 数Ⅰ
数Ⅰ
 数Ⅰ
数Ⅰ
【数学Ⅰ/テスト対策】絶対値を含む方程式・不等式③

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の不等式を解け。
$|2x+1| \lt x+5$
この動画を見る
次の不等式を解け。
$|2x+1| \lt x+5$
円 学芸大学附属 B
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
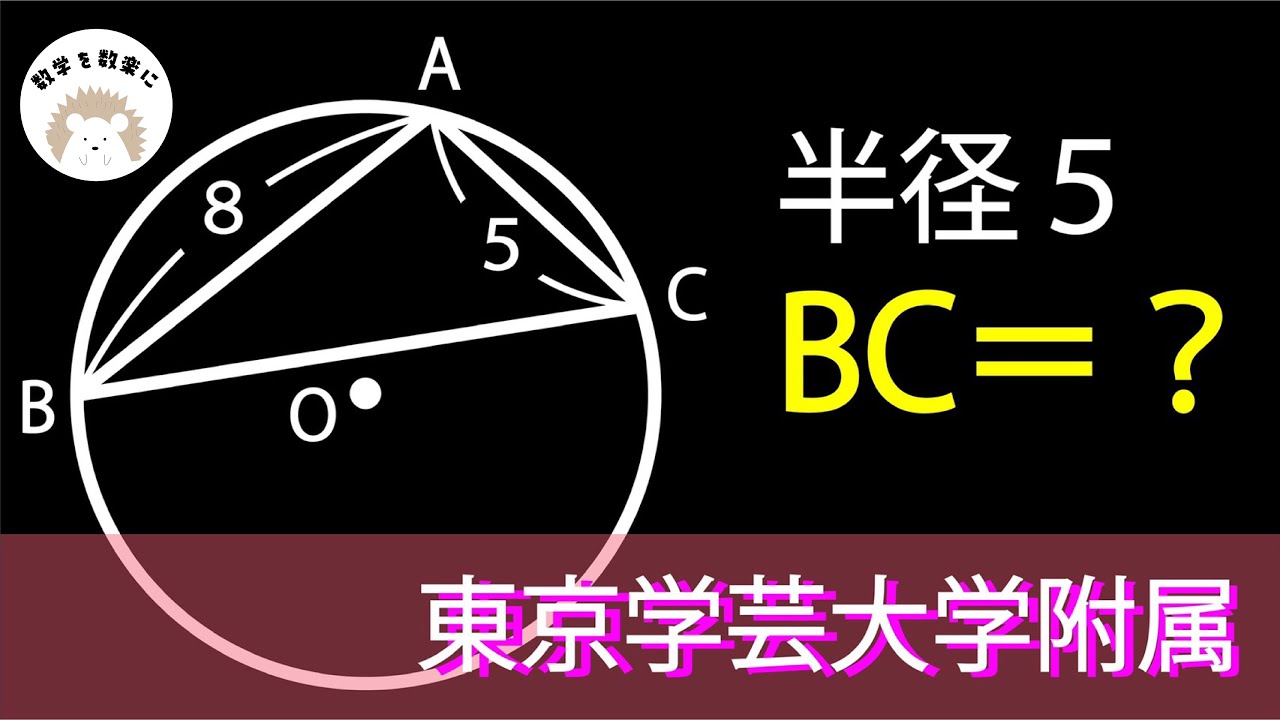
円の半径=5
BC=?
*図は動画内参照
東京学芸大学附属高校
この動画を見る
円の半径=5
BC=?
*図は動画内参照
東京学芸大学附属高校
福田の数学〜早稲田大学2021年人間科学部第7問〜双曲線と図形問題

単元:
#数Ⅰ#大学入試過去問(数学)#平面上の曲線#図形と計量#2次曲線#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{7}}$ 原点を$O$とする座標平面上で、2点$(\sqrt5,0),$$(-\sqrt5,0)$を焦点とし、2点$A(1,0),$$A'(-1,0)$を頂点とする双曲線を$H$とする。$H$の方程式を$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$と表すとき、$a^2=\boxed{\ \ ネ\ \ },$ $b^2=\boxed{\ \ ノ\ \ }$である。双曲線Hの漸近線のうち、傾きが正であるものの方程式は$y=\boxed{\ \ ハ\ \ }x$である。$点P(p,q)$は双曲線$H$の$第1象限$の部分を動く点とする。$点P$から$x軸$に下ろした垂線の足を$Q$、$直線PQ$と$双曲線H$の漸近線との交点のうち、$第1象限$にあるものを$R$とする。$点P$における$H$の接線と$直線x=1$との交点を$M$とし、$直線OM$と$直線AP$との交点を$N$とする。$三角形OQR$の面積を$S$、$三角形OAN$の面積を$T$とするとき、$\frac{T}{S}$は、$p=\boxed{\ \ ヒ\ \ }$のとき、最大値$\frac{\boxed{\ \ フ\ \ }}{\boxed{\ \ ヘ\ \ }}$をとる。
2021早稲田大学人間科学部過去問
この動画を見る
${\Large\boxed{7}}$ 原点を$O$とする座標平面上で、2点$(\sqrt5,0),$$(-\sqrt5,0)$を焦点とし、2点$A(1,0),$$A'(-1,0)$を頂点とする双曲線を$H$とする。$H$の方程式を$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$と表すとき、$a^2=\boxed{\ \ ネ\ \ },$ $b^2=\boxed{\ \ ノ\ \ }$である。双曲線Hの漸近線のうち、傾きが正であるものの方程式は$y=\boxed{\ \ ハ\ \ }x$である。$点P(p,q)$は双曲線$H$の$第1象限$の部分を動く点とする。$点P$から$x軸$に下ろした垂線の足を$Q$、$直線PQ$と$双曲線H$の漸近線との交点のうち、$第1象限$にあるものを$R$とする。$点P$における$H$の接線と$直線x=1$との交点を$M$とし、$直線OM$と$直線AP$との交点を$N$とする。$三角形OQR$の面積を$S$、$三角形OAN$の面積を$T$とするとき、$\frac{T}{S}$は、$p=\boxed{\ \ ヒ\ \ }$のとき、最大値$\frac{\boxed{\ \ フ\ \ }}{\boxed{\ \ ヘ\ \ }}$をとる。
2021早稲田大学人間科学部過去問
【数学Ⅰ/テスト対策】絶対値を含む方程式・不等式①

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の方程式、不等式を解け。
(1)$|x+3|=2$
(2)$|3-x| \leqq 5$
(3)$|3x+2| \gt 7$
この動画を見る
次の方程式、不等式を解け。
(1)$|x+3|=2$
(2)$|3-x| \leqq 5$
(3)$|3x+2| \gt 7$
福田のわかった数学〜高校1年生033〜背理法(1)

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 背理法(1)
$\sqrt2,$$\sqrt[3]3$ が無理数であることを証明せよ。
この動画を見る
数学$\textrm{I}$ 背理法(1)
$\sqrt2,$$\sqrt[3]3$ が無理数であることを証明せよ。
よく間違える二次不等式

【中学数学】平方根・ルートの問題演習~計算の仕方~ 2-4.5【中3数学】

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
$\sqrt{ 147 }-\sqrt{ 27 }-\sqrt{ 48 }$
2⃣
$\displaystyle \frac{2\sqrt{ 6 }}{3} \div \displaystyle \frac{4\sqrt{ 2 }}{3} \times \displaystyle \frac{7\sqrt{ 5 }}{2}$
この動画を見る
1⃣
$\sqrt{ 147 }-\sqrt{ 27 }-\sqrt{ 48 }$
2⃣
$\displaystyle \frac{2\sqrt{ 6 }}{3} \div \displaystyle \frac{4\sqrt{ 2 }}{3} \times \displaystyle \frac{7\sqrt{ 5 }}{2}$
灘高校の式の値 伝えたいこと、たくさん
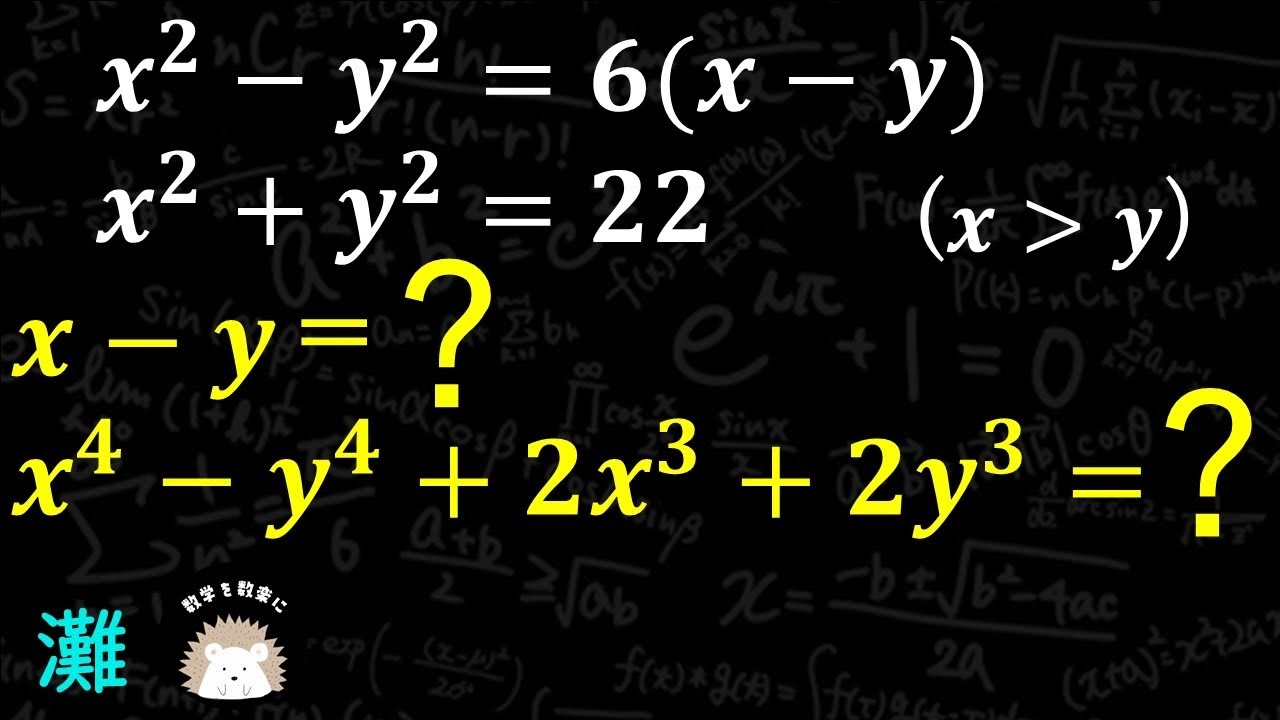
単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x^2-y^2=6(x-y)$ , $x^2+y^2 = 22$ (x>y)
$x-y=?$
$x^4-y^4+2x^3+2y^3=?$
灘高等学校
この動画を見る
$x^2-y^2=6(x-y)$ , $x^2+y^2 = 22$ (x>y)
$x-y=?$
$x^4-y^4+2x^3+2y^3=?$
灘高等学校
【中学数学】平方根・ルートの足し算をどこよりも分かりやすく 2-4.5【中3数学】

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
$5 \times 2\sqrt{ 3 }$
2⃣
$5\sqrt{ 2 }+7\sqrt{ 2 }$
3⃣
$2\sqrt{ 3 }+5\sqrt{ 2 }+3\sqrt{ 3 }+\sqrt{ 2 }$
この動画を見る
1⃣
$5 \times 2\sqrt{ 3 }$
2⃣
$5\sqrt{ 2 }+7\sqrt{ 2 }$
3⃣
$2\sqrt{ 3 }+5\sqrt{ 2 }+3\sqrt{ 3 }+\sqrt{ 2 }$
4の累乗の和で平方数を作れ

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a,b,c,n$は自然数である.
$4^a+4^b+4^c=n^2$
$10\lt a\lt b\lt c$を満たす$(a,b,c)$を1組与えよ.
この動画を見る
$a,b,c,n$は自然数である.
$4^a+4^b+4^c=n^2$
$10\lt a\lt b\lt c$を満たす$(a,b,c)$を1組与えよ.
補助線を引け!解説2通り
福田のわかった数学〜高校1年生032〜否定分の作り方(2)

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 否定分の作り方(2)
次の関数$f(x)$についての命題を否定せよ。
「$N$以上の全ての自然数$n$について$f(n) \leqq 2$」
が成り立つような自然数$N$が存在する。
この動画を見る
数学$\textrm{I}$ 否定分の作り方(2)
次の関数$f(x)$についての命題を否定せよ。
「$N$以上の全ての自然数$n$について$f(n) \leqq 2$」
が成り立つような自然数$N$が存在する。
垂線の長さの和=❓ B
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
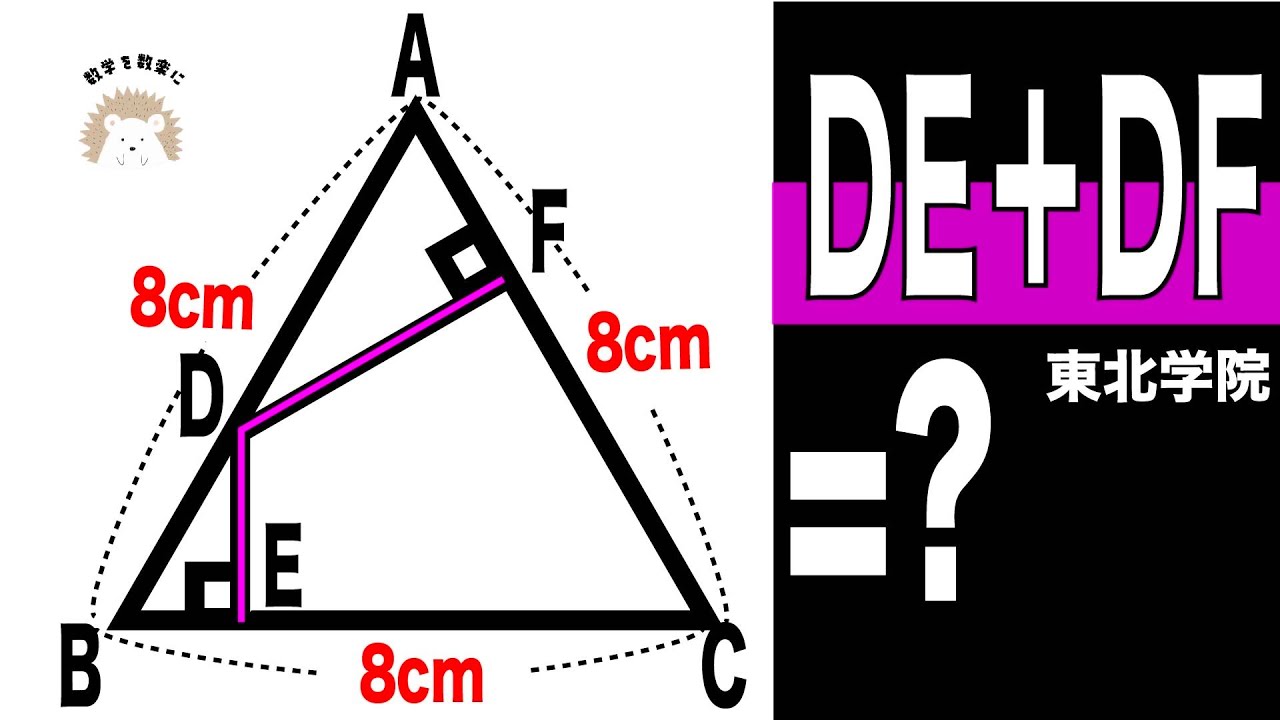
DE+EF=?
*図は動画内参照
東北学院高等学校
この動画を見る
DE+EF=?
*図は動画内参照
東北学院高等学校
【背理法はこう解け!】背理法の考え方と解法のテンプレはこうだ!【高校数学 数学】

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
$\sqrt{ 3 }$が無理数なことを証明せよ
この動画を見る
$\sqrt{ 3 }$が無理数なことを証明せよ
福田の数学〜早稲田大学2021年人間科学部第2問(2)〜3辺の長さから三角形の面積を求める

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$
(2)3辺の長さがそれぞれ$5,16,19$の三角形の面積は$\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}$である。
2021早稲田大学人間科学部過去問
この動画を見る
${\Large\boxed{2}}$
(2)3辺の長さがそれぞれ$5,16,19$の三角形の面積は$\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}$である。
2021早稲田大学人間科学部過去問
華麗に解こう

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$a+b+c=4$
$a^2+b^2+c^2=10$
$a^3+b^3+c^3=22$
$a^4+b^4+c^4=?$
この動画を見る
これを解け.
$a+b+c=4$
$a^2+b^2+c^2=10$
$a^3+b^3+c^3=22$
$a^4+b^4+c^4=?$
福田の数学〜早稲田大学2021年商学部第3問〜正の約数の総和が奇数になる条件

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$ 次の設問に答えよ。
(1)$225$の全ての正の約数の和を求めよ。
(2)$2021$以下の正の整数で、すべての正の約数の和が奇数であるものの個数を求めよ。
2021早稲田大学商学部過去問
この動画を見る
${\Large\boxed{3}}$ 次の設問に答えよ。
(1)$225$の全ての正の約数の和を求めよ。
(2)$2021$以下の正の整数で、すべての正の約数の和が奇数であるものの個数を求めよ。
2021早稲田大学商学部過去問
福田のわかった数学〜高校1年生031〜否定分の作り方(1)

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
数学\textrm{I} 否定分の作り方(1)\\
次の命題を否定せよ。\\
砂糖は甘い。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
数学\textrm{I} 否定分の作り方(1)\\
次の命題を否定せよ。\\
砂糖は甘い。
\end{eqnarray}
平均値より中央値の話

16和歌山県教員採用試験(数学:6番 対数の不等式)

単元:
#数Ⅰ#数Ⅱ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#指数関数と対数関数#対数関数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{6}$
$2\log_3 x-4\log_x 27 \leqq 5$を解け.
この動画を見る
$\boxed{6}$
$2\log_3 x-4\log_x 27 \leqq 5$を解け.
どっちがでかい?階乗の累乗根

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
どちらが大きい?
$\sqrt[8]{8!}$ VS $\sqrt[7]{7!}$
この動画を見る
どちらが大きい?
$\sqrt[8]{8!}$ VS $\sqrt[7]{7!}$
自分で考えろ!

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$42\times 37$の計算の様々なやり方に関して解説していきます.
この動画を見る
$42\times 37$の計算の様々なやり方に関して解説していきます.
数I 2次関数の最大に関する問題 (他の問題の解説もあり)
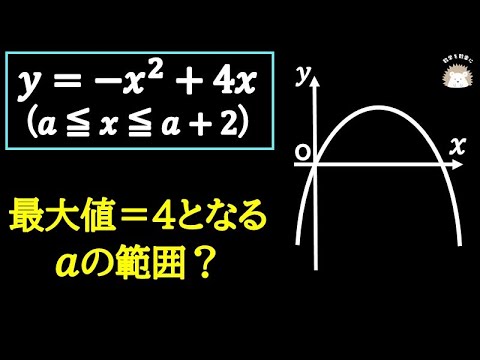
単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$y=-x^2+4x (a \leqq x \leqq a+2)$
(1)最大値=3となるaの値=?
(2)最大値=4となるaの範囲は?
この動画を見る
$y=-x^2+4x (a \leqq x \leqq a+2)$
(1)最大値=3となるaの値=?
(2)最大値=4となるaの範囲は?
素因数分解

奇数の平方の逆数の和になぜかあれが登場
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
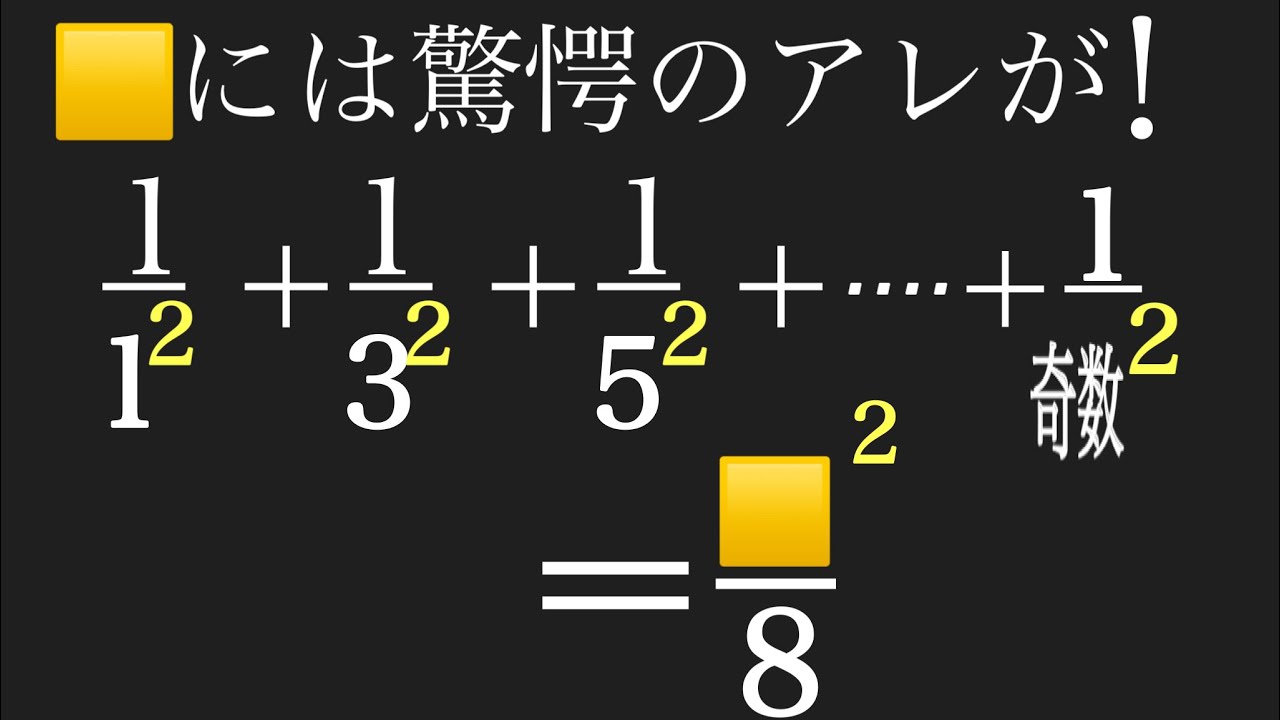
これを解け.$n\to \infty$である.
$\dfrac{1}{1^2}+\dfrac{1}{3^2}+\dfrac{1}{5^2}+\dfrac{1}{7^2}+・・・・・・$
$+\dfrac{1}{(2n-1)^2}=\dfrac{\Box^2}{8}$
この動画を見る
これを解け.$n\to \infty$である.
$\dfrac{1}{1^2}+\dfrac{1}{3^2}+\dfrac{1}{5^2}+\dfrac{1}{7^2}+・・・・・・$
$+\dfrac{1}{(2n-1)^2}=\dfrac{\Box^2}{8}$
【高校数学】三角関数の性質の考え方~θ+2nπ, -θ, θ+π, θ+π/2~ 4-3 【数学Ⅱ】

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
たくさんある三角比の公式
覚えないといけないと思っていませんか!?
暗記は不要です!!
この動画を見る
たくさんある三角比の公式
覚えないといけないと思っていませんか!?
暗記は不要です!!
【集合はこれだけ!】集合の問題の解き方のコツはベン図!【高校数学 数学】

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
全体集合$\cup=${$x|x$は10以下の自然数}とする
このとき、集合について以下のことが分かっている。
次の問いに答えよ
$A=${$1,3,4,6,8$}
$A \cap B=${$4,6,8$}
$A \cup B=${$1,2,3,4,6,7,8,9$}
(1)$B$
(2)$A \cap \overline{B}$
(3)$\overline{A \cup B}$
この動画を見る
全体集合$\cup=${$x|x$は10以下の自然数}とする
このとき、集合について以下のことが分かっている。
次の問いに答えよ
$A=${$1,3,4,6,8$}
$A \cap B=${$4,6,8$}
$A \cup B=${$1,2,3,4,6,7,8,9$}
(1)$B$
(2)$A \cap \overline{B}$
(3)$\overline{A \cup B}$
福田の数学〜早稲田大学2021年社会科学部第3問〜整式の割り算の余りと整数の余りの割り算の関係

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$ $k$を$3$以上の整数とする。k進法で$2021_{k}$と表される整数$N$を考える。次の問いに答えよ。
$(1)N$が$k-1$で割り切れるときの$k$の値を求めよ。
$(2)N$を$k+1$で割ったときの余りを$k$で表せ。
$(3)N$を$k+2$で割ったときの余りが$1$となる$k$を全て求めよ。
2021早稲田大学社会科学部過去問
この動画を見る
${\Large\boxed{3}}$ $k$を$3$以上の整数とする。k進法で$2021_{k}$と表される整数$N$を考える。次の問いに答えよ。
$(1)N$が$k-1$で割り切れるときの$k$の値を求めよ。
$(2)N$を$k+1$で割ったときの余りを$k$で表せ。
$(3)N$を$k+2$で割ったときの余りが$1$となる$k$を全て求めよ。
2021早稲田大学社会科学部過去問
累乗の桁数

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$2^{1000}$は$m$桁
$5^{1000}$は$n$桁
$m+n=\boxed{?}$
この動画を見る
$2^{1000}$は$m$桁
$5^{1000}$は$n$桁
$m+n=\boxed{?}$
ドラゴン桜 東大模試数学

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a^3+b^3-3ab=2020$を満たす自然数$a,b$は存在するか.
東大模試過去問
この動画を見る
$a^3+b^3-3ab=2020$を満たす自然数$a,b$は存在するか.
東大模試過去問
