 確率
確率
 確率
確率
福田の1.5倍速演習〜合格する重要問題095〜明治大学2020年度理工学部第1問(3)〜円順列と確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (3)A, B, C, D, Eの5人が、無作為に並び、手をつないでひとつの輪を作るという試行を考える。
(a)この試行を1回行うとき、AがBとCの2人と手をつなぐ確率は$\frac{\boxed{コ}}{\boxed{サ}}$である。
(b)この試行を3回行うとき、Aと3回手をつなぐ人が2人いる確率は$\frac{\boxed{シ}}{\boxed{スセ}}$である。
(c)この試行を3回行うとき、Aと3回手をつなぐ人が1人だけいる確率は$\frac{\boxed{ソ}}{\boxed{タ}}$である。
2020明治大学理工学部過去問
この動画を見る
$\Large\boxed{1}$ (3)A, B, C, D, Eの5人が、無作為に並び、手をつないでひとつの輪を作るという試行を考える。
(a)この試行を1回行うとき、AがBとCの2人と手をつなぐ確率は$\frac{\boxed{コ}}{\boxed{サ}}$である。
(b)この試行を3回行うとき、Aと3回手をつなぐ人が2人いる確率は$\frac{\boxed{シ}}{\boxed{スセ}}$である。
(c)この試行を3回行うとき、Aと3回手をつなぐ人が1人だけいる確率は$\frac{\boxed{ソ}}{\boxed{タ}}$である。
2020明治大学理工学部過去問
見掛け倒しの「どっちがでかい?」

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
どちらが大きいか?
$P_{2022} vs P_{2023}$
$P_n$はサイコロをn回ふって出た目の和が7の倍数になる確率を求めよ.
この動画を見る
どちらが大きいか?
$P_{2022} vs P_{2023}$
$P_n$はサイコロをn回ふって出た目の和が7の倍数になる確率を求めよ.
福田の1.5倍速演習〜合格する重要問題065〜中央大学2019年度理工学部第3問〜反復試行と確率漸化式

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$ Oを原点とする平面上の動点Rが$R_0$(1, 0)から出発して、単位円の周上を1秒ごとに反時計周りに移動する。移動するときの動径ORの回転角は、確率$\frac{1}{2}$で$\frac{\pi}{6}$、確率$\frac{1}{2}$で$\frac{\pi}{3}$である。n秒後のRの位置を$R_n$とする。以下の問いに答えよ。
(1)$R_5$が(-1, 0)である確率を求めよ。
(2)$R_9$がx軸上にある確率を求めよ。
次に、$R_n$がx軸上またはy軸上にある確率を$p_n$(n≧1)とする。
(3)$p_{n+1}$を$p_n$を用いて表せ。
(4)$p_n$を求めよ。
2019中央大学理工学部過去問
この動画を見る
$\boxed{3}$ Oを原点とする平面上の動点Rが$R_0$(1, 0)から出発して、単位円の周上を1秒ごとに反時計周りに移動する。移動するときの動径ORの回転角は、確率$\frac{1}{2}$で$\frac{\pi}{6}$、確率$\frac{1}{2}$で$\frac{\pi}{3}$である。n秒後のRの位置を$R_n$とする。以下の問いに答えよ。
(1)$R_5$が(-1, 0)である確率を求めよ。
(2)$R_9$がx軸上にある確率を求めよ。
次に、$R_n$がx軸上またはy軸上にある確率を$p_n$(n≧1)とする。
(3)$p_{n+1}$を$p_n$を用いて表せ。
(4)$p_n$を求めよ。
2019中央大学理工学部過去問
福田の1.5倍速演習〜合格する重要問題057〜慶應義塾大学大学2019年度商学部第3問〜グループ分けの確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{3}}$ 男子7人、女子5人の12人の中から3人を選んで第1グループを作る。次に、残った人の中から3人を選んで第2グループを作る。
(1)第1グループの男子の数が
0人である確率は$\displaystyle\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イウ\ \ }}$
1人である確率は$\displaystyle\frac{\boxed{\ \ エ\ \ }}{\boxed{\ \ オカ\ \ }}$
2人である確率は$\displaystyle\frac{\boxed{\ \ キク\ \ }}{\boxed{\ \ ケコ\ \ }}$
3人である確率は$\displaystyle\frac{\boxed{\ \ サ\ \ }}{\boxed{\ \ シス\ \ }}$
である。
(2)第1グループも第2グループも男子の数が1人である確率は$\frac{\boxed{\ \ セ\ \ }}{\boxed{\ \ ソタ\ \ }}$である。また、第2グループの男子の数が1人である確率は$\frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツテ\ \ }}$である。
(3)第2グループの男子の数が1人であるとき、第1グループの男子の数も1人である確率は$\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナニ\ \ }}$である。
2019慶應義塾大学商学部過去問
この動画を見る
$\Large{\boxed{3}}$ 男子7人、女子5人の12人の中から3人を選んで第1グループを作る。次に、残った人の中から3人を選んで第2グループを作る。
(1)第1グループの男子の数が
0人である確率は$\displaystyle\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イウ\ \ }}$
1人である確率は$\displaystyle\frac{\boxed{\ \ エ\ \ }}{\boxed{\ \ オカ\ \ }}$
2人である確率は$\displaystyle\frac{\boxed{\ \ キク\ \ }}{\boxed{\ \ ケコ\ \ }}$
3人である確率は$\displaystyle\frac{\boxed{\ \ サ\ \ }}{\boxed{\ \ シス\ \ }}$
である。
(2)第1グループも第2グループも男子の数が1人である確率は$\frac{\boxed{\ \ セ\ \ }}{\boxed{\ \ ソタ\ \ }}$である。また、第2グループの男子の数が1人である確率は$\frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツテ\ \ }}$である。
(3)第2グループの男子の数が1人であるとき、第1グループの男子の数も1人である確率は$\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナニ\ \ }}$である。
2019慶應義塾大学商学部過去問
【数A】確率:東北大 2008年 大問4(2)

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
点Pが次のルール (i), (i) に従って数直線上を移動するものとする。
(i)$1,2,3,4,5,6$の目が同じ割合で出るサイコロを振り, 出た目の数をkとする.
(ii)Pの座標aについて, $a\gt 0$ならば座標$a-k$の点へ移動し, $a\gt 0$ならば座標$a+k$の点へ移動する.
(iii)原点に移動したら終了し, そうでなければ(i) を繰り返す。
(2) Pの座標が$1,2,... 6$ のいずれかであるとき,
ちょうど n回サイコロを振って
原点で終了する確率を求めよ.
この動画を見る
点Pが次のルール (i), (i) に従って数直線上を移動するものとする。
(i)$1,2,3,4,5,6$の目が同じ割合で出るサイコロを振り, 出た目の数をkとする.
(ii)Pの座標aについて, $a\gt 0$ならば座標$a-k$の点へ移動し, $a\gt 0$ならば座標$a+k$の点へ移動する.
(iii)原点に移動したら終了し, そうでなければ(i) を繰り返す。
(2) Pの座標が$1,2,... 6$ のいずれかであるとき,
ちょうど n回サイコロを振って
原点で終了する確率を求めよ.
前澤じゃんけんで1000万円とる確率は?

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
下記質問の解説動画です
前澤じゃんけんで20回連続勝って1000万円とる確率は?
この動画を見る
下記質問の解説動画です
前澤じゃんけんで20回連続勝って1000万円とる確率は?
橋本環奈に年賀状届く確率は?

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
下記質問の解説動画です
片っ端から住所書いて橋本環奈に年賀状が届く確率は?
この動画を見る
下記質問の解説動画です
片っ端から住所書いて橋本環奈に年賀状が届く確率は?
福田の1.5倍速演習〜合格する重要問題043〜北海道大学2017年度文系第3問〜確率漸化式の定番問題

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数B
指導講師:
福田次郎
問題文全文(内容文):
正四面体ABCDの頂点を移動する点Pがある。点Pは、1秒ごとに、
隣の3頂点のいずれかに等しい確率$\frac{a}{3}$で移るか、もとの頂点に確率1-aで
留まる。初め頂点Aにいた点Pが、n秒後に頂点Aにいる確率を$p_n$とする。
ただし、$0 \lt a \lt 1$とし、nは自然数とする。
(1)数列$\left\{p_n\right\}$の漸化式を求めよ。
(2)確率$p_n$を求めよ。
2017北海道大学文系過去問
この動画を見る
正四面体ABCDの頂点を移動する点Pがある。点Pは、1秒ごとに、
隣の3頂点のいずれかに等しい確率$\frac{a}{3}$で移るか、もとの頂点に確率1-aで
留まる。初め頂点Aにいた点Pが、n秒後に頂点Aにいる確率を$p_n$とする。
ただし、$0 \lt a \lt 1$とし、nは自然数とする。
(1)数列$\left\{p_n\right\}$の漸化式を求めよ。
(2)確率$p_n$を求めよ。
2017北海道大学文系過去問
佐藤さんですか?と聞いて当たる確率は?

単元:
#数A#場合の数と確率#確率
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
下記質問の解説動画です
街中の人に「あなたは佐藤さんですか?」って聞いて的中する確率は?
この動画を見る
下記質問の解説動画です
街中の人に「あなたは佐藤さんですか?」って聞いて的中する確率は?
福田の1.5倍速演習〜合格する重要問題037〜慶應義塾大学2019年度医学部第1問(2)〜積事象と和事象の確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(2)赤玉1個、白玉2個、黒玉3個が入った袋が1つある。はじめにK君が
この袋から同時に2個の玉を取り出す。次にK君が取り出した玉をもとに
戻さずに、O君が袋から同時に2個の玉を取り出す。この試行において
「K君が取り出した2個の玉が同じ色である」という事象をA,
「O君が取り出した2個の玉が同じ色である」という事象をB,
とする。このとき、AとBの積事象$A \cap B$の確率は$\boxed{(う)}$であり、
和事象$A \cup B$の確率は$\boxed{(え)}$である。
2019慶應義塾大学医学部過去問
この動画を見る
(2)赤玉1個、白玉2個、黒玉3個が入った袋が1つある。はじめにK君が
この袋から同時に2個の玉を取り出す。次にK君が取り出した玉をもとに
戻さずに、O君が袋から同時に2個の玉を取り出す。この試行において
「K君が取り出した2個の玉が同じ色である」という事象をA,
「O君が取り出した2個の玉が同じ色である」という事象をB,
とする。このとき、AとBの積事象$A \cap B$の確率は$\boxed{(う)}$であり、
和事象$A \cup B$の確率は$\boxed{(え)}$である。
2019慶應義塾大学医学部過去問
最後にありがちん〇んって言う確率は??
福田の1.5倍速演習〜合格する重要問題023〜名古屋大学2016年度理系数学第3問〜確率漸化式

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学#数B
指導講師:
福田次郎
問題文全文(内容文):
玉が2個ずつ入った2つの袋A,Bがあるとき、袋Bから玉を1個取り出して
袋Aに入れ、次に袋Aから玉を1個取り出して袋Bに入れる。という操作を
1回の操作と数えることにする。Aに赤玉が2個、Bに白玉が2個入った状態から
始め、この操作をn回繰り返した後に袋Bに入っている赤玉の個数がk個で
ある確率を$P_n(k)(n=1,2,3,\cdots)$とする。このとき、次の問いに答えよ。
(1)$k=0,1,2$に対する$P_1(k)$を求めよ。
(2)$k=0,1,2$に対する$P_n(k)$を求めよ。
2016名古屋大学理系過去問
この動画を見る
玉が2個ずつ入った2つの袋A,Bがあるとき、袋Bから玉を1個取り出して
袋Aに入れ、次に袋Aから玉を1個取り出して袋Bに入れる。という操作を
1回の操作と数えることにする。Aに赤玉が2個、Bに白玉が2個入った状態から
始め、この操作をn回繰り返した後に袋Bに入っている赤玉の個数がk個で
ある確率を$P_n(k)(n=1,2,3,\cdots)$とする。このとき、次の問いに答えよ。
(1)$k=0,1,2$に対する$P_1(k)$を求めよ。
(2)$k=0,1,2$に対する$P_n(k)$を求めよ。
2016名古屋大学理系過去問
座標平面と確率
単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
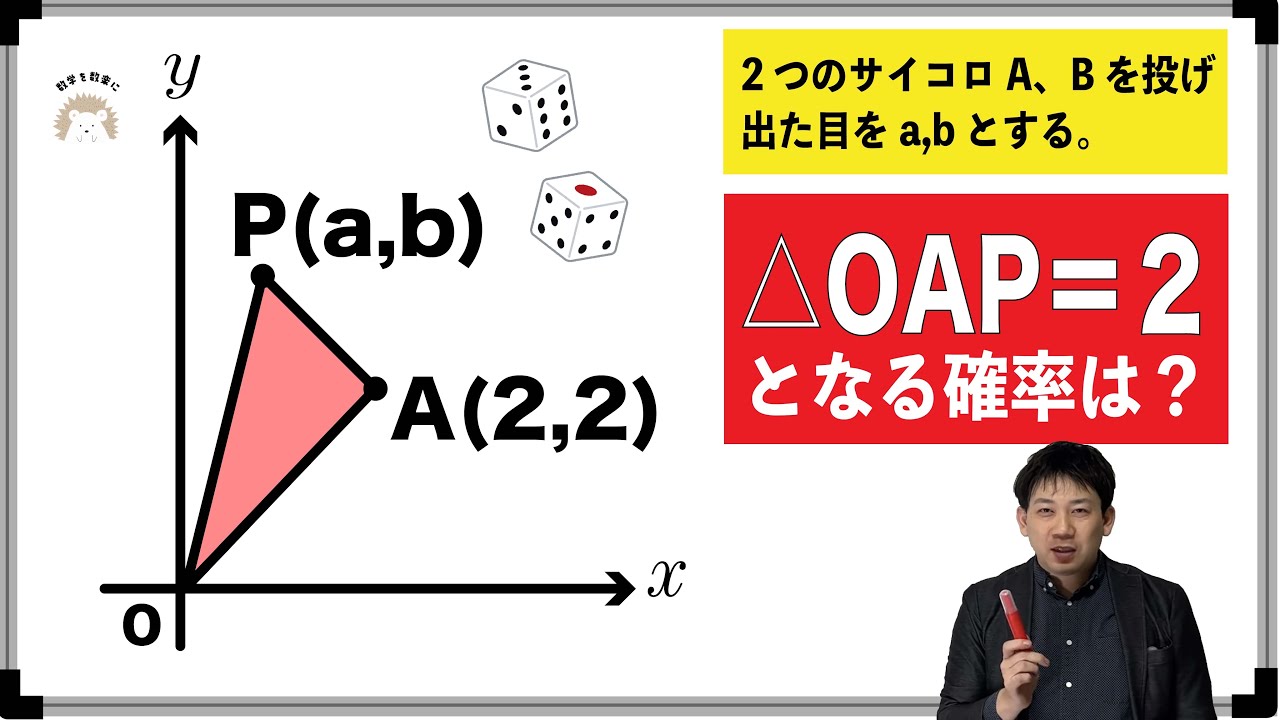
2つのサイコロA,Bを投げ出た目をa,bとする。
△OAP=2となる確率は?
*図は動画内参照
この動画を見る
2つのサイコロA,Bを投げ出た目をa,bとする。
△OAP=2となる確率は?
*図は動画内参照
福田の1.5倍速演習〜合格する重要問題003〜北海道大学2015年文系数学第4問〜隣り合う順列、隣り合わない順列

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
福田次郎
問題文全文(内容文):
ジョーカーを除く1組52枚のトランプのカードを1列に並べる思考を考える。
(1)番号7のカードが4枚連続して並ぶ確率を求めよ。
(2)番号7のカードが2枚ずつ隣り合い、4枚連続しては並ばない確率を求めよ。
8人の人が一列に並ぶとき、
(1)A,B,Cの3人が連続して並ぶ場合の数を求めよ。
(2)A,B,Cの3人が隣りあわないように並ぶ場合の数を求めよ。
2015北海道大学文系過去問
この動画を見る
ジョーカーを除く1組52枚のトランプのカードを1列に並べる思考を考える。
(1)番号7のカードが4枚連続して並ぶ確率を求めよ。
(2)番号7のカードが2枚ずつ隣り合い、4枚連続しては並ばない確率を求めよ。
8人の人が一列に並ぶとき、
(1)A,B,Cの3人が連続して並ぶ場合の数を求めよ。
(2)A,B,Cの3人が隣りあわないように並ぶ場合の数を求めよ。
2015北海道大学文系過去問
席替えで好きな人と隣になる確率は?

福田の数学〜中央大学2022年経済学部第1問(2)〜条件付き確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(2)赤玉4個と白玉8個が入っている袋から玉を
1個取り出し、
これをもとに戻さないで続けてもう1個玉を取り出す。
2個目に取り出した玉が白玉であるとき、
1個目に取り出した玉も白玉である確率を求めよ。
2022中央大学経済学部過去問
この動画を見る
(2)赤玉4個と白玉8個が入っている袋から玉を
1個取り出し、
これをもとに戻さないで続けてもう1個玉を取り出す。
2個目に取り出した玉が白玉であるとき、
1個目に取り出した玉も白玉である確率を求めよ。
2022中央大学経済学部過去問
福田の数学〜北里大学2022年医学部第3問〜確率と漸化式の融合問題

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
1つの箱を置ける台と2つの箱A, Bがある。箱Aには赤玉2個、青玉2個が
入っており、箱Bには白玉3個、青玉1個が入っている。台の上に箱Aを置き、
次の操作を繰り返す。
(操作) 台に置かれている箱から玉を1個取り出して色を調べてから箱に戻し、台
に置かれている箱を台から降ろす。取りだした玉が青球であれば箱Bを台
に置き、それ以外の色の玉であれば箱Aを台に置く。
正の整数nに対し、n回目の操作を終えたときに、台に箱Aが置かれている確率
をa_n、箱Bが置かれている確率をb_nとおく。次の問いに答えよ。
(1) 正の整数nに対し、$b_n$と$a_{n+1}$をそれぞれ $a_n$ を用いて表せ。
(2) 正の整数nに対し、$a_n$をnを用いて表せ。
(3) 正の整数nに対し、1回目からn回目までのn回の操作で白玉を1回も取り出
さない確率をnを用いて表せ。
(4)正の整数nに対し、1回目からn回目までのn回の操作で白玉をちょうど1回
だけ取り出す確率をnを用いて表せ。
2022北里大学医学部過去問
この動画を見る
1つの箱を置ける台と2つの箱A, Bがある。箱Aには赤玉2個、青玉2個が
入っており、箱Bには白玉3個、青玉1個が入っている。台の上に箱Aを置き、
次の操作を繰り返す。
(操作) 台に置かれている箱から玉を1個取り出して色を調べてから箱に戻し、台
に置かれている箱を台から降ろす。取りだした玉が青球であれば箱Bを台
に置き、それ以外の色の玉であれば箱Aを台に置く。
正の整数nに対し、n回目の操作を終えたときに、台に箱Aが置かれている確率
をa_n、箱Bが置かれている確率をb_nとおく。次の問いに答えよ。
(1) 正の整数nに対し、$b_n$と$a_{n+1}$をそれぞれ $a_n$ を用いて表せ。
(2) 正の整数nに対し、$a_n$をnを用いて表せ。
(3) 正の整数nに対し、1回目からn回目までのn回の操作で白玉を1回も取り出
さない確率をnを用いて表せ。
(4)正の整数nに対し、1回目からn回目までのn回の操作で白玉をちょうど1回
だけ取り出す確率をnを用いて表せ。
2022北里大学医学部過去問
橋本環奈と浜辺美波と会える確率は?
単元:
#数学(中学生)#中2数学#数A#場合の数と確率#確率#確率#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
橋本環奈と浜辺美波とディズニーで会える確率は?
この動画を見る
橋本環奈と浜辺美波とディズニーで会える確率は?
【数学Ⅰ・新課程】仮説検定の考え方【確率的に正しさを証明する】

単元:
#数Ⅰ#確率#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$(1)ある企業の新商品について20人中15人が「よい」と回答した.$
$この商品は「よい」商品であるか,仮説検定の考え方を用いて考察せよ.$
$(2)A,B,C,D,E,Fの6人の候補者がいる.$
$100人中25人がAを支持していると答えた.$
$Aの支持者は多いと言えるか,仮説検定の考え方を用いて考察せよ.$
この動画を見る
$(1)ある企業の新商品について20人中15人が「よい」と回答した.$
$この商品は「よい」商品であるか,仮説検定の考え方を用いて考察せよ.$
$(2)A,B,C,D,E,Fの6人の候補者がいる.$
$100人中25人がAを支持していると答えた.$
$Aの支持者は多いと言えるか,仮説検定の考え方を用いて考察せよ.$
自販機で当たりが出る確率は?
福田の数学〜上智大学2022年TEAP理系型第3問〜最後の目が得点になる確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#確率分布と統計的な推測#確率分布#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
各頂点に1から4までの数が1つずつ書いてあり、振るとそれらの1つが等し
い確率で得られる正四面体の形のさいころTがある。これを用いて、2人のプレイ
ヤA, B が以下のようなゲームをする。それぞれの枠内に記したルールに従い、各
プレイヤがTを1回以上振って、最後に出た数をそのプレイヤの得点とし、得点の
多い方を勝ちとする。ここで、同点のときには常にBの勝ちとする。また、振り直
すかどうかは、各プレイヤーとも自分が勝つ確率を最大にするように選択するとす
る。このとき、Aが勝つ確率pについて答えよ。ただし、以下のそれぞれの場合に
ついて、pは0以上の整数k, nを用いて$p =\frac{2k+1}{2^n}$と表せるので、このk, nを
答えよ。
(1)$A, B$がそれぞれ1回ずつTを振る
このときpを表すk, nは、$k=\boxed{ケ} ,\ n=\boxed{コ}$である。
(2)先にAが一回振る。次にBが2回まで振ってよい(Aの得点を知っている状
況で、1回振り直してよい)
このときpを表すk,nは、$k=\boxed{サ} ,\ n=\boxed{シ}$である。
(3)先にAが2回まで振ってよい(Bの得点がまだわからない状況で、1回振り直
してよい)。次にBが1回振る。
このときpを表すk,nは、$k=\boxed{ス} ,\ n=\boxed{セ }$である。
(4)先にAが2回まで振ってよい(Bの得点がまだわからない状況で、1回振り直
してよい)。次にBが2回まで振ってよい(Aの得点を知っている状況で、1回
振り直してよい)
このときpを表すk,nは、$k=\boxed{ソ} ,\ n=\boxed{タ}$である。
(5)先にAが3回まで振ってよい(Bの得点がまだわからない状況で、2回まで振
り直してよい)。次にBが2回まで振ってよい(Aの得点を知っている状況で、
1回振り直してよい)
このときpを表すk,nは、$k=\boxed{チ} ,\ n=\boxed{ツ}$である。
2022上智大学理系過去問
この動画を見る
各頂点に1から4までの数が1つずつ書いてあり、振るとそれらの1つが等し
い確率で得られる正四面体の形のさいころTがある。これを用いて、2人のプレイ
ヤA, B が以下のようなゲームをする。それぞれの枠内に記したルールに従い、各
プレイヤがTを1回以上振って、最後に出た数をそのプレイヤの得点とし、得点の
多い方を勝ちとする。ここで、同点のときには常にBの勝ちとする。また、振り直
すかどうかは、各プレイヤーとも自分が勝つ確率を最大にするように選択するとす
る。このとき、Aが勝つ確率pについて答えよ。ただし、以下のそれぞれの場合に
ついて、pは0以上の整数k, nを用いて$p =\frac{2k+1}{2^n}$と表せるので、このk, nを
答えよ。
(1)$A, B$がそれぞれ1回ずつTを振る
このときpを表すk, nは、$k=\boxed{ケ} ,\ n=\boxed{コ}$である。
(2)先にAが一回振る。次にBが2回まで振ってよい(Aの得点を知っている状
況で、1回振り直してよい)
このときpを表すk,nは、$k=\boxed{サ} ,\ n=\boxed{シ}$である。
(3)先にAが2回まで振ってよい(Bの得点がまだわからない状況で、1回振り直
してよい)。次にBが1回振る。
このときpを表すk,nは、$k=\boxed{ス} ,\ n=\boxed{セ }$である。
(4)先にAが2回まで振ってよい(Bの得点がまだわからない状況で、1回振り直
してよい)。次にBが2回まで振ってよい(Aの得点を知っている状況で、1回
振り直してよい)
このときpを表すk,nは、$k=\boxed{ソ} ,\ n=\boxed{タ}$である。
(5)先にAが3回まで振ってよい(Bの得点がまだわからない状況で、2回まで振
り直してよい)。次にBが2回まで振ってよい(Aの得点を知っている状況で、
1回振り直してよい)
このときpを表すk,nは、$k=\boxed{チ} ,\ n=\boxed{ツ}$である。
2022上智大学理系過去問
ここマダガスカルになる確率は?
単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
下記質問の解説動画です
ここ!マダガスカルってやって当たる確率は?
この動画を見る
下記質問の解説動画です
ここ!マダガスカルってやって当たる確率は?
円周率100桁適当に当たる確率は?
単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
下記質問の解説動画です
適当に数字言って円周率100桁当たる確率は?
この動画を見る
下記質問の解説動画です
適当に数字言って円周率100桁当たる確率は?
福田の数学〜上智大学2022年TEAP文系型第1問(3)〜サイコロの目による円と直線の位置関係の確率

単元:
#数A#数Ⅱ#大学入試過去問(数学)#場合の数と確率#確率#図形と方程式#点と直線#円と方程式#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
1個のさいころを投げる試行を2回繰り返し、
1回目に出た目をa,2回目に出た目をbとする。xy平面上で直線
$l:\frac{x}{a}+\frac{y}{b}=1$
を考える。lとx軸の交点をP、lとy軸の交点をQ、原点をOとし、
三角形OPQの周および内部をD、三角形OPQの面積をSとする。
(3)円$(x-3)^2+(y-3)^2=5$とlが共有点を持たない確率は$\frac{\boxed{サ}}{\boxed{シ}}$である。
2022上智大学文系過去問
この動画を見る
1個のさいころを投げる試行を2回繰り返し、
1回目に出た目をa,2回目に出た目をbとする。xy平面上で直線
$l:\frac{x}{a}+\frac{y}{b}=1$
を考える。lとx軸の交点をP、lとy軸の交点をQ、原点をOとし、
三角形OPQの周および内部をD、三角形OPQの面積をSとする。
(3)円$(x-3)^2+(y-3)^2=5$とlが共有点を持たない確率は$\frac{\boxed{サ}}{\boxed{シ}}$である。
2022上智大学文系過去問
福田の数学〜上智大学2022年TEAP文系型第1問(2)〜領域に属する確率

単元:
#数A#数Ⅱ#大学入試過去問(数学)#場合の数と確率#整数の性質#確率#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
1個のさいころを投げる試行を2回繰り返し、
1回目に出た目をa,2回目に出た目をbとする。xy平面上で直線
$l:\frac{x}{a}+\frac{y}{b}=1$
を考える。lとx軸の交点をP、lとy軸の交点をQ、原点をOとし、
三角形OPQの周および内部をD、三角形OPQの面積をSとする。
(2)点(2,\ 4)がDに含まれる確率は
$\frac{\boxed{キ}}{\boxed{ク}}$
点(2,\ 3)がDに含まれる確率は$\frac{\boxed{ケ}}{\boxed{コ}}$である。
2022上智大学文系過去問
この動画を見る
1個のさいころを投げる試行を2回繰り返し、
1回目に出た目をa,2回目に出た目をbとする。xy平面上で直線
$l:\frac{x}{a}+\frac{y}{b}=1$
を考える。lとx軸の交点をP、lとy軸の交点をQ、原点をOとし、
三角形OPQの周および内部をD、三角形OPQの面積をSとする。
(2)点(2,\ 4)がDに含まれる確率は
$\frac{\boxed{キ}}{\boxed{ク}}$
点(2,\ 3)がDに含まれる確率は$\frac{\boxed{ケ}}{\boxed{コ}}$である。
2022上智大学文系過去問
福田の数学〜上智大学2022年TEAP文系型第1問(1)〜サイコロの目の約数倍数の確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
1個のさいころを投げる試行を2回繰り返し、
1回目に出た目をa,2回目に出た目をbとする。xy平面上で直線
$l:\frac{x}{a}+\frac{y}{b}=1$
を考える。lとx軸の交点をP、lとy軸の交点をQ、原点をOとし、
三角形OPQの周および内部をD、三角形OPQの面積をSとする。
(1)Sが整数になる確率は$\frac{\boxed{ア}}{\boxed{イ}}$
Sが3の整数倍になる確率は$\frac{\boxed{ウ}}{\boxed{エ}}$
Sが4の整数倍になる確率は$\frac{\boxed{オ}}{\boxed{カ}}$である。
2022上智大学文系過去問
この動画を見る
1個のさいころを投げる試行を2回繰り返し、
1回目に出た目をa,2回目に出た目をbとする。xy平面上で直線
$l:\frac{x}{a}+\frac{y}{b}=1$
を考える。lとx軸の交点をP、lとy軸の交点をQ、原点をOとし、
三角形OPQの周および内部をD、三角形OPQの面積をSとする。
(1)Sが整数になる確率は$\frac{\boxed{ア}}{\boxed{イ}}$
Sが3の整数倍になる確率は$\frac{\boxed{ウ}}{\boxed{エ}}$
Sが4の整数倍になる確率は$\frac{\boxed{オ}}{\boxed{カ}}$である。
2022上智大学文系過去問
サイコロ3個目の積が10の倍数になる確率

単元:
#数A#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
サイコロ3個の目の積が5と10の倍数になる確率をそれぞれ求めよ.
福島大過去問
この動画を見る
サイコロ3個の目の積が5と10の倍数になる確率をそれぞれ求めよ.
福島大過去問
福田の数学〜青山学院大学2022年理工学部第1問〜サイコロの目の約数倍数の確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
1個のさいころを3回投げるとき、出た目を順にX_1,X_2,X_3とする。
また、$Y=\frac{X_2X_3}{X_1}$とする。
(1)$X_1=2$のとき、Yが整数となる確率は$\frac{\boxed{ア}}{\boxed{イ}}$である。
(2)$X_1=3$のとき、Yが整数となる確率は$\frac{\boxed{ウ}}{\boxed{エ}}\ である。
(3)$X_1=4$のとき、Yが整数となる確率は$\frac{\boxed{オ}}{\boxed{カキ}}$である。
(4)Yが整数となる確率は$\frac{\boxed{クケ}}{\boxed{コサ}}$である。
2022青山学院大学理工学部過去問
この動画を見る
1個のさいころを3回投げるとき、出た目を順にX_1,X_2,X_3とする。
また、$Y=\frac{X_2X_3}{X_1}$とする。
(1)$X_1=2$のとき、Yが整数となる確率は$\frac{\boxed{ア}}{\boxed{イ}}$である。
(2)$X_1=3$のとき、Yが整数となる確率は$\frac{\boxed{ウ}}{\boxed{エ}}\ である。
(3)$X_1=4$のとき、Yが整数となる確率は$\frac{\boxed{オ}}{\boxed{カキ}}$である。
(4)Yが整数となる確率は$\frac{\boxed{クケ}}{\boxed{コサ}}$である。
2022青山学院大学理工学部過去問
福田の数学〜立教大学2022年経済学部第1問(4)〜表が連続して出ない確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
コインを5回投げるとき、表が連続して2回以上出ない確率を求めよ。
ただし、コインを1回投げたとき、 表が出る確率および裏が出る確率はそれぞれ1/2であるとする。
2022立教大学経済学部過去問
この動画を見る
コインを5回投げるとき、表が連続して2回以上出ない確率を求めよ。
ただし、コインを1回投げたとき、 表が出る確率および裏が出る確率はそれぞれ1/2であるとする。
2022立教大学経済学部過去問
マークシート適当で満点の確率は?

