場合の数と確率
場合の数と確率
福田の数学〜立教大学2024年経済学部第1問(3)〜3回のさいころの目の積が4の倍数となる確率
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
さいころを $3$ 回投げて出る目をすべてかけた数が $4$ の倍数となる確率は $\fbox{カ}$ である。
この動画を見る
さいころを $3$ 回投げて出る目をすべてかけた数が $4$ の倍数となる確率は $\fbox{カ}$ である。
福田の数学〜立教大学2024年理学部第2問〜反復試行の確率
単元：
#数A#場合の数と確率#確率#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$1$ から $6$ の番号がひとつずつ重複なくつけられた $6$ つの箱がある。このとき、次の試行を行う。
$\fbox{さいころを $1$ つ投げて、出た目の番号のついた箱に玉を $1$ つ入れる。}$
この試行を繰り返し、いずれかの箱に玉が $3$ 個入った時点で終了する。ただし、$1$ 回目の試行を行う前は、どの箱にも玉は $1$ 個も入っていないとする。終了するまでに行った試行の回数を $N$ とする。
$(1)$ $N$ のとりうる最小値 $N_0$ と最大値 $N_1$ をそれぞれ求めよ。
$(2)$ $N=N_{0}$ となる確率を求めよ。
$(3)$ $N=N_{0}+1$ となる確率を求めよ。
$(4)$ 試行を $6$ 回行った時点で、すべての箱に $1$ つずつ玉が入るという事象を $A$ とする。また、$N=N_{1}$ となる事象を $B$ とする。事象 $A$ が起こったときの事象 $B$ が起こる条件付き確率 $P_{A}(B)$ を求めよ。
$(5)$ $N=N_{1}$ となる確率を $P$ とするとき、$6^{8}P$ は整数となる。その値を求めよ。
この動画を見る
$1$ から $6$ の番号がひとつずつ重複なくつけられた $6$ つの箱がある。このとき、次の試行を行う。
$\fbox{さいころを $1$ つ投げて、出た目の番号のついた箱に玉を $1$ つ入れる。}$
この試行を繰り返し、いずれかの箱に玉が $3$ 個入った時点で終了する。ただし、$1$ 回目の試行を行う前は、どの箱にも玉は $1$ 個も入っていないとする。終了するまでに行った試行の回数を $N$ とする。
$(1)$ $N$ のとりうる最小値 $N_0$ と最大値 $N_1$ をそれぞれ求めよ。
$(2)$ $N=N_{0}$ となる確率を求めよ。
$(3)$ $N=N_{0}+1$ となる確率を求めよ。
$(4)$ 試行を $6$ 回行った時点で、すべての箱に $1$ つずつ玉が入るという事象を $A$ とする。また、$N=N_{1}$ となる事象を $B$ とする。事象 $A$ が起こったときの事象 $B$ が起こる条件付き確率 $P_{A}(B)$ を求めよ。
$(5)$ $N=N_{1}$ となる確率を $P$ とするとき、$6^{8}P$ は整数となる。その値を求めよ。
『3×4=?』
福田の数学〜慶應義塾大学2024年経済学部第2問〜確率の基本性質と非復元抽出の条件付き確率
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large{\boxed{2}}$ 袋の中に、1から9までの番号を重複なく1つずつ記入したカードが9枚入っている。A,B,C,Dの4人のうちDがさいころを投げて、1の目が出たらAが、2または3の目が出たらBが、その他の目が出たらCが、袋の中からカードを1枚引き、カードに記入された番号を記録することを試行という。ただし、1度引いたカードは袋に戻さない。この試行を3回続けて行う。また、1回目の試行前のA,B,Cの点数をそれぞれ0としたうえで、以下の(a),(b)に従い、各回の試行後のA,B,Cの点数を定める。
(a)各回の試行においてカードを引いた人は、その回の試行前の自分の点数に、その回の試行で記録した番号を加え、試行後の点数とする。
(b)各回の試行においてカードを引いていない人は、その回の試行前の自分の点数を、そのまま試行後の点数とする。
(1)1回目の試行後、Bの点数が3の倍数となる確率は$\frac{\boxed{ア}}{\boxed{イ}}$である。ただし、0はすべての整数の倍数である。
(2)2回目の試行後、A,B,Cのうち、1人だけの点数が0である確率は$\frac{\boxed{ウエ}}{\boxed{オカ}}$である。
(3)2回目の試行後のAの点数が5以上となる確率は$\frac{\boxed{キク}}{\boxed{ケコ}}$である。
(4)2回目の試行後のAの点数が5以上であるとき、3回目の試行後のA,B,Cの点数がすべて5以上である条件付き確率は$\frac{\boxed{サシ}}{\boxed{スセソ}}$である。
この動画を見る
$\Large{\boxed{2}}$ 袋の中に、1から9までの番号を重複なく1つずつ記入したカードが9枚入っている。A,B,C,Dの4人のうちDがさいころを投げて、1の目が出たらAが、2または3の目が出たらBが、その他の目が出たらCが、袋の中からカードを1枚引き、カードに記入された番号を記録することを試行という。ただし、1度引いたカードは袋に戻さない。この試行を3回続けて行う。また、1回目の試行前のA,B,Cの点数をそれぞれ0としたうえで、以下の(a),(b)に従い、各回の試行後のA,B,Cの点数を定める。
(a)各回の試行においてカードを引いた人は、その回の試行前の自分の点数に、その回の試行で記録した番号を加え、試行後の点数とする。
(b)各回の試行においてカードを引いていない人は、その回の試行前の自分の点数を、そのまま試行後の点数とする。
(1)1回目の試行後、Bの点数が3の倍数となる確率は$\frac{\boxed{ア}}{\boxed{イ}}$である。ただし、0はすべての整数の倍数である。
(2)2回目の試行後、A,B,Cのうち、1人だけの点数が0である確率は$\frac{\boxed{ウエ}}{\boxed{オカ}}$である。
(3)2回目の試行後のAの点数が5以上となる確率は$\frac{\boxed{キク}}{\boxed{ケコ}}$である。
(4)2回目の試行後のAの点数が5以上であるとき、3回目の試行後のA,B,Cの点数がすべて5以上である条件付き確率は$\frac{\boxed{サシ}}{\boxed{スセソ}}$である。
福田のおもしろ数学172〜1000枚の1円玉を10個の袋に入れて1000円までのすべての金額が払えるようにする方法
単元：
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
1000枚の1円玉を10個の袋に分けます。適当な袋を組み合わせて1円から1000円まですべてを表せるようにするにはどう分ければいい？
この動画を見る
1000枚の1円玉を10個の袋に分けます。適当な袋を組み合わせて1円から1000円まですべてを表せるようにするにはどう分ければいい？
【わかりやすく】同じものを含む順列の求め方を解説！【数学A / 場合の数】
単元：
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師：
【ゼロから理解できる】高校数学・物理
問題文全文(内容文)：
$a,a,b,b,b,c,d$の7文字をすべて1列に並べる。
（1）全部で並べ方は何通りあるか。
（2）$c,d$がこの順になる並べ方は何通りあるか。
この動画を見る
$a,a,b,b,b,c,d$の7文字をすべて1列に並べる。
（1）全部で並べ方は何通りあるか。
（2）$c,d$がこの順になる並べ方は何通りあるか。
福田の数学〜神戸大学2024年文系第2問〜さいころの目と約数に関する確率
単元：
#数A#場合の数と確率#整数の性質#確率#約数・倍数・整数の割り算と余り・合同式#神戸大学
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{2}$ $n$を自然数とする。以下の問いに答えよ。
(1)1個のサイコロを投げて出た目が必ず$n$の約数となるような$n$で最小のものを求めよ。
(2)1個のサイコロを投げて出た目が$n$の約数となる確率が$\displaystyle\frac{5}{6}$であるような$n$で最小のものを求めよ。
(3)1個のサイコロを3回投げて出た目の積が20の約数となる確率を求めよ。
この動画を見る
$\Large\boxed{2}$ $n$を自然数とする。以下の問いに答えよ。
(1)1個のサイコロを投げて出た目が必ず$n$の約数となるような$n$で最小のものを求めよ。
(2)1個のサイコロを投げて出た目が$n$の約数となる確率が$\displaystyle\frac{5}{6}$であるような$n$で最小のものを求めよ。
(3)1個のサイコロを3回投げて出た目の積が20の約数となる確率を求めよ。
福田のおもしろ数学160〜星のカピイは能力を何個持てるか
単元：
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
星のカピイは敵の能力をコピーできます。2つの能力を組み合わせて別の能力にすることもできます。（同じ能力を組み合わせることも可能）能力は全部で12種類あります。さてカピイは何個の能力を使うことができるでしょう。
この動画を見る
星のカピイは敵の能力をコピーできます。2つの能力を組み合わせて別の能力にすることもできます。（同じ能力を組み合わせることも可能）能力は全部で12種類あります。さてカピイは何個の能力を使うことができるでしょう。
福田の数学〜神戸大学2024年理系第3問〜さいころの目と約数に関する確率
単元：
#数A#場合の数と確率#整数の性質#確率#約数・倍数・整数の割り算と余り・合同式#神戸大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{3}$ $n$を自然数とする。以下の問いに答えよ。
(1)1個のサイコロを投げて出た目が必ず$n$の約数となるような$n$を小さい順に3つ求めよ。
(2)1個のサイコロを投げて出た目が$n$の約数となる確率が$\displaystyle\frac{5}{6}$であるような$n$を小さい順に3つ求めよ。
(3)1個のサイコロを3回投げて出た目の積が160の約数となる確率を求めよ。
この動画を見る
$\Large\boxed{3}$ $n$を自然数とする。以下の問いに答えよ。
(1)1個のサイコロを投げて出た目が必ず$n$の約数となるような$n$を小さい順に3つ求めよ。
(2)1個のサイコロを投げて出た目が$n$の約数となる確率が$\displaystyle\frac{5}{6}$であるような$n$を小さい順に3つ求めよ。
(3)1個のサイコロを3回投げて出た目の積が160の約数となる確率を求めよ。
告白って成功確率50％なんじゃないん？
告白って成功確率50％なんじゃないん？
単元：
#数A#場合の数と確率#確率#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
下記質問の解説動画です
告白して付き合うか、振られるかの確率は50%?
この動画を見る
下記質問の解説動画です
告白して付き合うか、振られるかの確率は50%?
福田の数学〜名古屋大学2024年文系第3問〜反復試行の確率
単元：
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#確率#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{3}$ $n$を自然数とする。表と裏が出る確率がそれぞれ$\displaystyle\frac{1}{2}$のコインを$n$回投げ、以下のように得点を決める。
・最初に数直線上の原点に石を置き、コインを投げて表なら2、裏なら3だけ数直線上を正方向に石を移動させる。コインを$k$回投げた後の石の位置を$a_k$とする。
・$a_n$≠2$n$+2 の場合は得点を0、$a_n$≠2$n$+2 の場合は得点を$a_1$+$a_2$+...+$a_n$とする。
たとえば、$n$=3のとき、投げたコインが3回とも表のときは得点は0、投げたコインが順に裏、裏、表のときは得点は3+6+8=17 である。
(1)$n$解のうち裏の出る回数を$r$とするとき、$a_n$を求めよ。
(2)$n$=4とする。得点が0でない確率および25である確率をそれぞれ求めよ。
(3)$n$=9とする。得点が100である確率および奇数である確率をそれぞれ求めよ。
この動画を見る
$\Large\boxed{3}$ $n$を自然数とする。表と裏が出る確率がそれぞれ$\displaystyle\frac{1}{2}$のコインを$n$回投げ、以下のように得点を決める。
・最初に数直線上の原点に石を置き、コインを投げて表なら2、裏なら3だけ数直線上を正方向に石を移動させる。コインを$k$回投げた後の石の位置を$a_k$とする。
・$a_n$≠2$n$+2 の場合は得点を0、$a_n$≠2$n$+2 の場合は得点を$a_1$+$a_2$+...+$a_n$とする。
たとえば、$n$=3のとき、投げたコインが3回とも表のときは得点は0、投げたコインが順に裏、裏、表のときは得点は3+6+8=17 である。
(1)$n$解のうち裏の出る回数を$r$とするとき、$a_n$を求めよ。
(2)$n$=4とする。得点が0でない確率および25である確率をそれぞれ求めよ。
(3)$n$=9とする。得点が100である確率および奇数である確率をそれぞれ求めよ。
福田の数学〜名古屋大学2024年理系第4問〜反復試行の確率と漸化式と定積分の計算
単元：
#数A#場合の数と確率#確率#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{4}$ 袋の中にいくつかの赤玉の白玉が入っている。すべての玉に対する赤玉の割合を$p$(0≦$p$≦1)とする。袋から無作為に玉を一つ取り出して袋に戻す試行を行う。
試行を$n$回行うとき、赤玉を$k$回以上取り出す確率を$f(k)$とおく。
(1)$n$≧2に対して、$f(1)$と$f(2)$を求めよ。
(2)$k$=1,2,...,$n$に対して、等式
$f(k)$=$\displaystyle\frac{n!}{(k-1)!(n-k)!}\int_0^px^{k-1}(1-x)^{n-k}dx$
を示せ。
(3)自然数$k$に対して、定積分$I$=$\displaystyle\int_0^{\frac{1}{2}}x^k(1-x)^kdx$ を求めよ。
この動画を見る
$\Large\boxed{4}$ 袋の中にいくつかの赤玉の白玉が入っている。すべての玉に対する赤玉の割合を$p$(0≦$p$≦1)とする。袋から無作為に玉を一つ取り出して袋に戻す試行を行う。
試行を$n$回行うとき、赤玉を$k$回以上取り出す確率を$f(k)$とおく。
(1)$n$≧2に対して、$f(1)$と$f(2)$を求めよ。
(2)$k$=1,2,...,$n$に対して、等式
$f(k)$=$\displaystyle\frac{n!}{(k-1)!(n-k)!}\int_0^px^{k-1}(1-x)^{n-k}dx$
を示せ。
(3)自然数$k$に対して、定積分$I$=$\displaystyle\int_0^{\frac{1}{2}}x^k(1-x)^kdx$ を求めよ。
10回連続表なら次は裏なのか？
単元：
#数A#場合の数と確率#確率#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
下記質問の解説動画です
コインが10回連続表なら次は裏がでますか？
この動画を見る
下記質問の解説動画です
コインが10回連続表なら次は裏がでますか？
福田の数学〜慶應義塾大学2024年商学部第4問〜くじ引きと条件付き確率
単元：
#数A#場合の数と確率#確率#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{4}$ あるくじ引き店には、くじが10本入っている箱が5箱ある。5箱のうち4箱には当たりくじが1本、はずれくじが9本入っており、この4箱を「通常の箱」と呼ぶ。また、残りの1箱には当たりくじが5本、はずれくじが5本入っており、この箱を「有利な箱」と呼ぶ。通常の箱と有利な箱は見た目は同じであり、見分けることはできない。
(i)まず、Aが店に入り、5箱のうちの1箱を無作為に選び、その箱からくじを1本引いた。Aの選んだ箱が通常の箱であり、かつ、引いたくじがはずれである確率は$\frac{\boxed{アイ}}{\boxed{ウエ}}$である。また、Aの選んだ箱が有利な箱であり、かつ、引いたくじがはずれである確率は$\frac{\boxed{オ}}{\boxed{カキ}}$である。したがって、Aの引いたくじがはずれであったときに、Aの選んだ箱が有利な箱である確率は$\frac{\boxed{ク}}{\boxed{ケコ}}$である。
(ii)(i)の後、Aは引いたくじをもとの箱に戻し、よくかき混ぜたあと、同じ箱からもう一度くじを1本引いた。Aの引いたくじが1回目、2回目ともにはずれであったときに、Aの選んだ箱が有利な箱である確率は$\frac{\boxed{サシ}}{\boxed{スセソ}}$である。
(iii)(ii)の後、Aは引いたくじをもとの箱に戻して店を出た。その後、BとCが店に入った。Bは5箱のうち1箱を無作為に選び、CはBが選ばなかった4箱の中から1箱を無作為に選んだ。BはAと同じように、自分の選んだ箱からくじを1本引き、それをもとの箱に戻し、よくかき混ぜた後、同じ箱からもう一度くじを1本引いた。また、Cは自分の選んだ箱からくじを1本引いた。Bの引いたくじが1回目、2回目ともにはずれであり、かつ、Cが引いたくじが当たりであったときに、Bの選んだ箱が有利な箱である確率は$\frac{\boxed{タチ}}{\boxed{ツテト}}$であり、Cの選んだ箱が有利な箱である確率は$\frac{\boxed{ナニヌ}}{\boxed{ネノハ}}$である。
この動画を見る
$\Large\boxed{4}$ あるくじ引き店には、くじが10本入っている箱が5箱ある。5箱のうち4箱には当たりくじが1本、はずれくじが9本入っており、この4箱を「通常の箱」と呼ぶ。また、残りの1箱には当たりくじが5本、はずれくじが5本入っており、この箱を「有利な箱」と呼ぶ。通常の箱と有利な箱は見た目は同じであり、見分けることはできない。
(i)まず、Aが店に入り、5箱のうちの1箱を無作為に選び、その箱からくじを1本引いた。Aの選んだ箱が通常の箱であり、かつ、引いたくじがはずれである確率は$\frac{\boxed{アイ}}{\boxed{ウエ}}$である。また、Aの選んだ箱が有利な箱であり、かつ、引いたくじがはずれである確率は$\frac{\boxed{オ}}{\boxed{カキ}}$である。したがって、Aの引いたくじがはずれであったときに、Aの選んだ箱が有利な箱である確率は$\frac{\boxed{ク}}{\boxed{ケコ}}$である。
(ii)(i)の後、Aは引いたくじをもとの箱に戻し、よくかき混ぜたあと、同じ箱からもう一度くじを1本引いた。Aの引いたくじが1回目、2回目ともにはずれであったときに、Aの選んだ箱が有利な箱である確率は$\frac{\boxed{サシ}}{\boxed{スセソ}}$である。
(iii)(ii)の後、Aは引いたくじをもとの箱に戻して店を出た。その後、BとCが店に入った。Bは5箱のうち1箱を無作為に選び、CはBが選ばなかった4箱の中から1箱を無作為に選んだ。BはAと同じように、自分の選んだ箱からくじを1本引き、それをもとの箱に戻し、よくかき混ぜた後、同じ箱からもう一度くじを1本引いた。また、Cは自分の選んだ箱からくじを1本引いた。Bの引いたくじが1回目、2回目ともにはずれであり、かつ、Cが引いたくじが当たりであったときに、Bの選んだ箱が有利な箱である確率は$\frac{\boxed{タチ}}{\boxed{ツテト}}$であり、Cの選んだ箱が有利な箱である確率は$\frac{\boxed{ナニヌ}}{\boxed{ネノハ}}$である。
組合せの計算 なぜ？
1年間で必要な服の枚数は？
福田の数学〜早稲田大学2024年人間科学部第2問〜反復試行と条件付き確率
単元：
#数A#場合の数と確率#確率#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{2}$ $n$を2以上の自然数とする。1から$n$までの番号が1つずつつけられた$n$個の玉が中身の見えない袋に入っている。袋の中から1個の玉を選んで番号を確認して袋に戻すという操作を$n$回繰り返す。この$n$回の操作の中で、1から$n$－1までのいずれの番号の玉も選ばれているとき、番号が$n$の玉も選ばれている条件付き確率を$P(n)$とするとき、$P(3)$=$\frac{\boxed{オ}}{\boxed{カ}}$, $P(50)$=$\frac{\boxed{キ}}{\boxed{ク}}$ である。
この動画を見る
$\Large\boxed{2}$ $n$を2以上の自然数とする。1から$n$までの番号が1つずつつけられた$n$個の玉が中身の見えない袋に入っている。袋の中から1個の玉を選んで番号を確認して袋に戻すという操作を$n$回繰り返す。この$n$回の操作の中で、1から$n$－1までのいずれの番号の玉も選ばれているとき、番号が$n$の玉も選ばれている条件付き確率を$P(n)$とするとき、$P(3)$=$\frac{\boxed{オ}}{\boxed{カ}}$, $P(50)$=$\frac{\boxed{キ}}{\boxed{ク}}$ である。
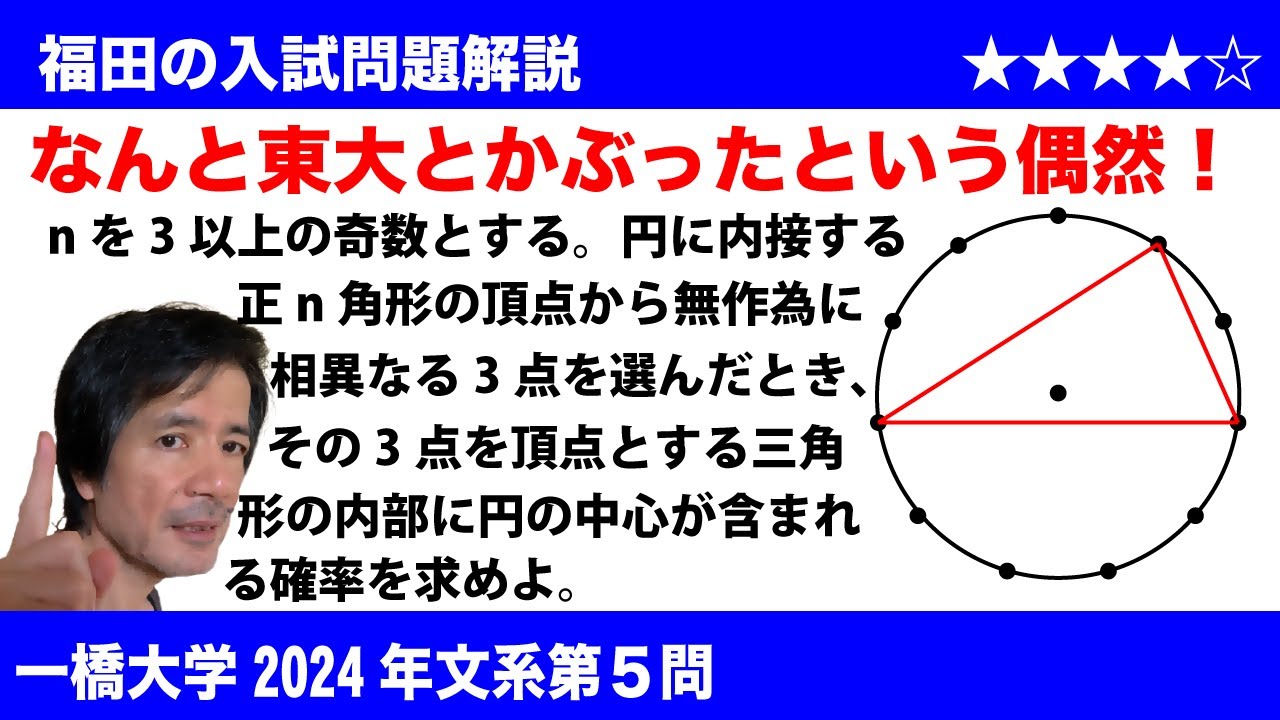
福田の数学〜一橋大学2024年文系第5問〜円の中心を含む三角形になる確率
単元：
#数A#場合の数と確率#確率#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{5}$ $n$を3以上の奇数とする。円に内接する正$n$角形の頂点から無作為に相異なる3点を選んだ時、その3点を頂点とする三角形の内部に円の中心が含まれる確率$p_n$を求めよ。
この動画を見る
$\Large\boxed{5}$ $n$を3以上の奇数とする。円に内接する正$n$角形の頂点から無作為に相異なる3点を選んだ時、その3点を頂点とする三角形の内部に円の中心が含まれる確率$p_n$を求めよ。
福田のおもしろ数学121〜この賭けは有理か不利か
単元：
#数A#場合の数と確率#確率#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
2つのサイコロを25回投げるとき少なくとも1回は両方のサイコロの目が共に6となる確率$p$を求めよ。
この動画を見る
2つのサイコロを25回投げるとき少なくとも1回は両方のサイコロの目が共に6となる確率$p$を求めよ。
福田の数学〜東北大学2024年理系第3問〜確率漸化式と複素数平面の融合
単元：
#数A#場合の数と確率#確率#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large{\boxed{3}}$ $n$ を2以上の整数とする。それぞれ $A$, $A$, $B$ と書かれた $3$ 枚のカードから無作為に $1$ 枚抜き出し、カードをもとに戻す試行を考える。この試行を $n$ 回繰り返し、抜き出したカードの文字を順に左から右に並べ、$n$ 文字の文字列を作る。作った文字列内に $AAA$ の並びがある場合は 不可 とする。また、作った文字列内に $BB$ の並びがある場合も 不可 とする。これらの場合以外は 可 とする。
例えば $n = 6$ のとき、文字列 $AAAABA$ や $ABBBAA$ や $ABBABB$ や $BBBAAA$ などは 不可 で、文字列 $BABAAB$ や $BABABA$ などは 可 である。
作った文字列が 可 でかつ右端の $2$ 文字が $AA$ である確率を $p_n$、作った文字列が 可 でかつ右端の $2$ 文字が $BA$ である確率を $q_n$、作った文字列が 可 でかつ右端の文字が $B$ である確率を $r_n$ とそれぞれおく。
(1) $p_2$, $q_2$, $r_2$ をそれぞれ求めよ。また、$p_{n+1}$, $q_{n+1}$, $r_{n+1}$ を $p_n$, $q_n$, $r_n$ を用いてそれぞれ表せ。
(2)$p_n$+$2q_n$+$2r_n$を$n$を用いて表せ。
(3)$p_n$+$iq_n$－$(1+i)r_n$を$n$を用いて表せ。ただし、$i$は虚数単位である。
(4)$p_n$=$r_n$ を満たすための、$n$の必要十分条件を求めよ。
この動画を見る
$\Large{\boxed{3}}$ $n$ を2以上の整数とする。それぞれ $A$, $A$, $B$ と書かれた $3$ 枚のカードから無作為に $1$ 枚抜き出し、カードをもとに戻す試行を考える。この試行を $n$ 回繰り返し、抜き出したカードの文字を順に左から右に並べ、$n$ 文字の文字列を作る。作った文字列内に $AAA$ の並びがある場合は 不可 とする。また、作った文字列内に $BB$ の並びがある場合も 不可 とする。これらの場合以外は 可 とする。
例えば $n = 6$ のとき、文字列 $AAAABA$ や $ABBBAA$ や $ABBABB$ や $BBBAAA$ などは 不可 で、文字列 $BABAAB$ や $BABABA$ などは 可 である。
作った文字列が 可 でかつ右端の $2$ 文字が $AA$ である確率を $p_n$、作った文字列が 可 でかつ右端の $2$ 文字が $BA$ である確率を $q_n$、作った文字列が 可 でかつ右端の文字が $B$ である確率を $r_n$ とそれぞれおく。
(1) $p_2$, $q_2$, $r_2$ をそれぞれ求めよ。また、$p_{n+1}$, $q_{n+1}$, $r_{n+1}$ を $p_n$, $q_n$, $r_n$ を用いてそれぞれ表せ。
(2)$p_n$+$2q_n$+$2r_n$を$n$を用いて表せ。
(3)$p_n$+$iq_n$－$(1+i)r_n$を$n$を用いて表せ。ただし、$i$は虚数単位である。
(4)$p_n$=$r_n$ を満たすための、$n$の必要十分条件を求めよ。
6年間ずっと同じクラスの確率は？
福田の数学〜北海道大学2024年文系第4問〜正八面体のサイコロと反復試行の確率
単元：
#数A#場合の数と確率#確率#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large{\boxed{4}}$ 各面に1つずつ数が書かれた正八面体のさいころがある。「1」、「2」、「3」が書かれた面がそれぞれ1つずつあり、残りの5つの面には「0」が書かれている。このさいころを水平な面に投げて、出た面に書かれた数を持ち点に加えるという試行を考える。最初の持ち点は0とし、この試行を繰り返す。例えば、3回の試行を行ったとき、出た面に書かれた数が「0」、「2」、「3」であれば、持ち点は5となる。なお、さいころが水平な床面にあるとき、さいころの上部の水平な面を出た面とよぶ。また、さいころを投げるとき、各面が出ることは同様に確からしいとする。
(1)この試行を2回行ったとき、持ち点が1である確率を求めよ。
(2)この試行を4回行ったとき、持ち点が10以下である確率を求めよ。
この動画を見る
$\Large{\boxed{4}}$ 各面に1つずつ数が書かれた正八面体のさいころがある。「1」、「2」、「3」が書かれた面がそれぞれ1つずつあり、残りの5つの面には「0」が書かれている。このさいころを水平な面に投げて、出た面に書かれた数を持ち点に加えるという試行を考える。最初の持ち点は0とし、この試行を繰り返す。例えば、3回の試行を行ったとき、出た面に書かれた数が「0」、「2」、「3」であれば、持ち点は5となる。なお、さいころが水平な床面にあるとき、さいころの上部の水平な面を出た面とよぶ。また、さいころを投げるとき、各面が出ることは同様に確からしいとする。
(1)この試行を2回行ったとき、持ち点が1である確率を求めよ。
(2)この試行を4回行ったとき、持ち点が10以下である確率を求めよ。
福田のおもしろ数学107〜京都大学の有名問題〜車両の色塗り
単元：
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$n$両編成($n$≧2)に各車両に赤、青、黄の3色のいずれかを塗る。隣り合った車両の少なくとも一方が赤になるような塗り方は何通りあるか。
この動画を見る
$n$両編成($n$≧2)に各車両に赤、青、黄の3色のいずれかを塗る。隣り合った車両の少なくとも一方が赤になるような塗り方は何通りあるか。
福田の数学〜北海道大学2024年理系第2問〜反復試行の確率と条件付き確率
単元：
#数A#場合の数と確率#確率#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{2}$ 各面に1つずつ数が書かれた正八面体のさいころがある。「1」、「2」、「3」が書かれた面がそれぞれ1つずつあり、残りの5つの面には「0」が書かれている。このさいころを水平な面に投げて、出た面に書かれた数を持ち点に加えるという試行を考える。最初の持ち点は0とし、この試行を繰り返す。例えば、3回の試行を行ったとき、出た面に書かれた数が「0」、「2」、「3」であれば、持ち点は5となる。なお、さいころが水平な床面にあるとき、さいころの上部の水平な面を出た面と呼ぶ。また、さいころを投げるとき、各面が出ることは同様に確からしいとする。
(1)この試行を$n$回行ったとき、持ち点が2以下である確率を求めよ。ただし、$n$は2以上の自然数とする。
(2)この試行を4回行って持ち点が10以上であった時に、さらにこの試行を2回行って持ち点が17以上である条件付き確率を求めよ。
この動画を見る
$\Large\boxed{2}$ 各面に1つずつ数が書かれた正八面体のさいころがある。「1」、「2」、「3」が書かれた面がそれぞれ1つずつあり、残りの5つの面には「0」が書かれている。このさいころを水平な面に投げて、出た面に書かれた数を持ち点に加えるという試行を考える。最初の持ち点は0とし、この試行を繰り返す。例えば、3回の試行を行ったとき、出た面に書かれた数が「0」、「2」、「3」であれば、持ち点は5となる。なお、さいころが水平な床面にあるとき、さいころの上部の水平な面を出た面と呼ぶ。また、さいころを投げるとき、各面が出ることは同様に確からしいとする。
(1)この試行を$n$回行ったとき、持ち点が2以下である確率を求めよ。ただし、$n$は2以上の自然数とする。
(2)この試行を4回行って持ち点が10以上であった時に、さらにこの試行を2回行って持ち点が17以上である条件付き確率を求めよ。
福田の数学〜慶應義塾大学2024年看護医療学部第1問(1)〜さいころの目の積が4の倍数になる確率
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{1}$ (1)4個のさいころを同時に投げるとき、出た目の積が偶数になる確率は$\boxed{\ \ ア\ \ }$であり、出た目の積が4の倍数になる確率は$\boxed{\ \ イ\ \ }$である。
この動画を見る
$\Large\boxed{1}$ (1)4個のさいころを同時に投げるとき、出た目の積が偶数になる確率は$\boxed{\ \ ア\ \ }$であり、出た目の積が4の倍数になる確率は$\boxed{\ \ イ\ \ }$である。
福田の数学〜慶應義塾大学2024年薬学部第3問〜ウイルスの保有と症状に関する条件付き確率
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{3}$ 10万人の集団があり、この集団に対してウイルスXとウイルスYの保有及び症状の有無を調べた。
この集団のうち2万人がウイルスXを保有し、ウイルスX保有者の$\frac{1}{4}$、ウイルスX非保有者の$\frac{1}{4}$がウイルスYを保有していた。ウイルスXが原因でみられる症状は発熱のみ、ウイルスYが原因でみられる症状は腹痛のみであり、ウイルスを保有していなくても発熱や腹痛がみられることがある。
過去の研究から、発熱はウイルスX保有者に確率$\frac{3}{4}$、ウイルスX非保有者に確率$\frac{1}{10}$でみられ、腹痛はウイルスY保有者に確率$\frac{9}{10}$、ウイルスY非保有者に確率$\frac{1}{5}$でみられることがわかっている。なお、発熱と腹痛はそれぞれ独立に発症し互いに影響しないものとする。
(1)この集団から無作為に選ばれた1人がウイルスXを保有していないが発熱がみられる確率は$\boxed{\ \ ト\ \ }$である。
(2)この集団から無作為に選ばれた1人がウイルスYを保有していないが発熱がみられる確率は$\boxed{\ \ ナ\ \ }$である。
(3)この集団から無作為に1人を選んでウイルスの保有および症状の有無を調べて集団に戻す試行を3回繰り返した。
(i)3回の試行で選ばれた人のうち、1人のみに腹痛がみられる確率は$\boxed{\ \ ニ\ \ }$である。
(ii)3回の試行で選ばれた人のうち、1人のみに腹痛がみられるとき、選ばれた人のうち少なくとも1人がウイルスYを保有している確率は$\boxed{\ \ ヌ\ \ }$である。
この動画を見る
$\Large\boxed{3}$ 10万人の集団があり、この集団に対してウイルスXとウイルスYの保有及び症状の有無を調べた。
この集団のうち2万人がウイルスXを保有し、ウイルスX保有者の$\frac{1}{4}$、ウイルスX非保有者の$\frac{1}{4}$がウイルスYを保有していた。ウイルスXが原因でみられる症状は発熱のみ、ウイルスYが原因でみられる症状は腹痛のみであり、ウイルスを保有していなくても発熱や腹痛がみられることがある。
過去の研究から、発熱はウイルスX保有者に確率$\frac{3}{4}$、ウイルスX非保有者に確率$\frac{1}{10}$でみられ、腹痛はウイルスY保有者に確率$\frac{9}{10}$、ウイルスY非保有者に確率$\frac{1}{5}$でみられることがわかっている。なお、発熱と腹痛はそれぞれ独立に発症し互いに影響しないものとする。
(1)この集団から無作為に選ばれた1人がウイルスXを保有していないが発熱がみられる確率は$\boxed{\ \ ト\ \ }$である。
(2)この集団から無作為に選ばれた1人がウイルスYを保有していないが発熱がみられる確率は$\boxed{\ \ ナ\ \ }$である。
(3)この集団から無作為に1人を選んでウイルスの保有および症状の有無を調べて集団に戻す試行を3回繰り返した。
(i)3回の試行で選ばれた人のうち、1人のみに腹痛がみられる確率は$\boxed{\ \ ニ\ \ }$である。
(ii)3回の試行で選ばれた人のうち、1人のみに腹痛がみられるとき、選ばれた人のうち少なくとも1人がウイルスYを保有している確率は$\boxed{\ \ ヌ\ \ }$である。
福田の数学〜東京工業大学2024年理系第4問〜表の出る確率が異なるコインを投げたときの表が奇数枚出る確率と極限
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#関数と極限#数列の極限#関数の極限#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{4}$ $n$を正の整数とし、$C_1$,...,$C_n$を$n$枚の硬貨とする。各$k$=1,...,$n$に対し、硬貨$C_k$を投げて表が出る確率を$p_k$、裏が出る確率を1－$p_k$とする。この$n$枚の硬貨を同時に投げ、表が出た硬貨の枚数が奇数であれば成功、というゲームを考える。
(1)$p_k$=$\frac{1}{3}$ ($k$=1,...,$n$)のとき、このゲームで成功する確率$X_n$を求めよ。
(2)$p_k$=$\frac{1}{2(k+1)}$ ($k$=1,...,$n$)のとき、このゲームで成功する確率$Y_n$を求めよ。
(3)$n$=$3m$($m$は正の定数)で$k$=1,...,$3m$に対して
$p_k$=$\left\{\begin{array}{1}
\frac{1}{3m} (k=1,...,m) \\
\frac{2}{3m} (k=m+1,...,2m)\\
\frac{1}{m} (k=2m+1,...,3m)\\
\end{array}\right.$
とする。このゲームで成功する確率を$Z_{3m}$とするとき、$\displaystyle\lim_{m \to \infty}Z_{3m}$ を求めよ。
この動画を見る
$\Large\boxed{4}$ $n$を正の整数とし、$C_1$,...,$C_n$を$n$枚の硬貨とする。各$k$=1,...,$n$に対し、硬貨$C_k$を投げて表が出る確率を$p_k$、裏が出る確率を1－$p_k$とする。この$n$枚の硬貨を同時に投げ、表が出た硬貨の枚数が奇数であれば成功、というゲームを考える。
(1)$p_k$=$\frac{1}{3}$ ($k$=1,...,$n$)のとき、このゲームで成功する確率$X_n$を求めよ。
(2)$p_k$=$\frac{1}{2(k+1)}$ ($k$=1,...,$n$)のとき、このゲームで成功する確率$Y_n$を求めよ。
(3)$n$=$3m$($m$は正の定数)で$k$=1,...,$3m$に対して
$p_k$=$\left\{\begin{array}{1}
\frac{1}{3m} (k=1,...,m) \\
\frac{2}{3m} (k=m+1,...,2m)\\
\frac{1}{m} (k=2m+1,...,3m)\\
\end{array}\right.$
とする。このゲームで成功する確率を$Z_{3m}$とするとき、$\displaystyle\lim_{m \to \infty}Z_{3m}$ を求めよ。
名古屋大学2024年の確率と積分の融合問題をその場で解きながら解説してみた！#shorts #高校数学 #名古屋大学
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#積分とその応用#不定積分#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師：
理数個別チャンネル
問題文全文(内容文)：
名古屋大学2024年の確率と積分の融合問題をその場で解きながら解説してみた！
この動画を見る
名古屋大学2024年の確率と積分の融合問題をその場で解きながら解説してみた！
灘問！！懐かしいと感じるのは私だけ？2024
単元：
#数A#場合の数と確率#確率#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
異なる5つのマスに黒石を1個ずつ置く
縦、横、斜めのうち少なくとも1列に3個の黒石が並ぶ並び方は全部で何通り？
2024灘中学校
この動画を見る
異なる5つのマスに黒石を1個ずつ置く
縦、横、斜めのうち少なくとも1列に3個の黒石が並ぶ並び方は全部で何通り？
2024灘中学校