 図形の性質
図形の性質
 図形の性質
図形の性質
サクッと解こう!高校入試レベル
チェバの定理使わずに解ける? 香川誠陵 2022入試問題解説23問目
単元:
#数学(中学生)#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
チェバの定理は使わない
AF:FCを求めよ
*図は動画内参照
2022香川誠陵高等学校
この動画を見る
チェバの定理は使わない
AF:FCを求めよ
*図は動画内参照
2022香川誠陵高等学校
15度75度90度の直角三角形の面積を求める
2つの接線に囲まれた円の面積 西武文理 2022入試問題解説 20問目
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
円の面積は?
*図は動画内参照
2022西武学園文理高等学校
この動画を見る
円の面積は?
*図は動画内参照
2022西武学園文理高等学校
球 中央大学附属(推薦)2022入試問題解説18問目

単元:
#数学(中学生)#数A#図形の性質#方べきの定理と2つの円の関係#立体図形#体積・表面積・回転体・水量・変化のグラフ#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
半径の差が1
表面積の和が34π
2つの球の体積の和は?
2022中央大学附属高等学校(推薦)
この動画を見る
半径の差が1
表面積の和が34π
2つの球の体積の和は?
2022中央大学附属高等学校(推薦)
福田の共通テスト解答速報〜2022年共通テスト数学IA問題5。平面幾何の問題。

単元:
#数A#大学入試過去問(数学)#図形の性質#内心・外心・重心とチェバ・メネラウス#方べきの定理と2つの円の関係#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
第5問 $\triangle ABC$の重心をGとし、線分AG上で点Aとは異なる位置に点Dをとる。
直線AGと辺BCの交点をEとする。また、直線BC上で辺BC上にはない位置に点Fをとる。
直線DFと辺ABの交点をP、直線DFと辺ACの交点をQとする。
(1)点Dは線分AGの中点であるとする。
このとき、$\triangle ABC$の形状に関係なく$\frac{AD}{DE}=\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$
である。また、点Fの位置に関係なく$\frac{BP}{AP}=\boxed{\ \ ウ\ \ }×\frac{\boxed{\ \ エ\ \ }}{\boxed{\ \ オ\ \ }},$
$\frac{CQ}{AQ}=\boxed{\ \ カ\ \ }×\frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ ク\ \ }}$であるので、常に$\frac{BP}{AP}+\frac{CQ}{AQ}=\boxed{\ \ ケ\ \ }$
$\boxed{\ \ エ\ \ }~\boxed{\ \ ケ\ \ }$の解答群
⓪BC ①BF ②CF ③EF ④FP ⑤FQ ⑥PQ
(2)$AB=9, BC=8, AC=6$とし、(1)と同様に、点Dは線分AGの中点であるとする。
ここで、4点B,C,Q,Pが同一円周上にあるように点Fをとる。このとき、
$AQ=\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\ AP$であるから
$AP=\frac{\boxed{\ \ シス\ \ }}{\boxed{\ \ セ\ \ }}, AQ=\frac{\boxed{\ \ ソタ\ \ }}{\boxed{\ \ チ\ \ }}$であり、
$CF=\frac{\boxed{\ \ ツテ\ \ }}{\boxed{\ \ トナ\ \ }}$である。
(3)$\triangle ABC$の形状や点Fの位置に関係なく、常に$\frac{BP}{AP}+\frac{CQ}{AQ}=10$となるのは
$\frac{AD}{DG}=\frac{\boxed{\ \ ニ\ \ }}{\boxed{\ \ ヌ\ \ }}$のときである。
2022共通テスト数学過去問
この動画を見る
第5問 $\triangle ABC$の重心をGとし、線分AG上で点Aとは異なる位置に点Dをとる。
直線AGと辺BCの交点をEとする。また、直線BC上で辺BC上にはない位置に点Fをとる。
直線DFと辺ABの交点をP、直線DFと辺ACの交点をQとする。
(1)点Dは線分AGの中点であるとする。
このとき、$\triangle ABC$の形状に関係なく$\frac{AD}{DE}=\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$
である。また、点Fの位置に関係なく$\frac{BP}{AP}=\boxed{\ \ ウ\ \ }×\frac{\boxed{\ \ エ\ \ }}{\boxed{\ \ オ\ \ }},$
$\frac{CQ}{AQ}=\boxed{\ \ カ\ \ }×\frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ ク\ \ }}$であるので、常に$\frac{BP}{AP}+\frac{CQ}{AQ}=\boxed{\ \ ケ\ \ }$
$\boxed{\ \ エ\ \ }~\boxed{\ \ ケ\ \ }$の解答群
⓪BC ①BF ②CF ③EF ④FP ⑤FQ ⑥PQ
(2)$AB=9, BC=8, AC=6$とし、(1)と同様に、点Dは線分AGの中点であるとする。
ここで、4点B,C,Q,Pが同一円周上にあるように点Fをとる。このとき、
$AQ=\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\ AP$であるから
$AP=\frac{\boxed{\ \ シス\ \ }}{\boxed{\ \ セ\ \ }}, AQ=\frac{\boxed{\ \ ソタ\ \ }}{\boxed{\ \ チ\ \ }}$であり、
$CF=\frac{\boxed{\ \ ツテ\ \ }}{\boxed{\ \ トナ\ \ }}$である。
(3)$\triangle ABC$の形状や点Fの位置に関係なく、常に$\frac{BP}{AP}+\frac{CQ}{AQ}=10$となるのは
$\frac{AD}{DG}=\frac{\boxed{\ \ ニ\ \ }}{\boxed{\ \ ヌ\ \ }}$のときである。
2022共通テスト数学過去問
キレイに解けます 立命館高校
単元:
#数学(中学生)#中2数学#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#三角形と四角形#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
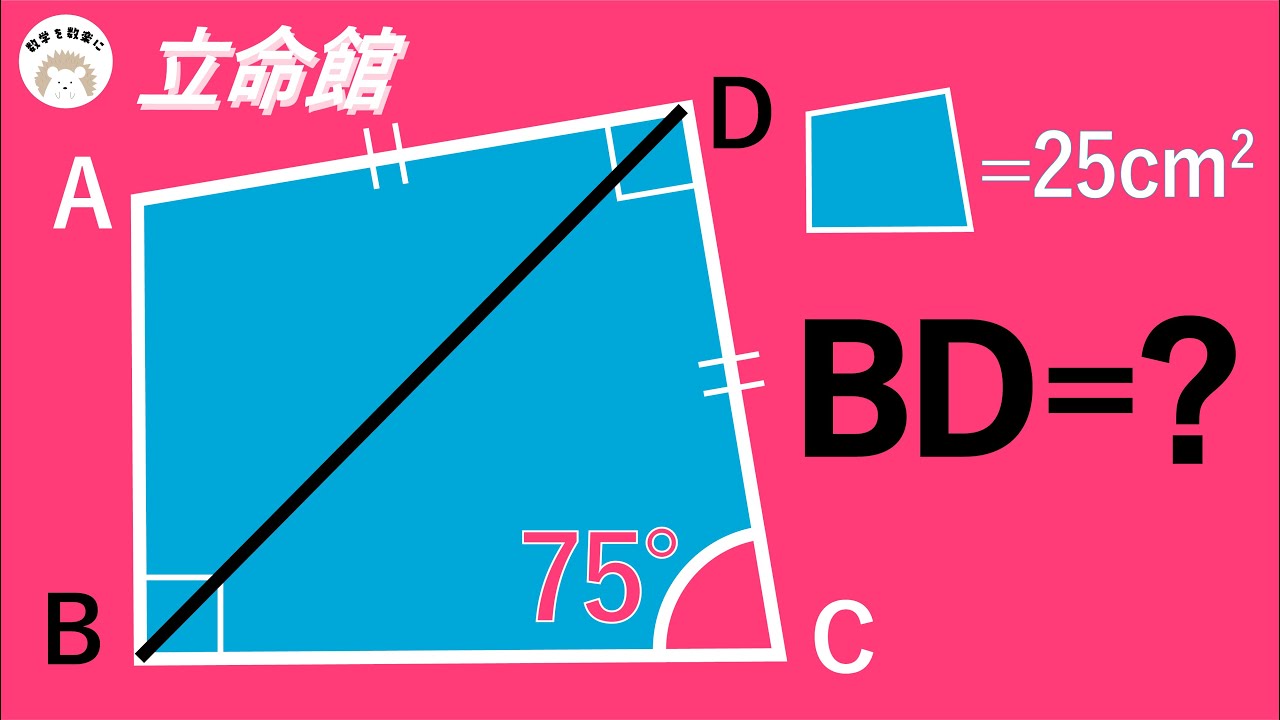
四角形ABCD=25㎠のとき
BD=?
*図は動画内参照
立命館高等学校
この動画を見る
四角形ABCD=25㎠のとき
BD=?
*図は動画内参照
立命館高等学校
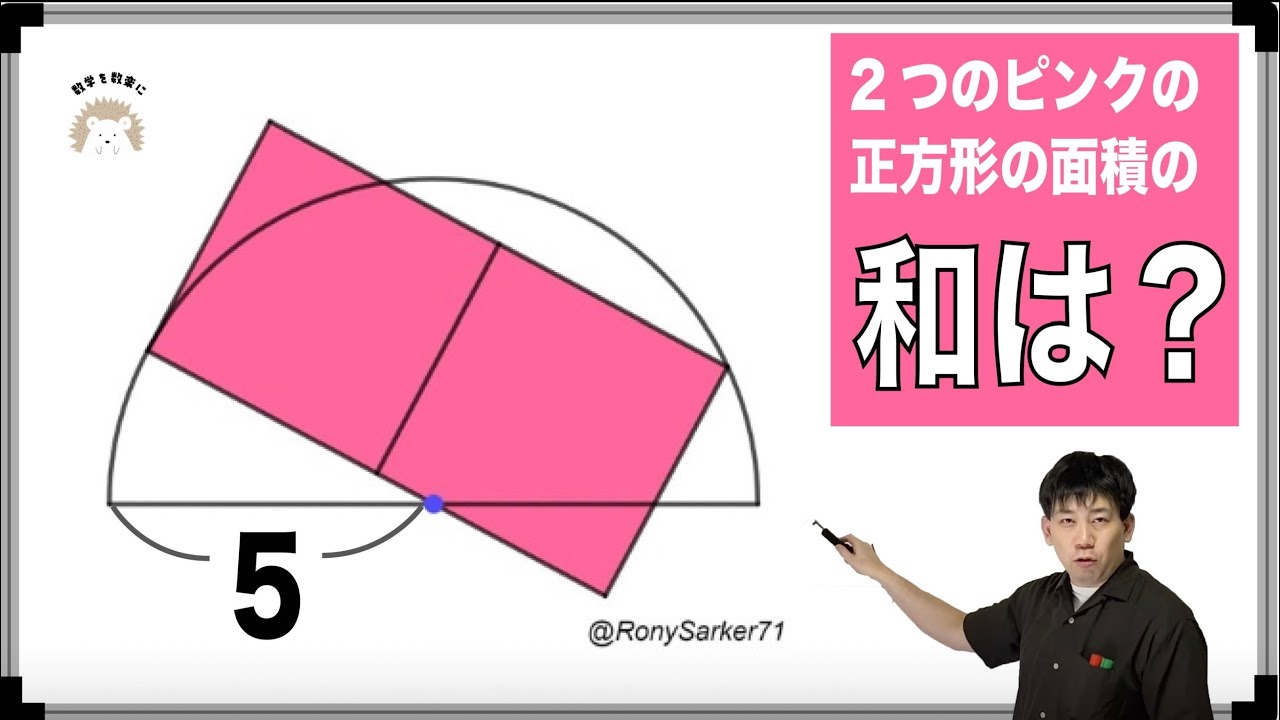
Rony先生の問題はやっぱり面白い!!3通りで解説!!
2通りで解説!!京都女子
単元:
#数学(中学生)#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
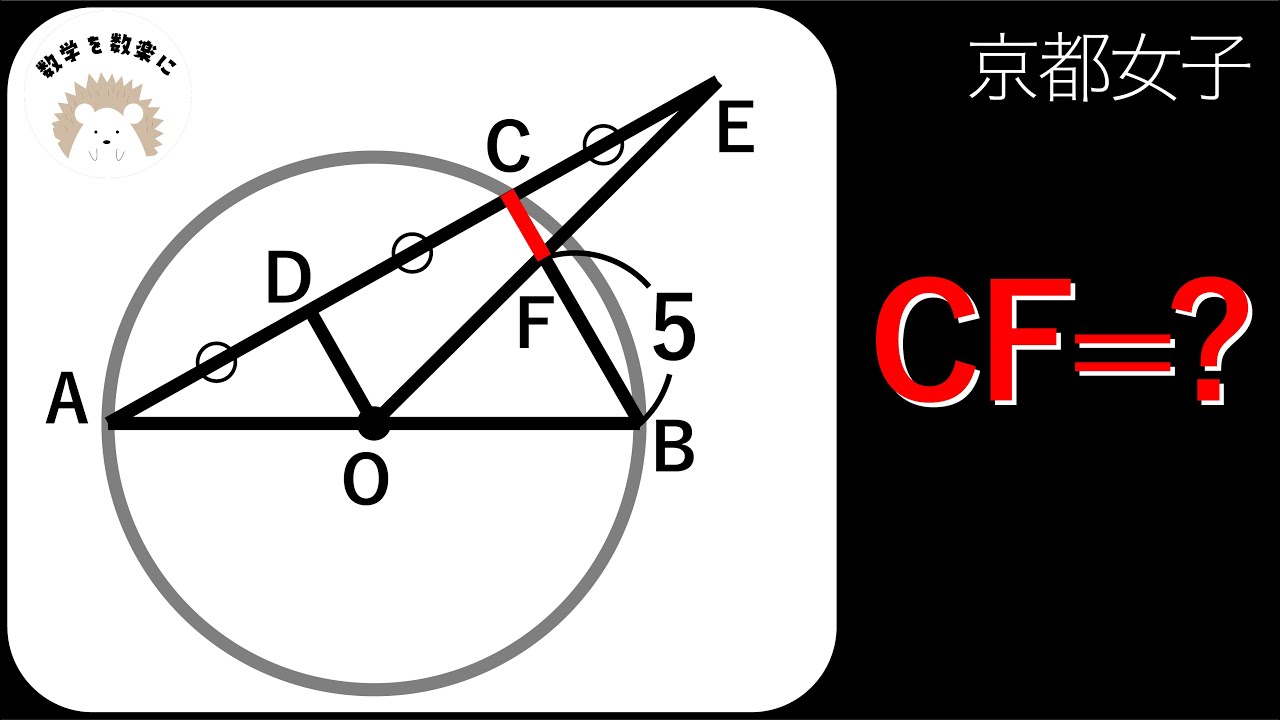
CF=?
*図は動画内参照
京都女子高等学校
この動画を見る
CF=?
*図は動画内参照
京都女子高等学校
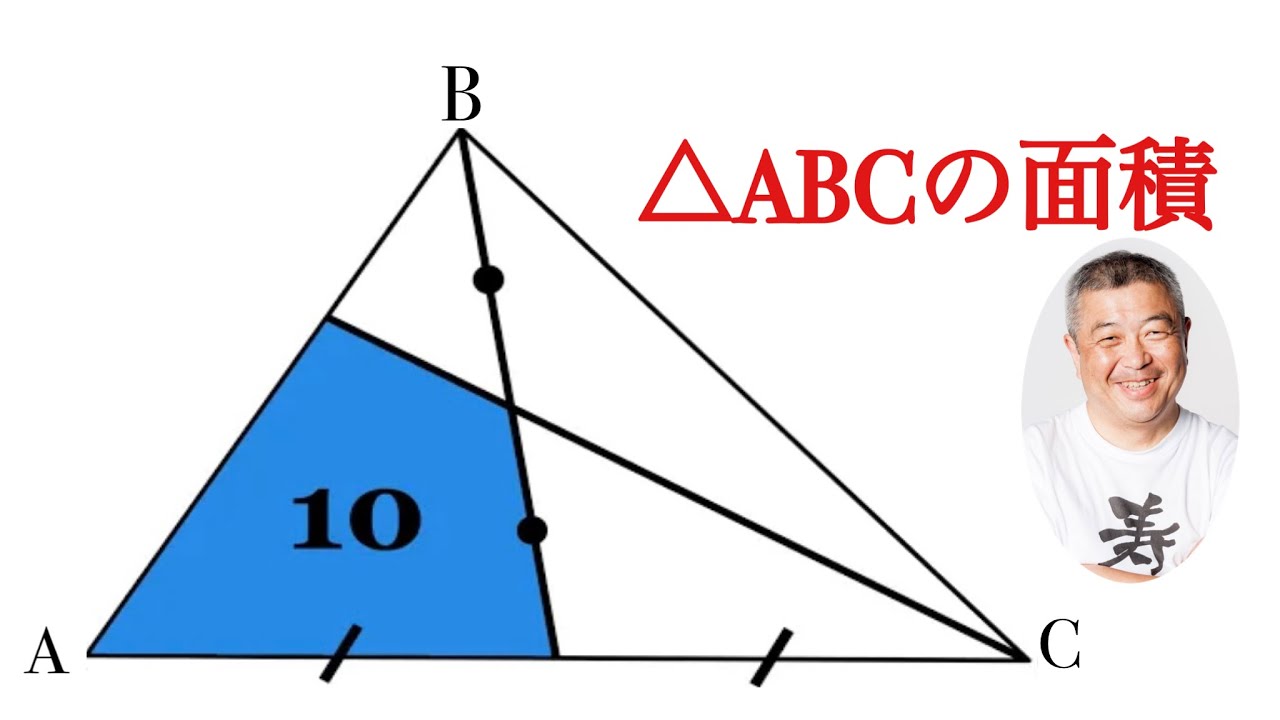
中学入試・高校入試頻出メネラウスの定理は使う?
単元:
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
メネラウスの定理が定期試験に出る頻度に関して解説していきます.
この動画を見る
メネラウスの定理が定期試験に出る頻度に関して解説していきます.
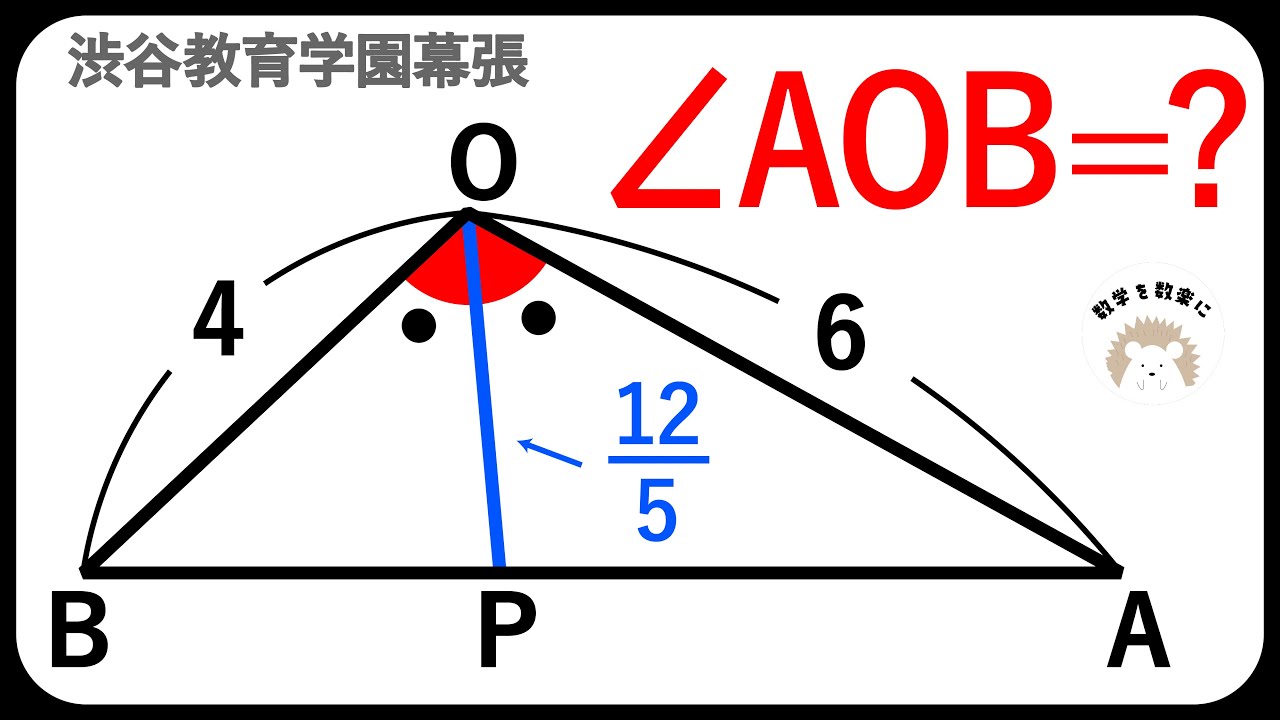
角度が出てないのに角度が出る問題 渋谷教育学園幕張高校
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle AOB =?$
*図は動画内参照
渋谷教育学園幕張高校
この動画を見る
$\angle AOB =?$
*図は動画内参照
渋谷教育学園幕張高校
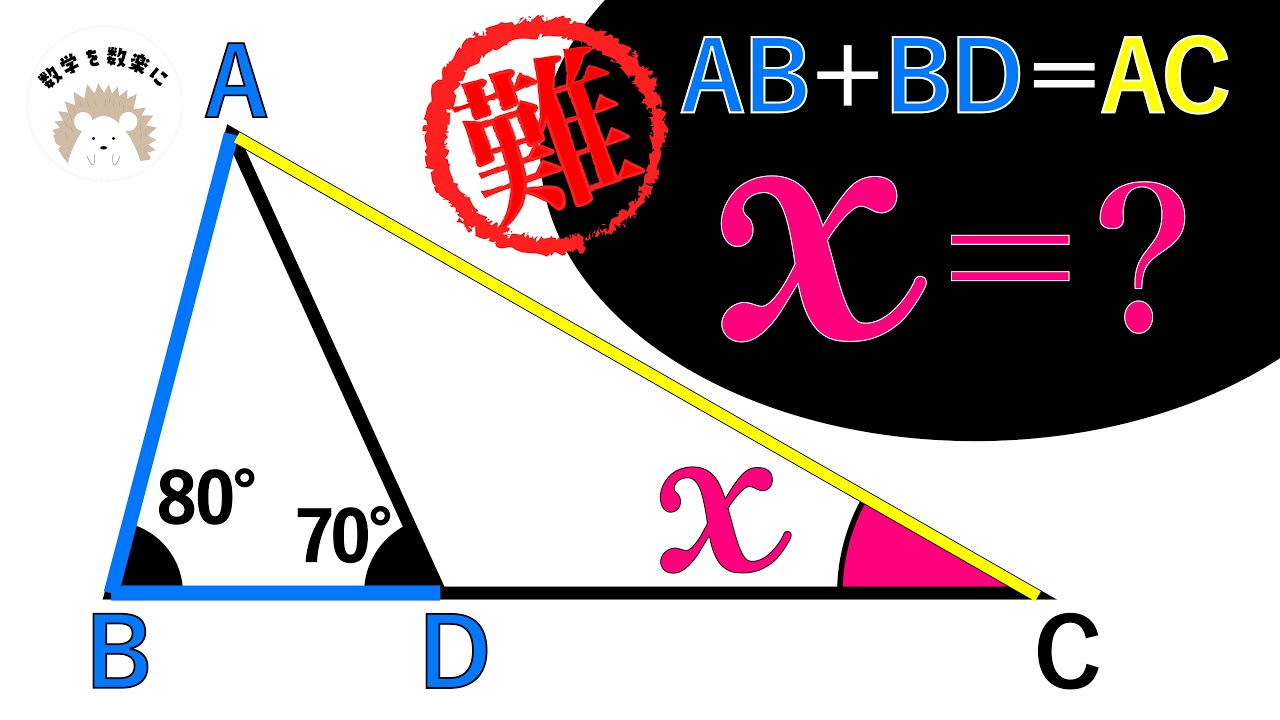
直角に凹ませました

補助線どう引く?
単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#平面図形#角度と面積#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
AB+BD=AC
x=?
*図は動画内参照
この動画を見る
AB+BD=AC
x=?
*図は動画内参照
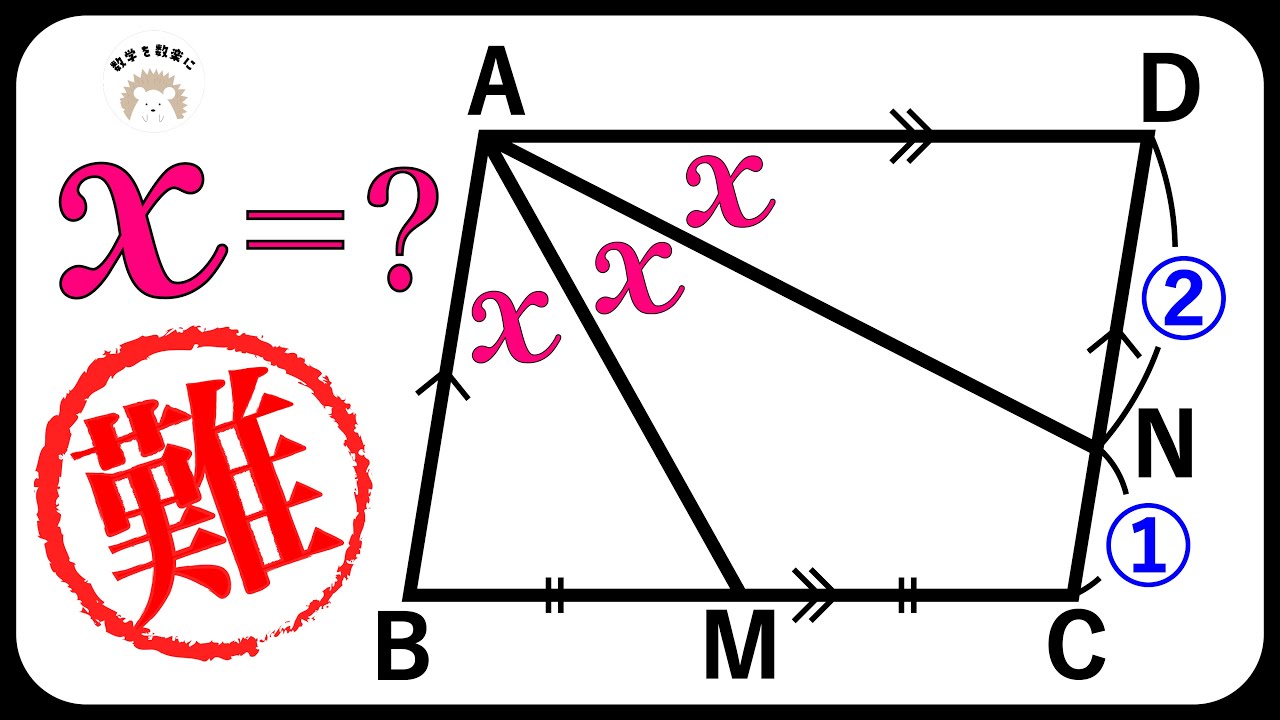
難問!?まさかの答え。
単元:
#数学(中学生)#中2数学#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#三角形と四角形#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
x=?
*図は動画内参照
この動画を見る
x=?
*図は動画内参照
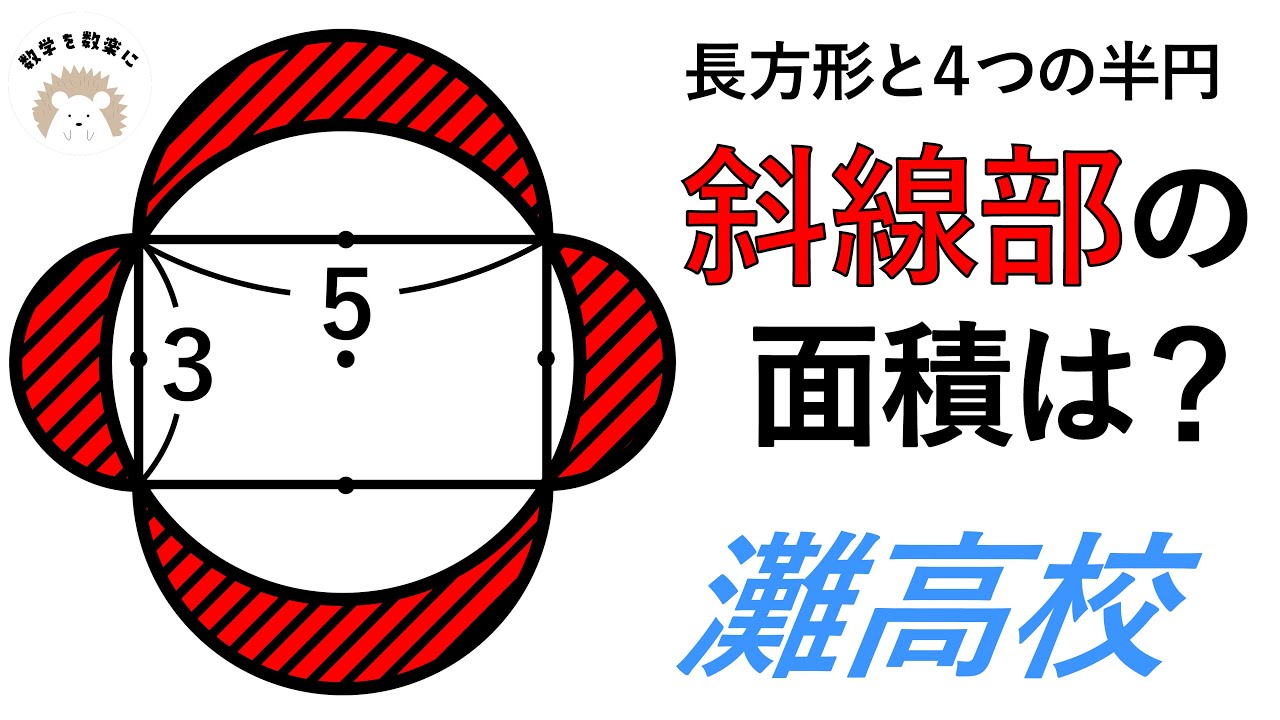
灘高校に受かるのは難だけど、この問題は難てこともない問題
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
長方形と4つの半円
斜線部の面積は?
*図は動画内参照
灘高等学校
この動画を見る
長方形と4つの半円
斜線部の面積は?
*図は動画内参照
灘高等学校
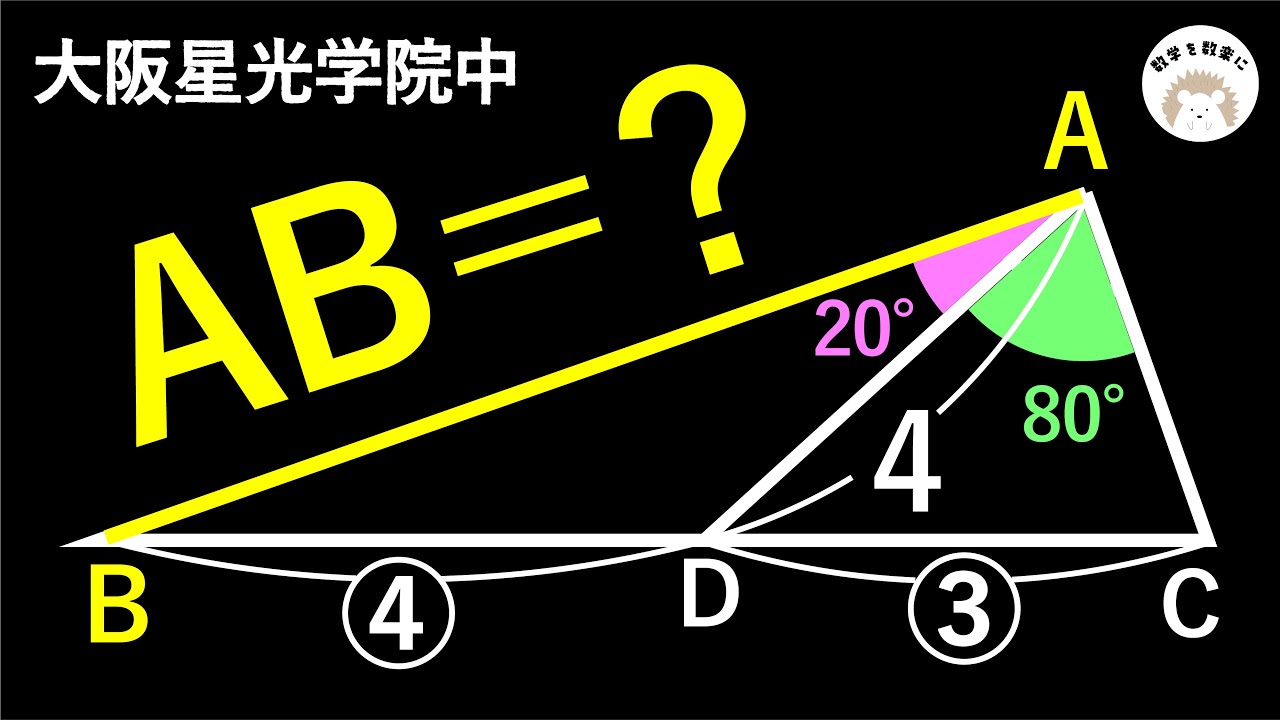
補助線引けるかな??
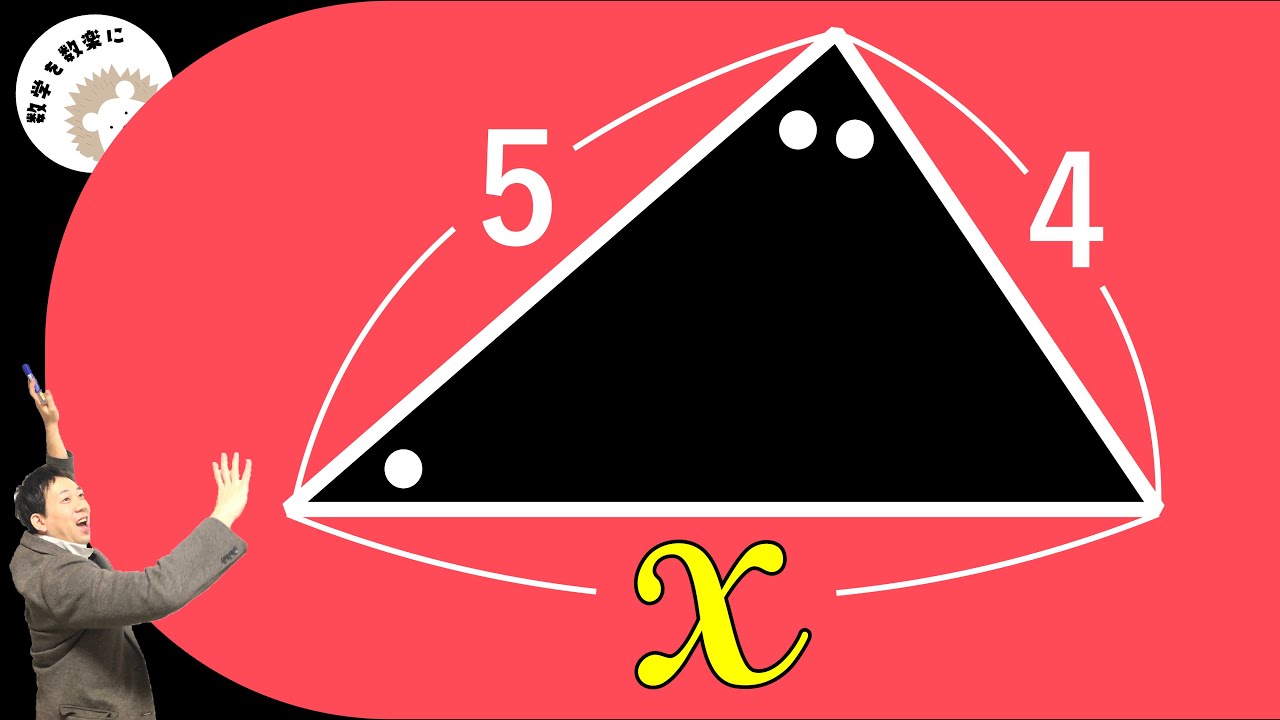
補助線どこ引く? 大阪星光学院中
単元:
#算数(中学受験)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#過去問解説(学校別)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
AB=?
*図は動画内参照
大阪星光学院中学校
この動画を見る
AB=?
*図は動画内参照
大阪星光学院中学校
初見で解けたら認めよう。2通りで解説。
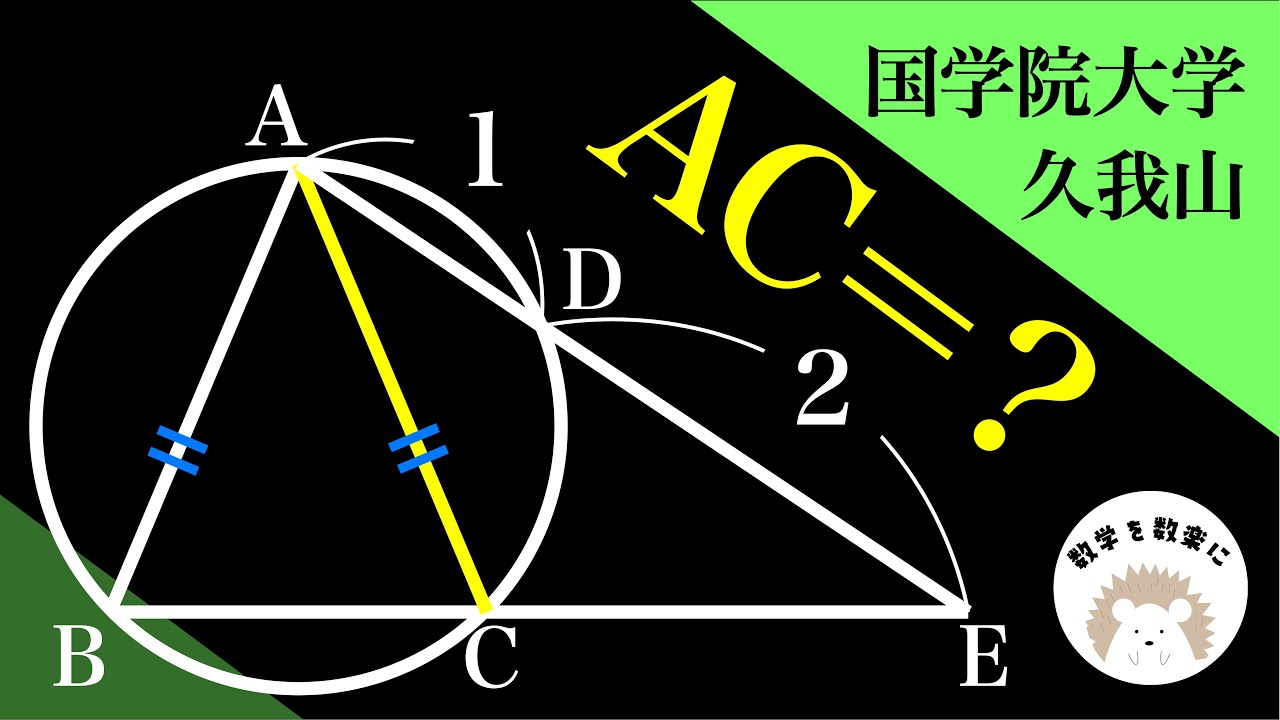
単元:
#数学(中学生)#中3数学#数A#図形の性質#三平方の定理#方べきの定理と2つの円の関係#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
AC=?
*図は動画内参照
國學院大學久我山高等学校
この動画を見る
AC=?
*図は動画内参照
國學院大學久我山高等学校
中3生も解けるし どっちが大きい?
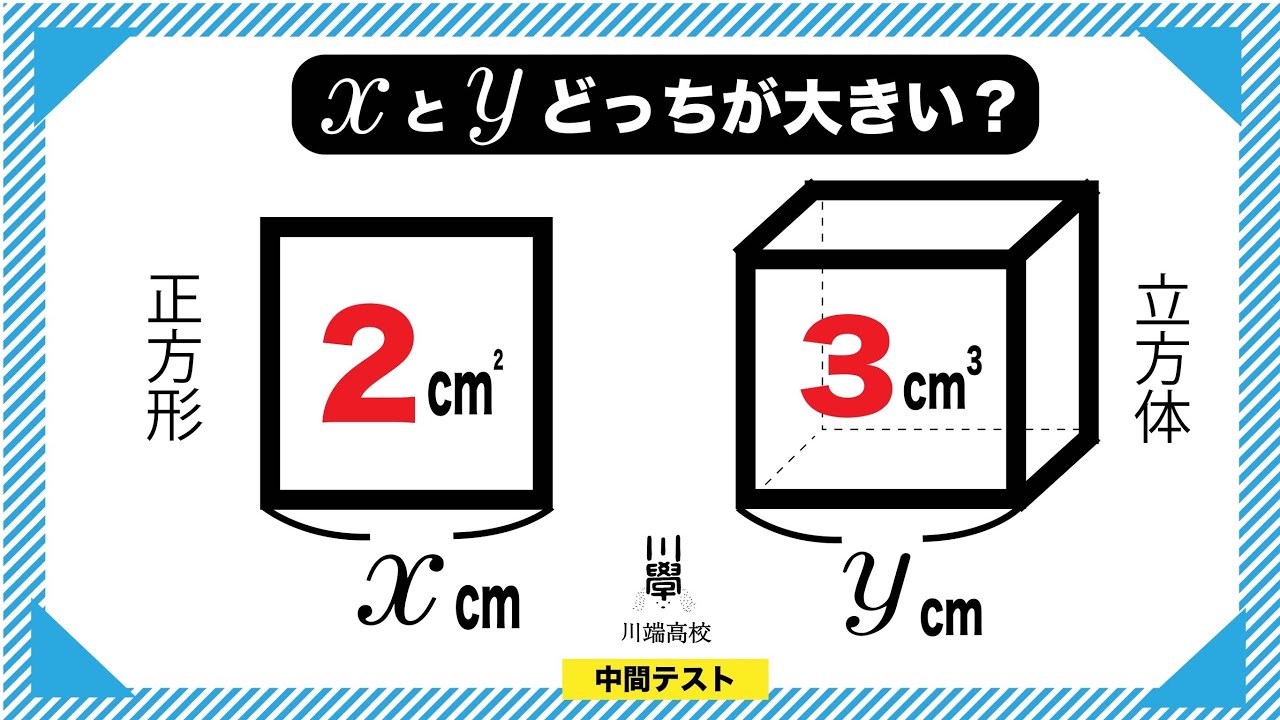
円と接線と角度 慶應義塾高校
単元:
#数学(中学生)#中3数学#数A#図形の性質#円#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
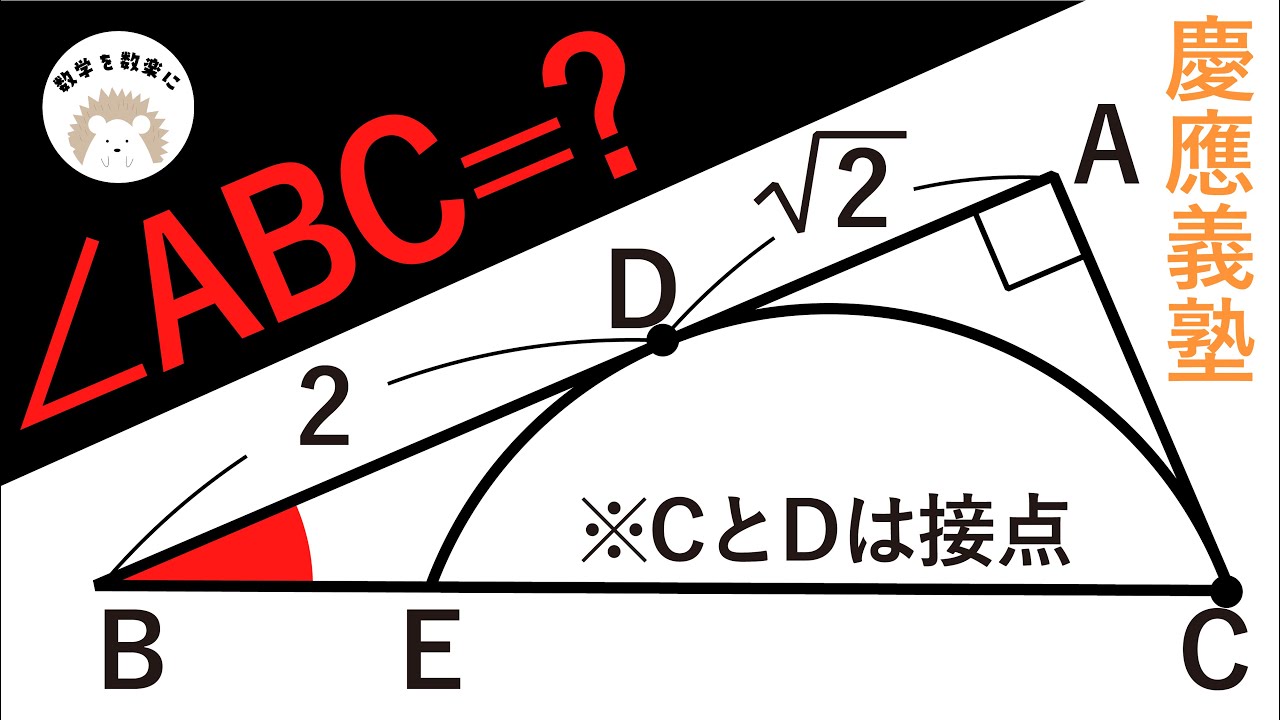
点Cと点Dは接点
$\angle ABC=?$
*図は動画内参照
慶應義塾高等学校
この動画を見る
点Cと点Dは接点
$\angle ABC=?$
*図は動画内参照
慶應義塾高等学校
空間上の3本の直線

単元:
#数A#図形の性質#空間における垂直と平行と多面体(オイラーの法則)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
空間内の3本の直線l,m,nに対して、l⊥m、かつl⊥nならば、
常にm$/\!/$n
この動画を見る
空間内の3本の直線l,m,nに対して、l⊥m、かつl⊥nならば、
常にm$/\!/$n
慶應義塾高校 円
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
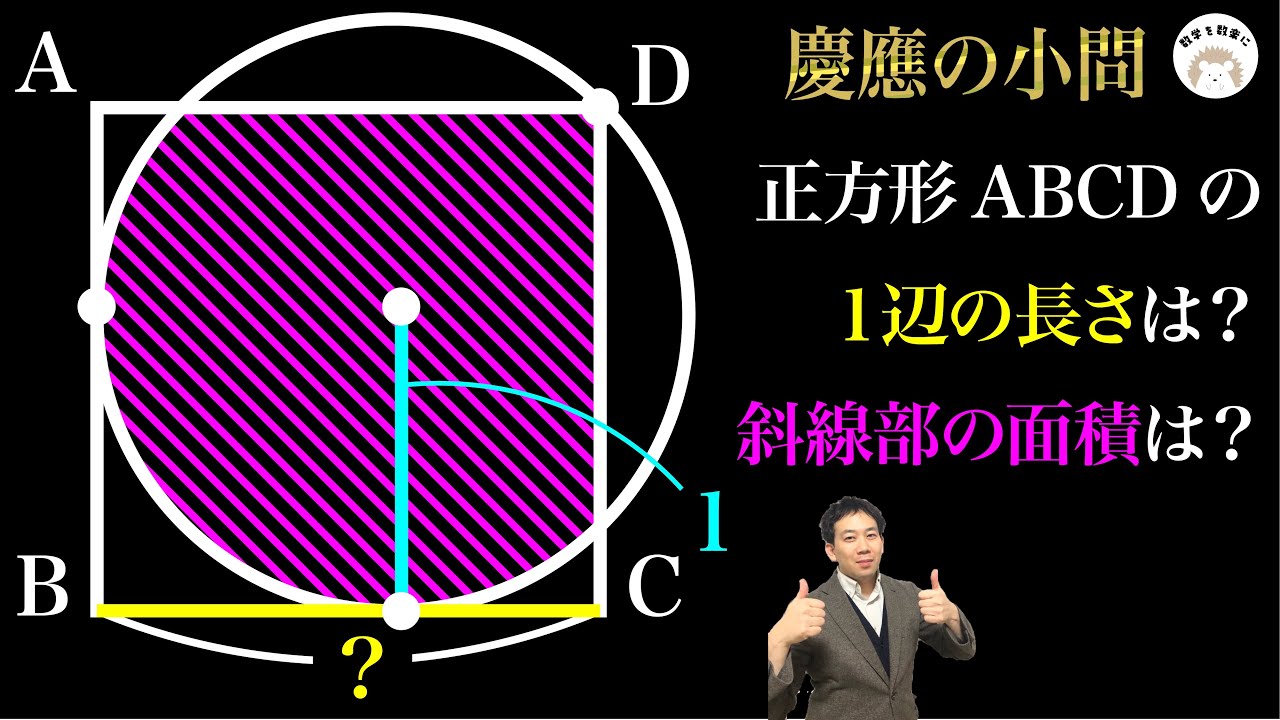
円の半径=1
正方形ABCDの1辺=?
斜線部の面積=?
*図は動画内参照
慶應義塾高等学校
この動画を見る
円の半径=1
正方形ABCDの1辺=?
斜線部の面積=?
*図は動画内参照
慶應義塾高等学校
〇〇を教えるときに注意していること
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
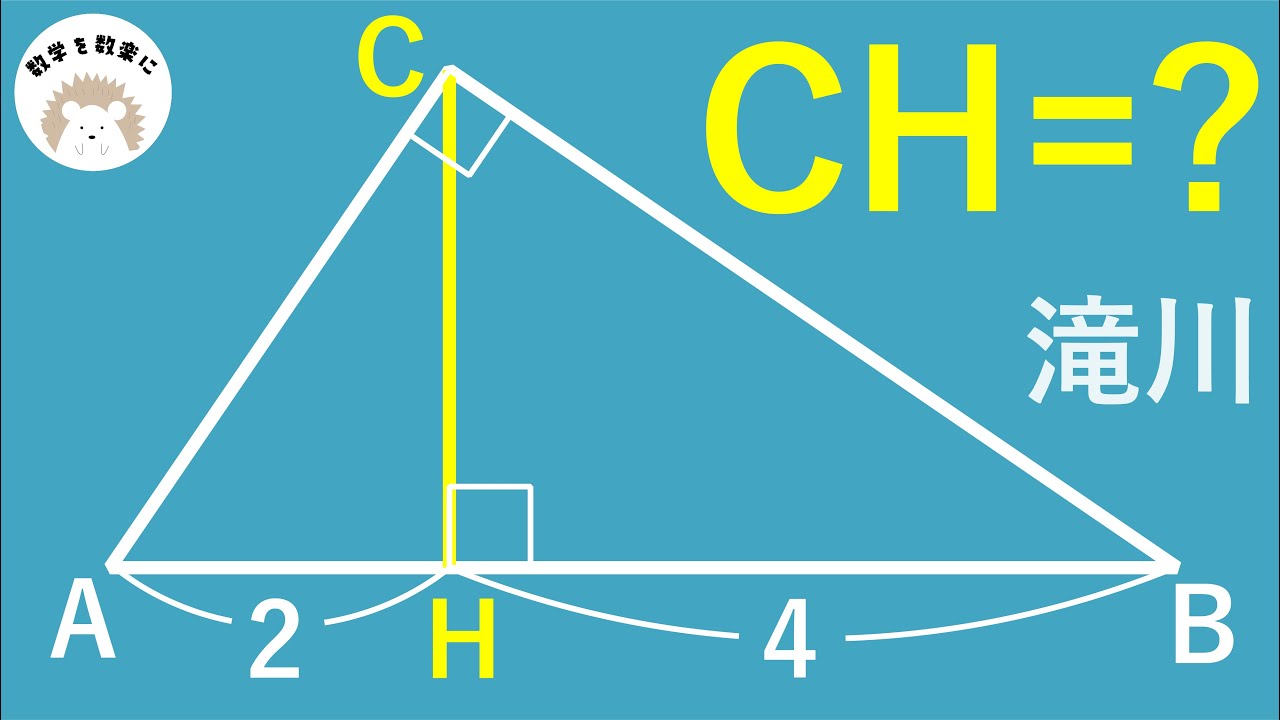
CH=?
*図は動画内参照
滝川高等学校
この動画を見る
CH=?
*図は動画内参照
滝川高等学校
補助線引けるかな?
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
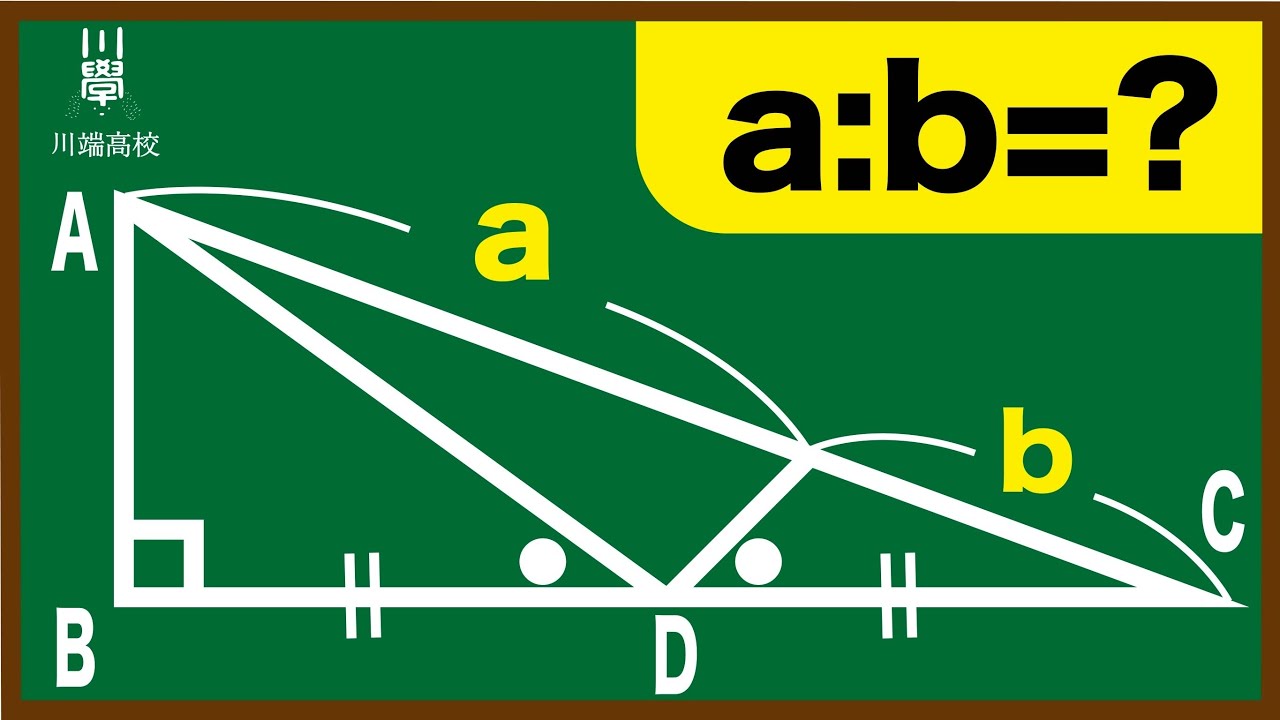
a:b=?
*図は動画内参照
川端高校
この動画を見る
a:b=?
*図は動画内参照
川端高校
座標平面上の角の二等分線
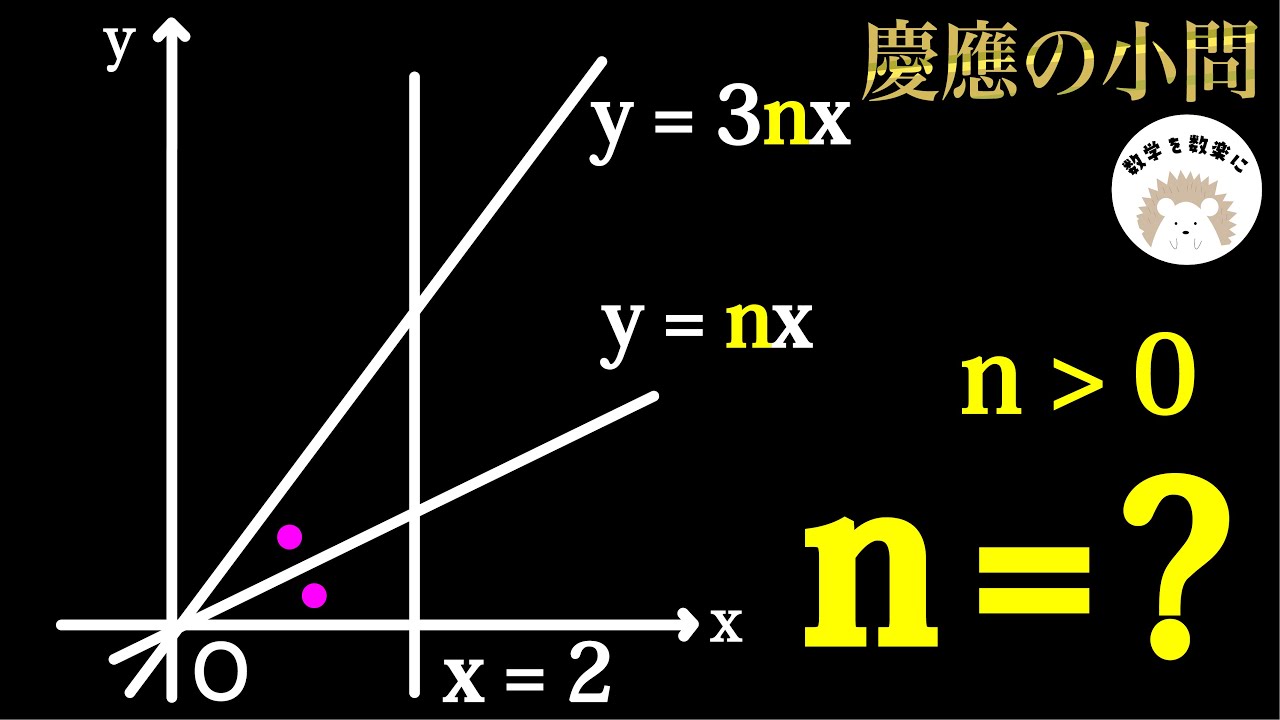
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
y=3nx
y=nx
*図は動画内参照
n=? (n>0)
慶應義塾高等学校
この動画を見る
y=3nx
y=nx
*図は動画内参照
n=? (n>0)
慶應義塾高等学校
高校入試の軌跡の問題
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
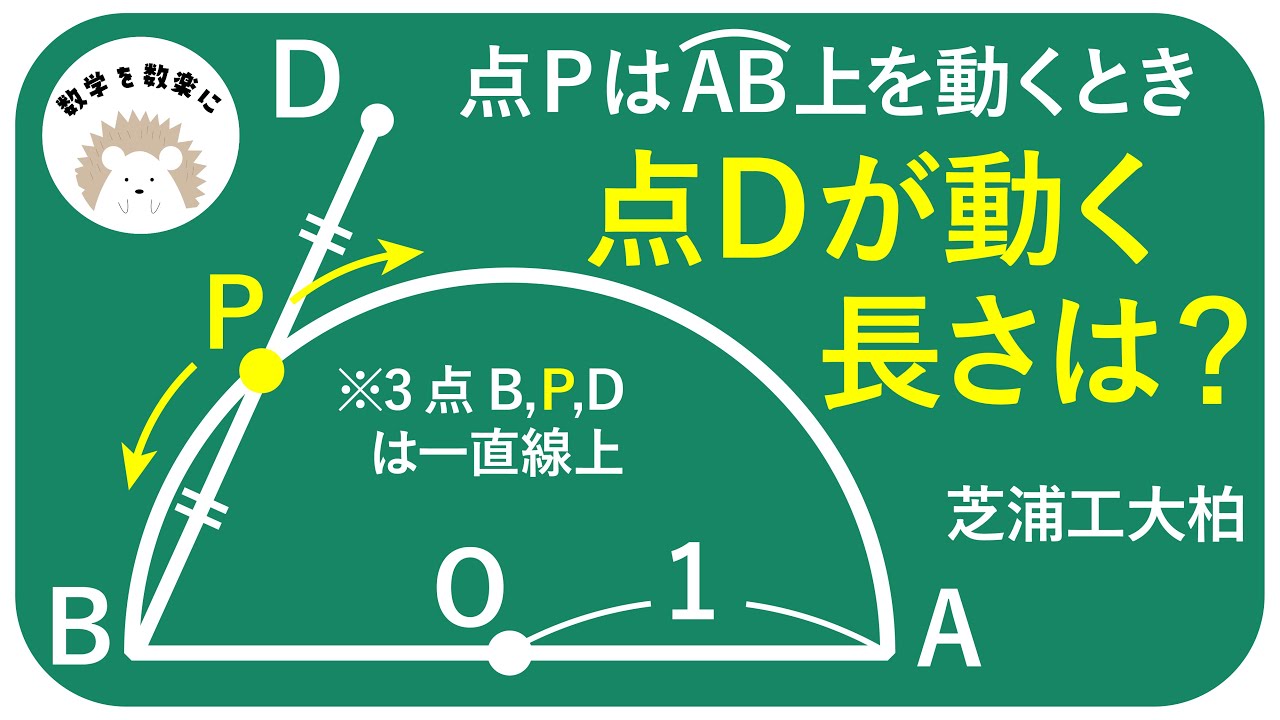
点Pは$\stackrel{\huge\frown}{AB}$上を動く。
BP=DPとなるように点Dを定めるとき点Dが動く長さは?
芝浦工業大学柏高等学校
この動画を見る
点Pは$\stackrel{\huge\frown}{AB}$上を動く。
BP=DPとなるように点Dを定めるとき点Dが動く長さは?
芝浦工業大学柏高等学校
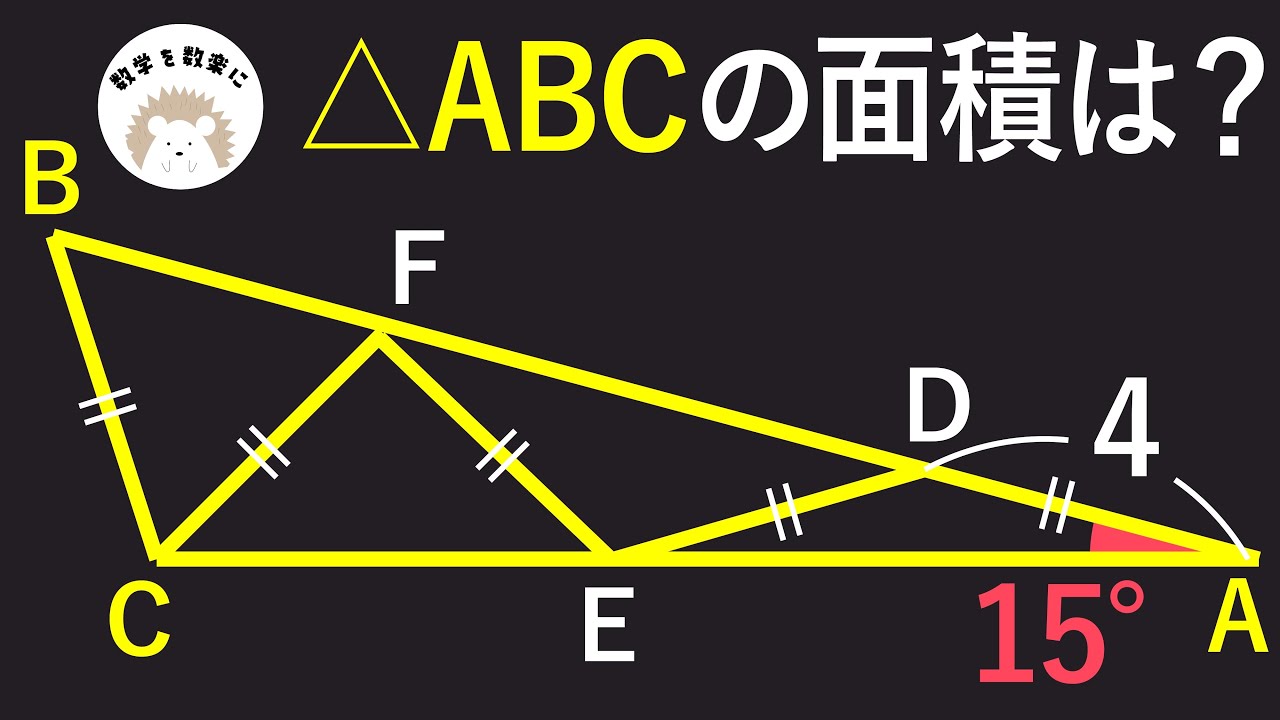
たった4という数字だけで。。。
単元:
#中1数学#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#平面図形#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
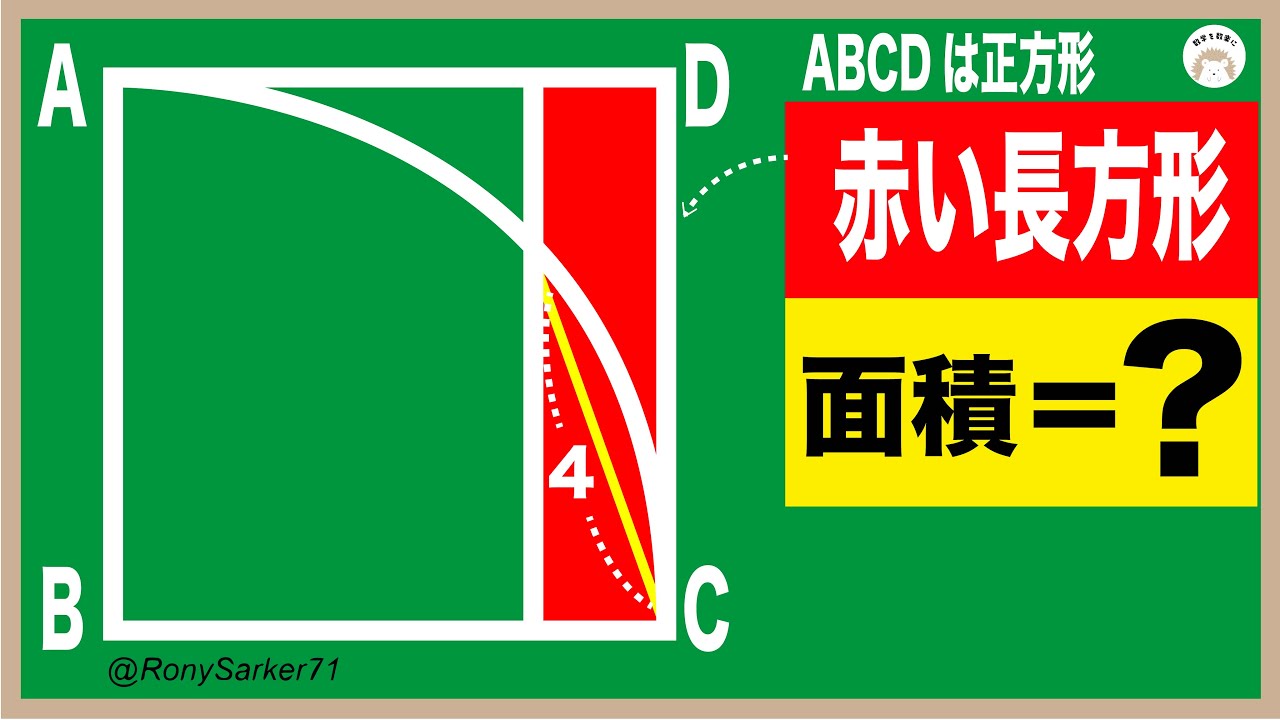
長方形の面積=?
*図は動画内参照
この動画を見る
長方形の面積=?
*図は動画内参照
京都と言ったら八つ橋くらい定番です
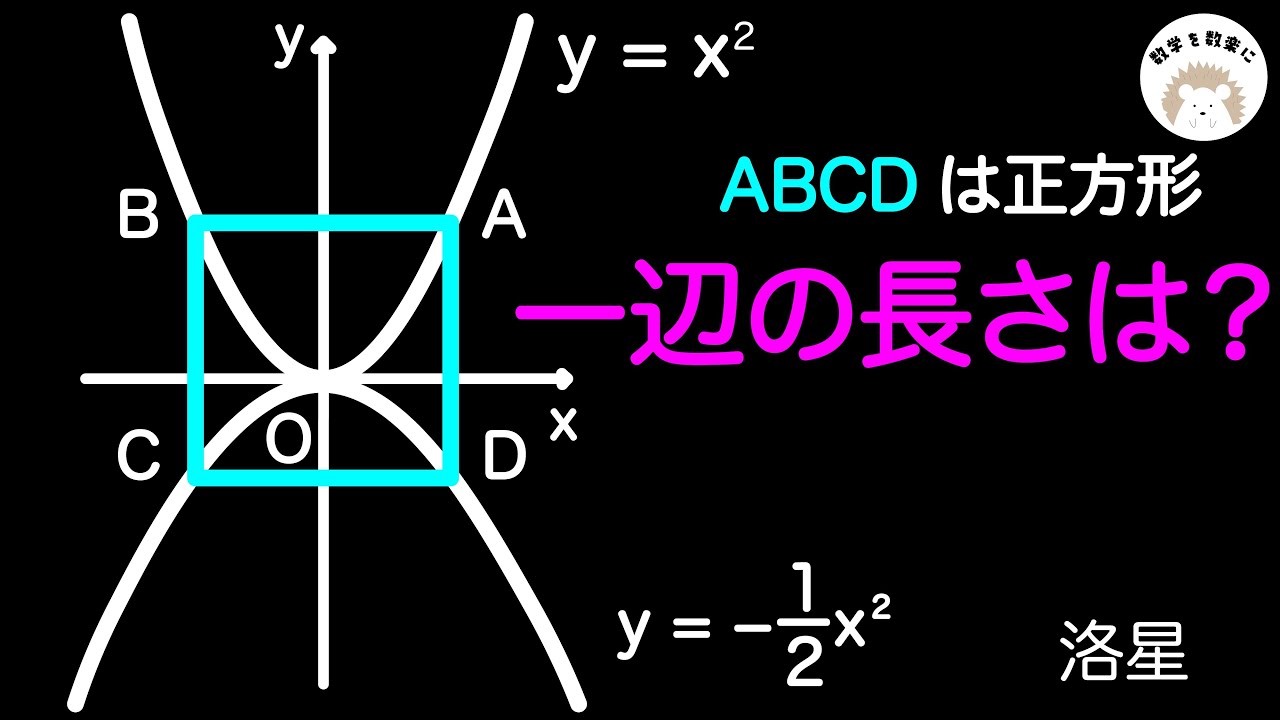
「長さ等しい」がいっぱい
高校入試最上級レベル 球の断面積
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
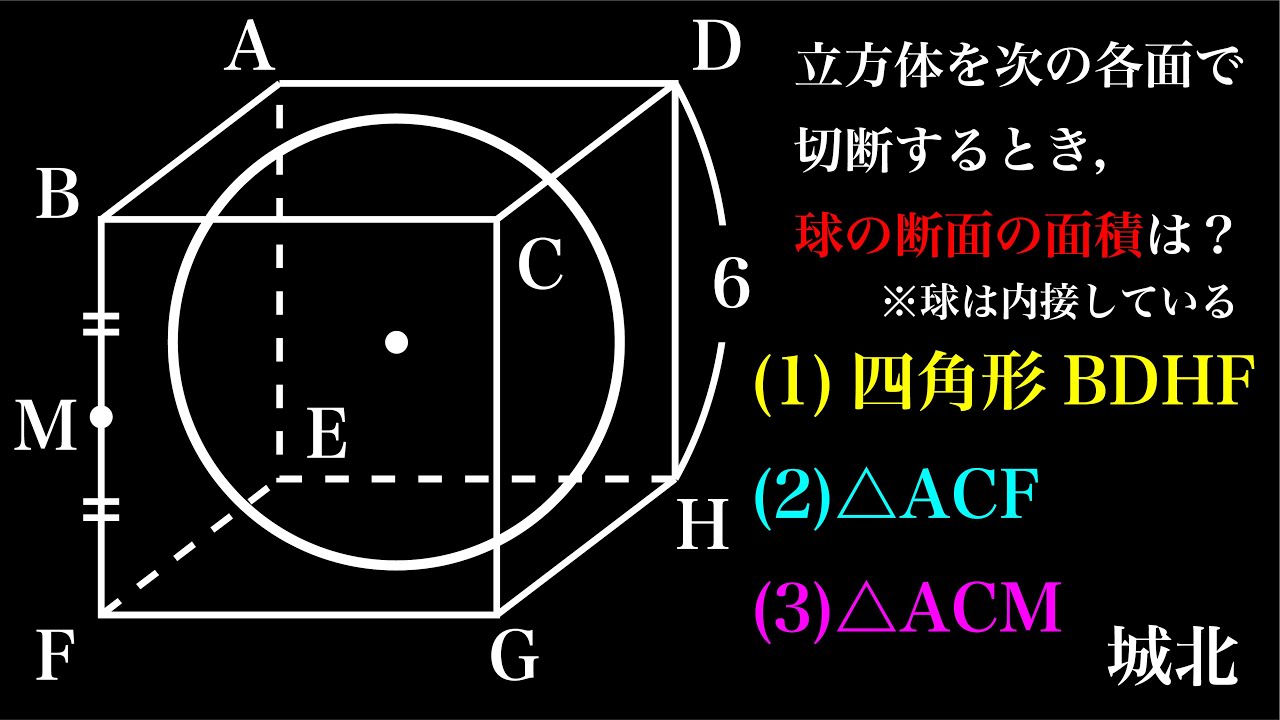
問題文全文(内容文):
立方体を次の各面で切断したときの球の断面積=?
(1)四角形BDHF
(2)△ACF
(3)△ACH
*図は動画内参照
城北高等学校
この動画を見る
立方体を次の各面で切断したときの球の断面積=?
(1)四角形BDHF
(2)△ACF
(3)△ACH
*図は動画内参照
城北高等学校
