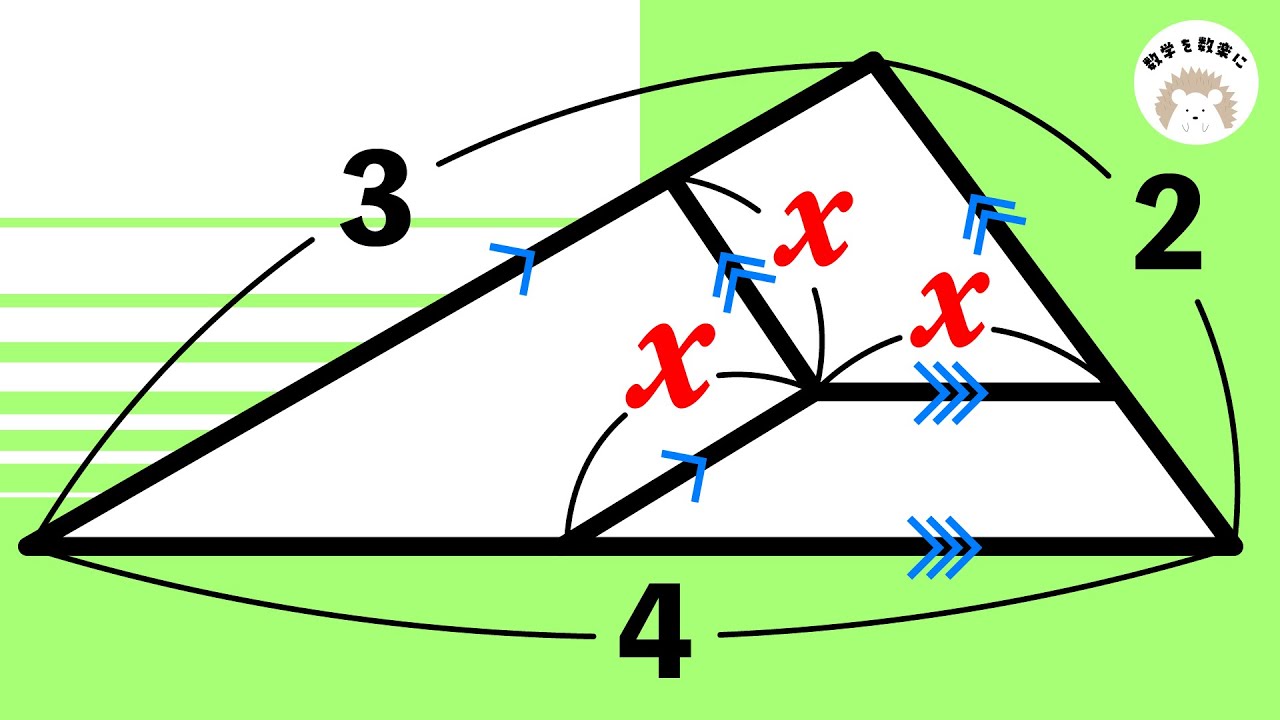
図形の性質
図形の性質
 図形の性質
図形の性質
福田の数学〜九州大学2023年文系第2問〜2直線のなす角と外接円の半径

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#内心・外心・重心とチェバ・メネラウス#周角と円に内接する四角形・円と接線・接弦定理#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ xy平面上の曲線C:$y$=$x^3$-$x$ を考える。変数$t$>0に対して、曲線C上の点A($t$, $t^3$-$t$)における接線を$l$とする。直線$l$と直線$y$=-$x$の交点をB、三角形OABの外接円の中心をPとする。以下の問いに答えよ。
(1)点Bの座標を$t$を用いて表せ。
(2)θ=$\angle$OBAとする。$\sin^2\theta$を$t$を用いて表せ。
(3)$f(t)$=$\frac{OP}{OA}$とする。$t$>0のとき、$f(t)$を最小にする$t$の値と$f(t)$の最小値を求めよ。
2023九州大学文系過去問
この動画を見る
$\Large\boxed{2}$ xy平面上の曲線C:$y$=$x^3$-$x$ を考える。変数$t$>0に対して、曲線C上の点A($t$, $t^3$-$t$)における接線を$l$とする。直線$l$と直線$y$=-$x$の交点をB、三角形OABの外接円の中心をPとする。以下の問いに答えよ。
(1)点Bの座標を$t$を用いて表せ。
(2)θ=$\angle$OBAとする。$\sin^2\theta$を$t$を用いて表せ。
(3)$f(t)$=$\frac{OP}{OA}$とする。$t$>0のとき、$f(t)$を最小にする$t$の値と$f(t)$の最小値を求めよ。
2023九州大学文系過去問
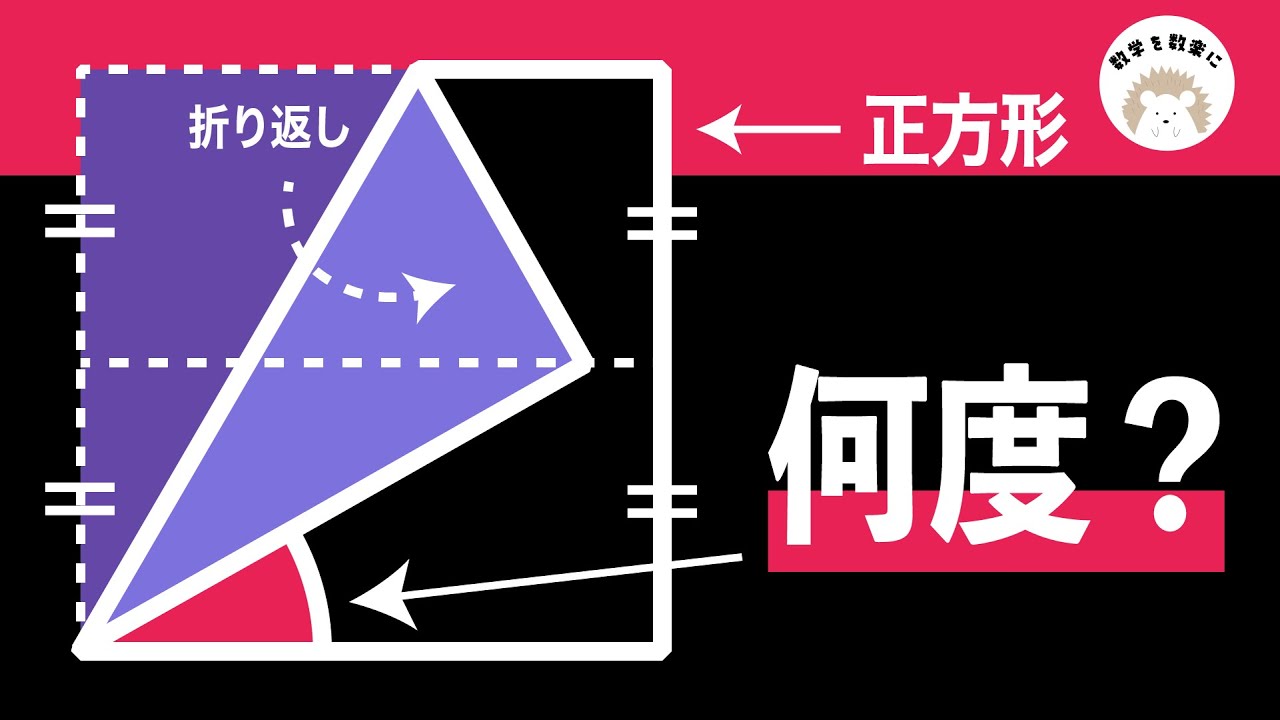
気付けば一瞬!! 正方形の折り返し 角度
見えないものを見ようとして 福岡大附属大濠
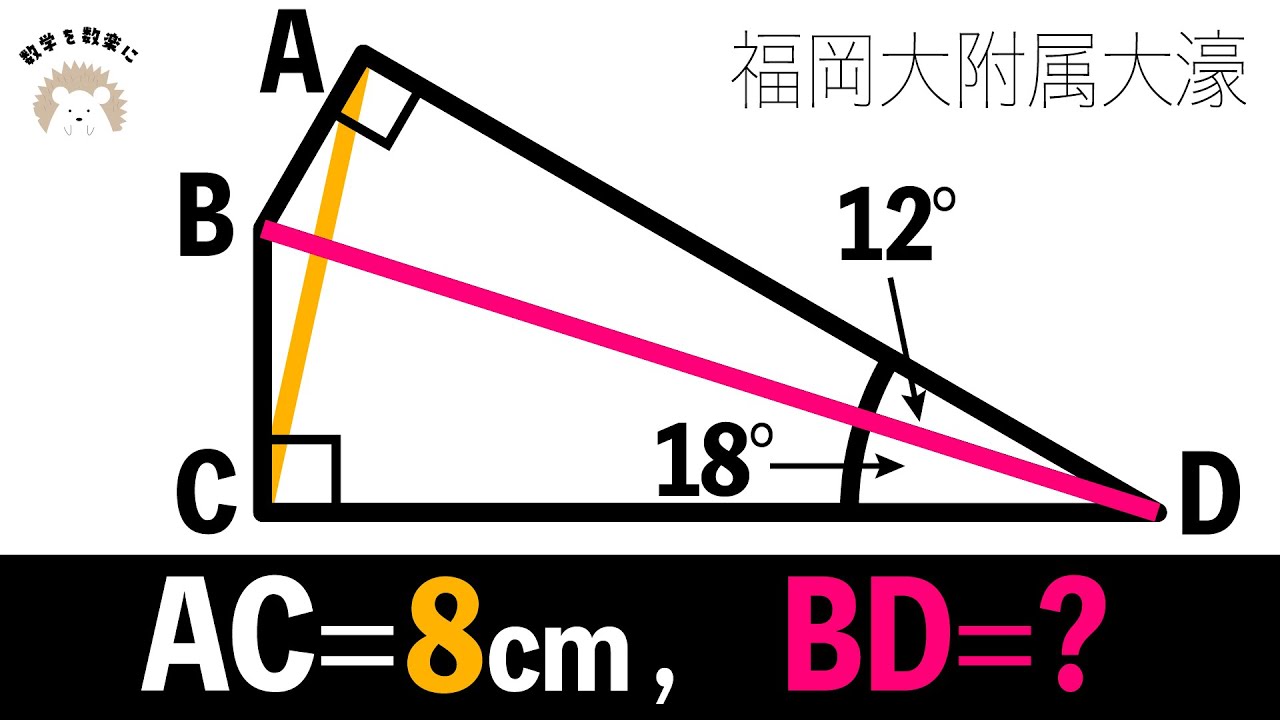
単元:
#数A#大学入試過去問(数学)#図形の性質#三角形の辺の比(内分・外分・二等分線)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
AC=8cm, BD=?
*図は動画内参照
福岡大学附属大濠高等学校
この動画を見る
AC=8cm, BD=?
*図は動画内参照
福岡大学附属大濠高等学校
福田の数学〜名古屋大学2023年文系第2問〜空間図形と体積の最小
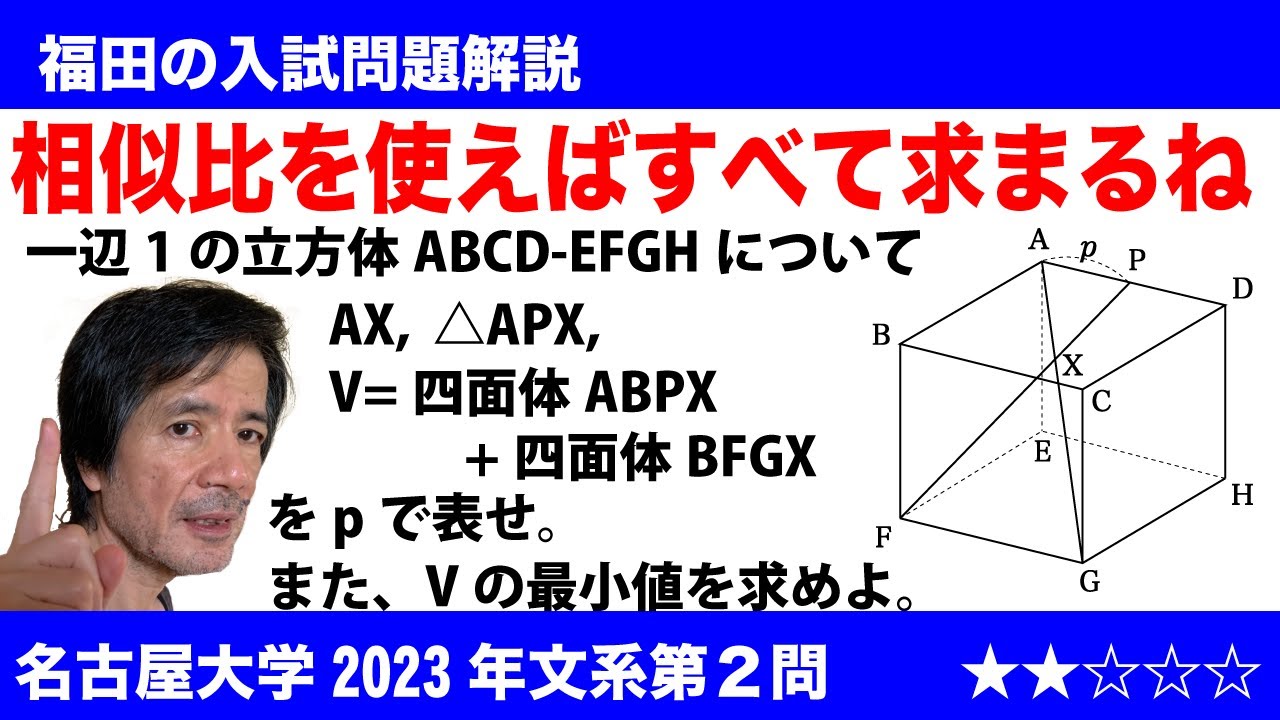
単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#式と証明#学校別大学入試過去問解説(数学)#空間における垂直と平行と多面体(オイラーの法則)#数学(高校生)#名古屋大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 図のような1辺の長さが1の立方体ABCD-EFGHにおいて、辺AD上に点Pをとり、線分APの長さをpとする。このとき、線分AGと線分FPは四角形ADGF上で交わる。その交点をXとする。(※図は動画参照)
(1)線分AXの長さをpを用いて表せ。
(2)三角形APXの面積をpを用いて表せ。
(3)四面体ABPXと四面体EFGXの体積の和をVとする。
Vをpを用いて表せ。
(4)点Pを辺AD上で動かすとき、Vの最小値を求めよ。
2023名古屋大学文系過去問
この動画を見る
$\Large\boxed{2}$ 図のような1辺の長さが1の立方体ABCD-EFGHにおいて、辺AD上に点Pをとり、線分APの長さをpとする。このとき、線分AGと線分FPは四角形ADGF上で交わる。その交点をXとする。(※図は動画参照)
(1)線分AXの長さをpを用いて表せ。
(2)三角形APXの面積をpを用いて表せ。
(3)四面体ABPXと四面体EFGXの体積の和をVとする。
Vをpを用いて表せ。
(4)点Pを辺AD上で動かすとき、Vの最小値を求めよ。
2023名古屋大学文系過去問
葉っぱの面積
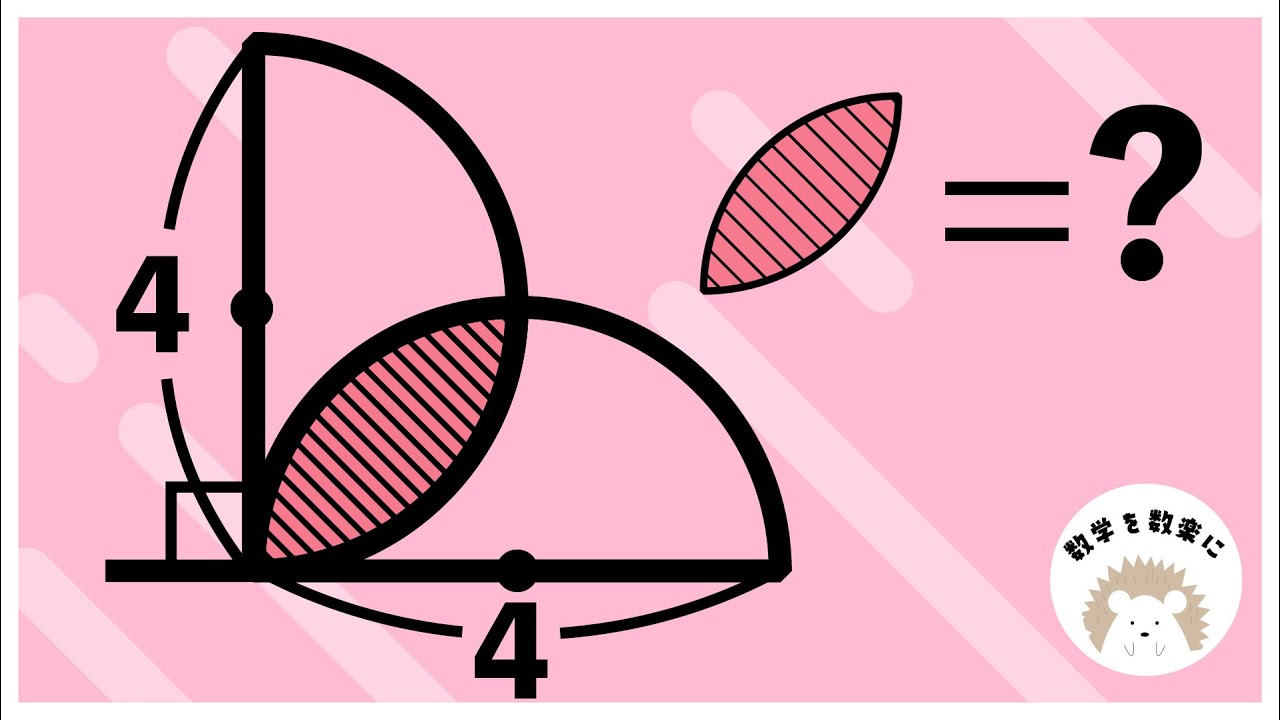
気付けば一瞬!!小学生も解ける!2つの正方形 たくさんの別解はコメント欄に!
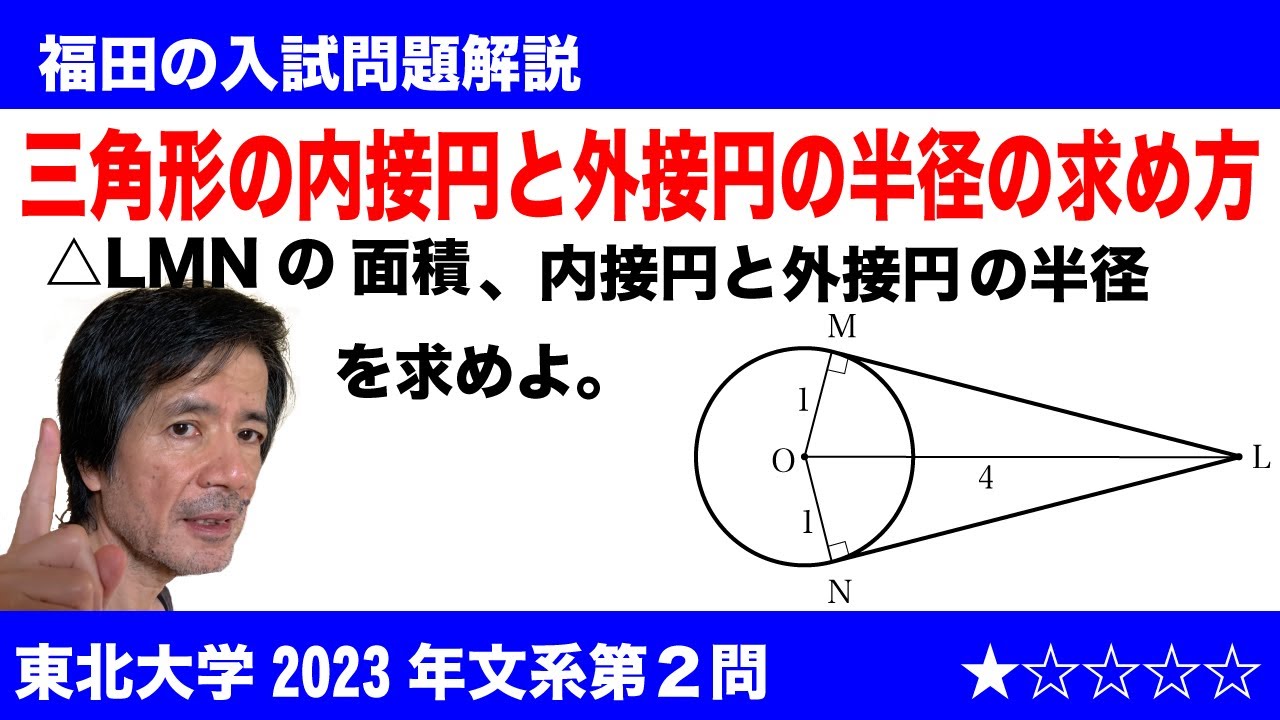
福田の数学〜東北大学2023年文系第1問〜三角形の面積と内接円と外接円の半径
単元:
#数Ⅰ#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#三角形の辺の比(内分・外分・二等分線)#周角と円に内接する四角形・円と接線・接弦定理#三角関数#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 平面上の半径1の円Cの中心Oから距離4だけ離れた点Lをとる。点Lを通る円Cの2本の接線と円Cの接点をそれぞれM、Nとする。以下の問いに答えよ。
(1)三角形LMNの面積を求めよ。
(2)三角形LMNの内接円の半径をrと、三角形LMNの外接円の半径Rをそれぞれ求めよ。
2023東北大学文系過去問
この動画を見る
$\Large\boxed{2}$ 平面上の半径1の円Cの中心Oから距離4だけ離れた点Lをとる。点Lを通る円Cの2本の接線と円Cの接点をそれぞれM、Nとする。以下の問いに答えよ。
(1)三角形LMNの面積を求めよ。
(2)三角形LMNの内接円の半径をrと、三角形LMNの外接円の半径Rをそれぞれ求めよ。
2023東北大学文系過去問
【数検準2級】高校数学:数学検定準2級2次:問3

単元:
#数A#数学検定・数学甲子園・数学オリンピック等#図形の性質#三角形の辺の比(内分・外分・二等分線)#数学検定#数学検定準2級#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
問3.次の問いに答えなさい。
(4) 右の図の四角形ABCDは平行四辺形です。また、点E、F、Gは辺ABを4等分する点で、点H、I、Jは辺CDを4等分する点です。
斜線部分の面積が10㎝²であるとき、四角形ABCDの面積を求めなさい。この問題は答えだけを書いてください。
この動画を見る
問3.次の問いに答えなさい。
(4) 右の図の四角形ABCDは平行四辺形です。また、点E、F、Gは辺ABを4等分する点で、点H、I、Jは辺CDを4等分する点です。
斜線部分の面積が10㎝²であるとき、四角形ABCDの面積を求めなさい。この問題は答えだけを書いてください。
図形の性質 作図問題【TAKAHASHI名人がていねいに解説】

単元:
#数A#図形の性質#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
線分ABが与えられたとき, 線分ABを斜辺とし, $\angle BAC=60°$ である直角三角形ABC を作図せよ。
右の図のような円があり,その周上に点Aがある。
Aを頂点の1つとし、他の5つの頂点がいずれもこの円周上にあるような正六角形を作図せよ。
右の図のように,直線と円Oおよびその中心が与えられている。
直線lに平行な円Oの接線を作図せよ。
この動画を見る
線分ABが与えられたとき, 線分ABを斜辺とし, $\angle BAC=60°$ である直角三角形ABC を作図せよ。
右の図のような円があり,その周上に点Aがある。
Aを頂点の1つとし、他の5つの頂点がいずれもこの円周上にあるような正六角形を作図せよ。
右の図のように,直線と円Oおよびその中心が与えられている。
直線lに平行な円Oの接線を作図せよ。
図形の性質 方べきの定理【TAKAHASHI名人がていねいに解説】
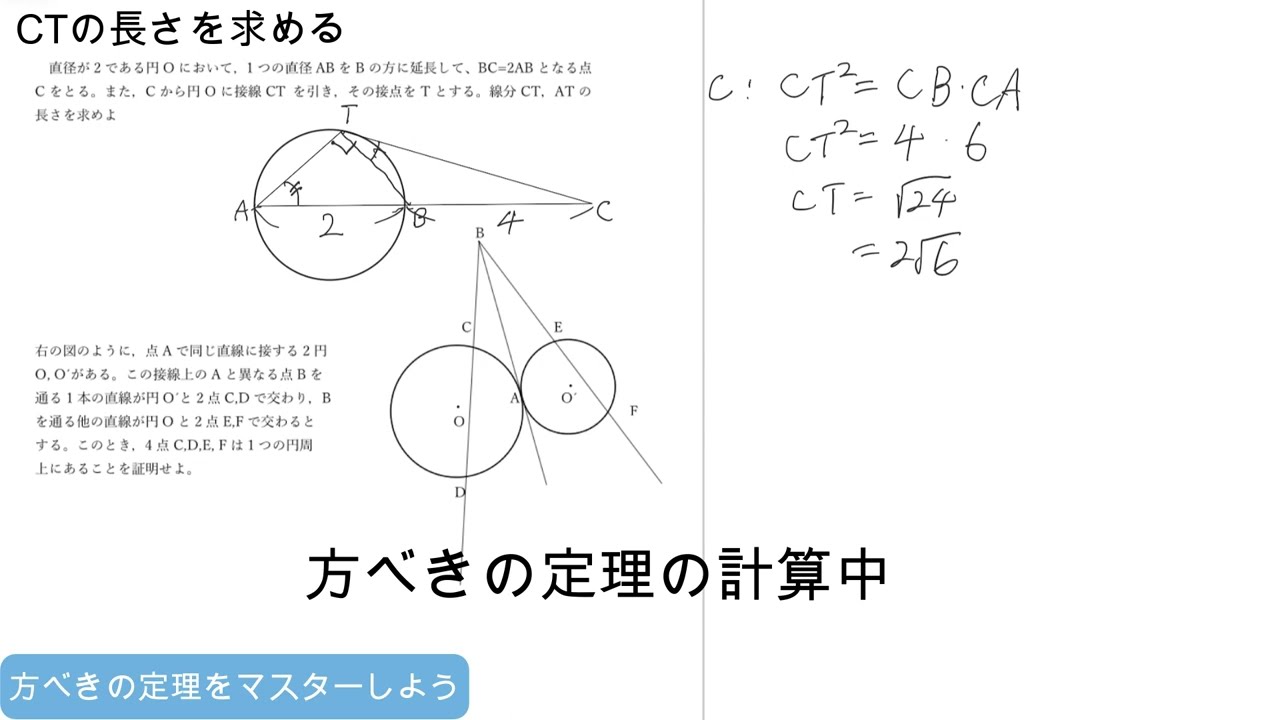
単元:
#数A#図形の性質#方べきの定理と2つの円の関係#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
■問題文
直径が2である円Oにおいて、1つの直径ABをBの方に延長して、BC=2ABとなる点Cをとる。また、Cから円Oに接線CTを引き、その接点をTとする。線分CT,ATの長さを求めよ。
右の図のように、点Aで同じ直線に接する2円O、O´がある。
この接線上のAと異なる点Bを通る1本の直線が円Oと2点C,Dで交わり, Bを通る他の直線が円 O′と2点E,Fで交わるとする。このとき, 4点 C, D, E, F は1つの円周上にあることを証明せよ。
この動画を見る
■問題文
直径が2である円Oにおいて、1つの直径ABをBの方に延長して、BC=2ABとなる点Cをとる。また、Cから円Oに接線CTを引き、その接点をTとする。線分CT,ATの長さを求めよ。
右の図のように、点Aで同じ直線に接する2円O、O´がある。
この接線上のAと異なる点Bを通る1本の直線が円Oと2点C,Dで交わり, Bを通る他の直線が円 O′と2点E,Fで交わるとする。このとき, 4点 C, D, E, F は1つの円周上にあることを証明せよ。
15度75度90度の直角三角形の比は受験生は覚えた方が良い。また、導けますか?

福田の数学〜慶應義塾大学2023年医学部第4問PART2〜円に内接する円の性質
単元:
#数A#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
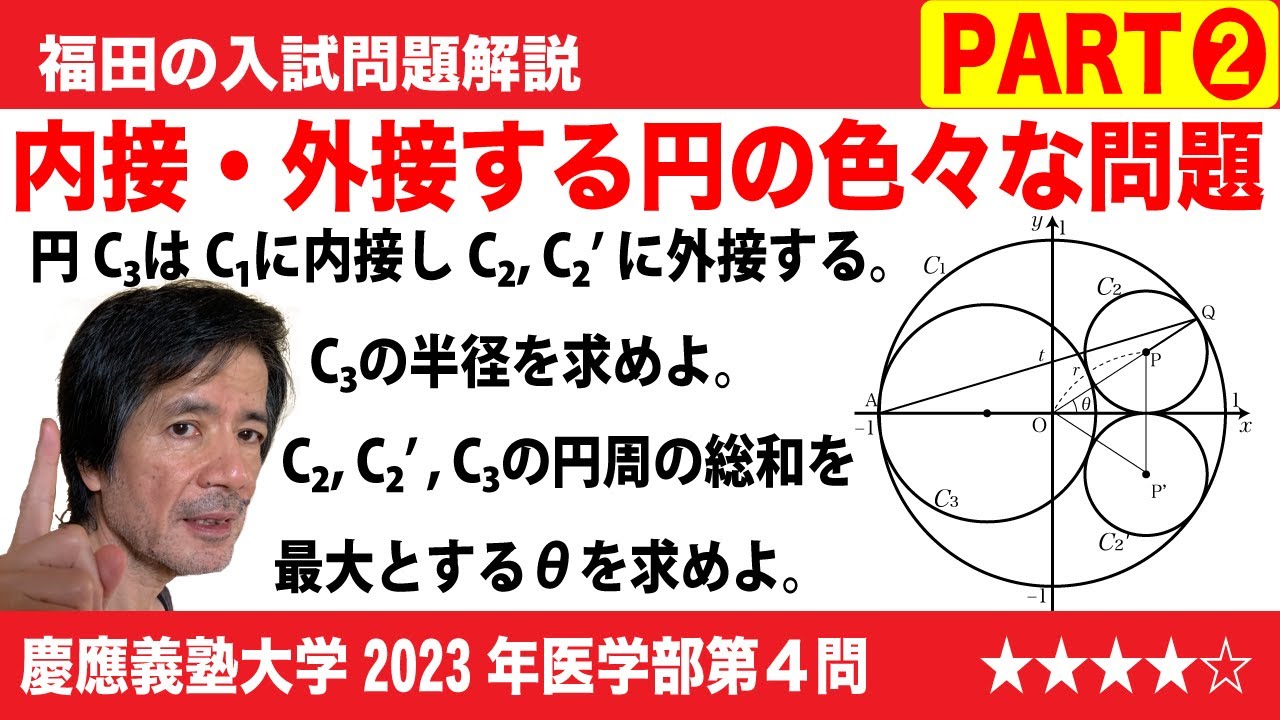
$\Large\boxed{4}$ 座標平面において原点Oを中心とする半径1の円を$C_1$とし、$C_1$の内部にある第1象限の点Pの極座標を(r, θ)とする。さらに点Pを中心とする円$C_2$が$C_1$上の点Qにおいて$C_1$に内接し、x軸上の点Rにおいてx軸に接しているとする。
また、極座標が(1, π)である$C_1$上の点をAとし、直線AQのy切片をtとする。
(1)rをθの式で表すとr=$\boxed{\ \ あ\ \ }$となり、tの式で表すとr=$\boxed{\ \ い\ \ }$となる。
(2)円$C_2$と同じ半径をもち、x軸に関して円$C_2$と対称な位置にある円$C'_2$の中心P'とする。三角形POP'の面積はθ=$\boxed{\ \ う\ \ }$のとき最大値$\boxed{\ \ え\ \ }$をとる。θ=$\boxed{\ \ う\ \ }$は条件t=$\boxed{\ \ お\ \ }$と同値である。
(3)円$C_1$に内接し、円$C_2$と$C'_2$の両方に外接する円のうち大きい方を$C_3$とする。円$C_3$の半径bをtの式で表すとb=$\boxed{\ \ か\ \ }$となる。
(4)3つの円$C_2$, $C'_2$, $C_3$の周の長さの和はθ=$\boxed{\ \ き\ \ }$の最大値$\boxed{\ \ く\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{4}$ 座標平面において原点Oを中心とする半径1の円を$C_1$とし、$C_1$の内部にある第1象限の点Pの極座標を(r, θ)とする。さらに点Pを中心とする円$C_2$が$C_1$上の点Qにおいて$C_1$に内接し、x軸上の点Rにおいてx軸に接しているとする。
また、極座標が(1, π)である$C_1$上の点をAとし、直線AQのy切片をtとする。
(1)rをθの式で表すとr=$\boxed{\ \ あ\ \ }$となり、tの式で表すとr=$\boxed{\ \ い\ \ }$となる。
(2)円$C_2$と同じ半径をもち、x軸に関して円$C_2$と対称な位置にある円$C'_2$の中心P'とする。三角形POP'の面積はθ=$\boxed{\ \ う\ \ }$のとき最大値$\boxed{\ \ え\ \ }$をとる。θ=$\boxed{\ \ う\ \ }$は条件t=$\boxed{\ \ お\ \ }$と同値である。
(3)円$C_1$に内接し、円$C_2$と$C'_2$の両方に外接する円のうち大きい方を$C_3$とする。円$C_3$の半径bをtの式で表すとb=$\boxed{\ \ か\ \ }$となる。
(4)3つの円$C_2$, $C'_2$, $C_3$の周の長さの和はθ=$\boxed{\ \ き\ \ }$の最大値$\boxed{\ \ く\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
福田の数学〜慶應義塾大学2023年医学部第4問PART1〜円に内接する円の性質
単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#複素数平面#周角と円に内接する四角形・円と接線・接弦定理#図形と方程式#円と方程式#微分とその応用#複素数平面#図形への応用#微分法#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
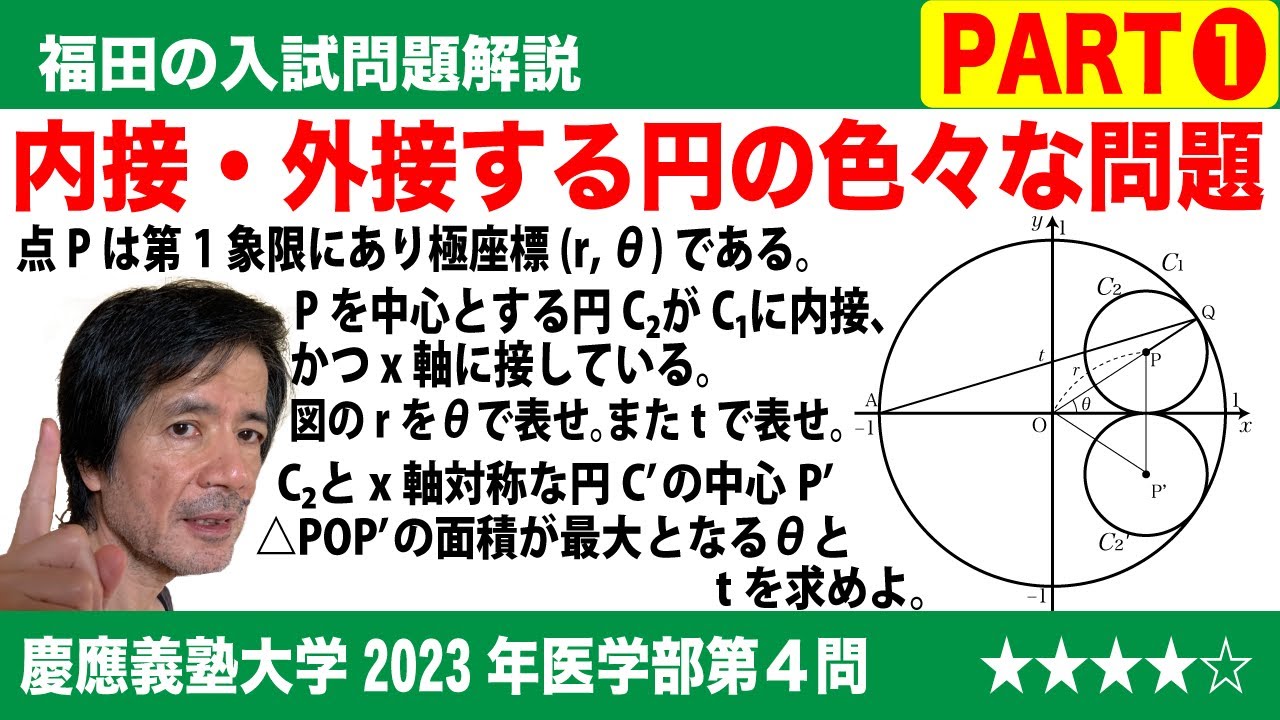
$\Large\boxed{4}$ 座標平面において原点Oを中心とする半径1の円を$C_1$とし、$C_1$の内部にある第1象限の点Pの極座標を(r, θ)とする。さらに点Pを中心とする円$C_2$が$C_1$上の点Qにおいて$C_1$に内接し、x軸上の点Rにおいてx軸に接しているとする。
また、極座標が(1, π)である$C_1$上の点をAとし、直線AQのy切片をtとする。
(1)rをθの式で表すとr=$\boxed{\ \ あ\ \ }$となり、tの式で表すとr=$\boxed{\ \ い\ \ }$となる。
(2)円$C_2$と同じ半径をもち、x軸に関して円$C_2$と対称な位置にある円$C'_2$の中心P'とする。三角形POP'の面積はθ=$\boxed{\ \ う\ \ }$のとき最大値$\boxed{\ \ え\ \ }$をとる。θ=$\boxed{\ \ う\ \ }$は条件t=$\boxed{\ \ お\ \ }$と同値である。
(3)円$C_1$に内接し、円$C_2$と$C'_2$の両方に外接する円のうち大きい方を$C_3$とする。円$C_3$の半径bをtの式で表すとb=$\boxed{\ \ か\ \ }$となる。
(4)3つの円$C_2$, $C'_2$, $C_3$の周の長さの和はθ=$\boxed{\ \ き\ \ }$の最大値$\boxed{\ \ く\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{4}$ 座標平面において原点Oを中心とする半径1の円を$C_1$とし、$C_1$の内部にある第1象限の点Pの極座標を(r, θ)とする。さらに点Pを中心とする円$C_2$が$C_1$上の点Qにおいて$C_1$に内接し、x軸上の点Rにおいてx軸に接しているとする。
また、極座標が(1, π)である$C_1$上の点をAとし、直線AQのy切片をtとする。
(1)rをθの式で表すとr=$\boxed{\ \ あ\ \ }$となり、tの式で表すとr=$\boxed{\ \ い\ \ }$となる。
(2)円$C_2$と同じ半径をもち、x軸に関して円$C_2$と対称な位置にある円$C'_2$の中心P'とする。三角形POP'の面積はθ=$\boxed{\ \ う\ \ }$のとき最大値$\boxed{\ \ え\ \ }$をとる。θ=$\boxed{\ \ う\ \ }$は条件t=$\boxed{\ \ お\ \ }$と同値である。
(3)円$C_1$に内接し、円$C_2$と$C'_2$の両方に外接する円のうち大きい方を$C_3$とする。円$C_3$の半径bをtの式で表すとb=$\boxed{\ \ か\ \ }$となる。
(4)3つの円$C_2$, $C'_2$, $C_3$の周の長さの和はθ=$\boxed{\ \ き\ \ }$の最大値$\boxed{\ \ く\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
視聴者さんからの出題

単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\stackrel{\huge\frown}{AP}$+$\stackrel{\huge\frown}{BQ}$ =?
*図は動画内参照
この動画を見る
$\stackrel{\huge\frown}{AP}$+$\stackrel{\huge\frown}{BQ}$ =?
*図は動画内参照
図形の性質 図形の性質の基本②【中学受験のドラえもんがていねいに解説】
単元:
#数A#図形の性質#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
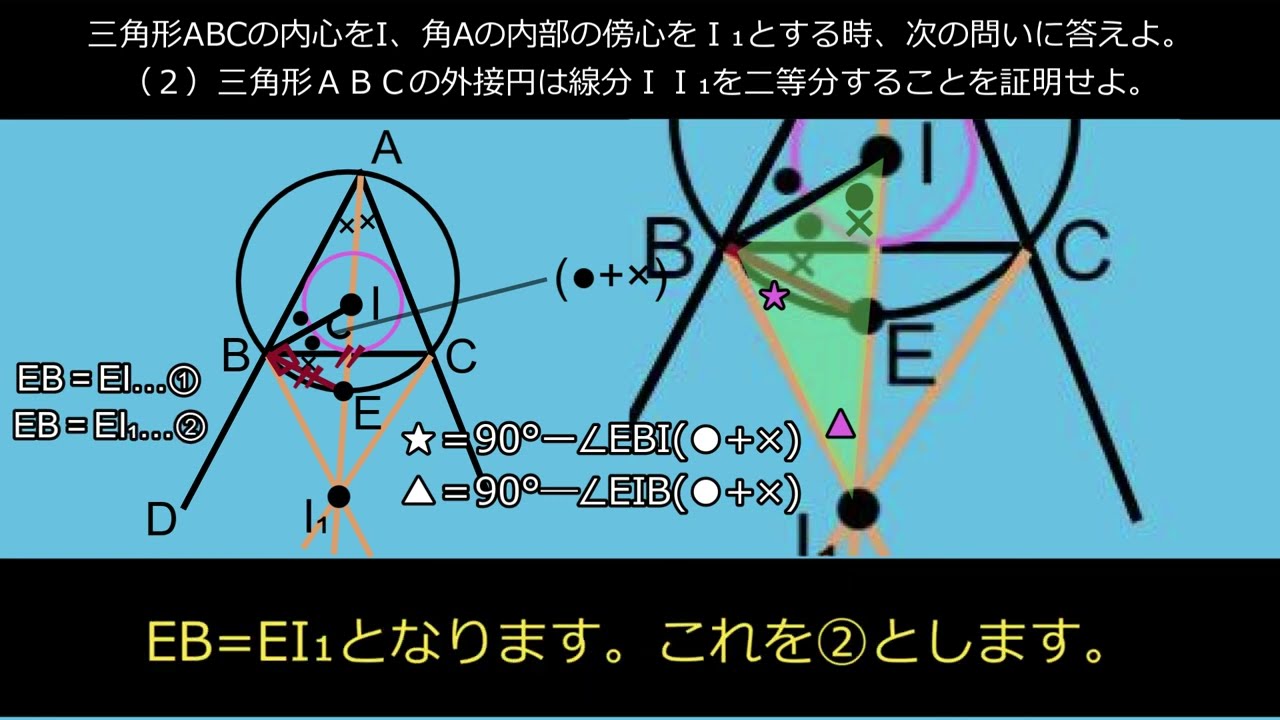
三角形ABCの内心をIとし、3辺BC、CA、ABに関してIと対称な点をそれぞれP,Q,Rとする。Iは三角形PQRについてどのような点か?
三角形ABCの内心をI、角Aの内部の傍心をI₁とする時、次の問いに答えよ。
(1)角IBI₁の大きさを求めよ。
(2)三角形ABCの外接円は線分II₁を二等分することを証明せよ。
AB=ACである二等辺三角形ABCの頂点Aから辺BCに下ろした垂線をADとする。
角Bの内部の傍接円IBの半径はADに等しいことを証明せよ。
この動画を見る
三角形ABCの内心をIとし、3辺BC、CA、ABに関してIと対称な点をそれぞれP,Q,Rとする。Iは三角形PQRについてどのような点か?
三角形ABCの内心をI、角Aの内部の傍心をI₁とする時、次の問いに答えよ。
(1)角IBI₁の大きさを求めよ。
(2)三角形ABCの外接円は線分II₁を二等分することを証明せよ。
AB=ACである二等辺三角形ABCの頂点Aから辺BCに下ろした垂線をADとする。
角Bの内部の傍接円IBの半径はADに等しいことを証明せよ。
福田の数学〜慶應義塾大学2023年医学部第3問〜接線が作る三角形

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#三角形の辺の比(内分・外分・二等分線)#図形と方程式#微分法と積分法#軌跡と領域#接線と増減表・最大値・最小値#関数と極限#微分とその応用#積分とその応用#数列の極限#微分法#定積分#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 座標平面上の曲線y=$\frac{1}{x^2}$ (x $\ne$ 0)をCとする。$a_1$を正の実数とし、点$A_1$$\left(a_1, \frac{1}{a_1^2}\right)$におけるCの接線を$l_1$とする。$l_1$とCの交点で$A_1$と異なるものを$A_2$$\left(a_2, \frac{1}{a_2^2}\right)$とする。次に点$A_2$におけるCの接線を$l_2$とCの交点で$A_2$と異なるものを$A_3$$\left(a_3, \frac{1}{a_3^2}\right)$とする。以下、同様にしてn=3,4,5,...に対して、$A_n$$\left(a_n, \frac{1}{a_n^2}\right)$におけるCの接線を$l_n$とし、$l_n$とCの交点で$A_n$と異なるものを$A_{n+1}$$\left(a_{n+1}, \frac{1}{a_{n+1}^2}\right)$とする。
(1)$\frac{a_2}{a_1}$=$\boxed{\ \ あ\ \ }$であり、$\frac{a_3}{a_1}$=$\boxed{\ \ い\ \ }$である。
(2)$a_n$を$a_1$で表すと$a_n$=$\boxed{\ \ う\ \ }$である。無限級数$\displaystyle\sum_{n=1}^{\infty}a_n$の和をTを$a_1$を用いて表すとT=$\boxed{\ \ え\ \ }$である。
(3)$a_1$を正の実数すべてにわたって動かすとき、三角形$A_1A_2A_3$の重心が描く軌跡の方程式をy=f(x)の形で求めるとf(x)=$\boxed{\ \ お\ \ }$となる。
(4)三角形$A_1A_2A_3$が鋭角三角形になるための条件は$\boxed{\ \ か\ \ }$<$a_1$<$\boxed{\ \ き\ \ }$である。
(5)x軸上に2点$A'_1$($a_1$, 0), $A'_2$($a_2$, 0)をとり、台形$A_1A_2A'_2A'_1$の面積を$S_1$とする。また、点$A_1$から点$A_3$にいたる曲線Cの部分、および線分$A_3A_2$と$A_2A_1$で囲まれた図形の面積を$S_2$とする。このとき、$S_1$:$S_2$=$\boxed{\ \ く\ \ }$:$\boxed{\ \ け\ \ }$である。ただし、$\boxed{\ \ く\ \ }$と$\boxed{\ \ け\ \ }$は互いに素な自然数である。
2023慶應義塾大学医学部過去問
この動画を見る
$\Large\boxed{3}$ 座標平面上の曲線y=$\frac{1}{x^2}$ (x $\ne$ 0)をCとする。$a_1$を正の実数とし、点$A_1$$\left(a_1, \frac{1}{a_1^2}\right)$におけるCの接線を$l_1$とする。$l_1$とCの交点で$A_1$と異なるものを$A_2$$\left(a_2, \frac{1}{a_2^2}\right)$とする。次に点$A_2$におけるCの接線を$l_2$とCの交点で$A_2$と異なるものを$A_3$$\left(a_3, \frac{1}{a_3^2}\right)$とする。以下、同様にしてn=3,4,5,...に対して、$A_n$$\left(a_n, \frac{1}{a_n^2}\right)$におけるCの接線を$l_n$とし、$l_n$とCの交点で$A_n$と異なるものを$A_{n+1}$$\left(a_{n+1}, \frac{1}{a_{n+1}^2}\right)$とする。
(1)$\frac{a_2}{a_1}$=$\boxed{\ \ あ\ \ }$であり、$\frac{a_3}{a_1}$=$\boxed{\ \ い\ \ }$である。
(2)$a_n$を$a_1$で表すと$a_n$=$\boxed{\ \ う\ \ }$である。無限級数$\displaystyle\sum_{n=1}^{\infty}a_n$の和をTを$a_1$を用いて表すとT=$\boxed{\ \ え\ \ }$である。
(3)$a_1$を正の実数すべてにわたって動かすとき、三角形$A_1A_2A_3$の重心が描く軌跡の方程式をy=f(x)の形で求めるとf(x)=$\boxed{\ \ お\ \ }$となる。
(4)三角形$A_1A_2A_3$が鋭角三角形になるための条件は$\boxed{\ \ か\ \ }$<$a_1$<$\boxed{\ \ き\ \ }$である。
(5)x軸上に2点$A'_1$($a_1$, 0), $A'_2$($a_2$, 0)をとり、台形$A_1A_2A'_2A'_1$の面積を$S_1$とする。また、点$A_1$から点$A_3$にいたる曲線Cの部分、および線分$A_3A_2$と$A_2A_1$で囲まれた図形の面積を$S_2$とする。このとき、$S_1$:$S_2$=$\boxed{\ \ く\ \ }$:$\boxed{\ \ け\ \ }$である。ただし、$\boxed{\ \ く\ \ }$と$\boxed{\ \ け\ \ }$は互いに素な自然数である。
2023慶應義塾大学医学部過去問
気付けば一瞬!! 気付けば爽快!! 中学数学

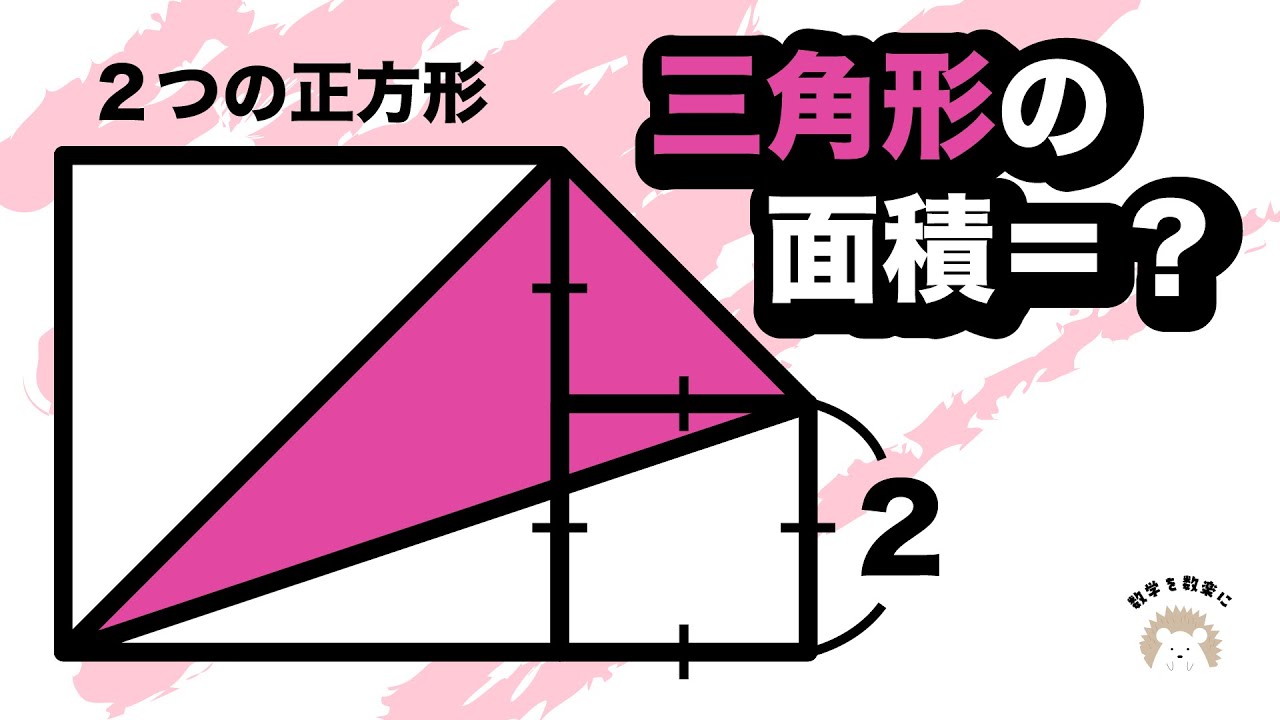
三角形を台形として考える 正方形と面積比
図形と計量 円に内接する四角形の面積【烈's study!がていねいに解説】
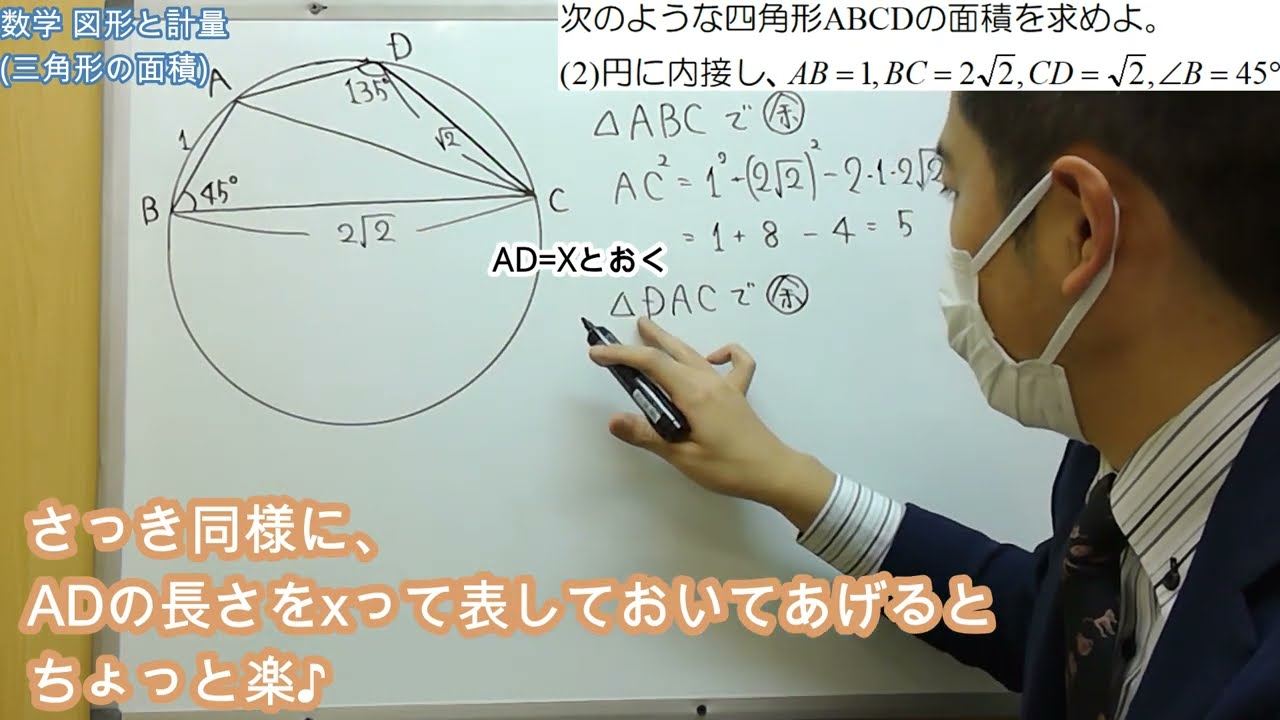
単元:
#数Ⅰ#数A#図形の性質#図形と計量#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のような四角形ABCDの面積を求めよ。
(1)円に内接し、$AB=4、BC=3、CD=1、\angle B=60°$
(2)円に内接し、$AB=1、BC=2\sqrt2、CD=\sqrt2、\angle B=45°$
この動画を見る
次のような四角形ABCDの面積を求めよ。
(1)円に内接し、$AB=4、BC=3、CD=1、\angle B=60°$
(2)円に内接し、$AB=1、BC=2\sqrt2、CD=\sqrt2、\angle B=45°$
図形と計量 四角形の面積【烈's study!がていねいに解説】

単元:
#数Ⅰ#数A#図形の性質#図形と計量#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のような四角形ABCDの面積を求めよ。
(1)$\angle A=135°,\angle C=45°,AB=1,BC=3,CD=\sqrt2,DA=\sqrt2$
(2)$\angle B=120°,AB=3,BC=5,CD=5,DA=4$
この動画を見る
次のような四角形ABCDの面積を求めよ。
(1)$\angle A=135°,\angle C=45°,AB=1,BC=3,CD=\sqrt2,DA=\sqrt2$
(2)$\angle B=120°,AB=3,BC=5,CD=5,DA=4$
【数A】【難問】正二十面体の体積を求めよ。

単元:
#数A#図形の性質#空間における垂直と平行と多面体(オイラーの法則)#数学(高校生)
教材:
#チャート式#青チャートⅠ・A#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
1辺の長さが1の正二十面体の体積を求めなさい。
この動画を見る
1辺の長さが1の正二十面体の体積を求めなさい。
気付けば一瞬!!!!2つのおうぎ形
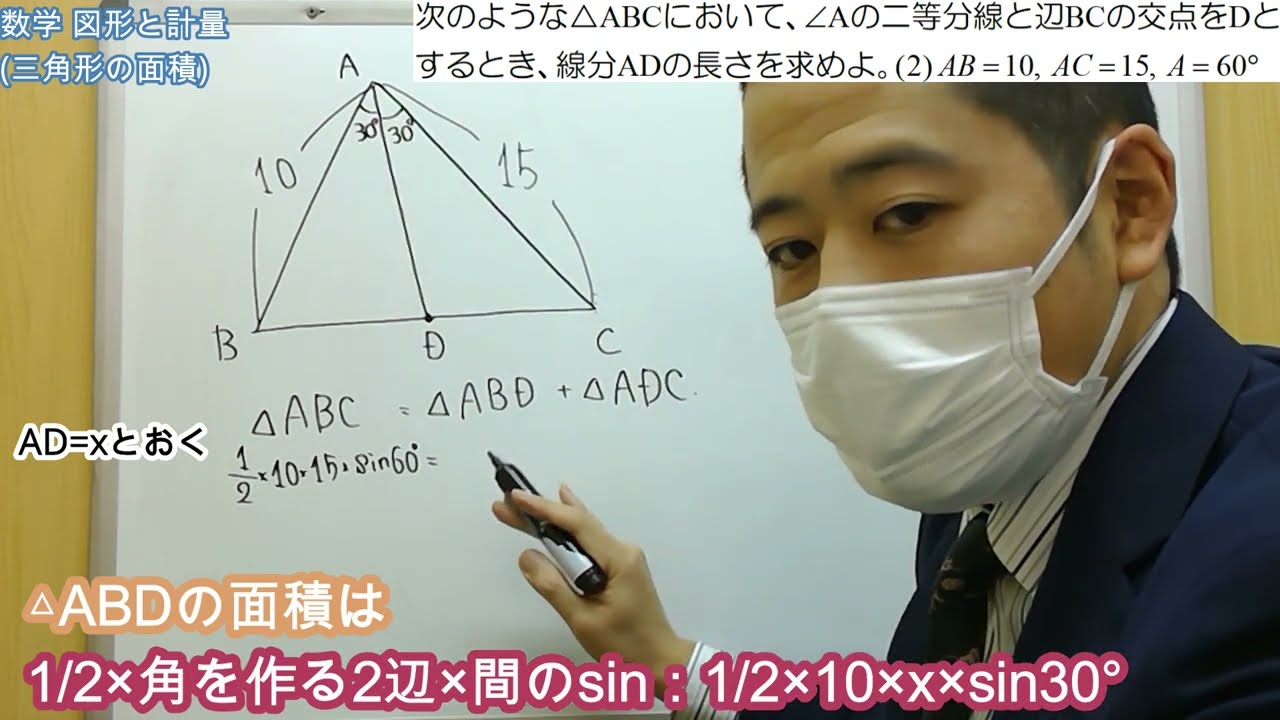
図形と計量 三角形の面積 二等分線の利用【烈's study!がていねいに解説】
単元:
#数Ⅰ#数A#図形の性質#図形と計量#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のような$△ABC$について、$\angle A$の二等分線と辺BCの交点をDとするとき、線分ADの長さを求めよ。
(1)$AB=4、AC=3、A=120°$
(2)$AB=10、AC=15、A=60°$
この動画を見る
次のような$△ABC$について、$\angle A$の二等分線と辺BCの交点をDとするとき、線分ADの長さを求めよ。
(1)$AB=4、AC=3、A=120°$
(2)$AB=10、AC=15、A=60°$
気付けば一瞬!? 等〇変形
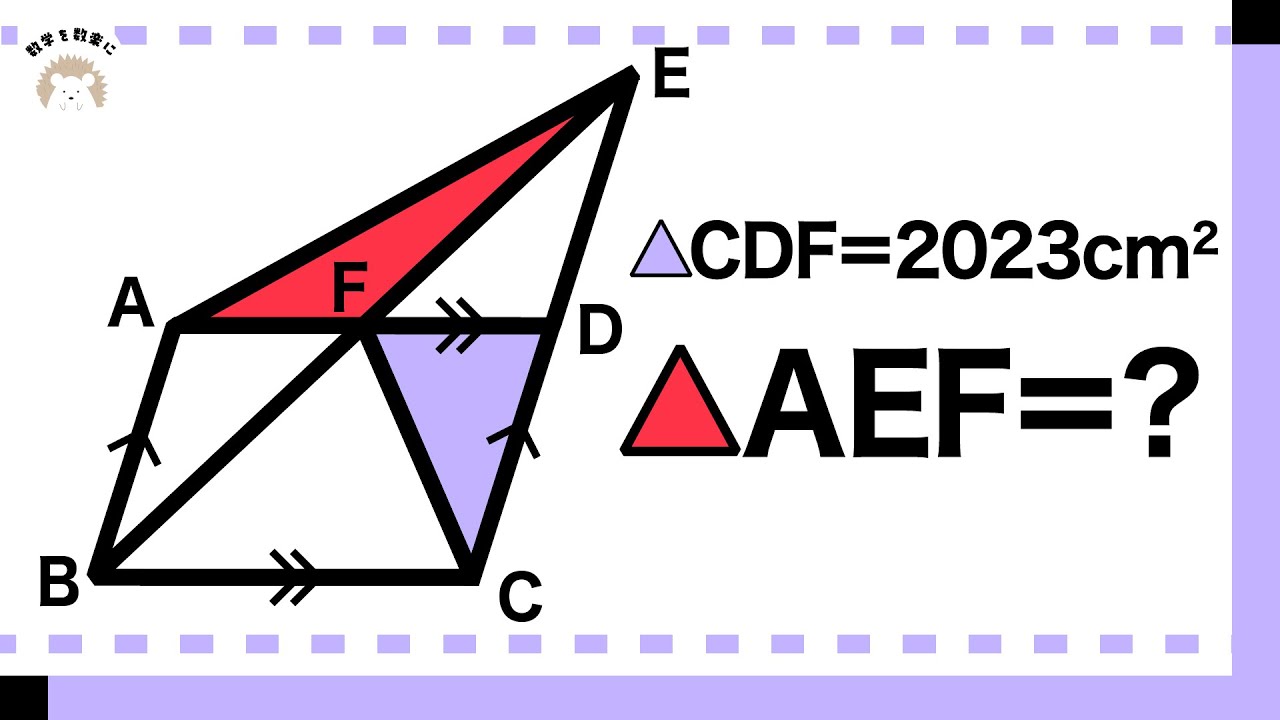
基礎ができるからこそ応用につながる 長方形は何こ?

もはやパズル!!三平方の定理禁止!!大阪教育大附属天王寺中
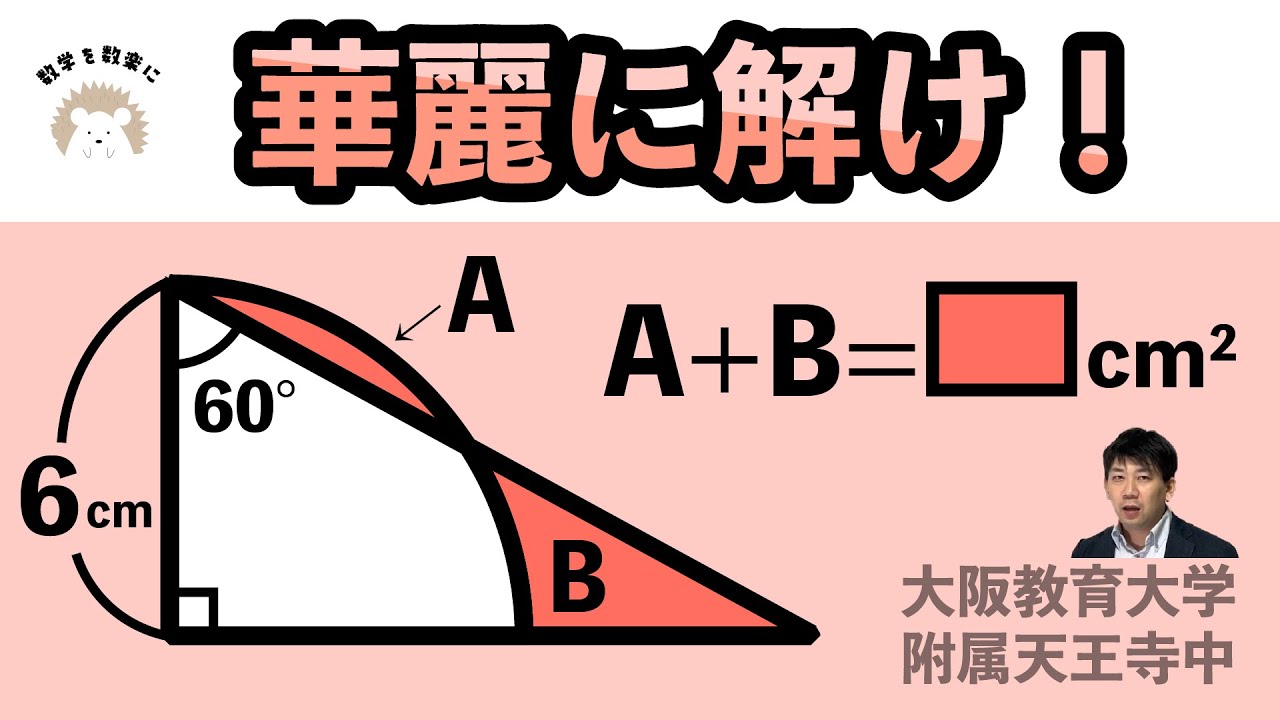
単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
A + B = ▢ ㎠
*図は動画内参照
大阪教育大学付属天王寺中学校
この動画を見る
A + B = ▢ ㎠
*図は動画内参照
大阪教育大学付属天王寺中学校
福田の数学〜慶應義塾大学2023年薬学部第1問(2)〜折れ線の最小と内接円の半径

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#図形と方程式#三角関数#点と直線#加法定理とその応用#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (2)aは正の定数とする。原点をOとするxy平面上に直線l:y=$\frac{2}{3}$xと2点A(0,a), B(17,20)がある。直線l上にとった動点Pと2点A,Bそれぞれを線分で結び、2つの線分の長さの和AP+BPが最小となったとき、$\angle APO$=45°であった。AP+BPが最小であるとき、直線BPを表す方程式はy=$\boxed{\ \ ウ\ \ }$であり、三角形ABPの内接円の半径は$\boxed{\ \ エ\ \ }$である。
2023慶應義塾大学薬学部過去問
この動画を見る
$\Large\boxed{1}$ (2)aは正の定数とする。原点をOとするxy平面上に直線l:y=$\frac{2}{3}$xと2点A(0,a), B(17,20)がある。直線l上にとった動点Pと2点A,Bそれぞれを線分で結び、2つの線分の長さの和AP+BPが最小となったとき、$\angle APO$=45°であった。AP+BPが最小であるとき、直線BPを表す方程式はy=$\boxed{\ \ ウ\ \ }$であり、三角形ABPの内接円の半径は$\boxed{\ \ エ\ \ }$である。
2023慶應義塾大学薬学部過去問
正方形と円
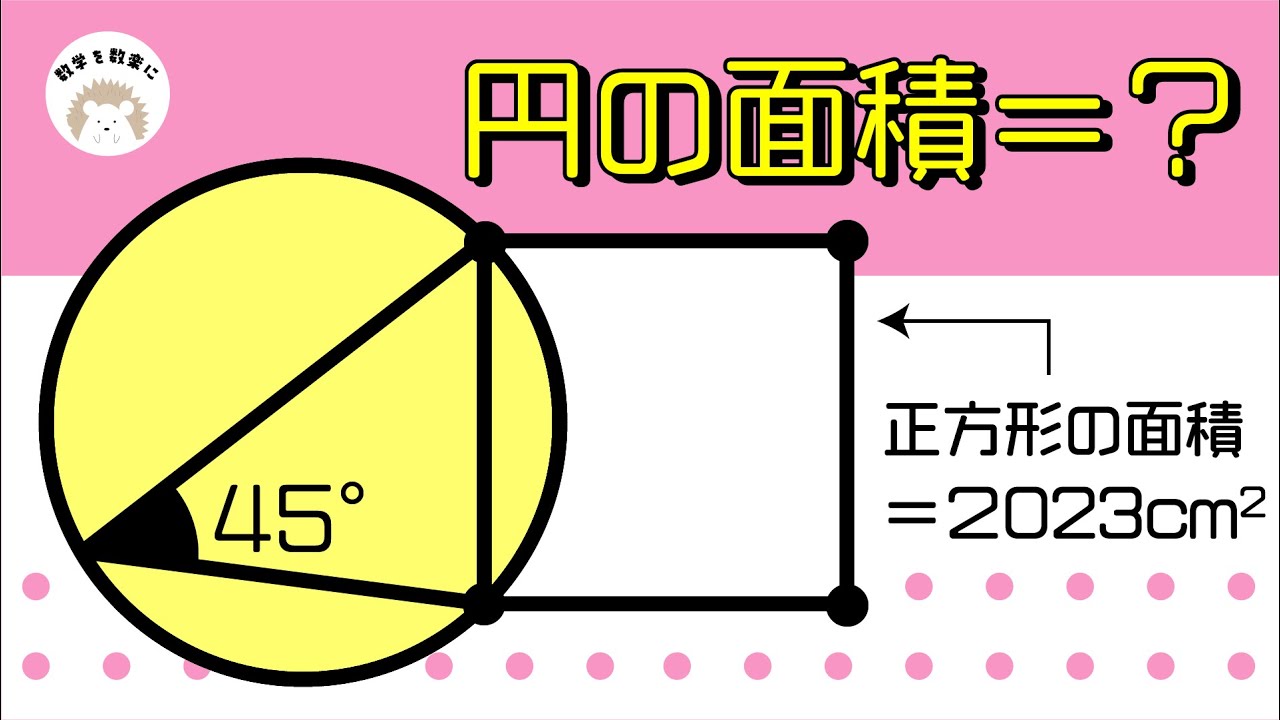
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
正方形の面積= 2023㎠
円の面積=?
*図は動画内参照
この動画を見る
正方形の面積= 2023㎠
円の面積=?
*図は動画内参照
気付けば、知っていれば一瞬!!
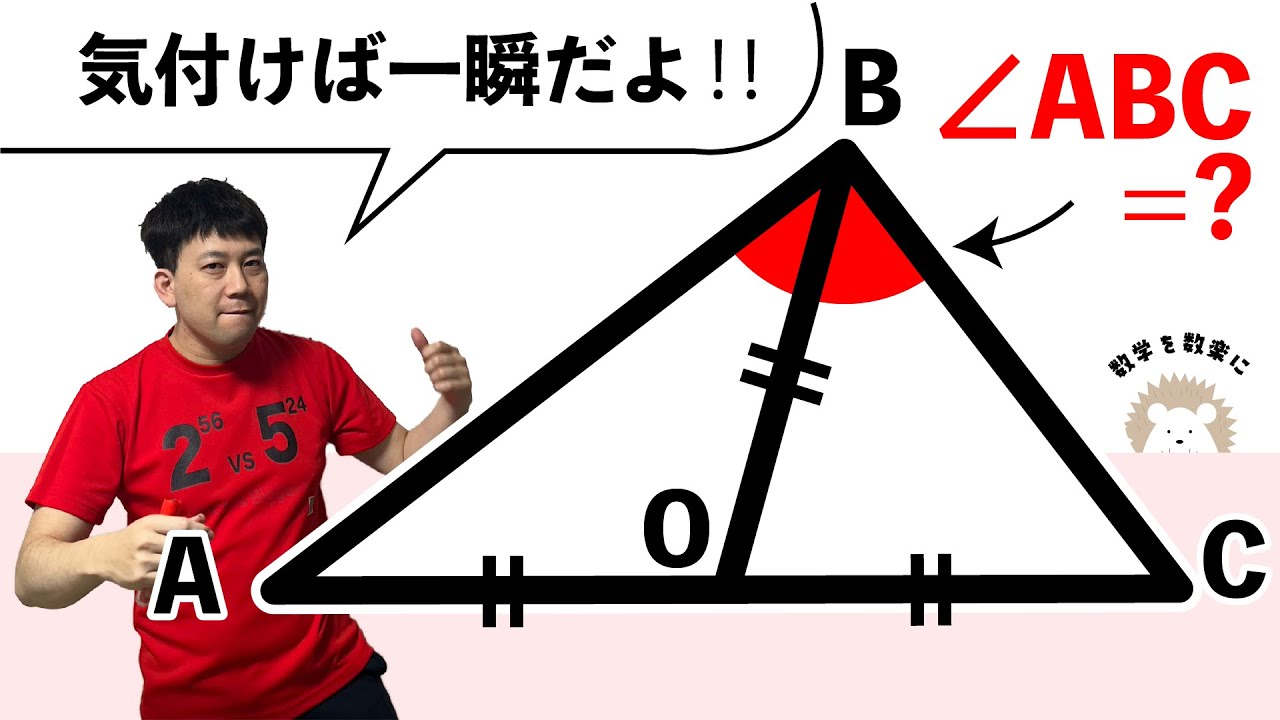
補助線引ける?