整数の性質
整数の性質
３通りの解法 首都大
単元：
#数A#数Ⅱ#整数の性質#約数・倍数・整数の割り算と余り・合同式#指数関数と対数関数#対数関数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\log_{10}x+\log_{10}y=\log_{10}(y+2x^2+1)$
整数＄(x,y)$を全て求めよ.
2008首都大過去問
この動画を見る
$\log_{10}x+\log_{10}y=\log_{10}(y+2x^2+1)$
整数＄(x,y)$を全て求めよ.
2008首都大過去問
14岡山県教員採用試験（数学：1-6 行列）
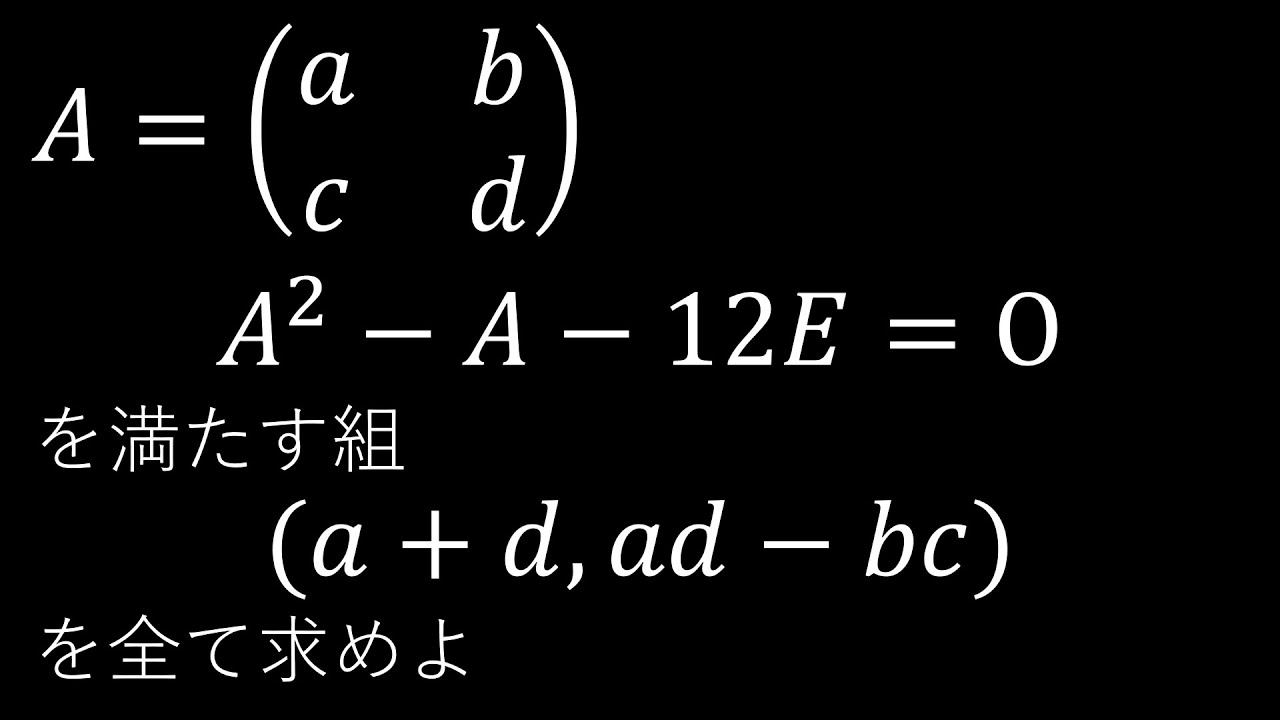
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{1}-(6)$
$\begin{pmatrix}
a & b \\
c & d
\end{pmatrix}$
$A^2-A-12E=\theta$を満たすとき,
$(a+d,ad-bc)$を全て求めよ.
この動画を見る
$\boxed{1}-(6)$
$\begin{pmatrix}
a & b \\
c & d
\end{pmatrix}$
$A^2-A-12E=\theta$を満たすとき,
$(a+d,ad-bc)$を全て求めよ.
13愛知県教員採用試験（数学：10番 行列）
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{10}$
$A=\begin{pmatrix}
2 & 3 \\
1 & 2
\end{pmatrix}$とする.
$A^3-4A^2+3A+E$を求めよ.
この動画を見る
$\boxed{10}$
$A=\begin{pmatrix}
2 & 3 \\
1 & 2
\end{pmatrix}$とする.
$A^3-4A^2+3A+E$を求めよ.
【高校数学】ユークリッドの互除法をどこよりも丁寧に教えます 5-7【数学A】
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
1⃣
667と299の最大公約数を求めよ
2⃣
31$x$+22$y$=1を満たす整数$x,y$の組を1つ求めよ
この動画を見る
1⃣
667と299の最大公約数を求めよ
2⃣
31$x$+22$y$=1を満たす整数$x,y$の組を1つ求めよ
兵庫医大 普通の基本問題 指数方程式
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$4^x-2^{x+2}+a^2-3a+4=0$が異なる2つの正の解をもつ$a$の範囲を求めよ.
2019兵庫医大過去問
この動画を見る
$4^x-2^{x+2}+a^2-3a+4=0$が異なる2つの正の解をもつ$a$の範囲を求めよ.
2019兵庫医大過去問
数学「大学入試良問集」【3−6不定方程式②】を宇宙一わかりやすく
単元：
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文)：
$3$以上$9999$以下の奇数$a$で、$a^2-a$が$10000$で割り切れるものをすべて求めよ。
この動画を見る
$3$以上$9999$以下の奇数$a$で、$a^2-a$が$10000$で割り切れるものをすべて求めよ。
数学「大学入試良問集」【3−5 ユークリッド互除法】を宇宙一わかりやすく
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文)：
（1）
自然数$a,b,c,d$に$\displaystyle \frac{b}{a}=\displaystyle \frac{c}{a}+d$の関係があるとき、$a$と$c$が互いに素であれば、$a$と$b$も互いに素であることを証明せよ。
（2）
任意の自然数$n$に対し、$28n+5$と$21n+4$は互いに素であることを証明せよ。
この動画を見る
（1）
自然数$a,b,c,d$に$\displaystyle \frac{b}{a}=\displaystyle \frac{c}{a}+d$の関係があるとき、$a$と$c$が互いに素であれば、$a$と$b$も互いに素であることを証明せよ。
（2）
任意の自然数$n$に対し、$28n+5$と$21n+4$は互いに素であることを証明せよ。
指数方程式を解け
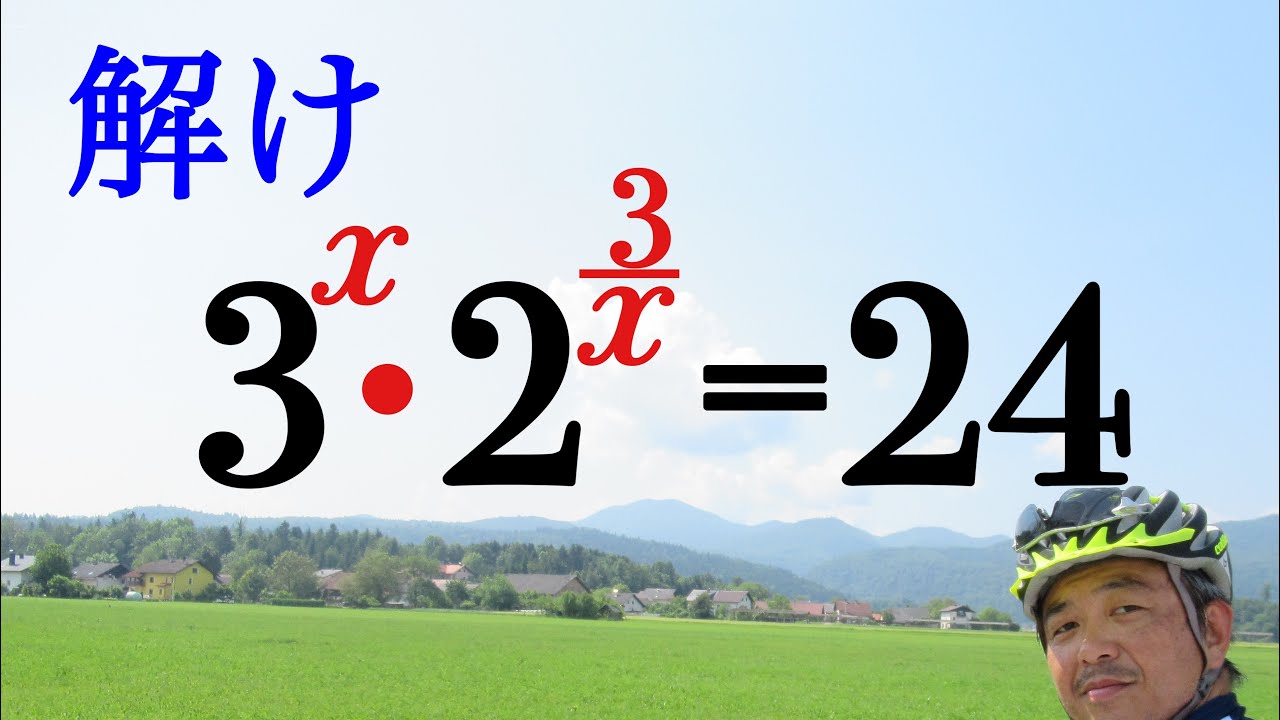
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
これを解け.
$3^x・2^{\frac{3}{x}}=24$
この動画を見る
これを解け.
$3^x・2^{\frac{3}{x}}=24$
数学「大学入試良問集」【3−4 整数 n進法】を宇宙一わかりやすく
単元：
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師：
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文)：
7進法で表すと3けたとなる正の整数がある。
これを11進法で表すと、やはり3けたで、数字の順序がもととちょうど反対となる。
このような整数を10進法で表せ。
この動画を見る
7進法で表すと3けたとなる正の整数がある。
これを11進法で表すと、やはり3けたで、数字の順序がもととちょうど反対となる。
このような整数を10進法で表せ。
数学「大学入試良問集」【3−3 整数 余りによる分類②】を宇宙一わかりやすく
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師：
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文)：
（1）
$p,2p+1,4p+1$がいずれも素数であるような$p$をすべて求めよ。
（2）
$q,2q+1,4q-1,6q-1,8q+1$がいずれも素数であるような$q$をすべて求めよ。
この動画を見る
（1）
$p,2p+1,4p+1$がいずれも素数であるような$p$をすべて求めよ。
（2）
$q,2q+1,4q-1,6q-1,8q+1$がいずれも素数であるような$q$をすべて求めよ。
整数問題 筑紫女学園（改）
単元：
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$n^3-4n=105$をみたす自然数n=?
筑紫女学園高等学校（改）
この動画を見る
$n^3-4n=105$をみたす自然数n=?
筑紫女学園高等学校（改）
数学「大学入試良問集」【3−2 整数 余りによる分類①】を宇宙一わかりやすく
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#関西大学
指導講師：
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文)：
$a,b,c$を正の整数とする。
（1）$a^2$を3で割った余りは0または1であることを示せ。
（2）$a^2+b^2=c^2$を満たすとき、$a,b,c$の積$abc$が3の倍数であることを示せ。
（3）$a^2+b^2=225$を満たす$a,b$の値を求めよ。
この動画を見る
$a,b,c$を正の整数とする。
（1）$a^2$を3で割った余りは0または1であることを示せ。
（2）$a^2+b^2=c^2$を満たすとき、$a,b,c$の積$abc$が3の倍数であることを示せ。
（3）$a^2+b^2=225$を満たす$a,b$の値を求めよ。
数学「大学入試良問集」【3−1 整数 不定方程式】を宇宙一わかりやすく
単元：
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#学校別大学入試過去問解説(数学)#数学(高校生)#鳥取大学
指導講師：
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文)：
$p,q,r$は不等式$p \leqq q \leqq r$を満たす正の整数とする。
このとき、次の各問いに答えよ。
（1）
$\displaystyle \frac{1}{p}+\displaystyle \frac{1}{q}=1$を満たす$p,q$をすべて求めよ。
（2）
$\displaystyle \frac{1}{p}+\displaystyle \frac{1}{q}+\displaystyle \frac{1}{r}=1$を満たす$p,q,r$をすべて求めよ。
この動画を見る
$p,q,r$は不等式$p \leqq q \leqq r$を満たす正の整数とする。
このとき、次の各問いに答えよ。
（1）
$\displaystyle \frac{1}{p}+\displaystyle \frac{1}{q}=1$を満たす$p,q$をすべて求めよ。
（2）
$\displaystyle \frac{1}{p}+\displaystyle \frac{1}{q}+\displaystyle \frac{1}{r}=1$を満たす$p,q,r$をすべて求めよ。
【高校数学】合同式の例題～modを使いこなそう～ 5-6.5【数学A】
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
1⃣
$\alpha$は7で割れば3余る自然数、$\beta$は7で割れば4余る自然数である。
このとき、次の数を7で割った余りを求めよ。
(a) $\alpha + 2 \beta$
(b) $\alpha^3$
(c) $\beta⁵⁰$
2⃣
$2000²⁰⁰⁰$を12で割ったときの余りを求めよ。
3⃣
$49¹²³$の一の位の数字を求めよ。
この動画を見る
1⃣
$\alpha$は7で割れば3余る自然数、$\beta$は7で割れば4余る自然数である。
このとき、次の数を7で割った余りを求めよ。
(a) $\alpha + 2 \beta$
(b) $\alpha^3$
(c) $\beta⁵⁰$
2⃣
$2000²⁰⁰⁰$を12で割ったときの余りを求めよ。
3⃣
$49¹²³$の一の位の数字を求めよ。
横浜市立（医）ド・モアブルと７倍角
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
(1)ド・モアブルの定理を用いて$\sin7\theta$を$\sin\theta,\cos\theta$およびその累乗を用いて表せ.
(2)$7x^3-35x^2+21x-1=0$を解け.
(3)$\dfrac{1}{\tan^2\dfrac{\pi}{7}}+\dfrac{1}{\tan^2\dfrac{2\pi}{7}}+\dfrac{1}{\tan^2\dfrac{3\pi}{7}}$の値を求めよ.
2016横浜市立(医)
この動画を見る
(1)ド・モアブルの定理を用いて$\sin7\theta$を$\sin\theta,\cos\theta$およびその累乗を用いて表せ.
(2)$7x^3-35x^2+21x-1=0$を解け.
(3)$\dfrac{1}{\tan^2\dfrac{\pi}{7}}+\dfrac{1}{\tan^2\dfrac{2\pi}{7}}+\dfrac{1}{\tan^2\dfrac{3\pi}{7}}$の値を求めよ.
2016横浜市立(医)
札幌医科大学2021 整数問題
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
自然数$n$に対し$N=(n+2)^3-n(n+1)(n+2)$が$36$の倍数になるような$n$をすべて求めよ.
2021札幌医大過去問
この動画を見る
自然数$n$に対し$N=(n+2)^3-n(n+1)(n+2)$が$36$の倍数になるような$n$をすべて求めよ.
2021札幌医大過去問
良問！！整数問題
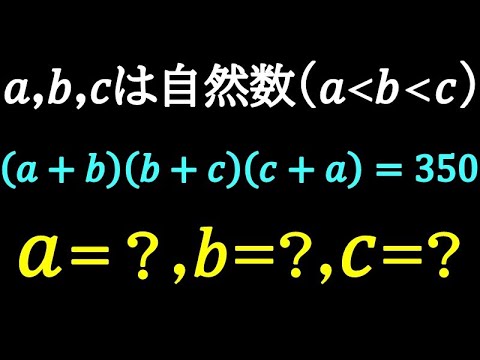
単元：
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
a=? b=? c=?
a,b,cは自然数でa<b<c
(a+b)(b+c)(c+a)=350
この動画を見る
a=? b=? c=?
a,b,cは自然数でa<b<c
(a+b)(b+c)(c+a)=350
12岡山県教員採用試験（数学：1-(4) 整数問題）
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{1}-(4)$
$\sqrt{n^2+55}$が自然数となるような
$n\in IN$を全て求めよ.
この動画を見る
$\boxed{1}-(4)$
$\sqrt{n^2+55}$が自然数となるような
$n\in IN$を全て求めよ.
【数A・算数】整数の性質：割り算の筆算で余りを出すときに・・・
単元：
#算数(中学受験)#計算と数の性質#数の性質その他#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
割り算の筆算で余りを出すときに・・・
この動画を見る
割り算の筆算で余りを出すときに・・・
指数方程式
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
実数解を求めよ.
$3^{x^2-2\sqrt5 x}=\dfrac{1}{121}$
この動画を見る
実数解を求めよ.
$3^{x^2-2\sqrt5 x}=\dfrac{1}{121}$
Σと合同式OnlineMathContest
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$1\leqq S,t\leqq 2020$であり,$S$は整数,$t$は奇数である.
$\displaystyle \sum_{k=1}^S k^t$が$S$の倍数となる$(s,t)$の組数を求めよ.
この動画を見る
$1\leqq S,t\leqq 2020$であり,$S$は整数,$t$は奇数である.
$\displaystyle \sum_{k=1}^S k^t$が$S$の倍数となる$(s,t)$の組数を求めよ.
合同式【高校数学ⅠA】を宇宙一わかりやすく
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文)：
【高校数学ⅠA】合同式の解説動画です
この動画を見る
【高校数学ⅠA】合同式の解説動画です
コメント欄はありがたい 素晴らしい別解
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$p,q,r$は自然数であり,$p+q+r=10$である.
$\dfrac{10!}{p!q!r!}$の総和を求めよ.
この動画を見る
$p,q,r$は自然数であり,$p+q+r=10$である.
$\dfrac{10!}{p!q!r!}$の総和を求めよ.
多項定理の応用OnlineMathContest
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$p,q,r$は自然数であり,$p+q+r=10$である.
$\dfrac{10!}{p!q!r!}$の総和を求めよ.
この動画を見る
$p,q,r$は自然数であり,$p+q+r=10$である.
$\dfrac{10!}{p!q!r!}$の総和を求めよ.
方程式 整数解OnlineMathContest
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$x^2-2(m-480)x+4m+97=0$が正整数解のみをもつ整数$m$を求めよ.
この動画を見る
$x^2-2(m-480)x+4m+97=0$が正整数解のみをもつ整数$m$を求めよ.
04大阪府教員採用試験（数学：1番 整数問題・数列）95東工大，07筑波大
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和（等差・等比・階差・Σ）#その他#数学(高校生)#数B#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{1}$
$2\leqq n \in IN$
1から$n$の異なる2つの積の総和を求めよ.
この動画を見る
$\boxed{1}$
$2\leqq n \in IN$
1から$n$の異なる2つの積の総和を求めよ.
2021富山大 整数問題
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$P\gt 3$,$P$と$P+4$は素数である.
(1)$P$を6で割った余りを示せ.
(2)$P+2$は3の倍数であることを示せ.
(3)$(P+1)(P+2)(P+3)$は$120$の倍数であることを示せ.
2021富山大過去問
この動画を見る
$P\gt 3$,$P$と$P+4$は素数である.
(1)$P$を6で割った余りを示せ.
(2)$P+2$は3の倍数であることを示せ.
(3)$(P+1)(P+2)(P+3)$は$120$の倍数であることを示せ.
2021富山大過去問
大阪大 積分のフリした整数問題
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$a,b,c$を整数とする.
$\displaystyle \int_{a}^{c}(x^2+bx)dx=\displaystyle \int_{b}^{c}(x^2+ax)dx$
①$a\neq b$なら$c$は3の倍数であることを示せ.
②$a\lt b,c=3600$ 整数$(a,b)$は何組であるか?
2021大阪大過去問
この動画を見る
$a,b,c$を整数とする.
$\displaystyle \int_{a}^{c}(x^2+bx)dx=\displaystyle \int_{b}^{c}(x^2+ax)dx$
①$a\neq b$なら$c$は3の倍数であることを示せ.
②$a\lt b,c=3600$ 整数$(a,b)$は何組であるか?
2021大阪大過去問
ルートを外せ11 B 2021 中央大附属
単元：
#数学(中学生)#数Ⅰ#数A#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$\sqrt{60(n+1)(n^2-1)}$が整数となるような2ケタの整数nをすべて求めよ。
2021中央大学附属高等学校
この動画を見る
$\sqrt{60(n+1)(n^2-1)}$が整数となるような2ケタの整数nをすべて求めよ。
2021中央大学附属高等学校
17大阪府教員採用試験（数学：3番 整数問題）
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{3}$
$x,y,z,a \Leftarrow IR$
$x+y+z=a$
$\dfrac{1}{x}+\dfrac{1}{y}+dfrac{1}{z}=\dfrac{1}{a}$をみたすとき,
(1)$x,y,z$のどれか1つは$a$と等しい.
(2)$n$が奇数のとき,$\dfrac{1}{x^n}+\dfrac{1}{y^n}+\dfrac{1}{z^n}=\dfrac{1}{x^n+y^n+z^n}$
この動画を見る
$\boxed{3}$
$x,y,z,a \Leftarrow IR$
$x+y+z=a$
$\dfrac{1}{x}+\dfrac{1}{y}+dfrac{1}{z}=\dfrac{1}{a}$をみたすとき,
(1)$x,y,z$のどれか1つは$a$と等しい.
(2)$n$が奇数のとき,$\dfrac{1}{x^n}+\dfrac{1}{y^n}+\dfrac{1}{z^n}=\dfrac{1}{x^n+y^n+z^n}$