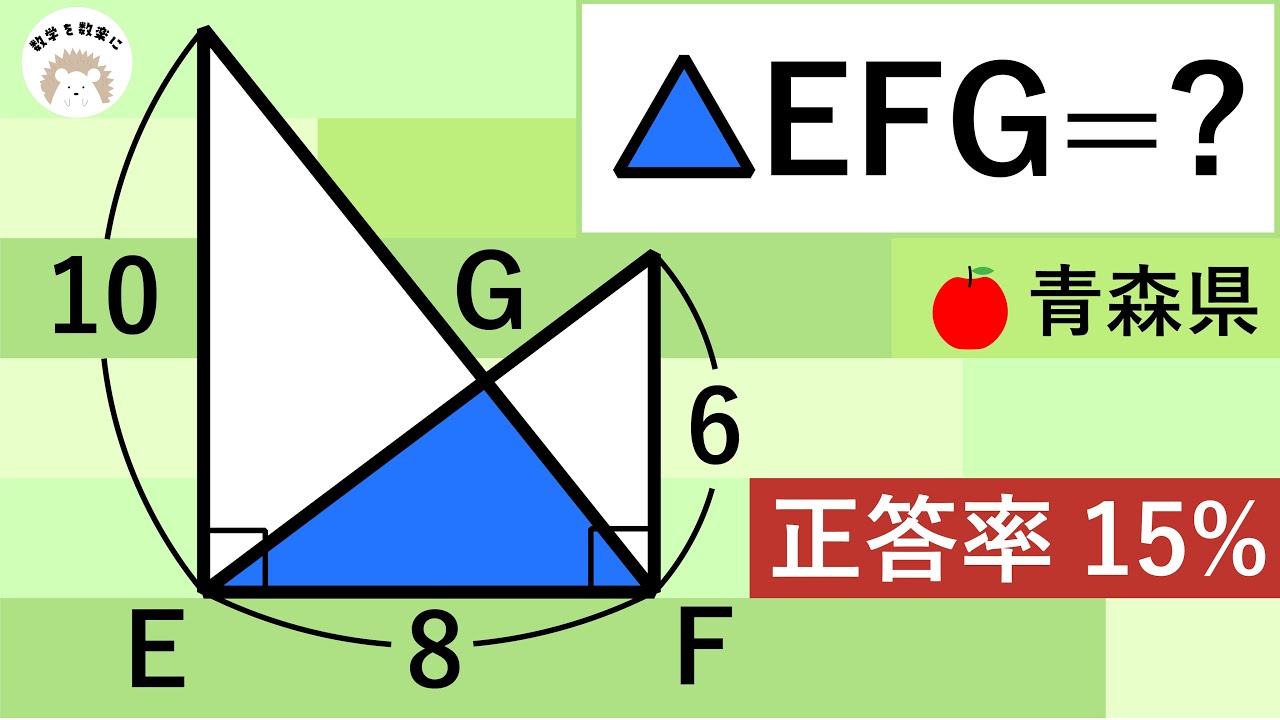
 数A
数A
 数A
数A
青森県 正答率15%
【高校数学あるある】階乗の末尾に0はいくつ並ぶ? #Shorts

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
150!の末尾が0の個数を求めよ。
この動画を見る
150!の末尾が0の個数を求めよ。
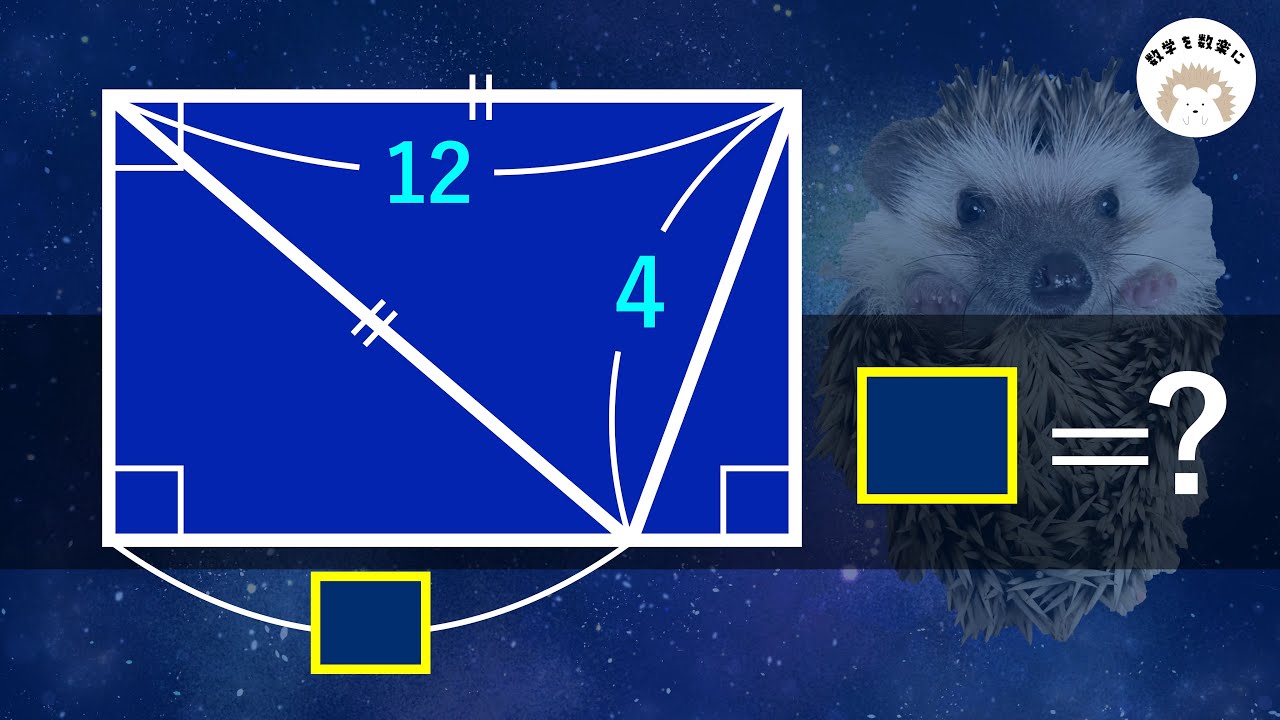
長方形の中にある二等辺三角形
素数が絡んだ整数問題(再アップ)【青山学院大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
素数$p,q$および自然数$n$に対し,$\dfrac{1}{p}+\dfrac{1}{q}+\dfrac{1}{pq}=\dfrac{1}{n}$が成り立つような$(p,q,n)$の組をすべて求めよ。
青山学院大過去問
この動画を見る
素数$p,q$および自然数$n$に対し,$\dfrac{1}{p}+\dfrac{1}{q}+\dfrac{1}{pq}=\dfrac{1}{n}$が成り立つような$(p,q,n)$の組をすべて求めよ。
青山学院大過去問
福田の数学〜立教大学2022年理学部第1問(3)〜垂線の足の位置ベクトル

単元:
#数A#大学入試過去問(数学)#図形の性質#平面上のベクトル#三角形の辺の比(内分・外分・二等分線)#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
三角形ABCにおいて、$AB=5,\ AC=6$、角Aの大きさは$\frac{\pi}{3}$であるとする。
Aから辺BCに垂線AHを下ろす。このとき$BH:CH=\boxed{ウ}:\boxed{エ}$である。
2022立教大学理学部過去問
この動画を見る
三角形ABCにおいて、$AB=5,\ AC=6$、角Aの大きさは$\frac{\pi}{3}$であるとする。
Aから辺BCに垂線AHを下ろす。このとき$BH:CH=\boxed{ウ}:\boxed{エ}$である。
2022立教大学理学部過去問
補助線引けるかな
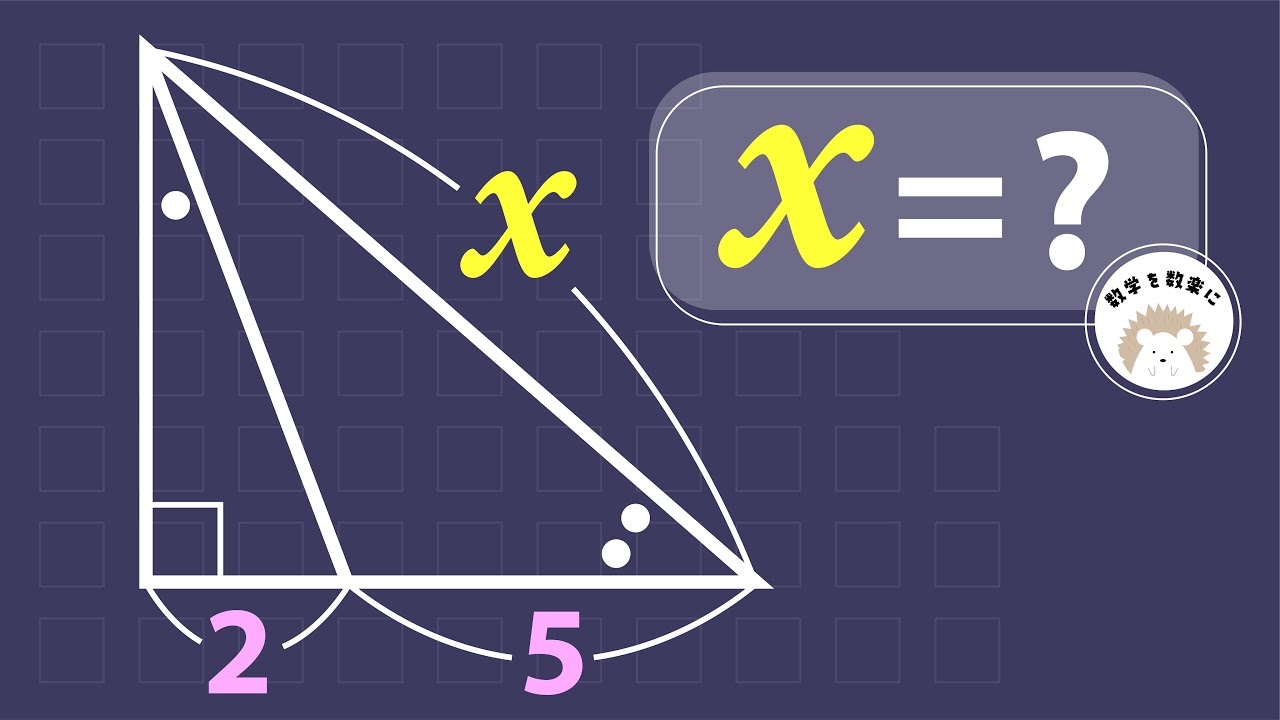
福田の数学〜立教大学2022年理学部第1問(2)〜余事象と確率の加法定理

単元:
#数A#数Ⅱ#大学入試過去問(数学)#場合の数と確率#確率#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
下図のように1から9までの数字が1つずつ記入された、9枚のカードがある。
$\boxed{1}\ \ \ \boxed{2}\ \ \ \boxed{3}\ \ \ \boxed{4}\ \ \ \boxed{5}\ \ \ \boxed{6}\ \ \ \boxed{7}\ \ \ \boxed{8}\ \ \ \boxed{9}$
これら9枚のカードから同時に取り出した3枚のカードの数字の積が
10で割り切れる確率は$\boxed{イ}$である。
2022立教大学理学部過去問
この動画を見る
下図のように1から9までの数字が1つずつ記入された、9枚のカードがある。
$\boxed{1}\ \ \ \boxed{2}\ \ \ \boxed{3}\ \ \ \boxed{4}\ \ \ \boxed{5}\ \ \ \boxed{6}\ \ \ \boxed{7}\ \ \ \boxed{8}\ \ \ \boxed{9}$
これら9枚のカードから同時に取り出した3枚のカードの数字の積が
10で割り切れる確率は$\boxed{イ}$である。
2022立教大学理学部過去問
精度90%の検査で陽性だったら90%陽性?答えが直感と違う?慶應(看護)

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
サイコロを3つ振ったら出た目の最小値が2であった.3つの目がどの2つも互いに素である確率を求めよ.
慶應(看護)過去問
この動画を見る
サイコロを3つ振ったら出た目の最小値が2であった.3つの目がどの2つも互いに素である確率を求めよ.
慶應(看護)過去問
ただの分数式だけど

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
a,bは正の整数である.
$\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{3}{2018}$を満たす(a,b)を全て求めよ.ただし1009は素数とする.
この動画を見る
a,bは正の整数である.
$\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{3}{2018}$を満たす(a,b)を全て求めよ.ただし1009は素数とする.
数のいれかえ 東海高校(改)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
ある2つの位の数をいれかえるともとの整数より90大きくなる。
このような3ケタの自然数は何個ある?
東海高等学校(改)
この動画を見る
ある2つの位の数をいれかえるともとの整数より90大きくなる。
このような3ケタの自然数は何個ある?
東海高等学校(改)
【数学】確率:センター試験(平成30年)本試

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#センター試験・共通テスト関連#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
1枚のコインを最大で5回投げるゲームを行う。このゲームでは、1回投げるごとに表が出たら持ち点に2点を加え、裏が出たら持ち点に -1点を加える。はじめの持ち点は0点とし、ゲーム終了のルールを次のように定める。
・持ち点が再び0点になった場合は、その時点で終了する。
・持ち点が再び0点にならない場合は、コインを5回投げ終わった時点で終了する。
(1) コインを2回投げ終わって持ち点が -2点である確率は □
である。また、コインを2回投げ終わって持ち点が1点である確率は □
である。
(2) 持ち点が再び0点になることが起こるのは、コインを
□ 回投げ終わったときである。コインを □回投げ終わって持ち点が0点になる確率は
□である。
(3) ゲームが終了した時点で持ち点が4点である確率は □である。
(4) ゲームが終了した時点で持ち点が4点であるとき、コインを2回投げ終わって持ち点が1点である条件付き確率は□である。
この動画を見る
1枚のコインを最大で5回投げるゲームを行う。このゲームでは、1回投げるごとに表が出たら持ち点に2点を加え、裏が出たら持ち点に -1点を加える。はじめの持ち点は0点とし、ゲーム終了のルールを次のように定める。
・持ち点が再び0点になった場合は、その時点で終了する。
・持ち点が再び0点にならない場合は、コインを5回投げ終わった時点で終了する。
(1) コインを2回投げ終わって持ち点が -2点である確率は □
である。また、コインを2回投げ終わって持ち点が1点である確率は □
である。
(2) 持ち点が再び0点になることが起こるのは、コインを
□ 回投げ終わったときである。コインを □回投げ終わって持ち点が0点になる確率は
□である。
(3) ゲームが終了した時点で持ち点が4点である確率は □である。
(4) ゲームが終了した時点で持ち点が4点であるとき、コインを2回投げ終わって持ち点が1点である条件付き確率は□である。
福田の数学〜明治大学2022年理工学部第2問〜平面図形の計量

単元:
#数Ⅰ#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#英語(高校生)#平面図形#大学入試過去問(英語)#学校別大学入試過去問解説(英語)#明治大学#数学(高校生)#明治大学
指導講師:
福田次郎
問題文全文(内容文):
平面上の長さ3の線分AB上に、$AP=t\ (0 \lt t \lt 3)$を満たす点Pをとる。
中心を$O$とする半径1の円Oが、線分ABと点Pで接しているとする。
$\alpha=\angle OAB,\ \beta=\angle OBA$
とおく。$\tan\alpha,\ \tan\beta,\tan(\alpha+\beta)$を$t$で表すと、
$\tan\alpha=\boxed{あ},\ \tan\beta=\boxed{い},$
$\ \tan(\alpha+\beta)=\boxed{う}$である。
$0 \lt \alpha+\beta \lt \frac{\pi}{2}$であるようなtの範囲は$\boxed{え}$である。
tは$\boxed{え}$の範囲にあるとする。点$A,\ B$から円Oに引いた接線の接点のうち、
Pでないものをそれぞれ$Q,\ R$とすると、$\angle QAB+\angle RBA \lt \pi$である。
したがって、線分AQのQの方への延長と線分BRのRの方への延長は交わり、
その交点をCとすると、円Oは三角形ABCの内接円である。
このとき、線分CQの長さをtで表すと$\ \boxed{お}$である。
また、$t$が$\boxed{え}$の範囲を動くとき、三角形ABCの面積Sの取り得る値の範囲は$\boxed{か}$である。
2022明治大学理工学部過去問
この動画を見る
平面上の長さ3の線分AB上に、$AP=t\ (0 \lt t \lt 3)$を満たす点Pをとる。
中心を$O$とする半径1の円Oが、線分ABと点Pで接しているとする。
$\alpha=\angle OAB,\ \beta=\angle OBA$
とおく。$\tan\alpha,\ \tan\beta,\tan(\alpha+\beta)$を$t$で表すと、
$\tan\alpha=\boxed{あ},\ \tan\beta=\boxed{い},$
$\ \tan(\alpha+\beta)=\boxed{う}$である。
$0 \lt \alpha+\beta \lt \frac{\pi}{2}$であるようなtの範囲は$\boxed{え}$である。
tは$\boxed{え}$の範囲にあるとする。点$A,\ B$から円Oに引いた接線の接点のうち、
Pでないものをそれぞれ$Q,\ R$とすると、$\angle QAB+\angle RBA \lt \pi$である。
したがって、線分AQのQの方への延長と線分BRのRの方への延長は交わり、
その交点をCとすると、円Oは三角形ABCの内接円である。
このとき、線分CQの長さをtで表すと$\ \boxed{お}$である。
また、$t$が$\boxed{え}$の範囲を動くとき、三角形ABCの面積Sの取り得る値の範囲は$\boxed{か}$である。
2022明治大学理工学部過去問
英国数学オリンピック 高校入試レベルの問題

単元:
#数A#数Ⅱ#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
すべてのxで次の式が成り立つ整数(a,b,c)をすべて求めよ.
$(x-10)(x-a)+1=(x+a)(x+c)$
英国数学オリンピック過去問
この動画を見る
すべてのxで次の式が成り立つ整数(a,b,c)をすべて求めよ.
$(x-10)(x-a)+1=(x+a)(x+c)$
英国数学オリンピック過去問
【整数問題】超典型的な問題!解けますか?【数学 入試問題】

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$\dfrac{1}{m}+\dfrac{1}{n}=\dfrac{1}{6}$かつ$m<n$を満たす正の整数$m,n$の組($m,n$)をすべて求めよ。
この動画を見る
$\dfrac{1}{m}+\dfrac{1}{n}=\dfrac{1}{6}$かつ$m<n$を満たす正の整数$m,n$の組($m,n$)をすべて求めよ。
直角2つで〇〇なる

イラン数学オリンピック 整数問題

単元:
#数A#数Ⅱ#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
Pが5以上の素数ならば,$7^P-6^P-1$は43の倍数であることを示せ.
イラン数学オリンピック過去問
この動画を見る
Pが5以上の素数ならば,$7^P-6^P-1$は43の倍数であることを示せ.
イラン数学オリンピック過去問
指数が絡んだ整数問題

単元:
#数A#数Ⅱ#整数の性質#約数・倍数・整数の割り算と余り・合同式#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$2^m - 2^n = 2016$
$m=?$ $n=?$
(mとnは自然数)
この動画を見る
$2^m - 2^n = 2016$
$m=?$ $n=?$
(mとnは自然数)
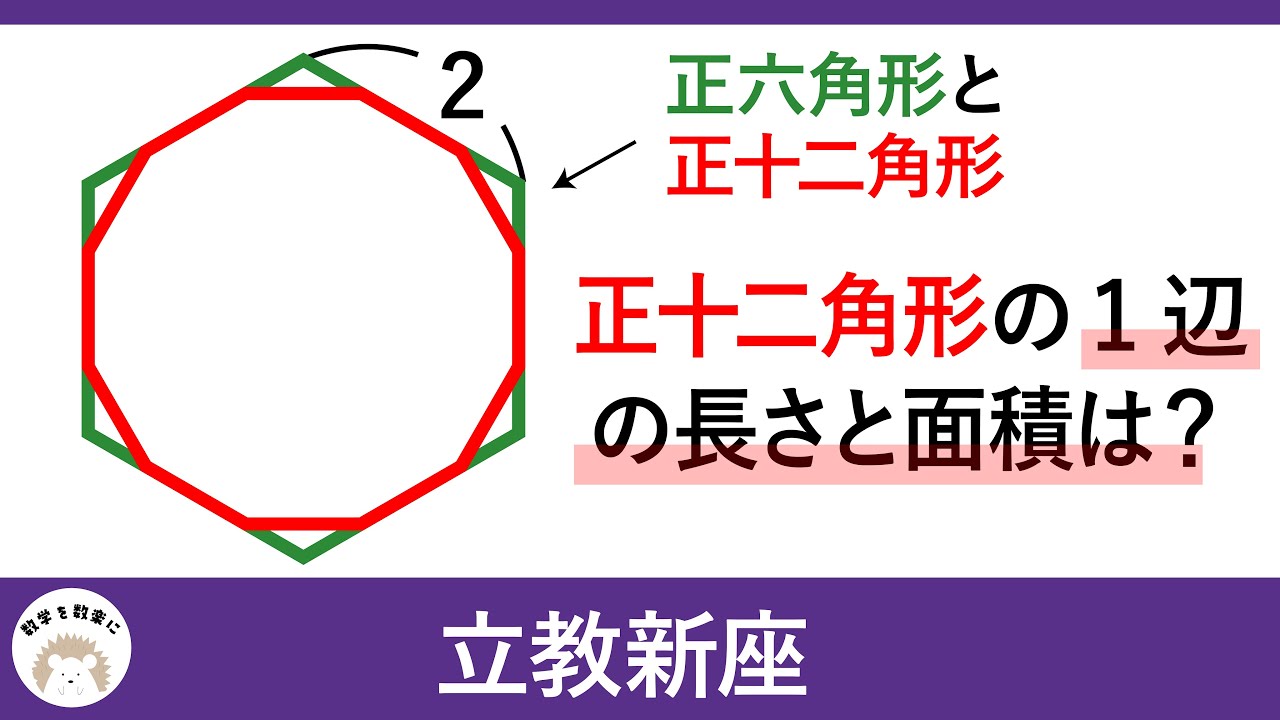
正12角形の一辺の長さと面積 立教新座
単元:
#数学(中学生)#中1数学#数Ⅰ#数A#図形の性質#図形と計量#平面図形#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
正六角形と正十二角形
正十二角形の1辺の長さと面積は?
立教新座高等学校
この動画を見る
正六角形と正十二角形
正十二角形の1辺の長さと面積は?
立教新座高等学校
【高校数学】「これ」知ってる? フェルマーが愛した無限降下法という証明方法 #Shorts

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$\sqrt3 $が無理数であることを証明せよ。
この動画を見る
$\sqrt3 $が無理数であることを証明せよ。
素数であることの証明【京都大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$n$を2以上の整数とする。$3^n-2^n$が素数ならば$n$も素数であることを示せ。
京都大過去問
この動画を見る
$n$を2以上の整数とする。$3^n-2^n$が素数ならば$n$も素数であることを示せ。
京都大過去問
福田の数学〜明治大学2022年全学部統一入試理系第4問〜サイコロの目で決まる複素数の値に関する確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#複素数平面#確率#複素数平面#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$i$を虚数単位とし、$z=\frac{1}{2}+\frac{\sqrt3}{2}\ i\$とおく。
さいころを3回ふり、出た目を順に$a,\ b,\ c$とする。
このとき、積$\ abc$が3の倍数となる確率は$\frac{\boxed{アイ}}{\boxed{ウエ}}$である。
また、$z^{abc}=-1$となる確率は$\frac{\boxed{オカ}}{\boxed{キクケ}}$であり、
$z^{abc}=1$となる確率は$\frac{\boxed{コサシ}}{\boxed{スセソ}}$である。
2022明治大学全統理系過去問
この動画を見る
$i$を虚数単位とし、$z=\frac{1}{2}+\frac{\sqrt3}{2}\ i\$とおく。
さいころを3回ふり、出た目を順に$a,\ b,\ c$とする。
このとき、積$\ abc$が3の倍数となる確率は$\frac{\boxed{アイ}}{\boxed{ウエ}}$である。
また、$z^{abc}=-1$となる確率は$\frac{\boxed{オカ}}{\boxed{キクケ}}$であり、
$z^{abc}=1$となる確率は$\frac{\boxed{コサシ}}{\boxed{スセソ}}$である。
2022明治大学全統理系過去問
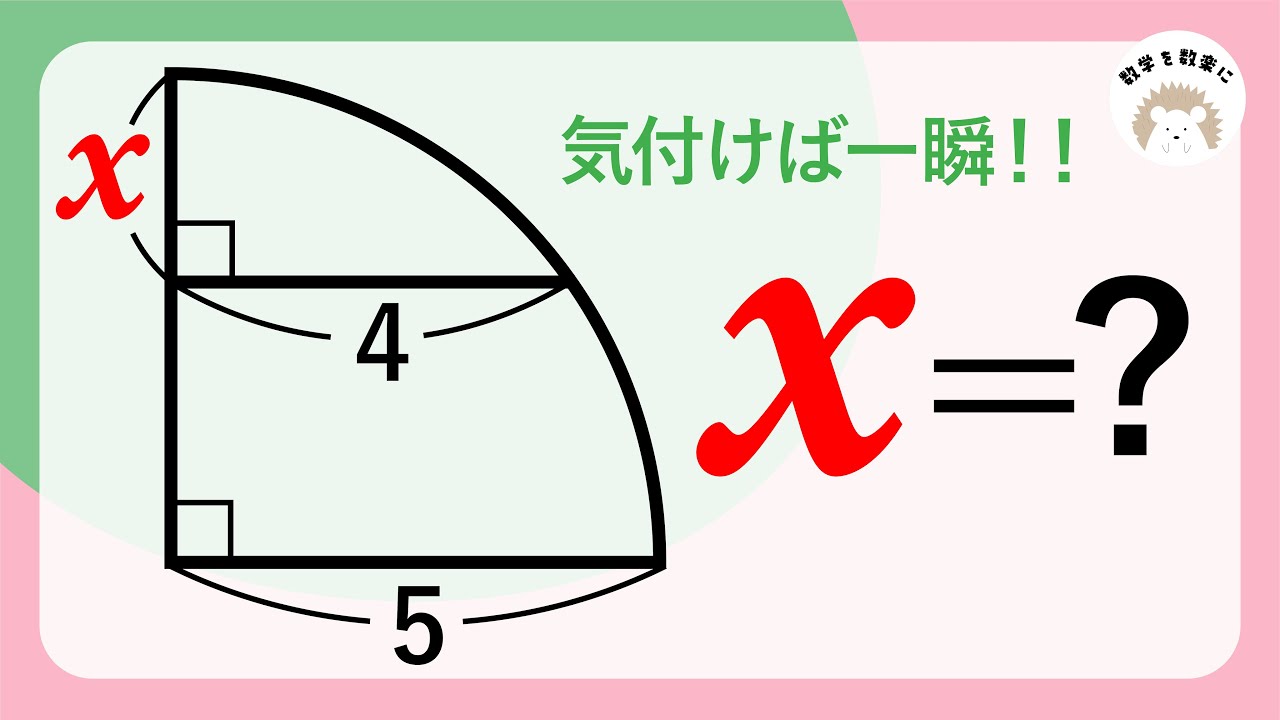
気付けば一瞬!! 4分の1円
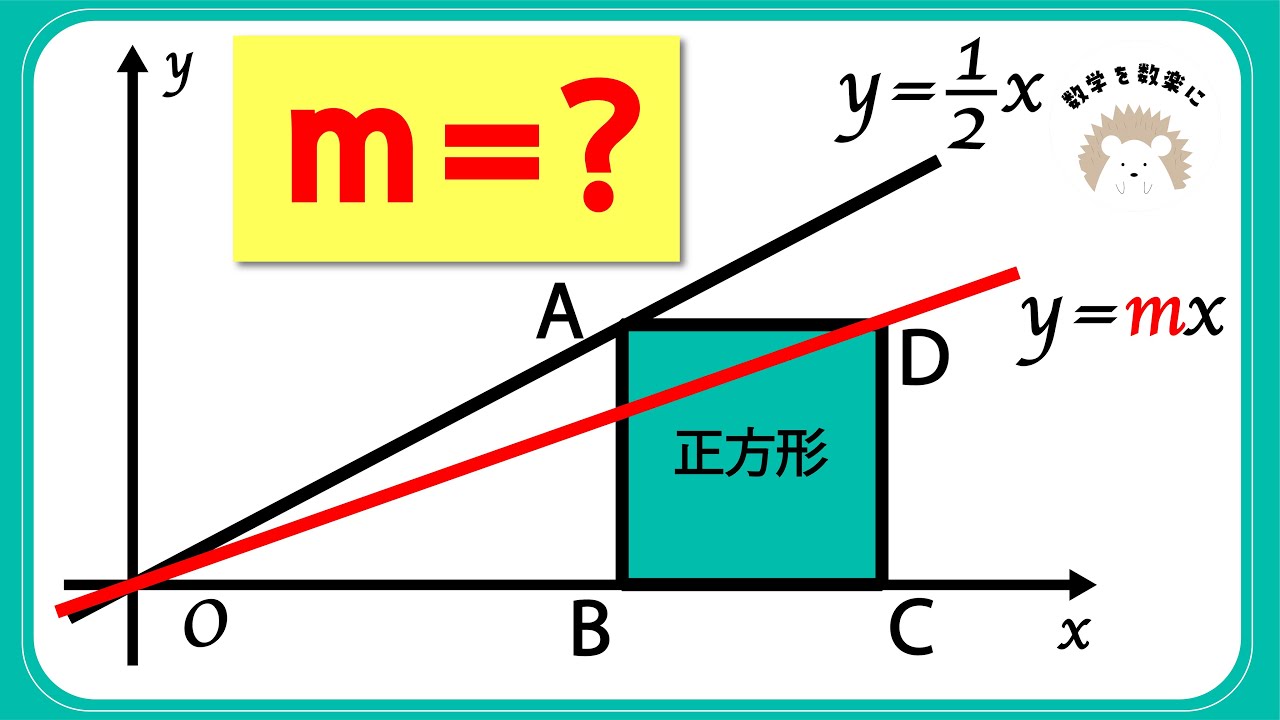
瞬殺せよ!傾き
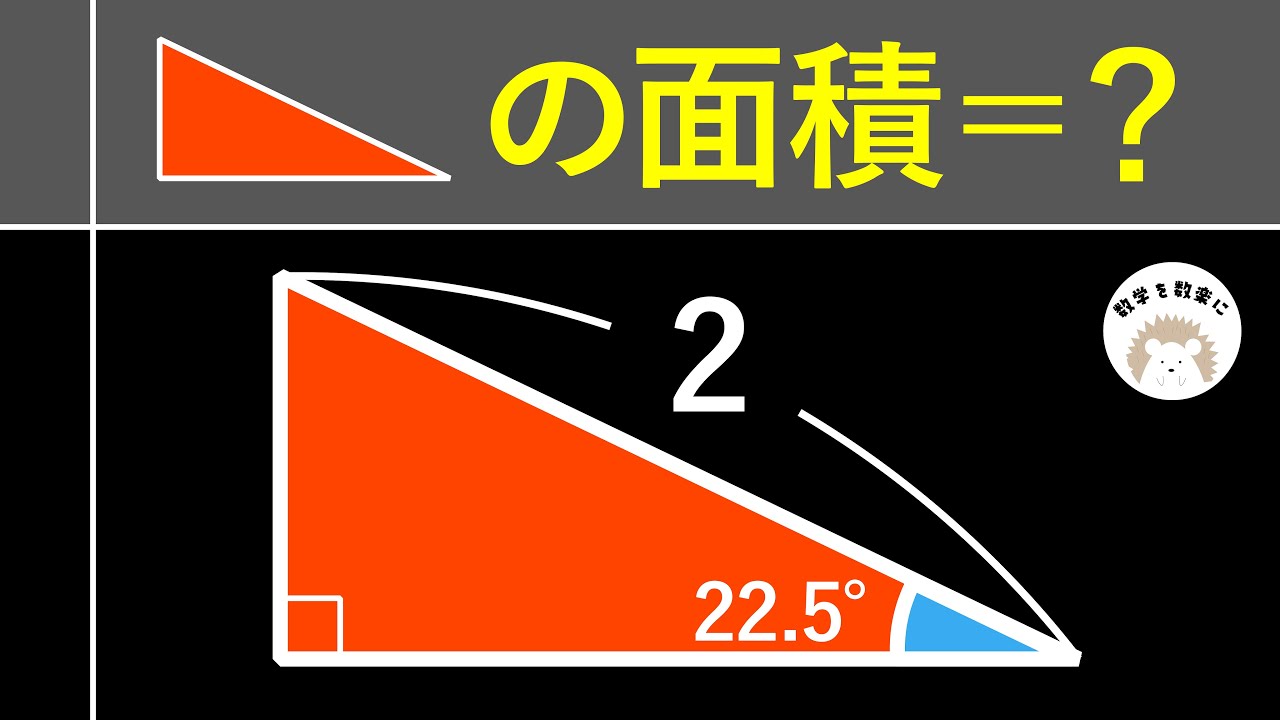
22.5度
【良問】素数を扱え!考え方をきっちり理解したい整数問題です【京都大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$p$が素数ならば,$p^4+14$は素数でないことを示せ。
京都大過去問
この動画を見る
$p$が素数ならば,$p^4+14$は素数でないことを示せ。
京都大過去問
インド数学オリンピック
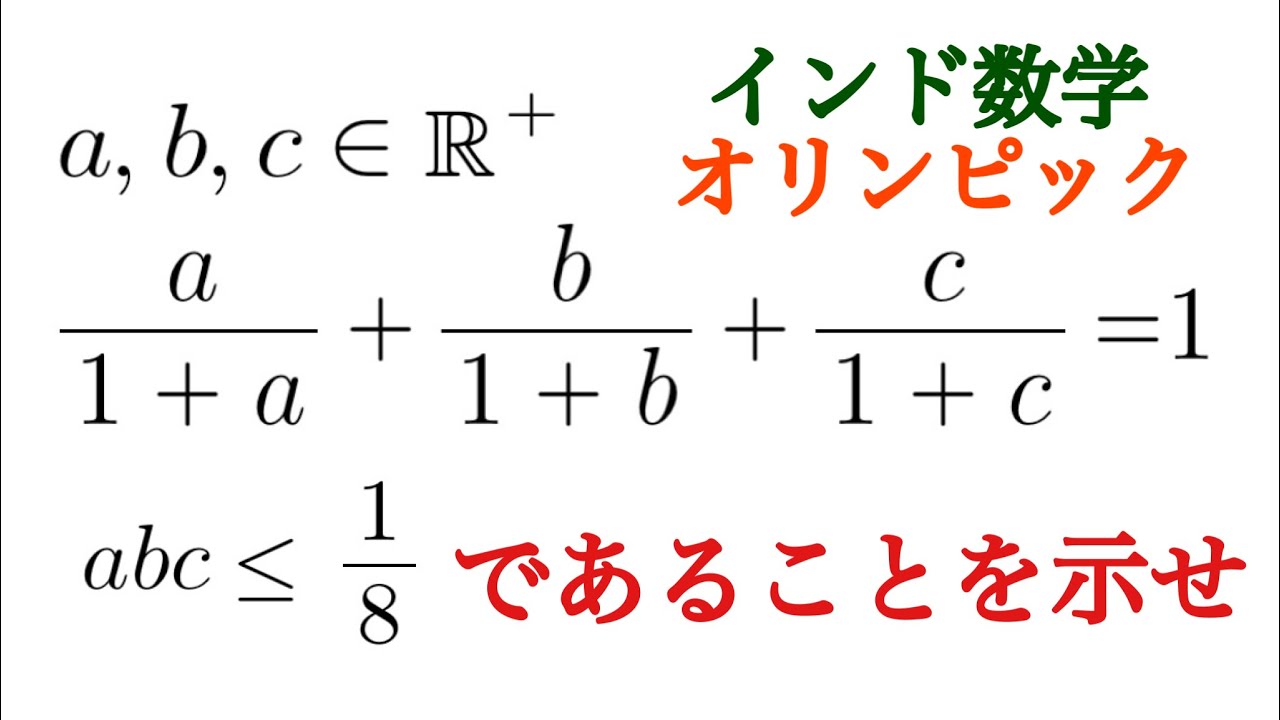
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
a,b,cは正の実数である.
$\dfrac{a}{1+a}+\dfrac{b}{1+b}+\dfrac{c}{1+c}=1$を満たす
$abc \leqq \dfrac{1}{8}$を示せ.
インド数学オリンピック過去問
この動画を見る
a,b,cは正の実数である.
$\dfrac{a}{1+a}+\dfrac{b}{1+b}+\dfrac{c}{1+c}=1$を満たす
$abc \leqq \dfrac{1}{8}$を示せ.
インド数学オリンピック過去問
正方形何個できる? 福岡大附属大濠

単元:
#数A#場合の数と確率#図形の性質#場合の数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
縦横等間隔に並ぶ16個の点
4つの点を選んで正方形をつくる。
何通りできる?
*図は動画内参照
福岡大附属大濠高等学校
この動画を見る
縦横等間隔に並ぶ16個の点
4つの点を選んで正方形をつくる。
何通りできる?
*図は動画内参照
福岡大附属大濠高等学校
素数を合成数の和で表す

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
13以上の素数はすべて2つの合成数の和で表せることを示せ.
この動画を見る
13以上の素数はすべて2つの合成数の和で表せることを示せ.
整数問題 昭和学院秀英

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$xy=(x+2)^2$をみたす自然数の組(x,y)をすべて求めよ。
昭和学院秀英高等学校
この動画を見る
$xy=(x+2)^2$をみたす自然数の組(x,y)をすべて求めよ。
昭和学院秀英高等学校
福田の数学〜明治大学2022年全学部統一入試12AB第3問〜漸化式の図形への応用

単元:
#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数列#漸化式#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
(1)三角形$ABC$の内接円が辺$AB$と接する点をPとし、
辺$BC$と接する点を$Q$とし、辺$CA$と接する点をRとする。
$\angle A$の大きさを$θ$とすると、$\angle APR=\boxed{ア}$であり、
$\angle PQR=\boxed{ア}$である。
$\boxed{ア}$の解答群
$⓪0 ①\frac{\pi}{2} ②θ ③\frac{θ}{2} ④\frac{\pi}{2}-θ ⑤\frac{\pi-θ}{2}$
$⑥\pi-\frac{θ}{2} ⑦\pi-θ ⑧\frac{\pi-3θ}{2} ⑨\frac{\pi}{2}-3θ$
(2)三角形$T_1$の3つの角のうち、角の大きさが最小のものは$\frac{\pi}{6}$で、
最大のものは$\frac{\pi}{2}$であるとする。
$n=1,\ 2,\ 3,\ ...$について、三角形$T_n$の内接円を$O_n$とし、
$T_n$と$O_n$とが接する3つの点を頂点とするような三角形を$T_{n+1}$とする。
このとき、三角形$T_2$の3つの角のうち、
角の大きさが最小のものは$\frac{\pi}{\boxed{イ}}$で、
最大のものは$\frac{\boxed{ウ}\ \pi}{\boxed{エオ}}$である。
$n=1,\ 2,\ 3,\ ...$について、三角形$T_n$の3つの角のうち、
角の大きさが最小のものを$a_n$とし、最大のものを$b_n$とする。三角形$T_{n+1}$について、
$a_{n+1}=\boxed{カ},\ \ \ b_{n+1}=\boxed{キ}$
と表せる。この式より
$a_n+b_n=\frac{\boxed{ク}}{\boxed{ケ}}\pi,$
$b_n-a_n=\frac{\pi}{\boxed{コ}・\boxed{サ}^{n-1}}$
であり、$a_n=\frac{\pi}{\boxed{シ}}(1-\frac{1}{\boxed{ス}^n}) $である。
$\boxed{カ}、\boxed{キ}$の解答群
$⓪\frac{a_n}{2} ①\frac{b_n}{2} ②\frac{\pi}{2}-a_n ③\frac{\pi}{2}-b_n ④\frac{\pi-a_n}{2}$
$⑤\frac{\pi-b_n}{2} ⑥\pi-\frac{a_n}{2} ⑦\pi-\frac{b_n}{2} ⑧\pi-a_n ⑨\pi-b_n$
2022明治大学全統過去問
この動画を見る
(1)三角形$ABC$の内接円が辺$AB$と接する点をPとし、
辺$BC$と接する点を$Q$とし、辺$CA$と接する点をRとする。
$\angle A$の大きさを$θ$とすると、$\angle APR=\boxed{ア}$であり、
$\angle PQR=\boxed{ア}$である。
$\boxed{ア}$の解答群
$⓪0 ①\frac{\pi}{2} ②θ ③\frac{θ}{2} ④\frac{\pi}{2}-θ ⑤\frac{\pi-θ}{2}$
$⑥\pi-\frac{θ}{2} ⑦\pi-θ ⑧\frac{\pi-3θ}{2} ⑨\frac{\pi}{2}-3θ$
(2)三角形$T_1$の3つの角のうち、角の大きさが最小のものは$\frac{\pi}{6}$で、
最大のものは$\frac{\pi}{2}$であるとする。
$n=1,\ 2,\ 3,\ ...$について、三角形$T_n$の内接円を$O_n$とし、
$T_n$と$O_n$とが接する3つの点を頂点とするような三角形を$T_{n+1}$とする。
このとき、三角形$T_2$の3つの角のうち、
角の大きさが最小のものは$\frac{\pi}{\boxed{イ}}$で、
最大のものは$\frac{\boxed{ウ}\ \pi}{\boxed{エオ}}$である。
$n=1,\ 2,\ 3,\ ...$について、三角形$T_n$の3つの角のうち、
角の大きさが最小のものを$a_n$とし、最大のものを$b_n$とする。三角形$T_{n+1}$について、
$a_{n+1}=\boxed{カ},\ \ \ b_{n+1}=\boxed{キ}$
と表せる。この式より
$a_n+b_n=\frac{\boxed{ク}}{\boxed{ケ}}\pi,$
$b_n-a_n=\frac{\pi}{\boxed{コ}・\boxed{サ}^{n-1}}$
であり、$a_n=\frac{\pi}{\boxed{シ}}(1-\frac{1}{\boxed{ス}^n}) $である。
$\boxed{カ}、\boxed{キ}$の解答群
$⓪\frac{a_n}{2} ①\frac{b_n}{2} ②\frac{\pi}{2}-a_n ③\frac{\pi}{2}-b_n ④\frac{\pi-a_n}{2}$
$⑤\frac{\pi-b_n}{2} ⑥\pi-\frac{a_n}{2} ⑦\pi-\frac{b_n}{2} ⑧\pi-a_n ⑨\pi-b_n$
2022明治大学全統過去問
