 数A
数A
 数A
数A
【数A】整数の性質:pを素数、aとbを自然数とする。p=a³-b³のとき、p-1が6の倍数であることを証明せよ。

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
pを素数、aとbを自然数とする。$p=a^3-b^3$のとき、p-1が6の倍数であることを証明せよ。
この動画を見る
pを素数、aとbを自然数とする。$p=a^3-b^3$のとき、p-1が6の倍数であることを証明せよ。
東北大 対数方程式
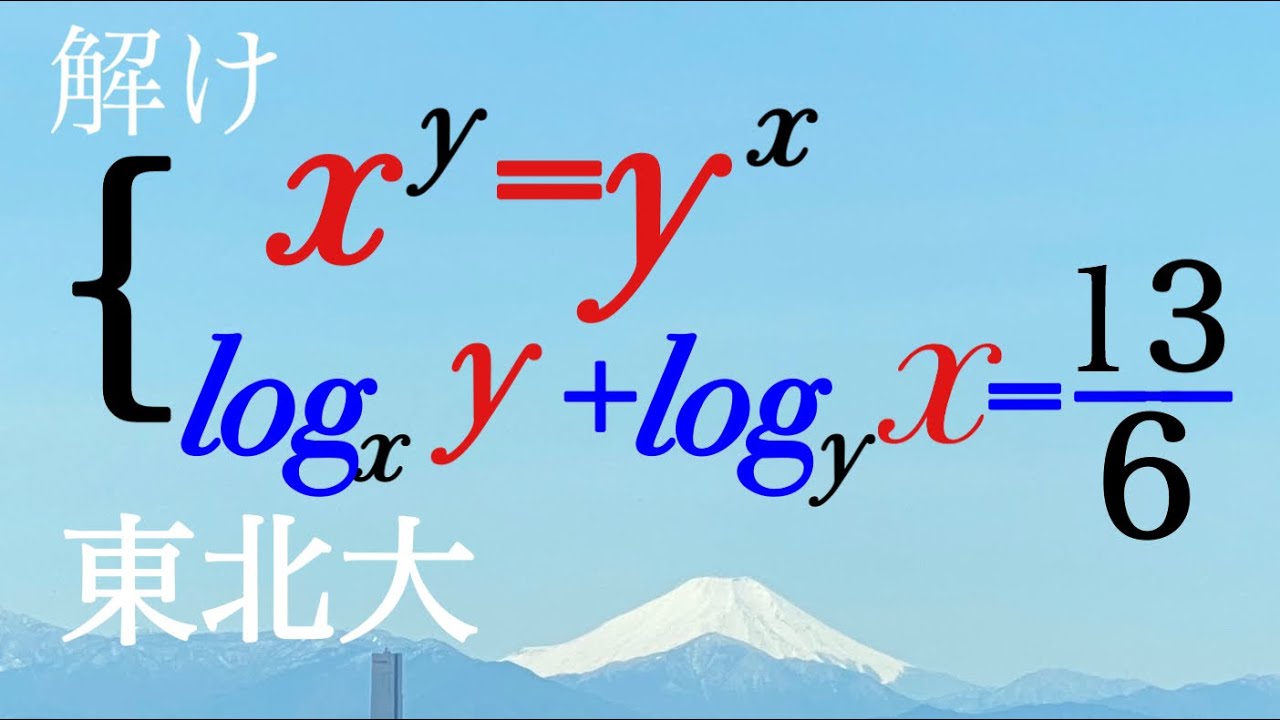
単元:
#数A#数Ⅱ#整数の性質#ユークリッド互除法と不定方程式・N進法#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
連立方程式を解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^y=y^x \\
\log_x y+\log_y x=\dfrac{13}{6}
\end{array}
\right.
\end{eqnarray}$
東北大過去問
この動画を見る
連立方程式を解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^y=y^x \\
\log_x y+\log_y x=\dfrac{13}{6}
\end{array}
\right.
\end{eqnarray}$
東北大過去問
【数A】整数の性質:n³+5nが6の倍数であることを証明せよ。

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$n^3+5n$が6の倍数であることを証明せよ。
この動画を見る
$n^3+5n$が6の倍数であることを証明せよ。
2021問題
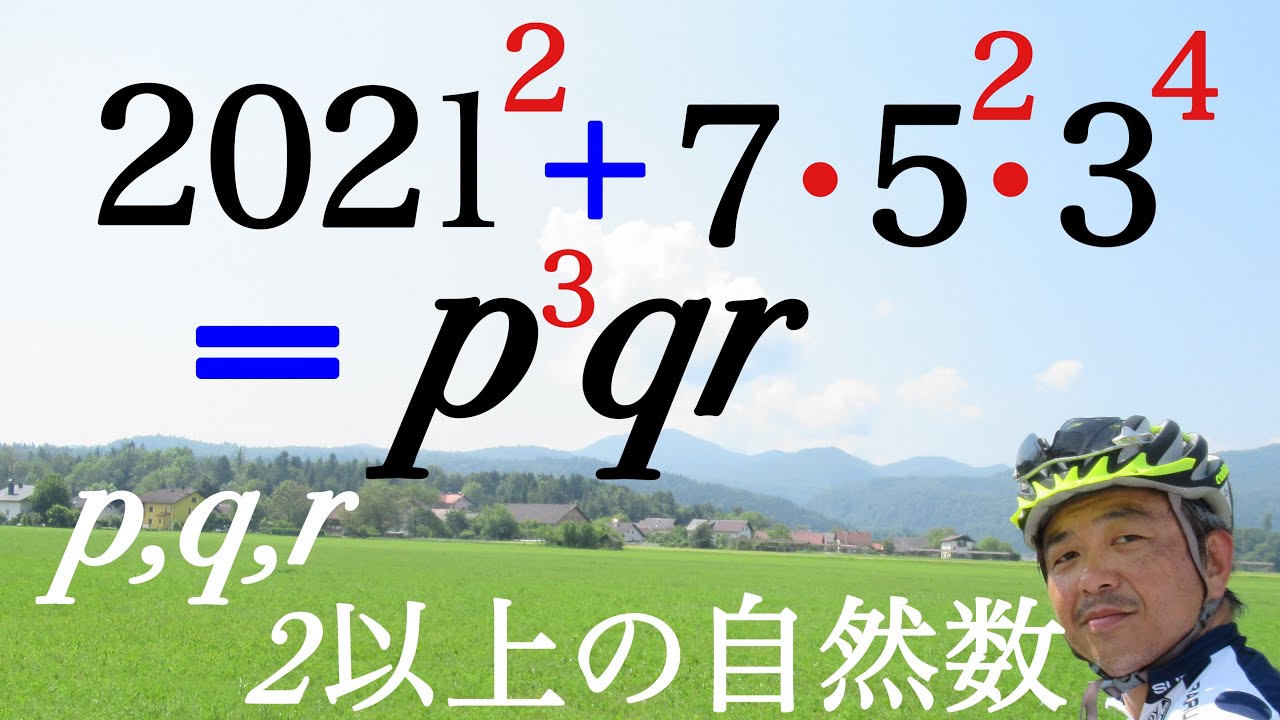
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$2021^2+7・5^2・3^4=p^3qr$
$p,q,r$は2以上の自然数である.
この動画を見る
これを解け.
$2021^2+7・5^2・3^4=p^3qr$
$p,q,r$は2以上の自然数である.

単元:
#数Ⅰ#数A#数Ⅱ#大学入試過去問(数学)#センター試験・共通テスト関連#共通テスト#数学(高校生)#数B
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
共通対策「数学で9割超える勉強法」についてお話しています。
この動画を見る
共通対策「数学で9割超える勉強法」についてお話しています。
04神奈川県教員採用試験(数学:1番 整数問題)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣$x,y \in \mathbb{N}$ , $1 \leqq x, y \leqq 9$
$\frac{10+x}{10x+y} = \frac{1}{y}$
をみたす組(x,y)を全て求めよ。
この動画を見る
1⃣$x,y \in \mathbb{N}$ , $1 \leqq x, y \leqq 9$
$\frac{10+x}{10x+y} = \frac{1}{y}$
をみたす組(x,y)を全て求めよ。
東大 不定方程式

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x,y,z$は自然数とする.
①$x+y+z=xyz$を満たす$(x,y,z)$をすべて求めよ.$(x\leqq y\leqq z)$
②$x^3+y^3+z^3=xyz$を満たす$(x,y,z)$は存在しないことを示せ.
2006東大過去問
この動画を見る
$x,y,z$は自然数とする.
①$x+y+z=xyz$を満たす$(x,y,z)$をすべて求めよ.$(x\leqq y\leqq z)$
②$x^3+y^3+z^3=xyz$を満たす$(x,y,z)$は存在しないことを示せ.
2006東大過去問
北海道大 整数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x,y$を自然数とする.
(1)$\dfrac{3x}{x^2+2}$が自然数となる$x$を求めよ.
(2)$\dfrac{3x}{x^2+2}+\dfrac{1}{y}$が自然数となる$(x,y)$を求めよ.
2016北海道大過去問
この動画を見る
$x,y$を自然数とする.
(1)$\dfrac{3x}{x^2+2}$が自然数となる$x$を求めよ.
(2)$\dfrac{3x}{x^2+2}+\dfrac{1}{y}$が自然数となる$(x,y)$を求めよ.
2016北海道大過去問
津田塾大 基本対称式

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a,b,c$は自然数である.
$abc,ab+bc+ca$,$a+b+c$がすべて3の倍数なら,$a,b,c$はすべて3の倍数であることを示せ.
2016津田塾大過去問
この動画を見る
$a,b,c$は自然数である.
$abc,ab+bc+ca$,$a+b+c$がすべて3の倍数なら,$a,b,c$はすべて3の倍数であることを示せ.
2016津田塾大過去問
聖マリアンナ医大 整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$p$は素数であり,$x,y,z$は整数である.
$x^3+py^3+p^2z^3-p^3xyz=0$ならば,$x=y=z=0$であることを示せ.
2016聖マリアンナ医大過去問
この動画を見る
$p$は素数であり,$x,y,z$は整数である.
$x^3+py^3+p^2z^3-p^3xyz=0$ならば,$x=y=z=0$であることを示せ.
2016聖マリアンナ医大過去問
整数問題2021

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$2021^{2021^{2021}}$の下3桁を求めよ.
この動画を見る
$2021^{2021^{2021}}$の下3桁を求めよ.
2021!を5の504乗で割ったあまり

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$2021!$を$5^{504}$で割った余りを求めよ.
この動画を見る
$2021!$を$5^{504}$で割った余りを求めよ.
旭川医科大 整数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
p^3-q^3-27r^3-9pqr=0 \\
p^2-10q-30r=11
\end{array}
\right.
\end{eqnarray}$
を満たす自然数$(p,q,r)$の組をすべて求めよ.
2015旭川医科大過去問
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
p^3-q^3-27r^3-9pqr=0 \\
p^2-10q-30r=11
\end{array}
\right.
\end{eqnarray}$
を満たす自然数$(p,q,r)$の組をすべて求めよ.
2015旭川医科大過去問
15愛知県教員採用試験(数学:1番 整数問題)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$x,y \in \mathbb{N}$ , $7x+4y=175$
(1)(x,y)の個数
(2)|x-y|の最大値
この動画を見る
$x,y \in \mathbb{N}$ , $7x+4y=175$
(1)(x,y)の個数
(2)|x-y|の最大値
合同式の基本 2021問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$2021^{2021}$を$15$で割った余りを求めよ.
この動画を見る
$2021^{2021}$を$15$で割った余りを求めよ.
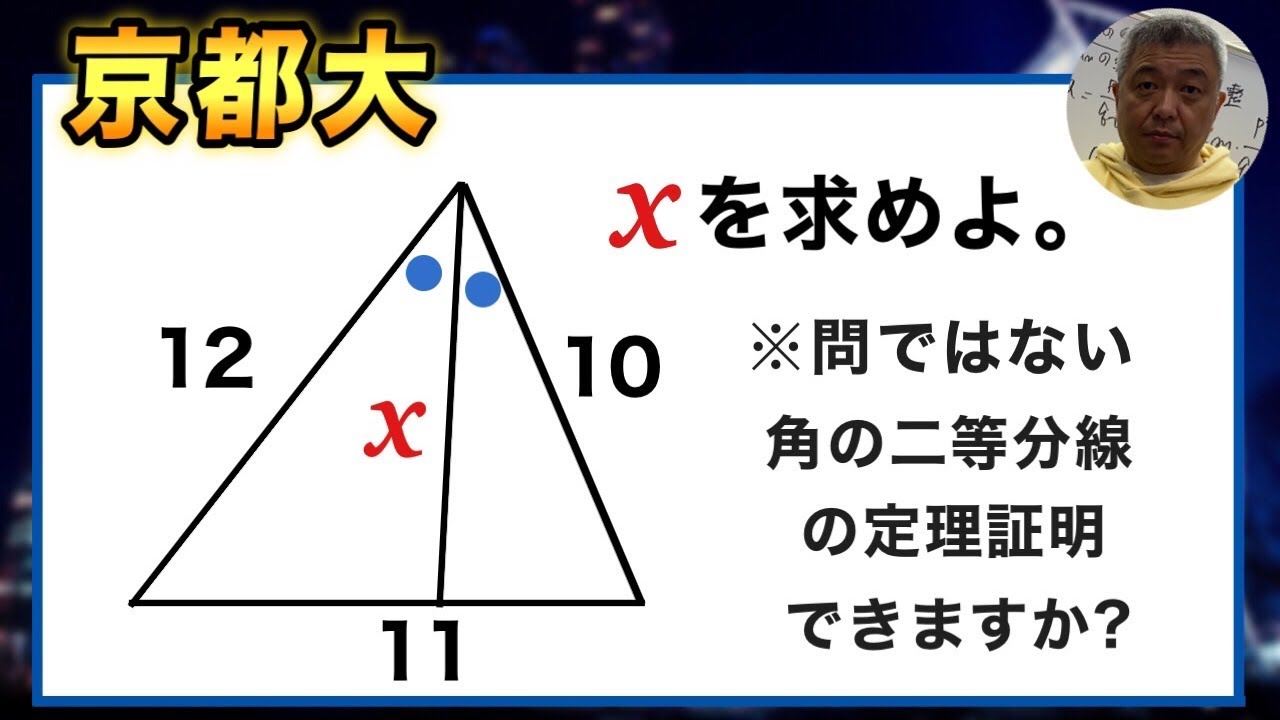
京都大 角の二等分線の定理
芝浦工大 1の4n+1乗根

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$は自然数とする.
$z^{4n+1}=1$の相異なる解を$1,\alpha_1,\alpha_2,\alpha_3・・・・・・\alpha_{4n}$とする.
$\alpha_1,\alpha_2,\alpha_3・・・・・・\alpha_{4n}=\Box$
$(\alpha_1-i)(\alpha_2-i)(\alpha_3-i)・・・・・・(\alpha_{4n}-i)=\Box$
$\Box$を求めよ.
芝浦工大過去問
この動画を見る
$n$は自然数とする.
$z^{4n+1}=1$の相異なる解を$1,\alpha_1,\alpha_2,\alpha_3・・・・・・\alpha_{4n}$とする.
$\alpha_1,\alpha_2,\alpha_3・・・・・・\alpha_{4n}=\Box$
$(\alpha_1-i)(\alpha_2-i)(\alpha_3-i)・・・・・・(\alpha_{4n}-i)=\Box$
$\Box$を求めよ.
芝浦工大過去問
慶應義塾大 方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^2-x+1=0$の解を$\alpha$とし,$x^2+x-1=0$の解を$\beta$とする.
(1)$\alpha\beta$を解にもつ4次方程式を1つ求めよ.
(2)(1)で求めた4次方程式の4つの解の平方の和を求めよ.
1996慶應(環境情報)過去問
この動画を見る
$x^2-x+1=0$の解を$\alpha$とし,$x^2+x-1=0$の解を$\beta$とする.
(1)$\alpha\beta$を解にもつ4次方程式を1つ求めよ.
(2)(1)で求めた4次方程式の4つの解の平方の和を求めよ.
1996慶應(環境情報)過去問
北海道大 数1

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\dfrac{1}{x}$の小数部分が$\dfrac{x}{2}$に等しくなるような正の数$x$をすべて求めよ.
ただし,正の数$a$の部分とは,$a$を越えない最大の整数$n$との差$a-n$のことをいう.
北海道大過去問
この動画を見る
$\dfrac{1}{x}$の小数部分が$\dfrac{x}{2}$に等しくなるような正の数$x$をすべて求めよ.
ただし,正の数$a$の部分とは,$a$を越えない最大の整数$n$との差$a-n$のことをいう.
北海道大過去問
奇数が分母の数列の和に突如あれが登場

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\Box$を求めよ.
$\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{5}-\dfrac{1}{7}+・・・・・・=\dfrac{\Box}{4}$
この動画を見る
$\Box$を求めよ.
$\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{5}-\dfrac{1}{7}+・・・・・・=\dfrac{\Box}{4}$
整数問題
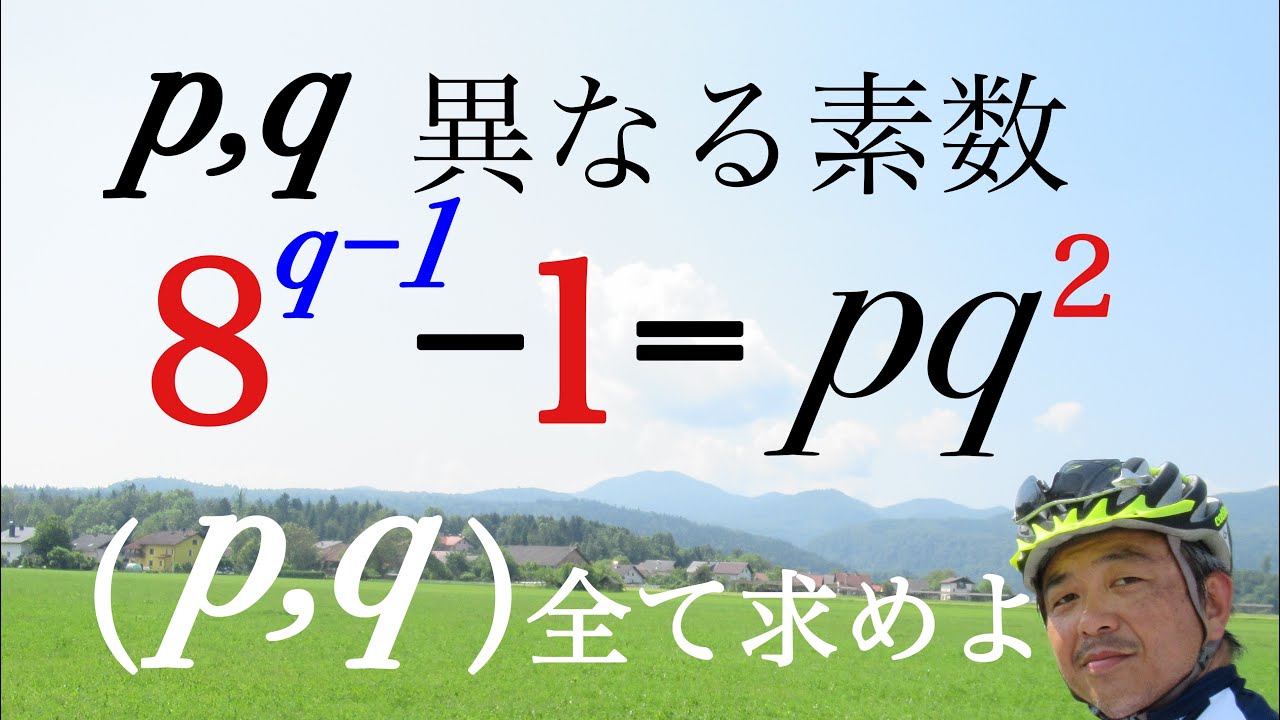
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$p,q$は異なる素数である.
$8^{q-1}-1=pq^2$の$(p,q)$を求めよ.
この動画を見る
$p,q$は異なる素数である.
$8^{q-1}-1=pq^2$の$(p,q)$を求めよ.
慶應義塾高校 入試問題 整数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\dfrac{3007}{3201}$を既約分数にせよ.
2020慶應義塾高過去問
この動画を見る
$\dfrac{3007}{3201}$を既約分数にせよ.
2020慶應義塾高過去問
一橋大 確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
サイコロを$n$回ふって
(1)$n$回目にはじめて積が$12$になる確率を求めよ.
(2)積が$12$になる確率を求めよ.
1996一橋大過去問
この動画を見る
サイコロを$n$回ふって
(1)$n$回目にはじめて積が$12$になる確率を求めよ.
(2)積が$12$になる確率を求めよ.
1996一橋大過去問
999C n が5の倍数になる最小のn

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
${}_{999} \mathrm{ C }_n$が$5$の倍数となる最小の$n$を求めよ.
この動画を見る
${}_{999} \mathrm{ C }_n$が$5$の倍数となる最小の$n$を求めよ.
金沢大 N進法の循環小数

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#数学(高校生)#金沢大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x,y,z$は1桁の自然数とする.
$N=\boxed{x}\boxed{y}.\boxed{z}_{(5)}$,$N-1=\boxed{z}\boxed{y}.\boxed{x}_{(7)}$
$(x,y,z)$の値を求めよ.
1969金沢大過去問
この動画を見る
$x,y,z$は1桁の自然数とする.
$N=\boxed{x}\boxed{y}.\boxed{z}_{(5)}$,$N-1=\boxed{z}\boxed{y}.\boxed{x}_{(7)}$
$(x,y,z)$の値を求めよ.
1969金沢大過去問
【数学A】合同式を用いた証明

単元:
#数A#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
3つの整数$a,b,c$が$a^2+b^2=c^2$を満たす。
$a,b$のうち、少なくとも1つは3の倍数であることを示せ。
この動画を見る
3つの整数$a,b,c$が$a^2+b^2=c^2$を満たす。
$a,b$のうち、少なくとも1つは3の倍数であることを示せ。
一橋大(1)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x\neq 0$は実数である.
$x+\dfrac{1}{x}$が整数なら,$x^n+\dfrac{1}{x^n}$も整数であることを示せ.$n$は自然数である.
1991一橋大過去問
この動画を見る
$x\neq 0$は実数である.
$x+\dfrac{1}{x}$が整数なら,$x^n+\dfrac{1}{x^n}$も整数であることを示せ.$n$は自然数である.
1991一橋大過去問
東大 2015 独自解法

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ {}_{2015}\mathrm{C}_{m}$が偶数となる最小の$m$を求めよ.
$1\leqq m\leqq 2015$であり,$m$は自然数とする.
2015東大過去問
この動画を見る
$ {}_{2015}\mathrm{C}_{m}$が偶数となる最小の$m$を求めよ.
$1\leqq m\leqq 2015$であり,$m$は自然数とする.
2015東大過去問
不定方程式の解の個数

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$9x^2-y^2-6x=6^m-1$を満たす自然数$(x,y)$の組は何組あるか.
この動画を見る
$9x^2-y^2-6x=6^m-1$を満たす自然数$(x,y)$の組は何組あるか.
10兵庫県教員採用試験(数学:2番 整数問題)

単元:
#数A#整数の性質#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
2⃣ $n \in \mathbb{N} $ , $\sqrt n$の整数部分をA(n)
(1)A(10)を求めよ。
(2)A(n)=3をみたすnの個数
(3)$A(1)+A(2)+A(3)+\cdots+A(n)$
この動画を見る
2⃣ $n \in \mathbb{N} $ , $\sqrt n$の整数部分をA(n)
(1)A(10)を求めよ。
(2)A(n)=3をみたすnの個数
(3)$A(1)+A(2)+A(3)+\cdots+A(n)$
