 三角関数とグラフ
三角関数とグラフ
 三角関数とグラフ
三角関数とグラフ
福田の数学〜青山学院大学2025理工学部第3問〜三角関数のグラフと面積

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
$f(x)=\cos^3 x+\sin^3 x,g(x)=\sin x$とする。
(1)$0\leqq x \leqq \pi$において、
曲線$y=f(x)$の概形を描け。
ただし、凹凸は調べなくてよい。
(2)$0\leqq x \leqq \pi$において、
$2$曲線$y=f(x),y=g(x)$の共有点の座標を求めよ。
(3)$0\leqq x \leqq \pi$において、
$2$曲線$y=f(x),y=g(x)$で囲まれた図形の
面積$S$を求めよ。
$2025$年青山学院大学理工学部過去問題
この動画を見る
$\boxed{3}$
$f(x)=\cos^3 x+\sin^3 x,g(x)=\sin x$とする。
(1)$0\leqq x \leqq \pi$において、
曲線$y=f(x)$の概形を描け。
ただし、凹凸は調べなくてよい。
(2)$0\leqq x \leqq \pi$において、
$2$曲線$y=f(x),y=g(x)$の共有点の座標を求めよ。
(3)$0\leqq x \leqq \pi$において、
$2$曲線$y=f(x),y=g(x)$で囲まれた図形の
面積$S$を求めよ。
$2025$年青山学院大学理工学部過去問題
福田の数学〜早稲田大学2025社会科学部第3問〜三角関数の最大最小と三角方程式の解の個数

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#三角関数#円と方程式#三角関数とグラフ#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
$\theta$の関数
$f(\theta)=\cos 2\theta-\sqrt3 \sin 2\theta+4\cos\dfrac{\theta}{2}\left(\sin\dfrac{\theta}{2}-\sqrt3 \cos\dfrac{\theta}{2}\right)+2\sqrt3$
を考える。
ただし、$0\leqq \theta \leqq \pi$とする。次の問いに答えよ。
(1)$k=\sin\theta-\sqrt3 \cos \theta$とおくとき、
$f(\theta)$を$k$の関数で表せ。
(2)$f(\theta)$の最大値、最小値を求めよ。
また、そのときの$\theta$の値を求めよ。
(3) (1)の$k$に対して、$\theta$の方程式
$f(\theta)=ak$の解の個数を求めよ。
ただし、定数$a$は$0\lt a \leqq 3$とする。
$2025$年早稲田大学社会科学部過去問題
この動画を見る
$\boxed{3}$
$\theta$の関数
$f(\theta)=\cos 2\theta-\sqrt3 \sin 2\theta+4\cos\dfrac{\theta}{2}\left(\sin\dfrac{\theta}{2}-\sqrt3 \cos\dfrac{\theta}{2}\right)+2\sqrt3$
を考える。
ただし、$0\leqq \theta \leqq \pi$とする。次の問いに答えよ。
(1)$k=\sin\theta-\sqrt3 \cos \theta$とおくとき、
$f(\theta)$を$k$の関数で表せ。
(2)$f(\theta)$の最大値、最小値を求めよ。
また、そのときの$\theta$の値を求めよ。
(3) (1)の$k$に対して、$\theta$の方程式
$f(\theta)=ak$の解の個数を求めよ。
ただし、定数$a$は$0\lt a \leqq 3$とする。
$2025$年早稲田大学社会科学部過去問題
福田の数学〜九州大学2025文系第2問〜円周上の2点との距離の2乗の和の最大値

単元:
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#三角関数#三角関数とグラフ#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
半径$1$の円周$C$上の$2$点$A,B$は
$AB=\sqrt3$をみたすとする。
点$P$が円周$C$上を動くとき、
$AP^2+BP^2$の最大値を求めよ。
$2025$年九州大学文系過去問題
この動画を見る
$\boxed{2}$
半径$1$の円周$C$上の$2$点$A,B$は
$AB=\sqrt3$をみたすとする。
点$P$が円周$C$上を動くとき、
$AP^2+BP^2$の最大値を求めよ。
$2025$年九州大学文系過去問題
福田のおもしろ数学530〜三角関数の最大値

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$x_i \in R \ (i=1,2,\cdots,n)$
$n$は$2$以上の自然数
$\sin x_1 \cos x_2 +\sin x_2 \cos x_3+ \cdots + \sin x_n \cos x_1$
の最大値を求めよ。
この動画を見る
$x_i \in R \ (i=1,2,\cdots,n)$
$n$は$2$以上の自然数
$\sin x_1 \cos x_2 +\sin x_2 \cos x_3+ \cdots + \sin x_n \cos x_1$
の最大値を求めよ。
福田の数学〜立教大学2025経済学部第2問〜2点の位置関係と三角関数

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
$p,q$を正の実数とする。
原点を$O$とする座標平面上に
点$A(1,0)$、点$P\left(p,\dfrac{1}{p}\right)$,点$Q\left(q,\dfrac{2}{q}\right)$がある。
$\angle AOP=\alpha,\angle AOQ=\beta$とおき、
$P,Q$は$\alpha \lt \beta$を満たしながら動くものとする。
三角形$OPQ$の面積を$S$とし、
また、$T=\tan(\beta-\alpha)$とおく。
(1)$\cos\alpha,\sin\alpha$をそれぞれ$p$を用いて表せ。
また、$\cos\beta,\sin\beta$をそれぞれ$q$を用いて表せ。
(2)$T$を$p,q$を用いて表せ。
(3)$S$を$p,q$を用いて表せ。
(4)$t=pq$とおく。$\dfrac{S}{T}$を$t$を用いて表せ。
(5)$\dfrac{S}{T}$の最小値を求めよ。
$2025$年立教大学経済学部過去問題
この動画を見る
$\boxed{2}$
$p,q$を正の実数とする。
原点を$O$とする座標平面上に
点$A(1,0)$、点$P\left(p,\dfrac{1}{p}\right)$,点$Q\left(q,\dfrac{2}{q}\right)$がある。
$\angle AOP=\alpha,\angle AOQ=\beta$とおき、
$P,Q$は$\alpha \lt \beta$を満たしながら動くものとする。
三角形$OPQ$の面積を$S$とし、
また、$T=\tan(\beta-\alpha)$とおく。
(1)$\cos\alpha,\sin\alpha$をそれぞれ$p$を用いて表せ。
また、$\cos\beta,\sin\beta$をそれぞれ$q$を用いて表せ。
(2)$T$を$p,q$を用いて表せ。
(3)$S$を$p,q$を用いて表せ。
(4)$t=pq$とおく。$\dfrac{S}{T}$を$t$を用いて表せ。
(5)$\dfrac{S}{T}$の最小値を求めよ。
$2025$年立教大学経済学部過去問題
福田のおもしろ数学334〜sin3°の値を求める

福田の数学〜北里大学2024医学部第1問(1)〜三角関数の最大最小

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#加法定理とその応用#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
2つの実数x,yは$x^2+y^2 \leqq 4,x \geqq 0 $を満たすとする。このとき、$3x+4y-3$の最小値は$\boxed{ ア }$、最大値は$\boxed{ イ }$である。また、$3x^2+4xy-3y^2$の最大値は$\boxed{ ウ }$である。
この動画を見る
2つの実数x,yは$x^2+y^2 \leqq 4,x \geqq 0 $を満たすとする。このとき、$3x+4y-3$の最小値は$\boxed{ ア }$、最大値は$\boxed{ イ }$である。また、$3x^2+4xy-3y^2$の最大値は$\boxed{ ウ }$である。
福田のおもしろ数学293〜三角方程式を満たす正の整数xの最小値

単元:
#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#整数の性質#約数・倍数・整数の割り算と余り・合同式#三角関数とグラフ#加法定理とその応用
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle \tan 19x^{\circ}\ =\ \frac{\cos 96^{\circ}+\sin 96^{\circ}}{\cos 96^{\circ}-\sin 96^{\circ}}\ $を満たす最小の正の整数$\ x\ $を求めよ。
この動画を見る
$\displaystyle \tan 19x^{\circ}\ =\ \frac{\cos 96^{\circ}+\sin 96^{\circ}}{\cos 96^{\circ}-\sin 96^{\circ}}\ $を満たす最小の正の整数$\ x\ $を求めよ。
福田の数学〜東京理科大学2024創域理工学部第1問(2)〜三角不等式の解法

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#加法定理とその応用#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}(2)0 \leqq θ \lt 2π$のとき、次の不等式を解こう。
$sin2θ \gt 2cos(θ+\frac{π}{6})+\frac{\sqrt{3}}{2}・・・③$
$a=cosθ,b=sinθ$とおくと、次の不等式$③$は
$\boxed{キ}ab-\boxed{ク}\sqrt{\boxed{ケ}}a+\boxed{コ}b-\sqrt{2}\gt0 ・・・④$
となる。不等式$④$の左辺は
$(\boxed{サ}a+\boxed{シ})(\boxed{ス}b-\sqrt{セ})$
と因数分解できる。これより、不等式$③$の解は
$\frac{π}{\boxed{ソ}} \lt θ \lt \frac{\boxed{タ}}{\boxed{チ}}π$または$\frac{\boxed{ツ}}{\boxed{テ}}π \lt θ \lt\frac{\boxed{ト}}{\boxed{ナ}}π$
と求まる。
この動画を見る
$\boxed{1}(2)0 \leqq θ \lt 2π$のとき、次の不等式を解こう。
$sin2θ \gt 2cos(θ+\frac{π}{6})+\frac{\sqrt{3}}{2}・・・③$
$a=cosθ,b=sinθ$とおくと、次の不等式$③$は
$\boxed{キ}ab-\boxed{ク}\sqrt{\boxed{ケ}}a+\boxed{コ}b-\sqrt{2}\gt0 ・・・④$
となる。不等式$④$の左辺は
$(\boxed{サ}a+\boxed{シ})(\boxed{ス}b-\sqrt{セ})$
と因数分解できる。これより、不等式$③$の解は
$\frac{π}{\boxed{ソ}} \lt θ \lt \frac{\boxed{タ}}{\boxed{チ}}π$または$\frac{\boxed{ツ}}{\boxed{テ}}π \lt θ \lt\frac{\boxed{ト}}{\boxed{ナ}}π$
と求まる。
福田の数学〜上智大学2024TEAP利用型文系第3問(3)〜直線の回転

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}(3)$座標平面において、直線$y=2x-3$を、原点を中心に反時計回りに45°回転して得られる直線は$y=\boxed{メ}x+\boxed{モ}\sqrt{\boxed{ヤ}}$である。
この動画を見る
$\boxed{3}(3)$座標平面において、直線$y=2x-3$を、原点を中心に反時計回りに45°回転して得られる直線は$y=\boxed{メ}x+\boxed{モ}\sqrt{\boxed{ヤ}}$である。
大学入試問題#916「これは受験生に失礼」 #東海大学医学部2024 #三角関数

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#数学(高校生)#東海大学
指導講師:
ますただ
問題文全文(内容文):
$\sin\alpha-\sin\beta=\displaystyle \frac{1}{3}$
$\cos\alpha+\cos\beta=\displaystyle \frac{1}{5}$
のとき、$\cos(\alpha+\beta)$の値を求めよ。
出典:2024年東海大学医学部
この動画を見る
$\sin\alpha-\sin\beta=\displaystyle \frac{1}{3}$
$\cos\alpha+\cos\beta=\displaystyle \frac{1}{5}$
のとき、$\cos(\alpha+\beta)$の値を求めよ。
出典:2024年東海大学医学部
福田のおもしろ数学212〜三角形の内角に関する不等式の証明

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\triangle \mathrm{ABC}$において、$\frac{\sin A+\sin B}{2}\leqq \sin \frac{A+B}{2} \cdots (*)$を証明してください。
この動画を見る
$\triangle \mathrm{ABC}$において、$\frac{\sin A+\sin B}{2}\leqq \sin \frac{A+B}{2} \cdots (*)$を証明してください。
福田の数学〜立教大学2024年理学部第1問(1)〜三角方程式の基本

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ (1)実数$x$が$3\cos x$=$\sin^2x$ を満たすとき、$\cos x$の値は$\boxed{\ \ ア\ \ }$である。
この動画を見る
$\Large{\boxed{1}}$ (1)実数$x$が$3\cos x$=$\sin^2x$ を満たすとき、$\cos x$の値は$\boxed{\ \ ア\ \ }$である。
三角関数 数 三角関数の不等式2【NI・SHI・NOがていねいに解説】
単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$0\leqq θ\lt 2π$のとき,次の不等式を解け。
(1) $\sin (θ+\displaystyle \frac{π}{4})\leqq \displaystyle \frac{\sqrt{3}}{2}$
(2) $\tan (θ-\displaystyle \frac{π}{6})\gt 1$
(3) $\cos (θ-\displaystyle \frac{π}{3})\lt -\displaystyle \frac{\sqrt{3}}{2}$
(4) $\tan (θ+\displaystyle \frac{π}{6})\geqq -\sqrt{3}$
この動画を見る
$0\leqq θ\lt 2π$のとき,次の不等式を解け。
(1) $\sin (θ+\displaystyle \frac{π}{4})\leqq \displaystyle \frac{\sqrt{3}}{2}$
(2) $\tan (θ-\displaystyle \frac{π}{6})\gt 1$
(3) $\cos (θ-\displaystyle \frac{π}{3})\lt -\displaystyle \frac{\sqrt{3}}{2}$
(4) $\tan (θ+\displaystyle \frac{π}{6})\geqq -\sqrt{3}$
【高校数学】全て覚える必要はない!?三角関数の性質のコツ【数学のコツ】
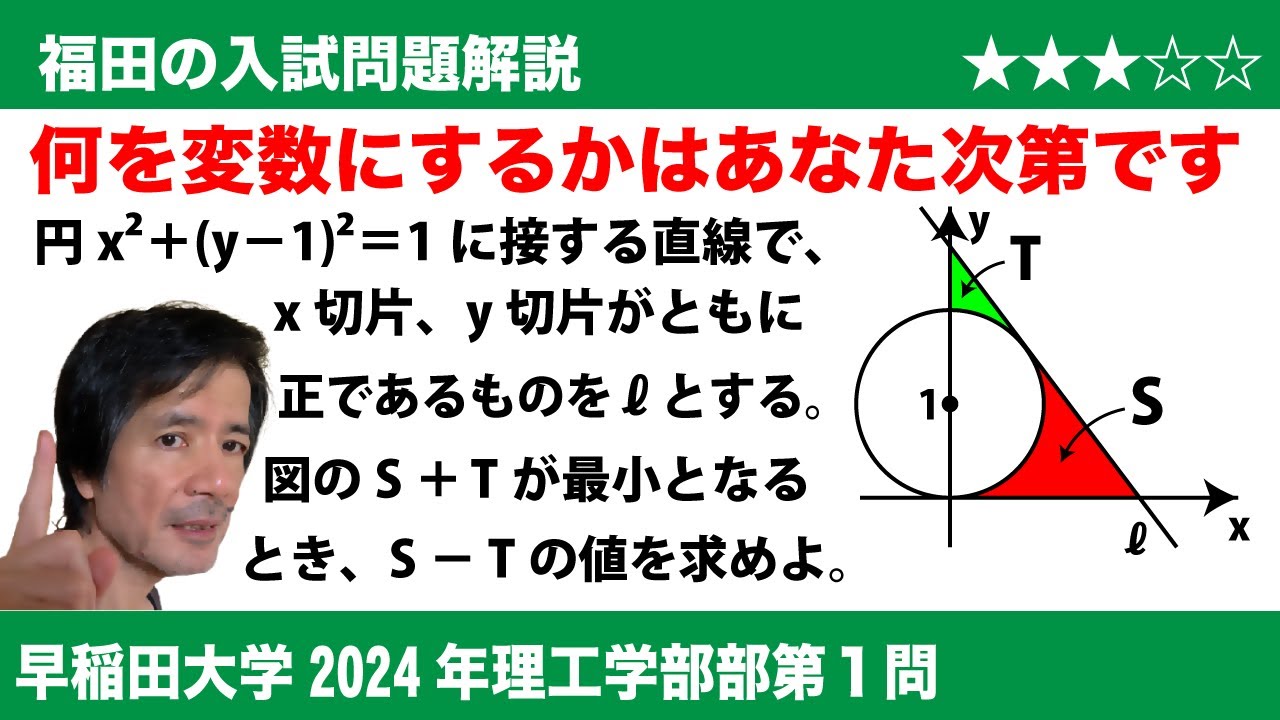
福田の数学〜早稲田大学2024年理工学部第1問〜円の接線で出来る図形の面積の最小
単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#微分法と積分法#三角関数とグラフ#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 円$C$:$x^2$+$(y-1)^2$=1 に接する直線で、$x$切片、$y$切片がともに正であるものを$l$とする。$C$と$l$と$x$軸により囲まれた部分の面積を$S$、$C$と$l$と$y$軸により囲まれた部分の面積を$T$とする。$S$+$T$が最小となるとき、$S$-$T$の値を求めよ。
この動画を見る
$\Large\boxed{1}$ 円$C$:$x^2$+$(y-1)^2$=1 に接する直線で、$x$切片、$y$切片がともに正であるものを$l$とする。$C$と$l$と$x$軸により囲まれた部分の面積を$S$、$C$と$l$と$y$軸により囲まれた部分の面積を$T$とする。$S$+$T$が最小となるとき、$S$-$T$の値を求めよ。
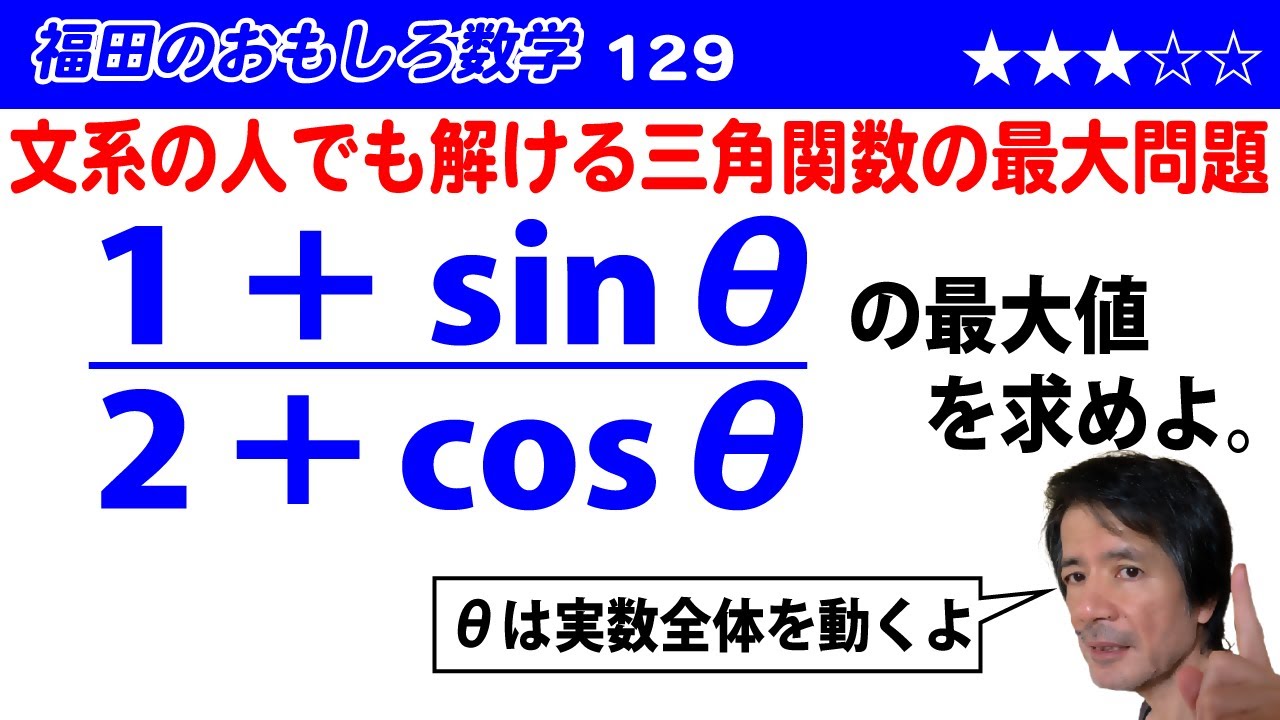
福田のおもしろ数学129〜三角関数の最大問題
単元:
#数Ⅱ#三角関数#三角関数とグラフ
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle\frac{1+\sin\theta}{2+\cos\theta}$($\theta$は実数)の最大値を求めよ。
この動画を見る
$\displaystyle\frac{1+\sin\theta}{2+\cos\theta}$($\theta$は実数)の最大値を求めよ。
福田のおもしろ数学122〜どれがどれですか?該当する関数を見つけてください

単元:
#数Ⅱ#三角関数#指数関数と対数関数#三角関数とグラフ
指導講師:
福田次郎
問題文全文(内容文):
$\begin{array}{|c|c|c|c|}
\hline
x & a & b & c\\ \hline
f_1(x) & 0.980 & 0.921 & 0.825 \\ \hline
f_2(x) & 0.063 & 0.251 & 0.565 \\ \hline
f_3(x) & 0.803 & 0.644 & 0.517 \\ \hline
f_4(x) & 0.199 & 0.389 & 0.565 \\ \hline
\end{array}$
上の数表において、$f_1(x)$, $f_2(x)$, $f_3(x)$, $f_4(x)$は関数
$\sin x$, $\cos x$, $\frac{\pi}{2}x^2$, $3^{-x}$
のうちのどれかである。どれがどれか?
ただし、$a$, $b$, $c$は0<$a$<$b$<$c$<$\frac{\pi}{2}$, $b$=$\frac{a+c}{2}$ を満たし、数値はどれも小数第4位を四捨五入してある。
この動画を見る
$\begin{array}{|c|c|c|c|}
\hline
x & a & b & c\\ \hline
f_1(x) & 0.980 & 0.921 & 0.825 \\ \hline
f_2(x) & 0.063 & 0.251 & 0.565 \\ \hline
f_3(x) & 0.803 & 0.644 & 0.517 \\ \hline
f_4(x) & 0.199 & 0.389 & 0.565 \\ \hline
\end{array}$
上の数表において、$f_1(x)$, $f_2(x)$, $f_3(x)$, $f_4(x)$は関数
$\sin x$, $\cos x$, $\frac{\pi}{2}x^2$, $3^{-x}$
のうちのどれかである。どれがどれか?
ただし、$a$, $b$, $c$は0<$a$<$b$<$c$<$\frac{\pi}{2}$, $b$=$\frac{a+c}{2}$ を満たし、数値はどれも小数第4位を四捨五入してある。
福田のおもしろ数学089〜サイン100乗とコサイン100乗の和の最大最小

単元:
#数Ⅱ#三角関数#三角関数とグラフ
指導講師:
福田次郎
問題文全文(内容文):
$\theta$がすべての実数を動くとき$\sin^{100}\theta$+$\cos^{100}\theta$ の最大値、最小値を求めよ。
この動画を見る
$\theta$がすべての実数を動くとき$\sin^{100}\theta$+$\cos^{100}\theta$ の最大値、最小値を求めよ。
【短時間でポイントチェック!!】三角関数の合成〔現役講師解説、数学〕

単元:
#数Ⅱ#三角関数#三角関数とグラフ#加法定理とその応用#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
$r \sin(\theta+\alpha)$の形に表せ。
ただし、$r>0,-\pi<\alpha≦\pi$とする。
①$\sin\theta-\cos\theta$
②$\frac{\sqrt{3}}{2}\sin\theta+\frac{1}{2}\cos\theta$
この動画を見る
$r \sin(\theta+\alpha)$の形に表せ。
ただし、$r>0,-\pi<\alpha≦\pi$とする。
①$\sin\theta-\cos\theta$
②$\frac{\sqrt{3}}{2}\sin\theta+\frac{1}{2}\cos\theta$
共テ数学90%取る勉強法

単元:
#数Ⅰ#数A#数Ⅱ#数と式#2次関数#場合の数と確率#式と証明#複素数と方程式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#2次関数とグラフ#整数の性質#場合の数#約数・倍数・整数の割り算と余り・合同式#三角関数#指数関数と対数関数#微分法と積分法#整式の除法・分数式・二項定理#複素数#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#三角関数とグラフ#指数関数#対数関数#平均変化率・極限・導関数#数列#数列とその和(等差・等比・階差・Σ)#数学的帰納法#数学(高校生)#数B
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
共通テスト数学90%取る勉強法説明動画です
この動画を見る
共通テスト数学90%取る勉強法説明動画です
数学どうにかしたい人へ

単元:
#数Ⅰ#数A#数Ⅱ#数と式#2次関数#場合の数と確率#図形の性質#式と証明#複素数と方程式#平面上のベクトル#空間ベクトル#平面上の曲線#複素数平面#図形と計量#データの分析#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#一次不等式(不等式・絶対値のある方程式・不等式)#集合と命題(集合・命題と条件・背理法)#2次方程式と2次不等式#2次関数とグラフ#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#データの分析#整数の性質#場合の数#確率#三角形の辺の比(内分・外分・二等分線)#内心・外心・重心とチェバ・メネラウス#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・N進法#図形と方程式#三角関数#指数関数と対数関数#微分法と積分法#整式の除法・分数式・二項定理#恒等式・等式・不等式の証明#複素数#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#円と方程式#軌跡と領域#三角関数とグラフ#加法定理とその応用#指数関数#対数関数#平均変化率・極限・導関数#接線と増減表・最大値・最小値#数列#確率分布と統計的な推測#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#空間ベクトル#数列とその和(等差・等比・階差・Σ)#漸化式#数学的帰納法#確率分布#統計的な推測#関数と極限#微分とその応用#積分とその応用#2次曲線#複素数平面#図形への応用#関数(分数関数・無理関数・逆関数と合成関数)#数列の極限#関数の極限#微分法#色々な関数の導関数#接線と法線・平均値の定理#関数の変化(グラフ・最大最小・方程式・不等式)#不定積分#定積分#面積・体積・長さ・速度#空間における垂直と平行と多面体(オイラーの法則)#不定積分・定積分#面積、体積#媒介変数表示と極座標#速度と近似式#数学(高校生)#数B#数C#数Ⅲ
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
数学が共通テストのみの人の勉強法紹介動画です
この動画を見る
数学が共通テストのみの人の勉強法紹介動画です
福田の数学〜中央大学2023年経済学部第1問(3)〜三角関数の最大

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$0\leqq x\leqq \require{physics}\flatfrac{\pi}{2}$のとき、次の関数が最大となる$x$の値を求めよ。
$y=\sin ^22x+2\cos^2x$
2023中央大学経済学部過去問
この動画を見る
$0\leqq x\leqq \require{physics}\flatfrac{\pi}{2}$のとき、次の関数が最大となる$x$の値を求めよ。
$y=\sin ^22x+2\cos^2x$
2023中央大学経済学部過去問
福田の数学〜上智大学2023年TEAP利用型文系第1問〜三角関数の最大最小

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 関数
$y$=2($\sin^3x$+$\cos^3x$)+8$\sin x\cos x$+5 (0≦$x$<2$\pi$)
を考える。$\sin x$+$\cos x$=$t$ とおく。
(1)$y$を$t$の式で表すと
$y$=$\boxed{\ \ ア\ \ }t^3$+$\boxed{\ \ イ\ \ }t^2$+$\boxed{\ \ ウ\ \ }t$+$\boxed{\ \ エ\ \ }$
である。
(2)関数$y$は$t$=$\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}$において最小値$\frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ ク\ \ }}$をとる。
(3)関数$y$は$x$=$\frac{\boxed{\ \ ケ\ \ }}{\boxed{\ \ コ\ \ }}\pi$において最大値$\boxed{\ \ サ\ \ }$+$\sqrt{\boxed{\ \ コ\ \ }}$をとる。
この動画を見る
$\Large\boxed{1}$ 関数
$y$=2($\sin^3x$+$\cos^3x$)+8$\sin x\cos x$+5 (0≦$x$<2$\pi$)
を考える。$\sin x$+$\cos x$=$t$ とおく。
(1)$y$を$t$の式で表すと
$y$=$\boxed{\ \ ア\ \ }t^3$+$\boxed{\ \ イ\ \ }t^2$+$\boxed{\ \ ウ\ \ }t$+$\boxed{\ \ エ\ \ }$
である。
(2)関数$y$は$t$=$\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}$において最小値$\frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ ク\ \ }}$をとる。
(3)関数$y$は$x$=$\frac{\boxed{\ \ ケ\ \ }}{\boxed{\ \ コ\ \ }}\pi$において最大値$\boxed{\ \ サ\ \ }$+$\sqrt{\boxed{\ \ コ\ \ }}$をとる。
【わかりやすく】三角不等式(2次不等式を利用)【数学Ⅰ三角比】

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
$0^{ \circ } \leqq \theta \leqq 180^{ \circ }$のとき、次の不等式を解け。
$2\cos^2\theta-\cos\theta \lt 0$
この動画を見る
$0^{ \circ } \leqq \theta \leqq 180^{ \circ }$のとき、次の不等式を解け。
$2\cos^2\theta-\cos\theta \lt 0$
【わかりやすく】三角方程式(2次方程式を利用)【数学Ⅰ三角比】

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
$0^{ \circ } \leqq \theta \leqq 180^{ \circ }$のとき、次の等式を満たす$\theta$を求めよ。
$2\sin^2\theta-3\cos\theta=0$
この動画を見る
$0^{ \circ } \leqq \theta \leqq 180^{ \circ }$のとき、次の等式を満たす$\theta$を求めよ。
$2\sin^2\theta-3\cos\theta=0$
【わかりやすく】弧度法について解説(数学Ⅱ 三角関数)

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の角を弧度法で表せ。
(1)
$30^{ \circ }$
(2)
$45^{ \circ }$
(3)
$120^{ \circ }$
(4)
$-90^{ \circ }$
(5)
$108^{ \circ }$
(6)
$390^{ \circ }$
(7)
$\displaystyle \frac{\pi}{3}$
(8)
$\displaystyle \frac{7}{6}\pi$
(9)
$\displaystyle \frac{9}{4}\pi$
(10)
$-\displaystyle \frac{5}{12}n$
(11)
$\displaystyle \frac{11}{2}\pi$
(12)
$3$
この動画を見る
次の角を弧度法で表せ。
(1)
$30^{ \circ }$
(2)
$45^{ \circ }$
(3)
$120^{ \circ }$
(4)
$-90^{ \circ }$
(5)
$108^{ \circ }$
(6)
$390^{ \circ }$
(7)
$\displaystyle \frac{\pi}{3}$
(8)
$\displaystyle \frac{7}{6}\pi$
(9)
$\displaystyle \frac{9}{4}\pi$
(10)
$-\displaystyle \frac{5}{12}n$
(11)
$\displaystyle \frac{11}{2}\pi$
(12)
$3$
大学入試問題#608「絶対値・・・・」 横浜市立大学(2009) #定積分

単元:
#数Ⅰ#数Ⅱ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#三角関数#三角関数とグラフ#加法定理とその応用#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\frac{\pi}{6}}^{\frac{\pi}{2}} |\sin2\ x| \sin\ x\ dx$
出典:2009年横浜市立大学 入試問題
この動画を見る
$\displaystyle \int_{-\frac{\pi}{6}}^{\frac{\pi}{2}} |\sin2\ x| \sin\ x\ dx$
出典:2009年横浜市立大学 入試問題
大学入試問題#607「やばい、忙しすぎる」 青山学院大学(2007) #定積分

単元:
#数Ⅱ#三角関数#三角関数とグラフ#微分とその応用#積分とその応用#微分法#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{\pi}{2}}^{\pi} x(\cos2x-\sin2x) dx$
出典:2007年青山学院大学 入試問題
この動画を見る
$\displaystyle \int_{\frac{\pi}{2}}^{\pi} x(\cos2x-\sin2x) dx$
出典:2007年青山学院大学 入試問題
【数学】2022年度 第2回 K塾記述高2模試 全問解説(ベクトルはおまけ)、※修正箇所:問1(1)(概要欄へ)

単元:
#数Ⅰ#数A#数Ⅱ#数と式#2次関数#場合の数と確率#図形の性質#複素数と方程式#図形と計量#式の計算(整式・展開・因数分解)#一次不等式(不等式・絶対値のある方程式・不等式)#2次方程式と2次不等式#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#確率#図形と方程式#三角関数#複素数#三角関数とグラフ#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
理数個別チャンネル
問題文全文(内容文):
2022年度第2回全統記述高2模試全問解説動画です!
この動画を見る
2022年度第2回全統記述高2模試全問解説動画です!
