 指数関数と対数関数
指数関数と対数関数
 指数関数と対数関数
指数関数と対数関数
微分の超頻出の問題!どこで最大値を取るかしっかり考えよう【大阪大学】【数学 入試問題】

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#微分法と積分法#対数関数#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
正の実数a,xに対して,
y=$(\log_{\frac{1}{2}}x)^{3}$+$a(\log_{\sqrt{ 2 } } x)(\log_{4} x^{3})$とする。
(1)t=$\log_{ 2 } x$とするとき,yをa,tを用いて表せ。
(2)xが$\dfrac{1}{2}$≦x≦8の範囲を動くとき,yの最大値Mをaを用いて表せ。
大阪大過去問
この動画を見る
正の実数a,xに対して,
y=$(\log_{\frac{1}{2}}x)^{3}$+$a(\log_{\sqrt{ 2 } } x)(\log_{4} x^{3})$とする。
(1)t=$\log_{ 2 } x$とするとき,yをa,tを用いて表せ。
(2)xが$\dfrac{1}{2}$≦x≦8の範囲を動くとき,yの最大値Mをaを用いて表せ。
大阪大過去問
福田の数学〜慶應義塾大学2023年薬学部第1問(6)〜指数方程式が解をもたない条件

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (6)aを実数とする。実数xの関数f(x)=$4^x$+$4^{-x}$+a($2^x$+$2^{-x}$)+$\frac{1}{3}a^2$-1 がある。
(i)t=$2^x$+$2^{-x}$とおくときtの最小値は$\boxed{\ \ ソ\ \ }$であり、f(x)をtの式で表すと$\boxed{\ \ タ\ \ }$である。
(ii)a=-3のとき、方程式f(x)=0の解をすべて求めると、x=$\boxed{\ \ チ\ \ }$である。
(iii)方程式f(x)=0が実数解を持たないようなaの値の範囲は$\boxed{\ \ ツ\ \ }$である。
この動画を見る
$\Large\boxed{1}$ (6)aを実数とする。実数xの関数f(x)=$4^x$+$4^{-x}$+a($2^x$+$2^{-x}$)+$\frac{1}{3}a^2$-1 がある。
(i)t=$2^x$+$2^{-x}$とおくときtの最小値は$\boxed{\ \ ソ\ \ }$であり、f(x)をtの式で表すと$\boxed{\ \ タ\ \ }$である。
(ii)a=-3のとき、方程式f(x)=0の解をすべて求めると、x=$\boxed{\ \ チ\ \ }$である。
(iii)方程式f(x)=0が実数解を持たないようなaの値の範囲は$\boxed{\ \ ツ\ \ }$である。
福田の数学〜慶應義塾大学2023年薬学部第1問(3)〜3次関数と絶対不等式

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#指数関数と対数関数#微分法と積分法#指数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (3)a,bを実数とし、実数xの関数f(x)をf(x)=$x^3$+$ax^2$+$bx$-6とおく。
方程式f(x)=0はx=-1を解に持ち、f'(-1)=-7である。
(i)a=$\boxed{\ \ オ\ \ }$, b=$\boxed{\ \ カ\ \ }$である。
(ii)cは正の実数とする。f(x)≧3$x^2$+4(3c-1)$x$-16がx≧0において常に成立するとき、cの値の範囲は$\boxed{\ \ キ\ \ }$である。
2023慶應義塾大学薬学部過去問
この動画を見る
$\Large\boxed{1}$ (3)a,bを実数とし、実数xの関数f(x)をf(x)=$x^3$+$ax^2$+$bx$-6とおく。
方程式f(x)=0はx=-1を解に持ち、f'(-1)=-7である。
(i)a=$\boxed{\ \ オ\ \ }$, b=$\boxed{\ \ カ\ \ }$である。
(ii)cは正の実数とする。f(x)≧3$x^2$+4(3c-1)$x$-16がx≧0において常に成立するとき、cの値の範囲は$\boxed{\ \ キ\ \ }$である。
2023慶應義塾大学薬学部過去問
昔の人は偉い!対数の近似値の求め方

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\log_{10}2=0.3010299956・・・・・・=x,$
近似値を求めよ.
この動画を見る
$\log_{10}2=0.3010299956・・・・・・=x,$
近似値を求めよ.
対数の近似値 立命館

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\log_{10}7$を小数第2位まで求めよ.
$\log_{10}2=0.3010$,
$\log_{10}3=0.4771$
立命館大過去問
この動画を見る
$\log_{10}7$を小数第2位まで求めよ.
$\log_{10}2=0.3010$,
$\log_{10}3=0.4771$
立命館大過去問
一つとは限らない
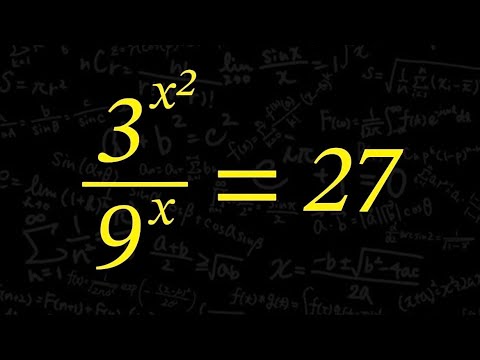
福岡大(医)連立指数方程式
単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#対数関数#学校別大学入試過去問解説(数学)#数学(高校生)#福岡大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x,y$は1でない正の実数であるとする.これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^{x+y}=y^{10} \\
y^{x+y}=x^{90}
\end{array}
\right.
\end{eqnarray}$
福岡大(医)過去問
この動画を見る
$x,y$は1でない正の実数であるとする.これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^{x+y}=y^{10} \\
y^{x+y}=x^{90}
\end{array}
\right.
\end{eqnarray}$
福岡大(医)過去問
中学生にはキツいよ
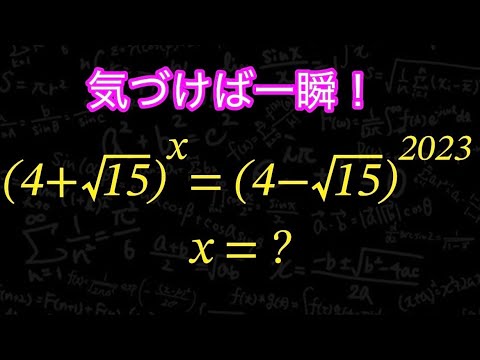
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(4+\sqrt {15})^x = (4 - \sqrt {15})^{2023}$
x=?
この動画を見る
$(4+\sqrt {15})^x = (4 - \sqrt {15})^{2023}$
x=?
答えはわかるでしょう。
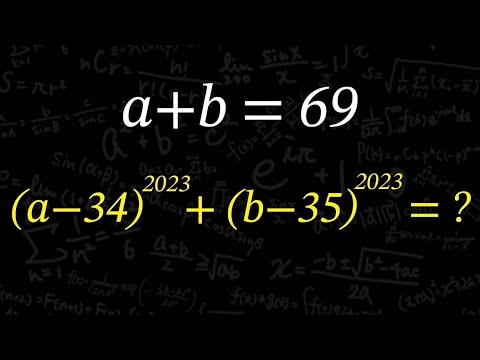
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
a+b=69
$(a - 34)^{2024} + (b-35)^{2023} = ?$
この動画を見る
a+b=69
$(a - 34)^{2024} + (b-35)^{2023} = ?$
分数の小数乗
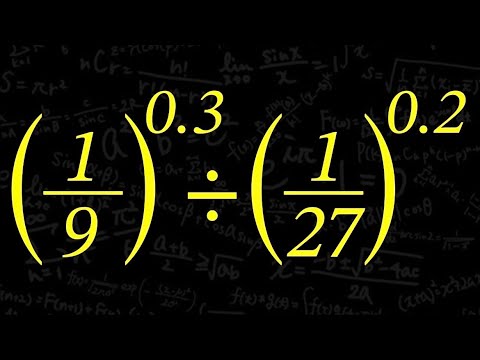
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(\frac{1}{9})^{0.3} \div (\frac{1}{27})^{0.2}$
この動画を見る
$(\frac{1}{9})^{0.3} \div (\frac{1}{27})^{0.2}$
中学生も解ける!! 指数
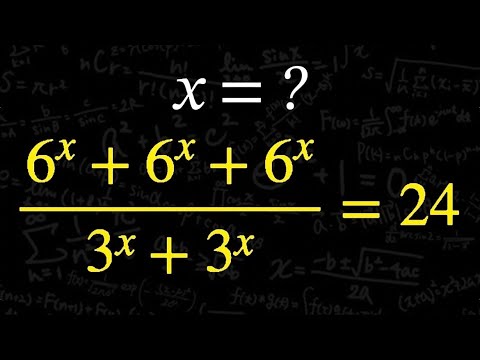
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
x=?
$\frac{6^x+6^x+6^x}{3^x+3^x} =24$
この動画を見る
x=?
$\frac{6^x+6^x+6^x}{3^x+3^x} =24$
福田の数学〜大阪大学2023年文系第2問〜対数関数と3次関数の最大

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 正の実数a, xに対して
y=$(\log_{\frac{1}{2}}x)^3$+$a\log_{\sqrt 2}x$$(\log_4x^3)$
とする。
(1)t=$\log_2x$とするとき、yをa, tを用いて表せ。
(2)xが$\frac{1}{2}$≦x≦8の範囲を動くとき、yの最大値Mをaを用いて表せ。
2023大阪大学文系過去問
この動画を見る
$\Large\boxed{2}$ 正の実数a, xに対して
y=$(\log_{\frac{1}{2}}x)^3$+$a\log_{\sqrt 2}x$$(\log_4x^3)$
とする。
(1)t=$\log_2x$とするとき、yをa, tを用いて表せ。
(2)xが$\frac{1}{2}$≦x≦8の範囲を動くとき、yの最大値Mをaを用いて表せ。
2023大阪大学文系過去問
指数の計算

小数のマイナス乗
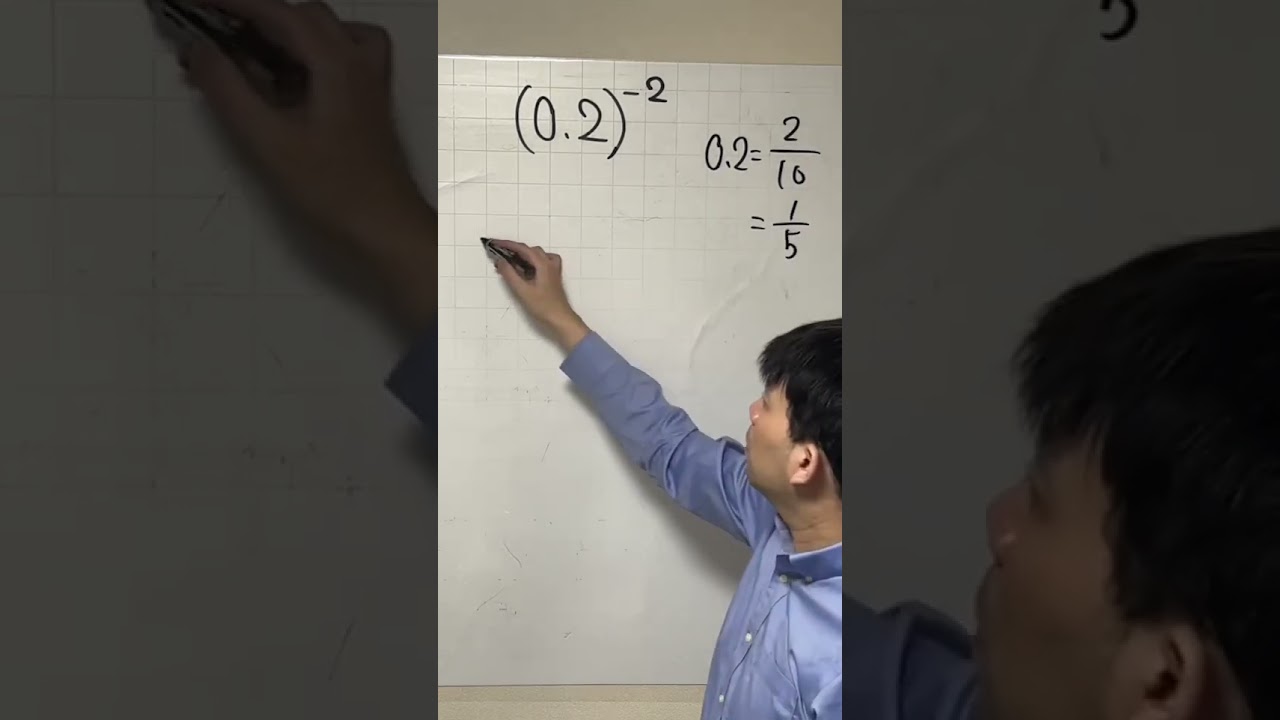
どっちがでかい?僅差!

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$2^{\sqrt{5}}と3^{\sqrt{2}}ではどちらが大きいか?$
この動画を見る
$2^{\sqrt{5}}と3^{\sqrt{2}}ではどちらが大きいか?$
大学入試問題#458「これはさすがに落とせない!」 横浜国立大学(2000) #定積分

単元:
#大学入試過去問(数学)#対数関数#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{2} \displaystyle \frac{log\ x}{(1+x)^2} dx$
出典:2000年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{2} \displaystyle \frac{log\ x}{(1+x)^2} dx$
出典:2000年横浜国立大学 入試問題
浜松医大 対数の基本 数3不要

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)2進法で30桁の自然数nを10進法で表すと何桁か,
$\log_{10}=0.3010$
(2)自然数nを2進法で表すと$a_n$桁となる.
$\displaystyle \lim_{ n \to \(x) } \dfrac{\log_{10}n}{a_n}$を求めよ.
浜松医大過去問
この動画を見る
(1)2進法で30桁の自然数nを10進法で表すと何桁か,
$\log_{10}=0.3010$
(2)自然数nを2進法で表すと$a_n$桁となる.
$\displaystyle \lim_{ n \to \(x) } \dfrac{\log_{10}n}{a_n}$を求めよ.
浜松医大過去問
どっちがでかい?対数勝負 昭和(医)

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#数学(高校生)#昭和大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \log a\sqrt{ab}$ vs $\log_{\sqrt{ab}}b$
$a>1,b<1,a \neq b$とするとき,どちらが大きいか?
昭和(医)過去問
この動画を見る
$ \log a\sqrt{ab}$ vs $\log_{\sqrt{ab}}b$
$a>1,b<1,a \neq b$とするとき,どちらが大きいか?
昭和(医)過去問
多くの単元が絡んだ問題!解けますか?【一橋大学】【数学 入試問題】

単元:
#数A#数Ⅱ#大学入試過去問(数学)#整数の性質#三角関数#指数関数と対数関数#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$0≦θ≦2\pi$とする。$\log_{ 2 }(4\sin^2θ+3\cosθ-4),$
$\log_{ 2 }(-4\cos^3θ+3\cosθ+1)$がともに整数となるような$θ$の値をすべて求めよ。
一橋大過去問
この動画を見る
$0≦θ≦2\pi$とする。$\log_{ 2 }(4\sin^2θ+3\cosθ-4),$
$\log_{ 2 }(-4\cos^3θ+3\cosθ+1)$がともに整数となるような$θ$の値をすべて求めよ。
一橋大過去問
大学入試問題#453「落とせない問題」 信州大学(2022) #定積分

単元:
#大学入試過去問(数学)#対数関数#積分とその応用#関数(分数関数・無理関数・逆関数と合成関数)#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{e}^{e^2} \displaystyle \frac{dx}{x(1+log\ x^3)log\ x}$
出典:2022年信州大学 入試問題
この動画を見る
$\displaystyle \int_{e}^{e^2} \displaystyle \frac{dx}{x(1+log\ x^3)log\ x}$
出典:2022年信州大学 入試問題
大学入試問題#452「解き方は色々とあるかと思います」 横浜国立大学(2002) #定積分

単元:
#大学入試過去問(数学)#対数関数#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{a} log(a^2+x^2) dx$
出典:2002年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{a} log(a^2+x^2) dx$
出典:2002年横浜国立大学 入試問題
指数・対数連立不等式 京都府立大

単元:
#2次関数#2次方程式と2次不等式#2次関数とグラフ#指数関数と対数関数#指数関数#対数関数
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a>0,a \neq 1$とする.
$\begin{eqnarray}
\left\{
\begin{array}{l}
a^{2x-4}-1<a^{x+1}-a^{x-5} \\
2\log_a(x-2)\geqq \log_a(x-2)+\log_a5
\end{array}
\right.
\end{eqnarray}$
連立不等式を解け.
この動画を見る
$a>0,a \neq 1$とする.
$\begin{eqnarray}
\left\{
\begin{array}{l}
a^{2x-4}-1<a^{x+1}-a^{x-5} \\
2\log_a(x-2)\geqq \log_a(x-2)+\log_a5
\end{array}
\right.
\end{eqnarray}$
連立不等式を解け.
指数・対数 × 整数問題!落としたくない問題です【大阪大学】【数学 入試問題】

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
連立方程式$\begin{eqnarray}
\left\{
\begin{array}{l}
2^x+3^y=43 \\
\log_{ 2 } x-\log_{ 3 } y=1
\end{array}
\right.
\end{eqnarray}$を考える。
(1)この連立方程式を満たす自然数$x,y$の組を求めよ。
(2)この連立方程式を満たす正の実数$x,y$は、(1)で求めた自然数の組以外に存在しないことを示せ。
大阪大過去問
この動画を見る
連立方程式$\begin{eqnarray}
\left\{
\begin{array}{l}
2^x+3^y=43 \\
\log_{ 2 } x-\log_{ 3 } y=1
\end{array}
\right.
\end{eqnarray}$を考える。
(1)この連立方程式を満たす自然数$x,y$の組を求めよ。
(2)この連立方程式を満たす正の実数$x,y$は、(1)で求めた自然数の組以外に存在しないことを示せ。
大阪大過去問
満点は激ムズ!?常用対数の難問です【お茶の水女子大学】【数学 入試問題】

単元:
#数Ⅱ#指数関数と対数関数#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
以下の問いに答えよ。ただし、必要があれば、
$0.3010<\log_{10} 2<0.3011$
$0.4771<\log_{10} 3<0.4772$であることを用いてもよい。
(1)$3^{53}$の桁数を求めよ。
(2)$3^{53}$の最高位の数と1の位の数をそれぞれ求めよ。
(3)$|3^{53}-2^m|$が最小となる整数$m$を求めよ。
お茶の水女子大過去問
この動画を見る
以下の問いに答えよ。ただし、必要があれば、
$0.3010<\log_{10} 2<0.3011$
$0.4771<\log_{10} 3<0.4772$であることを用いてもよい。
(1)$3^{53}$の桁数を求めよ。
(2)$3^{53}$の最高位の数と1の位の数をそれぞれ求めよ。
(3)$|3^{53}-2^m|$が最小となる整数$m$を求めよ。
お茶の水女子大過去問
指数方程式
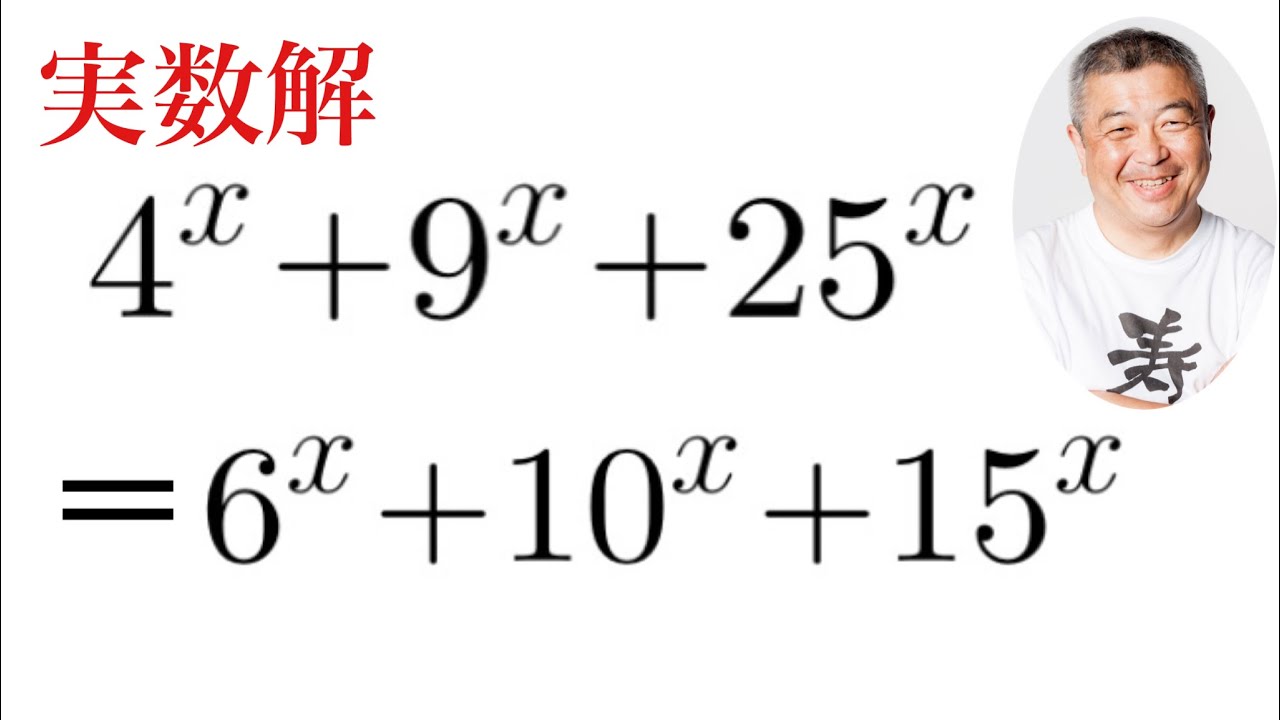
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 4^x+9^x+25^x=6^x+10^x+15^x$
これの実数解を求めよ.
この動画を見る
$ 4^x+9^x+25^x=6^x+10^x+15^x$
これの実数解を求めよ.
福田の数学〜2023年共通テスト速報〜数学IIB第1問三角関数と対数〜三角不等式と対数が有理数とならない条件

単元:
#数Ⅰ#数A#数Ⅱ#大学入試過去問(数学)#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#整数の性質#ユークリッド互除法と不定方程式・N進法#三角関数#指数関数と対数関数#三角関数とグラフ#指数関数#対数関数#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
第一問
[ 1 ] 三角関数の値の大小関係について考えよう。
(1) $x=\displaystyle\frac{\pi}{6}$のとき$\sin x\boxed{\boxed{\ \ ア\ \ }}\sin 2x$であり、$x=\frac{2}{3}\pi$のとき$\sin x\boxed{\boxed{\ \ イ\ \ }}\sin 2x$である。
$\boxed{\boxed{\ \ ア\ \ }}$, $\boxed{\boxed{\ \ イ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪< ①= ②>
(2) $\sin x$と$\sin 2x$の値の大小関係を詳しく調べよう。
$\sin 2x$-$\sin x$=$\sin 2x\left(\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ }\right)$
であるから、$\sin 2x$-$\sin x$>0が成り立つことは
「$\sin x$>0かつ $\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ } \gt 0$」... ①
「$\sin x$<0かつ $\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ } \lt 0$」... ②
が成り立つことと同値である。$0 \leqq x \leqq 2\pi$のとき、①が成り立つようなxの値の範囲は
$0 \lt x \lt \displaystyle\frac{\pi}{\boxed{\ \ オ\ \ }}$
であり、②が成り立つようなxの値の範囲は
$\pi \lt x \lt \displaystyle\frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ\ \ }}\pi$
である。よって、$0 \leqq x \leqq 2\pi$のとき、$\sin 2x \gt \sin x$が成り立つようなxの値の範囲は
$0 \lt x \lt \displaystyle\frac{\pi}{\boxed{\ \ オ\ \ }}, \pi \lt x \lt \displaystyle\frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ\ \ }}\pi$
である。
(3)$\sin 3x$と$\sin 4x$の値の大小関係を調べよう。
三角関数の加法定理を用いると、等式
$\sin(\alpha+\beta)$-$\sin(\alpha-\beta)$=$2\cos\alpha\sin\beta$...③
が得られる。$\alpha+\beta=4x$, $\alpha-\beta=3x$を満たす$\alpha$, $\beta$に対して③を用いることにより、$\sin 4x-\sin 3x \gt 0$が成り立つことは
「$\cos\boxed{\boxed{\ \ ク\ \ }} \gt 0$ かつ $\sin\boxed{\boxed{\ \ ケ\ \ }} \gt 0$」...④
または
「$\cos\boxed{\boxed{\ \ ク\ \ }} \lt 0$ かつ $\sin\boxed{\boxed{\ \ ケ\ \ }} \lt 0$」...⑤
が成り立つことと同値であることがわかる。
$0 \leqq x \leqq \pi$のとき、④,⑤により、$\sin 4x$>$\sin 3x$が成り立つようなxの値の範囲は
$0 \leqq x \leqq \displaystyle\frac{\pi}{\boxed{\ \ コ\ \ }}$, $\displaystyle\frac{\boxed{\ \ サ\ \ }}{\boxed{\ \ シ\ \ }}\pi \lt x \lt \frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}\pi$
である。
$\boxed{\boxed{\ \ ク\ \ }}$, $\boxed{\boxed{\ \ ケ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪0 ①x ②2x ③3x
④4x ⑤5x ⑥6x ⑦$\frac{x}{2}$
⑧$\frac{3}{2}x$ ⑨$\frac{5}{2}x$ ⓐ$\frac{7}{2}x$ ⓑ$\frac{9}{2}x$
(4)(2), (3)の考察から、$0 \leqq x \leqq \pi$のとき、$\sin 3x \gt \sin 4x \gt \sin 2x$が成り立つようなxの値の範囲は
$\displaystyle\frac{\pi}{\boxed{\ \ コ\ \ }}$ $\lt$ $\displaystyle\frac{\pi}{\boxed{\ \ ソ\ \ }}$, $\displaystyle\frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}\pi \lt x \lt \frac{\boxed{\ \ タ\ \ }}{\boxed{\ \ チ\ \ }}\pi$
であることがわかる。
[ 2 ]
(1)$a \gt 0$, $a \ne 1$, $b \gt 0$のとき、$\log_ab=x$とおくと、$\boxed{\boxed{\ \ ツ\ \ }}$が成り立つ。
$\boxed{\boxed{\ \ ツ\ \ }}$の解答群
⓪$x^a=b$ ①$x^b=a$ ②$a^x=b$
③$b^x=a$ ④$a^b=x$ ⑤$b^a=x$
(2)様々な対数の値が有理数か無理数かについて考えよう。
(i)$\log_5 25=\boxed{\ \ テ\ \ }$, $\log_9 27=\displaystyle\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}$であり、どちらも有理数である。
(ii)$\log_2 3$が有理数と無理数のどちらかであるかを考えよう。
$\log_2 3$が有理数であると仮定すると、$\log_2 3$>0であるので、二つの自然数p, qを用いて$\log_2 3=\displaystyle\frac{p}{q}$と表すことができる。このとき、(1)により$\log_2 3=\displaystyle\frac{p}{q}$は$\boxed{\boxed{\ \ ニ\ \ }}$と変形できる。いま、2は偶数であり3は奇数であるので、$\boxed{\boxed{\ \ ニ\ \ }}$を満たす自然数p, qは存在しない。
したがって、$\log_2 3$は無理数であることがわかる。
(iii)a, bを2以上の自然数とするとき、(ii)と同様に考えると、「$\boxed{\boxed{\ \ ヌ\ \ }}$ならば$\log_a b$は常に無理数である」ことがわかる。
$\boxed{\boxed{\ \ ヌ\ \ }}$の解答群
⓪aが偶数 ①bが偶数 ②aが奇数
③bが奇数 ④aとbがともに偶数、またはaとbがともに奇数 ⑤aとbのいずれか一方が偶数で、もう一方が奇数
2023共通テスト過去問
この動画を見る
第一問
[ 1 ] 三角関数の値の大小関係について考えよう。
(1) $x=\displaystyle\frac{\pi}{6}$のとき$\sin x\boxed{\boxed{\ \ ア\ \ }}\sin 2x$であり、$x=\frac{2}{3}\pi$のとき$\sin x\boxed{\boxed{\ \ イ\ \ }}\sin 2x$である。
$\boxed{\boxed{\ \ ア\ \ }}$, $\boxed{\boxed{\ \ イ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪< ①= ②>
(2) $\sin x$と$\sin 2x$の値の大小関係を詳しく調べよう。
$\sin 2x$-$\sin x$=$\sin 2x\left(\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ }\right)$
であるから、$\sin 2x$-$\sin x$>0が成り立つことは
「$\sin x$>0かつ $\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ } \gt 0$」... ①
「$\sin x$<0かつ $\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ } \lt 0$」... ②
が成り立つことと同値である。$0 \leqq x \leqq 2\pi$のとき、①が成り立つようなxの値の範囲は
$0 \lt x \lt \displaystyle\frac{\pi}{\boxed{\ \ オ\ \ }}$
であり、②が成り立つようなxの値の範囲は
$\pi \lt x \lt \displaystyle\frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ\ \ }}\pi$
である。よって、$0 \leqq x \leqq 2\pi$のとき、$\sin 2x \gt \sin x$が成り立つようなxの値の範囲は
$0 \lt x \lt \displaystyle\frac{\pi}{\boxed{\ \ オ\ \ }}, \pi \lt x \lt \displaystyle\frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ\ \ }}\pi$
である。
(3)$\sin 3x$と$\sin 4x$の値の大小関係を調べよう。
三角関数の加法定理を用いると、等式
$\sin(\alpha+\beta)$-$\sin(\alpha-\beta)$=$2\cos\alpha\sin\beta$...③
が得られる。$\alpha+\beta=4x$, $\alpha-\beta=3x$を満たす$\alpha$, $\beta$に対して③を用いることにより、$\sin 4x-\sin 3x \gt 0$が成り立つことは
「$\cos\boxed{\boxed{\ \ ク\ \ }} \gt 0$ かつ $\sin\boxed{\boxed{\ \ ケ\ \ }} \gt 0$」...④
または
「$\cos\boxed{\boxed{\ \ ク\ \ }} \lt 0$ かつ $\sin\boxed{\boxed{\ \ ケ\ \ }} \lt 0$」...⑤
が成り立つことと同値であることがわかる。
$0 \leqq x \leqq \pi$のとき、④,⑤により、$\sin 4x$>$\sin 3x$が成り立つようなxの値の範囲は
$0 \leqq x \leqq \displaystyle\frac{\pi}{\boxed{\ \ コ\ \ }}$, $\displaystyle\frac{\boxed{\ \ サ\ \ }}{\boxed{\ \ シ\ \ }}\pi \lt x \lt \frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}\pi$
である。
$\boxed{\boxed{\ \ ク\ \ }}$, $\boxed{\boxed{\ \ ケ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪0 ①x ②2x ③3x
④4x ⑤5x ⑥6x ⑦$\frac{x}{2}$
⑧$\frac{3}{2}x$ ⑨$\frac{5}{2}x$ ⓐ$\frac{7}{2}x$ ⓑ$\frac{9}{2}x$
(4)(2), (3)の考察から、$0 \leqq x \leqq \pi$のとき、$\sin 3x \gt \sin 4x \gt \sin 2x$が成り立つようなxの値の範囲は
$\displaystyle\frac{\pi}{\boxed{\ \ コ\ \ }}$ $\lt$ $\displaystyle\frac{\pi}{\boxed{\ \ ソ\ \ }}$, $\displaystyle\frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}\pi \lt x \lt \frac{\boxed{\ \ タ\ \ }}{\boxed{\ \ チ\ \ }}\pi$
であることがわかる。
[ 2 ]
(1)$a \gt 0$, $a \ne 1$, $b \gt 0$のとき、$\log_ab=x$とおくと、$\boxed{\boxed{\ \ ツ\ \ }}$が成り立つ。
$\boxed{\boxed{\ \ ツ\ \ }}$の解答群
⓪$x^a=b$ ①$x^b=a$ ②$a^x=b$
③$b^x=a$ ④$a^b=x$ ⑤$b^a=x$
(2)様々な対数の値が有理数か無理数かについて考えよう。
(i)$\log_5 25=\boxed{\ \ テ\ \ }$, $\log_9 27=\displaystyle\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}$であり、どちらも有理数である。
(ii)$\log_2 3$が有理数と無理数のどちらかであるかを考えよう。
$\log_2 3$が有理数であると仮定すると、$\log_2 3$>0であるので、二つの自然数p, qを用いて$\log_2 3=\displaystyle\frac{p}{q}$と表すことができる。このとき、(1)により$\log_2 3=\displaystyle\frac{p}{q}$は$\boxed{\boxed{\ \ ニ\ \ }}$と変形できる。いま、2は偶数であり3は奇数であるので、$\boxed{\boxed{\ \ ニ\ \ }}$を満たす自然数p, qは存在しない。
したがって、$\log_2 3$は無理数であることがわかる。
(iii)a, bを2以上の自然数とするとき、(ii)と同様に考えると、「$\boxed{\boxed{\ \ ヌ\ \ }}$ならば$\log_a b$は常に無理数である」ことがわかる。
$\boxed{\boxed{\ \ ヌ\ \ }}$の解答群
⓪aが偶数 ①bが偶数 ②aが奇数
③bが奇数 ④aとbがともに偶数、またはaとbがともに奇数 ⑤aとbのいずれか一方が偶数で、もう一方が奇数
2023共通テスト過去問
福田の1.5倍速演習〜合格する重要問題072〜上智大学2019年度理工学部第3問〜ガウス記号で定義された数列

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{3}}$ $\alpha=\log_23$とし、自然数nに対して
$a_n=[n\alpha]$, $b_n=\left[\displaystyle\frac{n\alpha}{\alpha-1}\right]$
とする。ただし、実数xに対して[x]はxを超えない最大の整数を表す。
(1)$a_5=\boxed{\ \ ス\ \ }$である。
(2)$b_3=k$とおくと、不等式$\displaystyle\frac{3^{k+c}}{2^k} \leqq 1 \lt \frac{3^{k+1+c}}{2^{k+1}}$が整数$c=\boxed{\ \ セ\ \ }$で成り立ち、
$b_3=\boxed{\ \ ソ\ \ }$であることがわかる。
(3)$a_n \leqq$ 10を満たす自然数nの個数は$\boxed{\ \ タ\ \ }$である。
(4)$b_n \leqq$ 10を満たす自然数nの個数は$\boxed{\ \ チ\ \ }$である。
(5)$a_n \leqq$ 50を満たす自然数nの個数をsとし、$b_n \leqq$ 50を満たす自然数nの個数をtとする。このとき、s+t=$\boxed{\ \ ツ\ \ }$である。
2019上智大学理工学部過去問
この動画を見る
$\Large{\boxed{3}}$ $\alpha=\log_23$とし、自然数nに対して
$a_n=[n\alpha]$, $b_n=\left[\displaystyle\frac{n\alpha}{\alpha-1}\right]$
とする。ただし、実数xに対して[x]はxを超えない最大の整数を表す。
(1)$a_5=\boxed{\ \ ス\ \ }$である。
(2)$b_3=k$とおくと、不等式$\displaystyle\frac{3^{k+c}}{2^k} \leqq 1 \lt \frac{3^{k+1+c}}{2^{k+1}}$が整数$c=\boxed{\ \ セ\ \ }$で成り立ち、
$b_3=\boxed{\ \ ソ\ \ }$であることがわかる。
(3)$a_n \leqq$ 10を満たす自然数nの個数は$\boxed{\ \ タ\ \ }$である。
(4)$b_n \leqq$ 10を満たす自然数nの個数は$\boxed{\ \ チ\ \ }$である。
(5)$a_n \leqq$ 50を満たす自然数nの個数をsとし、$b_n \leqq$ 50を満たす自然数nの個数をtとする。このとき、s+t=$\boxed{\ \ ツ\ \ }$である。
2019上智大学理工学部過去問
福田の1.5倍速演習〜合格する重要問題056〜神戸大学2017年度文系第1問〜3次関数の最大最小

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#接線と増減表・最大値・最小値#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ tを正の実数とする。$f(x)=x^3+3x^2-3(t^2-1)x+2t^3-3t^2+1$とおく。
以下の問いに答えよ。
(1)2t^3-3t^2+1 を因数分解せよ。
(2)$f(x)$が極小値0をもつことを示せ。
(3)$-1 \leqq x \leqq 2$における$f(x)$の最小値$m$と最大値$M$をtの式で表せ。
2017神戸大学文系過去問
この動画を見る
$\Large{\boxed{1}}$ tを正の実数とする。$f(x)=x^3+3x^2-3(t^2-1)x+2t^3-3t^2+1$とおく。
以下の問いに答えよ。
(1)2t^3-3t^2+1 を因数分解せよ。
(2)$f(x)$が極小値0をもつことを示せ。
(3)$-1 \leqq x \leqq 2$における$f(x)$の最小値$m$と最大値$M$をtの式で表せ。
2017神戸大学文系過去問
解けるように作られた指数方程式
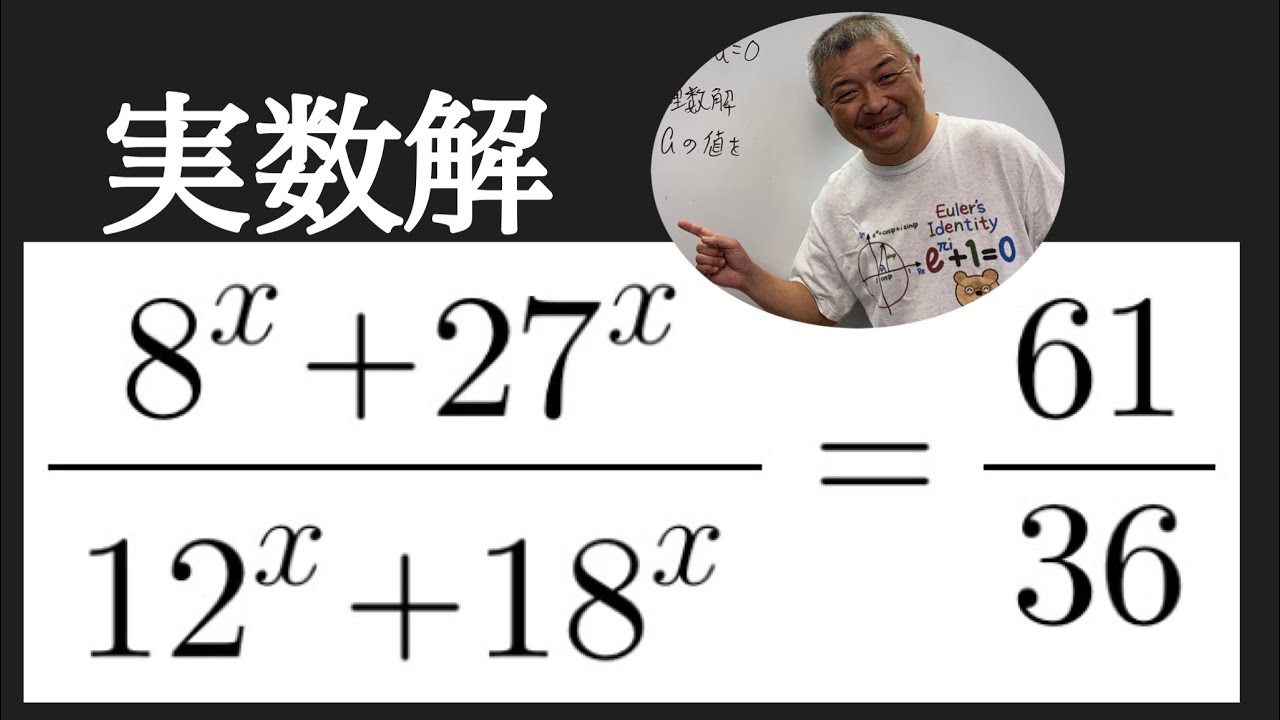
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$実数解 $\dfrac{8^x+27^x}{12^x+18^x}=\dfrac{61}{36}$
これを求めよ.
この動画を見る
$実数解 $\dfrac{8^x+27^x}{12^x+18^x}=\dfrac{61}{36}$
これを求めよ.
問題は解けるようにできている。 指数の計算 早実
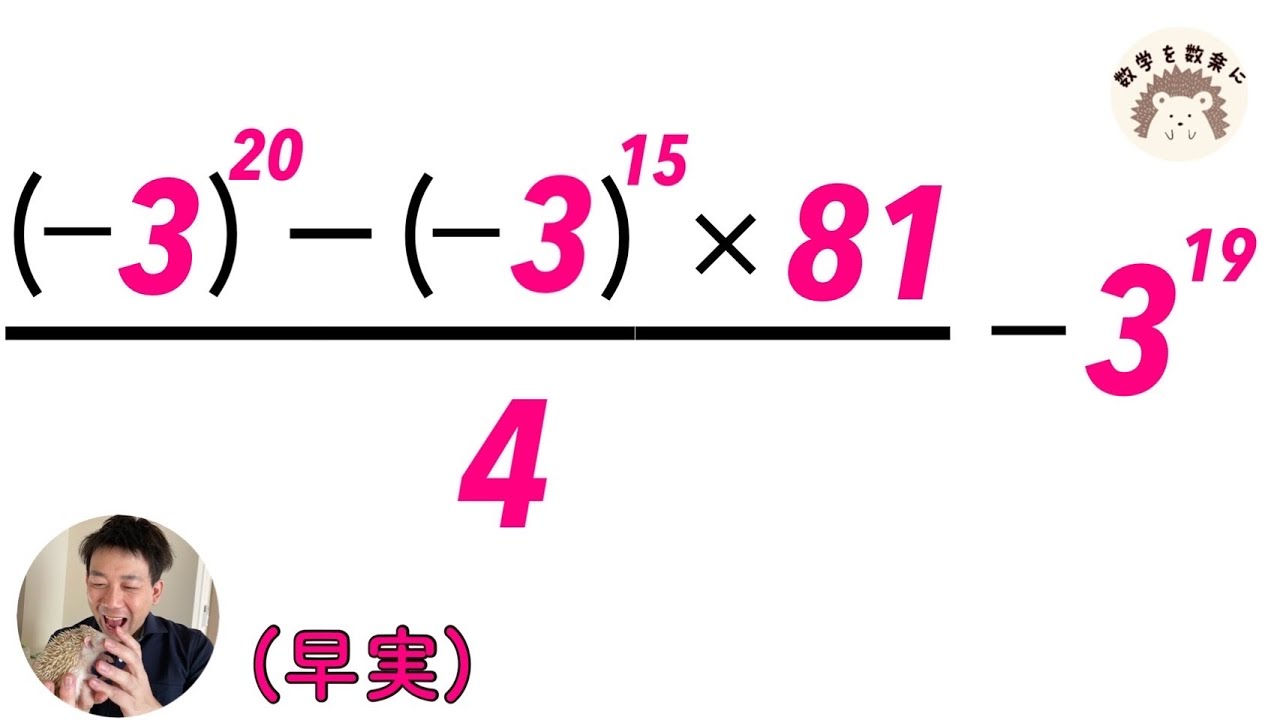
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{(-3)^{20}-(-3)^{15} \times 81}{4} -3^{19}$
早稲田実業学校
この動画を見る
$\frac{(-3)^{20}-(-3)^{15} \times 81}{4} -3^{19}$
早稲田実業学校
