 数Ⅱ
数Ⅱ
 数Ⅱ
数Ⅱ
【高校数学】不等式の証明~どこよりも丁寧に~ 1-11【数学Ⅱ】

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
(1) x > 1,y > 1のとき次の不等式が成り立つことを証明せよ
xy + 1 > x + y
(2) 不等式 a²- ab + b² ≧0を証明せよ
また、等号が成り立つのはどのようなときか。
この動画を見る
(1) x > 1,y > 1のとき次の不等式が成り立つことを証明せよ
xy + 1 > x + y
(2) 不等式 a²- ab + b² ≧0を証明せよ
また、等号が成り立つのはどのようなときか。
【短時間でマスター!!】直線の方程式(平行と垂直)の求め方を解説!〔現役講師解説、数学〕

単元:
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
数学2B
直線の方程式
並行と垂直の条件
①点$(1,-3)$を通り、直線$4x+5y=2$に平行な直線
②点$(0,1)$を通り、直線$y=-3x-1$に垂直な直線
この動画を見る
数学2B
直線の方程式
並行と垂直の条件
①点$(1,-3)$を通り、直線$4x+5y=2$に平行な直線
②点$(0,1)$を通り、直線$y=-3x-1$に垂直な直線
福田の数学〜早稲田大学2023年人間科学部第6問〜関数の極値と回転体の体積

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{6}$ 関数$y$=$e^x\sin x$は$x$=$a$(0<$a$<$\pi$)において極値を取る。このとき、
$a$=$\frac{\boxed{シ}}{\boxed{ス}}\pi$である。また、曲線$y$=$e^x\sin x$(0≦$x$≦$a$)と直線$x$=$a$および$x$軸によって囲まれた図形を$x$軸のまわりに1回転してできる立体の体積Vは、
$p$=$\frac{\boxed{セ}}{\boxed{ソ}}$として、V=$\frac{\boxed{タ}e^{px}+\boxed{チ}}{\boxed{ツ}}\pi$
である。
この動画を見る
$\Large\boxed{6}$ 関数$y$=$e^x\sin x$は$x$=$a$(0<$a$<$\pi$)において極値を取る。このとき、
$a$=$\frac{\boxed{シ}}{\boxed{ス}}\pi$である。また、曲線$y$=$e^x\sin x$(0≦$x$≦$a$)と直線$x$=$a$および$x$軸によって囲まれた図形を$x$軸のまわりに1回転してできる立体の体積Vは、
$p$=$\frac{\boxed{セ}}{\boxed{ソ}}$として、V=$\frac{\boxed{タ}e^{px}+\boxed{チ}}{\boxed{ツ}}\pi$
である。
式の証明 山梨大
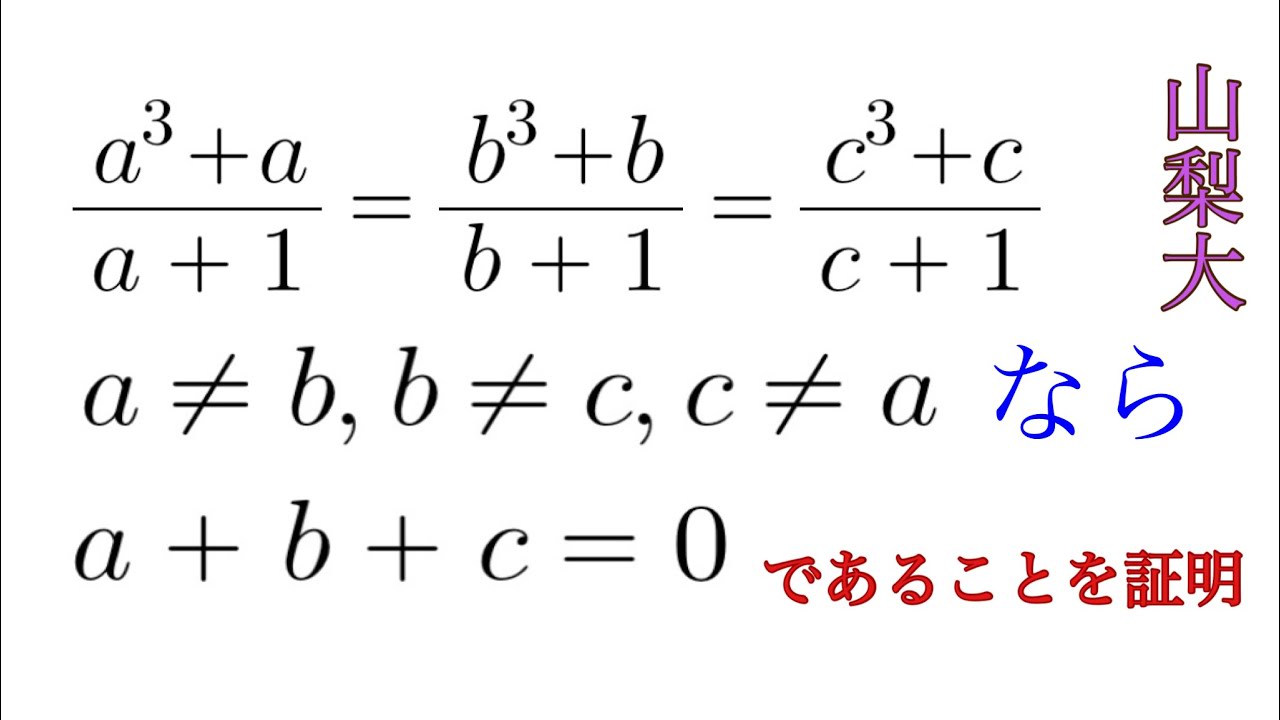
単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#山梨大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
2019年 山梨大学 過去問
$\frac{a^3+a}{a+1}=\frac{b^3+b}{b+1}=\frac{c^3+c}{c+1}$
$a \neq b$、$b \neq c、c \neq a$のとき
a+b+c=0であることを証明せよ。
この動画を見る
2019年 山梨大学 過去問
$\frac{a^3+a}{a+1}=\frac{b^3+b}{b+1}=\frac{c^3+c}{c+1}$
$a \neq b$、$b \neq c、c \neq a$のとき
a+b+c=0であることを証明せよ。
福田の数学〜早稲田大学2023年人間科学部第2問〜対数不等式

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 不等式
$\log_4(16-x^2-y^2)$≧$\displaystyle\frac{3}{2}$+2$\log_{16}(2-x)$
を満たす点P($x$,$y$)の中で、$x$座標と$y$座標がともに整数であるものは$\boxed{\ \ オ\ \ }$個ある。このうち、$x$座標が最小となる点は($\boxed{\ \ カ\ \ }$, $\boxed{\ \ キ\ \ }$)である。
この動画を見る
$\Large\boxed{2}$ 不等式
$\log_4(16-x^2-y^2)$≧$\displaystyle\frac{3}{2}$+2$\log_{16}(2-x)$
を満たす点P($x$,$y$)の中で、$x$座標と$y$座標がともに整数であるものは$\boxed{\ \ オ\ \ }$個ある。このうち、$x$座標が最小となる点は($\boxed{\ \ カ\ \ }$, $\boxed{\ \ キ\ \ }$)である。
福田の数学〜早稲田大学2023年人間科学部第1問(3)〜指数不等式

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#対数関数#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (3)$5^{n+5}$>$11^n$ を満たす自然数$n$は$\boxed{\ \ エ\ \ }$個ある。
ただし、$log_511$=1.49 とする。
この動画を見る
$\Large\boxed{1}$ (3)$5^{n+5}$>$11^n$ を満たす自然数$n$は$\boxed{\ \ エ\ \ }$個ある。
ただし、$log_511$=1.49 とする。
福田の数学〜早稲田大学2023年人間科学部第1問(2)〜式の値と1の3乗根

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (2)$x^2$+$x$+1=0 のとき、$x^{20}$+$x$=$\boxed{\ \ ウ\ \ }$ である。
この動画を見る
$\Large\boxed{1}$ (2)$x^2$+$x$+1=0 のとき、$x^{20}$+$x$=$\boxed{\ \ ウ\ \ }$ である。
整数問題 2通りの解法で

単元:
#数A#数Ⅱ#整数の性質#約数・倍数・整数の割り算と余り・合同式#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$ 自然数
$7^{2n-1}+9^{2n-1}+47^{2n-1}$
は63の倍数であることを示せ。
この動画を見る
$n$ 自然数
$7^{2n-1}+9^{2n-1}+47^{2n-1}$
は63の倍数であることを示せ。
大学入試問題#614「これは、時間内で解くのは大変かもしれない」 立命館大学(2023) #曲線の長さ

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#学校別大学入試過去問解説(数学)#数学(高校生)#立命館大学
指導講師:
ますただ
問題文全文(内容文):
次の曲線の長さ$L$を求めよ。
$\begin{eqnarray}
\left\{
\begin{array}{l}
x=\cos^4\theta \\
y=\sin^4\theta
\end{array}
\right.
\end{eqnarray}$
$(0 \leqq \theta \leqq \displaystyle \frac{\pi}{2})$
出典:2023年立命館大学 入試問題
この動画を見る
次の曲線の長さ$L$を求めよ。
$\begin{eqnarray}
\left\{
\begin{array}{l}
x=\cos^4\theta \\
y=\sin^4\theta
\end{array}
\right.
\end{eqnarray}$
$(0 \leqq \theta \leqq \displaystyle \frac{\pi}{2})$
出典:2023年立命館大学 入試問題
連立方程式
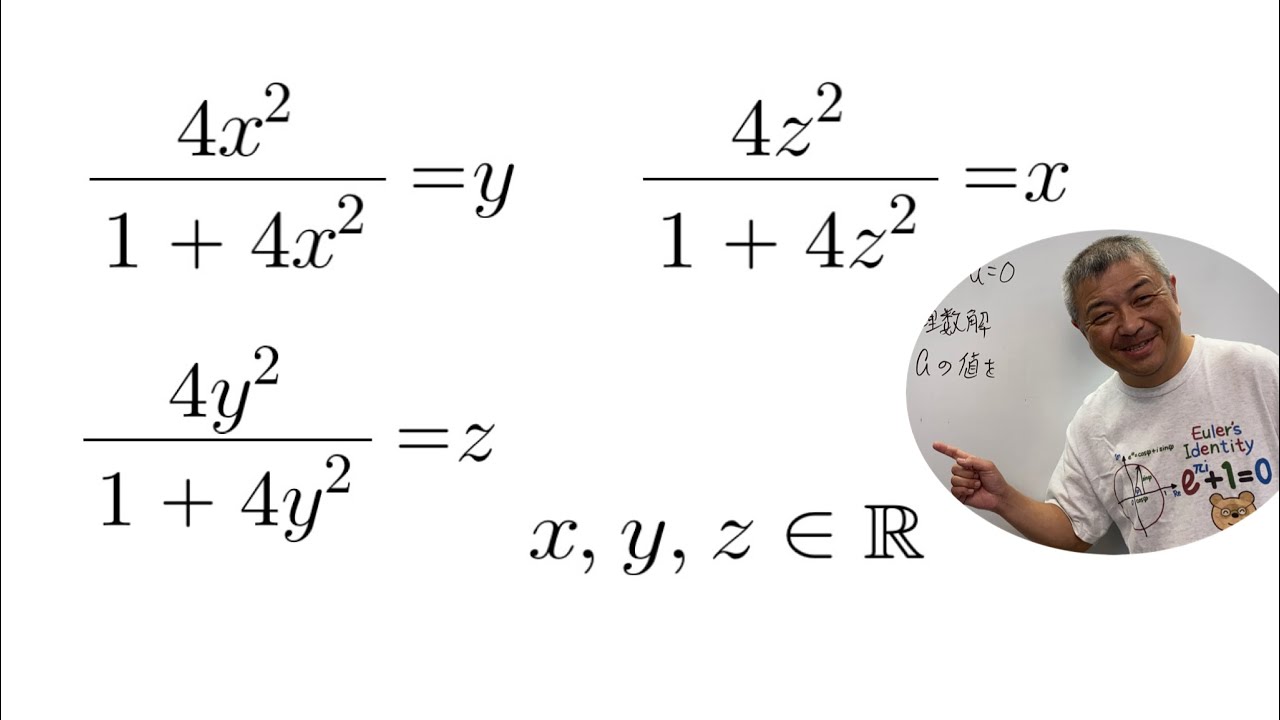
単元:
#連立方程式#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x,y,z$は実数とする.これを解け.
これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
xy+x+y=1 \\
x^2y^2+x^2+y^2=31
\end{array}
\right.
\end{eqnarray}$
この動画を見る
$x,y,z$は実数とする.これを解け.
これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
xy+x+y=1 \\
x^2y^2+x^2+y^2=31
\end{array}
\right.
\end{eqnarray}$
福田の数学〜浜松医科大学2023年医学部第2問〜定積分と極限とグラフ

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#浜松医科大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
医療で使われる技術の1つとして、磁気共鳴画像法 (MRI) がある。
MRI は画像の濃淡を表す関数、例えば
$M(x)=\displaystyle \lim_{ n \to \infty } I_n(x) $ (xは実数)
を用いて体内の様子を可視化する技術である。 ここで $I_n(x) $ は
$I_n(x) = \displaystyle \int_0^n e^{ -t }cos(tx)dt $
(n=1, 2, 3, ...)である。以下の問いに答えよ。
(1) 定積分$I_n(x) $を求めよ。
(2) $M(x)=\displaystyle \lim_{ n \to \infty } I_n(x) $ を求めよ
2023浜松医科大学医過去問
(3) 関数 $y= M(x)$ について、増減、極値、グラフの凹凸および変曲点を調べて、そのグラフをかけ。
この動画を見る
医療で使われる技術の1つとして、磁気共鳴画像法 (MRI) がある。
MRI は画像の濃淡を表す関数、例えば
$M(x)=\displaystyle \lim_{ n \to \infty } I_n(x) $ (xは実数)
を用いて体内の様子を可視化する技術である。 ここで $I_n(x) $ は
$I_n(x) = \displaystyle \int_0^n e^{ -t }cos(tx)dt $
(n=1, 2, 3, ...)である。以下の問いに答えよ。
(1) 定積分$I_n(x) $を求めよ。
(2) $M(x)=\displaystyle \lim_{ n \to \infty } I_n(x) $ を求めよ
2023浜松医科大学医過去問
(3) 関数 $y= M(x)$ について、増減、極値、グラフの凹凸および変曲点を調べて、そのグラフをかけ。
千葉大 複素数の方程式

単元:
#数Ⅱ#複素数と方程式#複素数#解と判別式・解と係数の関係#千葉大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
2023千葉大学過去問題
①$z^3=i$を解け
②$z^{100}=i$の解で 実部$\leqq \frac{1}{2}$
かつ虚部$\geqq 0$は何個あるか?
この動画を見る
2023千葉大学過去問題
①$z^3=i$を解け
②$z^{100}=i$の解で 実部$\leqq \frac{1}{2}$
かつ虚部$\geqq 0$は何個あるか?
【短時間でマスター!!】円の方程式(中心と半径)の求め方を解説!〔現役講師解説、数学〕

単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
数学2B
円の方程式
中心と半径の求め方について解説します。
次の方程式はどのような図形を表すか。
①$x^2+y^2+2y-3=0$
②$x^2+y^2+4x-6y-4=0$
この動画を見る
数学2B
円の方程式
中心と半径の求め方について解説します。
次の方程式はどのような図形を表すか。
①$x^2+y^2+2y-3=0$
②$x^2+y^2+4x-6y-4=0$
福田の数学〜浜松医科大学2023年医学部第1問〜高次方程式の解

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
次の条件を満たす係数が整数の多項式 $f(x)$ を考える。
(I) $f(0)$ は4で割り切れない。
(II) 方程式$f(x) = 0 $は$ x = 1 $で重解をもつ。
(III) 方程式$f(x)=x(x-1)(x-2)$ は異なる整数解をもつ。
このとき、$f(4)$ を36で割ったときの余りを求めよ。
2023浜松医科大学医過去問
この動画を見る
次の条件を満たす係数が整数の多項式 $f(x)$ を考える。
(I) $f(0)$ は4で割り切れない。
(II) 方程式$f(x) = 0 $は$ x = 1 $で重解をもつ。
(III) 方程式$f(x)=x(x-1)(x-2)$ は異なる整数解をもつ。
このとき、$f(4)$ を36で割ったときの余りを求めよ。
2023浜松医科大学医過去問
cosの和を求める

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\cos \dfrac{\pi}{7}-\cos \dfrac{2\pi}{7}+\cos \dfrac{3\pi}{7}$を求めよ
この動画を見る
$\cos \dfrac{\pi}{7}-\cos \dfrac{2\pi}{7}+\cos \dfrac{3\pi}{7}$を求めよ
内角と外角 愛工大名電(愛知県)

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#円と方程式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
正n角形の頂点における内角の大きさが外角の大きさより90°大きいときnの値を求めよ。
愛知工業大学名電高等学校
この動画を見る
正n角形の頂点における内角の大きさが外角の大きさより90°大きいときnの値を求めよ。
愛知工業大学名電高等学校
筑波大 4次方程式
単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
2006年 国立大学法人筑波大学 過去問
$f(x)=x^4+2x^2-4x+8$
$(x^2+t)^2-f(x)=(px+q)^2$
を満たす整数$p,q,t$
$f(x)=0$を解け
この動画を見る
2006年 国立大学法人筑波大学 過去問
$f(x)=x^4+2x^2-4x+8$
$(x^2+t)^2-f(x)=(px+q)^2$
を満たす整数$p,q,t$
$f(x)=0$を解け
サッカーボールの頂点の個数は? 共栄学園(東東京)

単元:
#数Ⅱ#点と直線#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
12個の正五角形と20個の正六角形の合わせて32面からなる多面体
どの頂点にも1個の正五角形と2個の正六角形の面が集まっている
この多面体の頂点の個数は?
共栄学園高等学校
この動画を見る
12個の正五角形と20個の正六角形の合わせて32面からなる多面体
どの頂点にも1個の正五角形と2個の正六角形の面が集まっている
この多面体の頂点の個数は?
共栄学園高等学校
大学入試問題#608「絶対値・・・・」 横浜市立大学(2009) #定積分

単元:
#数Ⅰ#数Ⅱ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#三角関数#三角関数とグラフ#加法定理とその応用#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\frac{\pi}{6}}^{\frac{\pi}{2}} |\sin2\ x| \sin\ x\ dx$
出典:2009年横浜市立大学 入試問題
この動画を見る
$\displaystyle \int_{-\frac{\pi}{6}}^{\frac{\pi}{2}} |\sin2\ x| \sin\ x\ dx$
出典:2009年横浜市立大学 入試問題
大学入試問題#607「やばい、忙しすぎる」 青山学院大学(2007) #定積分

単元:
#数Ⅱ#三角関数#三角関数とグラフ#微分とその応用#積分とその応用#微分法#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{\pi}{2}}^{\pi} x(\cos2x-\sin2x) dx$
出典:2007年青山学院大学 入試問題
この動画を見る
$\displaystyle \int_{\frac{\pi}{2}}^{\pi} x(\cos2x-\sin2x) dx$
出典:2007年青山学院大学 入試問題
福田の数学〜千葉大学2023年第7問〜三角関数と定積分の最大Part1

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#積分とその応用#定積分#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{7}$ 関数
$f(x)$=$\displaystyle\left|\cos x-\sqrt5\sin x-\frac{3\sqrt2}{2}\right|$
について、以下の問いに答えよ。
(1)$f(x)$の最大値を求めよ。
(2)$\displaystyle\int_0^{2\pi}f(x)dx$ を求めよ。
(3)$S(t)$=$\displaystyle\int_t^{t+\frac{\pi}{3}}f(x)dx$ とおく。このとき$S(t)$の最大値を求めよ。
この動画を見る
$\Large\boxed{7}$ 関数
$f(x)$=$\displaystyle\left|\cos x-\sqrt5\sin x-\frac{3\sqrt2}{2}\right|$
について、以下の問いに答えよ。
(1)$f(x)$の最大値を求めよ。
(2)$\displaystyle\int_0^{2\pi}f(x)dx$ を求めよ。
(3)$S(t)$=$\displaystyle\int_t^{t+\frac{\pi}{3}}f(x)dx$ とおく。このとき$S(t)$の最大値を求めよ。
【数学】2022年度 第2回 K塾記述高2模試 全問解説(ベクトルはおまけ)、※修正箇所:問1(1)(概要欄へ)

単元:
#数Ⅰ#数A#数Ⅱ#数と式#2次関数#場合の数と確率#図形の性質#複素数と方程式#図形と計量#式の計算(整式・展開・因数分解)#一次不等式(不等式・絶対値のある方程式・不等式)#2次方程式と2次不等式#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#確率#図形と方程式#三角関数#複素数#三角関数とグラフ#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
理数個別チャンネル
問題文全文(内容文):
2022年度第2回全統記述高2模試全問解説動画です!
この動画を見る
2022年度第2回全統記述高2模試全問解説動画です!
福井大 微分積分いい気分

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#面積、体積#数学(高校生)#福井大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
2016福井大学過去問題
$f(x)=x^3,g(x)=x^3-4$
①f(x),g(x)の両方と接する直線l
②g(x)とlとで囲まれる面積
この動画を見る
2016福井大学過去問題
$f(x)=x^3,g(x)=x^3-4$
①f(x),g(x)の両方と接する直線l
②g(x)とlとで囲まれる面積
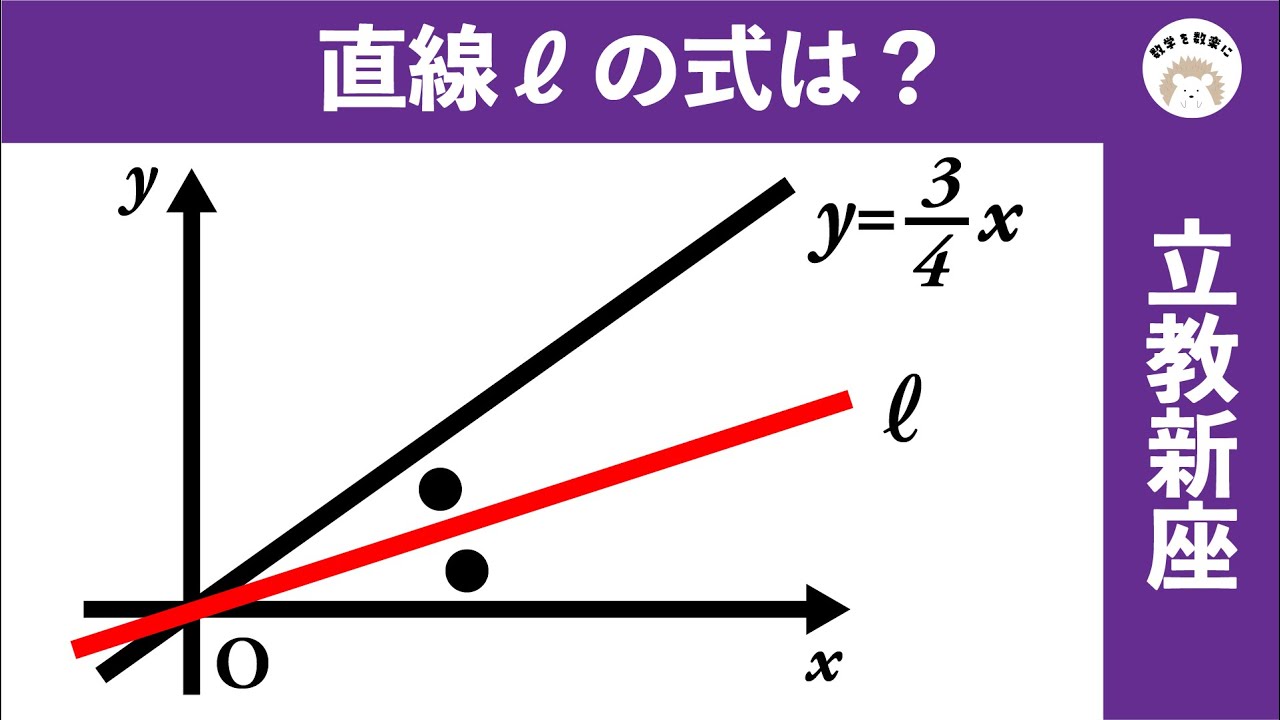
内角を二等分する直線の式 立教新座
福田の数学〜千葉大学2023年第3問〜2次関数と定積分で表された関数

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#2次関数#2次関数とグラフ#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 以下の問いに答えよ。
(1)$p$を実数とする。曲線$y$=|$x^2$+$x$-2|と直線$y$=$x$+$p$ の共有点の個数を求めよ。
(2)等式$f(x)$=$x^2$+$\displaystyle\int_{-1}^2(xf(t)-t)dt$ を満たす関数$f(x)$を求めよ。
この動画を見る
$\Large\boxed{3}$ 以下の問いに答えよ。
(1)$p$を実数とする。曲線$y$=|$x^2$+$x$-2|と直線$y$=$x$+$p$ の共有点の個数を求めよ。
(2)等式$f(x)$=$x^2$+$\displaystyle\int_{-1}^2(xf(t)-t)dt$ を満たす関数$f(x)$を求めよ。
大学入試問題#600「合同式使ってみた」 山梨大学医学部(2014) #整式

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#複素数と方程式#整式の除法・分数式・二項定理#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#山梨大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$x^{2014}$を$x^4+x^3+x^2+x+1$で割った余りを求めよ
出典:2014年山梨大学 入試問題
この動画を見る
$x^{2014}$を$x^4+x^3+x^2+x+1$で割った余りを求めよ
出典:2014年山梨大学 入試問題
福田の数学〜千葉大学2023年第1問〜三角形の面積と軌跡
単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
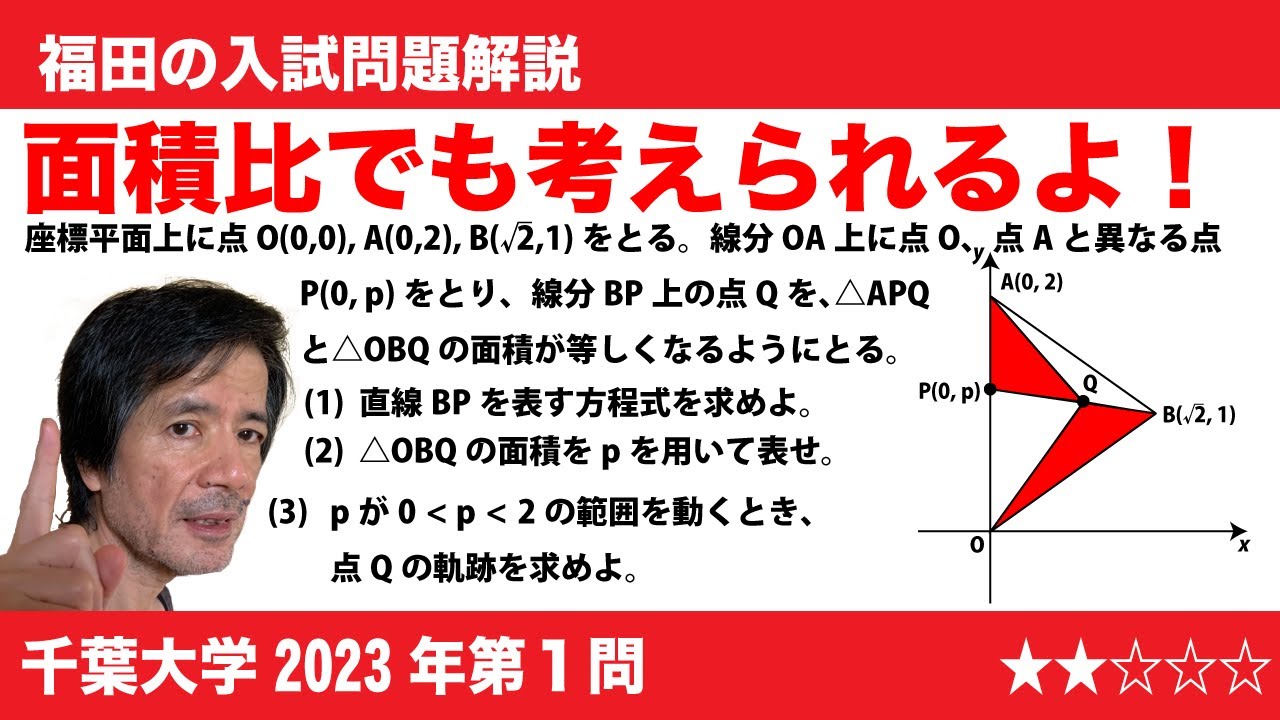
$\Large\boxed{1}$ 座標平面上に点O(0,0), A(0,2), B($\sqrt 2$, 1)をとる。線分OA上に点O、点Aと異なる点P(0,$p$)をとり、線分BP上の点Qを、$\triangle$APQと$\triangle$OBQの面積が等しくなるようにとる。
(1)直線BPを表す方程式を求めよ。
(2)$\triangle$OBQの面積を$p$を用いて表せ。
(3)$p$が0<$p$<2の範囲を動くとき、点Qの軌跡を求めよ。
この動画を見る
$\Large\boxed{1}$ 座標平面上に点O(0,0), A(0,2), B($\sqrt 2$, 1)をとる。線分OA上に点O、点Aと異なる点P(0,$p$)をとり、線分BP上の点Qを、$\triangle$APQと$\triangle$OBQの面積が等しくなるようにとる。
(1)直線BPを表す方程式を求めよ。
(2)$\triangle$OBQの面積を$p$を用いて表せ。
(3)$p$が0<$p$<2の範囲を動くとき、点Qの軌跡を求めよ。
16次式が正である証明

複素数のいい問題 山形大

単元:
#数Ⅱ#複素数と方程式#複素数#解と判別式・解と係数の関係#数学(高校生)#山形大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
山形大学過去問題
複素数平面上の相異なる3点A(α),B(β),C(γ)において
$α^2+β^2+γ^2=αβ+βγ+αγ$が成り立つなら△ABCは正三角形であることを示せ
この動画を見る
山形大学過去問題
複素数平面上の相異なる3点A(α),B(β),C(γ)において
$α^2+β^2+γ^2=αβ+βγ+αγ$が成り立つなら△ABCは正三角形であることを示せ
【数Ⅱ】二項定理を覚えられない人へ

