 数Ⅱ
数Ⅱ
 数Ⅱ
数Ⅱ
数学は学んだことを実際の問題に当てはめるのが大切~全国入試問題解法 #shorts #数学 #高校入試 #sound #動体視力 #素数

単元:
#数学(中学生)#数Ⅱ#式と証明#恒等式・等式・不等式の証明#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ ab=9991 $となる2以上の自然数$ a,b $の値をそれぞれ求めなさい.
立命館高校過去問
この動画を見る
$ ab=9991 $となる2以上の自然数$ a,b $の値をそれぞれ求めなさい.
立命館高校過去問
福田の数学〜北海道大学2023年理系第5問〜中間値の定理と関数の増減PART1

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#点と直線#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ a,bを$a^2$+$b^2$<1をみたす正の実数とする。また、座標平面上で原点を中心とする半径1の円をCとし、Cの内部にある2点A(a,0), B(0,b)を考える。
0<θ<$\frac{\pi}{2}$に対してC上の点P($\cos\theta$, $\sin\theta$)を考え、PにおけるCの接線に関してBと対称な点をDとおく。
(1)f(θ)=ab$\cos2\theta$+a$\sin\theta$-b$\cos\theta$とおく。方程式f(θ)=0の解が0<θ<$\frac{\pi}{2}$の範囲に少なくとも1つ存在することを示せ。
(2)Dの座標をa, $\theta$を用いて表せ。
(3)θが0<θ<$\frac{\pi}{2}$の範囲を動くとき、3点A,P,Dが同一直線上にあるようなθは少なくとも1つ存在することを示せ。また、このようなθはただ1つであることを示せ。
2023北海道大学理系過去問
この動画を見る
$\Large\boxed{5}$ a,bを$a^2$+$b^2$<1をみたす正の実数とする。また、座標平面上で原点を中心とする半径1の円をCとし、Cの内部にある2点A(a,0), B(0,b)を考える。
0<θ<$\frac{\pi}{2}$に対してC上の点P($\cos\theta$, $\sin\theta$)を考え、PにおけるCの接線に関してBと対称な点をDとおく。
(1)f(θ)=ab$\cos2\theta$+a$\sin\theta$-b$\cos\theta$とおく。方程式f(θ)=0の解が0<θ<$\frac{\pi}{2}$の範囲に少なくとも1つ存在することを示せ。
(2)Dの座標をa, $\theta$を用いて表せ。
(3)θが0<θ<$\frac{\pi}{2}$の範囲を動くとき、3点A,P,Dが同一直線上にあるようなθは少なくとも1つ存在することを示せ。また、このようなθはただ1つであることを示せ。
2023北海道大学理系過去問
福岡大(医)連立指数方程式
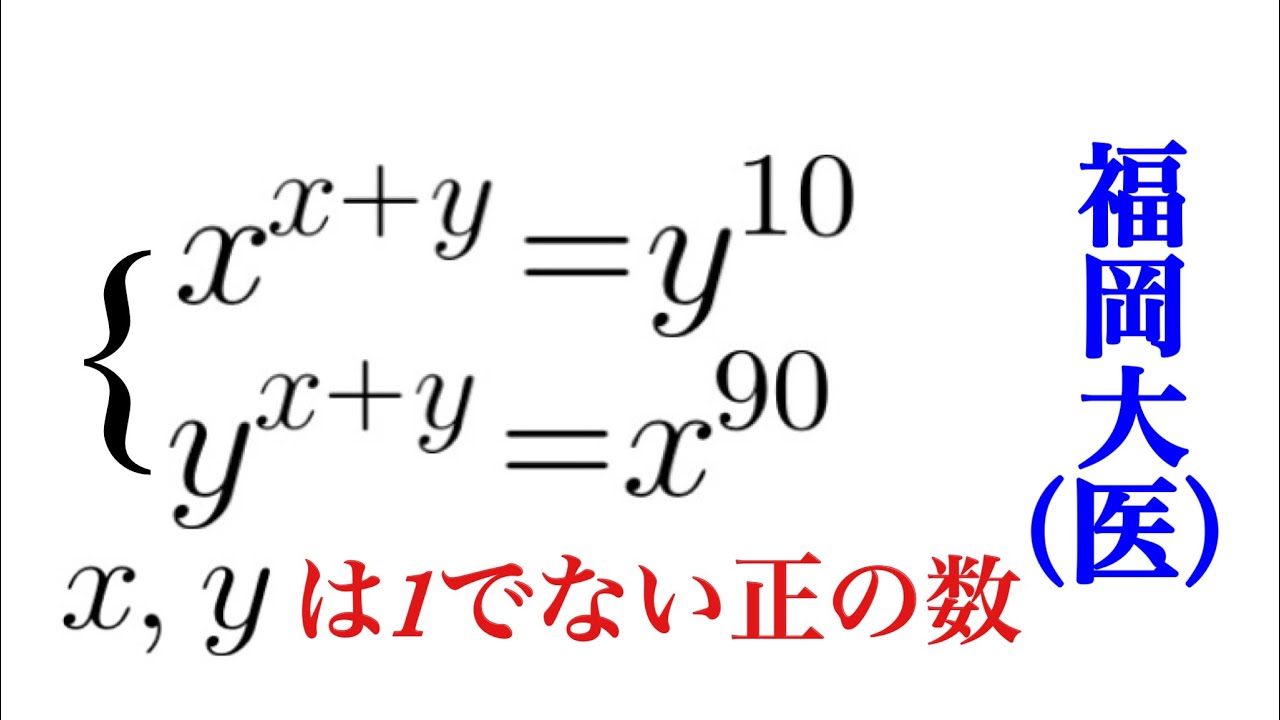
単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#対数関数#学校別大学入試過去問解説(数学)#数学(高校生)#福岡大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x,y$は1でない正の実数であるとする.これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^{x+y}=y^{10} \\
y^{x+y}=x^{90}
\end{array}
\right.
\end{eqnarray}$
福岡大(医)過去問
この動画を見る
$x,y$は1でない正の実数であるとする.これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^{x+y}=y^{10} \\
y^{x+y}=x^{90}
\end{array}
\right.
\end{eqnarray}$
福岡大(医)過去問
中学生にはキツいよ
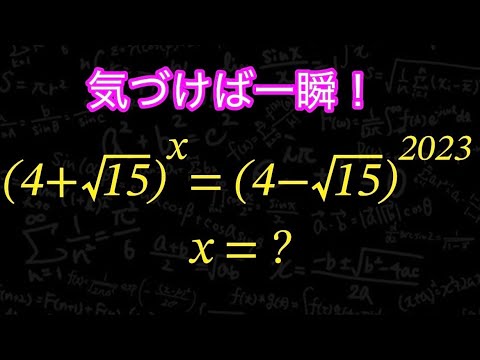
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(4+\sqrt {15})^x = (4 - \sqrt {15})^{2023}$
x=?
この動画を見る
$(4+\sqrt {15})^x = (4 - \sqrt {15})^{2023}$
x=?
答えはわかるでしょう。
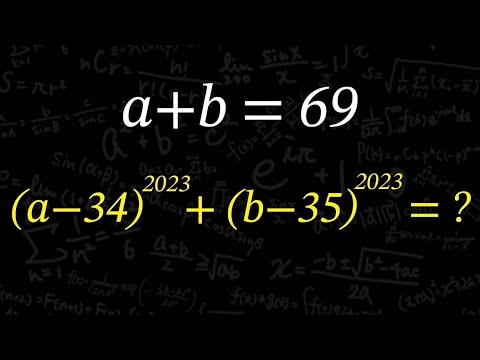
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
a+b=69
$(a - 34)^{2024} + (b-35)^{2023} = ?$
この動画を見る
a+b=69
$(a - 34)^{2024} + (b-35)^{2023} = ?$
分数の小数乗
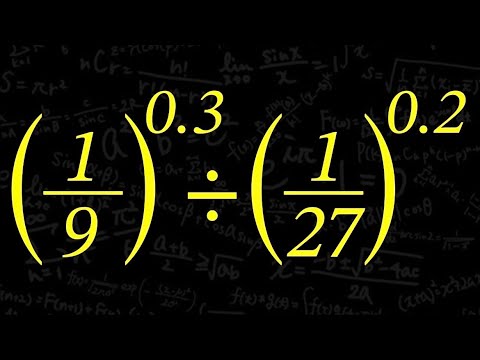
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(\frac{1}{9})^{0.3} \div (\frac{1}{27})^{0.2}$
この動画を見る
$(\frac{1}{9})^{0.3} \div (\frac{1}{27})^{0.2}$
ざ・解と係数の関係

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^3+2x^2-2x-1=0$の3つの解を$\alpha,\beta,\delta$とする.
$\dfrac{1}{(\delta-3)(\beta-3)},\dfrac{1}{(\delta-3)(\delta-3)},\dfrac{1}{(\delta-3)(\alpha-3)}$を解にもつ3次方程式を求めよ.
この動画を見る
$x^3+2x^2-2x-1=0$の3つの解を$\alpha,\beta,\delta$とする.
$\dfrac{1}{(\delta-3)(\beta-3)},\dfrac{1}{(\delta-3)(\delta-3)},\dfrac{1}{(\delta-3)(\alpha-3)}$を解にもつ3次方程式を求めよ.
中学生も解ける!! 指数
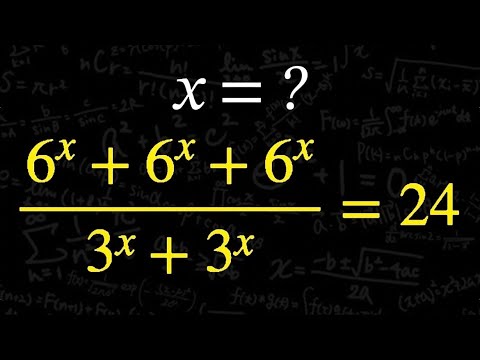
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
x=?
$\frac{6^x+6^x+6^x}{3^x+3^x} =24$
この動画を見る
x=?
$\frac{6^x+6^x+6^x}{3^x+3^x} =24$
福田の数学〜大阪大学2023年文系第2問〜対数関数と3次関数の最大

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 正の実数a, xに対して
y=$(\log_{\frac{1}{2}}x)^3$+$a\log_{\sqrt 2}x$$(\log_4x^3)$
とする。
(1)t=$\log_2x$とするとき、yをa, tを用いて表せ。
(2)xが$\frac{1}{2}$≦x≦8の範囲を動くとき、yの最大値Mをaを用いて表せ。
2023大阪大学文系過去問
この動画を見る
$\Large\boxed{2}$ 正の実数a, xに対して
y=$(\log_{\frac{1}{2}}x)^3$+$a\log_{\sqrt 2}x$$(\log_4x^3)$
とする。
(1)t=$\log_2x$とするとき、yをa, tを用いて表せ。
(2)xが$\frac{1}{2}$≦x≦8の範囲を動くとき、yの最大値Mをaを用いて表せ。
2023大阪大学文系過去問
福田の数学〜大阪大学2023年文系第1問〜三角方程式と解の存在範囲

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#2次関数#2次関数とグラフ#図形と方程式#三角関数#円と方程式#三角関数とグラフ#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
a,bを実数とする。θについての方程式
$\cos 2θ =a\sin θ +b$
が実数解をもつような点(a,b)の存在範囲を座標平面上に図示せよ
2023大阪大学文系過去問
この動画を見る
a,bを実数とする。θについての方程式
$\cos 2θ =a\sin θ +b$
が実数解をもつような点(a,b)の存在範囲を座標平面上に図示せよ
2023大阪大学文系過去問
久留米大(医)4次方程式

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#学校別大学入試過去問解説(数学)#数学(高校生)#久留米大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x=1+\sqrt{3}c$が解である$x^4+ax^3+ax^2+(6-a)x+b=0$の
実数$a,b$を求めよ.
久留米大(医)過去問
この動画を見る
$x=1+\sqrt{3}c$が解である$x^4+ax^3+ax^2+(6-a)x+b=0$の
実数$a,b$を求めよ.
久留米大(医)過去問
【高校数学】2文字の恒等式について~問題演習~ 1-7.5【数学Ⅱ】

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
等式3x²-2xy+7y²=a(x+y)²+b(x+y)(x-y)+c(x-y)²
がx,yについての恒等式となるように定数a,b,cの値を求めよ。
この動画を見る
等式3x²-2xy+7y²=a(x+y)²+b(x+y)(x-y)+c(x-y)²
がx,yについての恒等式となるように定数a,b,cの値を求めよ。
福田の数学〜大阪大学2023年理系第4問〜空間ベクトルと軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#空間ベクトル#図形と方程式#軌跡と領域#空間ベクトル#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
a,b を$a^2+b^2>1$かつ b≠0 をみたす実数の定数とする。
座標空間のA (a,0,b) と点 P(x, y, 0) をとる。
点O(0, 0, 0) を通り直線APと垂直な平面をαとし、平面と直線AP との交点をQとする。
$(\overrightarrow{ AP }・\overrightarrow{ AO })^2=|\overrightarrow{ AP }|^2|\overrightarrow{ AQ }|^2$が成り立つことを示せ。
$|\overrightarrow{ OQ }|^2=1$ をみたすように点P(x,y,0) が xy平面上を動くとき、点Pの軌跡を求めよ。
2023大阪大学理系過去問
この動画を見る
a,b を$a^2+b^2>1$かつ b≠0 をみたす実数の定数とする。
座標空間のA (a,0,b) と点 P(x, y, 0) をとる。
点O(0, 0, 0) を通り直線APと垂直な平面をαとし、平面と直線AP との交点をQとする。
$(\overrightarrow{ AP }・\overrightarrow{ AO })^2=|\overrightarrow{ AP }|^2|\overrightarrow{ AQ }|^2$が成り立つことを示せ。
$|\overrightarrow{ OQ }|^2=1$ をみたすように点P(x,y,0) が xy平面上を動くとき、点Pの軌跡を求めよ。
2023大阪大学理系過去問
指数の計算

福田の数学〜大阪大学2023年理系第3問〜三角方程式の解の個数

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#円と方程式#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ Pを座標平面上の点とし、点Pの座標を(a,b)とする。-π≦t≦πの範囲にある実数tのうち、曲線y=$\cos x$上の点(t, $\cos t$)における接線が点Pを通るという条件をみたすものの個数をN(P)とする。N(P)=4かつ0<a<πをみたすような点Pの存在範囲を座標平面上に図示せよ。
2023大阪大学理系過去問
この動画を見る
$\Large\boxed{3}$ Pを座標平面上の点とし、点Pの座標を(a,b)とする。-π≦t≦πの範囲にある実数tのうち、曲線y=$\cos x$上の点(t, $\cos t$)における接線が点Pを通るという条件をみたすものの個数をN(P)とする。N(P)=4かつ0<a<πをみたすような点Pの存在範囲を座標平面上に図示せよ。
2023大阪大学理系過去問
小数のマイナス乗
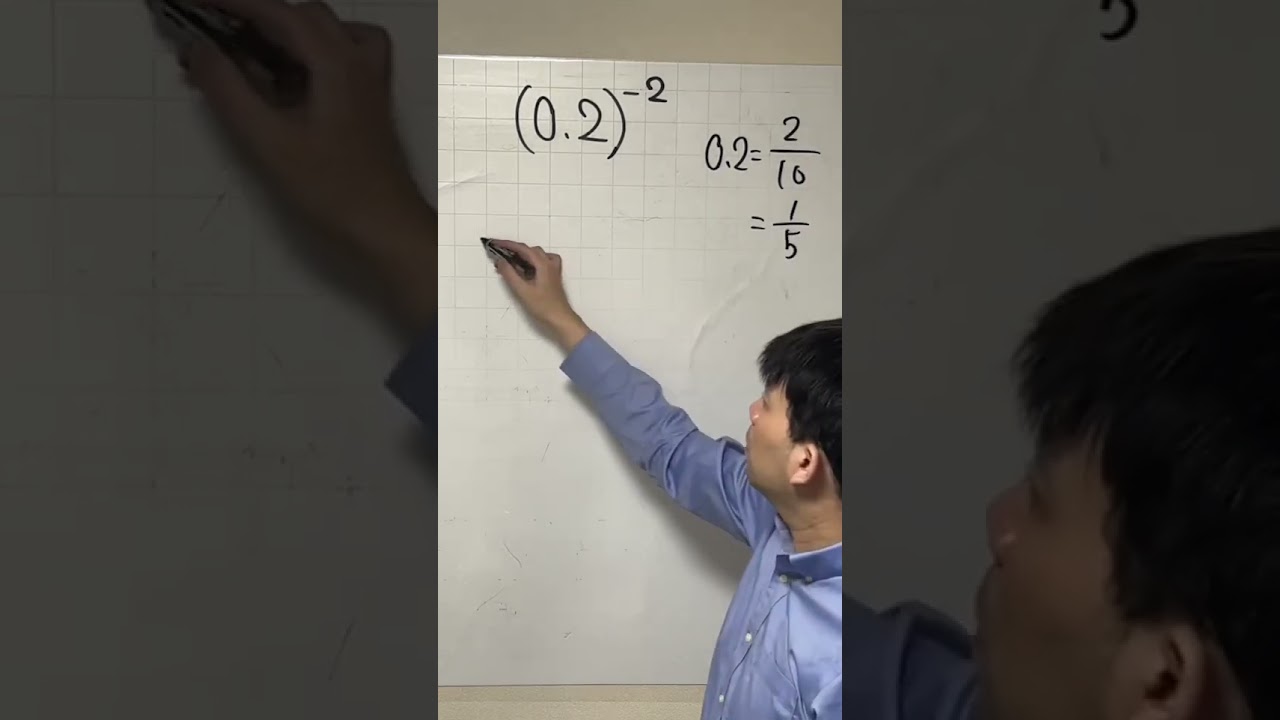
福田の数学〜東京慈恵会医科大学2023年医学部第3問〜無理数である証明

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#式と証明#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ Oを原点とする座標平面において、第1象限に属する点P($\sqrt 2r$, $\sqrt 3s$)(r,sは有理数)をとるとき、線分OPの長さは無理数となることを示せ。
2023東京慈恵会医科大学医学部過去問
この動画を見る
$\Large\boxed{3}$ Oを原点とする座標平面において、第1象限に属する点P($\sqrt 2r$, $\sqrt 3s$)(r,sは有理数)をとるとき、線分OPの長さは無理数となることを示せ。
2023東京慈恵会医科大学医学部過去問
【0≦θ≦πを問題文に追加】微分すると大変かも・・・ By ~らん~
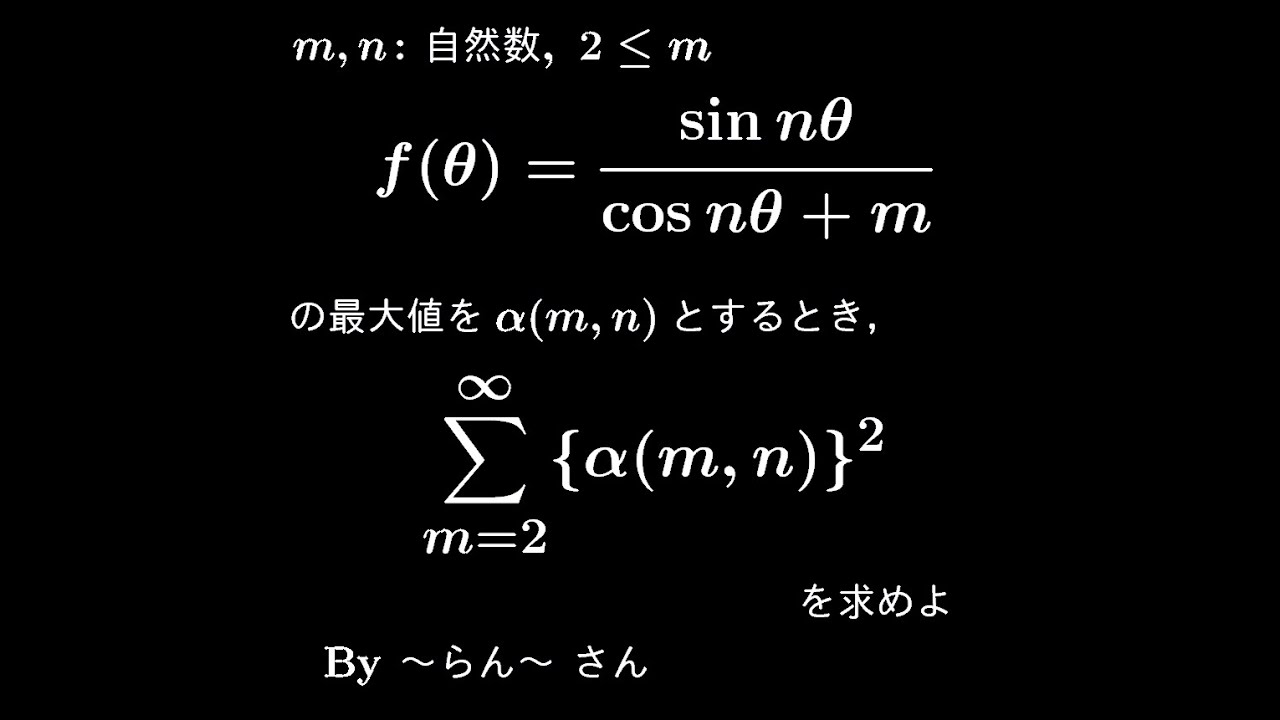
単元:
#数Ⅱ#三角関数#三角関数とグラフ#数列#数列とその和(等差・等比・階差・Σ)#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数列の極限#関数の極限#数学(高校生)#数B#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$m,n$:自然数
$m \geqq 2$
$f(\theta)=\displaystyle \frac{\sin\ n\theta}{\cos\ n\theta+m}$の最大値を$\alpha(m,n)$とする
$\displaystyle \sum_{m=2}^\infty \{\alpha(m,n)\}^2$を求めよ
この動画を見る
$m,n$:自然数
$m \geqq 2$
$f(\theta)=\displaystyle \frac{\sin\ n\theta}{\cos\ n\theta+m}$の最大値を$\alpha(m,n)$とする
$\displaystyle \sum_{m=2}^\infty \{\alpha(m,n)\}^2$を求めよ
福田の数学〜大阪大学2023年理系第2問〜ベクトルと領域

単元:
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#図形と方程式#軌跡と領域#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 平面上の3点O,A,Bが
|2$\overrightarrow{OA}$+$\overrightarrow{OB}$|=|$\overrightarrow{OA}$+2$\overrightarrow{OB}$|=1 かつ (2$\overrightarrow{OA}$+$\overrightarrow{OB}$)・($\overrightarrow{OA}$+$\overrightarrow{OB}$)=$\displaystyle\frac{1}{3}$
を満たすとする。
(1)(2$\overrightarrow{OA}$+$\overrightarrow{OB}$)・($\overrightarrow{OA}$+2$\overrightarrow{OB}$)を求めよ。
(2)平面上の点Pが
|$\overrightarrow{OP}$ー($\overrightarrow{OA}$+$\overrightarrow{OB}$)|≦$\frac{1}{3}$ かつ $\overrightarrow{OP}$・(2$\overrightarrow{OA}$+$\overrightarrow{OB}$)≦$\frac{1}{3}$
を満たすように動くとき、|$\overrightarrow{OP}$|の最大値と最小値を求めよ。
2023大阪大学理系過去問
この動画を見る
$\Large\boxed{2}$ 平面上の3点O,A,Bが
|2$\overrightarrow{OA}$+$\overrightarrow{OB}$|=|$\overrightarrow{OA}$+2$\overrightarrow{OB}$|=1 かつ (2$\overrightarrow{OA}$+$\overrightarrow{OB}$)・($\overrightarrow{OA}$+$\overrightarrow{OB}$)=$\displaystyle\frac{1}{3}$
を満たすとする。
(1)(2$\overrightarrow{OA}$+$\overrightarrow{OB}$)・($\overrightarrow{OA}$+2$\overrightarrow{OB}$)を求めよ。
(2)平面上の点Pが
|$\overrightarrow{OP}$ー($\overrightarrow{OA}$+$\overrightarrow{OB}$)|≦$\frac{1}{3}$ かつ $\overrightarrow{OP}$・(2$\overrightarrow{OA}$+$\overrightarrow{OB}$)≦$\frac{1}{3}$
を満たすように動くとき、|$\overrightarrow{OP}$|の最大値と最小値を求めよ。
2023大阪大学理系過去問
大学入試問題#489「これは教科書の例題」 兵庫医科大学(2023) #定積分

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} (x+2)(x-1)^9 dx$
出典:2023年兵庫医科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} (x+2)(x-1)^9 dx$
出典:2023年兵庫医科大学 入試問題
福田の数学〜大阪大学2023年理系第1問〜不等式の証明と極限

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#関数と極限#微分とその応用#数列の極限#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ nを2以上の自然数とする。
(1)0≦x≦1のとき、次の不等式が成り立つことを示せ。
$\frac{1}{2}x^2$≦$\displaystyle(-1)^n\left\{\frac{1}{x+1}-1-\sum\_{k=2}^n(-x)^{k-1}\right\}$≦$x^n-\frac{1}{2}x^{n+1}$
(2)$a_n$=$\displaystyle\sum_{k=1}^n\frac{(-1)^{k-1}}{k}$ とするとき、次の極限値を求めよ。
$\displaystyle\lim_{n \to \infty}(-1)^nn(a_n-\log 2)$
2023大阪大学理系過去問
この動画を見る
$\Large\boxed{5}$ nを2以上の自然数とする。
(1)0≦x≦1のとき、次の不等式が成り立つことを示せ。
$\frac{1}{2}x^2$≦$\displaystyle(-1)^n\left\{\frac{1}{x+1}-1-\sum\_{k=2}^n(-x)^{k-1}\right\}$≦$x^n-\frac{1}{2}x^{n+1}$
(2)$a_n$=$\displaystyle\sum_{k=1}^n\frac{(-1)^{k-1}}{k}$ とするとき、次の極限値を求めよ。
$\displaystyle\lim_{n \to \infty}(-1)^nn(a_n-\log 2)$
2023大阪大学理系過去問
福田の数学〜京都大学2023年文系第5問〜定積分で表された関数

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ 整式f(x)が恒等式
f(x)+$\displaystyle\int_{-1}^1(x-y)^2f(y)dy$=$2x^2$+$x$+$\frac{5}{3}$
を満たすとき、f(x)を求めよ。
2023京都大学文系過去問
この動画を見る
$\Large\boxed{5}$ 整式f(x)が恒等式
f(x)+$\displaystyle\int_{-1}^1(x-y)^2f(y)dy$=$2x^2$+$x$+$\frac{5}{3}$
を満たすとき、f(x)を求めよ。
2023京都大学文系過去問
【高校数学】分数式の恒等式~どこよりも分かりやすく丁寧に~ 1-7.5【数学Ⅱ】

福田の数学〜京都大学2023年文系第1問〜3乗根の有理化

単元:
#数Ⅰ#数A#数Ⅱ#大学入試過去問(数学)#数と式#場合の数と確率#式と証明#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#確率#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 問1 nを自然数とする。1個のさいころをn回投げるとき、出た目の積が5で割り切れる確率を求めよ。
問2 次の式の分母を有理化し、分母に3乗根の記号が含まれない式として表せ。
$\frac{55}{2\sqrt[3]{9}+\sqrt[3]{3}+5}$
2023京都大学文系過去問
この動画を見る
$\Large\boxed{1}$ 問1 nを自然数とする。1個のさいころをn回投げるとき、出た目の積が5で割り切れる確率を求めよ。
問2 次の式の分母を有理化し、分母に3乗根の記号が含まれない式として表せ。
$\frac{55}{2\sqrt[3]{9}+\sqrt[3]{3}+5}$
2023京都大学文系過去問
大学入試問題#485「計算ミスに注意」 九州歯科大学(2016) #定積分 視聴者の僚太さんの紹介で投稿しました。

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#面積、体積#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-2}^{3} (3\sqrt{ x^4-6x^2+9 }-4x) dx$
出典:2016年九州歯科大学 入試問題
この動画を見る
$\displaystyle \int_{-2}^{3} (3\sqrt{ x^4-6x^2+9 }-4x) dx$
出典:2016年九州歯科大学 入試問題
福田の数学〜京都大学2023年理系第6問〜チェビシェフの多項式と論証(PART2)

単元:
#式の計算(単項式・多項式・式の四則計算)#数Ⅱ#大学入試過去問(数学)#三角関数#学校別大学入試過去問解説(数学)#その他#推理と論証#推理と論証#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{6}$ pを3以上の素数とする。また、θを実数とする。
(1)$\cos3\theta$と$\cos4\theta$を$\cos\theta$の式として表せ。
(2)$\cos\theta$=$\frac{1}{p}$のとき、θ=$\frac{m}{n}$・$\pi$となるような正の整数m,nが存在するか否かを理由をつけて判定せよ。
チェビシェフの多項式
$\cos n\theta$=$T_n$($\cos\theta$)を満たすn次の多項式$T_n(x)$が存在し、その係数はすべて整数であり、最高次の係数が$2^{n-1}$である。
これが、すべての自然数nについて成り立つことを数学的帰納法で証明せよ。
2023京都大学理系過去問
この動画を見る
$\Large\boxed{6}$ pを3以上の素数とする。また、θを実数とする。
(1)$\cos3\theta$と$\cos4\theta$を$\cos\theta$の式として表せ。
(2)$\cos\theta$=$\frac{1}{p}$のとき、θ=$\frac{m}{n}$・$\pi$となるような正の整数m,nが存在するか否かを理由をつけて判定せよ。
チェビシェフの多項式
$\cos n\theta$=$T_n$($\cos\theta$)を満たすn次の多項式$T_n(x)$が存在し、その係数はすべて整数であり、最高次の係数が$2^{n-1}$である。
これが、すべての自然数nについて成り立つことを数学的帰納法で証明せよ。
2023京都大学理系過去問
福田の数学〜京都大学2023年理系第6問〜チェビシェフの多項式と論証(PART1)

単元:
#式の計算(単項式・多項式・式の四則計算)#数Ⅱ#大学入試過去問(数学)#三角関数#学校別大学入試過去問解説(数学)#その他#推理と論証#推理と論証#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{6}$ pを3以上の素数とする。また、θを実数とする。
(1)$\cos3\theta$と$\cos4\theta$を$\cos\theta$の式として表せ。
(2)$\cos\theta$=$\frac{1}{p}$のとき、θ=$\frac{m}{n}$・$\pi$となるような正の整数m,nが存在するか否かを理由をつけて判定せよ。
チェビシェフの多項式
$\cos n\theta$=$T_n$($\cos\theta$)を満たすn次の多項式$T_n(x)$が存在し、その係数はすべて整数であり、最高次の係数が$2^{n-1}$である。
これが、すべての自然数nについて成り立つことを数学的帰納法で証明せよ。
2023京都大学理系過去問
この動画を見る
$\Large\boxed{6}$ pを3以上の素数とする。また、θを実数とする。
(1)$\cos3\theta$と$\cos4\theta$を$\cos\theta$の式として表せ。
(2)$\cos\theta$=$\frac{1}{p}$のとき、θ=$\frac{m}{n}$・$\pi$となるような正の整数m,nが存在するか否かを理由をつけて判定せよ。
チェビシェフの多項式
$\cos n\theta$=$T_n$($\cos\theta$)を満たすn次の多項式$T_n(x)$が存在し、その係数はすべて整数であり、最高次の係数が$2^{n-1}$である。
これが、すべての自然数nについて成り立つことを数学的帰納法で証明せよ。
2023京都大学理系過去問
大学入試問題#483「作成時間がありませんでした」 近畿大学医学部(2023) #解と係数の関係

単元:
#数Ⅱ#複素数と方程式#複素数#解と判別式・解と係数の関係#数列#漸化式#数B
指導講師:
ますただ
問題文全文(内容文):
$x^2-x+1=0$の解を$\alpha,\beta$とする
$\alpha^9+\beta^9$の値を求めよ
出典:2023年近畿大学医学 入試問題
この動画を見る
$x^2-x+1=0$の解を$\alpha,\beta$とする
$\alpha^9+\beta^9$の値を求めよ
出典:2023年近畿大学医学 入試問題
綺麗な三次方程式

単元:
#数Ⅱ#式と証明#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(x-3)^3+(x-2)^3+(x-1)^3=x^3$
これを解け.
この動画を見る
$(x-3)^3+(x-2)^3+(x-1)^3=x^3$
これを解け.
福田の数学〜京都大学2023年理系第2問〜空間の位置ベクトルと直線のベクトル方程式

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#空間ベクトル#剰余の定理・因数定理・組み立て除法と高次方程式#空間ベクトル#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 空間内の4点O,A,B,Cは同一平面上にないとする。点D,P,Qを次のように定める。点Dは$\overrightarrow{OD}$=$\overrightarrow{OA}$+$2\overrightarrow{OB}$+$3\overrightarrow{OC}$を満たし、点Pは線分OAを1:2に内分し、点Qは線分OBの中点である。さらに、直線OD上の点Rを、直線QRと直線PCが交点を持つように定める。このとき、線分ORの長さと線分RDの長さの比OR:RDを求めよ。
2023京都大学理系過去問
この動画を見る
$\Large\boxed{2}$ 空間内の4点O,A,B,Cは同一平面上にないとする。点D,P,Qを次のように定める。点Dは$\overrightarrow{OD}$=$\overrightarrow{OA}$+$2\overrightarrow{OB}$+$3\overrightarrow{OC}$を満たし、点Pは線分OAを1:2に内分し、点Qは線分OBの中点である。さらに、直線OD上の点Rを、直線QRと直線PCが交点を持つように定める。このとき、線分ORの長さと線分RDの長さの比OR:RDを求めよ。
2023京都大学理系過去問
