 数Ⅱ
数Ⅱ
 数Ⅱ
数Ⅱ
福田の数学〜京都大学2022年文系第4問〜線分の中点の軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
a,bを正の実数とする。直線$L:ax+by=1$と曲線$y=-\frac{1}{x}$との2つの交点
のうち、y座標が正のものをP、負のものをQとする。また、Lとx軸との交点を
Rとし、Lとy軸との交点をSとする。a,bが条件
$\frac{PQ}{RS}=\sqrt2$
を満たしながら動くとき、線分PQの中点の軌跡を求めよ。
2022京都大学文系過去問
この動画を見る
a,bを正の実数とする。直線$L:ax+by=1$と曲線$y=-\frac{1}{x}$との2つの交点
のうち、y座標が正のものをP、負のものをQとする。また、Lとx軸との交点を
Rとし、Lとy軸との交点をSとする。a,bが条件
$\frac{PQ}{RS}=\sqrt2$
を満たしながら動くとき、線分PQの中点の軌跡を求めよ。
2022京都大学文系過去問
2022九州大

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
kは実数であり,整式f(x)を$ f(x)=x^4+6x^3-kx^2+2kx-64 $で定める.
f(x)=0が虚数解をもつとき,
(1)f(x)はx-2で割り切れることを示せ.
(2)f(x)=0は負の実数解をもつことを示せ.
(3)f(x)=0のすべての実数解が整数で,すべての虚数解の実部と虚部が
ともに整数である.kの値を求めよ.
2022九州大過去問
この動画を見る
kは実数であり,整式f(x)を$ f(x)=x^4+6x^3-kx^2+2kx-64 $で定める.
f(x)=0が虚数解をもつとき,
(1)f(x)はx-2で割り切れることを示せ.
(2)f(x)=0は負の実数解をもつことを示せ.
(3)f(x)=0のすべての実数解が整数で,すべての虚数解の実部と虚部が
ともに整数である.kの値を求めよ.
2022九州大過去問
福田の数学〜京都大学2022年文系第3問〜放物線と直交する2接線で囲まれる面積

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
xy平面上の2直線$L_1,L_2$は直交し、交点のx座標は$\frac{3}{2}$である。
また、$L_1,L_2$は共に曲線$C:y=\frac{x^2}{4}$に接している。このとき、$L_1,L_2$およびCで
囲まれる図形の面積を求めよ。
2022京都大学文系過去問
この動画を見る
xy平面上の2直線$L_1,L_2$は直交し、交点のx座標は$\frac{3}{2}$である。
また、$L_1,L_2$は共に曲線$C:y=\frac{x^2}{4}$に接している。このとき、$L_1,L_2$およびCで
囲まれる図形の面積を求めよ。
2022京都大学文系過去問
整式の剰余

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^{2022}$を$(x+1)(x^2+1)(x^4+1)(x^8+1)$で割った余りを求めよ.
この動画を見る
$x^{2022}$を$(x+1)(x^2+1)(x^4+1)(x^8+1)$で割った余りを求めよ.
中学生もわかる!と思う!指数の方程式
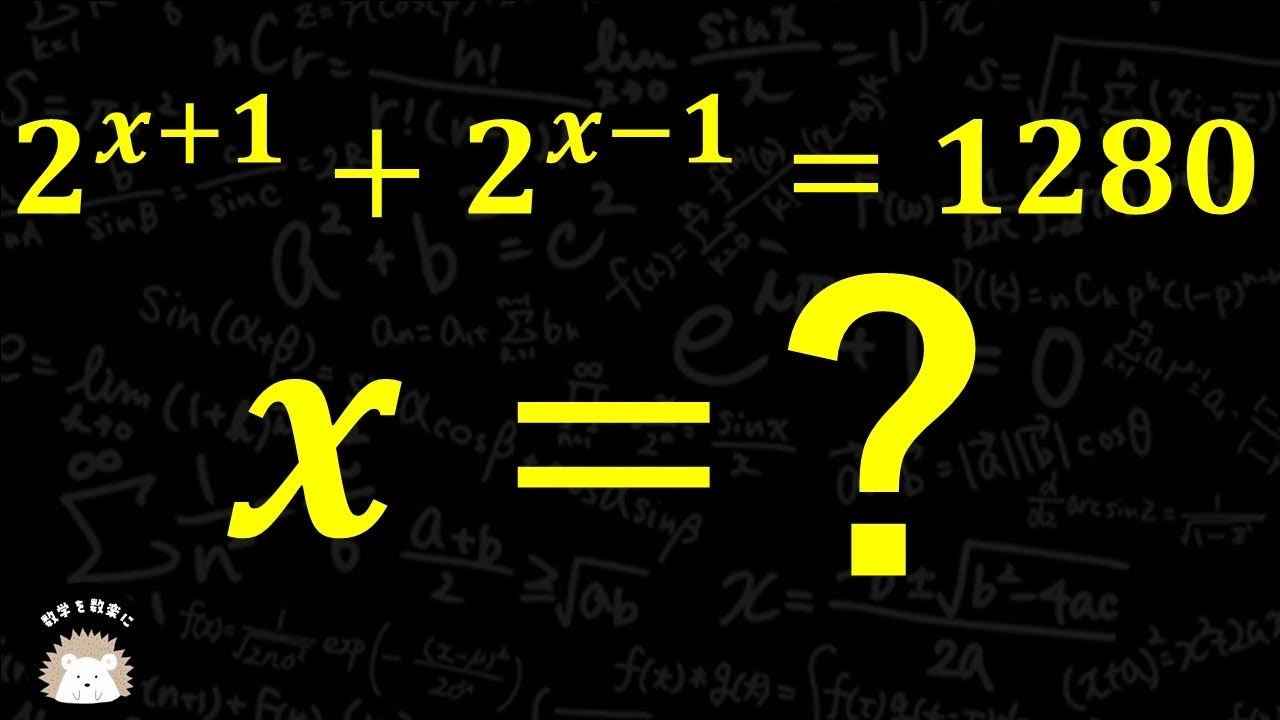
単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$2^{x+1}+2^{x-1} = 1280$
x=?
この動画を見る
$2^{x+1}+2^{x-1} = 1280$
x=?
2022早稲田大(社)整式の剰余

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
整式P(x)をx-1で割ると1あまり,$ (x+1)^2 $で割ると3x+2あまる.
P(x)を次の式で割ったあまりは?
(1)$ x+1$ (2)$(x+1)(x-1)$ (3)$(x-1)(x+1)^2$
2022早稲田大過去問
この動画を見る
整式P(x)をx-1で割ると1あまり,$ (x+1)^2 $で割ると3x+2あまる.
P(x)を次の式で割ったあまりは?
(1)$ x+1$ (2)$(x+1)(x-1)$ (3)$(x-1)(x+1)^2$
2022早稲田大過去問
【数Ⅱ】2つの円の位置関係・交点を通る直線または円の方程式【知らないと解けない知識問題】

単元:
#数Ⅱ#図形と方程式#点と直線#円と方程式#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$ 2円x^2+y^2-10=0,x^2+y^2+2x-2y-6=0が2点で交わることを示せ.$
この動画を見る
$ 2円x^2+y^2-10=0,x^2+y^2+2x-2y-6=0が2点で交わることを示せ.$
福田の数学・入試問題解説〜東北大学2022年理系第4問〜2つの直線に接し互いに外接する2つの円の性質

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
xy平面の第1象限内において、直線$l:y=mx (m \gt 0)$とx軸の両方に
接している半径aの円をCとし、円Cの中心を通る直線$y=tx (t \gt 0)$を考える。
また、直線lとx軸、および、円Cの全てにそれぞれ1点で接する円の半径をbとする。
ただし、$b \gt a$とする。
(1)mを用いてtを表せ。
(2)tを用いて$\frac{b}{a}$を表せ。
(3)極限値$\lim_{m \to +0}\frac{1}{m}(\frac{b}{a}-1)$を求めよ。
2022東北大学理系過去問
この動画を見る
xy平面の第1象限内において、直線$l:y=mx (m \gt 0)$とx軸の両方に
接している半径aの円をCとし、円Cの中心を通る直線$y=tx (t \gt 0)$を考える。
また、直線lとx軸、および、円Cの全てにそれぞれ1点で接する円の半径をbとする。
ただし、$b \gt a$とする。
(1)mを用いてtを表せ。
(2)tを用いて$\frac{b}{a}$を表せ。
(3)極限値$\lim_{m \to +0}\frac{1}{m}(\frac{b}{a}-1)$を求めよ。
2022東北大学理系過去問
解けるように作られた問題

単元:
#数Ⅱ#複素数と方程式#微分法と積分法#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^3-x-1=0 $の実数解を$ \alpha $とするとき,
$ \sqrt[3]{3\alpha^2-4\alpha}+\sqrt[3]{3\alpha^2+4\alpha+2}$の値を求めよ.
この動画を見る
$ x^3-x-1=0 $の実数解を$ \alpha $とするとき,
$ \sqrt[3]{3\alpha^2-4\alpha}+\sqrt[3]{3\alpha^2+4\alpha+2}$の値を求めよ.
解けるように作られた方程式
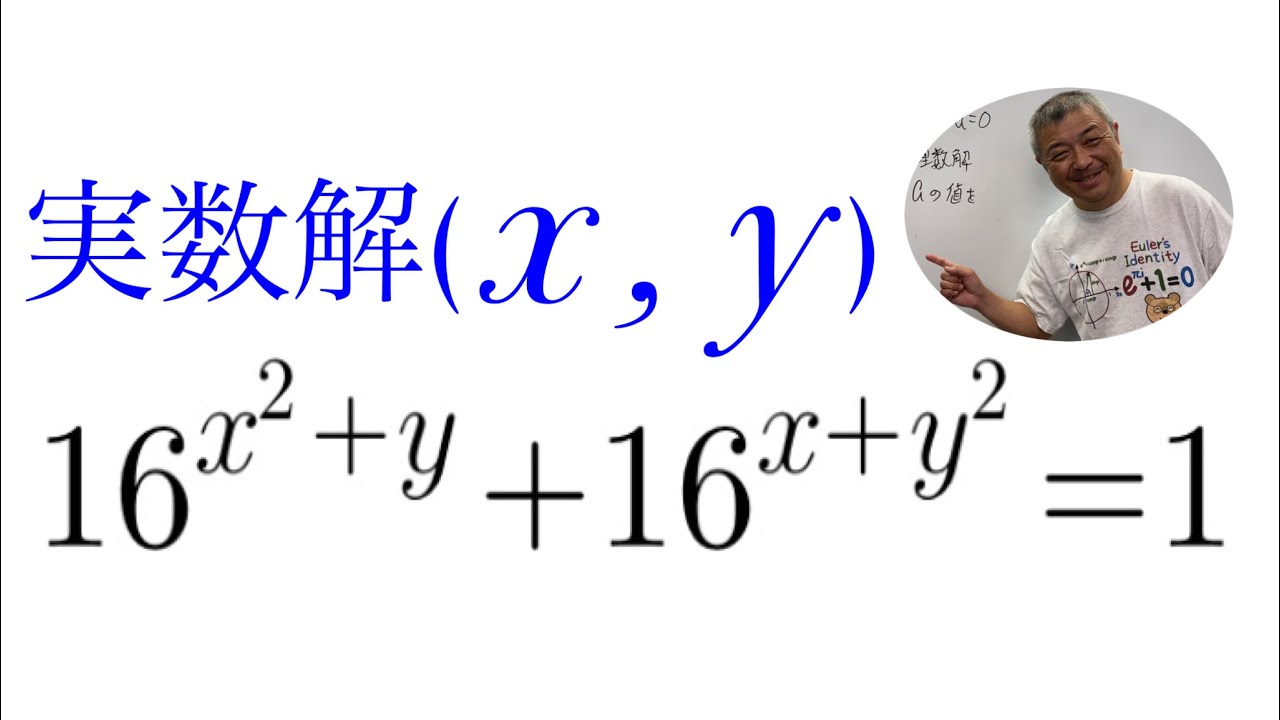
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解$(x,y)$を求めよ.
$ 16^{x^2+y}+16^{x+y^2}=1$
この動画を見る
実数解$(x,y)$を求めよ.
$ 16^{x^2+y}+16^{x+y^2}=1$
指数方程式
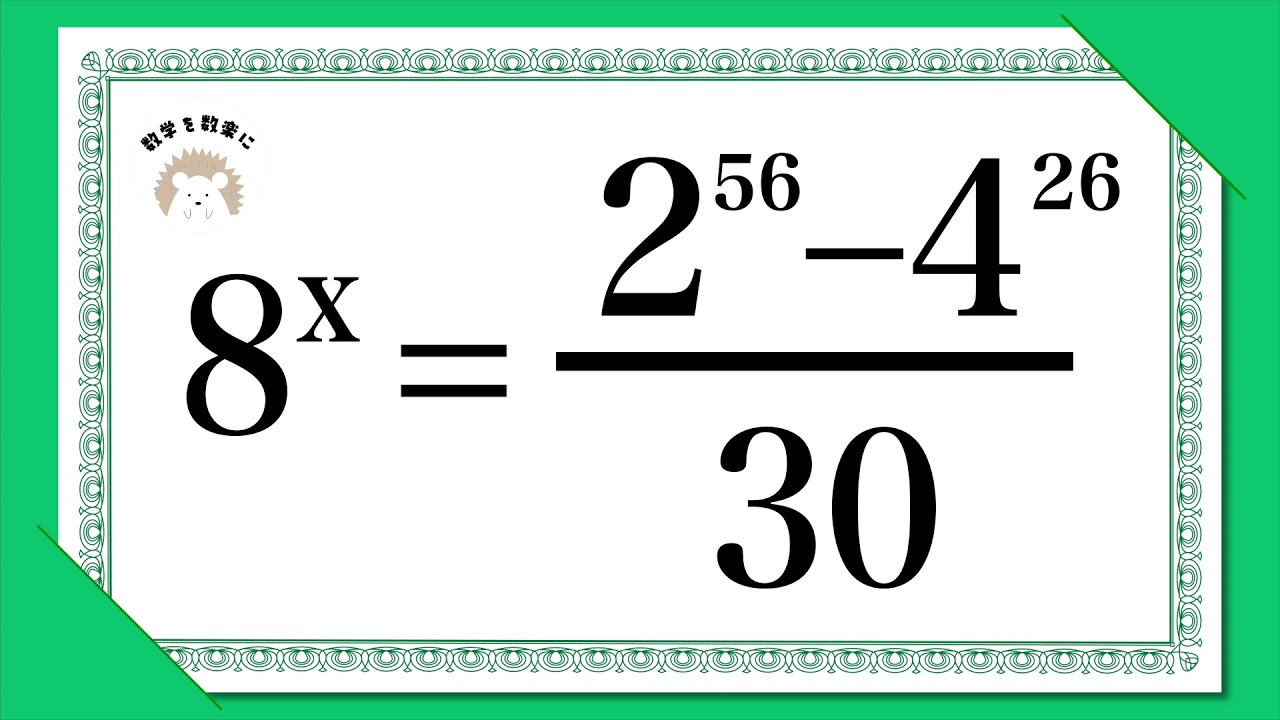
単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$8^x=\frac{2^{56}-4^{26}}{30}$のときx=?
この動画を見る
$8^x=\frac{2^{56}-4^{26}}{30}$のときx=?
福田の数学・入試問題解説〜東北大学2022年理系第2問〜4次関数の極値と最小値

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#微分法と積分法#指数関数#接線と増減表・最大値・最小値#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
aを実数とし、実数xの関数$f(x)=(x^2+3x+a)(x+1)^2$を考える。
(1)f(x)の最小値が負となるようなaのとりうる値の範囲を求めよ。
(2)$a \lt 2$のとき、f(x)は2つの極小値をもつ。このときf(x)が極小となる
xの値を$\alpha_1,\alpha_2(\alpha_1 \lt \alpha_2)$とする。
$f(\alpha_1) \lt f(\alpha_2)$を示せ。
(3)f(x)が$x \lt \beta$において単調減少し、かつ、$x=\beta$において最小値をとるとする。
このとき、aのとりうる値の範囲を求めよ。
2022東北大学理系過去問
この動画を見る
aを実数とし、実数xの関数$f(x)=(x^2+3x+a)(x+1)^2$を考える。
(1)f(x)の最小値が負となるようなaのとりうる値の範囲を求めよ。
(2)$a \lt 2$のとき、f(x)は2つの極小値をもつ。このときf(x)が極小となる
xの値を$\alpha_1,\alpha_2(\alpha_1 \lt \alpha_2)$とする。
$f(\alpha_1) \lt f(\alpha_2)$を示せ。
(3)f(x)が$x \lt \beta$において単調減少し、かつ、$x=\beta$において最小値をとるとする。
このとき、aのとりうる値の範囲を求めよ。
2022東北大学理系過去問
福田の入試問題解説〜東京大学2022年文系第2問〜3次関数の法施線とグラフとの交点

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#微分法と積分法#指数関数#接線と増減表・最大値・最小値#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$y=x^3-x$により定まる座標平面上の曲線をCとする。
C上の点P$(\alpha,\alpha^3-\alpha)$を通り、
点PにおけるCの接線と垂直に交わる直線をlとする。Cとlは相異なる3点で交わるとする。
(1)$\alpha$のとりうる値の範囲を求めよ。
(2)Cとlの点P以外の2つの交点のx座標を$\beta,\gamma$とする。ただし$\beta \lt \gamma$とする。
$\beta^2+\beta\gamma+\gamma^2-1\neq 0$ となることを示せ。
(3)(2)の$\beta,\gamma$を用いて、
$u=4\alpha^3+\frac{1}{\beta^2+\beta\gamma+\gamma^2-1}$
と定める。このとき、uの取りうる値の範囲を求めよ。
2022東京大学文系過去問
この動画を見る
$y=x^3-x$により定まる座標平面上の曲線をCとする。
C上の点P$(\alpha,\alpha^3-\alpha)$を通り、
点PにおけるCの接線と垂直に交わる直線をlとする。Cとlは相異なる3点で交わるとする。
(1)$\alpha$のとりうる値の範囲を求めよ。
(2)Cとlの点P以外の2つの交点のx座標を$\beta,\gamma$とする。ただし$\beta \lt \gamma$とする。
$\beta^2+\beta\gamma+\gamma^2-1\neq 0$ となることを示せ。
(3)(2)の$\beta,\gamma$を用いて、
$u=4\alpha^3+\frac{1}{\beta^2+\beta\gamma+\gamma^2-1}$
と定める。このとき、uの取りうる値の範囲を求めよ。
2022東京大学文系過去問
【丁寧に解説】テストによく出る繁分数式(分数の中に分数)を解説!
単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
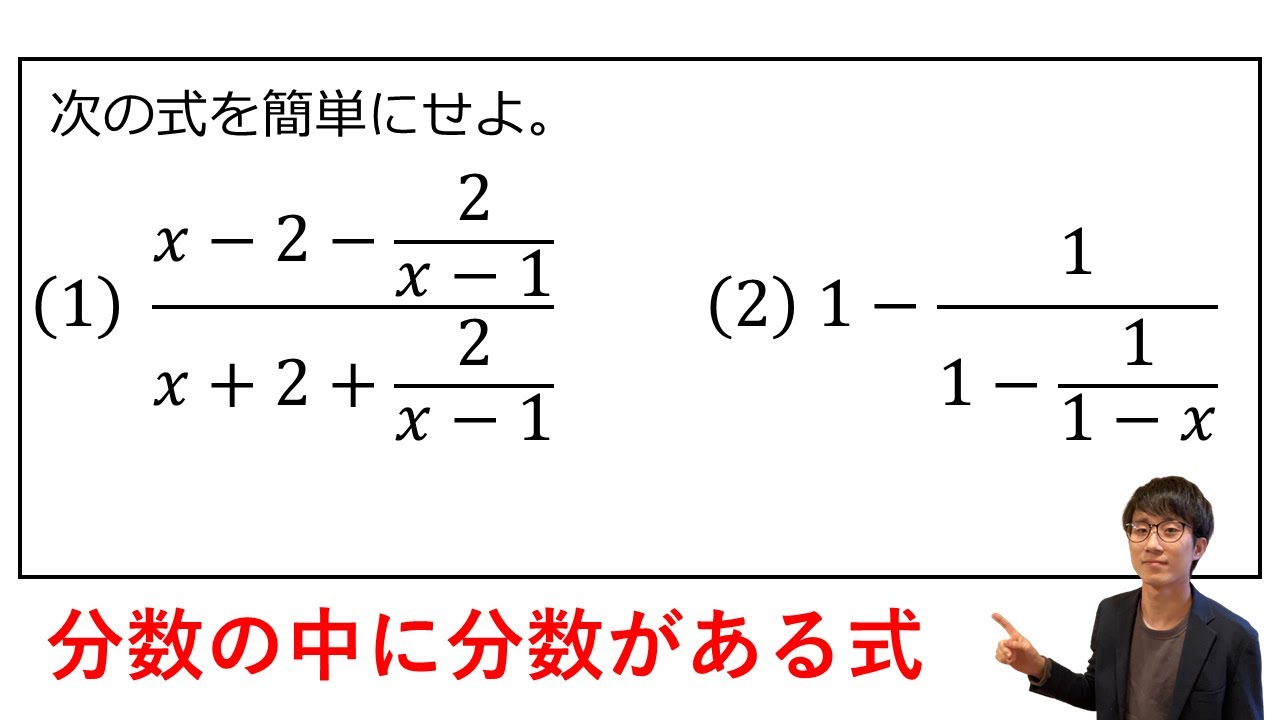
次の式を簡単にせよ。
(1)
$\displaystyle \frac{x-2-\displaystyle \frac{2}{x-1}}{x+2+\displaystyle \frac{2}{x-1}}$
(2)
$1-\displaystyle \frac{1}{1-\displaystyle \frac{1}{1-x}}$
この動画を見る
次の式を簡単にせよ。
(1)
$\displaystyle \frac{x-2-\displaystyle \frac{2}{x-1}}{x+2+\displaystyle \frac{2}{x-1}}$
(2)
$1-\displaystyle \frac{1}{1-\displaystyle \frac{1}{1-x}}$
【ゼロからわかる】整式の割り算②(高校数学Ⅱ)

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の問いに答えよ。
(1)
$x^2-6x+3$で割ると、商が$2x-3,$余りが$3x$である整数$A$を求めよ。
(2)
$x^3+3x^2+2x+1$を$B$で割ると、商が$x+1,$余りが$x+2$になる。
整数$B$を求めよ。
この動画を見る
次の問いに答えよ。
(1)
$x^2-6x+3$で割ると、商が$2x-3,$余りが$3x$である整数$A$を求めよ。
(2)
$x^3+3x^2+2x+1$を$B$で割ると、商が$x+1,$余りが$x+2$になる。
整数$B$を求めよ。
【数Ⅱ】円外の点から引いた接線【頻出問題 4S数学問題集で解く】

単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$ 点(3,1)を通り,円x^2+y^2=5に接する直線の方程式を求めよ.$
この動画を見る
$ 点(3,1)を通り,円x^2+y^2=5に接する直線の方程式を求めよ.$
整式の剰余2022

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^{2022}$を$ x^6-x^5+x^4-x^3+x^2-x+1$で割った余りを求めよ.
この動画を見る
$ x^{2022}$を$ x^6-x^5+x^4-x^3+x^2-x+1$で割った余りを求めよ.
福田の入試問題解説〜北海道大学2022年理系第5問〜複素数平面上の点の軌跡とドモアブルの定理

単元:
#数Ⅱ#大学入試過去問(数学)#複素数平面#図形と方程式#軌跡と領域#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数C
指導講師:
福田次郎
問題文全文(内容文):
複素数zに関する次の2つの方程式を考える。ただし、$\bar{ z }$はzと共役な複素数とし、
iを虚数単位とする。
$z\bar{ z }=4 \ldots\ldots$① $|z|=|z-\sqrt3+i| \ldots\ldots②$
(1)①、②それぞれの方程式について、その解z全体が表す図形を複素数平面上に
図示せよ。
(2)①、②の共通解となる複素数を全て求めよ。
(3)(2)で求めた全ての複素数の積をwとおく。このとき$w^n$が負の実数となる
ための整数nの必要十分条件を求めよ。
2022北海道大学理系過去問
この動画を見る
複素数zに関する次の2つの方程式を考える。ただし、$\bar{ z }$はzと共役な複素数とし、
iを虚数単位とする。
$z\bar{ z }=4 \ldots\ldots$① $|z|=|z-\sqrt3+i| \ldots\ldots②$
(1)①、②それぞれの方程式について、その解z全体が表す図形を複素数平面上に
図示せよ。
(2)①、②の共通解となる複素数を全て求めよ。
(3)(2)で求めた全ての複素数の積をwとおく。このとき$w^n$が負の実数となる
ための整数nの必要十分条件を求めよ。
2022北海道大学理系過去問
いくつでしょうか?

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
この値を求めよ.
$2^{\frac{1}{4}}・4^{\frac{1}{8}}・8^{\frac{1}{16}}・16^{\frac{1}{32}}・・・・・・\infty$
この動画を見る
この値を求めよ.
$2^{\frac{1}{4}}・4^{\frac{1}{8}}・8^{\frac{1}{16}}・16^{\frac{1}{32}}・・・・・・\infty$
指数の計算 敬愛学園 令和4年度 2022 入試問題100題解説92問目!

単元:
#数学(中学生)#数Ⅱ#指数関数と対数関数#指数関数#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$2^{13}+2^{13}+2^{14}+2^{15}=2^▢$
2022敬愛学園
この動画を見る
$2^{13}+2^{13}+2^{14}+2^{15}=2^▢$
2022敬愛学園
福田の入試問題解説〜北海道大学2022年理系第3問〜指数不等式の領域が表す面積の最小

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
以下の問いに答えよ。
(1)連立不等式$x \geqq 2, 2^x \leqq x^y \leqq x^2$の表す領域をxy平面上に図示せよ。
ただし、自然対数の底eが$2 \lt e \lt 3$を満たすことを用いてよい。
(2)$a \gt 0$に対して、連立不等式$2 \leqq x \leqq 6, (x^y-2^x)(x^a-x^y) \geqq 0$
の表すxy平面上の領域の面積をS(a)とする。
$S(a)$を最小にするaの値を求めよ。
2022北海道大学理系過去問
この動画を見る
以下の問いに答えよ。
(1)連立不等式$x \geqq 2, 2^x \leqq x^y \leqq x^2$の表す領域をxy平面上に図示せよ。
ただし、自然対数の底eが$2 \lt e \lt 3$を満たすことを用いてよい。
(2)$a \gt 0$に対して、連立不等式$2 \leqq x \leqq 6, (x^y-2^x)(x^a-x^y) \geqq 0$
の表すxy平面上の領域の面積をS(a)とする。
$S(a)$を最小にするaの値を求めよ。
2022北海道大学理系過去問
【ゼロからわかる】整式の割り算(高校数学Ⅱ)

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の整式$A,B$について、$A$を$B$で割った商と余りを求めよ。
(1)$A=a^2+6a+5,B=a+3$
(2)$A=4x^3-3x+2,B=2x+3$
この動画を見る
次の整式$A,B$について、$A$を$B$で割った商と余りを求めよ。
(1)$A=a^2+6a+5,B=a+3$
(2)$A=4x^3-3x+2,B=2x+3$
雑問

単元:
#数A#数Ⅱ#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 25^{63}\times 63^{25}$の下3桁を求めよ.
この動画を見る
$ 25^{63}\times 63^{25}$の下3桁を求めよ.
大学入試問題#137 秋田大学(2020) 三角関数

単元:
#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#数学(高校生)#秋田大学
指導講師:
ますただ
問題文全文(内容文):
$y=\displaystyle \frac{6+4\sin\theta+4\cos\theta+\sin2\theta}{2+\sin\theta+\cos\theta}$の最小値を求めよ。
出典:2020年秋田大学 入試問題
この動画を見る
$y=\displaystyle \frac{6+4\sin\theta+4\cos\theta+\sin2\theta}{2+\sin\theta+\cos\theta}$の最小値を求めよ。
出典:2020年秋田大学 入試問題
連立2元9次方程式
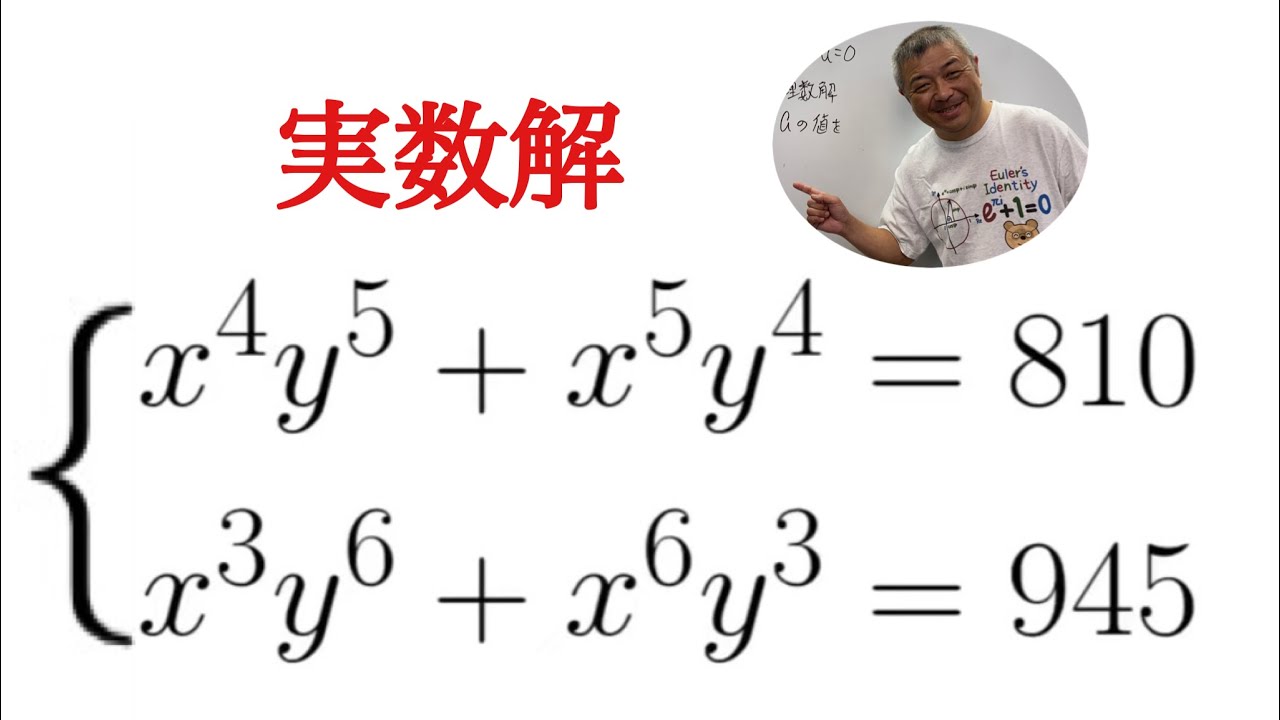
単元:
#数Ⅰ#数Ⅱ#数と式#2次関数#複素数と方程式#式の計算(整式・展開・因数分解)#2次方程式と2次不等式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \begin{eqnarray}
\left\{
\begin{array}{l}
x^4y^5+x^5y^4=810 \\
x^3y^6+x^6y^3=945
\end{array}
\right.
\end{eqnarray}$
実数解を求めよ.
この動画を見る
$ \begin{eqnarray}
\left\{
\begin{array}{l}
x^4y^5+x^5y^4=810 \\
x^3y^6+x^6y^3=945
\end{array}
\right.
\end{eqnarray}$
実数解を求めよ.
福田の数学〜京都大学2022年理系第5問〜方程式の解と不等式の証明

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#複素数と方程式#恒等式・等式・不等式の証明#解と判別式・解と係数の関係#微分とその応用#積分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
曲線$C:y=\cos^3x$ $(0 \leqq x \leqq \frac{\pi}{2})$,x軸およびy軸で囲まれる図形の面s系をS
とする。$0 \lt t \lt \frac{\pi}{2}$とし、C上の点Q$(t,\cos^3t)$と原点O,およびP$(t,o),R(0,\cos^3t)$
を頂点にもつ長方形OPQRの面積をf(t)とする。このとき、次の問いに答えよ。
(1)Sを求めよ。
(2)$f(t)$は最大値をただ一つのtでとることを示せ。そのときのtを$\alpha$とすると、
$f(\alpha)=\frac{\cos^4\alpha}{3\sin\alpha}$ であることを示せ。
(3)$\frac{f(\alpha)}{S} \lt \frac{9}{16}$ を示せ。
2022京都大学理系過去問
この動画を見る
曲線$C:y=\cos^3x$ $(0 \leqq x \leqq \frac{\pi}{2})$,x軸およびy軸で囲まれる図形の面s系をS
とする。$0 \lt t \lt \frac{\pi}{2}$とし、C上の点Q$(t,\cos^3t)$と原点O,およびP$(t,o),R(0,\cos^3t)$
を頂点にもつ長方形OPQRの面積をf(t)とする。このとき、次の問いに答えよ。
(1)Sを求めよ。
(2)$f(t)$は最大値をただ一つのtでとることを示せ。そのときのtを$\alpha$とすると、
$f(\alpha)=\frac{\cos^4\alpha}{3\sin\alpha}$ であることを示せ。
(3)$\frac{f(\alpha)}{S} \lt \frac{9}{16}$ を示せ。
2022京都大学理系過去問
2022藤田医科大の簡単な問題 メインはn個の相加相乗平均の証明

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#微分とその応用#微分法#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x\gt 0$において$\dfrac{x}{2}+\dfrac{2}{x^2}$の最小値を求めよ.
2022藤田医科大過去問
この動画を見る
$ x\gt 0$において$\dfrac{x}{2}+\dfrac{2}{x^2}$の最小値を求めよ.
2022藤田医科大過去問
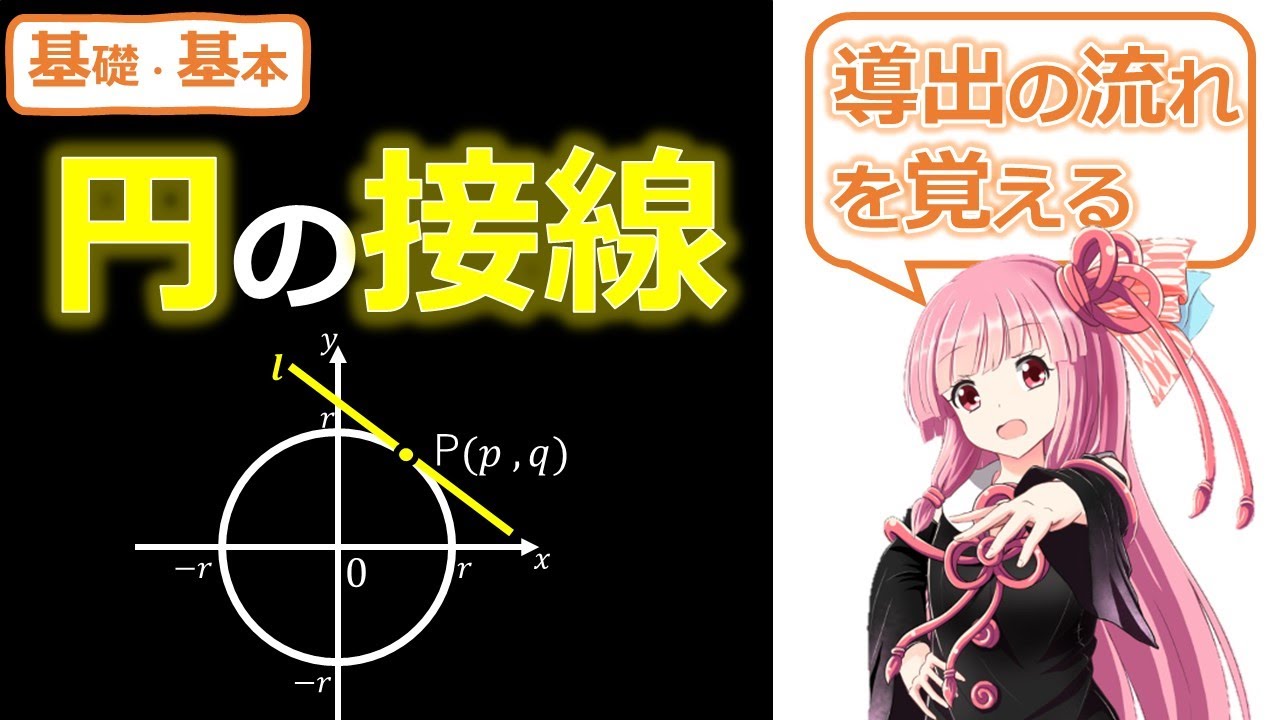
【数Ⅱ】円の接線【流れを覚えて自分で導出する】
#51 数検1級1次 過去問 逆三角関数

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#三角関数#三角関数とグラフ#数学検定#数学検定1級
指導講師:
ますただ
問題文全文(内容文):
$\sin(\sin^{-1}(-\displaystyle \frac{5}{13})+\cos^{-1}(\displaystyle \frac{4}{5}))$の値を求めよ。
出典:数検1級1次 過去問
この動画を見る
$\sin(\sin^{-1}(-\displaystyle \frac{5}{13})+\cos^{-1}(\displaystyle \frac{4}{5}))$の値を求めよ。
出典:数検1級1次 過去問
ざ・息抜き

単元:
#数Ⅰ#数Ⅱ#2次関数#2次方程式と2次不等式#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \sqrt{2022}x^{\log_{2022}x}=x^2$の解の積の下3桁を求めよ.
この動画を見る
$ \sqrt{2022}x^{\log_{2022}x}=x^2$の解の積の下3桁を求めよ.
