数Ⅱ
数Ⅱ
09三重県教員採用試験（数学：4番 不等式）
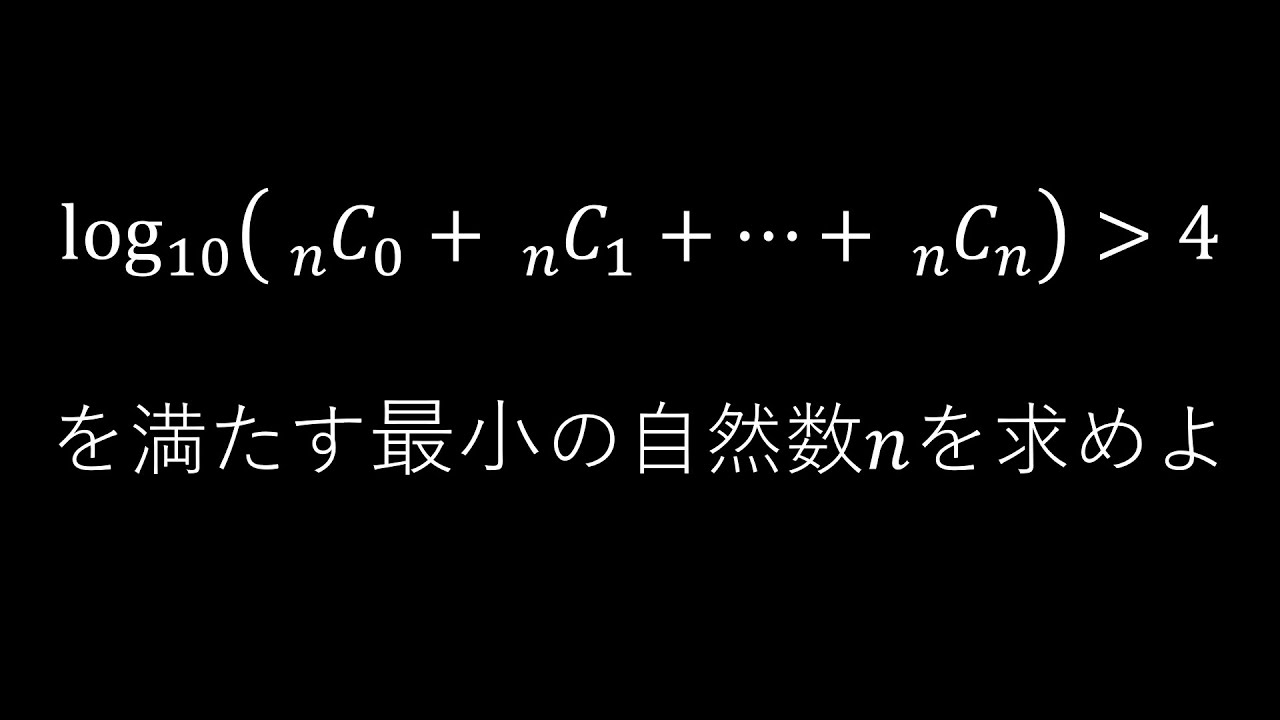
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{4}$
$\log_{10} ({n}_n \mathrm{C}_0+{n}_n \mathrm{C}_1+･･････+{n}_n \mathrm{C}_n)\gt 4$
をみたす最小の自然数$n$を求めよ.
この動画を見る
$\boxed{4}$
$\log_{10} ({n}_n \mathrm{C}_0+{n}_n \mathrm{C}_1+･･････+{n}_n \mathrm{C}_n)\gt 4$
をみたす最小の自然数$n$を求めよ.
高専数学 微積II #3 2次近似式
単元：
#数Ⅱ#微分法と積分法#微分とその応用#速度と近似式#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\sqrt[3]{1-x}$の$x=0$における2次近似式を用いて,
$\sqrt[3]{0.8}$の近似値を小数第三位まで求めよ.
この動画を見る
$\sqrt[3]{1-x}$の$x=0$における2次近似式を用いて,
$\sqrt[3]{0.8}$の近似値を小数第三位まで求めよ.
福田の数学〜慶應義塾大学2021年経済学部第６問〜3次関数の接線と面積
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#面積、体積#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{6}}$
F(x)は実数を係数とするxの3次式で、x^3の項の係数は1であり、$y=F(x)$で
定まる曲線をCとする。$\alpha \lt \beta$を満たす実数$\alpha,\ \beta$に対して、C上の点A$(\alpha,F(\alpha))$
におけるCの接線を$L_{\alpha}$とするとき、Cと$L_{\alpha}$とのA以外の共有点が$B(\beta,F(\beta))$
であるとする。さらに、BにおけるCの接線を$L_{\beta}$とのB以外の共有点を$(\gamma,F(\gamma))$
とする。
(1)接線$L_{\alpha}$の方程式を$y=l_{\alpha}(x)$とし、$G(x)=F(x)-l_{\alpha}(x)$とおく。さらに、
曲線$y=G(x)$上の点$(\beta,G(\beta))$における接線の方程式を$y=m(x)$とする。$G(x)$
および$m(x)$を、それぞれ$\alpha,\beta$を用いて因数分解された形に表せ。必要ならば
xの整式で表される関数$p(x),q(x)$とそれらの導関数に関して成り立つ公式
$\left\{p(x)q(x)\right\}'=p'(x)q(x)+p(x)q'(x)$
を用いてもよい。
(2)接線$L_{\beta}$の方程式は(1)で定めた$l_{\alpha}(x),\ m(x)$を用いて、$y=l_{\alpha}(x)+ m(x)$で
与えられることを示せ。さらに、$\gamma$を$\alpha,\beta$を用いて表せ。
(3)曲線Cおよび$L_{\beta}$で囲まれた図形の面積を$S$とする。$S$を$\alpha,\beta$を用いて表せ。
さらに$\alpha,\beta$が$-1 \lt \alpha \lt 0$かつ$1 \lt \beta \lt 2$を満たすとき、$S$の取り得る値の
範囲を求めよ。必要ならば$r \lt s$を満たす実数$r,s$に対して成り立つ公式
$\int_r^s(x-r)(x-s)^2dx=\frac{1}{12}(s-r)^4$
を用いてもよい。
2021慶應義塾大学経済学部過去問
この動画を見る
${\Large\boxed{6}}$
F(x)は実数を係数とするxの3次式で、x^3の項の係数は1であり、$y=F(x)$で
定まる曲線をCとする。$\alpha \lt \beta$を満たす実数$\alpha,\ \beta$に対して、C上の点A$(\alpha,F(\alpha))$
におけるCの接線を$L_{\alpha}$とするとき、Cと$L_{\alpha}$とのA以外の共有点が$B(\beta,F(\beta))$
であるとする。さらに、BにおけるCの接線を$L_{\beta}$とのB以外の共有点を$(\gamma,F(\gamma))$
とする。
(1)接線$L_{\alpha}$の方程式を$y=l_{\alpha}(x)$とし、$G(x)=F(x)-l_{\alpha}(x)$とおく。さらに、
曲線$y=G(x)$上の点$(\beta,G(\beta))$における接線の方程式を$y=m(x)$とする。$G(x)$
および$m(x)$を、それぞれ$\alpha,\beta$を用いて因数分解された形に表せ。必要ならば
xの整式で表される関数$p(x),q(x)$とそれらの導関数に関して成り立つ公式
$\left\{p(x)q(x)\right\}'=p'(x)q(x)+p(x)q'(x)$
を用いてもよい。
(2)接線$L_{\beta}$の方程式は(1)で定めた$l_{\alpha}(x),\ m(x)$を用いて、$y=l_{\alpha}(x)+ m(x)$で
与えられることを示せ。さらに、$\gamma$を$\alpha,\beta$を用いて表せ。
(3)曲線Cおよび$L_{\beta}$で囲まれた図形の面積を$S$とする。$S$を$\alpha,\beta$を用いて表せ。
さらに$\alpha,\beta$が$-1 \lt \alpha \lt 0$かつ$1 \lt \beta \lt 2$を満たすとき、$S$の取り得る値の
範囲を求めよ。必要ならば$r \lt s$を満たす実数$r,s$に対して成り立つ公式
$\int_r^s(x-r)(x-s)^2dx=\frac{1}{12}(s-r)^4$
を用いてもよい。
2021慶應義塾大学経済学部過去問
06滋賀県教員採用試験（数学：6番 面積）
単元：
#数Ⅱ#微分法と積分法#その他#面積、体積#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{6}$
曲線$\sqrt x+\sqrt y=1,$
$x$軸,$y$軸で囲まれた部分の面積を求めよ.
この動画を見る
$\boxed{6}$
曲線$\sqrt x+\sqrt y=1,$
$x$軸,$y$軸で囲まれた部分の面積を求めよ.
高専数学 微積II #2(3)(4) 2次近似式
単元：
#数Ⅱ#微分法と積分法#微分とその応用#速度と近似式#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$x=0$における2次近似式を求め等式で表せ.
(1)$\cos 2x$
(2)$\log (1+2x)$
この動画を見る
$x=0$における2次近似式を求め等式で表せ.
(1)$\cos 2x$
(2)$\log (1+2x)$
名古屋大学２００２どっちがでかいか？
単元：
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
どちらが大きいか?
①$\ell_n\left(1+\dfrac{1}{x}\right)$ vs $\dfrac{1}{x+1}$
②$\left(1+\dfrac{2002}{2001}\right)^{\frac{2001}{2002}}$ vs $\left(1+\dfrac{2001}{2002}\right)^{\frac{2002}{2001}}$
この動画を見る
どちらが大きいか?
①$\ell_n\left(1+\dfrac{1}{x}\right)$ vs $\dfrac{1}{x+1}$
②$\left(1+\dfrac{2002}{2001}\right)^{\frac{2001}{2002}}$ vs $\left(1+\dfrac{2001}{2002}\right)^{\frac{2002}{2001}}$
福田のわかった数学〜高校２年生037〜軌跡(4)反転の話その2
単元：
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
数学$\textrm{II}$
軌跡(4) 反転の話(2)
動点Pが直線$l:x+y=1$上を動く。
原点Oを端点とする半直線OP上で
$OP・OQ=1$
を満たす点Qの軌跡を求めよ。
この動画を見る
数学$\textrm{II}$
軌跡(4) 反転の話(2)
動点Pが直線$l:x+y=1$上を動く。
原点Oを端点とする半直線OP上で
$OP・OQ=1$
を満たす点Qの軌跡を求めよ。
高専数学 微積II #2(1)(2) 2次近似式
単元：
#数Ⅱ#微分法と積分法#微分とその応用#速度と近似式#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$x=0$における2次近似式を求め等式で表せ.
(1)$e^{3x}$
(2)$x\sqrt{1+x}$
この動画を見る
$x=0$における2次近似式を求め等式で表せ.
(1)$e^{3x}$
(2)$x\sqrt{1+x}$
20三重県教員採用試験（数学：1-(3) 対数）
単元：
#数Ⅱ#指数関数と対数関数#対数関数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{1}-(3)$
$x \geq 3,y \geq \dfrac{1}{3},xy^2=243$
のとき
$\left(\log_3 x\right)\left(\log_3 y\right)$
の最大値,最小値を求めよ.
この動画を見る
$\boxed{1}-(3)$
$x \geq 3,y \geq \dfrac{1}{3},xy^2=243$
のとき
$\left(\log_3 x\right)\left(\log_3 y\right)$
の最大値,最小値を求めよ.
21三重県教員採用試験（数学：1-(3) 解と係数の関係）
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{1}-(3)$
$x^3+ax^2+bx+21=0$の1つの解が
$x=2+\sqrt3 i$のとき
$a,b$の値と実数解を求めよ.
この動画を見る
$\boxed{1}-(3)$
$x^3+ax^2+bx+21=0$の1つの解が
$x=2+\sqrt3 i$のとき
$a,b$の値と実数解を求めよ.
高専数学 微積II n次近似式
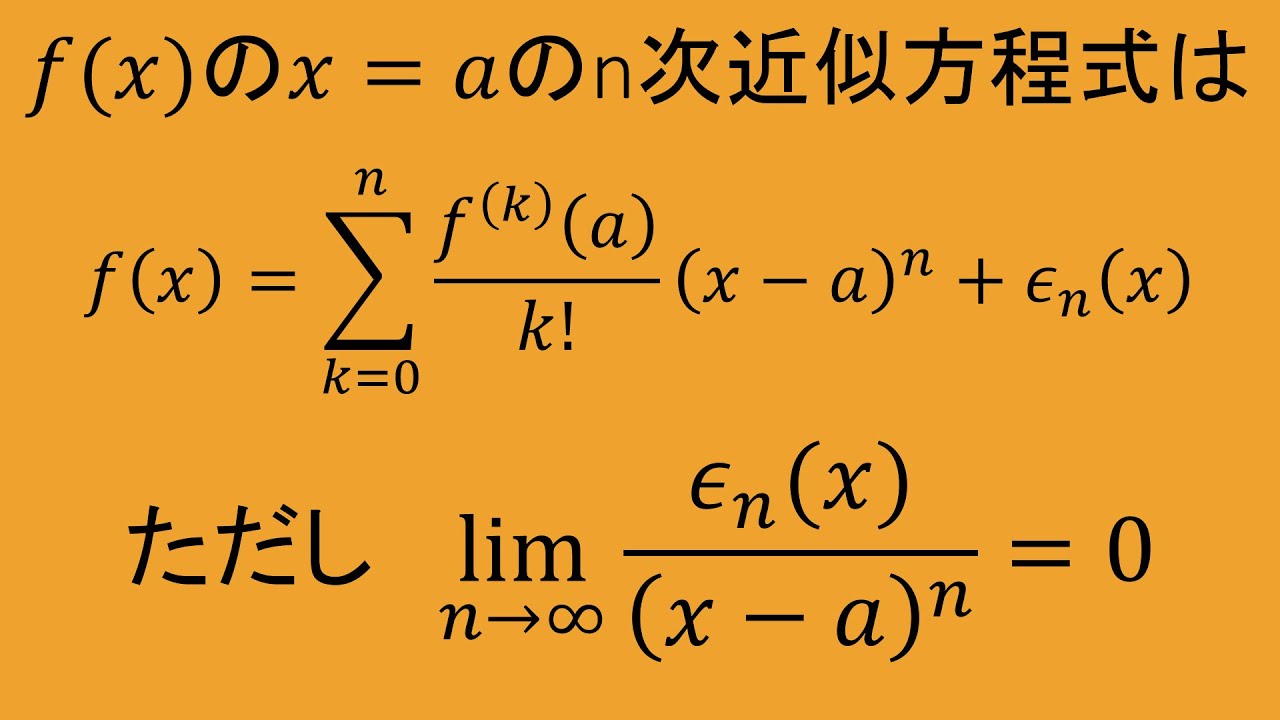
単元：
#数Ⅱ#微分法と積分法#微分とその応用#速度と近似式#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$f(x)$の$x=a$における$n$次近似式の等式は
$f(x)=\dfrac{f(a)}{O!}+\dfrac{f'(a)}{1!}(x-a)+･･････$
$+\dfrac{f^{(n)}(a)}{n!} (x-a)^n+\xi_n (x)$
つまり
$f(x)=\displaystyle \sum_{k=0}^{n}\dfrac{f^{(k)}(a)}{k!} (x-a)^k+\xi (x)$
ただし
$\displaystyle \lim_{x\to a} \dfrac{\xi_n(x)}{(x-a)^n}=0$
これを解け.
この動画を見る
$f(x)$の$x=a$における$n$次近似式の等式は
$f(x)=\dfrac{f(a)}{O!}+\dfrac{f'(a)}{1!}(x-a)+･･････$
$+\dfrac{f^{(n)}(a)}{n!} (x-a)^n+\xi_n (x)$
つまり
$f(x)=\displaystyle \sum_{k=0}^{n}\dfrac{f^{(k)}(a)}{k!} (x-a)^k+\xi (x)$
ただし
$\displaystyle \lim_{x\to a} \dfrac{\xi_n(x)}{(x-a)^n}=0$
これを解け.
ゆる言語学者に数学を教えるよ。その３ 複素数の掛け算
高専数学 微積II #1(1)(2) 1次近似式
単元：
#数Ⅱ#微分法と積分法#微分とその応用#速度と近似式#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$f(x)$の$x=a$における一次近似式は
$f(a)+f`(a)(x-a)$
次の点における一次近似式を求めよ.
(1)$e^{2x}\cos x \ (x=0)$
(2)$\dfrac{1}{x} \ (x=1)$
この動画を見る
$f(x)$の$x=a$における一次近似式は
$f(a)+f`(a)(x-a)$
次の点における一次近似式を求めよ.
(1)$e^{2x}\cos x \ (x=0)$
(2)$\dfrac{1}{x} \ (x=1)$
言語学オタクに数学を教えるよ！その２ ネイピア数とは
高専数学 微積I 254 広義積分
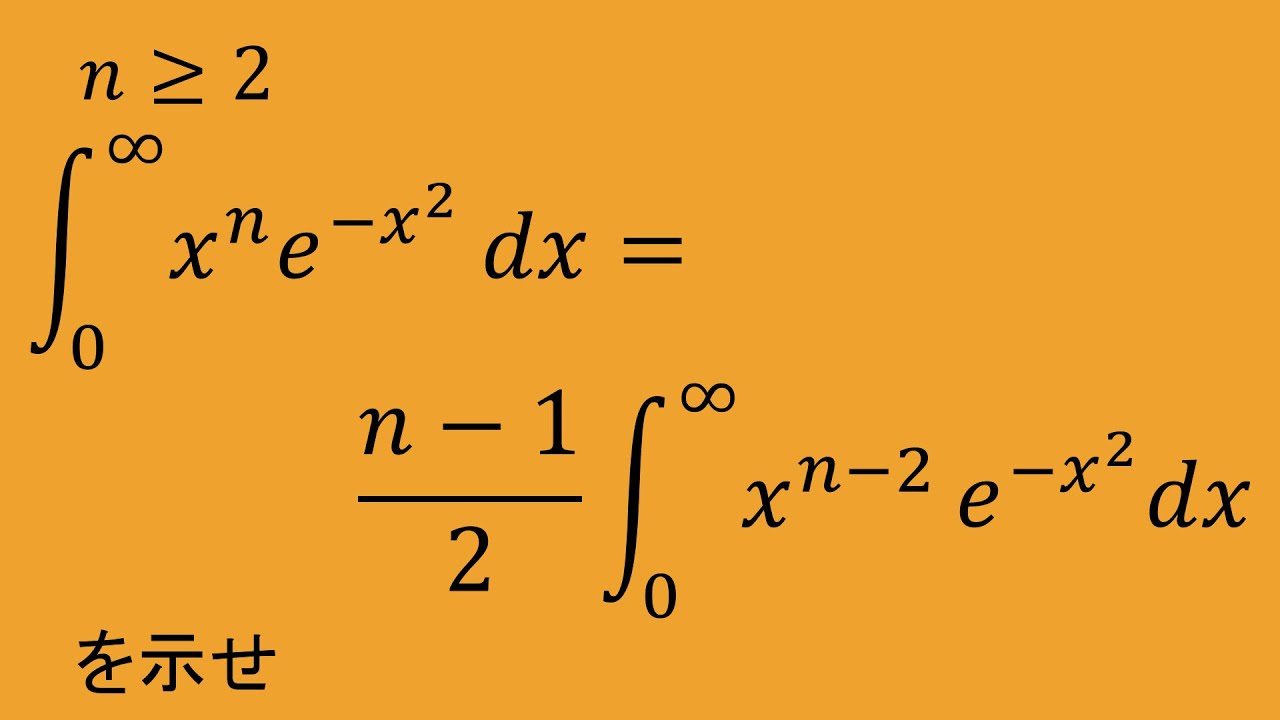
単元：
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$n\geqq 2$である.
$\displaystyle \int_{0}^{\infty} x^n e^{-x^2} dx=\dfrac{n-1}{2} \displaystyle \int_{0}^{\infty} x^{n-2} e^{-x^2} dx$
が成り立つことを示せ.
この動画を見る
$n\geqq 2$である.
$\displaystyle \int_{0}^{\infty} x^n e^{-x^2} dx=\dfrac{n-1}{2} \displaystyle \int_{0}^{\infty} x^{n-2} e^{-x^2} dx$
が成り立つことを示せ.
ゆる言語学者に数学を教えるよ！その１sinの微分
福田の数学〜慶應義塾大学2021年経済学部第１問〜2つの円に同時に外接する円の条件
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#集合と命題（集合・命題と条件・背理法）#図形と方程式#円と方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{1}}$ 座標平面上の原点を中心とする$半径2$の円を$C_1$、中心の座標が$(7,0)$、$半径3$の円を$C_2$とする。さらに$r$を正の実数とするとき、$C_1$と$C_2$に同時に外接する円で、その中心の座標が$(a,b)$、半径が$r$であるものを$C_3$とする。ただし、2つの円が外接するとは、それらが$1点$を共有し、中心が互いの外部にあるときをいう。
$(1)r$の最小値は$\boxed{\ \ ア\ \ }$であり、$a$の最大値は$\boxed{\ \ イ\ \ }$となる。
$(2)a$と$b$は関係式$b^2=\boxed{\ \ ウエ\ \ }(a+\boxed{\ \ オカ\ \ })(a-4)$を満たす。
$(3)C_3$が$直線x=-3$に接するとき、$a=\frac{\boxed{\ \ キク\ \ }}{\boxed{\ \ ケ\ \ }},$ $|b|=\frac{\sqrt{\boxed{\ \ コサシ\ \ }}}{\boxed{\ \ ス\ \ }}$である。
$(4)点(a,b)$と原点を通る直線と、$点(a,b)$と$点(7,0)$を通る直線が直交するとき、
$|b|=\frac{\boxed{\ \ セソ\ \ }}{\boxed{\ \ タ\ \ }}$となる。
2021慶應義塾大学経済学部過去問
この動画を見る
${\Large\boxed{1}}$ 座標平面上の原点を中心とする$半径2$の円を$C_1$、中心の座標が$(7,0)$、$半径3$の円を$C_2$とする。さらに$r$を正の実数とするとき、$C_1$と$C_2$に同時に外接する円で、その中心の座標が$(a,b)$、半径が$r$であるものを$C_3$とする。ただし、2つの円が外接するとは、それらが$1点$を共有し、中心が互いの外部にあるときをいう。
$(1)r$の最小値は$\boxed{\ \ ア\ \ }$であり、$a$の最大値は$\boxed{\ \ イ\ \ }$となる。
$(2)a$と$b$は関係式$b^2=\boxed{\ \ ウエ\ \ }(a+\boxed{\ \ オカ\ \ })(a-4)$を満たす。
$(3)C_3$が$直線x=-3$に接するとき、$a=\frac{\boxed{\ \ キク\ \ }}{\boxed{\ \ ケ\ \ }},$ $|b|=\frac{\sqrt{\boxed{\ \ コサシ\ \ }}}{\boxed{\ \ ス\ \ }}$である。
$(4)点(a,b)$と原点を通る直線と、$点(a,b)$と$点(7,0)$を通る直線が直交するとき、
$|b|=\frac{\boxed{\ \ セソ\ \ }}{\boxed{\ \ タ\ \ }}$となる。
2021慶應義塾大学経済学部過去問
福田のわかった数学〜高校２年生036〜軌跡(3)反転の話その１
単元：
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$数学\textrm{II}$ $軌跡(3)$ $反転の話(1)$
座標平面上で、$点P(4,3)$に対して
$OP・OQ=1$
となる$点Q$を$半直線OP$上にとる。
$点Q$の座標を求めよ。
この動画を見る
$数学\textrm{II}$ $軌跡(3)$ $反転の話(1)$
座標平面上で、$点P(4,3)$に対して
$OP・OQ=1$
となる$点Q$を$半直線OP$上にとる。
$点Q$の座標を求めよ。
高専数学 微積I #258 媒介変数表示曲線の面積
単元：
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師：
ますただ
問題文全文(内容文)：
$1 \leqq t \leqq 2$である.
曲線$x=t+\dfrac{1}{t},y=t-\dfrac{1}{t}$と
$x$軸,直線$x=\dfrac{5}{2}$で
囲まれた図形の面積$S$を求めよ.
この動画を見る
$1 \leqq t \leqq 2$である.
曲線$x=t+\dfrac{1}{t},y=t-\dfrac{1}{t}$と
$x$軸,直線$x=\dfrac{5}{2}$で
囲まれた図形の面積$S$を求めよ.
18兵庫県教員採用試験（数学：3 -(2) 解の個数）
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{3}-(2)$
$\vert x^2-2x-3 \vert =a(x+1)+2$
が異なる3個の実数解をもつような
$a$の値を求めよ.
この動画を見る
$\boxed{3}-(2)$
$\vert x^2-2x-3 \vert =a(x+1)+2$
が異なる3個の実数解をもつような
$a$の値を求めよ.
福田の数学〜慶應義塾大学2021年環境情報学部第６問〜領域における最大
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{6}}$ ある国の有識者会議が、経済活性化に資する公共サービスの$供給量x$と、医療・
公衆衛生に関する公共サービスの$供給量y$の組み合わせの検討を行っている。$供給量
(x,y)$は、予算やマンパワー、既存の法律など、さまざまな要因により、その実現可能性
に制約を受け、次の不等式を満たすものとする。
$\left\{\begin{array}{1}
2x+5y \leqq 405 \ldots(1)\\
x^2+75y \leqq 6075 \ldots(2)\\
x \geqq 0 \ldots(3)\\
y \geqq 0 \ldots(4)\\
\end{array}\right.$
$供給量(x,y)$を$x軸$と$y軸$の$2次元座標$で表すと、実現可能な供給量の組合せ$(x,y)$の値域は、$0 \leqq x \leqq \boxed{\ \ アイ\ \ }$の範囲で$(1)$と$(4)$を満たす$(x,y)$の部分の領域と、
$\boxed{\ \ アイ\ \ } \leqq x \leqq \sqrt{\boxed{\ \ オカ\ \ }}$の範囲で$(2)$と$(4)$を満たす$(x,y)$の部分の領域の$2$つ
からなることがわかる。
いま、有識者会議の目標が$xy$の最大化であるとすると、供給量の組合せを
$(x,y)=(\boxed{\ \ キク\ \ },\boxed{\ \ ケコ\ \ })$とする結論を得る。
次に、情勢の変化に伴って、上記の$(1),(2),(3),(4)$に新たな不等式
$x+y \leqq 93 \ldots(5)$
が加わったとすると、実現可能な$(x,y)$の領域は、$0 \leqq x \leqq \boxed{\ \ サシ\ \ }$の範囲で
$(1)と(4)$を満たす$(x,y)$の部分の領域と、$\boxed{\ \ サシ\ \ } \leqq x \leqq \boxed{\ \ スセ\ \ }$の範囲で
$(5)と(4)$を満たす$(x,y)$の部分の領域と、$\boxed{\ \ スセ\ \ } \leqq x \leqq \boxed{\ \ ウエ\ \ }\sqrt{\boxed{\ \ オカ\ \ }}$の範囲で
$(2)と(4)$を満たす$(x,y)$の部分の領域の$3つ$に分けることができる。
また、政府の方針にそって、有識者会議の目標が$x^2y$の最大化に変更されたとすると、
供給量の組合せを
$(x,y)=(\boxed{\ \ ソタ\ \ },\boxed{\ \ チツ\ \ })$
とする結論を導くことになる。
2021慶應義塾大学環境情報学部過去問
この動画を見る
${\Large\boxed{6}}$ ある国の有識者会議が、経済活性化に資する公共サービスの$供給量x$と、医療・
公衆衛生に関する公共サービスの$供給量y$の組み合わせの検討を行っている。$供給量
(x,y)$は、予算やマンパワー、既存の法律など、さまざまな要因により、その実現可能性
に制約を受け、次の不等式を満たすものとする。
$\left\{\begin{array}{1}
2x+5y \leqq 405 \ldots(1)\\
x^2+75y \leqq 6075 \ldots(2)\\
x \geqq 0 \ldots(3)\\
y \geqq 0 \ldots(4)\\
\end{array}\right.$
$供給量(x,y)$を$x軸$と$y軸$の$2次元座標$で表すと、実現可能な供給量の組合せ$(x,y)$の値域は、$0 \leqq x \leqq \boxed{\ \ アイ\ \ }$の範囲で$(1)$と$(4)$を満たす$(x,y)$の部分の領域と、
$\boxed{\ \ アイ\ \ } \leqq x \leqq \sqrt{\boxed{\ \ オカ\ \ }}$の範囲で$(2)$と$(4)$を満たす$(x,y)$の部分の領域の$2$つ
からなることがわかる。
いま、有識者会議の目標が$xy$の最大化であるとすると、供給量の組合せを
$(x,y)=(\boxed{\ \ キク\ \ },\boxed{\ \ ケコ\ \ })$とする結論を得る。
次に、情勢の変化に伴って、上記の$(1),(2),(3),(4)$に新たな不等式
$x+y \leqq 93 \ldots(5)$
が加わったとすると、実現可能な$(x,y)$の領域は、$0 \leqq x \leqq \boxed{\ \ サシ\ \ }$の範囲で
$(1)と(4)$を満たす$(x,y)$の部分の領域と、$\boxed{\ \ サシ\ \ } \leqq x \leqq \boxed{\ \ スセ\ \ }$の範囲で
$(5)と(4)$を満たす$(x,y)$の部分の領域と、$\boxed{\ \ スセ\ \ } \leqq x \leqq \boxed{\ \ ウエ\ \ }\sqrt{\boxed{\ \ オカ\ \ }}$の範囲で
$(2)と(4)$を満たす$(x,y)$の部分の領域の$3つ$に分けることができる。
また、政府の方針にそって、有識者会議の目標が$x^2y$の最大化に変更されたとすると、
供給量の組合せを
$(x,y)=(\boxed{\ \ ソタ\ \ },\boxed{\ \ チツ\ \ })$
とする結論を導くことになる。
2021慶應義塾大学環境情報学部過去問
福田のわかった数学〜高校３年生理系043〜極限(43)有名な極限の証明(3)
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
\begin{eqnarray}
数学\textrm{III} 有名な極限を証明(3)\\
\lim_{x \to \infty}\frac{\log x}{x}=0を既知として\\
\lim_{x \to +0}x\log x を求めよ。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
数学\textrm{III} 有名な極限を証明(3)\\
\lim_{x \to \infty}\frac{\log x}{x}=0を既知として\\
\lim_{x \to +0}x\log x を求めよ。
\end{eqnarray}
高専数学 微積I p 62ex(2) 広義積分
単元：
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{\infty}\log \left(1+\dfrac{3}{x^2}\right)dx$
を計算せよ.
この動画を見る
$\displaystyle \int_{1}^{\infty}\log \left(1+\dfrac{3}{x^2}\right)dx$
を計算せよ.
練習問題36 （数検1級1次 教採 極限値）
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{x\to\infty} \dfrac{e^x-e^{-x}}{\log (1+x)}$
を求めよ.
この動画を見る
$\displaystyle \lim_{x\to\infty} \dfrac{e^x-e^{-x}}{\log (1+x)}$
を求めよ.
対数の基本
単元：
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$a\gt 0,b\gt 0$
$a^2+b^2=1$
$\log_a b^2=\log_b ab$
実数$(a,b)$を求めよ.
この動画を見る
$a\gt 0,b\gt 0$
$a^2+b^2=1$
$\log_a b^2=\log_b ab$
実数$(a,b)$を求めよ.
福田の数学〜慶應義塾大学2021年環境情報学部第５問〜空間の領域に位置する直方体の体積
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{5}}$ $xyz空間$において、$直方体ABCD-EFGH$が$z \geqq x^2+y^2$
$(0 \leqq z \leqq 1)$を満たす立体の周辺および内部に存在する。この
直方体の$面ABCD,EFGH$は$xy平面$に平行であり、$頂点A,B,C,D$
は$平面z=1$上に、$頂点E,F,G,H$は$曲面z=x^2+y^2$上に存在する。
$(1)$$直方体ABCD-EFGH$の$面ABCD$および$EFGH$が$1辺$の$長さa$
の正方形のとき、正の実数である$a$の取り得る値の範囲は
$0 \lt a \lt \sqrt{\boxed{\ \ アイ\ \ }}$であり、この直方体の体積は$\frac{\boxed{\ \ ウエ\ \ }}{\boxed{\ \ オカ\ \ }}a^4+\boxed{\ \ キク\ \ }a^2$
である。
$(2)$$直方体ABCD-EFGH$の$面ABFE$および$DCGH$が$1辺$の$長さb$
の正方形のとき、正の実数である$b$の取り得る値の範囲は
$0 \lt b \lt \boxed{\ \ ケコ\ \ }+\boxed{\ \ サシ\ \ }\sqrt{\boxed{\ \ スセ\ \ }}$であり、この直方体の体積は
$b^2\sqrt{\boxed{\ \ ソタ\ \ }b^2+\boxed{\ \ チツ\ \ }b+\boxed{\ \ テト\ \ }}$である。
$(3)$$直方体ABCD-EFGH$の全ての面が$1辺$の$長さc$の正方形のとき、すなわち
$直方体ABCD-EFGH$が立方体のとき、正の実数である$c$の値は
$\boxed{\ \ ナニ\ \ }+\sqrt{\boxed{\ \ ヌネ\ \ }}$であり、$立方体ABCD-EFGH$の体積は
$\boxed{\ \ ノハヒ\ \ }+\boxed{\ \ フヘ\ \ }\sqrt{\boxed{\ \ ホマ\ \ }}$である。
この動画を見る
${\Large\boxed{5}}$ $xyz空間$において、$直方体ABCD-EFGH$が$z \geqq x^2+y^2$
$(0 \leqq z \leqq 1)$を満たす立体の周辺および内部に存在する。この
直方体の$面ABCD,EFGH$は$xy平面$に平行であり、$頂点A,B,C,D$
は$平面z=1$上に、$頂点E,F,G,H$は$曲面z=x^2+y^2$上に存在する。
$(1)$$直方体ABCD-EFGH$の$面ABCD$および$EFGH$が$1辺$の$長さa$
の正方形のとき、正の実数である$a$の取り得る値の範囲は
$0 \lt a \lt \sqrt{\boxed{\ \ アイ\ \ }}$であり、この直方体の体積は$\frac{\boxed{\ \ ウエ\ \ }}{\boxed{\ \ オカ\ \ }}a^4+\boxed{\ \ キク\ \ }a^2$
である。
$(2)$$直方体ABCD-EFGH$の$面ABFE$および$DCGH$が$1辺$の$長さb$
の正方形のとき、正の実数である$b$の取り得る値の範囲は
$0 \lt b \lt \boxed{\ \ ケコ\ \ }+\boxed{\ \ サシ\ \ }\sqrt{\boxed{\ \ スセ\ \ }}$であり、この直方体の体積は
$b^2\sqrt{\boxed{\ \ ソタ\ \ }b^2+\boxed{\ \ チツ\ \ }b+\boxed{\ \ テト\ \ }}$である。
$(3)$$直方体ABCD-EFGH$の全ての面が$1辺$の$長さc$の正方形のとき、すなわち
$直方体ABCD-EFGH$が立方体のとき、正の実数である$c$の値は
$\boxed{\ \ ナニ\ \ }+\sqrt{\boxed{\ \ ヌネ\ \ }}$であり、$立方体ABCD-EFGH$の体積は
$\boxed{\ \ ノハヒ\ \ }+\boxed{\ \ フヘ\ \ }\sqrt{\boxed{\ \ ホマ\ \ }}$である。
高専数学 微積I #259(2) 広義積分
単元：
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{e}^{\infty}\dfrac{1}{r(\log r)^2} dr$
を計算せよ.
この動画を見る
$\displaystyle \int_{e}^{\infty}\dfrac{1}{r(\log r)^2} dr$
を計算せよ.
05高知県教員採用試験（数学：3-(2) 複素数）
単元：
#数Ⅱ#複素数と方程式#複素数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{3}-(2)$
$z=1+\sqrt3 i$のとき,
$1+z+z^2+z^3+z^4+z^5$の値を求めよ.
この動画を見る
$\boxed{3}-(2)$
$z=1+\sqrt3 i$のとき,
$1+z+z^2+z^3+z^4+z^5$の値を求めよ.
騙していません！
福田のわかった数学〜高校３年生理系042〜極限(42)有名な極限の証明(2)
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
\begin{eqnarray}
数学\textrm{III} 有名な極限を証明(2)\\
\lim_{x \to \infty}xe^{-x}=0を既知として\\
\lim_{x \to \infty}\frac{\log x}{x} を求めよ。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
数学\textrm{III} 有名な極限を証明(2)\\
\lim_{x \to \infty}xe^{-x}=0を既知として\\
\lim_{x \to \infty}\frac{\log x}{x} を求めよ。
\end{eqnarray}