 数Ⅱ
数Ⅱ
 数Ⅱ
数Ⅱ
20年5月数検準1級1次試験(極限)
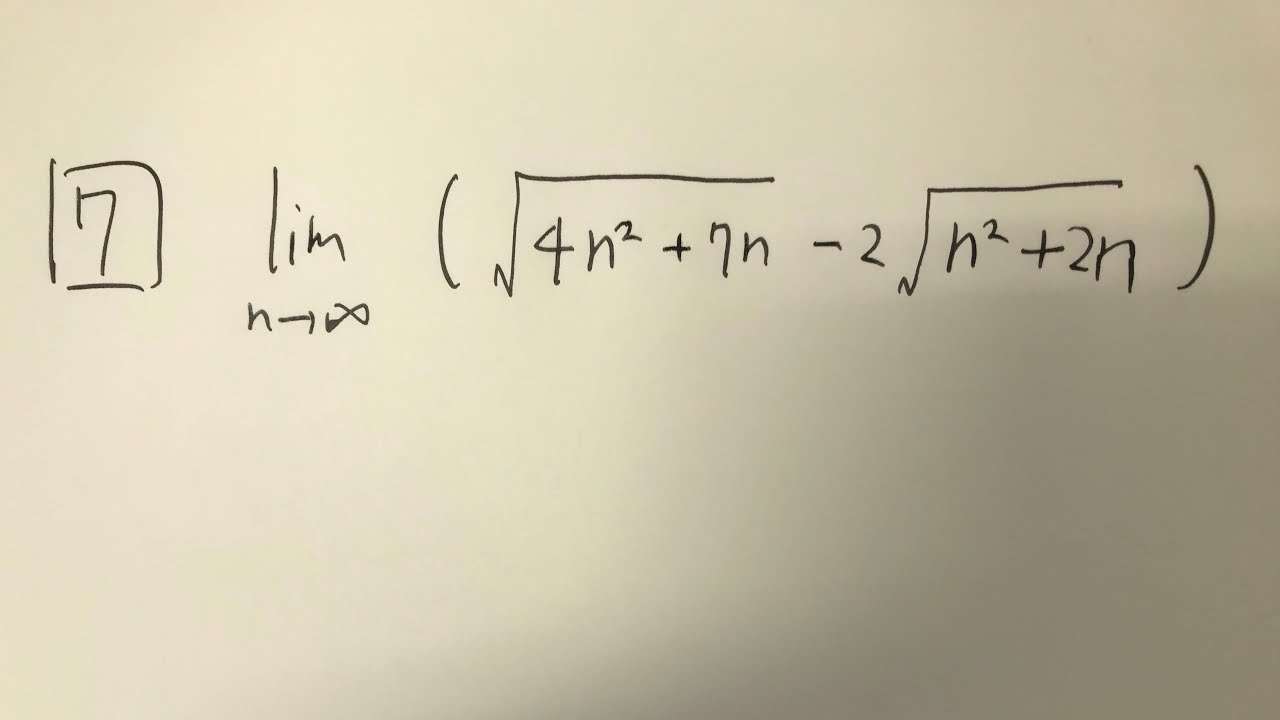
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#数学検定#数学検定準1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\boxed{7}$
$\displaystyle \lim_{n\to\infty}(\sqrt{4n^2+7n}-2\sqrt{n^2+2n})$
これを解け.
20年5月数検準1級1次試験(極限)過去問
この動画を見る
$\boxed{7}$
$\displaystyle \lim_{n\to\infty}(\sqrt{4n^2+7n}-2\sqrt{n^2+2n})$
これを解け.
20年5月数検準1級1次試験(極限)過去問
整式の剰余 大分大(医)その2

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$は自然数である.
(1)$x^n$を$x^5-1$で割った余りを求めよ.
(2)$x^{4n}+x^{3n}+x^{2n}+x^n$を$x^4+x^3+x^2+x+1$で割った余りを求めよ.
2005大分大(医)過去問
この動画を見る
$n$は自然数である.
(1)$x^n$を$x^5-1$で割った余りを求めよ.
(2)$x^{4n}+x^{3n}+x^{2n}+x^n$を$x^4+x^3+x^2+x+1$で割った余りを求めよ.
2005大分大(医)過去問
整式の剰余 大分大(医)

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$は自然数である.
$x^n$を$x^5-1$で割った余りを求めよ.
2005大分大(医)過去問
この動画を見る
$n$は自然数である.
$x^n$を$x^5-1$で割った余りを求めよ.
2005大分大(医)過去問
20年5月数学検定準1級1次試験(複素数)

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#複素数#数学検定#数学検定準1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\boxed{4}$
$\alpha=(-1+i)(1-\sqrt3 i)$
(1)$\vert \alpha \vert $を求めよ.
(2)$arg \alpha$を求めよ.
$0\leqq arg \alpha \lt 2\pi$
20年5月数学検定準1級1次試験(複素数)過去問
この動画を見る
$\boxed{4}$
$\alpha=(-1+i)(1-\sqrt3 i)$
(1)$\vert \alpha \vert $を求めよ.
(2)$arg \alpha$を求めよ.
$0\leqq arg \alpha \lt 2\pi$
20年5月数学検定準1級1次試験(複素数)過去問
整式の剰余(訂正版)

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$は自然数である.
$x^{6n}$を$x^4+x^2+1$で割った余りを求めよ.
この動画を見る
$n$は自然数である.
$x^{6n}$を$x^4+x^2+1$で割った余りを求めよ.
整式の剰余

20年5月数学検定準1級1次試験(円の方程式)

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#図形と方程式#数学検定#数学検定準1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
2⃣円$C_1$の中心は(-6,2)で直線$l:3x-4y+1=0$に接する。
このとき円$C_1$がx軸から切り取る線分の長さl'を求めよ。
この動画を見る
2⃣円$C_1$の中心は(-6,2)で直線$l:3x-4y+1=0$に接する。
このとき円$C_1$がx軸から切り取る線分の長さl'を求めよ。
20年5月数学検定準1級1次試験(円の方程式)

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#図形と方程式#円と方程式#数学検定#数学検定準1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\boxed{2}$
円$C_1$の中心は$(-6,2)$で直線$\ell:3x-4y+1=0$に接する.
このとき円$C_1$が$x$軸から切り取る線分の長さ$\ell^1$を求めよ.
20年5月数学検定準1級1次試験(円の方程式)過去問
この動画を見る
$\boxed{2}$
円$C_1$の中心は$(-6,2)$で直線$\ell:3x-4y+1=0$に接する.
このとき円$C_1$が$x$軸から切り取る線分の長さ$\ell^1$を求めよ.
20年5月数学検定準1級1次試験(円の方程式)過去問
20年5月数学検定準1級1次試験(積分)
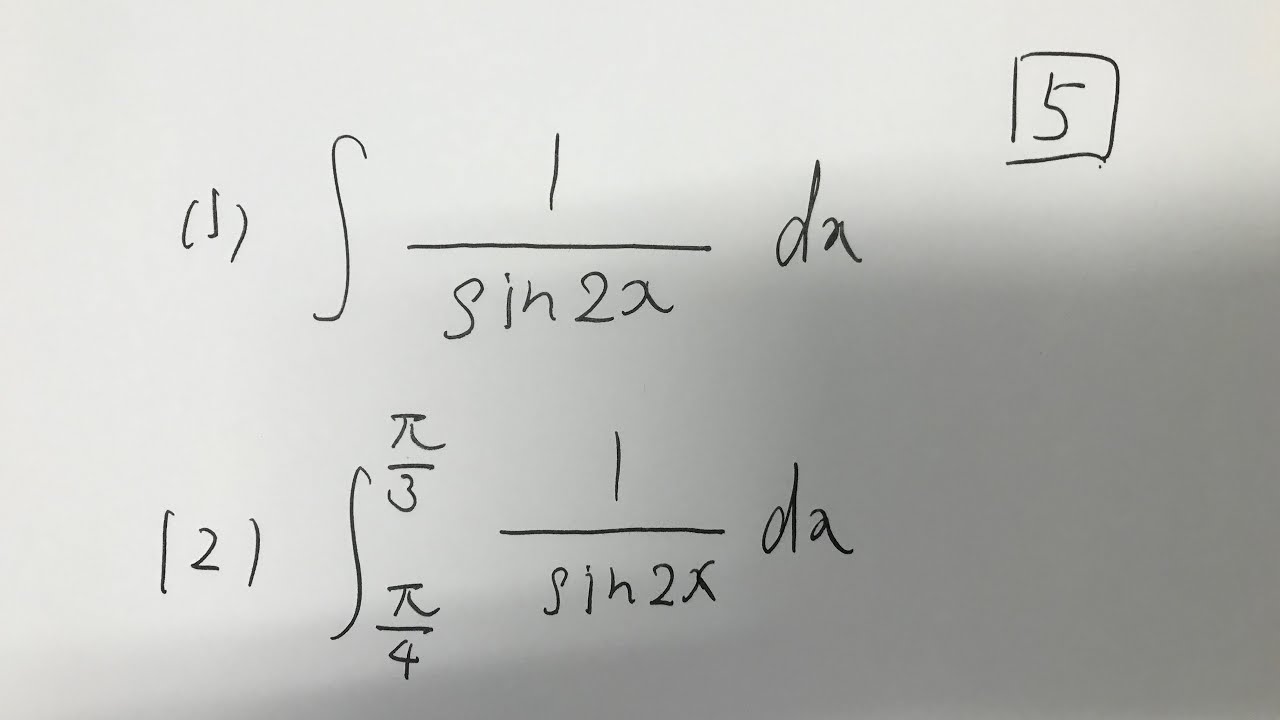
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#数学検定#数学検定準1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\boxed{5}$
(1)$\displaystyle \int_{}^{}\dfrac{dx}{\sin 2x}$
(2)$\displaystyle \int_{\frac{\pi}{4}}^{\frac{\pi}{3}}\dfrac{dx}{\sin 2x}$
20年5月数学検定準1級1次試験(積分)過去問
この動画を見る
$\boxed{5}$
(1)$\displaystyle \int_{}^{}\dfrac{dx}{\sin 2x}$
(2)$\displaystyle \int_{\frac{\pi}{4}}^{\frac{\pi}{3}}\dfrac{dx}{\sin 2x}$
20年5月数学検定準1級1次試験(積分)過去問
20年5月数学検定準1級1次試験(三角関数)
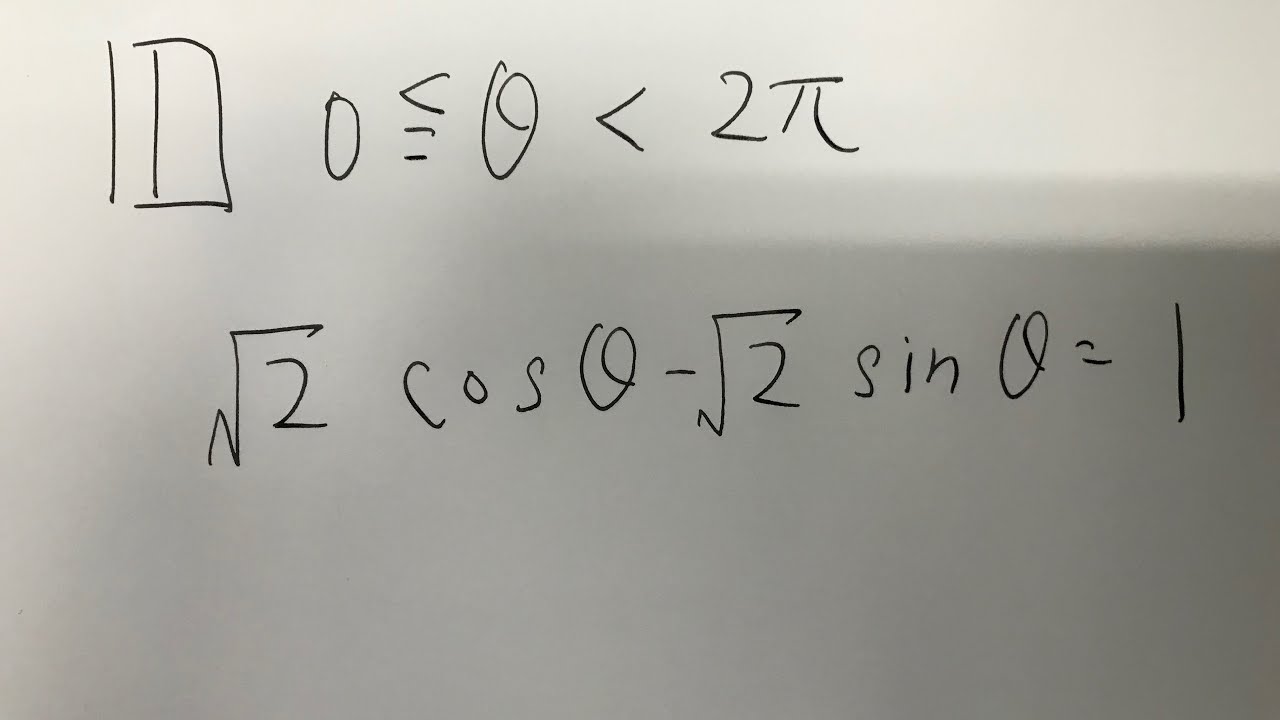
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#三角関数#三角関数とグラフ#数学検定#数学検定準1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
1⃣ $0 \leqq θ < 2\pi$
$\sqrt 2 cosθ - \sqrt 2 sinθ = 1$
この動画を見る
1⃣ $0 \leqq θ < 2\pi$
$\sqrt 2 cosθ - \sqrt 2 sinθ = 1$
20年5月数学検定準1級1次試験(三角関数)
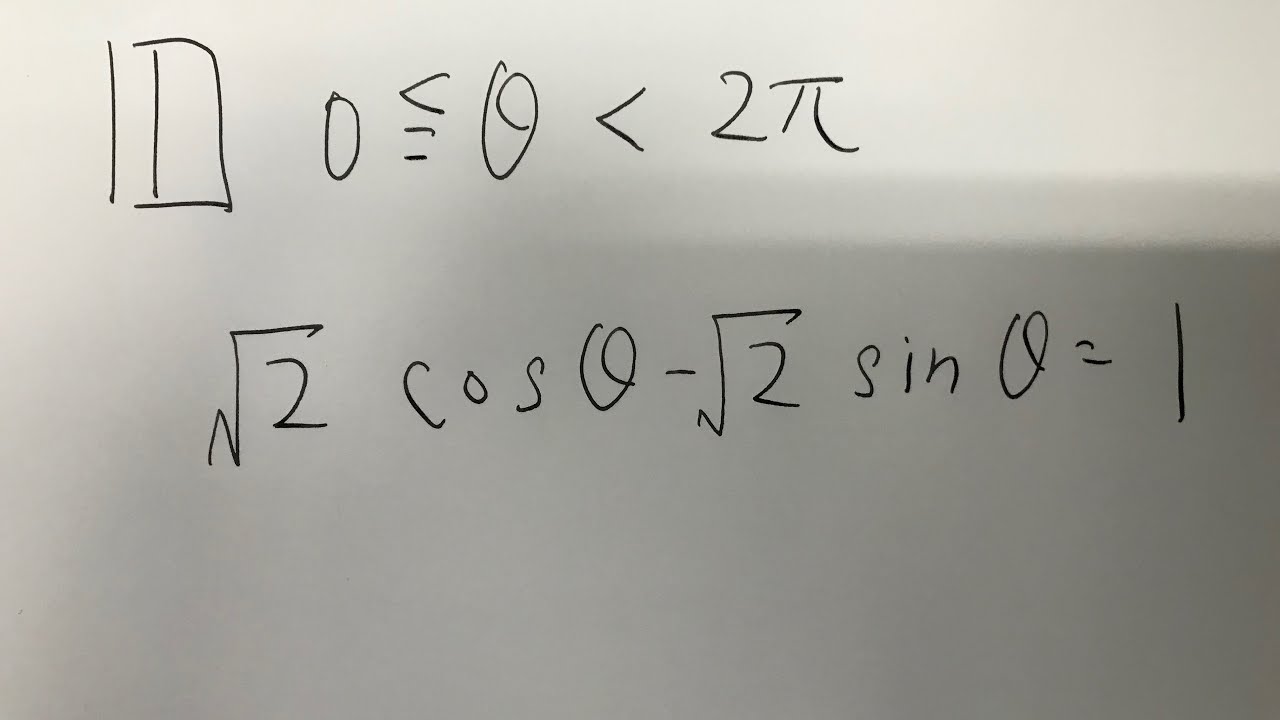
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#三角関数#数学検定#数学検定準1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\boxed{1}$
$0\leqq \theta \lt 2\pi$
$\sqrt2 \cos \theta -\sqrt2 \sin \theta=1$
20年5月数学検定準1級1次試験(三角関数)過去問
この動画を見る
$\boxed{1}$
$0\leqq \theta \lt 2\pi$
$\sqrt2 \cos \theta -\sqrt2 \sin \theta=1$
20年5月数学検定準1級1次試験(三角関数)過去問
【数Ⅱ】複素数と方程式:3次方程式が異なる3つの解を持つ条件:方程式x³+(a-1)x-a=0が異なる3つの実数解をもつとき、定数aの値の範囲を求めよ。

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
教材:
#ニュースコープ#ニュースコープ数学Ⅱ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
方程式$x^3+(a-1)x-a=0$が異なる3つの実数解をもつとき、定数aの値の範囲を求めよ。
この動画を見る
方程式$x^3+(a-1)x-a=0$が異なる3つの実数解をもつとき、定数aの値の範囲を求めよ。
【数Ⅱ】複素数と方程式:3次方程式が2重解を持つ条件:x³+6x²+ax+b=0が-1を2重解としてもつとき、定数a,bの値を求めよ。また、残りの解を求めよ。

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
教材:
#ニュースコープ#ニュースコープ数学Ⅱ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$x^3+6x^2+ax+b=0$が-1を2重解としてもつとき、定数a,bの値を求めよ。また、残りの解を求めよ。
この動画を見る
$x^3+6x^2+ax+b=0$が-1を2重解としてもつとき、定数a,bの値を求めよ。また、残りの解を求めよ。
複素数の5次方程式

単元:
#数Ⅱ#複素数と方程式#複素数#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.($\sin,\cos$は使わない)
$x^5=i$
この動画を見る
これを解け.($\sin,\cos$は使わない)
$x^5=i$
複素数 慈恵医大

単元:
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\theta=\dfrac{2}{9}\pi$
$\alpha=\cos\theta+i\sin\theta$
$\beta=\alpha+\alpha^8$である.
(1)$\beta$は実数であることを示せ.
(2)$\beta$を解にもつ整数係数の3次方程式を求めよ.
(3)(2)の3次方程式は有理数解をもたないことを示せ.
2004慈恵医大過去問
この動画を見る
$\theta=\dfrac{2}{9}\pi$
$\alpha=\cos\theta+i\sin\theta$
$\beta=\alpha+\alpha^8$である.
(1)$\beta$は実数であることを示せ.
(2)$\beta$を解にもつ整数係数の3次方程式を求めよ.
(3)(2)の3次方程式は有理数解をもたないことを示せ.
2004慈恵医大過去問
複素数 福井大

単元:
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\alpha^3=-4+\sqrt{11}i$,$c=\alpha+\overline{\alpha}$である.
(1)$\vert \alpha \vert$の値を求めよ.
(2)$c^3-9c$の値を求めよ.
(3)$c$の値を求めよ.
1999福井大過去問
この動画を見る
$\alpha^3=-4+\sqrt{11}i$,$c=\alpha+\overline{\alpha}$である.
(1)$\vert \alpha \vert$の値を求めよ.
(2)$c^3-9c$の値を求めよ.
(3)$c$の値を求めよ.
1999福井大過去問
複素数 日本大

単元:
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$z=\dfrac{\sqrt6+\sqrt2}{4}+\dfrac{\sqrt6-\sqrt2}{4}i$,$\displaystyle \sum_{n=1}^{23}z^n$
2000日大過去問
この動画を見る
これを解け.
$z=\dfrac{\sqrt6+\sqrt2}{4}+\dfrac{\sqrt6-\sqrt2}{4}i$,$\displaystyle \sum_{n=1}^{23}z^n$
2000日大過去問
複素数 広島大

単元:
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$z^2=8+6i$のとき,$z^3-16z-\dfrac{100}{z}$の値を求めよ.
1966広島大過去問
この動画を見る
$z^2=8+6i$のとき,$z^3-16z-\dfrac{100}{z}$の値を求めよ.
1966広島大過去問
19神奈川県教員採用試験(数学:面積の最小値)

単元:
#数Ⅱ#微分法と積分法#その他#不定積分・定積分#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$y=x^2-5x+4$と$y=m(x-2)$で囲まれた面積の最小値とそのときのmの値を求めよ。
この動画を見る
$y=x^2-5x+4$と$y=m(x-2)$で囲まれた面積の最小値とそのときのmの値を求めよ。
19神奈川県教員採用試験(数学:面積の最小値)

単元:
#数Ⅱ#微分法と積分法#面積、体積#その他#数学(高校生)#その他
指導講師:
ますただ
問題文全文(内容文):
$y=x^2-5x+4$と$y=m(n-2)$で囲まれた面積の最小値とそのときの$m$の値を求めよ.
19神奈川県教員採用試験(数学:面積の最小値)過去問
この動画を見る
$y=x^2-5x+4$と$y=m(n-2)$で囲まれた面積の最小値とそのときの$m$の値を求めよ.
19神奈川県教員採用試験(数学:面積の最小値)過去問
三角関数の基本 合成公式 図書館情報大

単元:
#数Ⅱ#三角関数#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\sqrt3\sin 2x+2\sin^2x-1$,$0\leqq x\lt \pi$における最大値,最小値を求めよ.
1985図書館情報大過去問
この動画を見る
$\sqrt3\sin 2x+2\sin^2x-1$,$0\leqq x\lt \pi$における最大値,最小値を求めよ.
1985図書館情報大過去問
18神奈川県採用試験(数学:複素数)
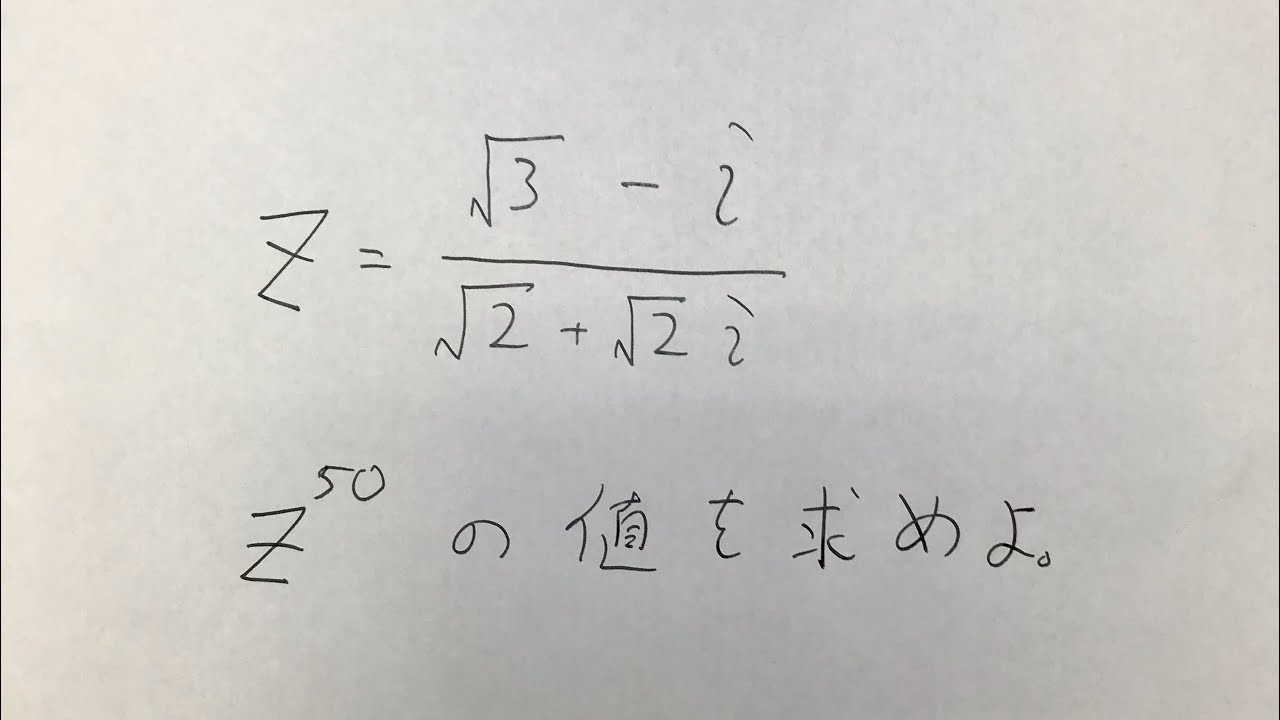
単元:
#数Ⅱ#複素数平面#三角関数#三角関数とグラフ#複素数平面#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$Z=\frac{\sqrt 3 - i}{\sqrt 2 + \sqrt 2 i } , Z^{50}$を求めよ。
この動画を見る
$Z=\frac{\sqrt 3 - i}{\sqrt 2 + \sqrt 2 i } , Z^{50}$を求めよ。
n乗根の方程式

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.$x,y$は実数である.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+y=10 \\
\sqrt[3]{x}+\sqrt[3]{y}=\dfrac{5}{2}\sqrt[6]{xy}
\end{array}
\right.
\end{eqnarray}$
この動画を見る
これを解け.$x,y$は実数である.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+y=10 \\
\sqrt[3]{x}+\sqrt[3]{y}=\dfrac{5}{2}\sqrt[6]{xy}
\end{array}
\right.
\end{eqnarray}$
整式の剰余
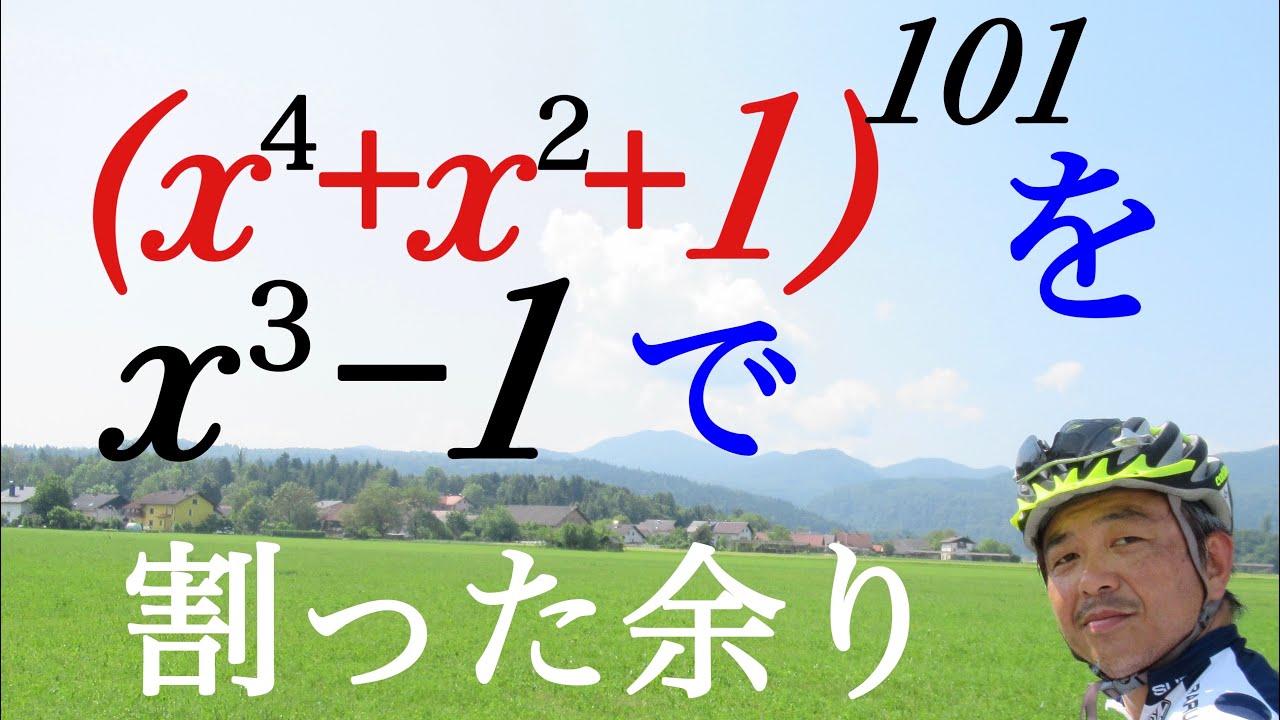
単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(x^4+x^2+1)^{101}$を$x^3-1$で割った余りを求めよ.
この動画を見る
$(x^4+x^2+1)^{101}$を$x^3-1$で割った余りを求めよ.
積分 帯広畜産大

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=x^4-4x^2-4x+3$と2点で接する直線の方程式を$g(x)$とする.
$f(x)$と$g(x)$で囲まれた面積を求めよ.
1979帯広畜産大過去問
この動画を見る
$f(x)=x^4-4x^2-4x+3$と2点で接する直線の方程式を$g(x)$とする.
$f(x)$と$g(x)$で囲まれた面積を求めよ.
1979帯広畜産大過去問
18神奈川県教員採用試験(数学:微分)

単元:
#数Ⅰ#数Ⅱ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#微分法と積分法#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$|x^3-3x^2-9x|-m=0$が異なる定数解を4個もつようにmの値の範囲を求めよ。
この動画を見る
$|x^3-3x^2-9x|-m=0$が異なる定数解を4個もつようにmの値の範囲を求めよ。
18神奈川県教員採用試験(数学:対数)

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$α= 5^{log_{25}^3}+1$のとき$4^{log_2^α}$の値を求めよ。
この動画を見る
$α= 5^{log_{25}^3}+1$のとき$4^{log_2^α}$の値を求めよ。
早稲田(商) 小問の難問

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$は自然数である.
$n\leqq (5+2\sqrt5)^{2019}\lt n+1$,$n$を$100$で割った余りを求めよ.
2019早稲田(商)過去問
この動画を見る
$n$は自然数である.
$n\leqq (5+2\sqrt5)^{2019}\lt n+1$,$n$を$100$で割った余りを求めよ.
2019早稲田(商)過去問
三次方程式の実数解 埼玉大

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$12x^3-21x^2+2x+4=0$
(1)正の実数を2つ,負の実数解を1つもつことを示せ.
(2)正の実数解を$\alpha,\beta(\alpha \lt \beta)$とするとき,$\vert \alpha-1 \vert,\vert \beta-1 \vert $の大小比較せよ.
1982埼玉大過去問
この動画を見る
$12x^3-21x^2+2x+4=0$
(1)正の実数を2つ,負の実数解を1つもつことを示せ.
(2)正の実数解を$\alpha,\beta(\alpha \lt \beta)$とするとき,$\vert \alpha-1 \vert,\vert \beta-1 \vert $の大小比較せよ.
1982埼玉大過去問
【数学II】軌跡がイマイチ掴めない人が「見えた!」を実感するための動画【軌跡と領域】

単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
【数学II】軌跡と領域について解説動画です
-----------------
①2点、A(1,0) B(6,0)からの距離の比が2:3である点Pの軌跡を求めよ。
②点Qが円$x^2+y^2=4$の同上を動くとき、A(8,0)と点Qとを結ぶ線分AQの中点Pの軌跡を求めよ。
この動画を見る
【数学II】軌跡と領域について解説動画です
-----------------
①2点、A(1,0) B(6,0)からの距離の比が2:3である点Pの軌跡を求めよ。
②点Qが円$x^2+y^2=4$の同上を動くとき、A(8,0)と点Qとを結ぶ線分AQの中点Pの軌跡を求めよ。
