数列
数列
福田のおもしろ数学426〜99個の分数の積を効率よく求める
単元：
#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師：
JiroFukuda Math Channel
問題文全文(内容文)：
$\begin{eqnarray}
\prod_{ k = 1 }^n ak=a_1a_2\cdots a_n
\end{eqnarray}$とするとき、
$\displaystyle \prod_{k=2}^{100} \dfrac{k^3+1}{k^3-1}$を求めよ。
この動画を見る
$\begin{eqnarray}
\prod_{ k = 1 }^n ak=a_1a_2\cdots a_n
\end{eqnarray}$とするとき、
$\displaystyle \prod_{k=2}^{100} \dfrac{k^3+1}{k^3-1}$を求めよ。
福田のおもしろ数学425〜8次方程式が等差数列をなす4つの実数解をもつ条件
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師：
JiroFukuda Math Channel
問題文全文(内容文)：
方程式$x^8+ax^4+1=0$が
等差数列をなす$4$つの実数解をもつとき、
実数$a$の値を求めよ。
この動画を見る
方程式$x^8+ax^4+1=0$が
等差数列をなす$4$つの実数解をもつとき、
実数$a$の値を求めよ。
福田の数学〜東京大学2025理系第5問〜バブルソートが題材となった数が整列する条件を漸化式にする
単元：
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数B
指導講師：
JiroFukuda Math Channel
問題文全文(内容文)：
$\boxed{5}$
$n$を$2$以上の整数とする。
$1$から$n$までの数字が書かれた札が各$1$枚ずつ合計$n$枚あり、
横一列におかれている。
$1$以上$(n-1)$以下の整数$i$に対して、
次の操作$(T_i)$を考える。
$(T_i)$左から$i$番目の札の数字が、
左から$(i+1)$番目の札の数字よりも大きければ、
これら$2$枚の札の位置を入れ替える。
そうでなければ、札の位置を変えない。
最初の状態において札の数字は左から
$A_1,A_2,\cdots A_n$であったとする。
この状態から$(n-1)$回の操作$(T_1),(T_2),\cdots (T_{n-1})$を
順に行った後、続けて$(n-1)$回の操作
$(T_{n-1}),\cdots ,(T_2),(T_1)$を順に行ったところ、
札の数字は左から$1,2,\cdots ,n$と小さい順に並んだ。
以下の問いに答えよ。
(1)$A_1$と$A_2$の少なくとも一方は$2$以下であることを示せ。
(2)最初の状態としてありうる札の数字の並び方
$A_1,A_2,\cdots 、A_n$no総数を$c_n$とする。
$n$が$4$以上の整数であるとき、
$c_n$を$c_{n-1}$と$c_{n-2}$を用いて表せ。
$2025$年東京大学理系過去問題
この動画を見る
$\boxed{5}$
$n$を$2$以上の整数とする。
$1$から$n$までの数字が書かれた札が各$1$枚ずつ合計$n$枚あり、
横一列におかれている。
$1$以上$(n-1)$以下の整数$i$に対して、
次の操作$(T_i)$を考える。
$(T_i)$左から$i$番目の札の数字が、
左から$(i+1)$番目の札の数字よりも大きければ、
これら$2$枚の札の位置を入れ替える。
そうでなければ、札の位置を変えない。
最初の状態において札の数字は左から
$A_1,A_2,\cdots A_n$であったとする。
この状態から$(n-1)$回の操作$(T_1),(T_2),\cdots (T_{n-1})$を
順に行った後、続けて$(n-1)$回の操作
$(T_{n-1}),\cdots ,(T_2),(T_1)$を順に行ったところ、
札の数字は左から$1,2,\cdots ,n$と小さい順に並んだ。
以下の問いに答えよ。
(1)$A_1$と$A_2$の少なくとも一方は$2$以下であることを示せ。
(2)最初の状態としてありうる札の数字の並び方
$A_1,A_2,\cdots 、A_n$no総数を$c_n$とする。
$n$が$4$以上の整数であるとき、
$c_n$を$c_{n-1}$と$c_{n-2}$を用いて表せ。
$2025$年東京大学理系過去問題
福田のおもしろ数学420〜間に左右の数の和を次々と書き足していくときの総和
単元：
#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師：
JiroFukuda Math Channel
問題文全文(内容文)：
黒板の両端に$1$が書かれている。
$1$番の生徒がその間に
左右の数の和である$2$を書く。
$2$番の生徒が$2$カ所の間に
左右の数の和である$3$を書く。
この操作を繰り返したとき、
$n$番の生徒が書き終えたとき、数字の合計はいくらか？
図は動画内参照
この動画を見る
黒板の両端に$1$が書かれている。
$1$番の生徒がその間に
左右の数の和である$2$を書く。
$2$番の生徒が$2$カ所の間に
左右の数の和である$3$を書く。
この操作を繰り返したとき、
$n$番の生徒が書き終えたとき、数字の合計はいくらか？
図は動画内参照
福田のおもしろ数学415〜1から16の整数を直線または円形に並べ隣り合う2数の和を平方数とできるか
単元：
#数列#数列とその和（等差・等比・階差・Σ）#数B
指導講師：
JiroFukuda Math Channel
問題文全文(内容文)：
$1,2,3,\cdots 16$を並びかえて
(1)直線上に配置する。(それぞれの場合に)
(2)円周上に配置する。(それぞれの場合に)
隣り合う$2$つの数の和が
平方数になることは可能か？
この動画を見る
$1,2,3,\cdots 16$を並びかえて
(1)直線上に配置する。(それぞれの場合に)
(2)円周上に配置する。(それぞれの場合に)
隣り合う$2$つの数の和が
平方数になることは可能か？
福田のおもしろ数学414〜3辺の長さと内接円の直径で等差数列ができる三角形は直角三角形であることの証明
単元：
#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師：
JiroFukuda Math Channel
問題文全文(内容文)：
ある三角形の$3$辺の長さとその内接円の直径を
ある順序で並べると等差数列になるという。
この三角形が直角三角形であることを証明せよ。
この動画を見る
ある三角形の$3$辺の長さとその内接円の直径を
ある順序で並べると等差数列になるという。
この三角形が直角三角形であることを証明せよ。
福田のおもしろ数学413〜2024個の分数からk個選んできて積を作って合計しよう
単元：
#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師：
JiroFukuda Math Channel
問題文全文(内容文)：
$\dfrac{1}{2},\dfrac{1}{3},\dfrac{1}{4},\dfrac{1}{5},\cdots \dfrac{1}{2025}$の$2024$個の数から
異なる$k$個を選んで作った積の総和を$s(k)$とする。
$s(2)+s(4)+s(6)+\cdots +s(2024)$
の値を求めて下さい。
この動画を見る
$\dfrac{1}{2},\dfrac{1}{3},\dfrac{1}{4},\dfrac{1}{5},\cdots \dfrac{1}{2025}$の$2024$個の数から
異なる$k$個を選んで作った積の総和を$s(k)$とする。
$s(2)+s(4)+s(6)+\cdots +s(2024)$
の値を求めて下さい。
shape problems : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study
福田のおもしろ数学411〜漸化式で定まる数列の2020項までの和と2030項までの和から2025項までの和を求める
単元：
#数列#漸化式#数学(高校生)#数B
指導講師：
JiroFukuda Math Channel
問題文全文(内容文)：
数列$\{a_n\}$は$a_n=a_{n-1}-a_{n-2} (n\geqq 3)$を
満たしている。
$\displaystyle \sum_{n=1}^{2020}=2030$ $\quad $ $\displaystyle \sum_{n=1}^{2030}=2020$
を満たすとき
$\displaystyle \sum_{n=1}^{2025} a_n$の値を求めよ。
この動画を見る
数列$\{a_n\}$は$a_n=a_{n-1}-a_{n-2} (n\geqq 3)$を
満たしている。
$\displaystyle \sum_{n=1}^{2020}=2030$ $\quad $ $\displaystyle \sum_{n=1}^{2030}=2020$
を満たすとき
$\displaystyle \sum_{n=1}^{2025} a_n$の値を求めよ。
福田のおもしろ数学400〜2項展開の係数と次数に関する個数
単元：
#数Ⅰ#数A#数と式#式の計算（整式・展開・因数分解）#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師：
JiroFukuda Math Channel
問題文全文(内容文)：
$\left(\sqrt x+\dfrac{1}{2\sqrt[4]{x}}\right)^n$の展開式を降順に並べたとき、
最初の3項の$x$の係数が等差数列になった。
この展開式の中に$x$の次数が整数となる
項は何個あるか？
この動画を見る
$\left(\sqrt x+\dfrac{1}{2\sqrt[4]{x}}\right)^n$の展開式を降順に並べたとき、
最初の3項の$x$の係数が等差数列になった。
この展開式の中に$x$の次数が整数となる
項は何個あるか？
福田のおもしろ数学383〜関数方程式
単元：
#数列#数学的帰納法#数学(高校生)#数B
指導講師：
JiroFukuda Math Channel
問題文全文(内容文)：
$0$以上の整数の集合を$\mathbb{N}$$_0$とする。
$f:$$\mathbb{N}$$_0$→$\mathbb{N}$$_0$が任意の$x≧y\in $$\mathbb{N}$$_0$で$f(x^2)-f(y^2)=f(x+y)f(x-y)$を満たす。
$f(x)$を求めよ。
この動画を見る
$0$以上の整数の集合を$\mathbb{N}$$_0$とする。
$f:$$\mathbb{N}$$_0$→$\mathbb{N}$$_0$が任意の$x≧y\in $$\mathbb{N}$$_0$で$f(x^2)-f(y^2)=f(x+y)f(x-y)$を満たす。
$f(x)$を求めよ。
福田のおもしろ数学378〜ある漸化式で定められる数列の最初の2025項が正で2026番目が初めて負になることが可能かどうかの検証
単元：
#数Ⅱ#三角関数#加法定理とその応用#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師：
JiroFukuda Math Channel
問題文全文(内容文)：
$a_{0}>0, c>0, a_{n+1}=\frac{a_{n}+c}{1-a_{n}c}$で定まる数列${a_{n}}$に対し、$a_{0}, a_{1}, \cdots ,a_{2024}$がすべて正であり、$a_{2025}<0$となることは可能か。
この動画を見る
$a_{0}>0, c>0, a_{n+1}=\frac{a_{n}+c}{1-a_{n}c}$で定まる数列${a_{n}}$に対し、$a_{0}, a_{1}, \cdots ,a_{2024}$がすべて正であり、$a_{2025}<0$となることは可能か。
福田のおもしろ数学374〜365と366を1から365までの整数で割った余りの総和の大小比較
単元：
#数列#数列とその和（等差・等比・階差・Σ）#漸化式
指導講師：
JiroFukuda Math Channel
問題文全文(内容文)：
$360$を$1,2,3,…,365$で割った余りの総和を$A$、$366$を$1,2,3,…,365$で割った余りの総和を$B$とする。$A$と$B$の大小を比較せよ。
この動画を見る
$360$を$1,2,3,…,365$で割った余りの総和を$A$、$366$を$1,2,3,…,365$で割った余りの総和を$B$とする。$A$と$B$の大小を比較せよ。
福田のおもしろ数学371〜初項が素数で漸化式で定義された数列が素数でない項をもつ証明
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#漸化式#数学(高校生)#数B
指導講師：
JiroFukuda Math Channel
問題文全文(内容文)：
$a_1=p$(素数), $a_{n+1}=2a_n-1$で定まる数列には素数でない項が存在する。証明せよ。
この動画を見る
$a_1=p$(素数), $a_{n+1}=2a_n-1$で定まる数列には素数でない項が存在する。証明せよ。
福田のおもしろ数学366〜漸化式で定義された数列の周期性を示す
単元：
#数列#漸化式#数学(高校生)#数B
指導講師：
JiroFukuda Math Channel
問題文全文(内容文)：
数列 ${x_n}$ が $x_1$ を正の整数とし、
$
x_{n+1} =
\begin{cases}
\frac{1}{2}x_n & (x_n\text{ が偶数})\\
a+x_n & (x_n\text{ が奇数})
\end{cases}
$
($a$ は正の奇数) を満たしている。この数列の周期性を示せ。
この動画を見る
数列 ${x_n}$ が $x_1$ を正の整数とし、
$
x_{n+1} =
\begin{cases}
\frac{1}{2}x_n & (x_n\text{ が偶数})\\
a+x_n & (x_n\text{ が奇数})
\end{cases}
$
($a$ は正の奇数) を満たしている。この数列の周期性を示せ。
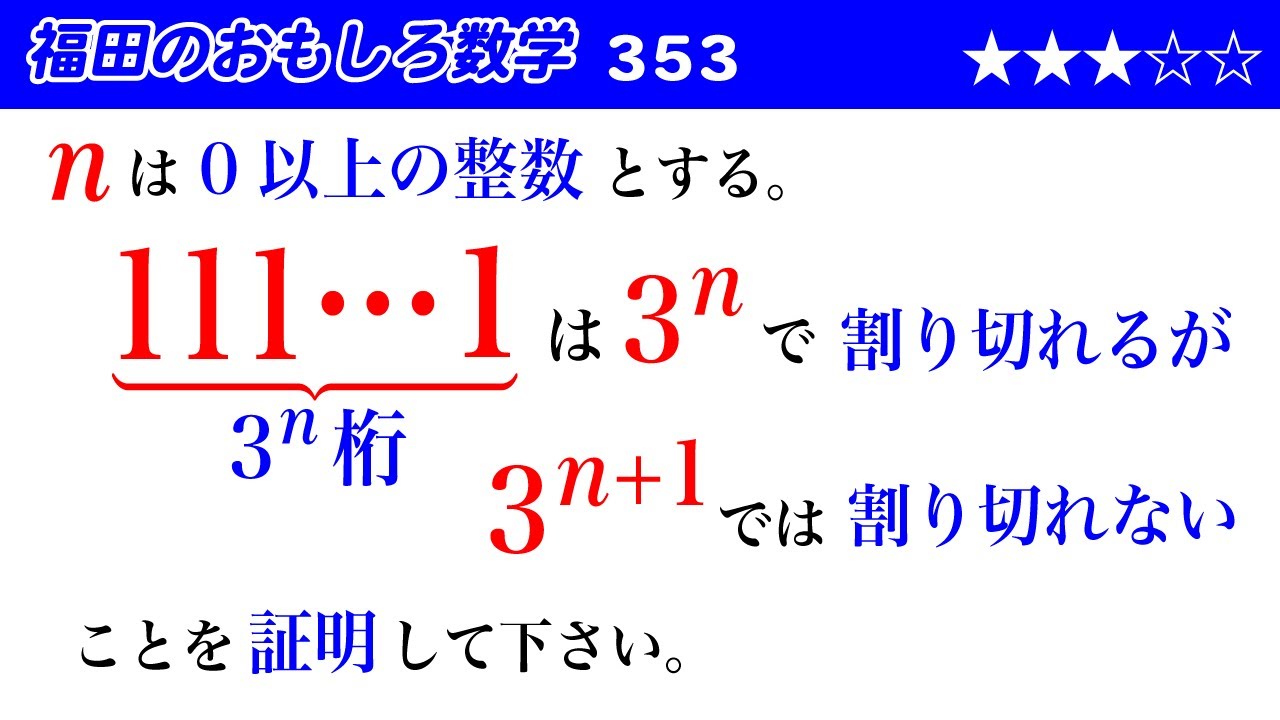
福田のおもしろ数学353〜1が連続3^n個並ぶ数は3^nで割り切れることの証明
単元：
#数列#数学的帰納法#数学(高校生)#数B
指導講師：
JiroFukuda Math Channel
問題文全文(内容文)：
$n$ は $0$ 以上の整数とする。$\underbrace{ 111\cdots111 }_{3^n 桁}$ は $3^n$ で割り切れるが、 $3^{n+1}$ で割り切れないことを証明してください。
この動画を見る
$n$ は $0$ 以上の整数とする。$\underbrace{ 111\cdots111 }_{3^n 桁}$ は $3^n$ で割り切れるが、 $3^{n+1}$ で割り切れないことを証明してください。
不等式の証明の難問！記号が多すぎる。。。 #Shorts #ずんだもん #勉強 #数学
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#数学(高校生)#数B#お茶の水女子大学
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
mを２以上の自然数、nを自然数とするとき、次の不等式 nmCn≧m^n≧Σ[i=0,n-1]m^i が成り立つことを示せ。
この動画を見る
mを２以上の自然数、nを自然数とするとき、次の不等式 nmCn≧m^n≧Σ[i=0,n-1]m^i が成り立つことを示せ。
福田のおもしろ数学351〜漸化式で定まる数列の第2025項の取り得る値の個数
単元：
#数列#漸化式#数学(高校生)#数B
指導講師：
JiroFukuda Math Channel
問題文全文(内容文)：
$a_1 = 1, a_{n+1} + a_n = ( a_{n+1} - a_n )^2$ で定まる、すべての項が正の数列 $\{ a_n \}$ に対し $a_2025$ の取りうる値は何個あるか。
この動画を見る
$a_1 = 1, a_{n+1} + a_n = ( a_{n+1} - a_n )^2$ で定まる、すべての項が正の数列 $\{ a_n \}$ に対し $a_2025$ の取りうる値は何個あるか。
福田のおもしろ数学339〜自然数の列から平方数を除いてできる列の第2024項の値
単元：
#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師：
JiroFukuda Math Channel
問題文全文(内容文)：
自然数の列$1,2,3,\cdots$から平方数を除いてできる列を$a_1,a_2,a_3,\cdots$とする。$a_{2024}$を求めて下さい。
この動画を見る
自然数の列$1,2,3,\cdots$から平方数を除いてできる列を$a_1,a_2,a_3,\cdots$とする。$a_{2024}$を求めて下さい。
福田のおもしろ数学323〜小数部分の和を不等式で評価する
単元：
#数列#数学的帰納法#数学(高校生)#数B
指導講師：
JiroFukuda Math Channel
問題文全文(内容文)：
$x$の小数部分を$\{x\}$で表すことにする。
$\displaystyle\{\sqrt{1}\}+\{\sqrt{2}\}+\{\sqrt{3}\}+・・・+\{\sqrt{n^2}\}\leqq \frac{n^2-1}{2}$
を証明せよ。
この動画を見る
$x$の小数部分を$\{x\}$で表すことにする。
$\displaystyle\{\sqrt{1}\}+\{\sqrt{2}\}+\{\sqrt{3}\}+・・・+\{\sqrt{n^2}\}\leqq \frac{n^2-1}{2}$
を証明せよ。
福田の数学〜北里大学2024医学部第3問〜確率漸化式
単元：
#数A#場合の数と確率#確率#数列#漸化式#数学(高校生)#数B
指導講師：
JiroFukuda Math Channel
問題文全文(内容文)：
箱Aには赤玉2個、白玉1個入っており、箱Bには白玉3個が入っている。2つの箱A、Bについて、次の操作を繰り返す。
（操作）2つの箱A,Bからそれぞれ1個ずつ玉を同時に取り出し、箱Aから取り出した玉を箱Bに入れて、箱Bから取り出した玉を箱Aに入れる。
ｎ回目の操作を終えたときに箱Aに入っている赤玉の個数が2個、1個、0個である確率をそれぞれ$p_n,q_n,r_n$とする。
（１）$p_1,q_1,p_2,q_2$を求め、$r_n$を$p_n$と$q_n$を用いて表せ。
（２）$p_{n+1}$を$p_n,q_n$で表せ。また$q_{n+1}$を$q_n$を用いて表せ。
（３）$q_n$を求めよ。
（４）$s_n=3^np_n$とおいて、$s_n$を求めよ。また、$p_n$を求めよ。
この動画を見る
箱Aには赤玉2個、白玉1個入っており、箱Bには白玉3個が入っている。2つの箱A、Bについて、次の操作を繰り返す。
（操作）2つの箱A,Bからそれぞれ1個ずつ玉を同時に取り出し、箱Aから取り出した玉を箱Bに入れて、箱Bから取り出した玉を箱Aに入れる。
ｎ回目の操作を終えたときに箱Aに入っている赤玉の個数が2個、1個、0個である確率をそれぞれ$p_n,q_n,r_n$とする。
（１）$p_1,q_1,p_2,q_2$を求め、$r_n$を$p_n$と$q_n$を用いて表せ。
（２）$p_{n+1}$を$p_n,q_n$で表せ。また$q_{n+1}$を$q_n$を用いて表せ。
（３）$q_n$を求めよ。
（４）$s_n=3^np_n$とおいて、$s_n$を求めよ。また、$p_n$を求めよ。
この求め方知ってた？
単元：
#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
図のように1辺1cmの正方形を並べて図形を作る。このときn番目図形の周の長さを求めよ。
※図は動画内参照
この動画を見る
図のように1辺1cmの正方形を並べて図形を作る。このときn番目図形の周の長さを求めよ。
※図は動画内参照
福田のおもしろ数学316〜x^n+x^{-n}が整数である証明と倍数
単元：
#数列#数学的帰納法#数学(高校生)#数B
指導講師：
JiroFukuda Math Channel
問題文全文(内容文)：
2より大きい整数$t$に対して$t=x+x^{-1}$を満たす実数$x$を考える。$t_n = x+x^{-n}$とするとき$t_n$は常に整数であることを示せ。また、$t_n$が$t$の倍数となるような正の整数$n$をすべて求めよ。
この動画を見る
2より大きい整数$t$に対して$t=x+x^{-1}$を満たす実数$x$を考える。$t_n = x+x^{-n}$とするとき$t_n$は常に整数であることを示せ。また、$t_n$が$t$の倍数となるような正の整数$n$をすべて求めよ。
福田の数学〜早稲田大学2024社会科学部第3問〜集合と数列
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題（集合・命題と条件・背理法）#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師：
JiroFukuda Math Channel
問題文全文(内容文)：
$n$を$n \geqq 3$である自然数とする。相異なる$n$個の正の数を小さい順に並べた集合$S=${ $a_{ 1 },a_{ 2 }・・・,a_{ n } $}を考える。$a_{ 1 }=k$とするとき、次の問いに答えよ。
(1)$a_{ i }-a_{ 1 }$$(i=2,3,・・・,n)$がすべての$S$の要素となるとき、$a_{ 2 }$を求めよ。
(2)(1)のとき、$a_{ n }$を$n$の式で表せ。
(3)$\frac{a_{ i }}{a_{ 1 }}$$(i=2,3,・・・,n)$がすべての$S$の要素となるとき、$a_{ n }$を$n$の式で表せ。
この動画を見る
$n$を$n \geqq 3$である自然数とする。相異なる$n$個の正の数を小さい順に並べた集合$S=${ $a_{ 1 },a_{ 2 }・・・,a_{ n } $}を考える。$a_{ 1 }=k$とするとき、次の問いに答えよ。
(1)$a_{ i }-a_{ 1 }$$(i=2,3,・・・,n)$がすべての$S$の要素となるとき、$a_{ 2 }$を求めよ。
(2)(1)のとき、$a_{ n }$を$n$の式で表せ。
(3)$\frac{a_{ i }}{a_{ 1 }}$$(i=2,3,・・・,n)$がすべての$S$の要素となるとき、$a_{ n }$を$n$の式で表せ。
福田のおもしろ数学311〜n個の積の和を最大にする方法
単元：
#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師：
JiroFukuda Math Channel
問題文全文(内容文)：
$n$個の実数 $a_1\leqq a_2\leqq \cdots \leqq a_n$と$n$個の実数を適当に並べたものを$b_1, b_2, \cdots ,b_n $ として、$s = a_1b_1+a_2b_2+\cdots + a_nb_n $を最大にするには$b_1 \leqq b_2 \leqq \cdots \leqq b_n $となるように並べたときである。これを証明して下さい。(ただし、$n\geqq 2$とする)
この動画を見る
$n$個の実数 $a_1\leqq a_2\leqq \cdots \leqq a_n$と$n$個の実数を適当に並べたものを$b_1, b_2, \cdots ,b_n $ として、$s = a_1b_1+a_2b_2+\cdots + a_nb_n $を最大にするには$b_1 \leqq b_2 \leqq \cdots \leqq b_n $となるように並べたときである。これを証明して下さい。(ただし、$n\geqq 2$とする)
福田のおもしろ数学309〜自然数から自然数への関数f(n)に関する関数方程式
単元：
#数Ⅰ#数と式#集合と命題（集合・命題と条件・背理法）#数列#数学的帰納法#数学(高校生)#数B
指導講師：
JiroFukuda Math Channel
問題文全文(内容文)：
$$自然数を自然数へ写す関数f(n)が次を満たす。$$
$$\frac{1}{a}+\frac{1}{b}=\frac{1}{c}\Rightarrow \frac{1}{f(a)}+\frac{1}{f(b)}=\frac{1}{f(c)}$$
$$このような関数f(n)をすべて求めて下さい。$$
この動画を見る
$$自然数を自然数へ写す関数f(n)が次を満たす。$$
$$\frac{1}{a}+\frac{1}{b}=\frac{1}{c}\Rightarrow \frac{1}{f(a)}+\frac{1}{f(b)}=\frac{1}{f(c)}$$
$$このような関数f(n)をすべて求めて下さい。$$
福田の数学〜早稲田大学2024商学部第1問(3)〜漸化式
単元：
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師：
JiroFukuda Math Channel
問題文全文(内容文)：
$C$を$1$でない正の実数とする。正の実数の数列$\{a_n\}$が次の条件を満たしている。
$a_1=C,$${a_n}^{n+1}{a_{n+1}}^n=C^{-(2n+1)}$
このとき、一般項$a_n$を$C$を用いて表せ。
この動画を見る
$C$を$1$でない正の実数とする。正の実数の数列$\{a_n\}$が次の条件を満たしている。
$a_1=C,$${a_n}^{n+1}{a_{n+1}}^n=C^{-(2n+1)}$
このとき、一般項$a_n$を$C$を用いて表せ。
福田の数学〜早稲田大学2024商学部第1問(2)〜不等式で決定される自然数の列
単元：
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師：
JiroFukuda Math Channel
問題文全文(内容文)：
$n$を$2$以上の整数とし、$a_1,a_2,a_3,・・・,a_n$を正の整数とする。
$a_1=1,{a_{i+3}}^3\lt 27{a_i}^4(i=1,2,3,・・・,n-1)$
$\displaystyle \sum_{i=1}^{n-1}\frac{a_i}{a_{i+1}}=\frac{a_1}{a_{2}}+\frac{a_2}{a_{3}}+\frac{a_3}{a_{4}}+・・・+\frac{a_{n-1}}{a_{n}}\lt 1$
であるとき、$a_n$のとりうる値の最大値は？
この動画を見る
$n$を$2$以上の整数とし、$a_1,a_2,a_3,・・・,a_n$を正の整数とする。
$a_1=1,{a_{i+3}}^3\lt 27{a_i}^4(i=1,2,3,・・・,n-1)$
$\displaystyle \sum_{i=1}^{n-1}\frac{a_i}{a_{i+1}}=\frac{a_1}{a_{2}}+\frac{a_2}{a_{3}}+\frac{a_3}{a_{4}}+・・・+\frac{a_{n-1}}{a_{n}}\lt 1$
であるとき、$a_n$のとりうる値の最大値は？
福田のおもしろ数学295〜与えられた不等式を満たす数列の1との大小関係
単元：
#数列#漸化式#数学(高校生)#数B
指導講師：
JiroFukuda Math Channel
問題文全文(内容文)：
どの項も正である数列$\{a_n\}$について
$(a_{n+1})^2+a_na_{n+2}\leqq a_n+a_{n+2}$
が成り立つとき、
$a_{2024}\leqq 1$を示せ。
この動画を見る
どの項も正である数列$\{a_n\}$について
$(a_{n+1})^2+a_na_{n+2}\leqq a_n+a_{n+2}$
が成り立つとき、
$a_{2024}\leqq 1$を示せ。
福田の数学〜慶應義塾大学2024環境情報学部第2問〜2べき乗表現の個数
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師：
JiroFukuda Math Channel
問題文全文(内容文)：
$b_k$を正の整数、$b_{k-1},\cdots,b_1,b_0$を負でない整数とする($k$は負でない整数であり、$k=0$のときは正の整数$b_0$のみを考える)。正の整数$n$に対して、$b_k,b_{k-1},\cdots,b_1,b_0$が$\ \ \ \ $
$\displaystyle 2^kb_k+2^{k-1}b_{k-1}+\cdots+2^2b_2+2b_1+b_0=\sum_{i=0}^k2^ib_i=n\ \\ $を満たすとき、$\langle b_k,b_{k-1},\cdots,b_1,b_0 \rangle$を$n$の2べき乗表現と呼ぶことにする。これは2進法による数の表現と似ているが、2進法の場合とは異なり、$b_i\ (i=0,1,\cdots,k)$は2以上の値も取りうる。そのため$n\geqq 2$において、$n$の2べき乗表現は1通りではない。$\\$
(1)$\ n=3$の2べき乗表現は$\langle 3 \rangle$と$\langle ア, イ\rangle$の2通りである。$\\ $(2)$\ \langle 3,2,1 \rangle$は$n=(ウエ)$の2べき乗表現である。$\\ $(3) $\ m$を正の整数とするとき、1から$m$までの整数を順に並べた$\langle 1,2,\cdots ,m \rangle$は$\ \ 2^{(m+オカ)}+(キク)m+(ケコ)\ $の2べき乗表現である。$\\ $ (4)$\ n$の2べき乗表現の個数を$a_n$とすると、$\ a_4=(サシ),\ a_5=(スセ),\ a_6=(ソタ),\cdots ,a_{10}=(チツ),\cdots , a_{20}=(テト)$である。
この動画を見る
$b_k$を正の整数、$b_{k-1},\cdots,b_1,b_0$を負でない整数とする($k$は負でない整数であり、$k=0$のときは正の整数$b_0$のみを考える)。正の整数$n$に対して、$b_k,b_{k-1},\cdots,b_1,b_0$が$\ \ \ \ $
$\displaystyle 2^kb_k+2^{k-1}b_{k-1}+\cdots+2^2b_2+2b_1+b_0=\sum_{i=0}^k2^ib_i=n\ \\ $を満たすとき、$\langle b_k,b_{k-1},\cdots,b_1,b_0 \rangle$を$n$の2べき乗表現と呼ぶことにする。これは2進法による数の表現と似ているが、2進法の場合とは異なり、$b_i\ (i=0,1,\cdots,k)$は2以上の値も取りうる。そのため$n\geqq 2$において、$n$の2べき乗表現は1通りではない。$\\$
(1)$\ n=3$の2べき乗表現は$\langle 3 \rangle$と$\langle ア, イ\rangle$の2通りである。$\\ $(2)$\ \langle 3,2,1 \rangle$は$n=(ウエ)$の2べき乗表現である。$\\ $(3) $\ m$を正の整数とするとき、1から$m$までの整数を順に並べた$\langle 1,2,\cdots ,m \rangle$は$\ \ 2^{(m+オカ)}+(キク)m+(ケコ)\ $の2べき乗表現である。$\\ $ (4)$\ n$の2べき乗表現の個数を$a_n$とすると、$\ a_4=(サシ),\ a_5=(スセ),\ a_6=(ソタ),\cdots ,a_{10}=(チツ),\cdots , a_{20}=(テト)$である。