 関数の極限
関数の極限
 関数の極限
関数の極限
06兵庫県教員採用試験(数学:5番類題 極限値)

単元:
#関数と極限#関数の極限#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
5⃣$\displaystyle \lim_{ x \to +0 } xlogx$
この動画を見る
5⃣$\displaystyle \lim_{ x \to +0 } xlogx$
08兵庫県教員採用試験(数学:4番 微積・極限値)

単元:
#関数と極限#微分とその応用#関数の極限#関数の変化(グラフ・最大最小・方程式・不等式)#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
4⃣$f_n(x)=\frac{logx}{x^n}$
(1)$log x < x ( x > 1)$
を示し$\displaystyle \lim_{ x \to \infty } f_n(x)$を求めよ。
(2)$y=f_n(x)$のグラフをかけ
(3)$x=a_n$(極大値をとるx座標)
$y=f_n(x),$x軸で囲まれた面積を$S_n$とする。
$\displaystyle \lim_{ n \to \infty } n^2S_n$を求めよ。
この動画を見る
4⃣$f_n(x)=\frac{logx}{x^n}$
(1)$log x < x ( x > 1)$
を示し$\displaystyle \lim_{ x \to \infty } f_n(x)$を求めよ。
(2)$y=f_n(x)$のグラフをかけ
(3)$x=a_n$(極大値をとるx座標)
$y=f_n(x),$x軸で囲まれた面積を$S_n$とする。
$\displaystyle \lim_{ n \to \infty } n^2S_n$を求めよ。
東京電機大 4次関数と直線の共有点

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#関数の極限#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=x^4-2x^3+x$と$y=k(x-1)$の共有点の個数を求めよ.
東京電機大過去問
この動画を見る
$f(x)=x^4-2x^3+x$と$y=k(x-1)$の共有点の個数を求めよ.
東京電機大過去問
16東京都教員採用試験(数学:1-7 極限値)
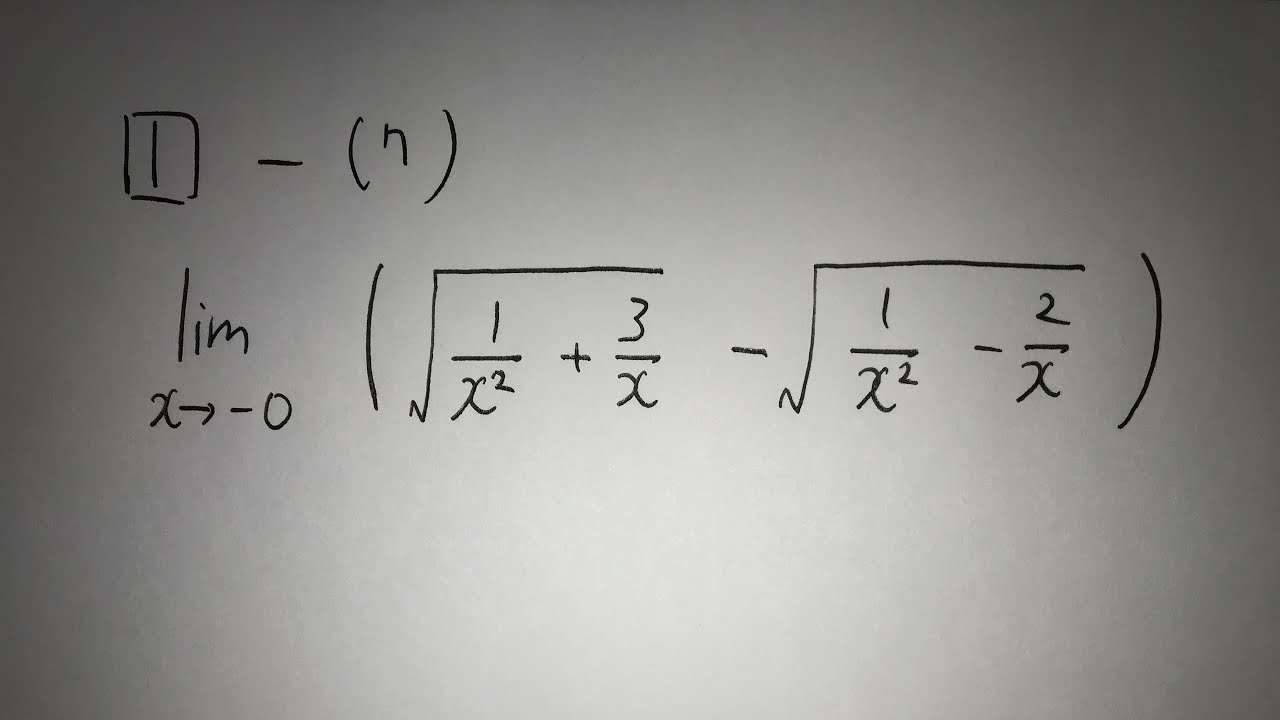
単元:
#関数と極限#関数の極限#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣-(7)
$\displaystyle \lim_{ n \to -0 } (\sqrt{\frac{1}{x^2}+\frac{3}{x}} - \sqrt{\frac{1}{x^2}-\frac{2}{x}})$
この動画を見る
1⃣-(7)
$\displaystyle \lim_{ n \to -0 } (\sqrt{\frac{1}{x^2}+\frac{3}{x}} - \sqrt{\frac{1}{x^2}-\frac{2}{x}})$
【数Ⅲ】極限:福島県立医大! 極限値lim[n→∞]l[n]_θ[n]を求めよ。

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
Oを原点とする座標平面上に2点A(2,0),B(0,1)がある。自然数nに対し、線分ABを1:nに内分する点を$P_n$とし,$∠AOP_n=θ_n$とする。ただし、$0<θ_n<\dfrac{\pi}{2}$である。線分$AP_n$の長さを$l_n$として、極限値$\displaystyle \lim_{n\to \infty}\dfrac{l_n}{\theta_n}$を求めよ。
この動画を見る
Oを原点とする座標平面上に2点A(2,0),B(0,1)がある。自然数nに対し、線分ABを1:nに内分する点を$P_n$とし,$∠AOP_n=θ_n$とする。ただし、$0<θ_n<\dfrac{\pi}{2}$である。線分$AP_n$の長さを$l_n$として、極限値$\displaystyle \lim_{n\to \infty}\dfrac{l_n}{\theta_n}$を求めよ。
東工大 末尾の0の個数問題

単元:
#関数と極限#数列の極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$は自然数である.
$f(n)$を$n!$の末尾に並ぶ$0$の個数とする.
(例)$f(10)=2,f(100)=24$
$\displaystyle \lim_{n\to\infty}\dfrac{f(10^n)}{10^n}$を求めよ.
1991東工大過去問
この動画を見る
$n$は自然数である.
$f(n)$を$n!$の末尾に並ぶ$0$の個数とする.
(例)$f(10)=2,f(100)=24$
$\displaystyle \lim_{n\to\infty}\dfrac{f(10^n)}{10^n}$を求めよ.
1991東工大過去問
慶応義塾大 4次方程式

単元:
#関数と極限#微分とその応用#関数(分数関数・無理関数・逆関数と合成関数)#関数の極限#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$3x^4-4x^3-12x^2-k=0$が相異なる4つの実数解をもつ$k$の範囲
そのときの4つの解のうち最大のものを$\alpha$とする。
$\alpha$の範囲を求めよ
出典:1989年慶應義塾大学 過去問
この動画を見る
$3x^4-4x^3-12x^2-k=0$が相異なる4つの実数解をもつ$k$の範囲
そのときの4つの解のうち最大のものを$\alpha$とする。
$\alpha$の範囲を求めよ
出典:1989年慶應義塾大学 過去問
ヨビノリのマンデー積分をぶっ飛ばせ!刺客は本人

単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#関数の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$自然数、$x,y$実数
$\displaystyle \int_{0}^{ 1 } (\sin(2n\pi t)-xt-y)^2dt$の最小値を$I_n$とおく
$\displaystyle \lim_{ n \to \infty }I_n$を求めよ
出典:2019年九州大学 過去問
この動画を見る
$n$自然数、$x,y$実数
$\displaystyle \int_{0}^{ 1 } (\sin(2n\pi t)-xt-y)^2dt$の最小値を$I_n$とおく
$\displaystyle \lim_{ n \to \infty }I_n$を求めよ
出典:2019年九州大学 過去問
自治医科大学

単元:
#大学入試過去問(数学)#複素数平面#関数と極限#複素数平面#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数C#数Ⅲ#自治医科大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)
$\alpha=\cos \displaystyle \frac{2}{7}\pi+i \sin \displaystyle \frac{2}{7}\pi$
$\displaystyle \frac{1}{1-\alpha}+\displaystyle \frac{1}{1-\alpha^2}+\displaystyle \frac{1}{1-\alpha^3}+\displaystyle \frac{1}{1-\alpha^4}+$
$\displaystyle \frac{1}{1-\alpha^5}+\displaystyle \frac{1}{1-\alpha^6}$
(2)
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{3\sin 4x}{x+\sin x}$
出典:2017年自治医科大学 過去問
この動画を見る
(1)
$\alpha=\cos \displaystyle \frac{2}{7}\pi+i \sin \displaystyle \frac{2}{7}\pi$
$\displaystyle \frac{1}{1-\alpha}+\displaystyle \frac{1}{1-\alpha^2}+\displaystyle \frac{1}{1-\alpha^3}+\displaystyle \frac{1}{1-\alpha^4}+$
$\displaystyle \frac{1}{1-\alpha^5}+\displaystyle \frac{1}{1-\alpha^6}$
(2)
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{3\sin 4x}{x+\sin x}$
出典:2017年自治医科大学 過去問
これから数Ⅲを学ぶ人に贈る「ネイピア数eってなんだよ?」

単元:
#数Ⅱ#指数関数と対数関数#指数関数#対数関数#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
①
$e=\displaystyle \lim_{ x \to \infty }(1+\displaystyle \frac{1}{n})^n$
$=\displaystyle \lim_{ h \to \infty }(1+h)^{\displaystyle \frac{1}{h}}$
②
$y=e^x$ $y^1=e^x$
③
動画内の図をみて求めよ
④
$y=log_{e}x$
$y^1=\displaystyle \frac{1}{x}$
この動画を見る
①
$e=\displaystyle \lim_{ x \to \infty }(1+\displaystyle \frac{1}{n})^n$
$=\displaystyle \lim_{ h \to \infty }(1+h)^{\displaystyle \frac{1}{h}}$
②
$y=e^x$ $y^1=e^x$
③
動画内の図をみて求めよ
④
$y=log_{e}x$
$y^1=\displaystyle \frac{1}{x}$
弘前大(医)3次方程式 極限 Japanese university entrance exam questions

単元:
#大学入試過去問(数学)#関数と極限#微分とその応用#関数の極限#微分法#数学(高校生)#弘前大学#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
弘前大学過去問題
n自然数
$x^3+3nx^2-(3n+2)=0$
(1)全ての自然数nについて正の解をただ1つしかもたないことを示せ。
(2)各自然数nに対して正の解を$a_n$とする。
$\displaystyle\lim_{n \to \infty}a_n$を求めよ。
この動画を見る
弘前大学過去問題
n自然数
$x^3+3nx^2-(3n+2)=0$
(1)全ての自然数nについて正の解をただ1つしかもたないことを示せ。
(2)各自然数nに対して正の解を$a_n$とする。
$\displaystyle\lim_{n \to \infty}a_n$を求めよ。
【数学Ⅲ】この公式を使った問題を5分で解いてみる

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
$\displaystyle \lim_{ x \to \infty } (1+\frac{4}{x})=???$
この動画を見る
$\displaystyle \lim_{ x \to \infty } (1+\frac{4}{x})=???$
東工大 極限値 高校数学 Japanese university entrance exam questions

単元:
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
1982東京工業大学過去問題
n自然数
半径$\frac{1}{n}$の円を重ならないように半径1の円に外接させる。このとき外接する円の最大個数を$a_n$とする。
$\displaystyle \lim_{n \to \infty} \frac{a_n}{n}$を求めよ。
この動画を見る
1982東京工業大学過去問題
n自然数
半径$\frac{1}{n}$の円を重ならないように半径1の円に外接させる。このとき外接する円の最大個数を$a_n$とする。
$\displaystyle \lim_{n \to \infty} \frac{a_n}{n}$を求めよ。
【高校数学】数Ⅲ-88 関数の連続性③

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①関数$f(x)=\lim_{n\to\infty}\dfrac{x^{2n+1}+1}{x^{2n}+1}$のグラフをかき、
$f(x)$が不連続となる$x$の値を求めよ。
この動画を見る
①関数$f(x)=\lim_{n\to\infty}\dfrac{x^{2n+1}+1}{x^{2n}+1}$のグラフをかき、
$f(x)$が不連続となる$x$の値を求めよ。
【高校数学】数Ⅲ-87 関数の連続性②

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の関数$f(x)$が、$x=0$で連続であるか不連続であるかを調べよ。
ただし、$[x]$は実数$x$を超えない最大の整数とする。
①$f(x)=3x^2$
②$f(x)=[\cos x]$
③$f(x)=x^2+\dfrac{x^2}{1+x^2}+\dfrac{x^2}{(1+x^2)^2}+・・・$
この動画を見る
次の関数$f(x)$が、$x=0$で連続であるか不連続であるかを調べよ。
ただし、$[x]$は実数$x$を超えない最大の整数とする。
①$f(x)=3x^2$
②$f(x)=[\cos x]$
③$f(x)=x^2+\dfrac{x^2}{1+x^2}+\dfrac{x^2}{(1+x^2)^2}+・・・$
【高校数学】数Ⅲ-86 関数の連続性①

単元:
#関数と極限#微分とその応用#関数の極限#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
(1)次の不等式を満たす実数$x$の値の範囲を、区間で示す記号で示せ。
①$3\lt x \lt 7$
②$-2 \leqq x \leqq 0$
③$-4 \lt x \leqq 5$
④$x \geqq 12$
(2)次の関数が連続である区間を求めよ。
⑤$f(x)=\sqrt{-3x+2}$
⑥$f(x)=\dfrac{x^2+1}{x^2-3x+2}$
⑦$f(x)=\log_2 \vert x \vert$
この動画を見る
(1)次の不等式を満たす実数$x$の値の範囲を、区間で示す記号で示せ。
①$3\lt x \lt 7$
②$-2 \leqq x \leqq 0$
③$-4 \lt x \leqq 5$
④$x \geqq 12$
(2)次の関数が連続である区間を求めよ。
⑤$f(x)=\sqrt{-3x+2}$
⑥$f(x)=\dfrac{x^2+1}{x^2-3x+2}$
⑦$f(x)=\log_2 \vert x \vert$
【高校数学】数Ⅲ-85 関数の決定問題

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$\displaystyle \lim_{x\to\infty} \dfrac{\sqrt{{x^2+2}-(ax+b)}}{x}=3$が成り立つように、
定数$a,b$の値を定めよ。
この動画を見る
①$\displaystyle \lim_{x\to\infty} \dfrac{\sqrt{{x^2+2}-(ax+b)}}{x}=3$が成り立つように、
定数$a,b$の値を定めよ。
【高校数学】数Ⅲ-80 関数の極限⑤(指数関数)

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の極限を求めよ。
①$\displaystyle \lim_{x\to \infty}(\sqrt 2)^x$
②$\displaystyle \lim_{x\to \infty}\left(\dfrac{1}{3}\right)^x$
③$\displaystyle \lim_{x\to \infty}2^{-x}$
④$\displaystyle \lim_{x\to \infty}\dfrac{5^x-7^x}{2^x+7^x}$
⑤$\displaystyle \lim_{x\to \infty}(2^x-3^x)$
⑥$\displaystyle \lim_{x\to \infty}(3^x-2^{2x+1})$
この動画を見る
次の極限を求めよ。
①$\displaystyle \lim_{x\to \infty}(\sqrt 2)^x$
②$\displaystyle \lim_{x\to \infty}\left(\dfrac{1}{3}\right)^x$
③$\displaystyle \lim_{x\to \infty}2^{-x}$
④$\displaystyle \lim_{x\to \infty}\dfrac{5^x-7^x}{2^x+7^x}$
⑤$\displaystyle \lim_{x\to \infty}(2^x-3^x)$
⑥$\displaystyle \lim_{x\to \infty}(3^x-2^{2x+1})$
ド・モアブルの定理を用いてオイラーの公式を導く

単元:
#複素数平面#関数と極限#複素数平面#関数の極限#数学(高校生)#数C#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
ド・モアブルの定理を用いてオイラーの公式を導く方法を解説していきます.
この動画を見る
ド・モアブルの定理を用いてオイラーの公式を導く方法を解説していきます.
ネイピア数 自然対数の底e とは

中学生の知識でオイラーの公式を理解しよう VOL 6 e ネイピア数の正体

単元:
#数Ⅱ#指数関数と対数関数#指数関数#関数と極限#微分とその応用#関数の極限#色々な関数の導関数#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
中学生の知識でオイラーの公式を理解しよう VOL 6 e ネイピア数の正体
この動画を見る
中学生の知識でオイラーの公式を理解しよう VOL 6 e ネイピア数の正体
