 数Ⅲ
数Ⅲ
 数Ⅲ
数Ⅲ
福田の数学〜慶應義塾大学薬学部2025第3問〜逆関数と定積分

単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#関数(分数関数・無理関数・逆関数と合成関数)#定積分#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
実数$x$に対して、関数
$f(x)=\dfrac{1}{3}x+\sqrt{\dfrac{1}{9}x^2+8}$
がある。ただし、定義域は$x\geqq 0$である。
$y=f(x)$の逆関数を$y=g(x)$とする。
(1)$g(x)$を求めると、$g(x)=\boxed{ナ}$であり、
$g(x)$定義域は$\boxed{ニ}$である。
(2)$\displaystyle \int_{2\sqrt2}^{4}g(x)dx$を求めると$\boxed{ヌ}$である。
(3)$\displaystyle \int_{0}^{3} f(x) dx$を求めると$\boxed{ネ}$である。
$2025$年慶應義塾大学薬学部過去問題
この動画を見る
$\boxed{3}$
実数$x$に対して、関数
$f(x)=\dfrac{1}{3}x+\sqrt{\dfrac{1}{9}x^2+8}$
がある。ただし、定義域は$x\geqq 0$である。
$y=f(x)$の逆関数を$y=g(x)$とする。
(1)$g(x)$を求めると、$g(x)=\boxed{ナ}$であり、
$g(x)$定義域は$\boxed{ニ}$である。
(2)$\displaystyle \int_{2\sqrt2}^{4}g(x)dx$を求めると$\boxed{ヌ}$である。
(3)$\displaystyle \int_{0}^{3} f(x) dx$を求めると$\boxed{ネ}$である。
$2025$年慶應義塾大学薬学部過去問題
福田の数学〜慶應義塾大学薬学部2025第1問(4)〜円柱を切ってできる立体の体積と側面積

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#立体図形#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(4)$xyz$空間において、
$xy$平面上に$(0,0,0)$を中心とする半径$2$の円がある。
この円と、$(0,0,2\sqrt3)$を中心とする半径$2$の円を
底面とする円柱を、
原点を通り$xz$平面と$30$度の角をなす平面によって
切断し、$2$つの立体に分ける。
いま$2$つの立体のうち、
体積の小さい方の立体について考える。
その立体の体積を$V$、切り口の面積を$S_1$、
円柱の側面であった部分の面積を$S_2$とする。
(i)$V=\boxed{ケ}$
(ii)$S_1=\boxed{コ},S_2=\boxed{サ}$である。
この動画を見る
$\boxed{1}$
(4)$xyz$空間において、
$xy$平面上に$(0,0,0)$を中心とする半径$2$の円がある。
この円と、$(0,0,2\sqrt3)$を中心とする半径$2$の円を
底面とする円柱を、
原点を通り$xz$平面と$30$度の角をなす平面によって
切断し、$2$つの立体に分ける。
いま$2$つの立体のうち、
体積の小さい方の立体について考える。
その立体の体積を$V$、切り口の面積を$S_1$、
円柱の側面であった部分の面積を$S_2$とする。
(i)$V=\boxed{ケ}$
(ii)$S_1=\boxed{コ},S_2=\boxed{サ}$である。
福田のおもしろ数学463〜2定点を見込む角を最大にする方法
単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
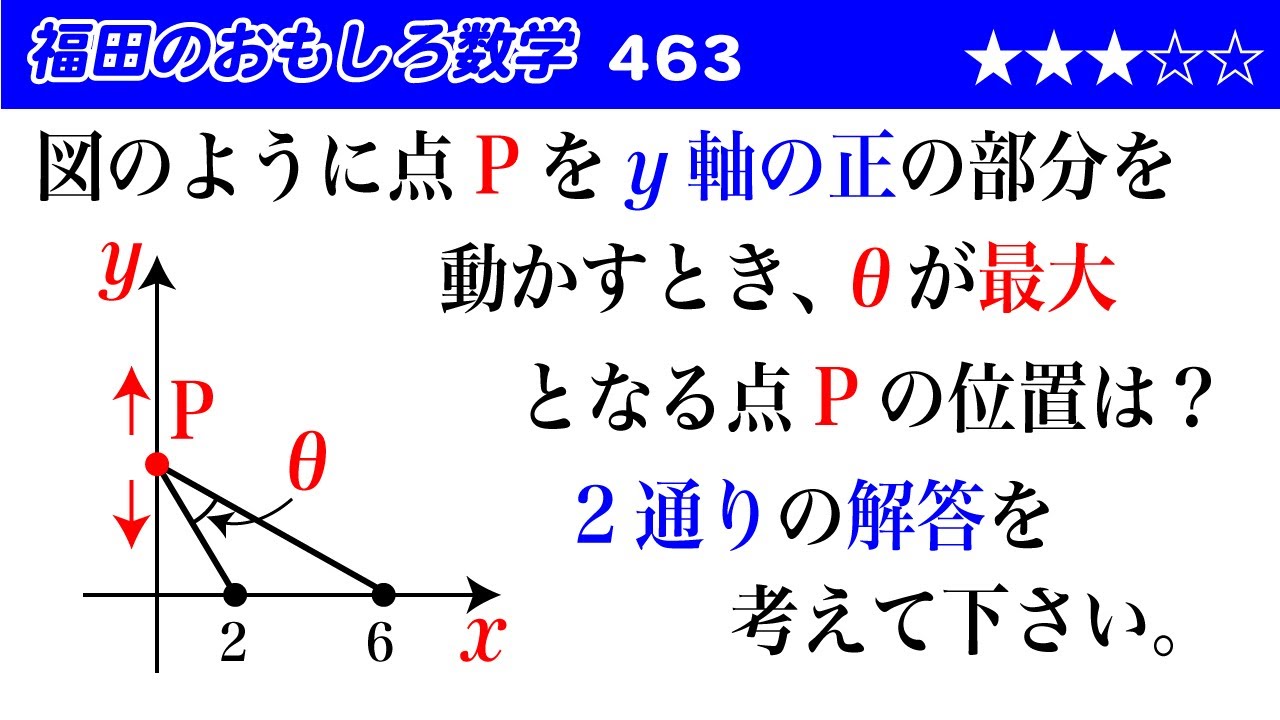
図のように点$P$を$y$軸の正の部分を
動かすとき、
$\theta$が最大となる点$P$の位置は?
$2$通りの解答を考えて下さい。
図は動画内参照
この動画を見る
図のように点$P$を$y$軸の正の部分を
動かすとき、
$\theta$が最大となる点$P$の位置は?
$2$通りの解答を考えて下さい。
図は動画内参照
福田のおもしろ数学461〜関数方程式

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$0$以上の実数で定義された実数値関数$f(x)$は
(i)$f(1)=1$
(ii)$f\left(\dfrac{1}{x+y}\right)=f\left(\dfrac{1}{x}\right)+f\left(\dfrac{1}{y}\right)$
$ \hspace{ 100pt } (x+y,x,y\neq 0)$
(iii)$(x+y)f(x+y)=xyf(x)f(y)$
$\hspace{ 100pt }(x+y,x,y\neq 0)$
を満たしている。$f(x)$を求めよ。
この動画を見る
$0$以上の実数で定義された実数値関数$f(x)$は
(i)$f(1)=1$
(ii)$f\left(\dfrac{1}{x+y}\right)=f\left(\dfrac{1}{x}\right)+f\left(\dfrac{1}{y}\right)$
$ \hspace{ 100pt } (x+y,x,y\neq 0)$
(iii)$(x+y)f(x+y)=xyf(x)f(y)$
$\hspace{ 100pt }(x+y,x,y\neq 0)$
を満たしている。$f(x)$を求めよ。
福田のおもしろ数学458〜関数方程式

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
整数から整数への関数$f(n)$が
$f(n)=f(n^2+n+1)$
を満たす偶関数であるとき、
$f(n)$を求めて下さい。
この動画を見る
整数から整数への関数$f(n)$が
$f(n)=f(n^2+n+1)$
を満たす偶関数であるとき、
$f(n)$を求めて下さい。
福田の数学〜東北大学2025理系第4問〜2曲線の相接と面積の極限

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{4}$
$n$を正の整数、$a$を正の実数とし、
関数$f(x)$と$g(x)$を次のように定める。
$f(x)=n\log x,\quad g(x)=ax^n$
また、曲線$y=f(x)$と曲線$y=g(x)$が共有点をもち、
その共有点における
$2$つの曲線の接線が一致しているとする。
このとき、以下の問いに答えよ。
(1)$a$の値を求めよ。
(2)この$2$つの曲線と$x$軸で囲まれた部分の面積
$S_n$を求めよ。
(3)$\quad $(2)で求めた$S_n$に対し、極限$\displaystyle \lim_{n\to\infty}S_n$を求めよ。
$2025$年東北大学理系過去問題
この動画を見る
$\boxed{4}$
$n$を正の整数、$a$を正の実数とし、
関数$f(x)$と$g(x)$を次のように定める。
$f(x)=n\log x,\quad g(x)=ax^n$
また、曲線$y=f(x)$と曲線$y=g(x)$が共有点をもち、
その共有点における
$2$つの曲線の接線が一致しているとする。
このとき、以下の問いに答えよ。
(1)$a$の値を求めよ。
(2)この$2$つの曲線と$x$軸で囲まれた部分の面積
$S_n$を求めよ。
(3)$\quad $(2)で求めた$S_n$に対し、極限$\displaystyle \lim_{n\to\infty}S_n$を求めよ。
$2025$年東北大学理系過去問題
福田の数学〜東北大学2025理系第3問〜4次関数が極大値をもつ条件

単元:
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
$a$を実数とし、関数$f(x)$を次のように定める。
$f(x)=x^4+\dfrac{4a}{3}x^3+(a+2)x^2$
このとき、以下の問いに答えよ。
(1)関数$f(x)$が極大値をもつような$a$のとり得る
値の範囲を求めよ。
(2)関数$f(x)$が$x=0$で極大値をもつような
$a$のとり得る値の範囲を求めよ。
$2025$年東北大学理系過去問題
この動画を見る
$\boxed{3}$
$a$を実数とし、関数$f(x)$を次のように定める。
$f(x)=x^4+\dfrac{4a}{3}x^3+(a+2)x^2$
このとき、以下の問いに答えよ。
(1)関数$f(x)$が極大値をもつような$a$のとり得る
値の範囲を求めよ。
(2)関数$f(x)$が$x=0$で極大値をもつような
$a$のとり得る値の範囲を求めよ。
$2025$年東北大学理系過去問題
福田のおもしろ数学454〜積分に関するシュワルツの不等式の証明と等号成立条件

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#積分とその応用#不定積分#定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$p\leqq x \leqq q$で定義された連続関数$f(x),g(x)$に対して
$\left(\displaystyle \int_{p}^{q} f(x)^2 dx\right)\left(\displaystyle \int_{p}^{q}g(x)^2 dx \right) \geqq \left(\displaystyle \int_{p}^{q} f(x)g(x)dx\right)^2$
を証明して下さい。
また等号成立条件も調べて下さい。
この動画を見る
$p\leqq x \leqq q$で定義された連続関数$f(x),g(x)$に対して
$\left(\displaystyle \int_{p}^{q} f(x)^2 dx\right)\left(\displaystyle \int_{p}^{q}g(x)^2 dx \right) \geqq \left(\displaystyle \int_{p}^{q} f(x)g(x)dx\right)^2$
を証明して下さい。
また等号成立条件も調べて下さい。
福田の数学〜北海道大学2025文系第4問〜関数方程式

単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{4}$
関数$f(x)$は、
すべての実数$x$およびすべての整数$n$について
$f(nx)={f(x)}^n$を満たし、
さらに$f(1)=2$を満たすとする。
ただし、$f(x)$のとりうる値は$0$でない実数とする。
(1)$f(n) \leqq 100$となるような最大の整数$n$を求めよ。
(2)すべての実数$x$について
$f(x)\gt 0$であることを証明せよ。
(3)$f(0.25)$を求めよ。
(4)$a$が有理数のとき、$f(a)$を$a$で表せ。
$2025$年北海道大学文系過去問題
この動画を見る
$\boxed{4}$
関数$f(x)$は、
すべての実数$x$およびすべての整数$n$について
$f(nx)={f(x)}^n$を満たし、
さらに$f(1)=2$を満たすとする。
ただし、$f(x)$のとりうる値は$0$でない実数とする。
(1)$f(n) \leqq 100$となるような最大の整数$n$を求めよ。
(2)すべての実数$x$について
$f(x)\gt 0$であることを証明せよ。
(3)$f(0.25)$を求めよ。
(4)$a$が有理数のとき、$f(a)$を$a$で表せ。
$2025$年北海道大学文系過去問題
【数Ⅲ】【積分とその応用】面積13 ※問題文は概要欄

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$k > 0$とする。曲線$y=\sin2x~~(0\leqq x\leqq \dfrac\pi2)$と$x$軸で囲まれた部分の面積を$y=k\sin x$が2等分するように定数$k$の値を定めよ。
この動画を見る
$k > 0$とする。曲線$y=\sin2x~~(0\leqq x\leqq \dfrac\pi2)$と$x$軸で囲まれた部分の面積を$y=k\sin x$が2等分するように定数$k$の値を定めよ。
【数Ⅲ】【積分とその応用】面積15 ※問題文は概要欄

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$x$軸に平行な直線と曲線$y=\sin x~~(0\leqq x \leqq 3\pi)$が4点で交わるとき、この直線と曲線で囲まれた3つの部分の面積の和が最小となるような直線の方程式を求めよ。
この動画を見る
$x$軸に平行な直線と曲線$y=\sin x~~(0\leqq x \leqq 3\pi)$が4点で交わるとき、この直線と曲線で囲まれた3つの部分の面積の和が最小となるような直線の方程式を求めよ。
【数Ⅲ】【積分とその応用】面積14 ※問題文は概要欄

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$1\leqq a\leqq e$とする。曲線$y=e^x-a$と$x$軸、$y$軸および直線$x=1$で囲まれた部分の面積を$S(a)$とする。
(1) $S(a)$を求めよ。
(2) $S(a)$の最小値とそのときの$a$の値を求めよ。
この動画を見る
$1\leqq a\leqq e$とする。曲線$y=e^x-a$と$x$軸、$y$軸および直線$x=1$で囲まれた部分の面積を$S(a)$とする。
(1) $S(a)$を求めよ。
(2) $S(a)$の最小値とそのときの$a$の値を求めよ。
【数Ⅲ】【積分とその応用】面積12 ※問題文は概要欄

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
曲線$\dfrac{\sqrt{x}}a+\dfrac{\sqrt{y}}b=1$は、直線$\dfrac x a+\dfrac y b=1$と$x$軸、$y$軸で囲まれた三角形を一定の面積の比に分割することを示せ。ただし、$a > 0,b > 0$とする。
この動画を見る
曲線$\dfrac{\sqrt{x}}a+\dfrac{\sqrt{y}}b=1$は、直線$\dfrac x a+\dfrac y b=1$と$x$軸、$y$軸で囲まれた三角形を一定の面積の比に分割することを示せ。ただし、$a > 0,b > 0$とする。
【数Ⅲ】【積分とその応用】面積11 ※問題文は概要欄

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
曲線$y=ax^2$と$y=\log x$はただ1点を共有し、その点におけるそれぞれの接線は一致するものとする。
(1)定数$a$の値と共有点の座標を求めよ。
(2)この2つの曲線と$x$軸で囲まれた部分の面積を求めよ。
この動画を見る
曲線$y=ax^2$と$y=\log x$はただ1点を共有し、その点におけるそれぞれの接線は一致するものとする。
(1)定数$a$の値と共有点の座標を求めよ。
(2)この2つの曲線と$x$軸で囲まれた部分の面積を求めよ。
【数Ⅲ】【積分とその応用】面積10 ※問題文は概要欄

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$x=\cos^4\theta,y=\sin^4\theta~~(0\leqq \theta \leqq \dfrac\pi2)$で表される曲線を$C$とし、曲線$C$の接線を$l$とする。曲線$C$と接線$l$、$x$軸で囲まれた部分の面積と、曲線$C$と接線$l$、$y$軸で囲まれた面積の和が$\frac{1}{24}$であるという。このとき、接線$l$の方程式を求めよ。
この動画を見る
$x=\cos^4\theta,y=\sin^4\theta~~(0\leqq \theta \leqq \dfrac\pi2)$で表される曲線を$C$とし、曲線$C$の接線を$l$とする。曲線$C$と接線$l$、$x$軸で囲まれた部分の面積と、曲線$C$と接線$l$、$y$軸で囲まれた面積の和が$\frac{1}{24}$であるという。このとき、接線$l$の方程式を求めよ。
福田のおもしろ数学449〜3次式が常に0以上となるxの範囲

単元:
#微分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
実数$a$に対して関数$f(x)$を考える。
$f(x)=x^3-2x^2+(2a-1)x-2a$
$0\leqq a \leqq 1$のとき、
常に$f(x)\geqq 0$となる$x$の範囲を求めよ。
この動画を見る
実数$a$に対して関数$f(x)$を考える。
$f(x)=x^3-2x^2+(2a-1)x-2a$
$0\leqq a \leqq 1$のとき、
常に$f(x)\geqq 0$となる$x$の範囲を求めよ。
福田の数学〜北海道大学2025文系第1問〜関数の増減と接線の方程式

単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
関数$f(x)=x^3-6x^2-15x+30$について考える。
$y=f(x)$のグラフを$C$とおく。
(1)$f(x)$が極大値、
極小値をとるような$x$をそれぞれ求め、
$f(x)$の極大値、極小値を求めよ。
(2)$C$上の点$(-3,-6)$を通り、
$C$に接する直線の方程式をすべて求めよ。
$2025$年北海道大学文系過去問題
この動画を見る
$\boxed{1}$
関数$f(x)=x^3-6x^2-15x+30$について考える。
$y=f(x)$のグラフを$C$とおく。
(1)$f(x)$が極大値、
極小値をとるような$x$をそれぞれ求め、
$f(x)$の極大値、極小値を求めよ。
(2)$C$上の点$(-3,-6)$を通り、
$C$に接する直線の方程式をすべて求めよ。
$2025$年北海道大学文系過去問題
福田のおもしろ数学447〜簡単な関数方程式を解こう

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
正の実数の集合を$R^{+}$と表す。
$f:R^{+}→R^{+}$が任意の$x,y \in R^{+}$に対し
$f(x)f(y)=f(xy)+\dfrac{1}{x}+\dfrac{1}{y}$
を満たしている。
このような$f(x)$をすべて求めて下さい。
この動画を見る
正の実数の集合を$R^{+}$と表す。
$f:R^{+}→R^{+}$が任意の$x,y \in R^{+}$に対し
$f(x)f(y)=f(xy)+\dfrac{1}{x}+\dfrac{1}{y}$
を満たしている。
このような$f(x)$をすべて求めて下さい。
福田の数学〜北海道大学2025理系第3問〜部分積分と極限

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
実数$a$および自然数$n$に対して、定積分
$I(a,n)=\displaystyle \int_{0}^{2\pi} e^{ax} \sin (nx) dx$
を考える。ここで$e$は自然対数の底である。
(1)$I(a,n)$を求めよ。
(2)$a_n=\dfrac{\log _n}{2\pi} (n=1,2,3,\cdots)$のとき、
極限$\displaystyle \lim_{n\to\infty} I(a_n,n)$を求めよ。
ただし、$\log_n$は$n$の自然対数である。
また、必要ならば$\displaystyle \lim_{n\to\infty}\dfrac{\log_n}{n}=0$である
ことを用いてもよい。
$2025$年北海道大学理系過去問題
この動画を見る
$\boxed{3}$
実数$a$および自然数$n$に対して、定積分
$I(a,n)=\displaystyle \int_{0}^{2\pi} e^{ax} \sin (nx) dx$
を考える。ここで$e$は自然対数の底である。
(1)$I(a,n)$を求めよ。
(2)$a_n=\dfrac{\log _n}{2\pi} (n=1,2,3,\cdots)$のとき、
極限$\displaystyle \lim_{n\to\infty} I(a_n,n)$を求めよ。
ただし、$\log_n$は$n$の自然対数である。
また、必要ならば$\displaystyle \lim_{n\to\infty}\dfrac{\log_n}{n}=0$である
ことを用いてもよい。
$2025$年北海道大学理系過去問題
福田のおもしろ数学445〜関数方程式

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
正の実数の集合を$R^{+}$と表す。
$f:R^{+}→R^{+}$が任意の$x,y \in R^{+}$に対し
$y^2f(x)=f\left(\dfrac{x}{y}\right)$を満たしている。
このような$f(x)$をすべて求めなさい。
この動画を見る
正の実数の集合を$R^{+}$と表す。
$f:R^{+}→R^{+}$が任意の$x,y \in R^{+}$に対し
$y^2f(x)=f\left(\dfrac{x}{y}\right)$を満たしている。
このような$f(x)$をすべて求めなさい。
【数Ⅲ】【積分とその応用】面積8 ※問題文は概要欄

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
曲線$x=\cos^3\theta,y=\sin^3\theta$で囲まれた部分の面積を求めよ。
この動画を見る
曲線$x=\cos^3\theta,y=\sin^3\theta$で囲まれた部分の面積を求めよ。
【数Ⅲ】【積分とその応用】面積7 ※問題文は概要欄

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の曲線と$x$軸で囲まれた部分の面積を求めよ。
(1) $x=1-t^4,y=t-t^3~~(0\leqq t \leqq 1)$
(2) $x=t+\sin t,y=1-\cos t~~(0\leqq \theta \leqq 2\pi)$
この動画を見る
次の曲線と$x$軸で囲まれた部分の面積を求めよ。
(1) $x=1-t^4,y=t-t^3~~(0\leqq t \leqq 1)$
(2) $x=t+\sin t,y=1-\cos t~~(0\leqq \theta \leqq 2\pi)$
【数Ⅲ】【積分とその応用】面積5 ※問題文は概要欄

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
曲線$5x^2+2xy+y^2=16$で囲まれた部分の面積$S$を求めよ。
この動画を見る
曲線$5x^2+2xy+y^2=16$で囲まれた部分の面積$S$を求めよ。
福田のおもしろ数学441〜ガウス記号を使って定義された数列の極限

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$a_n=\dfrac{1}{n^2} \displaystyle \sum_{k=1}^n [\sqrt{2n^2-k^2}]$とするとき、
$\displaystyle \lim_{n\to\infty} a_n$を求めて下さい。
$[x]$は$x$を超えない最大の整数とする。
この動画を見る
$a_n=\dfrac{1}{n^2} \displaystyle \sum_{k=1}^n [\sqrt{2n^2-k^2}]$とするとき、
$\displaystyle \lim_{n\to\infty} a_n$を求めて下さい。
$[x]$は$x$を超えない最大の整数とする。
【数Ⅲ】【積分とその応用】面積9 ※問題文は概要欄

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
座標平面上で、原点$\rm O$から曲線$y=\sin x$へ引いた接線の接点を${\rm T}(\alpha,\sin\alpha)$とする。ただし、$\pi < \alpha < \dfrac32\pi$とする。
(1)$\alpha$の満たす方程式を求めよ。
(2)曲線$y=\sin x$と線分$\rm OT$で囲まれた部分の面積$S$を、$\cos\alpha$で表せ。
この動画を見る
座標平面上で、原点$\rm O$から曲線$y=\sin x$へ引いた接線の接点を${\rm T}(\alpha,\sin\alpha)$とする。ただし、$\pi < \alpha < \dfrac32\pi$とする。
(1)$\alpha$の満たす方程式を求めよ。
(2)曲線$y=\sin x$と線分$\rm OT$で囲まれた部分の面積$S$を、$\cos\alpha$で表せ。
【数Ⅲ】【積分とその応用】面積6 ※問題文は概要欄

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
2つの曲線$y=x^2,\sqrt{x}+\sqrt{y}=2$と$y$軸で囲まれた部分の面積$S$を求めよ。
この動画を見る
2つの曲線$y=x^2,\sqrt{x}+\sqrt{y}=2$と$y$軸で囲まれた部分の面積$S$を求めよ。
【数Ⅲ】【積分とその応用】面積4 ※問題文は概要欄

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の曲線と$x$軸で囲まれた部分の面積を求めよ。
$x=\cos\theta$
$y=2\sin\theta~~(0\leqq \theta \leqq \pi)$
この動画を見る
次の曲線と$x$軸で囲まれた部分の面積を求めよ。
$x=\cos\theta$
$y=2\sin\theta~~(0\leqq \theta \leqq \pi)$
【数Ⅲ】【積分とその応用】面積3 ※問題文は概要欄

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の曲線で囲まれた図形の面積を求めよ。
(1) y²=x²(1-x)
(2) |y+1|=x|x-3|
この動画を見る
次の曲線で囲まれた図形の面積を求めよ。
(1) y²=x²(1-x)
(2) |y+1|=x|x-3|
【数Ⅲ】【積分とその応用】面積2 ※問題文は概要欄

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の楕円によって囲まれた図形の面積を求めよ。
(1) 2x²+3y²=6
(2) 3x²+4y²=1
この動画を見る
次の楕円によって囲まれた図形の面積を求めよ。
(1) 2x²+3y²=6
(2) 3x²+4y²=1
【数Ⅲ】【積分とその応用】面積1 ※問題文は概要欄

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の曲線や直線で囲まれた図形の面積を求めよ。
(1)$y=xe^{1-x}$,$y=xe^{x-1}$
(2)$y=x^2$,$y=xe^{1-x}$
(3)$y=e^x$,$y=e^{3x}$,$y=e^{2-x}$
(4)$y=(x-e)logx$,$y=0$
(5)$y=sinx$,$y=sin2x(0 \leqq x \leqq 2π)$
この動画を見る
次の曲線や直線で囲まれた図形の面積を求めよ。
(1)$y=xe^{1-x}$,$y=xe^{x-1}$
(2)$y=x^2$,$y=xe^{1-x}$
(3)$y=e^x$,$y=e^{3x}$,$y=e^{2-x}$
(4)$y=(x-e)logx$,$y=0$
(5)$y=sinx$,$y=sin2x(0 \leqq x \leqq 2π)$
