 数Ⅲ
数Ⅲ
 数Ⅲ
数Ⅲ
11和歌山県教員採用試験(数学:4番 微分と微分方程式)

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{4}$
$f(x)$:微分可能
任意の実数$x,y$に対して
$f(x+y)=f(x),f(y),f`(0)=2$
(1)$f(0)$を求めよ.
(2)$f(x)$を求めよ.
この動画を見る
$\boxed{4}$
$f(x)$:微分可能
任意の実数$x,y$に対して
$f(x+y)=f(x),f(y),f`(0)=2$
(1)$f(0)$を求めよ.
(2)$f(x)$を求めよ.
数学「大学入試良問集」【17−3① 解けない漸化式とはさみうちの原理】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#岐阜大学#数学(高校生)#数Ⅲ
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$a_1=2,a_{n+1}=\displaystyle \frac{1}{2}a_n+\displaystyle \frac{1}{a_n}$ $n=1,2,3,・・・$で定義される数列$\{a_n\}$について以下の問いに答えよ。
(1)$a_n \gt \sqrt{ 2 }(n=1,2,3,・・・)$を証明せよ。
(2)$a_{n+1}-\sqrt{ 2 } \lt \displaystyle \frac{1}{2}(a_n-\sqrt{ 2 })(n=1,2,3,・・・)$を証明せよ。
(3)$\displaystyle \lim_{ n \to \infty }a_n$を求めよ。
この動画を見る
$a_1=2,a_{n+1}=\displaystyle \frac{1}{2}a_n+\displaystyle \frac{1}{a_n}$ $n=1,2,3,・・・$で定義される数列$\{a_n\}$について以下の問いに答えよ。
(1)$a_n \gt \sqrt{ 2 }(n=1,2,3,・・・)$を証明せよ。
(2)$a_{n+1}-\sqrt{ 2 } \lt \displaystyle \frac{1}{2}(a_n-\sqrt{ 2 })(n=1,2,3,・・・)$を証明せよ。
(3)$\displaystyle \lim_{ n \to \infty }a_n$を求めよ。
【数Ⅲ】積分法:楕円で構成された図形の面積

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材:
#チャート式#青チャートⅢ#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
【高校数学 数学Ⅲ 積分法の応用】
2つの楕円$x^2+3y^2=4・・・①、3x^2+y^2=4・・・②$がある。
(1)2つの楕円の4つの交点の座標を求めよ。
(2)2つの楕円の内部の重なった部分の面積を求めよ。
(出典元)青チャート数学Ⅲより
この動画を見る
【高校数学 数学Ⅲ 積分法の応用】
2つの楕円$x^2+3y^2=4・・・①、3x^2+y^2=4・・・②$がある。
(1)2つの楕円の4つの交点の座標を求めよ。
(2)2つの楕円の内部の重なった部分の面積を求めよ。
(出典元)青チャート数学Ⅲより
福田のわかった数学〜高校3年生理系035〜極限(35)関数の極限、色々な極限(5)

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
数学\textrm{III} 色々な極限(5)\\
\lim_{x \to 0}\frac{a^x-1}{x} (a \gt 1)\\
を2通りの方法で求めよ。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
数学\textrm{III} 色々な極限(5)\\
\lim_{x \to 0}\frac{a^x-1}{x} (a \gt 1)\\
を2通りの方法で求めよ。
\end{eqnarray}
練習問題33 数検1級1次 微分方程式
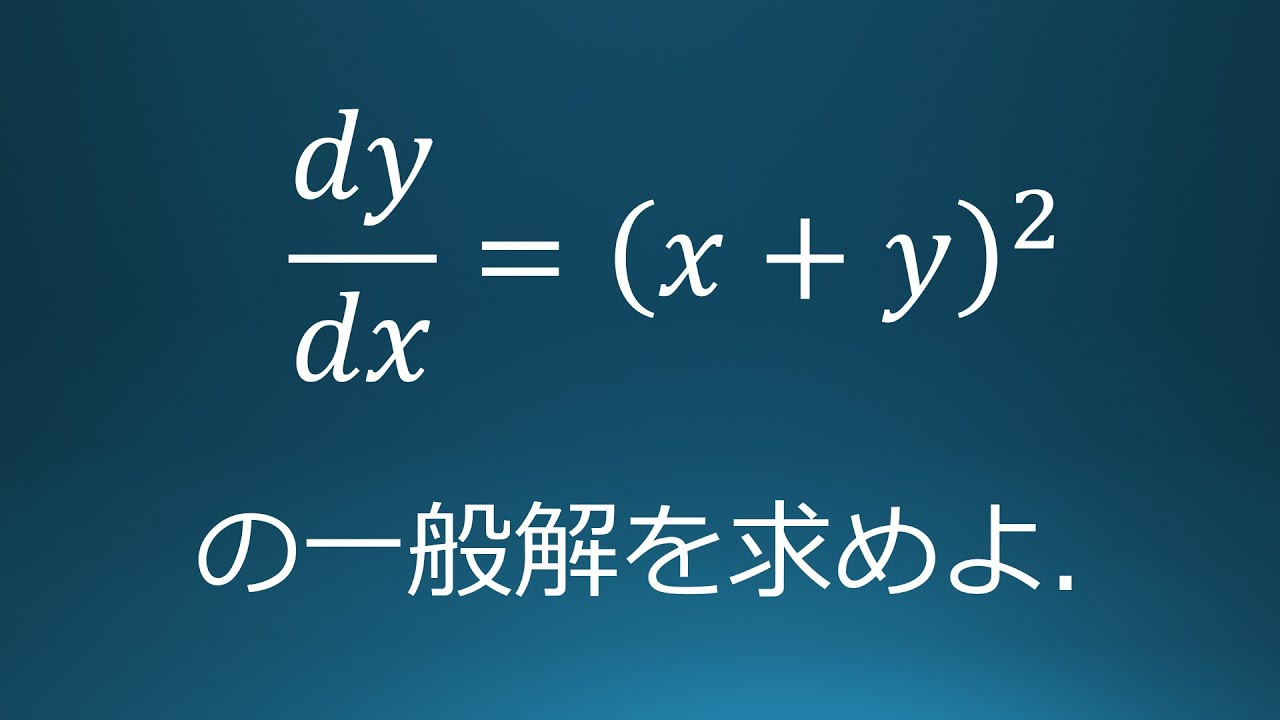
単元:
#数学検定・数学甲子園・数学オリンピック等#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\dfrac{dy}{dx}=(x+y)^2$
の一般解を求めよ.
この動画を見る
$\dfrac{dy}{dx}=(x+y)^2$
の一般解を求めよ.
08岡山県教員採用試験(数学:1-(4) 微分方程式)
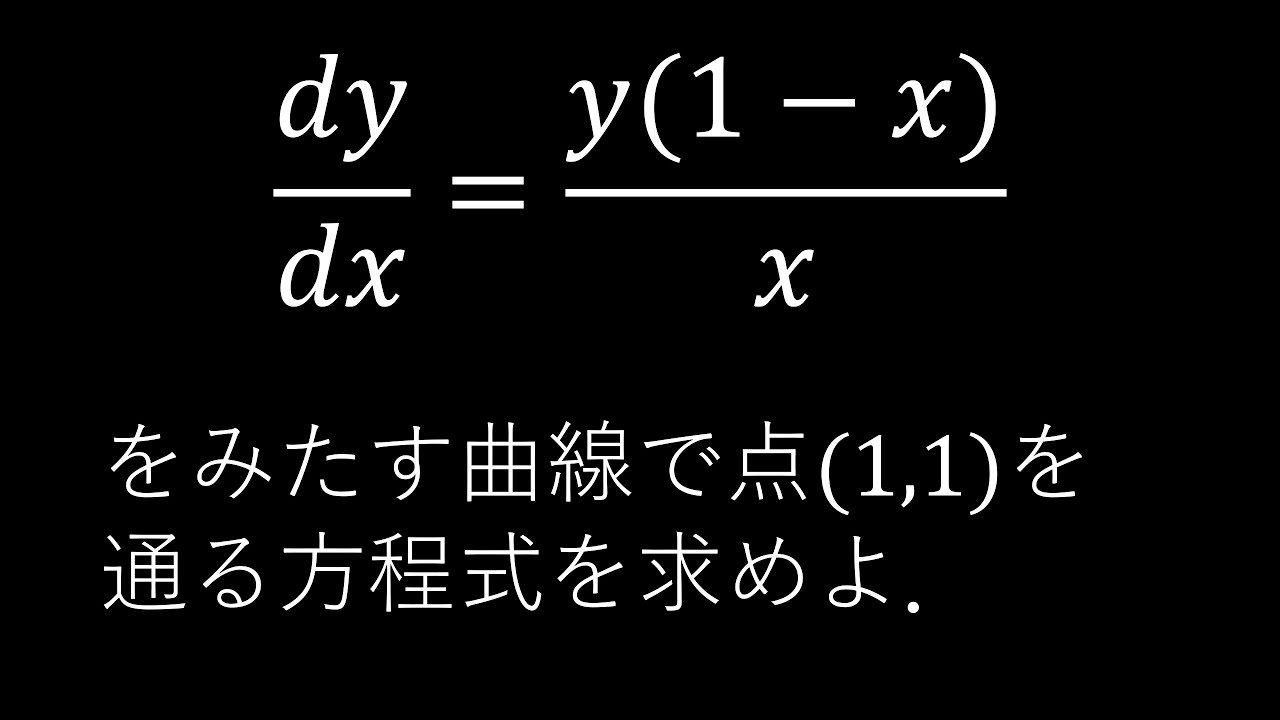
単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{1}-(4)$
$\dfrac{dy}{dx}=\dfrac{y(x-1)}{x}$
をみたす曲線で$(1,1)$を通る方程式を求めよ.
この動画を見る
$\boxed{1}-(4)$
$\dfrac{dy}{dx}=\dfrac{y(x-1)}{x}$
をみたす曲線で$(1,1)$を通る方程式を求めよ.
数学「大学入試良問集」【17−2 Sn入り漸化式と極限】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#熊本大学#数学(高校生)#数Ⅲ
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
数列$\{a_n\}$について、$S_n=\displaystyle \sum_{k=1}^n a_k$ $n=1,2,3,・・・,S_0=0$とおく。
$a_n=S_{n-1}+n・2^n$ $n=1,2,3,・・・$ が成り立つとき、次の各問いに答えよ。
(1)$S_n$を$n$の式で表せ。
(2)極限値$\displaystyle \lim_{ n \to \infty }\displaystyle \sum_{k=1}^n\displaystyle \frac{2^k}{a_k}$を求めよ。
この動画を見る
数列$\{a_n\}$について、$S_n=\displaystyle \sum_{k=1}^n a_k$ $n=1,2,3,・・・,S_0=0$とおく。
$a_n=S_{n-1}+n・2^n$ $n=1,2,3,・・・$ が成り立つとき、次の各問いに答えよ。
(1)$S_n$を$n$の式で表せ。
(2)極限値$\displaystyle \lim_{ n \to \infty }\displaystyle \sum_{k=1}^n\displaystyle \frac{2^k}{a_k}$を求めよ。
福田のわかった数学〜高校3年生理系034〜極限(34)関数の極限、色々な極限(4)

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
数学\textrm{III} 色々な極限(4)\\
\lim_{x \to 1}\frac{\sin\pi x}{x-1}\\
を2通りの方法で求めよ。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
数学\textrm{III} 色々な極限(4)\\
\lim_{x \to 1}\frac{\sin\pi x}{x-1}\\
を2通りの方法で求めよ。
\end{eqnarray}
古畑任三郎/刑事コロンボ問題

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\displaystyle \lim_{x\to \infty}\dfrac{[2x^2-x+3]}{x^2}$
この動画を見る
これを解け.
$\displaystyle \lim_{x\to \infty}\dfrac{[2x^2-x+3]}{x^2}$
数学「大学入試良問集」【17−1 隣接三項間漸化式と極限】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京医科大学#東京医科大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$a_1=1,a_2=2,n \geqq 3$のとき$a_n=\displaystyle \frac{1}{5}(3a_{n-1}+2a_{n-2})$で定義される数列$\{a_n\}$の極限値を求めよ。
この動画を見る
$a_1=1,a_2=2,n \geqq 3$のとき$a_n=\displaystyle \frac{1}{5}(3a_{n-1}+2a_{n-2})$で定義される数列$\{a_n\}$の極限値を求めよ。
福田のわかった数学〜高校3年生理系033〜極限(33)関数の極限、色々な極限(3)

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
数学\textrm{III} 色々な極限(3)\\
\lim_{x \to \infty}\frac{[3x]}{x} を求めよ。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
数学\textrm{III} 色々な極限(3)\\
\lim_{x \to \infty}\frac{[3x]}{x} を求めよ。
\end{eqnarray}
【数Ⅲ】極限:2021年高3第1回K塾記述模試

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#全統模試(河合塾)#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
初項$2p^2$、公比pの等比数列{$a_n$}がある。ただし、pは実数の定数とする。無限 等比級数$\displaystyle \sum_{n=1}^{\infty}a_n$が収束し、その和が1であるとき、次の問に答えよ。
(1)p の値を求めよ。
(2)母線の長さが1、高さがa[n]の円錐の体積を$V_n$とする。無限 級数$\displaystyle \sum_{n=1}^{\infty}V_n$は収束するか。収束するときはその和を求め、発散するとき はそのことを示せ。
(3)母線の長さが1、高さが$a_n$の円錐の側面積を$T_n$とす る。無限級数$\displaystyle \sum_{n=1}^{\infty}T_n$は収束するか。収束するときはその和を求め、発散 するときはそのことを示せ。
この動画を見る
初項$2p^2$、公比pの等比数列{$a_n$}がある。ただし、pは実数の定数とする。無限 等比級数$\displaystyle \sum_{n=1}^{\infty}a_n$が収束し、その和が1であるとき、次の問に答えよ。
(1)p の値を求めよ。
(2)母線の長さが1、高さがa[n]の円錐の体積を$V_n$とする。無限 級数$\displaystyle \sum_{n=1}^{\infty}V_n$は収束するか。収束するときはその和を求め、発散するとき はそのことを示せ。
(3)母線の長さが1、高さが$a_n$の円錐の側面積を$T_n$とす る。無限級数$\displaystyle \sum_{n=1}^{\infty}T_n$は収束するか。収束するときはその和を求め、発散 するときはそのことを示せ。
対数関数の微分公式
福田のわかった数学〜高校3年生理系032〜極限(32)関数の極限、色々な極限(2)

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
数学\textrm{III} 色々な極限(2)\\
\lim_{x \to 2}([2x]-[x]) を求めよ。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
数学\textrm{III} 色々な極限(2)\\
\lim_{x \to 2}([2x]-[x]) を求めよ。
\end{eqnarray}
福田のわかった数学〜高校3年生理系031〜極限(31)関数の極限、色々な極限(1)

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
数学\textrm{III} 色々な極限(1)\\
\lim_{x \to 1}\frac{(x-1)^2}{|x^2-1|} を求めよ。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
数学\textrm{III} 色々な極限(1)\\
\lim_{x \to 1}\frac{(x-1)^2}{|x^2-1|} を求めよ。
\end{eqnarray}
15滋賀県教員採用試験(数学:5番 グラフと極限)
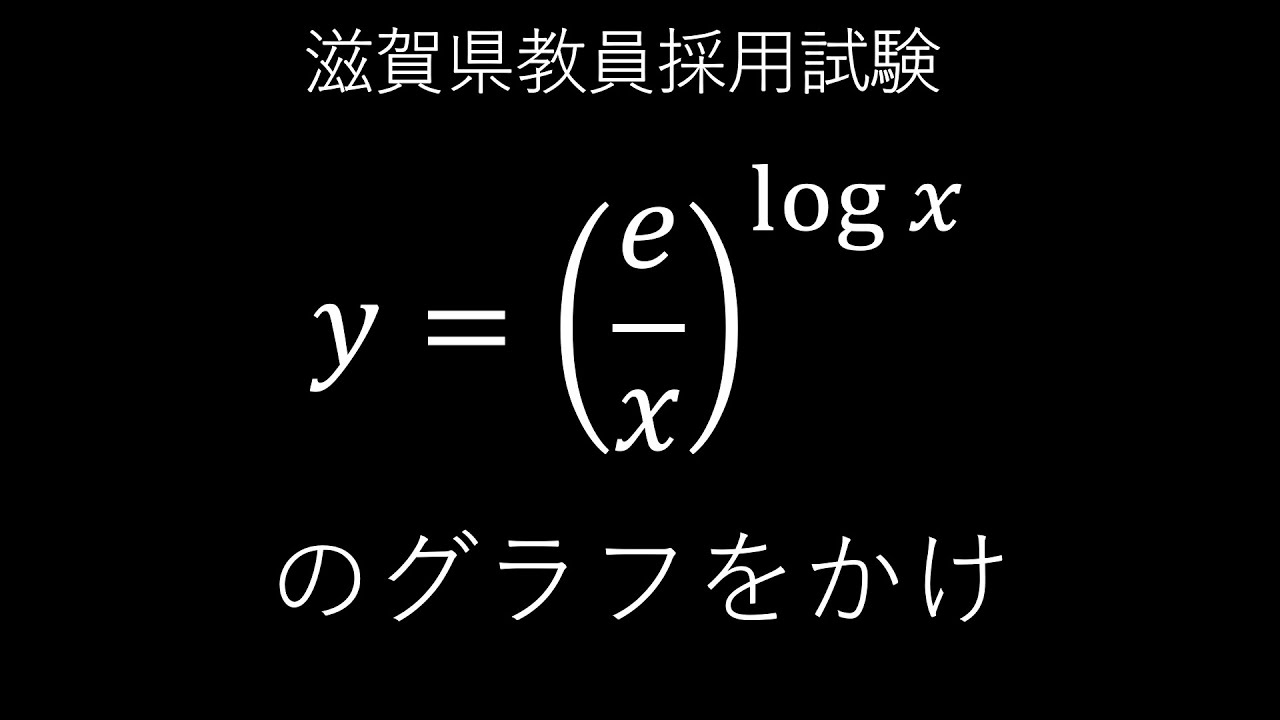
単元:
#関数と極限#微分とその応用#数列の極限#関数の極限#関数の変化(グラフ・最大最小・方程式・不等式)#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{5}$
$y=\left(\dfrac{e}{x}\right)^{\log x}$のグラフをかけ.
この動画を見る
$\boxed{5}$
$y=\left(\dfrac{e}{x}\right)^{\log x}$のグラフをかけ.
福田の数学〜早稲田大学2021年商学部第1問(2)〜整式と不等式

単元:
#大学入試過去問(数学)#微分とその応用#微分法#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$
(2)$n$を正の整数とする。$f(x)$は$x$の$n+1$次式で表される関数で、$x$が$0$以上$n$以下の整数のとき$f(x)=0$であり、$f(n+1)=n+1$である。このとき、
$\displaystyle \sum_{k=0}^n\frac{(1-\sqrt2)^k}{f'(k)} \gt 2^{2021}$
を満たす最小の$n$は$\boxed{\ \ イ\ \ }$である。
2021早稲田大学商学部過去問
この動画を見る
${\Large\boxed{1}}$
(2)$n$を正の整数とする。$f(x)$は$x$の$n+1$次式で表される関数で、$x$が$0$以上$n$以下の整数のとき$f(x)=0$であり、$f(n+1)=n+1$である。このとき、
$\displaystyle \sum_{k=0}^n\frac{(1-\sqrt2)^k}{f'(k)} \gt 2^{2021}$
を満たす最小の$n$は$\boxed{\ \ イ\ \ }$である。
2021早稲田大学商学部過去問
07滋賀県教員採用試験(数学:5番 接線の個数)
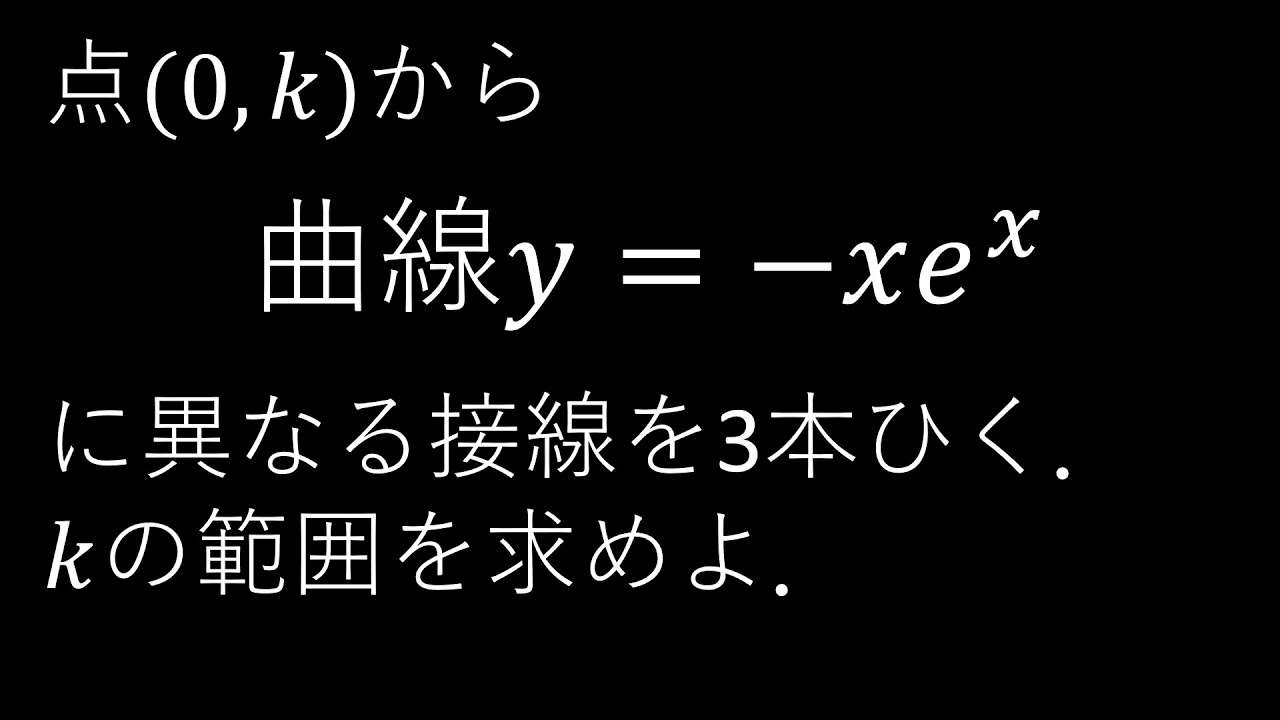
単元:
#微分とその応用#接線と法線・平均値の定理#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{5}$
点$(0,k)$から曲線$c$
$c:y=-xe^x$
に異なる3本の接線が引けるとき,
$k$の値の範囲を求めよ.
この動画を見る
$\boxed{5}$
点$(0,k)$から曲線$c$
$c:y=-xe^x$
に異なる3本の接線が引けるとき,
$k$の値の範囲を求めよ.
【数Ⅲ】微分法:sinを微分するとどうなる??グラフのイメージでサクッとわかる♪

福田のわかった数学〜高校3年生理系030〜極限(30)関数の極限、三角関数の極限(10)

単元:
#数Ⅱ#三角関数#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 三角関数の極限(10)
$\displaystyle \lim_{x \to 0}\frac{\sqrt{9-8x+7\cos2x}-(a+bx)}{x^2}$
が有限の値となる$a,b$とそのときの極限値
この動画を見る
数学$\textrm{III}$ 三角関数の極限(10)
$\displaystyle \lim_{x \to 0}\frac{\sqrt{9-8x+7\cos2x}-(a+bx)}{x^2}$
が有限の値となる$a,b$とそのときの極限値
12滋賀県教員採用試験(数学:5番 微分と微分方程式)

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{5}$任意の実数$s,t$に対して
$f(s+t)=f(s)f(t),f(1)\neq 0,f`(0)=a$である.
(1)$f(0)$
(2)任意の実数$x$に対して$f(x)\neq 0$を示せ.
(3)任意の実数$x$に対して$f`(x)=af(x)$を示せ.
(4)$f(x)$を求めよ.
この動画を見る
$\boxed{5}$任意の実数$s,t$に対して
$f(s+t)=f(s)f(t),f(1)\neq 0,f`(0)=a$である.
(1)$f(0)$
(2)任意の実数$x$に対して$f(x)\neq 0$を示せ.
(3)任意の実数$x$に対して$f`(x)=af(x)$を示せ.
(4)$f(x)$を求めよ.
福田のわかった数学〜高校3年生理系029〜極限(29)関数の極限、三角関数の極限(9)
単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
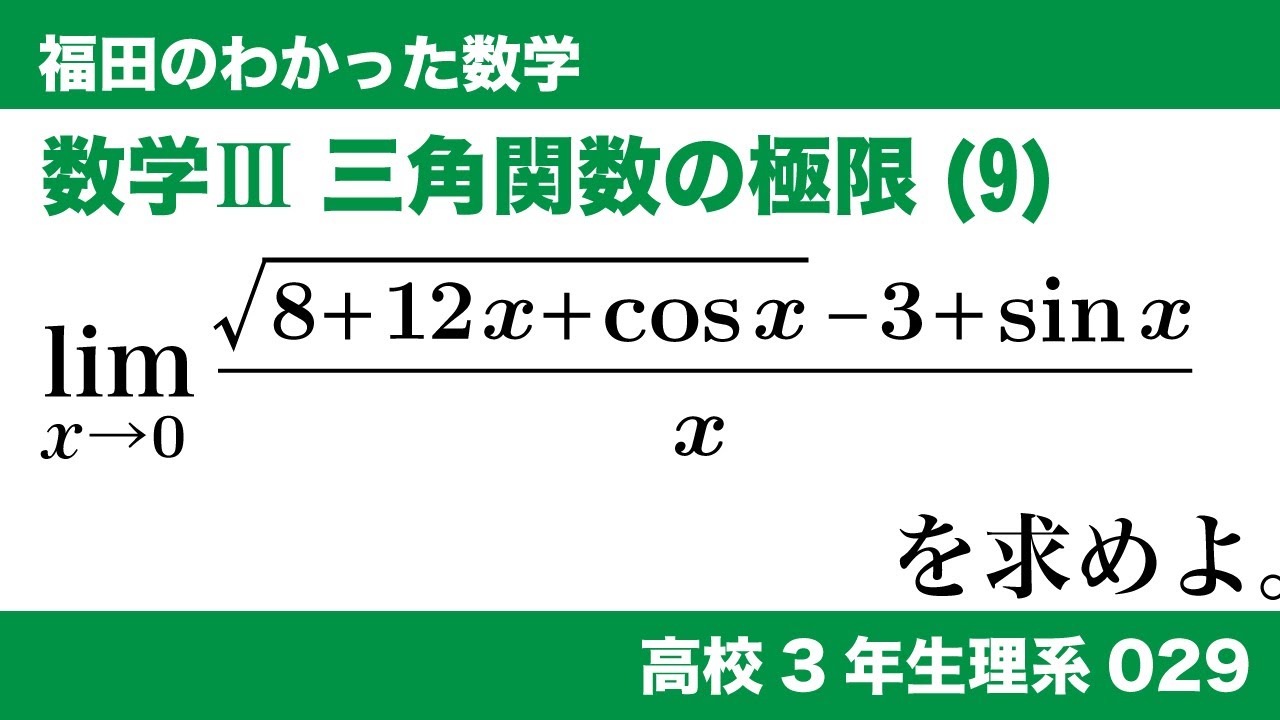
数学$\textrm{III}$ 三角関数の極限$(9)\\
\lim_{x \to 0}\frac{\sqrt{8+12x+\cos x}-3+\sin x}{x}$
を求めよ。
この動画を見る
数学$\textrm{III}$ 三角関数の極限$(9)\\
\lim_{x \to 0}\frac{\sqrt{8+12x+\cos x}-3+\sin x}{x}$
を求めよ。
岡山県教員採用試験:方程式の利用
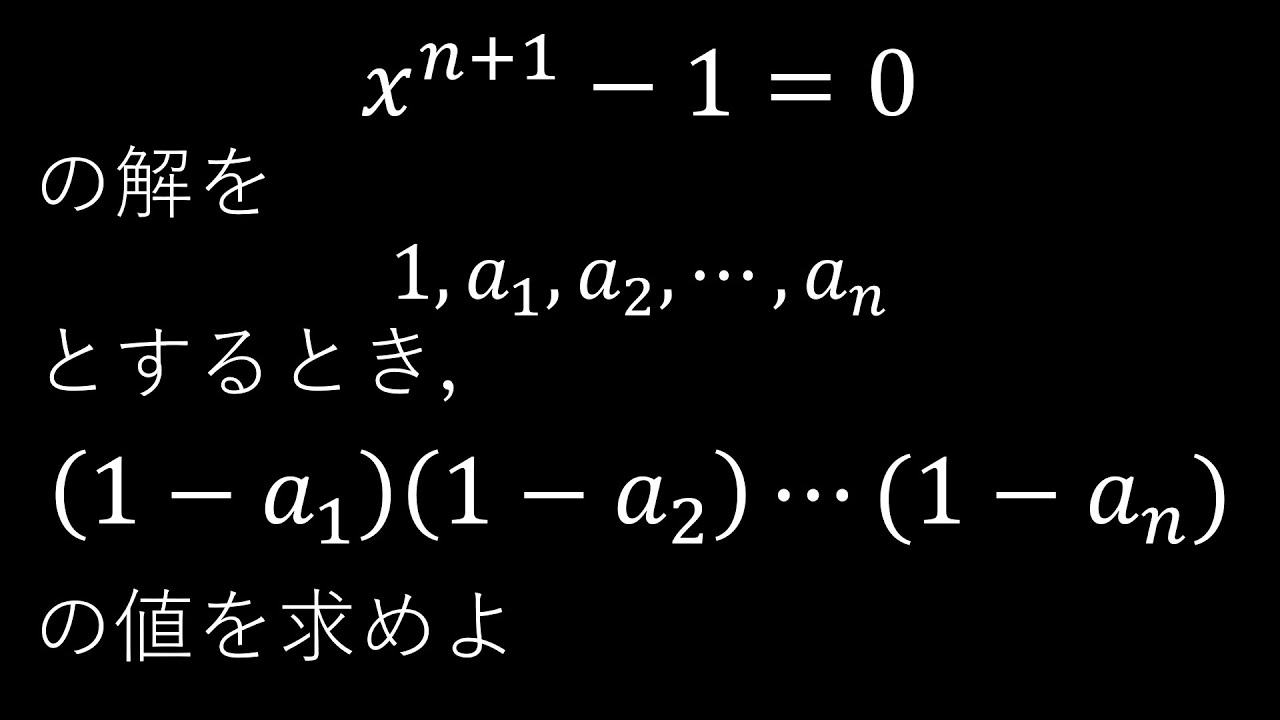
単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{1}$ $n$は自然数とする.
$x^{n+1}-1=0$の解を
$1,a_1,a_2,・・・,a_n$とするとき,
$(1-a_1)\times (1-a_2)\times ・・・ \times (1-a_n)$
の値を求めよ.
この動画を見る
$\boxed{1}$ $n$は自然数とする.
$x^{n+1}-1=0$の解を
$1,a_1,a_2,・・・,a_n$とするとき,
$(1-a_1)\times (1-a_2)\times ・・・ \times (1-a_n)$
の値を求めよ.
福田のわかった数学〜高校3年生理系028〜極限(28)関数の極限、三角関数の極限(8)

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
数学\textrm{III} 三角関数の極限(8)\\
\\
\lim_{x \to 0}(\frac{\sin2x}{2x}-\frac{\sin3x}{3x}) を求めよ。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
数学\textrm{III} 三角関数の極限(8)\\
\\
\lim_{x \to 0}(\frac{\sin2x}{2x}-\frac{\sin3x}{3x}) を求めよ。
\end{eqnarray}
福田のわかった数学〜高校3年生理系027〜極限(27)関数の極限、三角関数の極限(7)

単元:
#数Ⅱ#三角関数#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
数学\textrm{III} 三角関数の極限(7)\\
\\
\lim_{x \to 0}\frac{\sin(2\sin x)}{3x(1+2x)} を求めよ。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
数学\textrm{III} 三角関数の極限(7)\\
\\
\lim_{x \to 0}\frac{\sin(2\sin x)}{3x(1+2x)} を求めよ。
\end{eqnarray}
福田のわかった数学〜高校3年生理系026〜極限(26)関数の極限、三角関数の極限(6)

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
数学\textrm{III} 三角関数の極限(6)\\
\lim_{x \to \frac{\pi}{2}}\frac{1-\sin x}{(2x-\pi)^2} を求めよ。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
数学\textrm{III} 三角関数の極限(6)\\
\lim_{x \to \frac{\pi}{2}}\frac{1-\sin x}{(2x-\pi)^2} を求めよ。
\end{eqnarray}
15滋賀県教員採用試験(数学:4番 積分)

単元:
#積分とその応用#不定積分#定積分#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{4}$
$2\leqq n \gets IN$
$\log(n+1)\lt 1+\dfrac{1}{2}+・・・+\dfrac{1}{n}\lt 1+\log n$
を示せ.
この動画を見る
$\boxed{4}$
$2\leqq n \gets IN$
$\log(n+1)\lt 1+\dfrac{1}{2}+・・・+\dfrac{1}{n}\lt 1+\log n$
を示せ.
福田の数学〜早稲田大学2021年教育学部第1問(3)〜2曲線の相接

単元:
#大学入試過去問(数学)#微分とその応用#接線と法線・平均値の定理#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ (3)座標平面上の2つの曲線$y=ae^x$と$y=-x^2+2x$が共有点をもち、かつ、その
共有点において共通の接線をもつような正の定数$a$の値を求めよ。
2021早稲田大学教育学部過去問
この動画を見る
${\Large\boxed{1}}$ (3)座標平面上の2つの曲線$y=ae^x$と$y=-x^2+2x$が共有点をもち、かつ、その
共有点において共通の接線をもつような正の定数$a$の値を求めよ。
2021早稲田大学教育学部過去問
福田のわかった数学〜高校3年生理系025〜極限(25)関数の極限、三角関数の極限(5)

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 三角関数の極限(5)
$\lim_{x \to 0}\displaystyle \frac{\tan x°}{x}$ を求めよ。
この動画を見る
数学$\textrm{III}$ 三角関数の極限(5)
$\lim_{x \to 0}\displaystyle \frac{\tan x°}{x}$ を求めよ。
14京都府教員採用試験(数学:1-(6) 積分)

単元:
#積分とその応用#不定積分#定積分#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{2}$
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sin x\ \sin2x\ dx$
を求めよ.
この動画を見る
$\boxed{2}$
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sin x\ \sin2x\ dx$
を求めよ.
