 数Ⅲ
数Ⅲ
 数Ⅲ
数Ⅲ
福田の数学〜上智大学2024TEAP利用型理系第3問〜定積分で表された方程式

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
(1) $x \gt 0$ のとき、関数 $\displaystyle y = \frac{e^x}{x}$ の極値を求めて、そのグラフの概形をかけ。
(2) 次の等式を満たす正の定数 $a$ を求めよ。
\begin{eqnarray}
\int_a^{2a} \frac{e^x}{x} dx = \int_a^{2a} \frac{e^x}{x^2} dx
\end{eqnarray}
(3) 次の等式を満たす異なる正の整数 $m,n$ が存在しないことを証明せよ。
\begin{eqnarray}
\int_m^{n} \frac{e^x}{x} dx = \int_m^{n} \frac{e^x}{x^2} dx
\end{eqnarray}
この動画を見る
(1) $x \gt 0$ のとき、関数 $\displaystyle y = \frac{e^x}{x}$ の極値を求めて、そのグラフの概形をかけ。
(2) 次の等式を満たす正の定数 $a$ を求めよ。
\begin{eqnarray}
\int_a^{2a} \frac{e^x}{x} dx = \int_a^{2a} \frac{e^x}{x^2} dx
\end{eqnarray}
(3) 次の等式を満たす異なる正の整数 $m,n$ が存在しないことを証明せよ。
\begin{eqnarray}
\int_m^{n} \frac{e^x}{x} dx = \int_m^{n} \frac{e^x}{x^2} dx
\end{eqnarray}
福田の数学〜上智大学2024TEAP利用型理系第1問(3)〜対数不等式を満たす最小の整数

単元:
#大学入試過去問(数学)#指数関数と対数関数#対数関数#微分とその応用#色々な関数の導関数#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
(i) $\log_{10} 2=0.301$とする。このとき、$\log_{10} 1.28=0.\boxed{ウ}$である。
(ii)$n$は$2$以上の整数とする。$n^{100}<1.28^n$となる最小の$n$について、$2^a \leqq n < 2^{a+1}$となる整数$a$は$\boxed{エ}$
この動画を見る
(i) $\log_{10} 2=0.301$とする。このとき、$\log_{10} 1.28=0.\boxed{ウ}$である。
(ii)$n$は$2$以上の整数とする。$n^{100}<1.28^n$となる最小の$n$について、$2^a \leqq n < 2^{a+1}$となる整数$a$は$\boxed{エ}$
福田のおもしろ数学266〜直交する3つの円柱の共通部分の体積

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$x$軸、$y$軸、$z$軸を軸とする半径$1$の円柱$T_1,T_2,T_3$の共通部分の体積を求めて下さい。
この動画を見る
$x$軸、$y$軸、$z$軸を軸とする半径$1$の円柱$T_1,T_2,T_3$の共通部分の体積を求めて下さい。
福田のおもしろ数学259〜複雑な無理不等式の解

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle \frac{4x^2}{(1-\sqrt{2x+1})^2} \lt 2x+9$ を解け。
この動画を見る
$\displaystyle \frac{4x^2}{(1-\sqrt{2x+1})^2} \lt 2x+9$ を解け。
福田の数学〜青山学院大学2024理工学部第5問〜関数の増減と無限級数の収束発散の判定
単元:
#関数と極限#微分とその応用#積分とその応用#数列の極限#関数の変化(グラフ・最大最小・方程式・不等式)#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
以下の問いに答えよ。
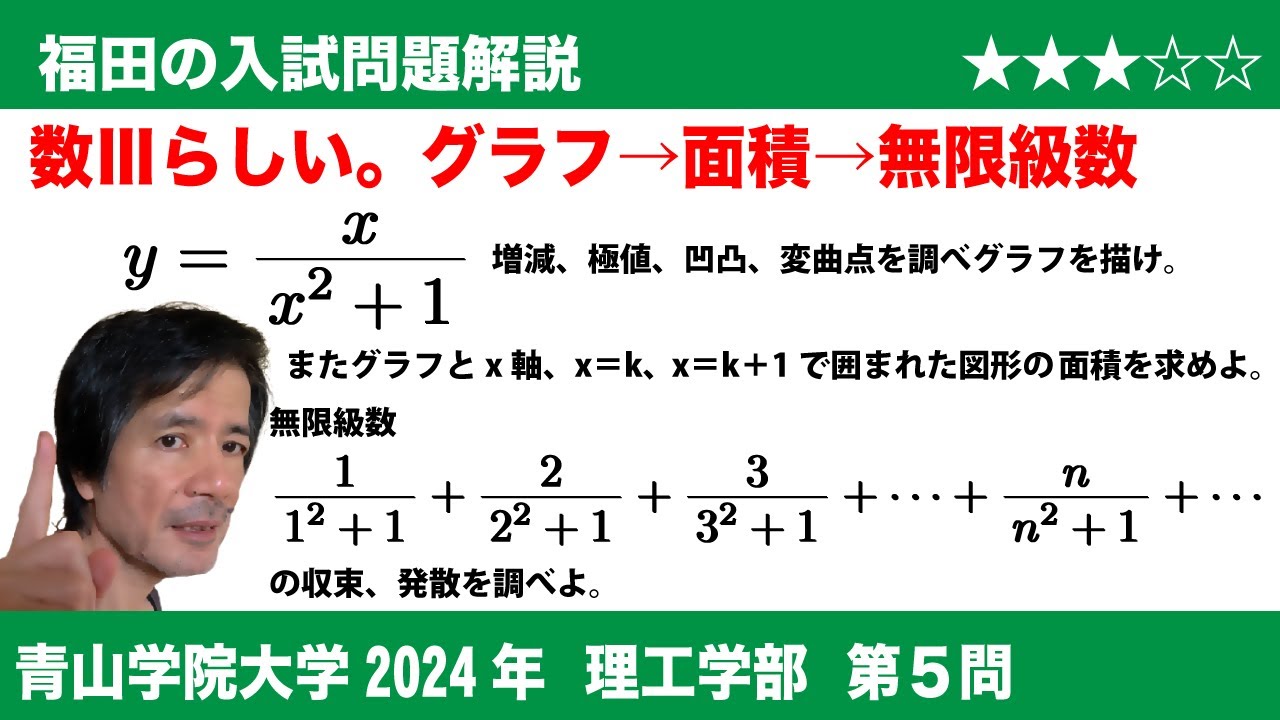
$(1)$ 関数 $\displaystyle{y=\frac{x}{x^2+1}}$ の増減、極値、グラフの凹凸および変曲点を調べて、そのグラフを描け。
$(2)$ $k$ を自然数とする。曲線 $\displaystyle{y=\frac{x}{x^2+1}}$ と $x$ 軸および2直線 $x=k$, $x=k+1$ で囲まれた図形の面積を $k$ を用いて表せ。
$(3)$ 無限級数
\begin{equation*}
\frac{1}{1^2+1}+\frac{2}{2^2+1}+\frac{3}{3^2+1}+\cdots+\frac{n}{n^2+1}+\cdots
\end{equation*}
の収束、発散を調べよ。
この動画を見る
以下の問いに答えよ。
$(1)$ 関数 $\displaystyle{y=\frac{x}{x^2+1}}$ の増減、極値、グラフの凹凸および変曲点を調べて、そのグラフを描け。
$(2)$ $k$ を自然数とする。曲線 $\displaystyle{y=\frac{x}{x^2+1}}$ と $x$ 軸および2直線 $x=k$, $x=k+1$ で囲まれた図形の面積を $k$ を用いて表せ。
$(3)$ 無限級数
\begin{equation*}
\frac{1}{1^2+1}+\frac{2}{2^2+1}+\frac{3}{3^2+1}+\cdots+\frac{n}{n^2+1}+\cdots
\end{equation*}
の収束、発散を調べよ。
福田のおもしろ数学255〜定積分の計算

福田の数学〜青山学院大学2024理工学部第2問〜法線と面積と回転体の体積

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
$f(x)=\tan{x}$とする。また、曲線
$\displaystyle C:y=f(x)(-\frac{\pi}{2}\lt x\lt \frac{\pi}{2})$
上の点$(\displaystyle \frac{\pi}{6},f(\frac{\pi}{6}))$における法線を$\ell$とする。
(1)法線$\ell$の方程式は$\displaystyle y=\frac{\fbox{アイ}}{\fbox{ウ}}x+\frac{\fbox{エ}}{\fbox{オ}}\pi+\frac{\sqrt{\fbox{カ}}}{\fbox{キ}}である。$
(2)曲線$C$と$x$軸および法線$\ell$で囲まれた図形の面積は
$\log{a}+b(a=\frac{\fbox{ク}\sqrt{\fbox{ケ}}}{\fbox{コ}},b=\frac{\fbox{サ}}{\fbox{シ}})$
この動画を見る
$f(x)=\tan{x}$とする。また、曲線
$\displaystyle C:y=f(x)(-\frac{\pi}{2}\lt x\lt \frac{\pi}{2})$
上の点$(\displaystyle \frac{\pi}{6},f(\frac{\pi}{6}))$における法線を$\ell$とする。
(1)法線$\ell$の方程式は$\displaystyle y=\frac{\fbox{アイ}}{\fbox{ウ}}x+\frac{\fbox{エ}}{\fbox{オ}}\pi+\frac{\sqrt{\fbox{カ}}}{\fbox{キ}}である。$
(2)曲線$C$と$x$軸および法線$\ell$で囲まれた図形の面積は
$\log{a}+b(a=\frac{\fbox{ク}\sqrt{\fbox{ケ}}}{\fbox{コ}},b=\frac{\fbox{サ}}{\fbox{シ}})$
福田のおもしろ数学254〜ルートx2乗+1の不定積分

単元:
#積分とその応用#不定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$
\{ \log(x+ \sqrt{x^2+1}) \}'= \frac{1}{ \sqrt{x^2+1}}
$
を使って
$
\int \sqrt{x^2+1}\ dx
$
を使って求めて下さい。
この動画を見る
$
\{ \log(x+ \sqrt{x^2+1}) \}'= \frac{1}{ \sqrt{x^2+1}}
$
を使って
$
\int \sqrt{x^2+1}\ dx
$
を使って求めて下さい。
福田のおもしろ数学253〜減衰曲線と定積分の極限

単元:
#積分とその応用#面積・体積・長さ・速度#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n \displaystyle \int_{(k-1)π}^{ kπ } |e^{-x}sinx| dx$を求めて下さい。
この動画を見る
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n \displaystyle \int_{(k-1)π}^{ kπ } |e^{-x}sinx| dx$を求めて下さい。
福田の数学〜明治大学2024理工学部第2問〜三角関数の増減と面積

単元:
#大学入試過去問(数学)#微分とその応用#積分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$f(x)=\sin{3x}-\sqrt3\cos{2x}$とし、座標平面上の曲線$y=f(x)$を$C$とする。
(1) 点$(0,f(0))$における曲線$C$の接線の方程式は$y=\boxed{あ}$である。
(2) $t$についての整式$g(t)$で、$f'(x)=g(\sin x)\cos x$が成り立つものを求めると、$g(t)=\boxed{い}$である。
(3) $x>0$の範囲で、$f'(x)=0$となる$x$の値を小さい順に$x_1,x_2,x_3,\cdots$とすると、$x_1=\boxed{う},x_2=\boxed{え},x_3=\boxed{お}$である。
(4) $0\leqq x\leqq \pi$の範囲での$f(x)$の最大値は$\boxed{か}$、最小値は$\boxed{き}$である。
(5) (4)で定めた$x_1$と$x_3$に対して、2点$(x_1,f(x_1)),(x_3,f(x_3))$を通る直線を$l$とする。このとき、$x_1\leqq x\leqq x_3$の範囲において直線$l$と曲線$C$で囲まれた部分の面積は$\boxed{く}$である。
この動画を見る
$f(x)=\sin{3x}-\sqrt3\cos{2x}$とし、座標平面上の曲線$y=f(x)$を$C$とする。
(1) 点$(0,f(0))$における曲線$C$の接線の方程式は$y=\boxed{あ}$である。
(2) $t$についての整式$g(t)$で、$f'(x)=g(\sin x)\cos x$が成り立つものを求めると、$g(t)=\boxed{い}$である。
(3) $x>0$の範囲で、$f'(x)=0$となる$x$の値を小さい順に$x_1,x_2,x_3,\cdots$とすると、$x_1=\boxed{う},x_2=\boxed{え},x_3=\boxed{お}$である。
(4) $0\leqq x\leqq \pi$の範囲での$f(x)$の最大値は$\boxed{か}$、最小値は$\boxed{き}$である。
(5) (4)で定めた$x_1$と$x_3$に対して、2点$(x_1,f(x_1)),(x_3,f(x_3))$を通る直線を$l$とする。このとき、$x_1\leqq x\leqq x_3$の範囲において直線$l$と曲線$C$で囲まれた部分の面積は$\boxed{く}$である。
福田の数学〜明治大学2024理工学部第1問(3)〜x軸まわりとy軸まわりの回転体の体積
単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
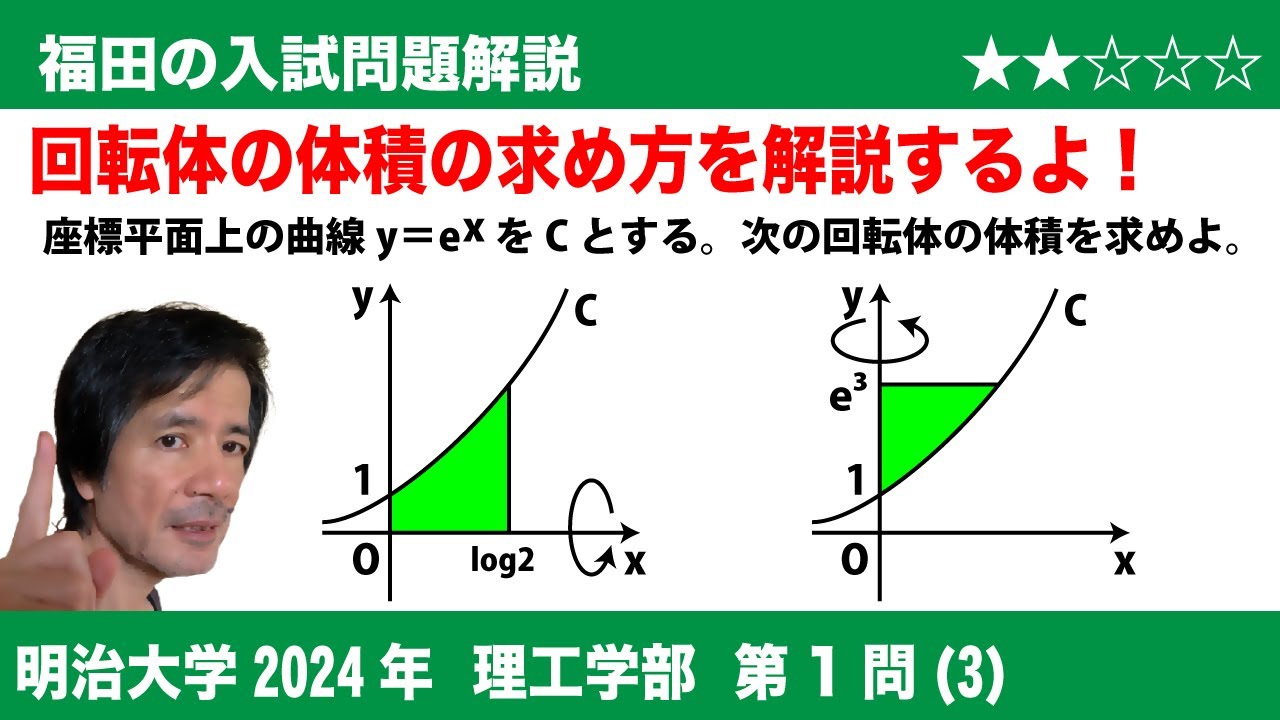
座標平面上の曲線 $y=e^x$ を $C$ とする。
(a) 曲線 $C$ と $x$ 軸および $2$ 直線 $x=0,x=\log 2$ で囲まれた部分を、 $x$ 軸のまわりに $1$ 回転してできる立体の体積は $\displaystyle \frac{\fbox{タ}}{\fbox{チ}}\pi$ である。
(b) 曲線 $C$ と $y$ 軸および直線 $y=e^3$ で囲まれた部分を、 $y$ 軸のまわりに $1$ 回転してできる立体の体積は $(\fbox{ツ}e^3-\fbox{テ})\pi$ である。
ただし、 $\log x$ は $x$ の自然対数を表し、 $e$ は自然対数の底である。
この動画を見る
座標平面上の曲線 $y=e^x$ を $C$ とする。
(a) 曲線 $C$ と $x$ 軸および $2$ 直線 $x=0,x=\log 2$ で囲まれた部分を、 $x$ 軸のまわりに $1$ 回転してできる立体の体積は $\displaystyle \frac{\fbox{タ}}{\fbox{チ}}\pi$ である。
(b) 曲線 $C$ と $y$ 軸および直線 $y=e^3$ で囲まれた部分を、 $y$ 軸のまわりに $1$ 回転してできる立体の体積は $(\fbox{ツ}e^3-\fbox{テ})\pi$ である。
ただし、 $\log x$ は $x$ の自然対数を表し、 $e$ は自然対数の底である。
福田のおもしろ数学249〜絶対値の付いた不等式が常に成り立つ条件

単元:
#微分とその応用#接線と法線・平均値の定理#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
任意の $x,y$ について $|\sin x - \sin y| \leqq k|x-y|$ が成り立つような定数 $k$ の最小値を求めよ。
この動画を見る
任意の $x,y$ について $|\sin x - \sin y| \leqq k|x-y|$ が成り立つような定数 $k$ の最小値を求めよ。
福田のおもしろ数学247〜複雑な無理方程式の解を1つ見つける

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$
5(\sqrt{1-x}+\sqrt{1+x})=6x+8\sqrt{1-x^2}
$の解を1つ求めて下さい。
この動画を見る
$
5(\sqrt{1-x}+\sqrt{1+x})=6x+8\sqrt{1-x^2}
$の解を1つ求めて下さい。
福田のおもしろ数学246〜分数式の極限と区分求積

単元:
#関数と極限#積分とその応用#関数の極限#定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } \frac{(1+2+…+n)^5}{(1^4+2^4+…+n^4)^2}$
を求めて下さい。
この動画を見る
$\displaystyle \lim_{ n \to \infty } \frac{(1+2+…+n)^5}{(1^4+2^4+…+n^4)^2}$
を求めて下さい。
難易度バリ高の極限 by 餃子n人前さん ※作成者の解答を参考に動画を作成しています。

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a_1=1,$ $a_{n+1}+a_n=\displaystyle \frac{1}{n}$のとき、
$\displaystyle \lim_{ n \to \infty } |na_n|$を求めよ
この動画を見る
$a_1=1,$ $a_{n+1}+a_n=\displaystyle \frac{1}{n}$のとき、
$\displaystyle \lim_{ n \to \infty } |na_n|$を求めよ
#岩手大学2024#定積分_34
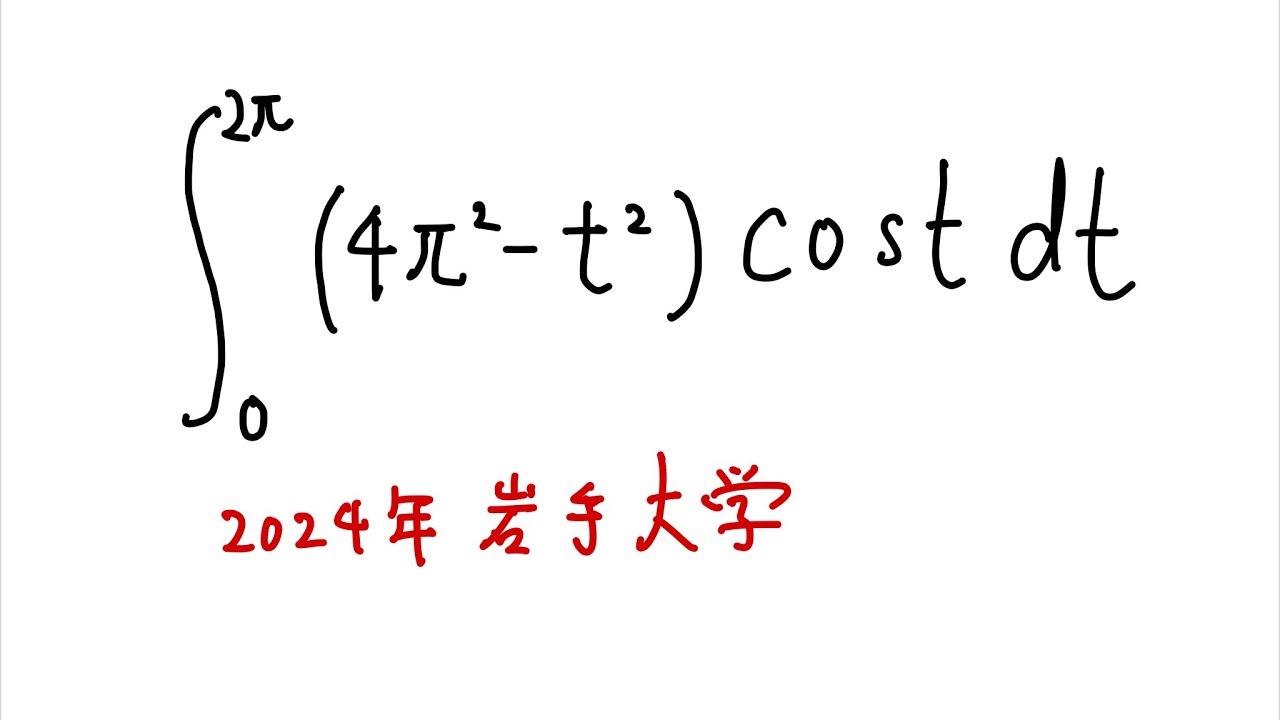
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#岩手大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{2\pi} (4\pi^2-t^2)\cos t dt$
出典:2024年岩手大学
この動画を見る
$\displaystyle \int_{0}^{2\pi} (4\pi^2-t^2)\cos t dt$
出典:2024年岩手大学
#福島大学2023#定積分_33

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\sqrt{ 3 }}^{ 1 } \sqrt{ 4-x^2 } dx$
出典:2023年福島大学
この動画を見る
$\displaystyle \int_{-\sqrt{ 3 }}^{ 1 } \sqrt{ 4-x^2 } dx$
出典:2023年福島大学
#南山大学2021#定積分_32
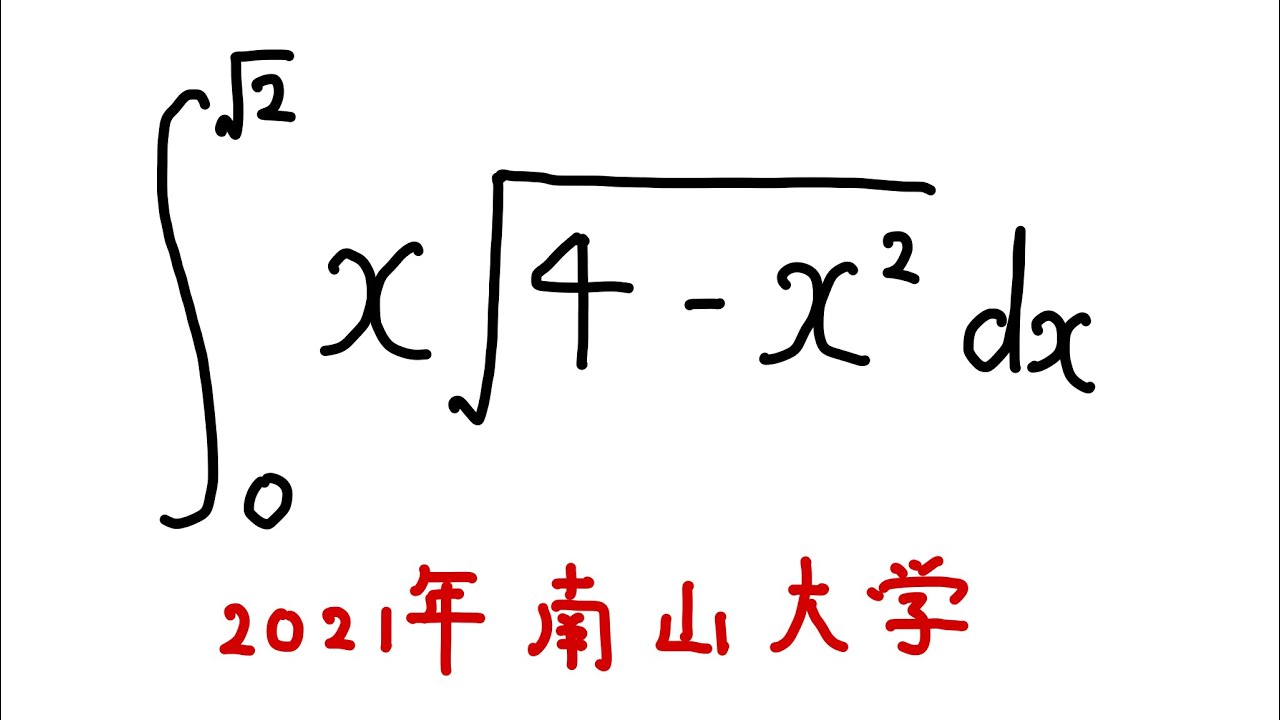
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#南山大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\sqrt{ 2 }} x\sqrt{ 4-x^2 } dx$
出典:2021年南山大学
この動画を見る
$\displaystyle \int_{0}^{\sqrt{ 2 }} x\sqrt{ 4-x^2 } dx$
出典:2021年南山大学
#福島大学2024#定積分_31#元高校教員
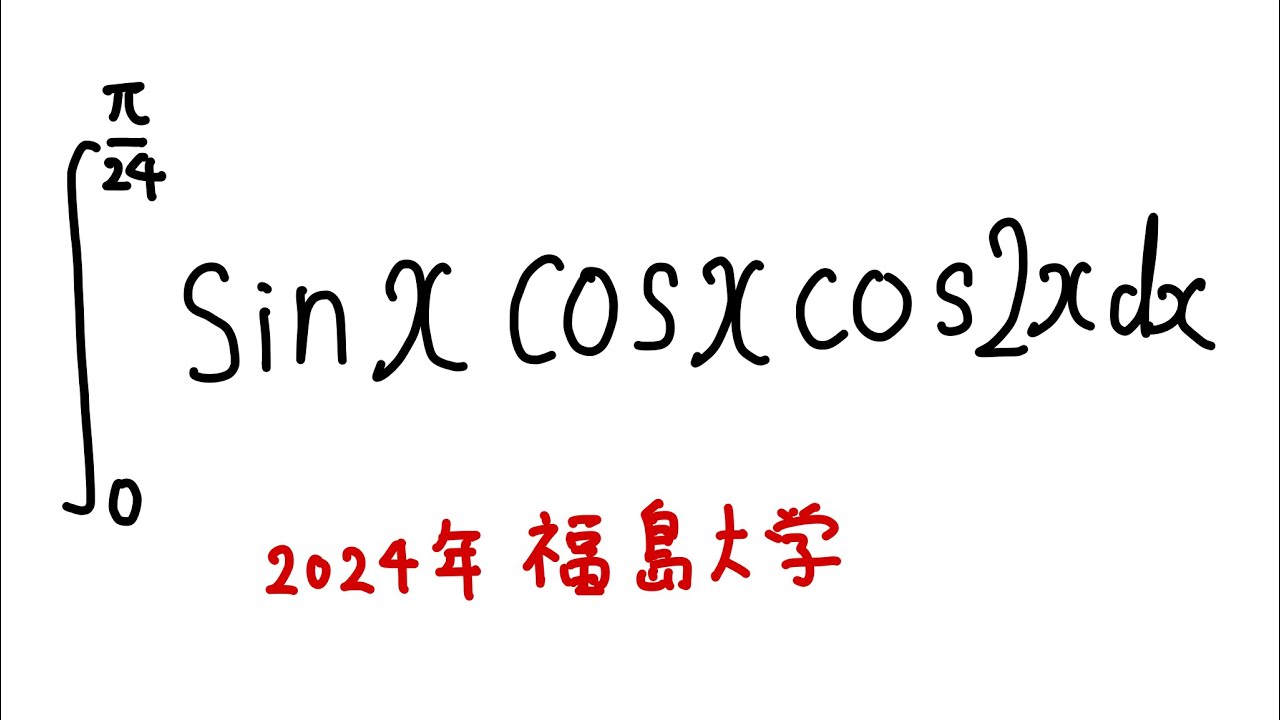
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{24}} \sin x\cos x\cos 2x dx$
出典:2024年福島大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{24}} \sin x\cos x\cos 2x dx$
出典:2024年福島大学
大学入試問題#922「できればスッと解きたい」

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{3}^{4} \displaystyle \frac{4x^2-9x+6}{(x-1)(x-2)^2} dx$
出典:2023年福島大学
この動画を見る
$\displaystyle \int_{3}^{4} \displaystyle \frac{4x^2-9x+6}{(x-1)(x-2)^2} dx$
出典:2023年福島大学
#青山学院大学2023#定積分_30#元高校教員

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#青山学院大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}} \cos3x\cos\displaystyle \frac{x}{3} dx$
出典:2023年 青山学院大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} \cos3x\cos\displaystyle \frac{x}{3} dx$
出典:2023年 青山学院大学
#広島市立大学2024#不定積分_29#元高校教員

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#広島市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{e^x}{e^{2x}-4} dx$
出典:2024年広島市立大学
この動画を見る
$\displaystyle \int \displaystyle \frac{e^x}{e^{2x}-4} dx$
出典:2024年広島市立大学
大学入試問題#921「癖がない綺麗な神問題」

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a \gt 1$
$I(a)=\displaystyle \int_{0}^{ \pi }\displaystyle \frac{a\sin\theta}{(a^2-2a \cos\theta+1)^{\frac{3}{2}}}d\theta$
1.$I(a)$を求めよ。
2.$\displaystyle \sum_{n=2}^{\infty} I(n)$の値を求めよ。
出典:1997年千葉大学
この動画を見る
$a \gt 1$
$I(a)=\displaystyle \int_{0}^{ \pi }\displaystyle \frac{a\sin\theta}{(a^2-2a \cos\theta+1)^{\frac{3}{2}}}d\theta$
1.$I(a)$を求めよ。
2.$\displaystyle \sum_{n=2}^{\infty} I(n)$の値を求めよ。
出典:1997年千葉大学
#京都大学1965#微分_28#元高校教員

単元:
#大学入試過去問(数学)#微分とその応用#微分法#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$f(x)=\displaystyle \frac{1}{x^3}$において
$f'(1)$を定義に従って求めよ。
出典:1965年京都大学
この動画を見る
$f(x)=\displaystyle \frac{1}{x^3}$において
$f'(1)$を定義に従って求めよ。
出典:1965年京都大学
#高知工科大学2024#定積分_27#元高校教員
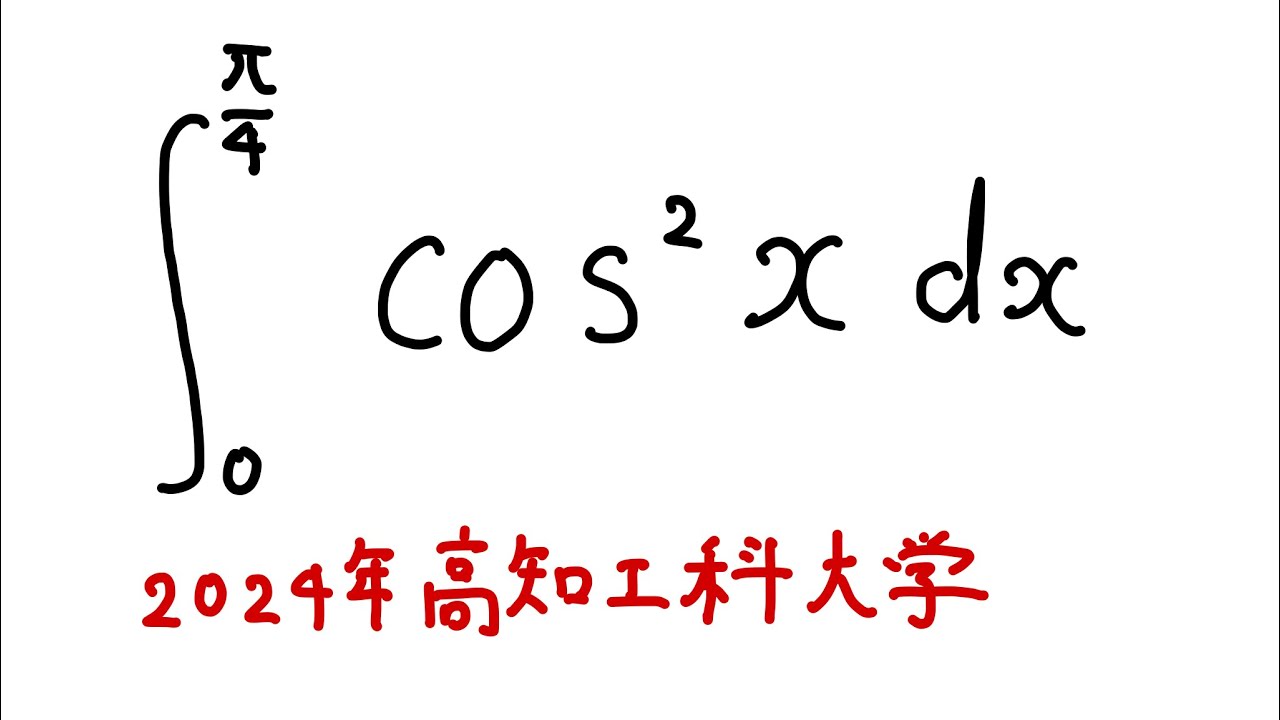
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#高知工科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{4}} \cos^2x dx$
出典:2024年高知工科大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}} \cos^2x dx$
出典:2024年高知工科大学
#高専#不定積分_19#元高専教員
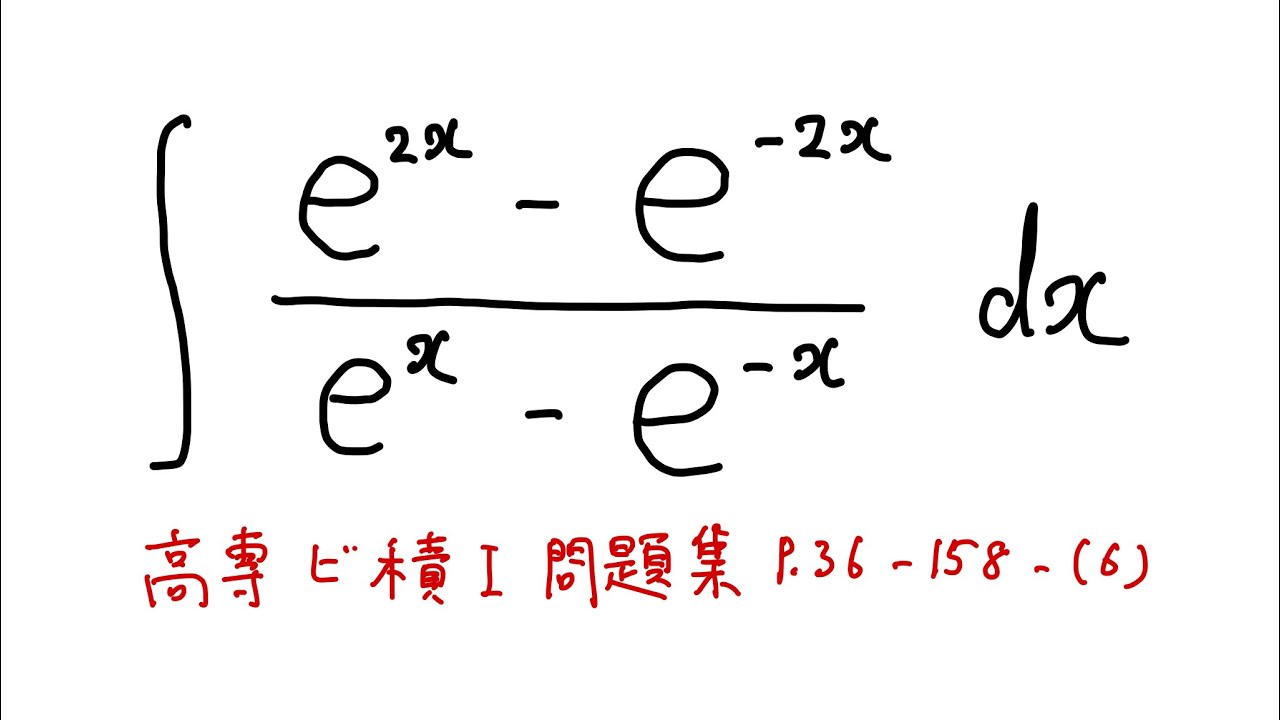
単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#高専(高等専門学校)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{e^{2x}-e^{-2x}}{e^x-e^{-x}} dx$
出典:国立高等専門学校機構
この動画を見る
$\displaystyle \int \displaystyle \frac{e^{2x}-e^{-2x}}{e^x-e^{-x}} dx$
出典:国立高等専門学校機構
#青山学院大学2023#定積分_26#元高校教員
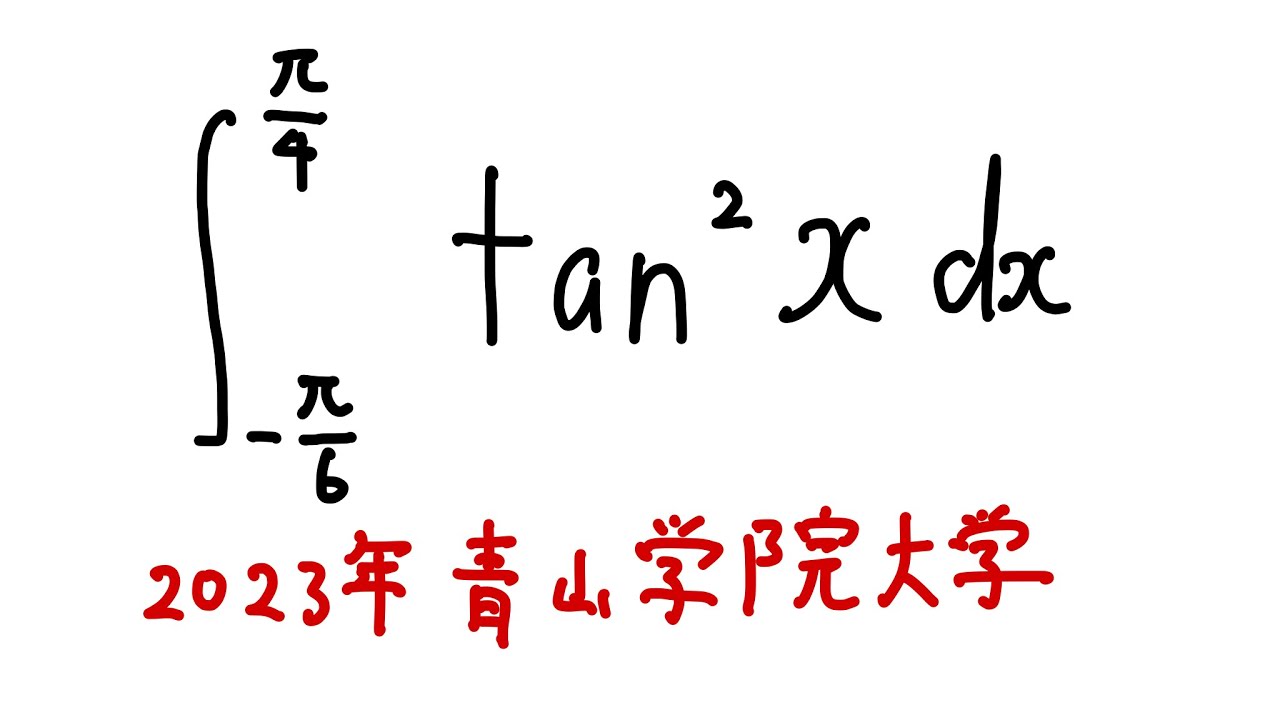
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#青山学院大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\frac{\pi}{6}}^{\frac{\pi}{4}} \tan^2x dx$
出典:2023年青山学院大学
この動画を見る
$\displaystyle \int_{-\frac{\pi}{6}}^{\frac{\pi}{4}} \tan^2x dx$
出典:2023年青山学院大学
福田のおもしろ数学241〜e^πとπ^eの大小

#高専#不定積分_18#元高専教員
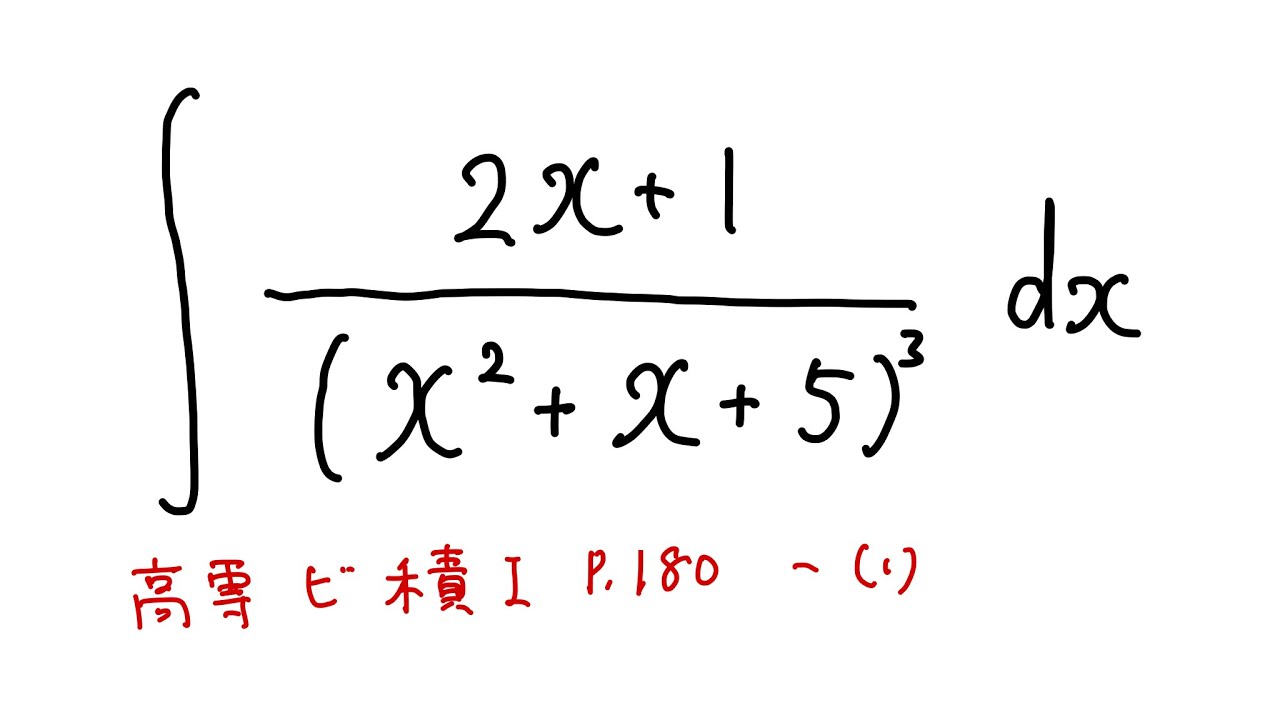
単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#高専(高等専門学校)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int\displaystyle \frac{2x+1}{(x^2+x+5)^3} dx$
出典:国立高等専門学校機構
この動画を見る
$\displaystyle \int\displaystyle \frac{2x+1}{(x^2+x+5)^3} dx$
出典:国立高等専門学校機構
大学入試問題#917「さすがに落とせん」

単元:
#大学入試過去問(数学)#微分とその応用#微分法#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\sqrt{ 1+x+x^2 }$
$x=1$における微分係数を定義に従って求めよ
出典:1965年京都大学
この動画を見る
$\sqrt{ 1+x+x^2 }$
$x=1$における微分係数を定義に従って求めよ
出典:1965年京都大学
