 複素数平面
複素数平面
 複素数平面
複素数平面
自治医科大学

単元:
#大学入試過去問(数学)#複素数平面#関数と極限#複素数平面#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数C#数Ⅲ#自治医科大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)
$\alpha=\cos \displaystyle \frac{2}{7}\pi+i \sin \displaystyle \frac{2}{7}\pi$
$\displaystyle \frac{1}{1-\alpha}+\displaystyle \frac{1}{1-\alpha^2}+\displaystyle \frac{1}{1-\alpha^3}+\displaystyle \frac{1}{1-\alpha^4}+$
$\displaystyle \frac{1}{1-\alpha^5}+\displaystyle \frac{1}{1-\alpha^6}$
(2)
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{3\sin 4x}{x+\sin x}$
出典:2017年自治医科大学 過去問
この動画を見る
(1)
$\alpha=\cos \displaystyle \frac{2}{7}\pi+i \sin \displaystyle \frac{2}{7}\pi$
$\displaystyle \frac{1}{1-\alpha}+\displaystyle \frac{1}{1-\alpha^2}+\displaystyle \frac{1}{1-\alpha^3}+\displaystyle \frac{1}{1-\alpha^4}+$
$\displaystyle \frac{1}{1-\alpha^5}+\displaystyle \frac{1}{1-\alpha^6}$
(2)
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{3\sin 4x}{x+\sin x}$
出典:2017年自治医科大学 過去問
名古屋大 3次式の係数決定

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=x^3+ax^2+bx+c$
$a,b,c$は整数
$f(\sqrt{ 2 })=0$
$w=\displaystyle \frac{-1+\sqrt{ 3 }i}{2}$
$f(w)$は実数
$a,b,c$の値を求めよ
出典:2006年名古屋大学 過去問
この動画を見る
$f(x)=x^3+ax^2+bx+c$
$a,b,c$は整数
$f(\sqrt{ 2 })=0$
$w=\displaystyle \frac{-1+\sqrt{ 3 }i}{2}$
$f(w)$は実数
$a,b,c$の値を求めよ
出典:2006年名古屋大学 過去問
横浜市立大(医)
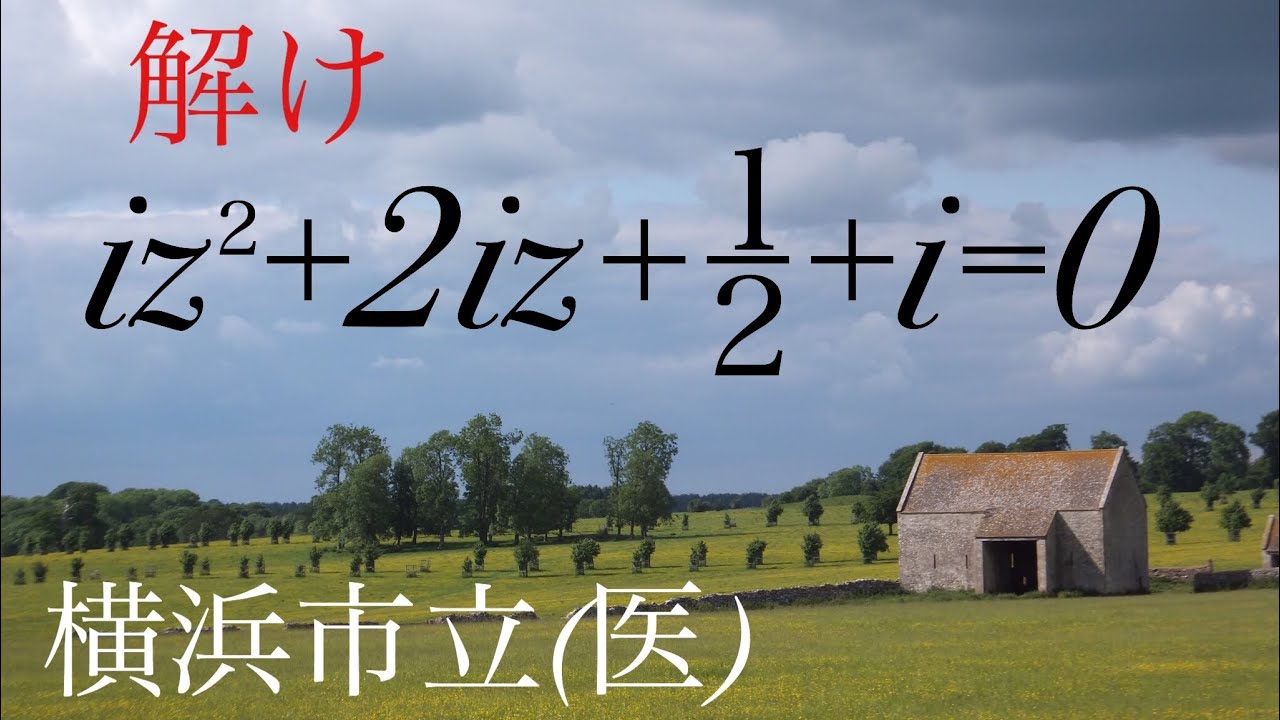
単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$iz^2+2iz+\displaystyle \frac{1}{2}+i=0$を解け
出典:2000年横浜市立大学 過去問
この動画を見る
$iz^2+2iz+\displaystyle \frac{1}{2}+i=0$を解け
出典:2000年横浜市立大学 過去問
京都大 複素数

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\displaystyle \frac{2Z+2i}{Z+2i}=\bar{ Z }$を満たす複素数$Z$をすべて求めよ
出典:2005年京都大学 過去問
この動画を見る
$\displaystyle \frac{2Z+2i}{Z+2i}=\bar{ Z }$を満たす複素数$Z$をすべて求めよ
出典:2005年京都大学 過去問
九州大 3次方程式:2次方程式 有理数解

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$Z=\cos20^{ \circ }+i \sin 20^{ \circ }$
$\alpha = Z+\bar{ Z }$←共役な複素数
(1)
$\alpha$が解となる整数係数3次方程式は?
(2)
(1)の3次方程式は、3つの実数解をもち、そのすべては有理数でないことを示せ
(3)
有理数係数の2次方程式で$\alpha$を解に持つものはないことを示せ
出典:2000年九州大学 過去問
この動画を見る
$Z=\cos20^{ \circ }+i \sin 20^{ \circ }$
$\alpha = Z+\bar{ Z }$←共役な複素数
(1)
$\alpha$が解となる整数係数3次方程式は?
(2)
(1)の3次方程式は、3つの実数解をもち、そのすべては有理数でないことを示せ
(3)
有理数係数の2次方程式で$\alpha$を解に持つものはないことを示せ
出典:2000年九州大学 過去問
千葉大 整式
単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
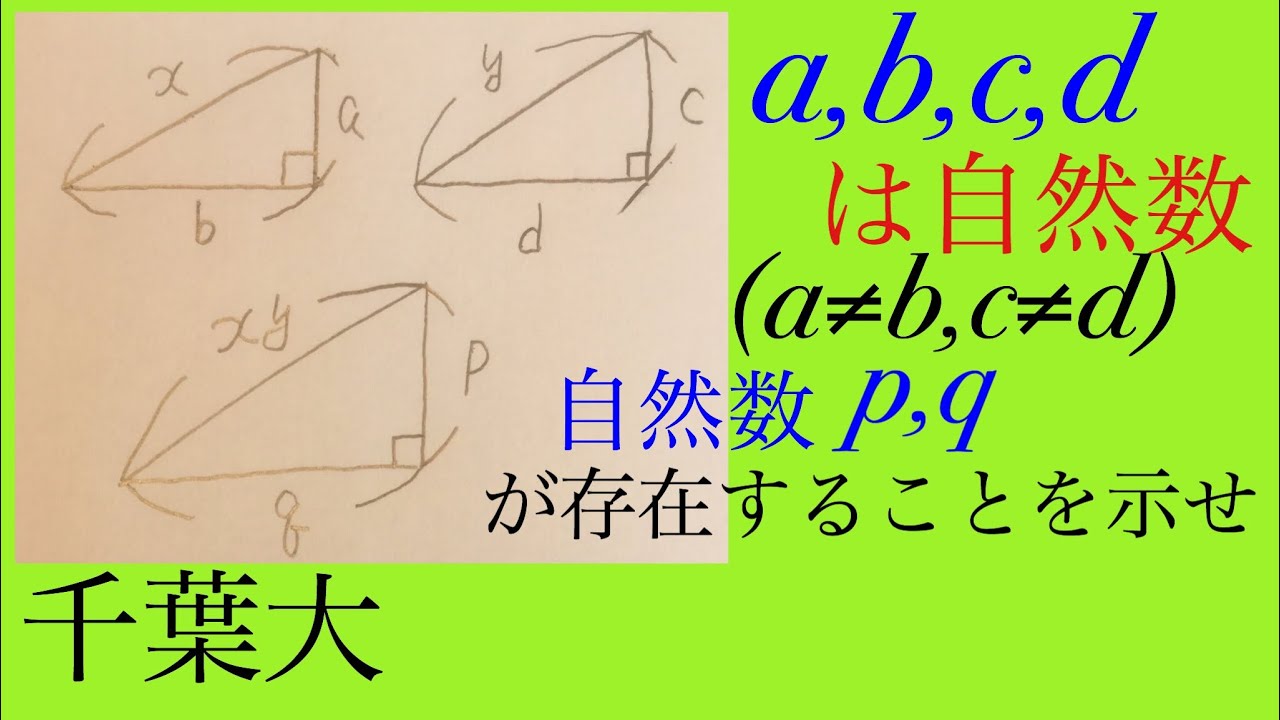
$a,b,c,d$は自然数
$a \neq b,c \neq d$
自然数$p,q$が存在することを示せ
出典:2004年千葉大学 過去問
この動画を見る
$a,b,c,d$は自然数
$a \neq b,c \neq d$
自然数$p,q$が存在することを示せ
出典:2004年千葉大学 過去問
早稲田大学 数列、複素数

単元:
#大学入試過去問(数学)#複素数平面#数列#漸化式#複素数平面#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$Z=1+2\sqrt{ 6 }i$
$Z^n=a_{n}+b_{n}i$
(1)
$a_{n}^2+b^2_{n}=5^{2n}$を示せ
(2)
$a_{n+2}=Pa_{n+1}+qa_{n}$ $P,q$の値
(3)
$a_{n}$は5の倍数でないことを示せ
(4)
$Z^n$は実数でないことを示せ
出典:2013年早稲田大学 過去問
この動画を見る
$Z=1+2\sqrt{ 6 }i$
$Z^n=a_{n}+b_{n}i$
(1)
$a_{n}^2+b^2_{n}=5^{2n}$を示せ
(2)
$a_{n+2}=Pa_{n+1}+qa_{n}$ $P,q$の値
(3)
$a_{n}$は5の倍数でないことを示せ
(4)
$Z^n$は実数でないことを示せ
出典:2013年早稲田大学 過去問
東京医科歯科大 複素数の入った2次方程式

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^2+dx+1+2i=0$が実数解をもつような複素数$\alpha$の絶対値の最小値を求めよ
出典:東京医科歯科大学 過去問
この動画を見る
$x^2+dx+1+2i=0$が実数解をもつような複素数$\alpha$の絶対値の最小値を求めよ
出典:東京医科歯科大学 過去問
三重大 複素数 Mathematics Japanese university entrance exam

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#三重大学#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^2-x+1=0$の2つの解を$\alpha, \beta$とする。
(1)
$\displaystyle \frac{1}{\alpha}+\displaystyle \frac{1}{\beta}$の値
(2)
$\alpha^{27},\beta^{27}$の値
(3)
$\alpha^n+\beta^n$の値
出典:三重大学 過去問
この動画を見る
$x^2-x+1=0$の2つの解を$\alpha, \beta$とする。
(1)
$\displaystyle \frac{1}{\alpha}+\displaystyle \frac{1}{\beta}$の値
(2)
$\alpha^{27},\beta^{27}$の値
(3)
$\alpha^n+\beta^n$の値
出典:三重大学 過去問
弘前大 3倍角 5倍角 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#大学入試過去問(数学)#複素数平面#三角関数#加法定理とその応用#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#弘前大学#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)
$\sin 3x$を$\sin x$で表せ
(2)
$\sin x + \cos x=4\sin x \cos ^2x$を満たす$x$を求めよ
出典:1986年弘前大学 過去問
この動画を見る
(1)
$\sin 3x$を$\sin x$で表せ
(2)
$\sin x + \cos x=4\sin x \cos ^2x$を満たす$x$を求めよ
出典:1986年弘前大学 過去問
これから数Ⅲを学ぶ人に贈る。複素数って何だよ?iって何?

甲南大 複素数 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数平面#複素数#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C#甲南大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$Z=\displaystyle \frac{\sqrt{ 3 }+i}{\sqrt{ 3 }-i}$
$Z+Z^2+Z^3+…+Z^{100}$
出典:2002年甲南大学 過去問
この動画を見る
$Z=\displaystyle \frac{\sqrt{ 3 }+i}{\sqrt{ 3 }-i}$
$Z+Z^2+Z^3+…+Z^{100}$
出典:2002年甲南大学 過去問
学習院大 複素数 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数平面#複素数#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C#学習院大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\displaystyle \frac{Z-1-3i}{Z-2}$が純虚数であるような複素数$Z$について
$\vert Z \vert$の最大・最小を求めよ。
出典:2003年学習院大学 過去問
この動画を見る
$\displaystyle \frac{Z-1-3i}{Z-2}$が純虚数であるような複素数$Z$について
$\vert Z \vert$の最大・最小を求めよ。
出典:2003年学習院大学 過去問
日本女子大 複素数 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数平面#複素数#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C#日本女子大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a=\displaystyle \frac{1+i}{\sqrt{ 3 }+i}$
$a^n$が正の実数となるような最小の自然数$n$
出典:日本女子大学 過去問
この動画を見る
$a=\displaystyle \frac{1+i}{\sqrt{ 3 }+i}$
$a^n$が正の実数となるような最小の自然数$n$
出典:日本女子大学 過去問
順天堂・御茶ノ水女子 複素数 高校数学 Mathematics Japanese university entrance exam

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C#順天堂大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
順天堂大学過去問題
1⃣
$α^4+α^3+α^2+α+1=0$
$α^6(α^7+1)(α+1)$の値
2⃣
$\sqrt3 + i +z$の絶対値を最大にする複素数Z
ただし|Z|=1
この動画を見る
順天堂大学過去問題
1⃣
$α^4+α^3+α^2+α+1=0$
$α^6(α^7+1)(α+1)$の値
2⃣
$\sqrt3 + i +z$の絶対値を最大にする複素数Z
ただし|Z|=1
学習院 複素数 絶対値の最大最小 Mathematics Japanese university entrance exam

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
学習院大学過去問題
複素数Z $(Z \neq 0)$
$ω=Z+\frac{1}{Z}+5$
|Z|=2
|ω|の最大値と最小値
この動画を見る
学習院大学過去問題
複素数Z $(Z \neq 0)$
$ω=Z+\frac{1}{Z}+5$
|Z|=2
|ω|の最大値と最小値
同志社 整式が割り切れる条件 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#複素数と方程式#複素数平面#剰余の定理・因数定理・組み立て除法と高次方程式#複素数平面#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
同志社大学過去問題
整式$x^{2n}+(x+1)^{2n}+1$が$x^2+x+1$で割り切れる自然数nの条件
この動画を見る
同志社大学過去問題
整式$x^{2n}+(x+1)^{2n}+1$が$x^2+x+1$で割り切れる自然数nの条件
長崎大 3乗根 Mathematics Japanese university entrance exam

単元:
#数A#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数平面#整数の性質#複素数#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#長崎大学#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
長崎大学過去問題
(1)$x^3=1$を解け
(2)$α=m+\sqrt7ni$とすると、$α^3=225+2\sqrt7i$が成り立つ。整数m,nを求めよ。
(3)$β^3=225+2\sqrt7i$を満たす複素数βをすべて求めよ。
この動画を見る
長崎大学過去問題
(1)$x^3=1$を解け
(2)$α=m+\sqrt7ni$とすると、$α^3=225+2\sqrt7i$が成り立つ。整数m,nを求めよ。
(3)$β^3=225+2\sqrt7i$を満たす複素数βをすべて求めよ。
横浜市大 複素数 cos36°,cos108° 高校数学 Mathematics Japanese university entrance exam

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#数学(高校生)#数C#横浜市立大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
横浜市立大学過去問題
(1)$x^2-x-1=0$解け
(2)複素数Z$(\neq 0)$,$\quad x=Z+\frac{1}{Z}$として、このxを(1)の方程式に代入して、すべての解を求めよ。
(3)$cos\frac{\pi}{5}$と$cos\frac{3\pi}{5}$の値
この動画を見る
横浜市立大学過去問題
(1)$x^2-x-1=0$解け
(2)複素数Z$(\neq 0)$,$\quad x=Z+\frac{1}{Z}$として、このxを(1)の方程式に代入して、すべての解を求めよ。
(3)$cos\frac{\pi}{5}$と$cos\frac{3\pi}{5}$の値
名古屋大 5次方程式 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数平面#剰余の定理・因数定理・組み立て除法と高次方程式#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
名古屋大学過去問題
次の方程式のすべての解を求めよ
$Z^5+2Z^4+4Z^3+8Z^2+16Z+32=0$
この動画を見る
名古屋大学過去問題
次の方程式のすべての解を求めよ
$Z^5+2Z^4+4Z^3+8Z^2+16Z+32=0$
岡山県立大 複素数 高校数学 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数平面#複素数#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C#岡山県立大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
岡山県立大学過去問題
$ω=\frac{-1+\sqrt3i}{2}$ n自然数
(1)$ω^{2005}$の値
(2)$ω^{n+1}+(ω+1)^{2n-1}=0$示せ
(3)整式$x^{n+1}+(x+1)^{2n-1}$は、$x^2+x+1$で割り切れる。示せ。
この動画を見る
岡山県立大学過去問題
$ω=\frac{-1+\sqrt3i}{2}$ n自然数
(1)$ω^{2005}$の値
(2)$ω^{n+1}+(ω+1)^{2n-1}=0$示せ
(3)整式$x^{n+1}+(x+1)^{2n-1}$は、$x^2+x+1$で割り切れる。示せ。
近畿大 茨城大 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数平面#複素数#剰余の定理・因数定理・組み立て除法と高次方程式#複素数平面#学校別大学入試過去問解説(数学)#近畿大学#数学(高校生)#数C#茨城大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
近畿大学過去問題
$x^4-Px^2+P^2-P-2=0$が相異4実根をもつPの範囲
茨城大学過去問題
$x^3=i$を解け
この動画を見る
近畿大学過去問題
$x^4-Px^2+P^2-P-2=0$が相異4実根をもつPの範囲
茨城大学過去問題
$x^3=i$を解け
島根大 愛知工大 整数・複素数 高校数学 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#複素数平面#恒等式・等式・不等式の証明#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#島根大学#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
島根大学過去問題
a,b,c実数
$a+b+c=3$
$ab+bc+ca \leqq 3$を示せ。
愛知工業大学過去問題
$Z=1-i$
$Z^7+Z^6+Z^5+Z^4+Z^3+Z^2+Z+1$の値
この動画を見る
島根大学過去問題
a,b,c実数
$a+b+c=3$
$ab+bc+ca \leqq 3$を示せ。
愛知工業大学過去問題
$Z=1-i$
$Z^7+Z^6+Z^5+Z^4+Z^3+Z^2+Z+1$の値
群馬大 複素数 Mathematics Japanese university entrance exam

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#群馬大学#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
群馬大学過去問題
$Z=\frac{\sqrt3-1}{2}+\frac{\sqrt3+1}{2}i$
(1)$\frac{Z}{1+i}$をa+biの形で(a,b実数)
(2)Zを極形式で表せ
(3)$Z^{12}$を計算せよ
この動画を見る
群馬大学過去問題
$Z=\frac{\sqrt3-1}{2}+\frac{\sqrt3+1}{2}i$
(1)$\frac{Z}{1+i}$をa+biの形で(a,b実数)
(2)Zを極形式で表せ
(3)$Z^{12}$を計算せよ
秋田大 慶応大 3次方程式 Σ 高校数学 Mathematics Japanese university entrance exam

単元:
#大学入試過去問(数学)#複素数平面#数列#数列とその和(等差・等比・階差・Σ)#複素数平面#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#秋田大学#数B#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
秋田大学過去問題
$2x^3-3x^2+ax-1=0$の1つの解は$x=\frac{1}{2}$,他の解をα,βとしたとき、$α^{30}+β^{30}$の値
慶応義塾大学過去問題
$\displaystyle\sum_{k=1}^nk・2^{k+2}$の値をnで表せ
この動画を見る
秋田大学過去問題
$2x^3-3x^2+ax-1=0$の1つの解は$x=\frac{1}{2}$,他の解をα,βとしたとき、$α^{30}+β^{30}$の値
慶応義塾大学過去問題
$\displaystyle\sum_{k=1}^nk・2^{k+2}$の値をnで表せ
鹿児島(医)慶應(理) 高校数学 Japanese university entrance exam questions

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#複素数平面#集合と命題(集合・命題と条件・背理法)#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#鹿児島大学#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
鹿児島大学過去問題・類慶応義塾大学
二つの整数の平方の和で表される数
全体からなる集合をA
・x,yが集合Aの要素であるとき、積xyも集合Aの要素であることを証明せよ
・5および$5^5$は集合Aの要素であることを示せ
この動画を見る
鹿児島大学過去問題・類慶応義塾大学
二つの整数の平方の和で表される数
全体からなる集合をA
・x,yが集合Aの要素であるとき、積xyも集合Aの要素であることを証明せよ
・5および$5^5$は集合Aの要素であることを示せ
東邦(医)正五角形の外接円と内接円の半径の比 高校数学 Japanese university entrance exam questions

単元:
#複素数平面#複素数平面#図形への応用#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
東邦大学過去問題
正五角形の外接円、内接円の半径をそれぞれR,rとする。
$\frac{r}{R}$の値を求めよ。
この動画を見る
東邦大学過去問題
正五角形の外接円、内接円の半径をそれぞれR,rとする。
$\frac{r}{R}$の値を求めよ。
和歌山大 ド・モアブルの定理 Japanese university entrance exam questions
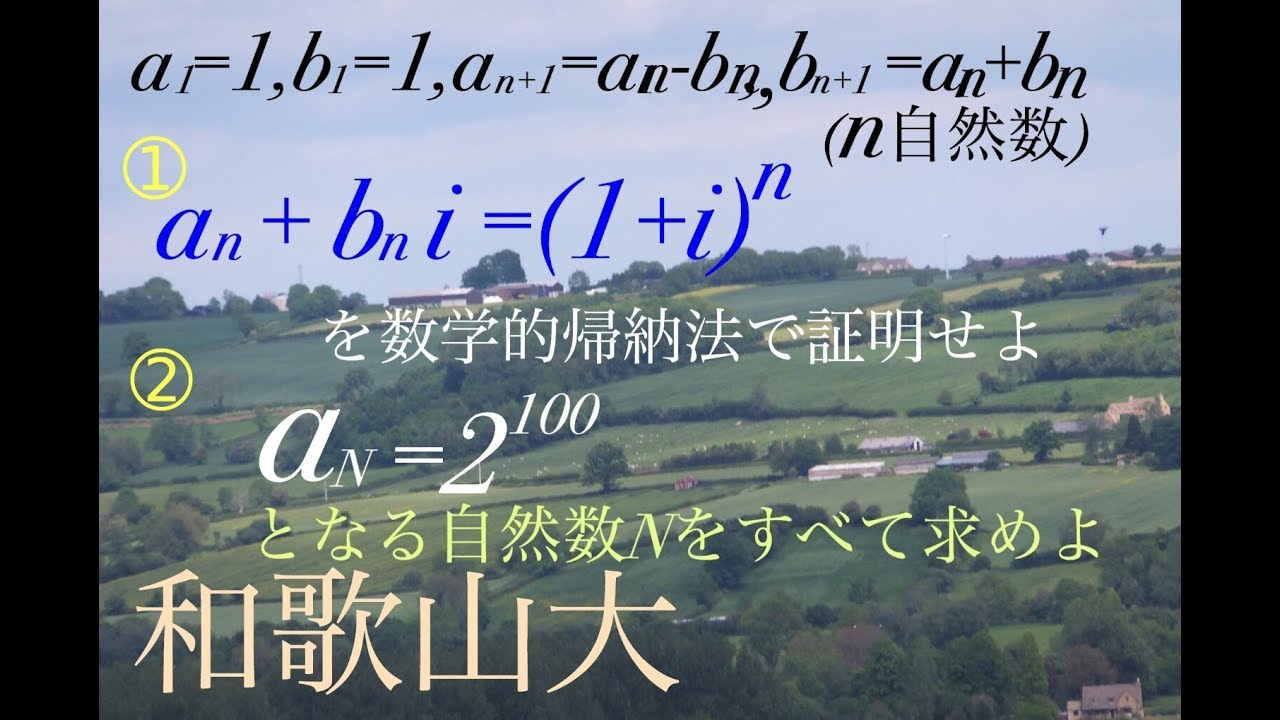
単元:
#大学入試過去問(数学)#複素数平面#数列#数学的帰納法#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#和歌山大学#数B#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
和歌山大学過去問題
$a_1=b_1=1$
$a_{n+1}=a_n-b_n$
$b_{n+1}=a_n+b_n$
(1)$a_n+b_ni= (1+i)^n$を数学的帰納法で証明せよ。
(2)$a_N=2^{100}$となる自然数Nをすべて求めよ。
この動画を見る
和歌山大学過去問題
$a_1=b_1=1$
$a_{n+1}=a_n-b_n$
$b_{n+1}=a_n+b_n$
(1)$a_n+b_ni= (1+i)^n$を数学的帰納法で証明せよ。
(2)$a_N=2^{100}$となる自然数Nをすべて求めよ。
福田の一夜漬け数学〜数学III 複素数平面〜京都大学の問題に挑戦
単元:
#大学入試過去問(数学)#複素数平面#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ $w$を$0$でない複素数、$x,y$を$w+\displaystyle \frac{1}{w}=x+yi$を満たす実数とする。
(1)実数$R$は$R \gt 1$を満たす定数とする。$w$が絶対値$R$の複素数
全体を動くとき、$xy$平面上の点$(x,\ y)$の軌跡を求めよ。
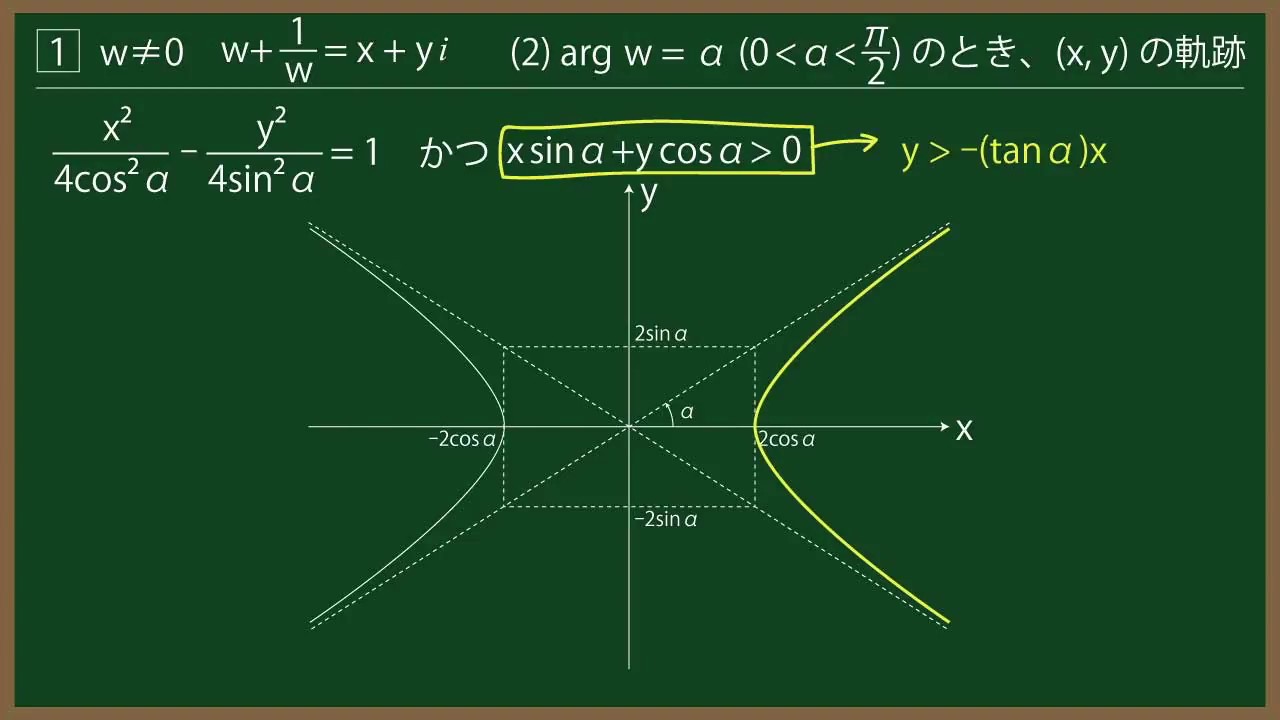
(2)実数$\alpha$は$0 \lt \alpha \lt \displaystyle \frac{\pi}{2}$を満たす定数とする。$w$が偏角$\alpha$の複素数
全体を動くとき、$xy$平面上の点$(x,\ y)$の軌跡を求めよ。
京都大学過去問
この動画を見る
${\Large\boxed{1}}$ $w$を$0$でない複素数、$x,y$を$w+\displaystyle \frac{1}{w}=x+yi$を満たす実数とする。
(1)実数$R$は$R \gt 1$を満たす定数とする。$w$が絶対値$R$の複素数
全体を動くとき、$xy$平面上の点$(x,\ y)$の軌跡を求めよ。
(2)実数$\alpha$は$0 \lt \alpha \lt \displaystyle \frac{\pi}{2}$を満たす定数とする。$w$が偏角$\alpha$の複素数
全体を動くとき、$xy$平面上の点$(x,\ y)$の軌跡を求めよ。
京都大学過去問
福田の一夜漬け数学〜数学III 複素数平面〜|z|, arg zの範囲

単元:
#複素数平面#図形への応用#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ 点$z$が、$|z+3-\sqrt3i|$$=\sqrt2|z$$+2-\sqrt3i|$ を満たしながら動く。
このとき、$|z|$の値の範囲と$z$の偏角$\theta$の範囲を求めよ。
ただし、$0 \leqq \theta \lt 2\pi$ とする。
この動画を見る
${\Large\boxed{1}}$ 点$z$が、$|z+3-\sqrt3i|$$=\sqrt2|z$$+2-\sqrt3i|$ を満たしながら動く。
このとき、$|z|$の値の範囲と$z$の偏角$\theta$の範囲を求めよ。
ただし、$0 \leqq \theta \lt 2\pi$ とする。
