 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
福田のおもしろ数学514〜指数方程式の解

福田の数学〜立教大学2025経済学部第1問(5)〜絶対値の付いた関数の定積分の計算

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(5)定積分$\displaystyle \int_{0}^{2} (x+1)\vert x-1 \vert dx$
の値は$\boxed{キ}$である。
$2025$年立教大学経済学部過去問題
この動画を見る
$\boxed{1}$
(5)定積分$\displaystyle \int_{0}^{2} (x+1)\vert x-1 \vert dx$
の値は$\boxed{キ}$である。
$2025$年立教大学経済学部過去問題
福田のおもしろ数学513〜3つの数のうち少なくとも2つは等しいことの証明

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$x,y,z$は正の実数であり、
任意の自然数$n$について$x^n,y^n,z^n$が
三角形の$3$辺をなすとき、
$x,y,z$の少なくとも$2$つは等しくことを
証明して下さい。
この動画を見る
$x,y,z$は正の実数であり、
任意の自然数$n$について$x^n,y^n,z^n$が
三角形の$3$辺をなすとき、
$x,y,z$の少なくとも$2$つは等しくことを
証明して下さい。
福田の数学〜立教大学2025経済学部第1問(4)〜2直線が1点で交わる条件

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(4)実数$a$は定数とする。
座標平面上の$2$つの直線$(a+1)x+ay=1$
$ax+(a+2)y=2$がただ$1$つの交点を持つための
$a$の条件は$\boxed{カ}$である。
$2025$年立教大学経済学部過去問題
この動画を見る
$\boxed{1}$
(4)実数$a$は定数とする。
座標平面上の$2$つの直線$(a+1)x+ay=1$
$ax+(a+2)y=2$がただ$1$つの交点を持つための
$a$の条件は$\boxed{カ}$である。
$2025$年立教大学経済学部過去問題
【数C】【ベクトルの内積】|a|=3,|b|=4,|a-b|=3のとき,|a+tb|を最小にする実数tの値とその最小値を求めよ。

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#平面上のベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
ベクトル$|\vec{a}|=3$、$|\vec{b}|=4$、$|\vec{a}-\vec{b}|=3$のとき、
$|\vec{a}+t\vec{b}|$を最小にする実数tの値とその最小値を求めよ。
この動画を見る
ベクトル$|\vec{a}|=3$、$|\vec{b}|=4$、$|\vec{a}-\vec{b}|=3$のとき、
$|\vec{a}+t\vec{b}|$を最小にする実数tの値とその最小値を求めよ。
福田のおもしろ数学512〜不定方程式の整数解

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$m^n-n^m=3$を満たす正の整数の組
$(m,n)$をすべて求めて下さい。
この動画を見る
$m^n-n^m=3$を満たす正の整数の組
$(m,n)$をすべて求めて下さい。
福田の数学〜立教大学2025経済学部第1問(3)〜等差中項と等比中項

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(3)$x,y,z$は実数であり、$x\lt y$を満たすとする。
$3$つの数$3,x,y$がこの順に等差数列となり、
さらに$4$つの数$4,x,y,z$がこの順に
等差数列となるとき、
$x=\boxed{ウ}、\boxed{エ}、\boxed{オ}$である。
$2025$年立教大学経済学部過去問題
この動画を見る
$\boxed{1}$
(3)$x,y,z$は実数であり、$x\lt y$を満たすとする。
$3$つの数$3,x,y$がこの順に等差数列となり、
さらに$4$つの数$4,x,y,z$がこの順に
等差数列となるとき、
$x=\boxed{ウ}、\boxed{エ}、\boxed{オ}$である。
$2025$年立教大学経済学部過去問題
【数C】【平面上の曲線】x²/16+y²/25 =1とy軸の交点をA、Bとする。楕円上の点をPとし、直線PA, PBとx軸の交点をそれぞれQ, R とするとき、 OQ・ORの値は一定であることを示せ。

単元:
#平面上の曲線#2次曲線#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#式と曲線
指導講師:
理数個別チャンネル
問題文全文(内容文):
原点を $\mathrm{O}$、楕円 $\displaystyle \frac{x^2}{16}+\frac{y^2}{25}=1$ と $y$ 軸の交点を $\mathrm{A,B}$ とする。
$\mathrm{A,B}$ 以外の楕円上の点を$\mathrm{P}$ とし、直線 $\mathrm{PA,\ PB}$ と $x$ 軸の交点をそれぞれ $\mathrm{Q,R}$ とするとき、
$\mathrm{OQ \cdot OR}$ の値は一定であることを示せ。
この動画を見る
原点を $\mathrm{O}$、楕円 $\displaystyle \frac{x^2}{16}+\frac{y^2}{25}=1$ と $y$ 軸の交点を $\mathrm{A,B}$ とする。
$\mathrm{A,B}$ 以外の楕円上の点を$\mathrm{P}$ とし、直線 $\mathrm{PA,\ PB}$ と $x$ 軸の交点をそれぞれ $\mathrm{Q,R}$ とするとき、
$\mathrm{OQ \cdot OR}$ の値は一定であることを示せ。
【数C】【平面上の曲線】2点 A(- 2, 0) , B(2, 0) と楕円 x²/36 + y²/9 = 1上の点Qでできる△AQBの重心Pの軌跡を求めよ。

単元:
#平面上の曲線#2次曲線#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#式と曲線
指導講師:
理数個別チャンネル
問題文全文(内容文):
$2$ 点 $\mathrm{A}(-2,\ 0),\ \mathrm{B}(2,\ 0)$と、
楕円 $\displaystyle \frac{x^2}{36}+\frac{y^2}{9}=1$ 上の点$\mathrm{Q}$でできる
$\triangle \mathrm{AQB}$ の重心$\mathrm{P}$の軌跡を求めよ。
この動画を見る
$2$ 点 $\mathrm{A}(-2,\ 0),\ \mathrm{B}(2,\ 0)$と、
楕円 $\displaystyle \frac{x^2}{36}+\frac{y^2}{9}=1$ 上の点$\mathrm{Q}$でできる
$\triangle \mathrm{AQB}$ の重心$\mathrm{P}$の軌跡を求めよ。
【数C】【平面上の曲線】長さ8の線分ABの端点Aは軸上を、 端点Bはy軸上を動くとする。(1) 線分ABを5:3に内分する点Pの軌跡を求めよ。(2) 線分ABを5:3に外分する点Qの軌跡を求めよ。

単元:
#平面上の曲線#2次曲線#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#式と曲線
指導講師:
理数個別チャンネル
問題文全文(内容文):
長さ $8$ の線分 $\mathrm{AB}$ の端点$\mathrm{A}$ は $x$ 軸上を、
端点$\mathrm{B}$ は $y$ 軸上を動くとする。
(1) 線分 $\mathrm{AB}$ を $5:3$ に内分する点 $\mathrm{P}$ の軌跡を求めよ。
(2) 線分 $\mathrm{AB}$ を $5:3$ に外分する点 $\mathrm{Q}$ の軌跡を求めよ。
この動画を見る
長さ $8$ の線分 $\mathrm{AB}$ の端点$\mathrm{A}$ は $x$ 軸上を、
端点$\mathrm{B}$ は $y$ 軸上を動くとする。
(1) 線分 $\mathrm{AB}$ を $5:3$ に内分する点 $\mathrm{P}$ の軌跡を求めよ。
(2) 線分 $\mathrm{AB}$ を $5:3$ に外分する点 $\mathrm{Q}$ の軌跡を求めよ。
何を折っているでしょう?

【数C】【平面上の曲線】次のような楕円の方程式を求めよ。ただし、中心は原点で、長軸はx軸上、短軸はy軸上にあるものとする。 (1) 長軸の長さが6,短軸の長さが4 (2) 2つの焦点間の距離が6,長軸の長さが10 (3) 2点(2,2√5/3), (-3√3/2,1)を通る

単元:
#平面上の曲線#2次曲線#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#式と曲線
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のような楕円の方程式を求めよ。
ただし、中心は原点で、長軸は $x$ 軸上、
短軸は $y$ 軸上にあるものとする。
(1) 長軸の長さが $6$ 、短軸の長さが $4$
(2) $2$ つの焦点間の距離が $6$, 長軸の長さが $10$
(3) $2$ 点 $\displaystyle (2,\ \frac{2\sqrt{5}}{3}),\ (-\frac{3\sqrt{3}}{2},\ 1)$を通る
この動画を見る
次のような楕円の方程式を求めよ。
ただし、中心は原点で、長軸は $x$ 軸上、
短軸は $y$ 軸上にあるものとする。
(1) 長軸の長さが $6$ 、短軸の長さが $4$
(2) $2$ つの焦点間の距離が $6$, 長軸の長さが $10$
(3) $2$ 点 $\displaystyle (2,\ \frac{2\sqrt{5}}{3}),\ (-\frac{3\sqrt{3}}{2},\ 1)$を通る
【数C】【平面上の曲線】楕円x²/9 + y²/4 = 1 上の点Pと点(2,0)の距離lの最小値、および最大値を求めよ

単元:
#平面上の曲線#2次曲線#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#式と曲線
指導講師:
理数個別チャンネル
問題文全文(内容文):
楕円 $\displaystyle \frac{x^2}{9}+\frac{y^2}{4}=1$ 上の
点 $\mathrm{P}$ と点$(2,\ 0)$ の距離 $l$ の最小値、および最大値を求めよ。
この動画を見る
楕円 $\displaystyle \frac{x^2}{9}+\frac{y^2}{4}=1$ 上の
点 $\mathrm{P}$ と点$(2,\ 0)$ の距離 $l$ の最小値、および最大値を求めよ。
福田のおもしろ数学511〜50の50乗と49の51乗の大小比較

福田の数学〜立教大学2025経済学部第1問(2)〜順列と確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(2)赤玉$3$個と白玉$4$個を無作為に$1$列に
並べるとき、
白玉が両端にある確率は$\boxed{イ}$である。
$2025$年立教大学経済学部過去問題
この動画を見る
$\boxed{1}$
(2)赤玉$3$個と白玉$4$個を無作為に$1$列に
並べるとき、
白玉が両端にある確率は$\boxed{イ}$である。
$2025$年立教大学経済学部過去問題
【数C】【平面上の曲線】辺が座標軸に平行な長方形が、楕円x²/16+y²/12=1に内接している。この長方形の周の長さが20であるとき、長方形の2辺の長さを求めよ。

単元:
#平面上の曲線#2次曲線#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説
指導講師:
理数個別チャンネル
問題文全文(内容文):
辺が座標軸に平行な長方形が、
楕円 $\displaystyle \frac{x^2}{16}+\frac{y^2}{12}=1$ に内接している。
この長方形の周の長さが $20$ であるとき、
長方形の $2$ 辺の長さを求めよ。
この動画を見る
辺が座標軸に平行な長方形が、
楕円 $\displaystyle \frac{x^2}{16}+\frac{y^2}{12}=1$ に内接している。
この長方形の周の長さが $20$ であるとき、
長方形の $2$ 辺の長さを求めよ。
福田のおもしろ数学510〜(n+1/n)のn乗がeより小であることの証明

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$n$を正の整数とするとき
$\left(1+\dfrac{1}{n}\right)^n \lt e$
を証明して下さい。
$e$は自然対数の底とする。
この動画を見る
$n$を正の整数とするとき
$\left(1+\dfrac{1}{n}\right)^n \lt e$
を証明して下さい。
$e$は自然対数の底とする。
福田の数学〜立教大学2025経済学部第1問(1)〜指数不等式

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(1)$2^{1-3x} \geqq \left(\dfrac{1}{\sqrt2}\right)^x$を満たす
実数$x$の値の範囲は$\boxed{ア}$である。
$2025$年立教大学経済学部過去問題
この動画を見る
$\boxed{1}$
(1)$2^{1-3x} \geqq \left(\dfrac{1}{\sqrt2}\right)^x$を満たす
実数$x$の値の範囲は$\boxed{ア}$である。
$2025$年立教大学経済学部過去問題
【数C】【ベクトルの内積】a = (4,2), b = (3,-1), x = (p,q)とする。xとb-aは平行で、x-bとaは垂直であるとき、pとqの値を求めよ。

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#平面上のベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\vec{a}=(4, 2), \vec{b}=(3, -1), \vec{x}=(p, q)$とする。
$\vec{x}$と$\vec{b}-\vec{a}$は平行で, $\vec{x}-\vec{b}$と$\vec{a}$は垂直であるとき,
pとqの値を求めよ。
この動画を見る
$\vec{a}=(4, 2), \vec{b}=(3, -1), \vec{x}=(p, q)$とする。
$\vec{x}$と$\vec{b}-\vec{a}$は平行で, $\vec{x}-\vec{b}$と$\vec{a}$は垂直であるとき,
pとqの値を求めよ。
【数C】【ベクトルの内積】a| =|b| = 2, a - b = -2のとき、 a+bとa+tbが垂直になるように、 実数tの値を定めよ。

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#平面上のベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
$|\vec{a}|=|\vec{b}|=2, \vec{a}\cdot\vec{b}=-2$のとき,
$\vec{a}+\vec{b}$と$\vec{a}+t\vec{b}$が垂直になるように,
実数tの値を定めよ。
この動画を見る
$|\vec{a}|=|\vec{b}|=2, \vec{a}\cdot\vec{b}=-2$のとき,
$\vec{a}+\vec{b}$と$\vec{a}+t\vec{b}$が垂直になるように,
実数tの値を定めよ。
【数C】【ベクトルの内積】a = √2, b = √5, a・b = -1のとき、 a+2bとa-bのなす角を求めよ。

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#平面上のベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
$|\vec{a}|=\sqrt{2}, |\vec{b}|=\sqrt{5}, \vec{a}\cdot\vec{b}=-1$のとき,
$\vec{a}+2\vec{b}$と$\vec{a}-\vec{b}$のなす角$\theta$を求めよ。
この動画を見る
$|\vec{a}|=\sqrt{2}, |\vec{b}|=\sqrt{5}, \vec{a}\cdot\vec{b}=-1$のとき,
$\vec{a}+2\vec{b}$と$\vec{a}-\vec{b}$のなす角$\theta$を求めよ。
福田のおもしろ数学509〜幾何の証明
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
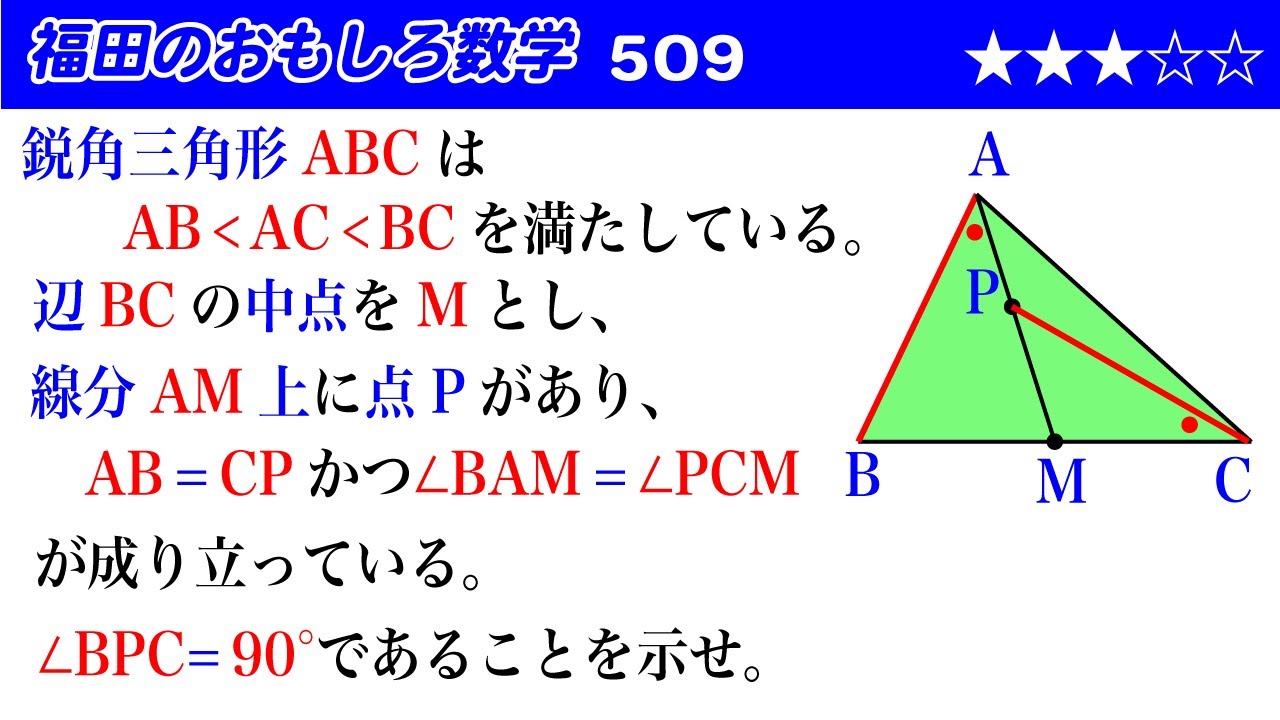
鋭角三角形$ABC$は
$AB \lt AC \lt BC$を満たしている。
辺$BC$の中点を$M$とし、
線分$AM$上に点$P$があり、
$AB = CP$かつ$\angle BAM=\angle PCM$が
成り立っている。
$\angle BPC=90°$であることを示せ。
図は動画内参照
この動画を見る
鋭角三角形$ABC$は
$AB \lt AC \lt BC$を満たしている。
辺$BC$の中点を$M$とし、
線分$AM$上に点$P$があり、
$AB = CP$かつ$\angle BAM=\angle PCM$が
成り立っている。
$\angle BPC=90°$であることを示せ。
図は動画内参照
福田の数学〜慶應義塾大学2025経済学部第6問〜放物線と直線で囲まれた図形の面積

単元:
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{6}$
$C$を$y=3x^2$で定まる曲線とし、
$C$上に異なる$2$点$A(a,3a^2)$
$B(b,3b^2)$をとる。ただし、$a\lt b$とする。
(1)$C$と直線$AB$で囲まれた図形の面積$S$を、
$a$と$b$を用いて表せ。
ただし、積分を用いて計算し、
積分の計算過程も書くこと。
(2)$2$点$A,B$間の距離が$3$のとき、
(1)で求めた面積$S$の取りうる値の最大値$T$を
求めよ。
(3)$2$点$A,B$間の距離が$3$のとき、
直線$AB$は点$(0,7)$を通らないことを示せ。
$2025$年慶應義塾大学経済学部過去問題
この動画を見る
$\boxed{6}$
$C$を$y=3x^2$で定まる曲線とし、
$C$上に異なる$2$点$A(a,3a^2)$
$B(b,3b^2)$をとる。ただし、$a\lt b$とする。
(1)$C$と直線$AB$で囲まれた図形の面積$S$を、
$a$と$b$を用いて表せ。
ただし、積分を用いて計算し、
積分の計算過程も書くこと。
(2)$2$点$A,B$間の距離が$3$のとき、
(1)で求めた面積$S$の取りうる値の最大値$T$を
求めよ。
(3)$2$点$A,B$間の距離が$3$のとき、
直線$AB$は点$(0,7)$を通らないことを示せ。
$2025$年慶應義塾大学経済学部過去問題
【数C】【平面上の曲線】2次曲線3 ※問題文は概要欄

単元:
#平面上の曲線#2次曲線#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#式と曲線
指導講師:
理数個別チャンネル
問題文全文(内容文):
放物線 $ C \mathrm{:} \ x^2 = 4y$ の焦点を $\mathrm{F}$、$C$ 上の点を $\mathrm{P}$ 、 $\mathrm{P}$ から準線に下した垂線を $\mathrm{PH}$ とする。 $\triangle \mathrm{PFH}$ が正三角形になるとき、 $\mathrm{P}$ の $x$ 座標 $a$ を求めよ。また、$ a \gt 0$ のとき、辺 $\mathrm{FH}$ と $C$ の交点 $\mathrm{Q}$ の $x$ 座標 $b$ と $\triangle \mathrm{PFQ}$ の面積 $S$ を求めよ。
この動画を見る
放物線 $ C \mathrm{:} \ x^2 = 4y$ の焦点を $\mathrm{F}$、$C$ 上の点を $\mathrm{P}$ 、 $\mathrm{P}$ から準線に下した垂線を $\mathrm{PH}$ とする。 $\triangle \mathrm{PFH}$ が正三角形になるとき、 $\mathrm{P}$ の $x$ 座標 $a$ を求めよ。また、$ a \gt 0$ のとき、辺 $\mathrm{FH}$ と $C$ の交点 $\mathrm{Q}$ の $x$ 座標 $b$ と $\triangle \mathrm{PFQ}$ の面積 $S$ を求めよ。
【数C】【平面上の曲線】2次曲線2 ※問題文は概要欄

単元:
#平面上の曲線#2次曲線#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#式と曲線
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の条件を満たす点 $\mathrm{P}$ の軌跡を求めよ。
(1) 直線 $x=-2$に接し、点 $(2,0)$を通る円の中心 $\mathrm{P}$
(2) 円 $ x^2 + (y+2)^2 = 1$ と直線 $y=1$の両方に接する円の中心 $\mathrm{P}$
この動画を見る
次の条件を満たす点 $\mathrm{P}$ の軌跡を求めよ。
(1) 直線 $x=-2$に接し、点 $(2,0)$を通る円の中心 $\mathrm{P}$
(2) 円 $ x^2 + (y+2)^2 = 1$ と直線 $y=1$の両方に接する円の中心 $\mathrm{P}$
福田の数学〜慶應義塾大学2025経済学部第5問〜空間における平面と平面の交線

単元:
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{5}$
座標平面の原点$O$を中心とする半径$1$の
球面を$C$、点$M(4,0,0)$を中心とする
半径$2$の球面上を$D$とする。
(1)$p,q$を実数とする。
$xy$平面上の直線$y=px+q$は、
球面$C$と$xy$平面が交わってできる円と
点$A_1$で接し、球面$D$と$xy$平面が交わって
できる円と点$A_2$で接し、かつ
$0 \lt p 1$を満たすとする。$p$と$q$の値を求めよ。
(2)$r,s$を実数とする。
$zx$平面上の直線$z=rx+s$は、球面$C$と
$zx$平面が交わってできる円と点$B_1$で接し、
球面$D$と$zx$平面が交わってできる円と点$B_2$で
接し、かつ、$r \lt -1$を満たすとする。
$r$と$s$の値を求めよ。
以下、点$E$は$\overrightarrow{ A_1 E }=(0,0,1)$を満たすとし、
$3$点$A_1,A_2,E$を通る平面を$\alpha$とする。
また、点$F$は$\overrightarrow{ B_1 E }=(0,1,0)$を満たすとし、
$3$点$B_1,B_2,F$を通る平面を$\beta$とする。
$\alpha$と$\beta$が交わってできる直線を
$\ell$とし、$\ell$と$xy$平面の交点を
$G,\ell$と$zx$平面の交点を$H$とする。
(3)$G$の座標を求めよ。
(4)$\ell$上の点$T$を、実数$t$を用いて
$\overrightarrow{OT}=\overrightarrow{OG}+t\overrightarrow{OH}$と表す。
$\triangle OMT$の面積が最小となる$t$の値の求めよ。
$2025$年慶應義塾大学経済学部過去問題
この動画を見る
$\boxed{5}$
座標平面の原点$O$を中心とする半径$1$の
球面を$C$、点$M(4,0,0)$を中心とする
半径$2$の球面上を$D$とする。
(1)$p,q$を実数とする。
$xy$平面上の直線$y=px+q$は、
球面$C$と$xy$平面が交わってできる円と
点$A_1$で接し、球面$D$と$xy$平面が交わって
できる円と点$A_2$で接し、かつ
$0 \lt p 1$を満たすとする。$p$と$q$の値を求めよ。
(2)$r,s$を実数とする。
$zx$平面上の直線$z=rx+s$は、球面$C$と
$zx$平面が交わってできる円と点$B_1$で接し、
球面$D$と$zx$平面が交わってできる円と点$B_2$で
接し、かつ、$r \lt -1$を満たすとする。
$r$と$s$の値を求めよ。
以下、点$E$は$\overrightarrow{ A_1 E }=(0,0,1)$を満たすとし、
$3$点$A_1,A_2,E$を通る平面を$\alpha$とする。
また、点$F$は$\overrightarrow{ B_1 E }=(0,1,0)$を満たすとし、
$3$点$B_1,B_2,F$を通る平面を$\beta$とする。
$\alpha$と$\beta$が交わってできる直線を
$\ell$とし、$\ell$と$xy$平面の交点を
$G,\ell$と$zx$平面の交点を$H$とする。
(3)$G$の座標を求めよ。
(4)$\ell$上の点$T$を、実数$t$を用いて
$\overrightarrow{OT}=\overrightarrow{OG}+t\overrightarrow{OH}$と表す。
$\triangle OMT$の面積が最小となる$t$の値の求めよ。
$2025$年慶應義塾大学経済学部過去問題
【数C】【平面上のベクトル】ベクトル方程式7 ※問題文は概要欄

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#平面上のベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
平面上の異なる2つの定点O, Aと任意の点Pに対し,
$\overrightarrow{OA}=\vec{a}$, $\overrightarrow{OP}=\vec{p}$とする。
次のベクトル方程式はどのような図形を表すか。
(1) $|\vec{p}+2\vec{a}|=|\vec{p}-2\vec{a}|$
(2) $2\vec{a}\cdot\vec{p}=|\vec{a}||\vec{p}|$
この動画を見る
平面上の異なる2つの定点O, Aと任意の点Pに対し,
$\overrightarrow{OA}=\vec{a}$, $\overrightarrow{OP}=\vec{p}$とする。
次のベクトル方程式はどのような図形を表すか。
(1) $|\vec{p}+2\vec{a}|=|\vec{p}-2\vec{a}|$
(2) $2\vec{a}\cdot\vec{p}=|\vec{a}||\vec{p}|$
【数C】【平面上のベクトル】ベクトル方程式6 ※問題文は概要欄

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#平面上のベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
平面上の$\triangle$ABCに対して,
条件$|\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}|=3$
を満たす動点Pはどのような図形を描くか。
この動画を見る
平面上の$\triangle$ABCに対して,
条件$|\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}|=3$
を満たす動点Pはどのような図形を描くか。
【数C】【平面上のベクトル】ベクトル方程式5 ※問題文は概要欄

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#平面上のベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\triangle$ABCの頂点A, B, Cの位置ベクトルを, それぞれ$\vec{a}$, $\vec{b}$, $\vec{c}$とする。
直線上の点をP($\vec{p}$)として, 次の直線のベクトル方程式を求めよ。
(1) Aから直線BCへの垂線$\qquad$
(2) Aと辺BCの中点を通る直線
この動画を見る
$\triangle$ABCの頂点A, B, Cの位置ベクトルを, それぞれ$\vec{a}$, $\vec{b}$, $\vec{c}$とする。
直線上の点をP($\vec{p}$)として, 次の直線のベクトル方程式を求めよ。
(1) Aから直線BCへの垂線$\qquad$
(2) Aと辺BCの中点を通る直線
福田のおもしろ数学507〜三角形の面がm個ありどの頂点にも4本の辺が集まる多面体

単元:
#数A#図形の性質#空間における垂直と平行と多面体(オイラーの法則)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
ある凸多面体において、
三角形の面が$m$枚あり、
(他の形の面も含まれている可能性がある)
すべての頂点にはちょうど$4$枚の辺が集まって
いるとする。
このとき、$m$の最小値を求めて下さい。
この動画を見る
ある凸多面体において、
三角形の面が$m$枚あり、
(他の形の面も含まれている可能性がある)
すべての頂点にはちょうど$4$枚の辺が集まって
いるとする。
このとき、$m$の最小値を求めて下さい。
