数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
福田の数学〜一橋大学2025文系第5問〜確率漸化式と条件付き確率

単元:
#数A#場合の数と確率#確率#数列#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{5}$
$5$点$A,B,C,D$が
下図のように線分で結ばれている。
点$P_1,P_2,P_3,\cdots $を次のように定めていく。
$P_1$を$A$とする。
正の整数$n$に対して、$P_n$を端点とする線分を
ひとつ無作為にえらび、その線分の$P_n$とは
異なる端点$P_{n+1}$とする。
(1)$P_n$が$A$または$B$である確率$p_n$を求めよ。
(2)$P_n$が$A$または$B$であるとき、
$k=1,2,\cdots ,n$のいずれに対しても$P_k=E$とは
ならない条件付き確率$q_n$を求めよ。
図は動画内参照
$2025$年一橋大学文系過去問題
この動画を見る
$\boxed{5}$
$5$点$A,B,C,D$が
下図のように線分で結ばれている。
点$P_1,P_2,P_3,\cdots $を次のように定めていく。
$P_1$を$A$とする。
正の整数$n$に対して、$P_n$を端点とする線分を
ひとつ無作為にえらび、その線分の$P_n$とは
異なる端点$P_{n+1}$とする。
(1)$P_n$が$A$または$B$である確率$p_n$を求めよ。
(2)$P_n$が$A$または$B$であるとき、
$k=1,2,\cdots ,n$のいずれに対しても$P_k=E$とは
ならない条件付き確率$q_n$を求めよ。
図は動画内参照
$2025$年一橋大学文系過去問題
福田のおもしろ数学492〜不定方程式の整数解

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$(x+y)^x-x^y$
を満たす正の整数$x,y$をすべて求めて下さい。
この動画を見る
$(x+y)^x-x^y$
を満たす正の整数$x,y$をすべて求めて下さい。
福田の数学〜一橋大学2025文系第4問〜ベクトル方程式と領域と角を2等分するベクトル

単元:
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#図形と方程式#軌跡と領域#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{4}$
原点を$O$とする座標空間内の
$2$点$A(0,3,-5),B(5,-2,10)$に対して
$\overrightarrow{OP}=s\left \{ (1-t)\overrightarrow{OA}+t\overrightarrow{OB} \right \},x\geqq 0,\dfrac{1}{5} \leqq t \leqq \dfrac{3}{5}$
で定まる点$P$が存在する範囲を$D$とする。
$D$に含まれる半径$10\sqrt2$の円のうち、
その中心と原点との距離が最小となるものを
$C$とする。
円$C$の中心の座標を求めよ。
$2025$年一橋大学文系過去問題
この動画を見る
$\boxed{4}$
原点を$O$とする座標空間内の
$2$点$A(0,3,-5),B(5,-2,10)$に対して
$\overrightarrow{OP}=s\left \{ (1-t)\overrightarrow{OA}+t\overrightarrow{OB} \right \},x\geqq 0,\dfrac{1}{5} \leqq t \leqq \dfrac{3}{5}$
で定まる点$P$が存在する範囲を$D$とする。
$D$に含まれる半径$10\sqrt2$の円のうち、
その中心と原点との距離が最小となるものを
$C$とする。
円$C$の中心の座標を求めよ。
$2025$年一橋大学文系過去問題
【初心者向け】数学が苦手でも偏差値70を超える唯一の勉強法

単元:
#その他#勉強法#数学(高校生)
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
【初心者向け】数学が苦手でも偏差値70を超える唯一の勉強法を解説していきます。
この動画を見る
【初心者向け】数学が苦手でも偏差値70を超える唯一の勉強法を解説していきます。
福田のおもしろ数学491〜三角関数の連立方程式

単元:
#連立方程式#数Ⅱ#三角関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$x,y$は実数であり
$\begin{eqnarray}
\left\{
\begin{array}{l}
\sin x+\cos y=1 \\
\cos x+\sin y=-1
\end{array}
\right.
\end{eqnarray}$
のとき、$\cos 2x=\cos 2y$となることを
証明せよ。
この動画を見る
$x,y$は実数であり
$\begin{eqnarray}
\left\{
\begin{array}{l}
\sin x+\cos y=1 \\
\cos x+\sin y=-1
\end{array}
\right.
\end{eqnarray}$
のとき、$\cos 2x=\cos 2y$となることを
証明せよ。
福田の数学〜一橋大学2025文系第3問〜定積分で表された方程式の解の個数

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
等式
$6\displaystyle \int_{0}^{2} \vert x^2-a \vert dx-a^2-2a+k$
が成り立つ実数$a$がちょうど$4$つ存在するような
実数$k$の範囲を求めよ。
$2025$年一橋大学文系過去問題
この動画を見る
$\boxed{3}$
等式
$6\displaystyle \int_{0}^{2} \vert x^2-a \vert dx-a^2-2a+k$
が成り立つ実数$a$がちょうど$4$つ存在するような
実数$k$の範囲を求めよ。
$2025$年一橋大学文系過去問題
【保存版】素因数分解のやり方

福田のおもしろ数学490〜3乗根混じりの2重根号を解消

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\sqrt[3]{1342\sqrt{167}+2005}$
の$2$重根号を解消せよ。
この動画を見る
$\sqrt[3]{1342\sqrt{167}+2005}$
の$2$重根号を解消せよ。
福田の数学〜一橋大学2025文系第2問〜円と円の交点を通る直線に対称な点の軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
座標平面上に原点を中心とす半径$3$の円$C_1$がある。
また、直線$x=2$上の点$P$を中心とする半径$1$の円を
$C_2$とする。
(1)$C_1$と$C_2$が共有点を$2$つ持つような$P$の
$y$座標の範囲を求めよ。
(2)$C_1$と$C_2$が共有点を$2$つ持つとき、
その$2$つの共有点を通る直線を$\ell$とする。
$\ell$に関して$P$と対称な位置にある点を$Q$とする。
ただし、$P$が$\ell$上にあるときは$Q=P$とする。
$P$の$y$座標が(1)で求めた範囲を動くとき、
点$Q$の軌跡を求め、図示せよ。
$2025$年一橋大学文系過去問題
この動画を見る
$\boxed{2}$
座標平面上に原点を中心とす半径$3$の円$C_1$がある。
また、直線$x=2$上の点$P$を中心とする半径$1$の円を
$C_2$とする。
(1)$C_1$と$C_2$が共有点を$2$つ持つような$P$の
$y$座標の範囲を求めよ。
(2)$C_1$と$C_2$が共有点を$2$つ持つとき、
その$2$つの共有点を通る直線を$\ell$とする。
$\ell$に関して$P$と対称な位置にある点を$Q$とする。
ただし、$P$が$\ell$上にあるときは$Q=P$とする。
$P$の$y$座標が(1)で求めた範囲を動くとき、
点$Q$の軌跡を求め、図示せよ。
$2025$年一橋大学文系過去問題
これ知ってた?

単元:
#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$(x+a)^{ 2 }=x^{ 2 }+2ax+a^{ 2 }$の考え方
この動画を見る
$(x+a)^{ 2 }=x^{ 2 }+2ax+a^{ 2 }$の考え方
福田のおもしろ数学489〜3本の光線のなす角と三角関数

単元:
#数Ⅱ#三角関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$3$本の光線が原点$O$から空間へ発射された。
$2$本ずつのなす角が
$\alpha,\beta,\gamma(0° \lt \alpha \leqq \beta \leqq \gamma \leqq 180°)$
であり、この$3$本の光線は同一平面上にない。
$\sin\dfrac{\alpha}{2}+\sin\dfrac{\beta}{2} \gt \sin\dfrac{\gamma}{2}$
を証明せよ。
この動画を見る
$3$本の光線が原点$O$から空間へ発射された。
$2$本ずつのなす角が
$\alpha,\beta,\gamma(0° \lt \alpha \leqq \beta \leqq \gamma \leqq 180°)$
であり、この$3$本の光線は同一平面上にない。
$\sin\dfrac{\alpha}{2}+\sin\dfrac{\beta}{2} \gt \sin\dfrac{\gamma}{2}$
を証明せよ。
福田の数学〜一橋大学2025文系第1問〜正の約数の個数と関数の最大値

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
正の整数$n$に対し、$n$の正の約数の個数を
$d(n)$とする。
たとえば、$6$の正の約数は$1,2,3,6$の$4$個なので、
$d(6)=4$である。また、
$f(n)=\dfrac{d(n)}{\sqrt n}$
とする。
(1)$f(2025)$を求めよ。
(2)素数$p$と正の整数$k$の組で
$f(p^k)\leqq f(p^{k+1})$を満たすものを求めよ。
(3)$f(n)$の最大値と、そのときの$n$を求めよ。
$2025$年一橋大学文系過去問題
この動画を見る
$\boxed{1}$
正の整数$n$に対し、$n$の正の約数の個数を
$d(n)$とする。
たとえば、$6$の正の約数は$1,2,3,6$の$4$個なので、
$d(6)=4$である。また、
$f(n)=\dfrac{d(n)}{\sqrt n}$
とする。
(1)$f(2025)$を求めよ。
(2)素数$p$と正の整数$k$の組で
$f(p^k)\leqq f(p^{k+1})$を満たすものを求めよ。
(3)$f(n)$の最大値と、そのときの$n$を求めよ。
$2025$年一橋大学文系過去問題
福田のおもしろ数学488〜関数方程式

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
実数から実数への関数$f(x)$が
任意の実数$x,y$に対して
$f(x+f(y))=x+f(f(y))$
を満たしている。また$f(2025)=2026$である。
$f(x)$を求めよ。
この動画を見る
実数から実数への関数$f(x)$が
任意の実数$x,y$に対して
$f(x+f(y))=x+f(f(y))$
を満たしている。また$f(2025)=2026$である。
$f(x)$を求めよ。
福田の数学〜慶應義塾大学看護医療学部2025第5問〜データの分析、平均と分散

単元:
#数Ⅰ#大学入試過去問(数学)#データの分析#データの分析#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{5}$
(1)$20$人の生徒に、$5$点満点の小テストを行った。
次の度数分布表は全員のテストの得点である。
この小テストの得点の平均値は$\boxed{ハ}$、
分散は$\boxed{ヒ}$である。
また、生徒のうちの$1$名の得点が$\boxed{フ}$点から
$\boxed{ヘ}$点に変更された場合、
生徒全員の得点の平均値は$3$、分散は$2$となる。
(2)確率変数$X$と$Y$は独立であり、$X$の平均が$m_x$、
分散が$\upsilon_x$であるとする。
また、$a,b$は定数とする。このとき、$aX+bY$の
平均は$\boxed{ホ}$、分散は$\boxed{マ}$である。
(3)確率変数$X_1,X_2,\cdots,X_n,X_{n+1}$は互いに
独立であり、
$T_n=\dfrac{1}{n}(X_1+X_2+\cdots + X_n)$
の平均が$m$、分散が$\upsilon$であるとする。
$X_{n+1}$の平均が$m'$、分散が$\upsilon'$であるとき、
$T_{n+1}=\dfrac{1}{n+1}(X_1+X_2+\cdots +X_n+X_{n+1})$
の平均は$\boxed{ミ}$、分散は$\boxed{ム}$である。
図は動画内参照
$2025$年慶應義塾大学看護医療学部過去問題
この動画を見る
$\boxed{5}$
(1)$20$人の生徒に、$5$点満点の小テストを行った。
次の度数分布表は全員のテストの得点である。
この小テストの得点の平均値は$\boxed{ハ}$、
分散は$\boxed{ヒ}$である。
また、生徒のうちの$1$名の得点が$\boxed{フ}$点から
$\boxed{ヘ}$点に変更された場合、
生徒全員の得点の平均値は$3$、分散は$2$となる。
(2)確率変数$X$と$Y$は独立であり、$X$の平均が$m_x$、
分散が$\upsilon_x$であるとする。
また、$a,b$は定数とする。このとき、$aX+bY$の
平均は$\boxed{ホ}$、分散は$\boxed{マ}$である。
(3)確率変数$X_1,X_2,\cdots,X_n,X_{n+1}$は互いに
独立であり、
$T_n=\dfrac{1}{n}(X_1+X_2+\cdots + X_n)$
の平均が$m$、分散が$\upsilon$であるとする。
$X_{n+1}$の平均が$m'$、分散が$\upsilon'$であるとき、
$T_{n+1}=\dfrac{1}{n+1}(X_1+X_2+\cdots +X_n+X_{n+1})$
の平均は$\boxed{ミ}$、分散は$\boxed{ム}$である。
図は動画内参照
$2025$年慶應義塾大学看護医療学部過去問題
福田のおもしろ数学487〜三角関数のシグマ計算の必殺テクニック

単元:
#数Ⅱ#三角関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
任意の自然数$m$に対して
$\displaystyle \sum_{k=1}^{m} (-1)^k \cos \dfrac{k\pi}{2m+1}=-\dfrac{1}{2}$
が成り立つことを証明して下さい。
この動画を見る
任意の自然数$m$に対して
$\displaystyle \sum_{k=1}^{m} (-1)^k \cos \dfrac{k\pi}{2m+1}=-\dfrac{1}{2}$
が成り立つことを証明して下さい。
福田の数学〜慶應義塾大学看護医療学部2025第4問〜放物線と接線の囲む面積と内積の最小値

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#図形と方程式#点と直線#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{4}$
$k$を実数の定数とし、
座標平面上に$2$点$A(1,-3),B(-1,k)$をとる。
また、放物線$y=x^2$を$C$とする。
以下に答えなさい。
(1)点$A$から曲線$C$に引いた$2$本の接線のうち、
傾きが正の接線を$\ell_1$とし、
傾きが負の接線を$\ell_2$とするとき、
直線$\ell_1$の方程式は$y=\boxed{テ}$であり、
直線$\ell_2$の方程式は$y=\boxed{ト}$である。
また、$2$直線$\ell_1,\ell_2$のなす角を$\theta$とすると、
$\tan\theta=\boxed{ナ}$である。
ただし、$0\lt\theta\lt\dfrac{\pi}{2}$とする。
さらに、曲線$C$と$2$直線$\ell_1,\ell_2$で囲まれた
図形の面積は$\boxed{ニ}$である。
(2)点$P$が曲線$C$全体を動くときの
$\overrightarrow{PA}・\overrightarrow{PB}$の最小値を$m$とする。
このとき、$m$を$k$を用いて表すと、
$k\geqq \boxed{ヌ}$のときは$m=\boxed{ネ}$であり、
$k\lt \boxed{ヌ}$のときは、$m=\boxed{ノ}$である。
$2025$年慶應義塾大学看護医療学部過去問題
この動画を見る
$\boxed{4}$
$k$を実数の定数とし、
座標平面上に$2$点$A(1,-3),B(-1,k)$をとる。
また、放物線$y=x^2$を$C$とする。
以下に答えなさい。
(1)点$A$から曲線$C$に引いた$2$本の接線のうち、
傾きが正の接線を$\ell_1$とし、
傾きが負の接線を$\ell_2$とするとき、
直線$\ell_1$の方程式は$y=\boxed{テ}$であり、
直線$\ell_2$の方程式は$y=\boxed{ト}$である。
また、$2$直線$\ell_1,\ell_2$のなす角を$\theta$とすると、
$\tan\theta=\boxed{ナ}$である。
ただし、$0\lt\theta\lt\dfrac{\pi}{2}$とする。
さらに、曲線$C$と$2$直線$\ell_1,\ell_2$で囲まれた
図形の面積は$\boxed{ニ}$である。
(2)点$P$が曲線$C$全体を動くときの
$\overrightarrow{PA}・\overrightarrow{PB}$の最小値を$m$とする。
このとき、$m$を$k$を用いて表すと、
$k\geqq \boxed{ヌ}$のときは$m=\boxed{ネ}$であり、
$k\lt \boxed{ヌ}$のときは、$m=\boxed{ノ}$である。
$2025$年慶應義塾大学看護医療学部過去問題
福田のおもしろ数学486〜1分チャレンジ!無理数の計算

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$x=\dfrac{\sqrt6+\sqrt2+\sqrt3+2}{\sqrt6-\sqrt2+\sqrt3-2},$
$y=\dfrac{\sqrt6+\sqrt2-\sqrt3-2}{\sqrt6-\sqrt2-\sqrt3+2}$
のとき$x^5+y^5$の値を求めて下さい。
この動画を見る
$x=\dfrac{\sqrt6+\sqrt2+\sqrt3+2}{\sqrt6-\sqrt2+\sqrt3-2},$
$y=\dfrac{\sqrt6+\sqrt2-\sqrt3-2}{\sqrt6-\sqrt2-\sqrt3+2}$
のとき$x^5+y^5$の値を求めて下さい。
福田の数学〜慶應義塾大学看護医療学部2025第3問〜空間ベクトルと四面体の体積

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
座標空間内に
$3$点$A(-1,1,6),B(0,3,6),C(1,1,5)$をとる。
このとき、$\vert \overrightarrow{AB} \vert =\boxed{ス},\overrightarrow{AB}・\overrightarrow{AC}=\boxed{セ}$であり、
$\angle BAC$の大きさを$\theta$とすると、
$\sin\theta=\boxed{ソ}$である。
ただし、$0\lt \theta \lt \pi$とする。
また、三角形$ABC$の面積は$\boxed{タ}$である。
さらに、
$3$点$A,B,C$の定める平面$ABC$に原点$O$から
垂線$OH$を下ろすと、点$H$の座標は$\boxed{チ}$であり、
四面体$OABC$の体積は$\boxed{ツ}$である。
$2025$年慶應義塾大学看護医療学部過去問題
この動画を見る
$\boxed{3}$
座標空間内に
$3$点$A(-1,1,6),B(0,3,6),C(1,1,5)$をとる。
このとき、$\vert \overrightarrow{AB} \vert =\boxed{ス},\overrightarrow{AB}・\overrightarrow{AC}=\boxed{セ}$であり、
$\angle BAC$の大きさを$\theta$とすると、
$\sin\theta=\boxed{ソ}$である。
ただし、$0\lt \theta \lt \pi$とする。
また、三角形$ABC$の面積は$\boxed{タ}$である。
さらに、
$3$点$A,B,C$の定める平面$ABC$に原点$O$から
垂線$OH$を下ろすと、点$H$の座標は$\boxed{チ}$であり、
四面体$OABC$の体積は$\boxed{ツ}$である。
$2025$年慶應義塾大学看護医療学部過去問題
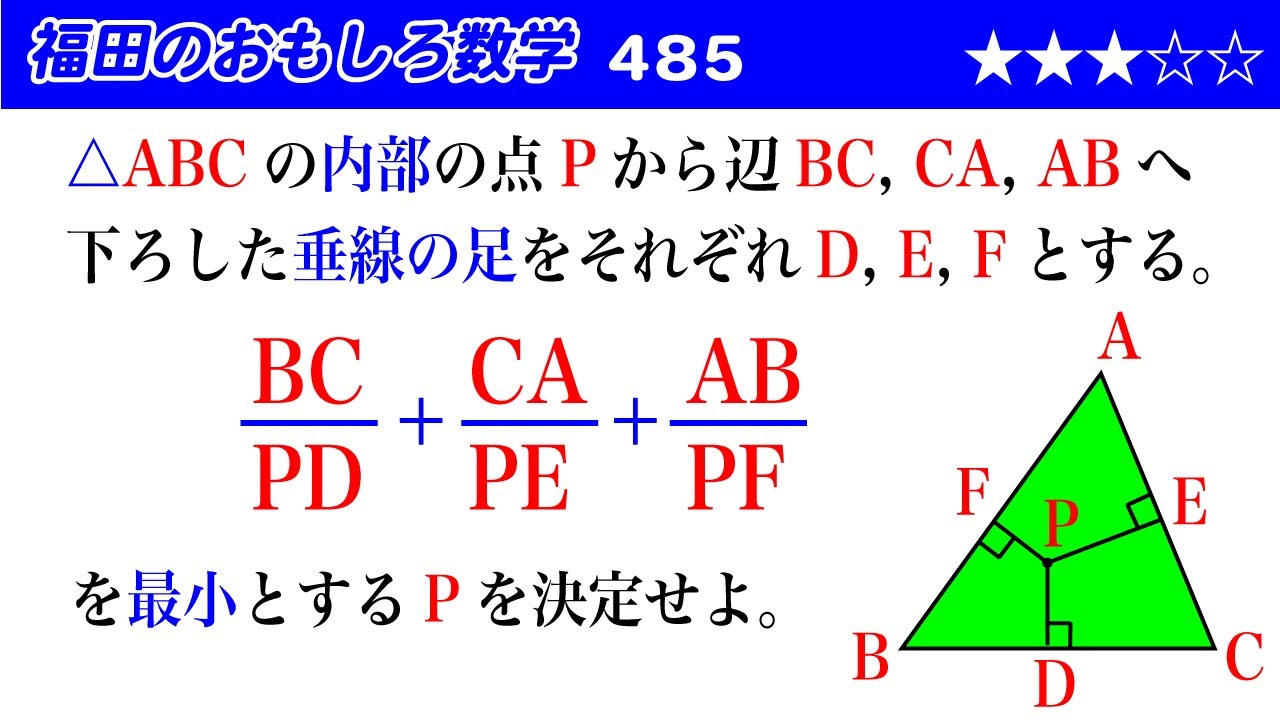
福田のおもしろ数学485〜三角形の内部の点から下ろした垂線の長さと最小値
単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\triangle ABC$の内部の点$P$から辺$BC,CA,AB$へ
下ろした垂線の足をそれぞれ$D,E,F$とする。
$\dfrac{BC}{PD}+\dfrac{CA}{PE}+\dfrac{AB}{PF}$
を最小とする$P$を決定せよ。
図は動画内参照
この動画を見る
$\triangle ABC$の内部の点$P$から辺$BC,CA,AB$へ
下ろした垂線の足をそれぞれ$D,E,F$とする。
$\dfrac{BC}{PD}+\dfrac{CA}{PE}+\dfrac{AB}{PF}$
を最小とする$P$を決定せよ。
図は動画内参照
福田の数学〜慶應義塾大学看護医療学部2025第2問(3)〜数学的帰納法

単元:
#大学入試過去問(数学)#数列#数学的帰納法#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
(3)自然数$n$に対して、
$3^n-2n-1$が
$4$の倍数であることの数学的帰納法を
用いた証明を記述しなさい。
$2025$年慶應義塾大学看護医療学部過去問題
この動画を見る
$\boxed{2}$
(3)自然数$n$に対して、
$3^n-2n-1$が
$4$の倍数であることの数学的帰納法を
用いた証明を記述しなさい。
$2025$年慶應義塾大学看護医療学部過去問題
福田のおもしろ数学484〜漸化式で定まる数列の連続する正の項の最大個数

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
実数列$a_1,a_2,a_3,\cdots $が
$a_n=a_{n-1}-a_{n+2} (n=1,2,3,4\cdots)$
を満たしている。
この数列の連続する要素のうちで、
すべてが正となるものの最大個数はいくつか?
この動画を見る
実数列$a_1,a_2,a_3,\cdots $が
$a_n=a_{n-1}-a_{n+2} (n=1,2,3,4\cdots)$
を満たしている。
この数列の連続する要素のうちで、
すべてが正となるものの最大個数はいくつか?
福田の数学〜慶應義塾大学看護医療学部2025第2問(2)〜円のベクトル方程式

単元:
#大学入試過去問(数学)#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
(2)平面上の異なる$2$点$A(\overrightarrow{a}),B(\overrightarrow{b})$に対して、
ベクトル方程式
$2 \vert \overrightarrow{p}-\overrightarrow{a}=\vert \overrightarrow{p}-\overrightarrow{b}\vert$
を満たす点$P(\overrightarrow{p})$全体の集合は円となる。
この円の中心の位置ベクトルは$\boxed{サ}$で半径は
$\boxed{シ}$となる。
ただし、$\boxed{シ}$では根号を用いない表記とすること。
$2025$年慶應義塾大学看護医療学部過去問題
この動画を見る
$\boxed{2}$
(2)平面上の異なる$2$点$A(\overrightarrow{a}),B(\overrightarrow{b})$に対して、
ベクトル方程式
$2 \vert \overrightarrow{p}-\overrightarrow{a}=\vert \overrightarrow{p}-\overrightarrow{b}\vert$
を満たす点$P(\overrightarrow{p})$全体の集合は円となる。
この円の中心の位置ベクトルは$\boxed{サ}$で半径は
$\boxed{シ}$となる。
ただし、$\boxed{シ}$では根号を用いない表記とすること。
$2025$年慶應義塾大学看護医療学部過去問題
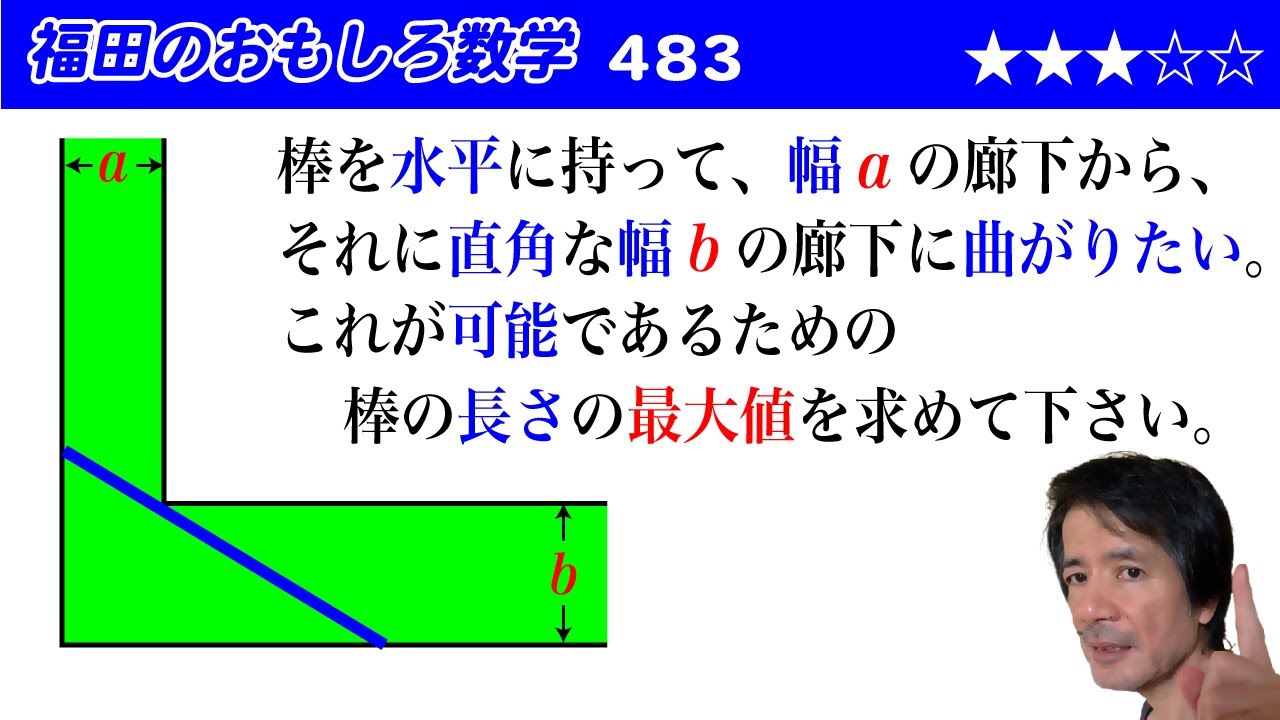
福田のおもしろ数学483〜直角に曲がった廊下を曲がれる棒の長さの最大値
単元:
#数Ⅰ#数A#図形の性質#図形と計量#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
棒を水平に持って、幅$a$の廊下から、
それに直角な幅$b$の廊下に曲がりたい。
これが可能であるための
棒の長さの最大値を求めて下さい。
図は動画内参照
この動画を見る
棒を水平に持って、幅$a$の廊下から、
それに直角な幅$b$の廊下に曲がりたい。
これが可能であるための
棒の長さの最大値を求めて下さい。
図は動画内参照
福田の数学〜慶應義塾大学看護医療学部2025第2問(1)〜極形式とド・モアブルの定理

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
(1)$x^3-3x^2+6x-4=0$の解で
虚部が正であるものを$\omega$としたとき、
$\omega$の絶対値は$\vert \omega \vert=\boxed{キ}$であり、
偏角$\theta$は$\theta=\boxed{ク}$である。
ただし、$0\leqq \theta \lt 2\pi$とする。
また、$\omega^{10} =\boxed{ケ}+\boxed{コ}i$である。
ただし、$\boxed{ケ},\boxed{コ}$は実数とする。
$2025$年慶應義塾大学看護医療学部過去問題
この動画を見る
$\boxed{2}$
(1)$x^3-3x^2+6x-4=0$の解で
虚部が正であるものを$\omega$としたとき、
$\omega$の絶対値は$\vert \omega \vert=\boxed{キ}$であり、
偏角$\theta$は$\theta=\boxed{ク}$である。
ただし、$0\leqq \theta \lt 2\pi$とする。
また、$\omega^{10} =\boxed{ケ}+\boxed{コ}i$である。
ただし、$\boxed{ケ},\boxed{コ}$は実数とする。
$2025$年慶應義塾大学看護医療学部過去問題
【数B】【数列】自然数の式の証明3 ※問題文は概要欄

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
理数個別チャンネル
問題文全文(内容文):
$n$は自然数とする。
$6^n+4= (5+1)^n+4$と変形することで、$6^n+4$が$5$の倍数であることを、二項定理を利用して証明せよ。
この動画を見る
$n$は自然数とする。
$6^n+4= (5+1)^n+4$と変形することで、$6^n+4$が$5$の倍数であることを、二項定理を利用して証明せよ。
【数B】【数列】自然数の式の証明2 ※問題文は概要欄

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
理数個別チャンネル
問題文全文(内容文):
$n$は整数とする。
(1)連続する2個の整数には、必ず$2$の倍数が含まれることを利用して、 $n^2+3n$が$2$の倍数であることを証明せよ。
(2)連続する3個の整数には、必ず$3$の倍数が含まれることを利用して、 $4n^3+3n^2+2n$が$3$の倍数であることを証明せよ。
この動画を見る
$n$は整数とする。
(1)連続する2個の整数には、必ず$2$の倍数が含まれることを利用して、 $n^2+3n$が$2$の倍数であることを証明せよ。
(2)連続する3個の整数には、必ず$3$の倍数が含まれることを利用して、 $4n^3+3n^2+2n$が$3$の倍数であることを証明せよ。
【数B】【数列】自然数の式の証明1 ※問題文は概要欄

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1) 整数$n$を$2$で割った余りで分類することで、$3n^2-n$が$2$の倍数であることを証明せよ。
(2) 整数$n$を$3$で割った余りで分類することで、 $n^3-n+9$が$3$の倍数であることを証明せよ。
この動画を見る
(1) 整数$n$を$2$で割った余りで分類することで、$3n^2-n$が$2$の倍数であることを証明せよ。
(2) 整数$n$を$3$で割った余りで分類することで、 $n^3-n+9$が$3$の倍数であることを証明せよ。
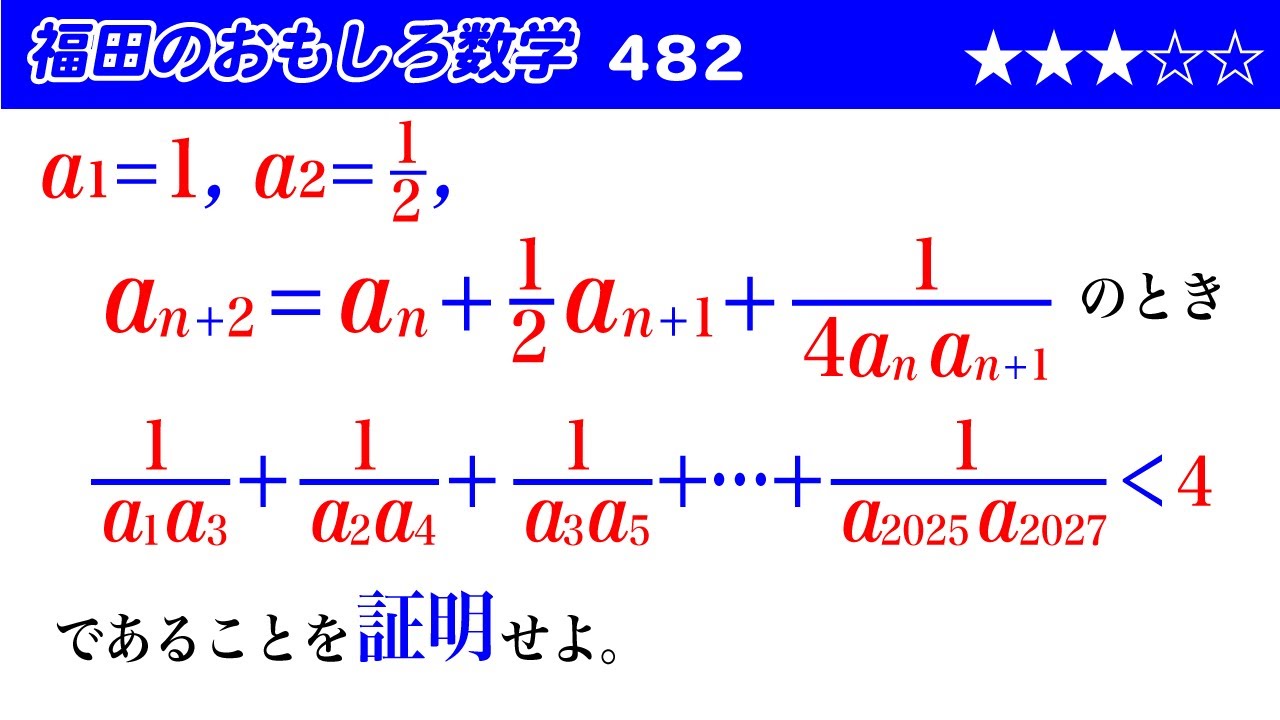
福田のおもしろ数学482〜漸化式で定まる数列に関する不等式の証明
単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数列#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$a_1=1,a_2=\dfrac{1}{2},$
$a_{n+2}=a_n+\dfrac{1}{2}a_{n+1}+\dfrac{1}{4a_na_{n+1}}$のとき、
$\dfrac{1}{a_1a_3}+\dfrac{1}{a_2a_4}+\dfrac{1}{a_3a_5}+\cdots +\dfrac{1}{a_{2025}a_{2027}}\lt 4$
であることを証明せよ。
この動画を見る
$a_1=1,a_2=\dfrac{1}{2},$
$a_{n+2}=a_n+\dfrac{1}{2}a_{n+1}+\dfrac{1}{4a_na_{n+1}}$のとき、
$\dfrac{1}{a_1a_3}+\dfrac{1}{a_2a_4}+\dfrac{1}{a_3a_5}+\cdots +\dfrac{1}{a_{2025}a_{2027}}\lt 4$
であることを証明せよ。
福田の数学〜慶應義塾大学看護医療学部2025第1問(4)〜三角関数の最大
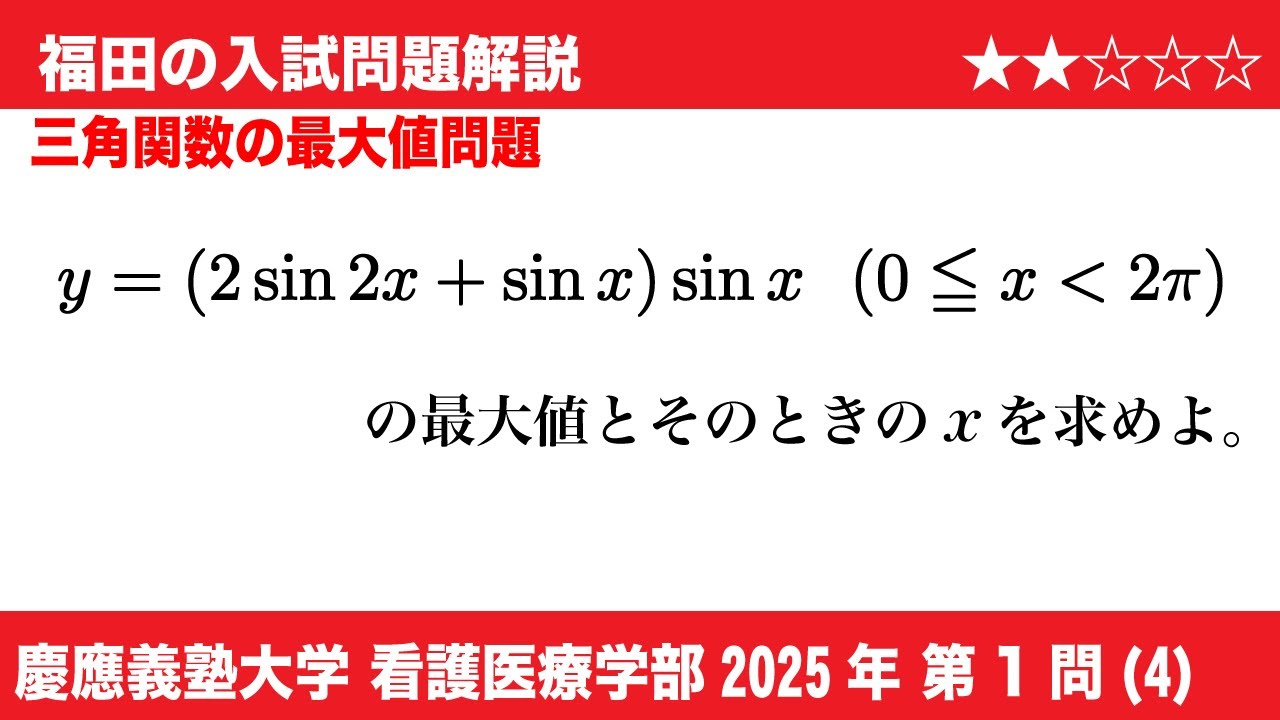
単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(4)関数$y=(2\sin 2x+\sin x)+\sin x (0\leqq x \lt 2\pi)$は、
$x=\boxed{オ}$のとき最大値$\boxed{カ}$をとる。
$2025$年慶應義塾大学看護医療学部過去問題
この動画を見る
$\boxed{1}$
(4)関数$y=(2\sin 2x+\sin x)+\sin x (0\leqq x \lt 2\pi)$は、
$x=\boxed{オ}$のとき最大値$\boxed{カ}$をとる。
$2025$年慶應義塾大学看護医療学部過去問題
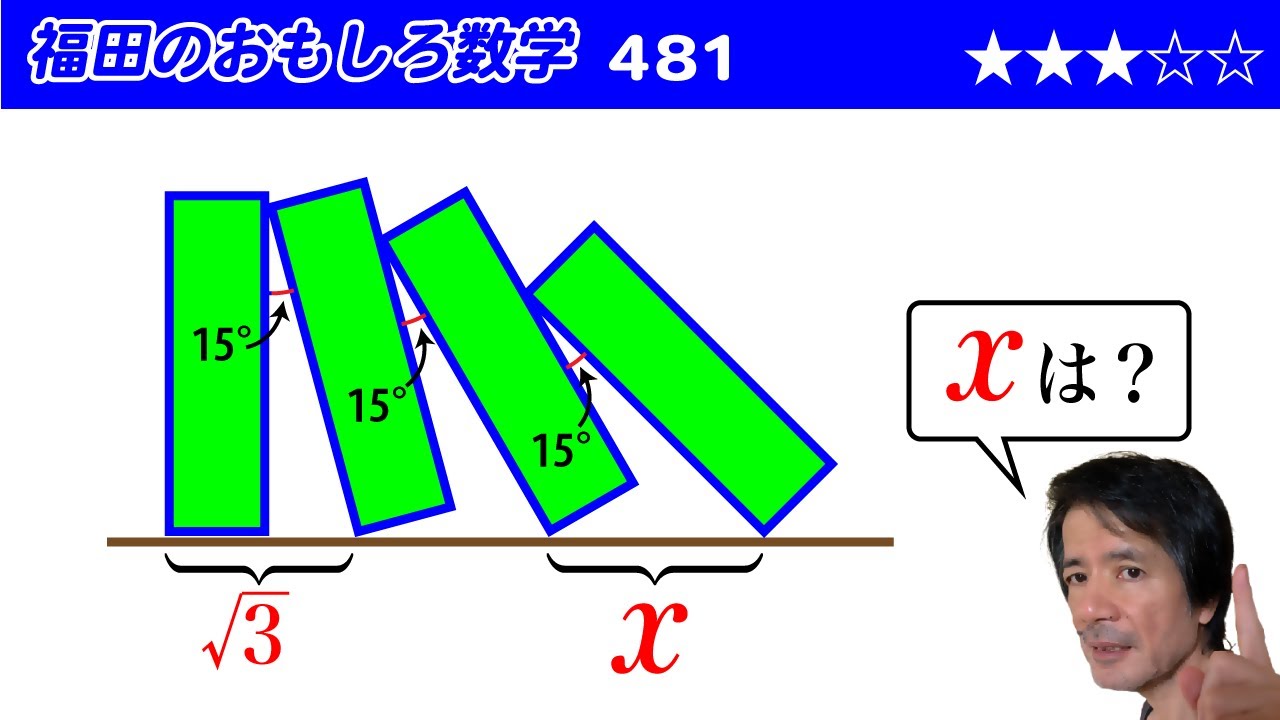
福田のおもしろ数学481〜長方形が15°ずつ傾いてずれていく