 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
【テストによく出る】数学A 一次不定方程式(ユークリッドの互除法を使って特殊解を求める)

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
不定方程式$90x-37y=1$の整数解を求めよ。
この動画を見る
不定方程式$90x-37y=1$の整数解を求めよ。
大学入試問題#106 明治薬科大学(2004) 整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$l,m,n$:自然数
$l \leqq m \leqq n$
$\displaystyle \frac{1}{l}+\displaystyle \frac{1}{m}+\displaystyle \frac{1}{n}=\displaystyle \frac{3}{2}$をみたす組$(l,m,n)$をすべて求めよ。
出典:2004年明治薬科大学 入試問題
この動画を見る
$l,m,n$:自然数
$l \leqq m \leqq n$
$\displaystyle \frac{1}{l}+\displaystyle \frac{1}{m}+\displaystyle \frac{1}{n}=\displaystyle \frac{3}{2}$をみたす組$(l,m,n)$をすべて求めよ。
出典:2004年明治薬科大学 入試問題
共通テスト追試ムズイぞ整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
共通テスト追試の整数問題を解説していきます.
この動画を見る
共通テスト追試の整数問題を解説していきます.
小数部分 立教新座 2022 入試問題解説 28問目 西大和学園も全く同じ問題でした。
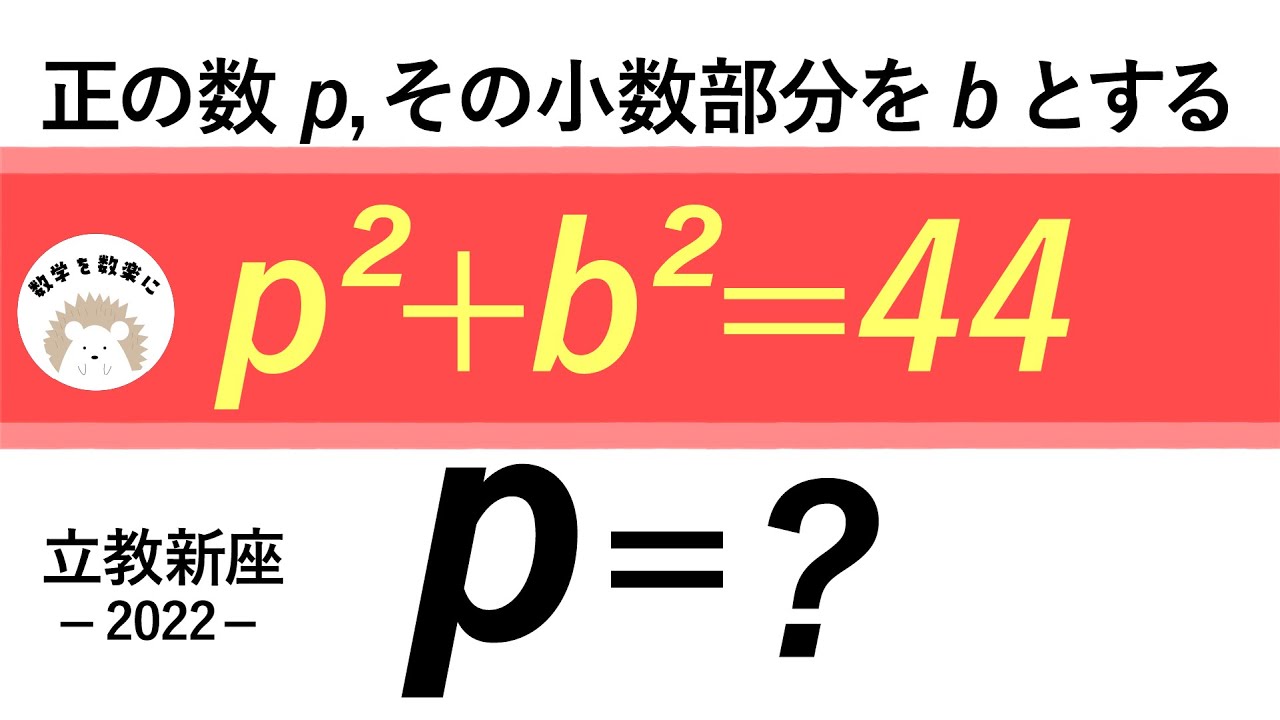
単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
正の数p、その小数部分をbとする
$p^2+b^2 = 44$
p=?
2022立教新座高等学校
この動画を見る
正の数p、その小数部分をbとする
$p^2+b^2 = 44$
p=?
2022立教新座高等学校
円周角 中央大杉並 推薦 2022入試問題解説27問目

単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle MBN = ?$
*図は動画内参照
2022中央大学杉並高等学校
この動画を見る
$\angle MBN = ?$
*図は動画内参照
2022中央大学杉並高等学校
篠原京大塾:2021年(文系数学)過去問解説【篠原好】

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
2021年(文系数学)過去問解説
この動画を見る
2021年(文系数学)過去問解説
2022藤田医科大 等差数列の超基本問題

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
公差が0でない整数の等差数列$a_n$がある
$\sum_{ }^{ } a_n$はn=7で
最大値119 $a_n$を求めよ。
藤田医学科大学
この動画を見る
公差が0でない整数の等差数列$a_n$がある
$\sum_{ }^{ } a_n$はn=7で
最大値119 $a_n$を求めよ。
藤田医学科大学
cosで合成 2通りで解説!

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{1}{2}cosθ+\frac{\sqrt 3}{2} sinθ$を
$▢cos(θ - ○)$の形に直せ
この動画を見る
$\frac{1}{2}cosθ+\frac{\sqrt 3}{2} sinθ$を
$▢cos(θ - ○)$の形に直せ
【0から理解できる】一次不定方程式を解説しました!(数学A・整数)

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の不定方程式の整数解を求めよ。
(1)$5x-3y=1$
(2)$5x-3y=4$
この動画を見る
次の不定方程式の整数解を求めよ。
(1)$5x-3y=1$
(2)$5x-3y=4$
大学入試問題#105 京都大学(2003) 数列
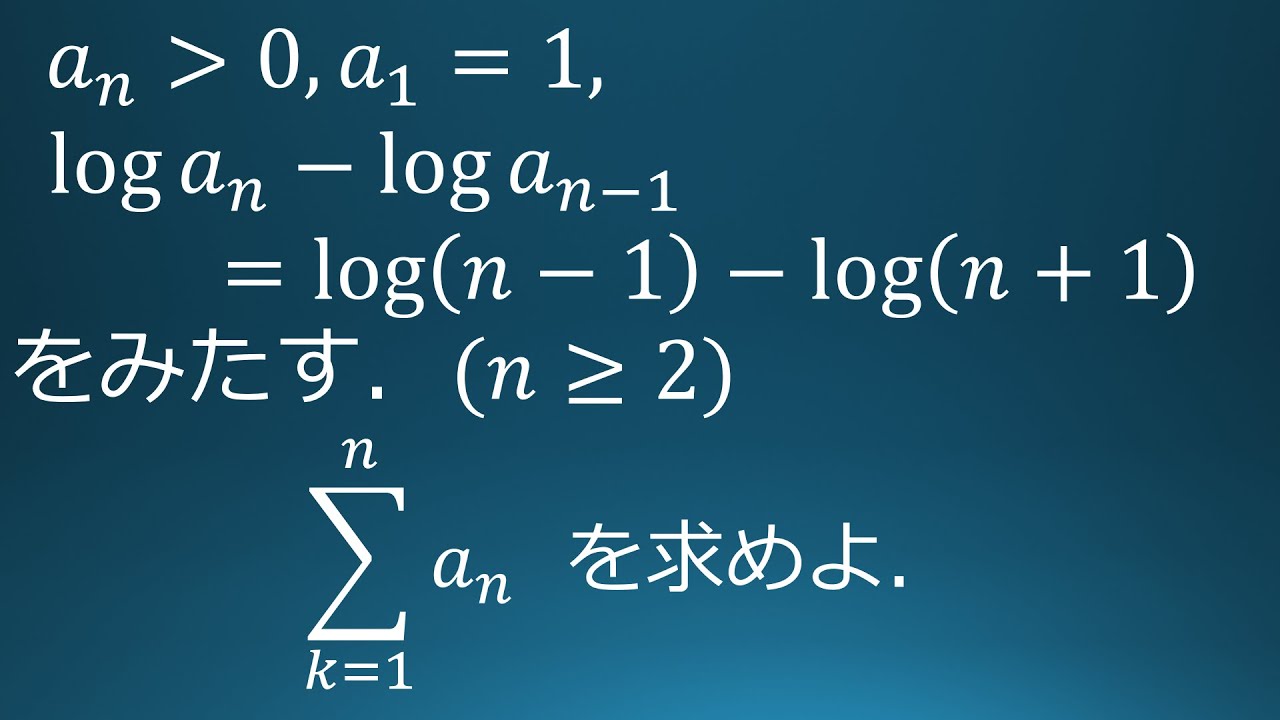
単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数B
指導講師:
ますただ
問題文全文(内容文):
$a_n \gt 0,\ a_1=1$
$n \geqq 2$のとき
$log\ a_n-log\ a_{n-1}=log(n-1)-log(n+1)$である。
$\displaystyle \sum_{k=1}^n a_k$を求めよ
出典:2003年京都大学 入試問題
この動画を見る
$a_n \gt 0,\ a_1=1$
$n \geqq 2$のとき
$log\ a_n-log\ a_{n-1}=log(n-1)-log(n+1)$である。
$\displaystyle \sum_{k=1}^n a_k$を求めよ
出典:2003年京都大学 入試問題
2022関西医科 超基本問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#関西医科大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x=\displaystyle \frac{6x^2+17x+10}{3x-2}$
(1)$f(x) \gt 0$を解け
(2)$f(n)$の値が自然数となる整数$n$
を求めよ。
2022年 関西医科過去問
この動画を見る
$x=\displaystyle \frac{6x^2+17x+10}{3x-2}$
(1)$f(x) \gt 0$を解け
(2)$f(n)$の値が自然数となる整数$n$
を求めよ。
2022年 関西医科過去問
【数Ⅱ】内分の公式・外分の公式を導出から丁寧に【公式を1つだけにする!?】

単元:
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$ 数直線上の点A(3),B(6)について,線分ABを3:2に内分する点Pの座標を求めよ.$
この動画を見る
$ 数直線上の点A(3),B(6)について,線分ABを3:2に内分する点Pの座標を求めよ.$
余りに関する問題 2022灘中(改)

単元:
#算数(中学受験)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#過去問解説(学校別)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$2^{2022}$を17で割った余りは?
2022灘中学校
この動画を見る
$2^{2022}$を17で割った余りは?
2022灘中学校
【数学A/整数】ユークリッドの互除法(文字式)

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
$7n+6$と$2n+3$の最大公約数が$3$になるような$20$以下の自然数$n$をすべて求めよ。
この動画を見る
$7n+6$と$2n+3$の最大公約数が$3$になるような$20$以下の自然数$n$をすべて求めよ。
大学入試問題#104 一橋大学(2006) ベクトル

単元:
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$|\vec{ a }|=5,|\vec{ b }|=3,|\vec{ c }|=1$
$\vec{ Z }=\vec{ a }+\vec{ b }+\vec{ c }$
(1)$|\vec{ Z }|$の最大値、最小値
(2)$\vec{ a }・\vec{ Z }=20$
をみたすとき
$|\vec{ Z }|$の最大値、最小値を求めよ
出典:2006年一橋大学 入試問題
この動画を見る
$|\vec{ a }|=5,|\vec{ b }|=3,|\vec{ c }|=1$
$\vec{ Z }=\vec{ a }+\vec{ b }+\vec{ c }$
(1)$|\vec{ Z }|$の最大値、最小値
(2)$\vec{ a }・\vec{ Z }=20$
をみたすとき
$|\vec{ Z }|$の最大値、最小値を求めよ
出典:2006年一橋大学 入試問題
整数問題 千葉大(医)類題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
整数$k,n$を
$k^2=3^n+360$
全て求めよ。
千葉大(医)過去問
この動画を見る
整数$k,n$を
$k^2=3^n+360$
全て求めよ。
千葉大(医)過去問
【数学A/整数】ユークリッドの互除法

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
1207と994の最大公約数を、ユークリッドの互除法を用いて求めよ。
この動画を見る
1207と994の最大公約数を、ユークリッドの互除法を用いて求めよ。
9で割り切れるのはなぜ?京都大(改)

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$n^9 - n^3$は9で割り切れるのはなぜ?(n:整数)
京都大学
この動画を見る
$n^9 - n^3$は9で割り切れるのはなぜ?(n:整数)
京都大学
大学入試問題#103 東海大学医学部(2017) 二項定理
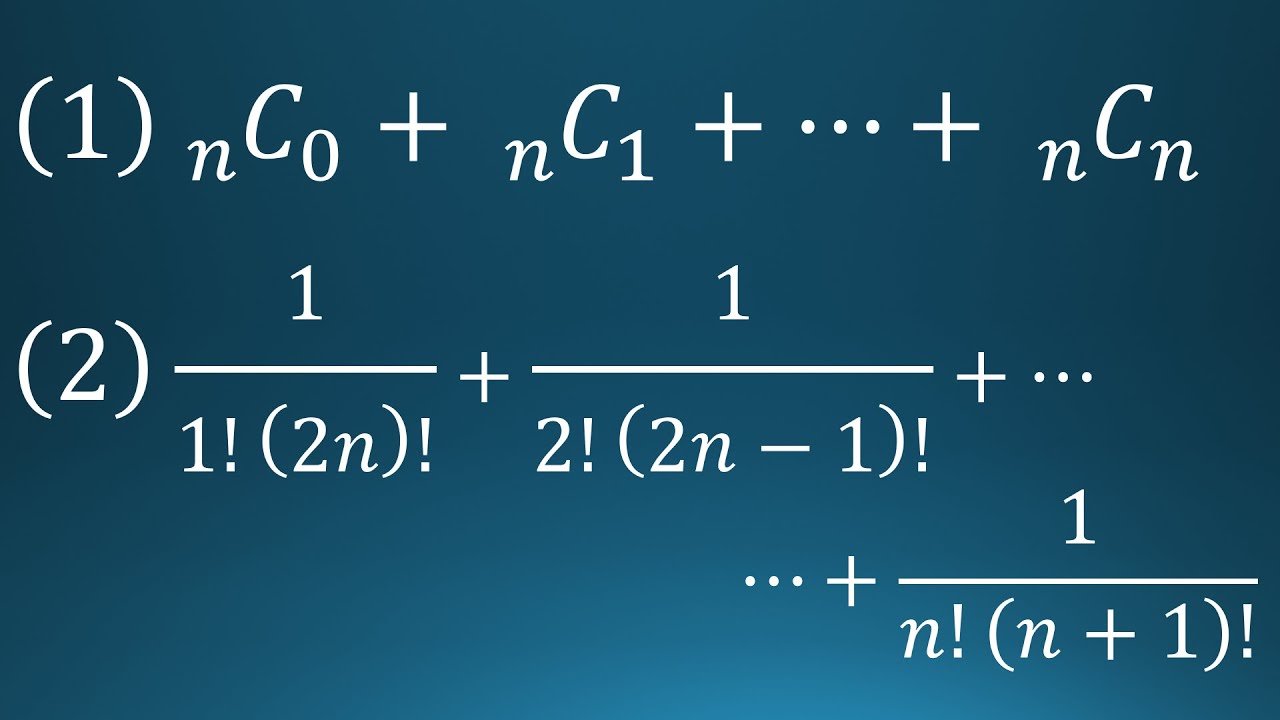
単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#数学(高校生)#東海大学
指導講師:
ますただ
問題文全文(内容文):
次の和を求めよ。
(1)
${}_{ n }C_0+{}_{ n }C_1+・・・+{}_{ n }C_n$
(2)
$\displaystyle \frac{1}{1!(2n)!}+\displaystyle \frac{1}{2(2n-1)!}+・・・+\displaystyle \frac{1}{n!(n+1)!}$
出典:2017年東海大学医学部 入試問題
この動画を見る
次の和を求めよ。
(1)
${}_{ n }C_0+{}_{ n }C_1+・・・+{}_{ n }C_n$
(2)
$\displaystyle \frac{1}{1!(2n)!}+\displaystyle \frac{1}{2(2n-1)!}+・・・+\displaystyle \frac{1}{n!(n+1)!}$
出典:2017年東海大学医学部 入試問題
これ解ける?

単元:
#その他#その他#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$3x-5y=4$のとき$\displaystyle \frac{27^{ x }}{243^{ y }}$を求めよ
この動画を見る
$3x-5y=4$のとき$\displaystyle \frac{27^{ x }}{243^{ y }}$を求めよ
チェバの定理使わずに解ける? 香川誠陵 2022入試問題解説23問目
単元:
#数学(中学生)#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
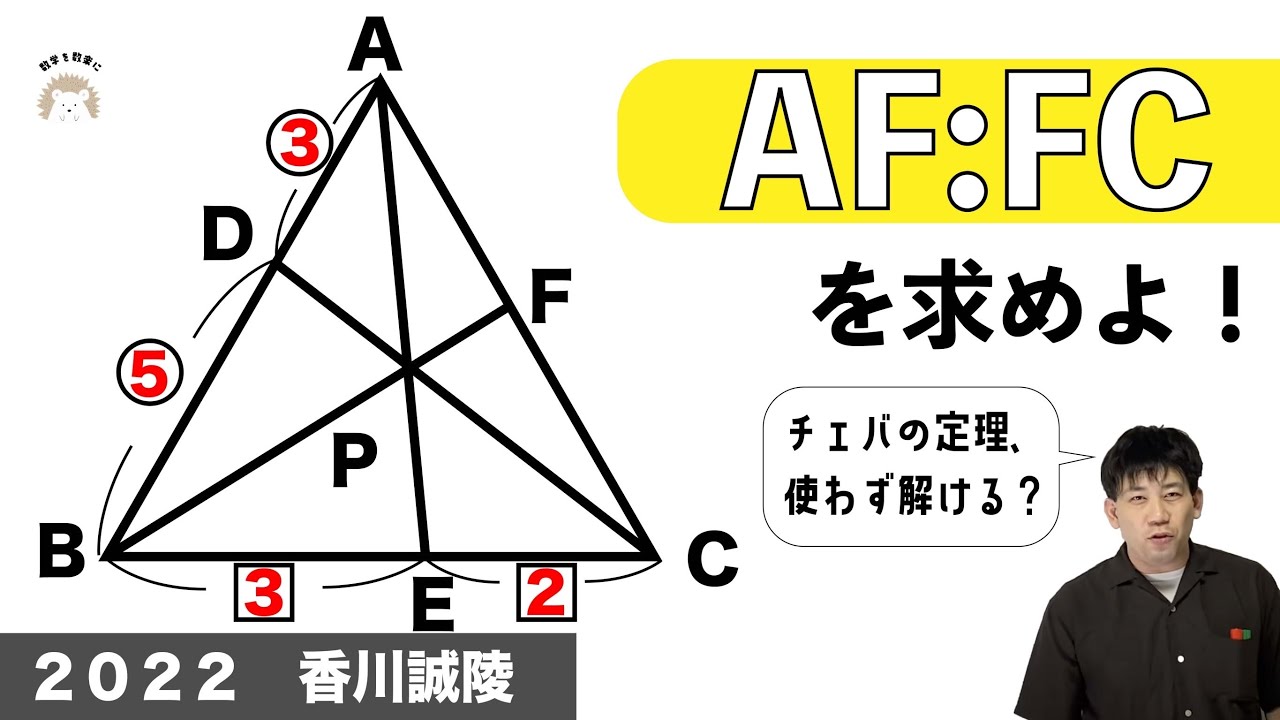
チェバの定理は使わない
AF:FCを求めよ
*図は動画内参照
2022香川誠陵高等学校
この動画を見る
チェバの定理は使わない
AF:FCを求めよ
*図は動画内参照
2022香川誠陵高等学校
【数学A/整数】最大公約数と最小公倍数を求める

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
120と252の最大公約数と最小公倍数を求めよ。
この動画を見る
120と252の最大公約数と最小公倍数を求めよ。
因数分解
大学入試問題#102 高知女子大学(1988) 無限級数
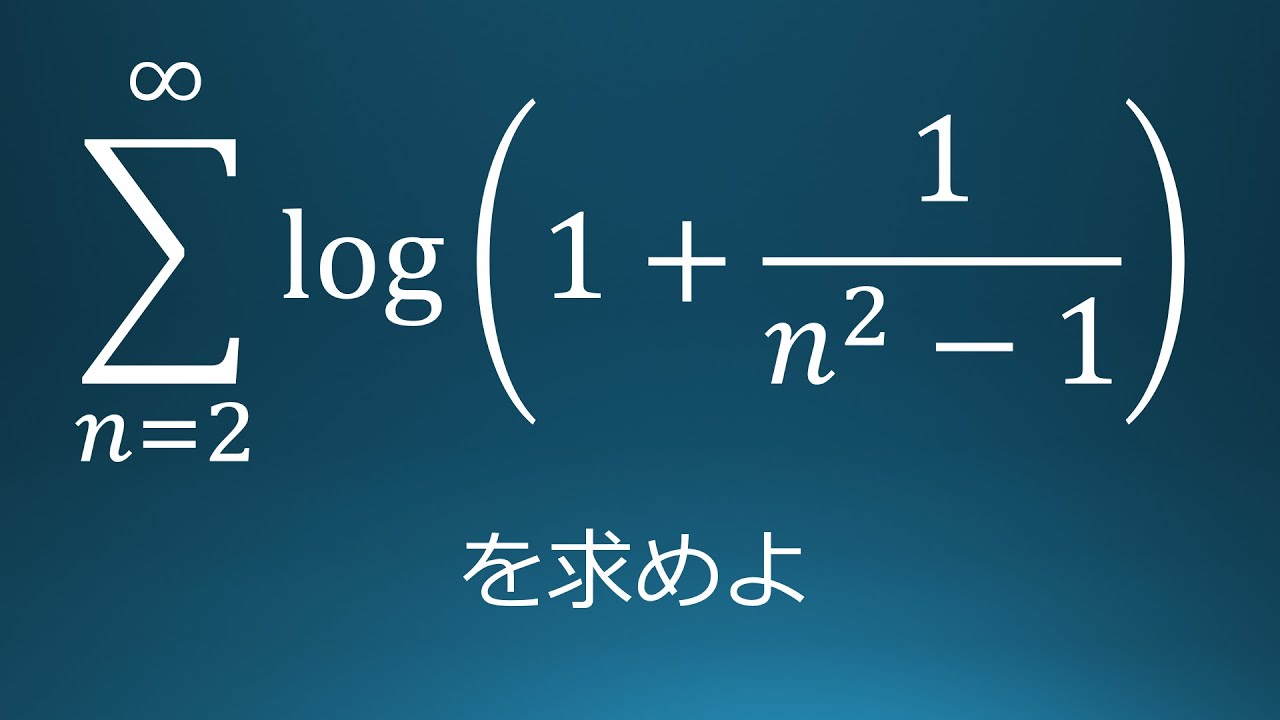
単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \sum_{n=2}^\infty log(1+\displaystyle \frac{1}{n^2-1})$を求めよ。
出典:1988年高知女子大学 入試問題
この動画を見る
$\displaystyle \sum_{n=2}^\infty log(1+\displaystyle \frac{1}{n^2-1})$を求めよ。
出典:1988年高知女子大学 入試問題
高校入試レベルだよ
指数方程式 解はアレだけじゃないよ

【高校数学】時間内で誰ができるねん~共通テスト数学ⅠA第4問解説~【大学受験】

単元:
#数A#大学入試過去問(数学)#整数の性質#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
(4) $11^4$を$2^4$で割ったときの余りは1に等しい。不定方程式
$11^5x-2^5y=1$
の整数解のうち、$x$が正の整数で最小になるのは、$x=$テト, $y=$ナニヌネノである
この動画を見る
(4) $11^4$を$2^4$で割ったときの余りは1に等しい。不定方程式
$11^5x-2^5y=1$
の整数解のうち、$x$が正の整数で最小になるのは、$x=$テト, $y=$ナニヌネノである
指数方程式 解はアレだけじゃないよ

【数学A/整数】約数の個数と総和

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
180の約数の個数とその総和を求めよ。
この動画を見る
180の約数の個数とその総和を求めよ。
sin sin sin sin sin sin sin sin sin sin sin sin
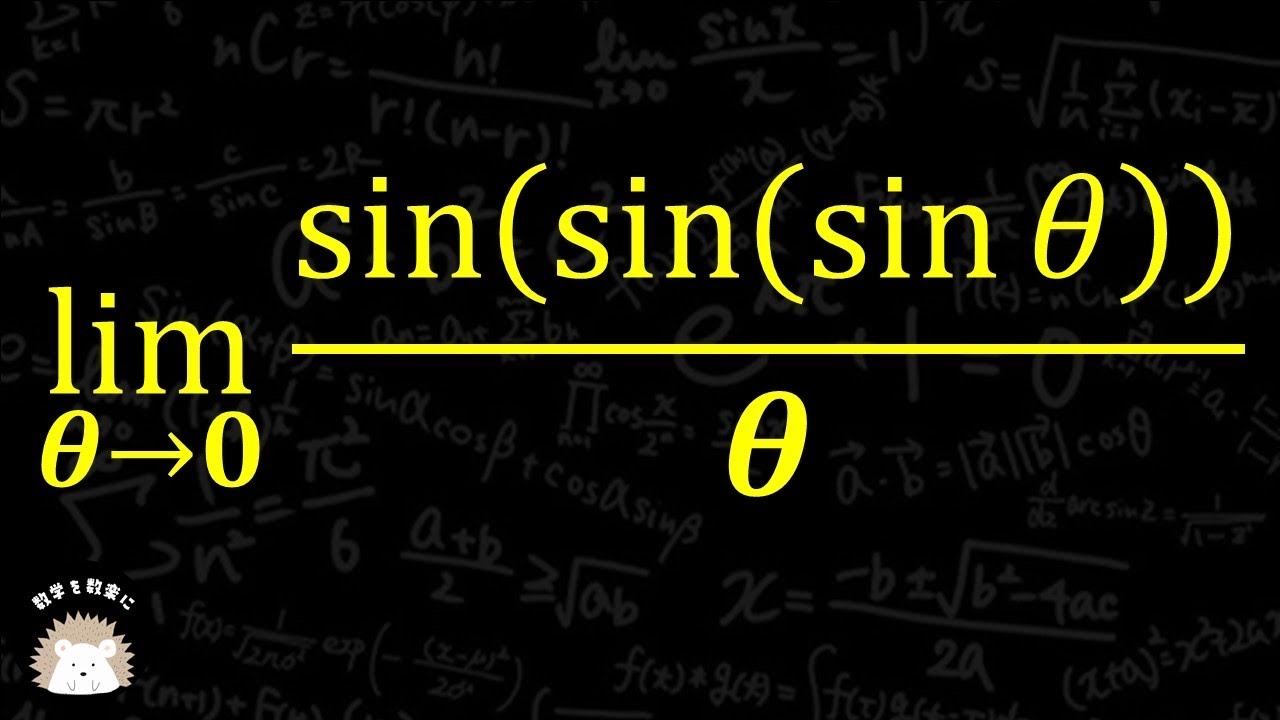
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$
\displaystyle \lim_{ θ \to 0 } \frac{sin(sin(sin θ))}{θ}
$
この動画を見る
$
\displaystyle \lim_{ θ \to 0 } \frac{sin(sin(sin θ))}{θ}
$
