 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
【理数個別の過去問解説】2020年度横浜国立大学 数学 第4問(1)解説

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
横浜国立大学2020年度大問4(1)
xyz空間に、2点A(1,2,9)、B(-3,6,7)を通る直線lがある。また、l上の点P、Qと、x軸上の点R、Sは
直線$PR⊥xy$平面、直線$QS⊥x$軸、直線$QS⊥l$
を満たす。次の問いに答えよ。
(1)P、Rの座標を求めよ。
(2)Q、Sの座標を求めよ。
(3)線分PQをx軸のまわりに1回転してできる局面と、Pを含みx軸に垂直な平面と、Qを含みx軸に垂直な平面で囲まれた立体の体積を求めよ。
この動画を見る
横浜国立大学2020年度大問4(1)
xyz空間に、2点A(1,2,9)、B(-3,6,7)を通る直線lがある。また、l上の点P、Qと、x軸上の点R、Sは
直線$PR⊥xy$平面、直線$QS⊥x$軸、直線$QS⊥l$
を満たす。次の問いに答えよ。
(1)P、Rの座標を求めよ。
(2)Q、Sの座標を求めよ。
(3)線分PQをx軸のまわりに1回転してできる局面と、Pを含みx軸に垂直な平面と、Qを含みx軸に垂直な平面で囲まれた立体の体積を求めよ。
福田の数学〜立教大学2021年理学部第1問(4)〜数列の和と不等式の評価

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ (4)一般項が$a_n=\frac{2}{n(n+2)}$であるような数列$\left\{a_n\right\}$の初項から第n項までの和
を$S_n$とする。$S_n \gt \frac{7}{6}$を満たす最小の自然数$n$は$\boxed{\ \ オ\ \ }$である。
2021立教大学理学部過去問
この動画を見る
${\Large\boxed{1}}$ (4)一般項が$a_n=\frac{2}{n(n+2)}$であるような数列$\left\{a_n\right\}$の初項から第n項までの和
を$S_n$とする。$S_n \gt \frac{7}{6}$を満たす最小の自然数$n$は$\boxed{\ \ オ\ \ }$である。
2021立教大学理学部過去問
福田のわかった数学〜高校3年生理系081〜グラフを描こう(3)対数関数のグラフ

単元:
#数Ⅱ#指数関数と対数関数#対数関数#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ グラフを描こう(3)
$y=x(\log x-1)^2$
のグラフを描け。ただし凹凸は調べなくてよい。
この動画を見る
数学$\textrm{III}$ グラフを描こう(3)
$y=x(\log x-1)^2$
のグラフを描け。ただし凹凸は調べなくてよい。
大学入試問題#26 東京理科大学(2021) 数列
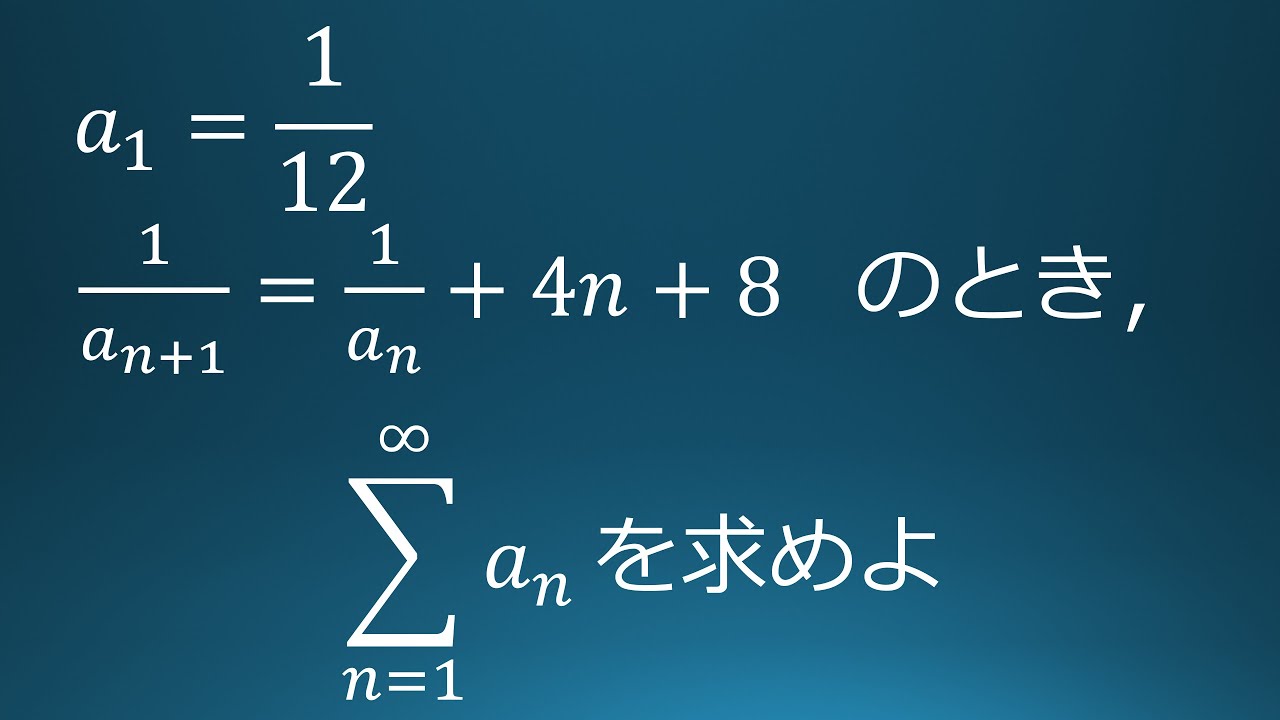
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$a_1=\displaystyle \frac{1}{12}$
$\displaystyle \frac{1}{a_{n+1}}=\displaystyle \frac{1}{a_n}+4n+8$
で定まる数列$\{a_n\}$において$\displaystyle \sum_{n=1}^\infty\ a_n$を求めよ
出典:2021年東京理科大学 入試問題
この動画を見る
$a_1=\displaystyle \frac{1}{12}$
$\displaystyle \frac{1}{a_{n+1}}=\displaystyle \frac{1}{a_n}+4n+8$
で定まる数列$\{a_n\}$において$\displaystyle \sum_{n=1}^\infty\ a_n$を求めよ
出典:2021年東京理科大学 入試問題
【理数個別の過去問解説】2020年度横浜国立大学 数学 第3問(3)解説

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
中身の見えない2つの箱A、Bがある。箱Aには白玉と赤玉がそれぞれ2個ずつ入っており、箱Bには白玉1個だけが入っている。このとき、nを正の整数として、次の操作(*)を考える。
(*)はじめに、箱Aの中身をよくかきまぜて、箱Aから玉を2個取り出し、色を確認しないで、箱Bに2個とも入れる。次に、「箱Bの中身をよくかきまぜて、箱Bから玉を1個取り出し、色を確認した後、箱Bに戻す」という作業をn回繰り返す。
操作(*)を一度行なったとき、箱Bから取り出した玉がn回ともすべて白玉である確率を$p_n$とし、箱Bから取り出した玉がn回ともすべて白玉であるという条件のもとで、はじめに箱Aから取り出した玉が2個とも白玉である条件付き確率を$q_n$とする。次の問いに答えよ。
(1)$p_2、q_2$を求めよ。
(2)$p_n、q_n$を求めよ。
(3)$q_n\gt \dfrac{1}{2}$をみたす最小のnの値を求めよ。
この動画を見る
中身の見えない2つの箱A、Bがある。箱Aには白玉と赤玉がそれぞれ2個ずつ入っており、箱Bには白玉1個だけが入っている。このとき、nを正の整数として、次の操作(*)を考える。
(*)はじめに、箱Aの中身をよくかきまぜて、箱Aから玉を2個取り出し、色を確認しないで、箱Bに2個とも入れる。次に、「箱Bの中身をよくかきまぜて、箱Bから玉を1個取り出し、色を確認した後、箱Bに戻す」という作業をn回繰り返す。
操作(*)を一度行なったとき、箱Bから取り出した玉がn回ともすべて白玉である確率を$p_n$とし、箱Bから取り出した玉がn回ともすべて白玉であるという条件のもとで、はじめに箱Aから取り出した玉が2個とも白玉である条件付き確率を$q_n$とする。次の問いに答えよ。
(1)$p_2、q_2$を求めよ。
(2)$p_n、q_n$を求めよ。
(3)$q_n\gt \dfrac{1}{2}$をみたす最小のnの値を求めよ。
超簡単な方程式

単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.$ 0\leqq x\leqq 2\pi$
$25^{\cos x}-6・5^{\cos x-\frac{1}{2}}+1=0$
この動画を見る
これを解け.$ 0\leqq x\leqq 2\pi$
$25^{\cos x}-6・5^{\cos x-\frac{1}{2}}+1=0$
【理数個別の過去問解説】2020年度横浜国立大学 数学 第3問(2)解説

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
中身の見えない2つの箱A、Bがある。箱Aには白玉と赤玉がそれぞれ2個ずつ入っており、箱Bには白玉1個だけが入っている。このとき、nを正の整数として、次の操作(*)を考える。
(*)はじめに、箱Aの中身をよくかきまぜて、箱Aから玉を2個取り出し、色を確認しないで、箱Bに2個とも入れる。次に、「箱Bの中身をよくかきまぜて、箱Bから玉を1個取り出し、色を確認した後、箱Bに戻す」という作業をn回繰り返す。
操作(*)を一度行なったとき、箱Bから取り出した玉がn回ともすべて白玉である確率を$p_n$とし、箱Bから取り出した玉がn回ともすべて白玉であるという条件のもとで、はじめに箱Aから取り出した玉が2個とも白玉である条件付き確率を$q_n$とする。次の問いに答えよ。
(1)$p_2、q_2$を求めよ。
(2)$p_n、q_n$を求めよ。
(3)$q_n\gt \dfrac{1}{2}$をみたす最小のnの値を求めよ。
この動画を見る
中身の見えない2つの箱A、Bがある。箱Aには白玉と赤玉がそれぞれ2個ずつ入っており、箱Bには白玉1個だけが入っている。このとき、nを正の整数として、次の操作(*)を考える。
(*)はじめに、箱Aの中身をよくかきまぜて、箱Aから玉を2個取り出し、色を確認しないで、箱Bに2個とも入れる。次に、「箱Bの中身をよくかきまぜて、箱Bから玉を1個取り出し、色を確認した後、箱Bに戻す」という作業をn回繰り返す。
操作(*)を一度行なったとき、箱Bから取り出した玉がn回ともすべて白玉である確率を$p_n$とし、箱Bから取り出した玉がn回ともすべて白玉であるという条件のもとで、はじめに箱Aから取り出した玉が2個とも白玉である条件付き確率を$q_n$とする。次の問いに答えよ。
(1)$p_2、q_2$を求めよ。
(2)$p_n、q_n$を求めよ。
(3)$q_n\gt \dfrac{1}{2}$をみたす最小のnの値を求めよ。
福田の数学〜立教大学2021年理学部第1問(3)〜じゃんけんの確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(3)4人でじゃんけんを1回するとき、ちょうど2人が勝つ確率は$\boxed{\ \ ウ\ \ }$であり、
また、だれも勝たない確率は$\boxed{\ \ エ\ \ }$である。
2021立教大学理学部過去問
この動画を見る
${\Large\boxed{1}}$(3)4人でじゃんけんを1回するとき、ちょうど2人が勝つ確率は$\boxed{\ \ ウ\ \ }$であり、
また、だれも勝たない確率は$\boxed{\ \ エ\ \ }$である。
2021立教大学理学部過去問
福田のわかった数学〜高校2年生063〜三角関数(2)三角関数の定義

単元:
#数Ⅱ#三角関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 三角関数(2) 三角関数の定義
一般角$\theta$に対して
$\sin\theta, \cos\theta$
の定義を説明せよ。
この動画を見る
数学$\textrm{II}$ 三角関数(2) 三角関数の定義
一般角$\theta$に対して
$\sin\theta, \cos\theta$
の定義を説明せよ。
大学入試問題#25 岩手大学(2020) 複素数

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#岩手大学
指導講師:
ますただ
問題文全文(内容文):
絶対値が1で偏角が$\displaystyle \frac{\pi}{5}$の複素数を$z$とする。
(1)$1+z+z^2+・・・+z^9$を求めよ。
(2)$z^4-z^3+z^2-z$を求めよ。
出典:2020年岩手大学 入試問題
この動画を見る
絶対値が1で偏角が$\displaystyle \frac{\pi}{5}$の複素数を$z$とする。
(1)$1+z+z^2+・・・+z^9$を求めよ。
(2)$z^4-z^3+z^2-z$を求めよ。
出典:2020年岩手大学 入試問題
【理数個別の過去問解説】2020年度横浜国立大学 数学 第3問(1)解説

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
横浜国立大学2020年度大問3(1)
中身の見えない2つの箱A、Bがある。箱Aには白玉と赤玉がそれぞれ2個ずつ入っており、箱Bには白玉1個だけが入っている。このとき、nを正の整数として、次の操作(*)を考える。
(*)はじめに、箱Aの中身をよくかきまぜて、箱Aから玉を2個取り出し、色を確認しないで、箱Bに2個とも入れる。次に、「箱Bの中身をよくかきまぜて、箱Bから玉を1個取り出し、色を確認した後、箱Bに戻す」という作業をn回繰り返す。
操作(*)を一度行なったとき、箱Bから取り出した玉がn回ともすべて白玉である確率を$p_n$とし、箱Bから取り出した玉がn回ともすべて白玉であるという条件のもとで、はじめに箱Aから取り出した玉が2個とも白玉である条件付き確率を$q_n$とする。次の問いに答えよ。
(1)$p_2、q_2$を求めよ。
(2)$p_n、q_n$を求めよ。
(3)$q_n\gt \dfrac{1}{2}$をみたす最小のnの値を求めよ。
この動画を見る
横浜国立大学2020年度大問3(1)
中身の見えない2つの箱A、Bがある。箱Aには白玉と赤玉がそれぞれ2個ずつ入っており、箱Bには白玉1個だけが入っている。このとき、nを正の整数として、次の操作(*)を考える。
(*)はじめに、箱Aの中身をよくかきまぜて、箱Aから玉を2個取り出し、色を確認しないで、箱Bに2個とも入れる。次に、「箱Bの中身をよくかきまぜて、箱Bから玉を1個取り出し、色を確認した後、箱Bに戻す」という作業をn回繰り返す。
操作(*)を一度行なったとき、箱Bから取り出した玉がn回ともすべて白玉である確率を$p_n$とし、箱Bから取り出した玉がn回ともすべて白玉であるという条件のもとで、はじめに箱Aから取り出した玉が2個とも白玉である条件付き確率を$q_n$とする。次の問いに答えよ。
(1)$p_2、q_2$を求めよ。
(2)$p_n、q_n$を求めよ。
(3)$q_n\gt \dfrac{1}{2}$をみたす最小のnの値を求めよ。
e^π>22 示せ
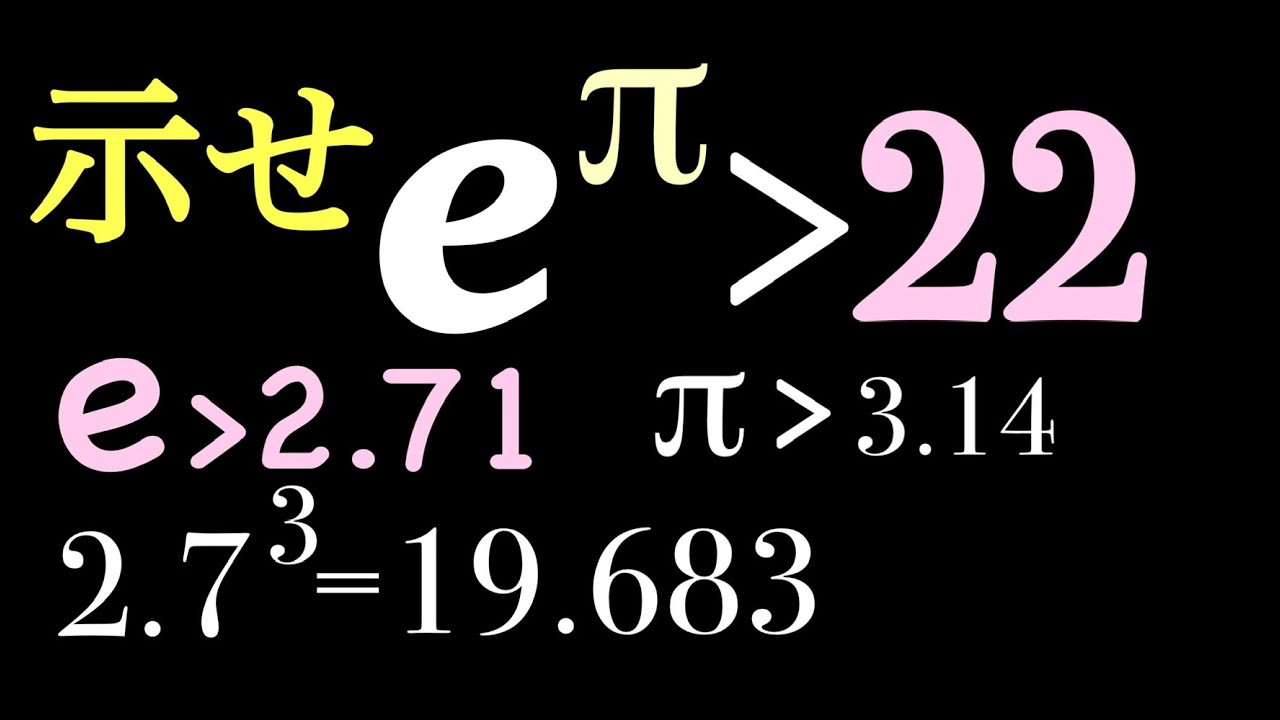
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$e^{\pi}\gt 22$を示せ.
$e \gt 2.71,\pi\gt 3.14$
この動画を見る
$e^{\pi}\gt 22$を示せ.
$e \gt 2.71,\pi\gt 3.14$
【英語】2021年第2回K塾記述模試解説大問4 -2~後編~

単元:
#大学入試過去問(数学)#全統模試(河合塾)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
和訳問題:Interesting as this sounds, the story has a flaw.
この動画を見る
和訳問題:Interesting as this sounds, the story has a flaw.
【困難は分割せよ!】関数:ラ・サール高等学校~全国入試問題解法

単元:
#数学(中学生)#関数(分数関数・無理関数・逆関数と合成関数)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 ラ・サール高等学校
$-1 \leqq x \leqq 2, 3 \leqq y \leqq 4$
のとき、
$x^2y-y$
の最大値と最小値を求めよ。
この動画を見る
入試問題 ラ・サール高等学校
$-1 \leqq x \leqq 2, 3 \leqq y \leqq 4$
のとき、
$x^2y-y$
の最大値と最小値を求めよ。
これ一瞬で約分出来たらすごくね?

単元:
#算数(中学受験)#数学(中学生)#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
正答率1%の問題
$\displaystyle\frac{x^6+a^2x^3y}{x^6-a^4y^2}$
この動画を見る
正答率1%の問題
$\displaystyle\frac{x^6+a^2x^3y}{x^6-a^4y^2}$
福田の数学〜立教大学2021年理学部第1問(2)〜3直線が1点で交わる条件

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#点と直線#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(2)$t$を実数とする。座標平面上の3つの直線
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+(2t-2)y-4t+2=0 \\
x+(2t+2)y-4t-2=0 \\
2tx+y-4t=0
\end{array}
\right.
(-2 \leqq t \leqq 1)
\end{eqnarray}$
が1つの点で交わるようなtの値を全て求めると$t=\boxed{イ}$である。
2021立教大学理学部過去問
この動画を見る
${\Large\boxed{1}}$(2)$t$を実数とする。座標平面上の3つの直線
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+(2t-2)y-4t+2=0 \\
x+(2t+2)y-4t-2=0 \\
2tx+y-4t=0
\end{array}
\right.
(-2 \leqq t \leqq 1)
\end{eqnarray}$
が1つの点で交わるようなtの値を全て求めると$t=\boxed{イ}$である。
2021立教大学理学部過去問
福田のわかった数学〜高校1年生063〜場合の数(2)完全順列

単元:
#数A#場合の数と確率#場合の数#数列#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 場合の数(2) 完全順列
1,2,3,4を1列に並べたものを$a_1a_2a_3a_4$とする。
$a_1\neq 1,a_2\neq 2,a_3\neq 3,a_4\neq 4$を満たす並べ方は何通りあるか。
この動画を見る
数学$\textrm{I}$ 場合の数(2) 完全順列
1,2,3,4を1列に並べたものを$a_1a_2a_3a_4$とする。
$a_1\neq 1,a_2\neq 2,a_3\neq 3,a_4\neq 4$を満たす並べ方は何通りあるか。
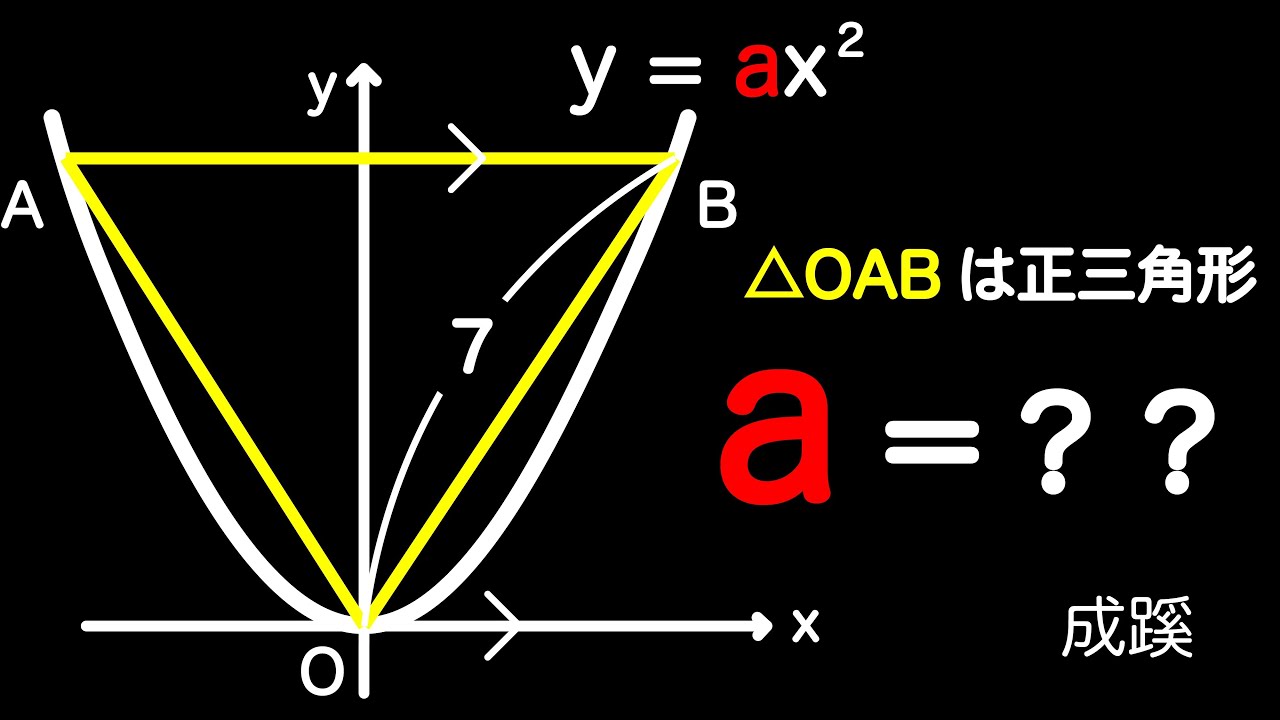
放物線と正三角形 成蹊
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△OABは正三角形
a=?
*図は動画内参照
成蹊高等学校
この動画を見る
△OABは正三角形
a=?
*図は動画内参照
成蹊高等学校
【数Ⅰ】データの分析の全用語を解説【これだけでデータの分析はバッチシ】

大学入試問題#24 秋田大学(2020) 定積分
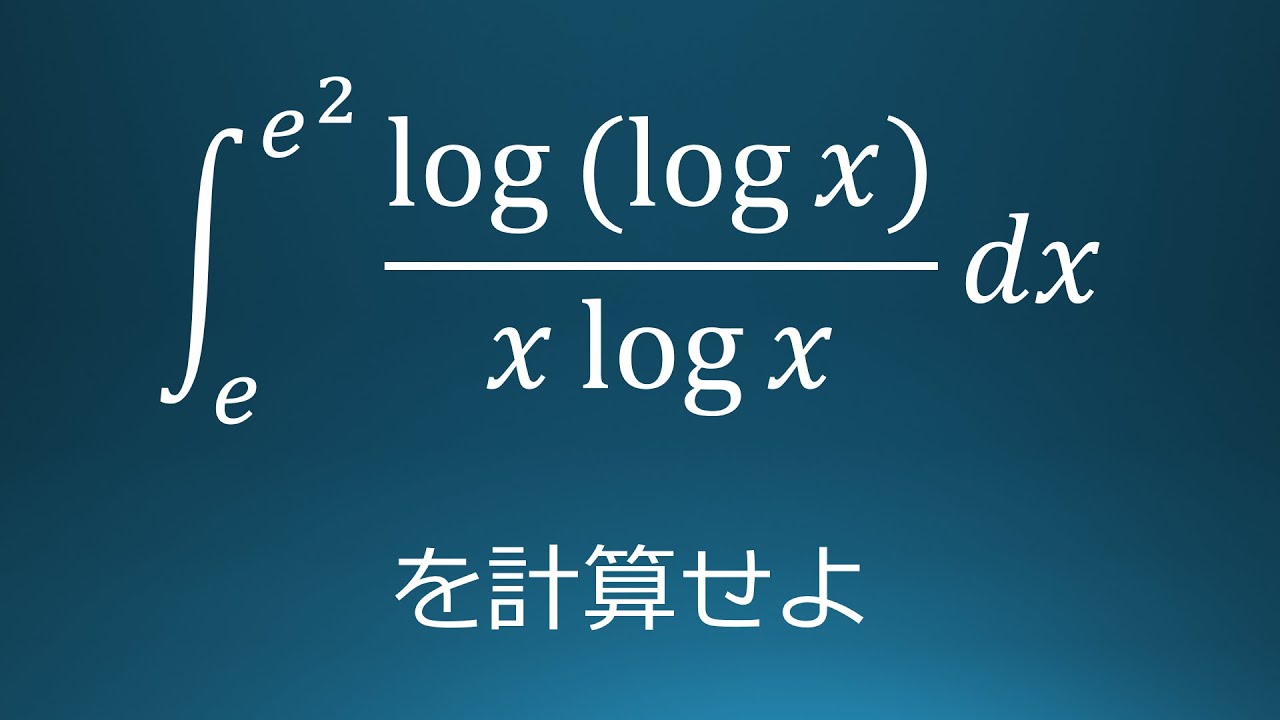
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#秋田大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{e}^{e^2}\displaystyle \frac{log(log\ x)}{x\ log\ x}\ dx$を計算せよ。
出典:2020年秋田大学 入試問題
この動画を見る
$\displaystyle \int_{e}^{e^2}\displaystyle \frac{log(log\ x)}{x\ log\ x}\ dx$を計算せよ。
出典:2020年秋田大学 入試問題
【理数個別の過去問解説】2020年度横浜国立大学 数学 第2問(2)解説

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
横浜国立大学2020年度大問2(2)
次の問いに答えよ。
(1)実数A,B,C,Dに対して、複素数zを
$z=\dfrac{A+\sqrt5 Bi}{C+\sqrt5 Di}$
で定める。ただし、$C+\sqrt5 Di\neq 0$とする。このとき、$x=x+yi$をみたす実数x,yをA,B,C,Dの式で表せ。
(2)次をみたす整数A,B,C,Dを求めよ。
$\dfrac{16+\sqrt5 i}{29}=\dfrac{A+\sqrt5 Bi}{C+\sqrt5 Di}$
$AD-BC=-1$
$D\gt 0$
この動画を見る
横浜国立大学2020年度大問2(2)
次の問いに答えよ。
(1)実数A,B,C,Dに対して、複素数zを
$z=\dfrac{A+\sqrt5 Bi}{C+\sqrt5 Di}$
で定める。ただし、$C+\sqrt5 Di\neq 0$とする。このとき、$x=x+yi$をみたす実数x,yをA,B,C,Dの式で表せ。
(2)次をみたす整数A,B,C,Dを求めよ。
$\dfrac{16+\sqrt5 i}{29}=\dfrac{A+\sqrt5 Bi}{C+\sqrt5 Di}$
$AD-BC=-1$
$D\gt 0$
【高校数学】明治大学の過去問~確率の問題演習~【大学受験】

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1から11までの番号をつけた11枚のカードから3枚を取り出すとき、
それらの番号の和が偶数となる確率は、
$\displaystyle \frac{□}{□}$で、それらの番号の積が偶数になる確率は、$\displaystyle \frac{□}{□}$
この動画を見る
1から11までの番号をつけた11枚のカードから3枚を取り出すとき、
それらの番号の和が偶数となる確率は、
$\displaystyle \frac{□}{□}$で、それらの番号の積が偶数になる確率は、$\displaystyle \frac{□}{□}$
福田の数学〜立教大学2021年理学部第1問(1)〜正六角形の対角線ベクトルの内積

単元:
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(1)1辺の長さが1の正六角形の頂点を反時計回りにA,B,C,D,E,Fとする。
このとき、2つのベクトル$\overrightarrow{ AC },\overrightarrow{ AD }$の内積$\overrightarrow{ AC }・\overrightarrow{ AD }$の値は$\boxed{\ \ ア\ \ }$である。
2021立教大学理学部過去問
この動画を見る
${\Large\boxed{1}}$(1)1辺の長さが1の正六角形の頂点を反時計回りにA,B,C,D,E,Fとする。
このとき、2つのベクトル$\overrightarrow{ AC },\overrightarrow{ AD }$の内積$\overrightarrow{ AC }・\overrightarrow{ AD }$の値は$\boxed{\ \ ア\ \ }$である。
2021立教大学理学部過去問
福田のわかった数学〜高校3年生理系080〜グラフを描こう(2)三角関数のグラフ

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ グラフを描こう(2)
$y=\cos2x-2\cos x (0 \leqq x \leqq 2\pi)$
のグラフを描け。ただし凹凸は調べなくてよい。
この動画を見る
数学$\textrm{III}$ グラフを描こう(2)
$y=\cos2x-2\cos x (0 \leqq x \leqq 2\pi)$
のグラフを描け。ただし凹凸は調べなくてよい。
【誘導あり 概要欄】大学入試問題#24 富山大学(2020) 微積の応用
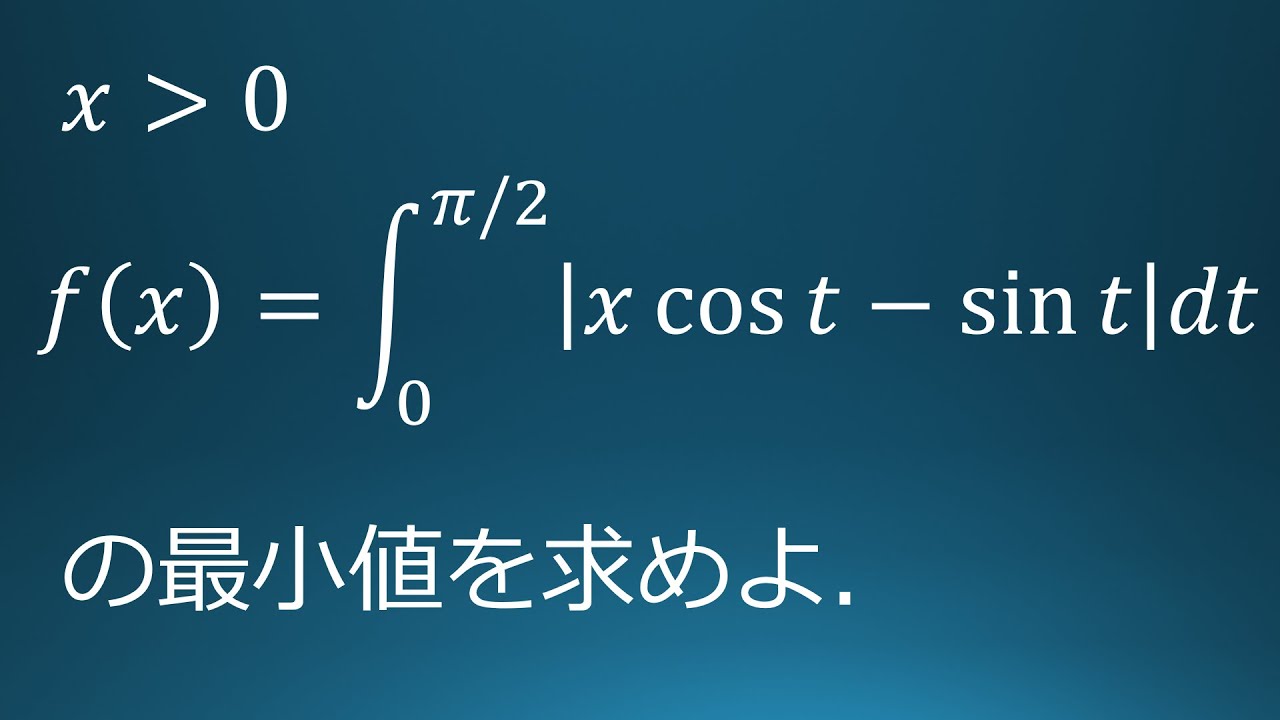
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#富山県立大学
指導講師:
ますただ
問題文全文(内容文):
(1)
$0 \lt \theta \lt \displaystyle \frac{\pi}{2}$
$x\ \cos\theta-\sin\theta=0$のとき
$\sin\theta,\cos\theta$を$x$で表せ。
(2)
$x \gt 0$
$f(x)=\displaystyle \int_{0}^{\frac{\pi}{2}}|x\ \cos\ t-\sin\ t|dt$の最小値を求めよ。
出典:2020年富山大学 入試問題
この動画を見る
(1)
$0 \lt \theta \lt \displaystyle \frac{\pi}{2}$
$x\ \cos\theta-\sin\theta=0$のとき
$\sin\theta,\cos\theta$を$x$で表せ。
(2)
$x \gt 0$
$f(x)=\displaystyle \int_{0}^{\frac{\pi}{2}}|x\ \cos\ t-\sin\ t|dt$の最小値を求めよ。
出典:2020年富山大学 入試問題
【理数個別の過去問解説】2020年度横浜国立大学 数学 第2問(1)解説

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
横浜国立大学2020年度大問2(1)
次の問いに答えよ。
(1)実数A,B,C,Dに対して、複素数zを
$z=\dfrac{A+\sqrt5 Bi}{C+\sqrt5 Di}$
で定める。ただし、$C+\sqrt5 Di\neq 0$とする。このとき、$x=x+yi$をみたす実数x,yをA,B,C,Dの式で表せ。
(2)次をみたす整数A,B,C,Dを求めよ。
$\dfrac{16+\sqrt5 i}{29}=\dfrac{A+\sqrt5 Bi}{C+\sqrt5 Di}$
$AD-BC=-1$
$D\gt 0$
この動画を見る
横浜国立大学2020年度大問2(1)
次の問いに答えよ。
(1)実数A,B,C,Dに対して、複素数zを
$z=\dfrac{A+\sqrt5 Bi}{C+\sqrt5 Di}$
で定める。ただし、$C+\sqrt5 Di\neq 0$とする。このとき、$x=x+yi$をみたす実数x,yをA,B,C,Dの式で表せ。
(2)次をみたす整数A,B,C,Dを求めよ。
$\dfrac{16+\sqrt5 i}{29}=\dfrac{A+\sqrt5 Bi}{C+\sqrt5 Di}$
$AD-BC=-1$
$D\gt 0$
x^πを微分せよ

補助線を引く喜びを
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
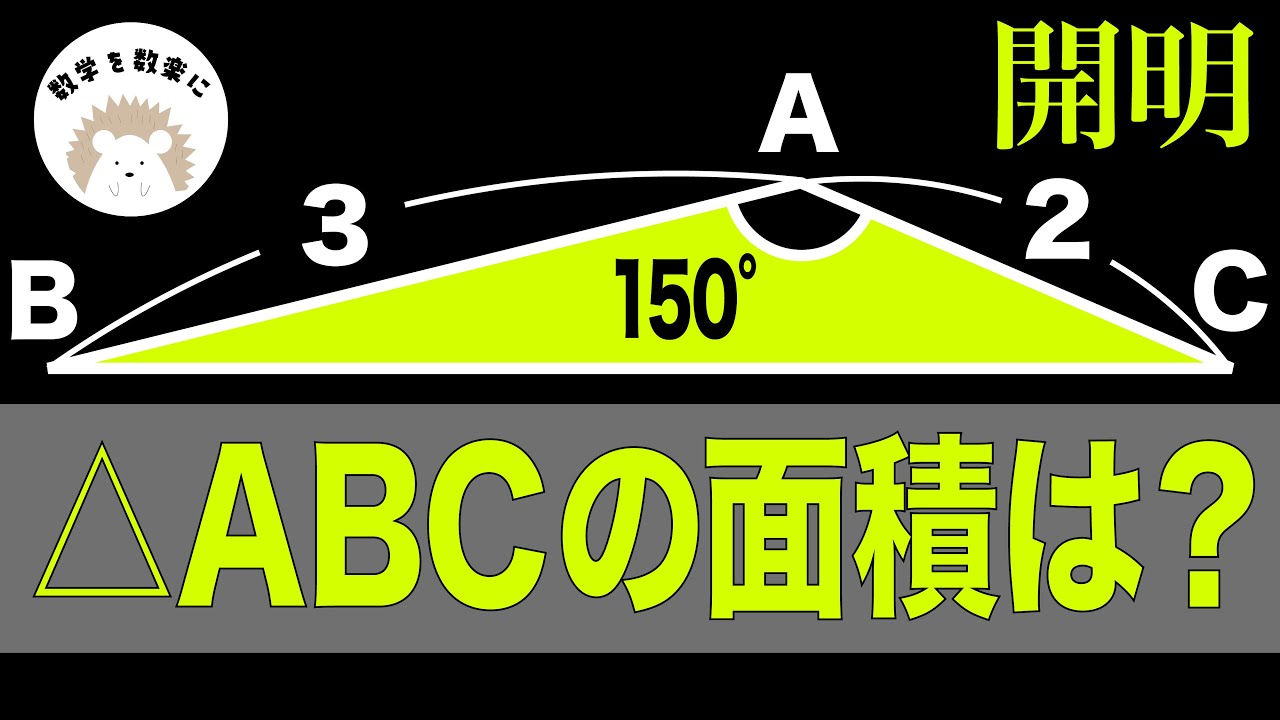
△ABC=?
*図は動画内参照
開明高等学校
この動画を見る
△ABC=?
*図は動画内参照
開明高等学校
【裏技】単位変換

単元:
#算数(中学受験)#計算と数の性質#数学(中学生)#単位・比と割合・比例・反比例#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
単位変換の説明動画です
この動画を見る
単位変換の説明動画です
福田の数学〜明治大学2021年理工学部第3問〜単位ベクトルと関数の増減

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#関数と極限#微分とその応用#関数の極限#微分法#数学(高校生)#大学入試解答速報#数学#明治大学#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$ Oを原点とする座標平面上の曲線$y=\log x$を$C$とする。正の実数$t$に対し、
曲線C上の点$P(t,\log t)$におけるCの法線Lの傾きは$\boxed{\ \ か\ \ }$である。Lに平行な
単位ベクトル$\overrightarrow{ n }$で、その$x$成分が正であるものは$\overrightarrow{ n }=(\boxed{\ \ き\ \ },\ \boxed{\ \ く\ \ })$である。
さらに、$r$を正の定数とし、点Qを$\overrightarrow{ OQ }=\overrightarrow{ OP }+r\ \overrightarrow{ n }$により定めると、
Qの座標は$(\boxed{\ \ け\ \ },\ \boxed{\ \ こ\ \ })$となる。ここで点Qのx座標とy座標をtの関数と見て、
それぞれ$X(t),\ Y(t)$とおくと$X(t),\ Y(t)$の導関数を成分とするベクトル$(X'(t),\ Y'(t))$
はrによらないベクトル$(1,\ \boxed{\ \ さ\ \ })$と平行であるか、零ベクトルである。
定数$r$の取り方によって関数$X(t)$の増減の様子は変わる。$X(t)$が区間$t \gt 0$で
常に増加するようなrの値の範囲は$\boxed{\ \ し\ \ }$である。また、$r=2\sqrt2$のとき、$X(t)$は
区間$\boxed{\ \ す\ \ } \leqq t \leqq \boxed{\ \ せ\ \ }$で減少し、区間$0 \lt t \leqq \boxed{\ \ す\ \ }$と区間$t \geqq \boxed{\ \ せ\ \ }$で増加する。
2021明治大学理工学部過去問
この動画を見る
${\Large\boxed{3}}$ Oを原点とする座標平面上の曲線$y=\log x$を$C$とする。正の実数$t$に対し、
曲線C上の点$P(t,\log t)$におけるCの法線Lの傾きは$\boxed{\ \ か\ \ }$である。Lに平行な
単位ベクトル$\overrightarrow{ n }$で、その$x$成分が正であるものは$\overrightarrow{ n }=(\boxed{\ \ き\ \ },\ \boxed{\ \ く\ \ })$である。
さらに、$r$を正の定数とし、点Qを$\overrightarrow{ OQ }=\overrightarrow{ OP }+r\ \overrightarrow{ n }$により定めると、
Qの座標は$(\boxed{\ \ け\ \ },\ \boxed{\ \ こ\ \ })$となる。ここで点Qのx座標とy座標をtの関数と見て、
それぞれ$X(t),\ Y(t)$とおくと$X(t),\ Y(t)$の導関数を成分とするベクトル$(X'(t),\ Y'(t))$
はrによらないベクトル$(1,\ \boxed{\ \ さ\ \ })$と平行であるか、零ベクトルである。
定数$r$の取り方によって関数$X(t)$の増減の様子は変わる。$X(t)$が区間$t \gt 0$で
常に増加するようなrの値の範囲は$\boxed{\ \ し\ \ }$である。また、$r=2\sqrt2$のとき、$X(t)$は
区間$\boxed{\ \ す\ \ } \leqq t \leqq \boxed{\ \ せ\ \ }$で減少し、区間$0 \lt t \leqq \boxed{\ \ す\ \ }$と区間$t \geqq \boxed{\ \ せ\ \ }$で増加する。
2021明治大学理工学部過去問
