 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
福田の数学〜明治大学2021年全学部統一入試Ⅲ第3問(1)〜定積分と極限

単元:
#関数と極限#積分とその応用#関数の極限#定積分#数学(高校生)#大学入試解答速報#数学#明治大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}} (1)\ k \gt 0$として、次の定積分を考える。
$F(k)=\int_0^1\frac{e^{kx}-1}{e^{kx}+1}\ dx$
このとき、$F(2)=\log(\boxed{\ \ ア\ \ })$となる。また、$\lim_{k \to \infty}F(k)=\boxed{\ \ イ\ \ }$である。
$\boxed{\ \ ア\ \ }$の解答群
$⓪\ \frac{e+1}{e} ①\ \frac{e^2+1}{e} ②\ \frac{e^4+1}{e} ③\ \frac{e^6+1}{e} ④\ \frac{e^8+1}{e}$
$⑤\ \frac{e+1}{2e} ⑥\ \frac{e^2+1}{2e} ⑦\ \frac{e^4+1}{2e} ⑧\ \frac{e^6+1}{2e} ⑨\ \frac{e^8+1}{2e}$
2021明治大学全統過去問
この動画を見る
${\Large\boxed{3}} (1)\ k \gt 0$として、次の定積分を考える。
$F(k)=\int_0^1\frac{e^{kx}-1}{e^{kx}+1}\ dx$
このとき、$F(2)=\log(\boxed{\ \ ア\ \ })$となる。また、$\lim_{k \to \infty}F(k)=\boxed{\ \ イ\ \ }$である。
$\boxed{\ \ ア\ \ }$の解答群
$⓪\ \frac{e+1}{e} ①\ \frac{e^2+1}{e} ②\ \frac{e^4+1}{e} ③\ \frac{e^6+1}{e} ④\ \frac{e^8+1}{e}$
$⑤\ \frac{e+1}{2e} ⑥\ \frac{e^2+1}{2e} ⑦\ \frac{e^4+1}{2e} ⑧\ \frac{e^6+1}{2e} ⑨\ \frac{e^8+1}{2e}$
2021明治大学全統過去問
福田のわかった数学〜高校3年生理系077〜極値(1)極大値をもつ条件

単元:
#数Ⅱ#三角関数#三角関数とグラフ#微分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 極値(1)
$f(x)=\frac{a-\cos x}{a+\sin x}\ が0 \lt x \lt \frac{\pi}{2}$の範囲で
極大値をもつように定数aの値の範囲を定めよ。
この動画を見る
数学$\textrm{III}$ 極値(1)
$f(x)=\frac{a-\cos x}{a+\sin x}\ が0 \lt x \lt \frac{\pi}{2}$の範囲で
極大値をもつように定数aの値の範囲を定めよ。
大学入試問題#15 慶應義塾大学(2021) 整数問題

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$a,b,c,d:$正の整数
$a^3=b^2$
$c^3=d^2$
$c-a=9$のとき$a,b,c,d$の値を求めよ。
出典:2021年慶應義塾大学 入試問題
この動画を見る
$a,b,c,d:$正の整数
$a^3=b^2$
$c^3=d^2$
$c-a=9$のとき$a,b,c,d$の値を求めよ。
出典:2021年慶應義塾大学 入試問題
もっちゃんと数学 フェルマーの小定理

単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
フェルマーの定理に関して解説していきます.
この動画を見る
フェルマーの定理に関して解説していきます.
早稲田高等学院 整数 数字がない!!

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$
\begin{eqnarray}
\left\{
\begin{array}{l}
x + y = m \\
xy = n \\
x>y\\
m,nは素数
\end{array}
\right.
\end{eqnarray}
$
自然数x,y,m,nを求めよ
早稲田大学高等学院
この動画を見る
$
\begin{eqnarray}
\left\{
\begin{array}{l}
x + y = m \\
xy = n \\
x>y\\
m,nは素数
\end{array}
\right.
\end{eqnarray}
$
自然数x,y,m,nを求めよ
早稲田大学高等学院
数学「大学入試良問集」【19−21 定積分関数の超良問(面積)】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
関数$f(x)$を$f(x)=\displaystyle \int_{0}^{x}\displaystyle \frac{1}{1+t^2}dt$で定める。
(1)$y=f(x)$の$x=1$における法線の方程式を求めよ。
(2)(1)で求めた法線と$x$軸および$y=f(x)$のグラフによって囲まれる図形の面積を求めよ。
この動画を見る
関数$f(x)$を$f(x)=\displaystyle \int_{0}^{x}\displaystyle \frac{1}{1+t^2}dt$で定める。
(1)$y=f(x)$の$x=1$における法線の方程式を求めよ。
(2)(1)で求めた法線と$x$軸および$y=f(x)$のグラフによって囲まれる図形の面積を求めよ。
【数Ⅲ】微分法:媒介変数で表された関数の2回微分

単元:
#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
xの関数yが、$\theta$を媒介変数として、$x=\cos\theta-1、y=2\sin\theta+1$と表される時、$\dfrac{d^2y}{dx^2}$を$\theta$の関数として表そう。
この動画を見る
xの関数yが、$\theta$を媒介変数として、$x=\cos\theta-1、y=2\sin\theta+1$と表される時、$\dfrac{d^2y}{dx^2}$を$\theta$の関数として表そう。
【裏技】これすげぇ

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#数学(中学生)#中1数学#中2数学#中3数学#約数・倍数を利用する問題#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
約分のテクニック紹介動画です
この動画を見る
約分のテクニック紹介動画です
福田の数学〜明治大学2021年全学部統一入試Ⅲ第2問(2)〜2次方程式の解が同一円周上にある条件

単元:
#数Ⅱ#2次関数#図形の性質#複素数平面#2次方程式と2次不等式#周角と円に内接する四角形・円と接線・接弦定理#複素数平面#数学(高校生)#大学入試解答速報#数学#明治大学#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$(2)方程式$x^2+x+1=0$の2つの解を$\alpha,\ \beta$とする。またbを実数として、
方程式$x^2+x+1=0$の2つの解を$\gamma,\ \delta$とする。複素数平面上で、4点$A(\alpha),$
$B(\beta),C(\gamma),D(\delta)$が同じ円上にあるとき、bの値は$±\frac{\sqrt{\boxed{\ \ キ\ \ }}}{\boxed{\ \ ク\ \ }}$となる。
2021明治大学全統過去問
この動画を見る
${\Large\boxed{2}}$(2)方程式$x^2+x+1=0$の2つの解を$\alpha,\ \beta$とする。またbを実数として、
方程式$x^2+x+1=0$の2つの解を$\gamma,\ \delta$とする。複素数平面上で、4点$A(\alpha),$
$B(\beta),C(\gamma),D(\delta)$が同じ円上にあるとき、bの値は$±\frac{\sqrt{\boxed{\ \ キ\ \ }}}{\boxed{\ \ ク\ \ }}$となる。
2021明治大学全統過去問
福田のわかった数学〜高校2年生059〜対称式と領域(1)

単元:
#数Ⅰ#数Ⅱ#2次関数#2次方程式と2次不等式#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$対称式と領域(1)
実数$x,\ yがx^2+y^2 \leqq 1$を
満たしながら動くとき、
次の点の存在範囲を図示せよ。
(1)$P(x+y,\ x-y) (2)Q(x+y,\ xy)$
この動画を見る
数学$\textrm{II}$対称式と領域(1)
実数$x,\ yがx^2+y^2 \leqq 1$を
満たしながら動くとき、
次の点の存在範囲を図示せよ。
(1)$P(x+y,\ x-y) (2)Q(x+y,\ xy)$
【数Ⅲ】極限:関数の極限 ガウス記号を含む極限

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の極限を調べよう。
(1)$\displaystyle \lim_{x\to 2}[x],$
(2)$\displaystyle \lim_{x\to 1}([2x]-[x])$
この動画を見る
次の極限を調べよう。
(1)$\displaystyle \lim_{x\to 2}[x],$
(2)$\displaystyle \lim_{x\to 1}([2x]-[x])$
ガチャ問題 東大大島さんと数学

【演習編!】平面図形の知識を演習で効率的に整理!〔高校数学 数学〕

単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#内心・外心・重心とチェバ・メネラウス#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
平面図形の解き方について解説します。
この動画を見る
平面図形の解き方について解説します。
油断禁物!!整数問題 大阪星光学院

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x^2-28x+160$が素数となる整数xを求めよ。
この動画を見る
$x^2-28x+160$が素数となる整数xを求めよ。
数学「大学入試良問集」【19−20 媒介変数のグラフと曲線の長さ、面積】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東邦大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$r$を正の定数とする。
$xy$平面上を時刻$t=0$から$t=\pi$まで運動する点$P(x,y)$の座標が$x=2r(t-\sin\ t\cos\ t),y=2r\ \sin^2t$であるとき、以下の問いに答えよ。
(1)
点$P$が描く曲線の概形を、$xy$平面上にかけ。
(2)
点$P$が時刻$t=0$から$t=\pi$までに動く道のり$S$は、
$S=\displaystyle \int_{0}^{\pi}\sqrt{ \left[ \dfrac{ dx }{ dt } \right]^2+\left[ \dfrac{ dy }{ dt } \right]^2 }\ dt$で与えられる。
このとき、$S$の値を求めよ。
(3)点$P$が描く曲線と$x$軸で囲まれた部分を、$x$軸の周りに1回転させてできる立体の体積を求めよ。
この動画を見る
$r$を正の定数とする。
$xy$平面上を時刻$t=0$から$t=\pi$まで運動する点$P(x,y)$の座標が$x=2r(t-\sin\ t\cos\ t),y=2r\ \sin^2t$であるとき、以下の問いに答えよ。
(1)
点$P$が描く曲線の概形を、$xy$平面上にかけ。
(2)
点$P$が時刻$t=0$から$t=\pi$までに動く道のり$S$は、
$S=\displaystyle \int_{0}^{\pi}\sqrt{ \left[ \dfrac{ dx }{ dt } \right]^2+\left[ \dfrac{ dy }{ dt } \right]^2 }\ dt$で与えられる。
このとき、$S$の値を求めよ。
(3)点$P$が描く曲線と$x$軸で囲まれた部分を、$x$軸の周りに1回転させてできる立体の体積を求めよ。
【数学】分かりやすい講義系参考書・問題集はどれがおすすめか?独学数学勉強法【篠原好】

【数Ⅲ】極限:関数の極限 x=-tの置換

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の極限を求めよう。
$\displaystyle \lim_{x\to-\infty}(\sqrt{x^2+2x+3}+x)$
この動画を見る
次の極限を求めよう。
$\displaystyle \lim_{x\to-\infty}(\sqrt{x^2+2x+3}+x)$
【5分で理解する平方根と整数の性質!】整数:中央大学附属高等学校~全国入試問題解法

単元:
#数学(中学生)#平方根#整数の性質#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 中央大学附属高等学校
$\sqrt{ 60(n+1)(n^2-1)}$
が整数となるような
2桁の整数$n$をすべて求めなさい。
この動画を見る
入試問題 中央大学附属高等学校
$\sqrt{ 60(n+1)(n^2-1)}$
が整数となるような
2桁の整数$n$をすべて求めなさい。
3通りで解説しました
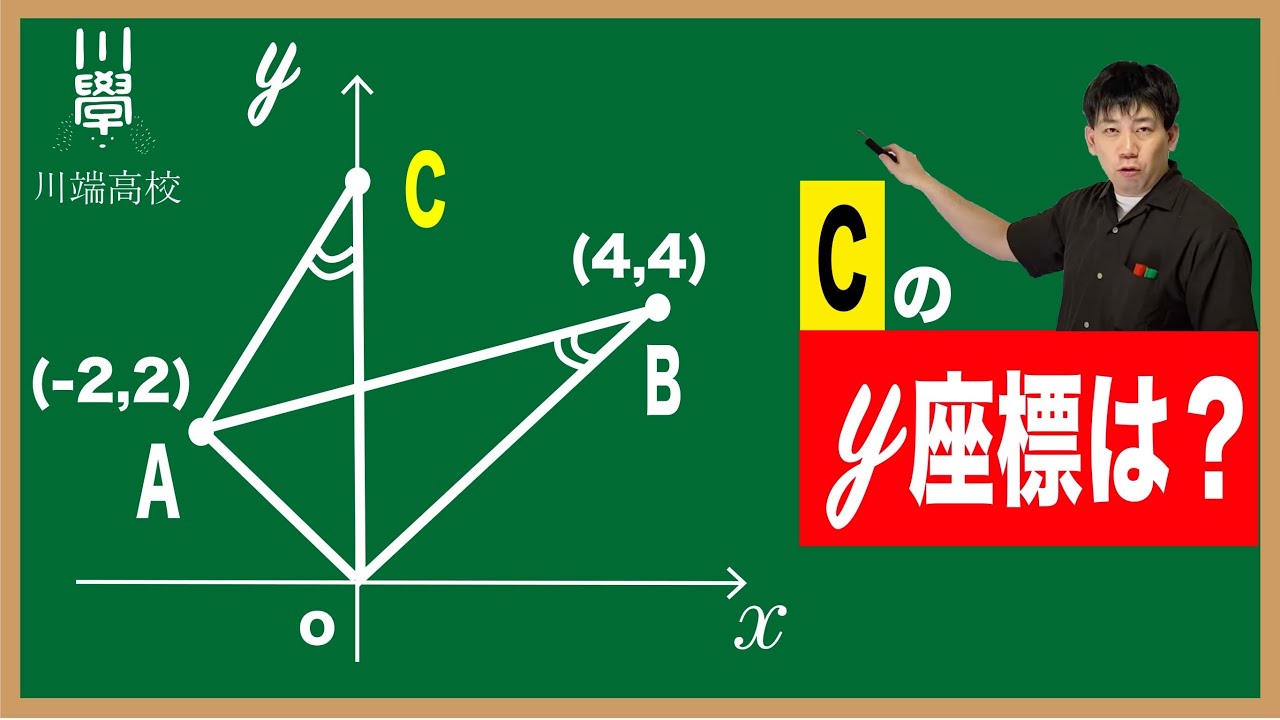
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
cのy座標は?
*図は動画内参照
川端高校
この動画を見る
cのy座標は?
*図は動画内参照
川端高校
福田の数学〜明治大学2021年全学部統一入試Ⅲ第2問(1)〜楕円と複素数平面

単元:
#平面上の曲線#複素数平面#図形と計量#三角比(三角比・拡張・相互関係・単位円)#2次曲線#複素数平面#大学入試解答速報#数学#明治大学#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$(1)座標平面において、点$(-1,\ 0)$からの距離と点$(1,\ 0)$からの距離の和が4
である点は方程式$\frac{x^2}{\boxed{\ \ ア\ \ }}+\frac{y^2}{\boxed{\ \ イ\ \ }}=1$で表される曲線C上にある。点$(x,\ y)$
が曲線C上を動くとき、点$(x,\ y)$と点$(-1,\ 0)$の距離をdとおけば、dの最小値
は$\boxed{\ \ ウ\ \ }$、最大値は$\boxed{\ \ エ\ \ }$となる。複素数$z$が$|z|+|z-4|=8$を満たすとき、
$|z|$のとりうる範囲は$\boxed{\ \ オ\ \ } \leqq |z| \leqq \boxed{\ \ カ\ \ }$である。
2021明治大学全統過去問
この動画を見る
${\Large\boxed{2}}$(1)座標平面において、点$(-1,\ 0)$からの距離と点$(1,\ 0)$からの距離の和が4
である点は方程式$\frac{x^2}{\boxed{\ \ ア\ \ }}+\frac{y^2}{\boxed{\ \ イ\ \ }}=1$で表される曲線C上にある。点$(x,\ y)$
が曲線C上を動くとき、点$(x,\ y)$と点$(-1,\ 0)$の距離をdとおけば、dの最小値
は$\boxed{\ \ ウ\ \ }$、最大値は$\boxed{\ \ エ\ \ }$となる。複素数$z$が$|z|+|z-4|=8$を満たすとき、
$|z|$のとりうる範囲は$\boxed{\ \ オ\ \ } \leqq |z| \leqq \boxed{\ \ カ\ \ }$である。
2021明治大学全統過去問
福田のわかった数学〜高校1年生059〜図形の計量(10)正四面体の各辺に接する球の半径

単元:
#数A#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 図形の計量(10)
1辺の長さがaの正四面体の全ての辺に接する球の半径を求めよ。
この動画を見る
数学$\textrm{I}$ 図形の計量(10)
1辺の長さがaの正四面体の全ての辺に接する球の半径を求めよ。
大学入試問題#14 津田塾大学(2021) 微積の応用

単元:
#微分とその応用#積分とその応用#微分法#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$0 \leqq x \leqq \displaystyle \frac{\pi}{x}$
$f(x)=\displaystyle \int_{0}^{\frac{\pi}{2}}\sin|x-t|dt$の最小値、最大値を求めよ。
出典:2021年津田塾大学 入試問題
この動画を見る
$0 \leqq x \leqq \displaystyle \frac{\pi}{x}$
$f(x)=\displaystyle \int_{0}^{\frac{\pi}{2}}\sin|x-t|dt$の最小値、最大値を求めよ。
出典:2021年津田塾大学 入試問題
【数Ⅲ】極限:3乗根を含む極限、3乗根の有理化:次の極限を求めよう。lim[x→0]{∛(1+x)-∛(1-x)}/x

単元:
#関数と極限#数列の極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の極限を求めよう。
$\displaystyle \lim_{x\to 0}\dfrac{\sqrt[3]{1+x}-\sqrt[3]{1-x}}{x}$
この動画を見る
次の極限を求めよう。
$\displaystyle \lim_{x\to 0}\dfrac{\sqrt[3]{1+x}-\sqrt[3]{1-x}}{x}$
指数方程式だよ
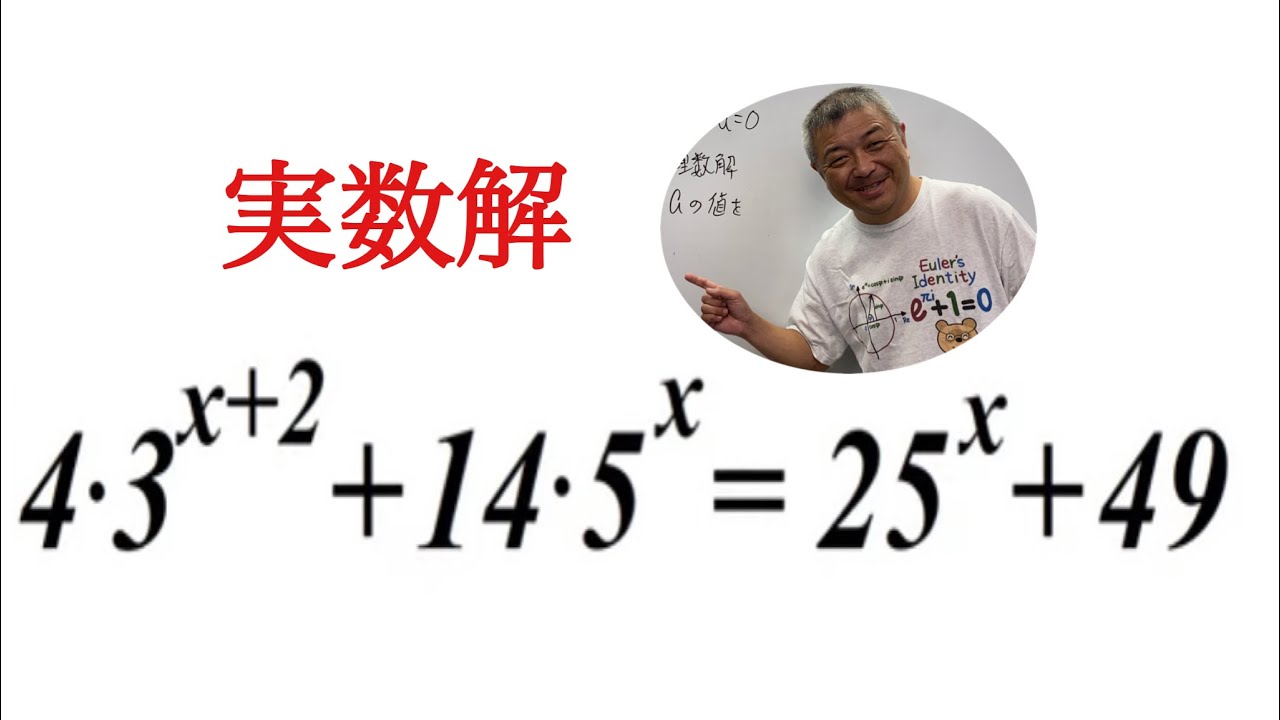
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解$x$を求めよ.
$4・3^{x+2}+14・5^x~25^x+49$
この動画を見る
実数解$x$を求めよ.
$4・3^{x+2}+14・5^x~25^x+49$
【数Ⅲ】極限:3乗根を含む極限、3乗根の有理化

数学「大学入試良問集」【19−19 定積分で示された関数の最大最小】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#中京大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
関数$f(x)=\displaystyle \int_{0}^{x}(x\ \cos\ t-\sin\ t)dt(0 \leqq x \leqq 2\pi)$について次の問いに答えよ。
(1)$f(x)$を微分せよ。
(2)$f(x)$の最大値と最小値、およびそのときの$x$の値を求めよ。
この動画を見る
関数$f(x)=\displaystyle \int_{0}^{x}(x\ \cos\ t-\sin\ t)dt(0 \leqq x \leqq 2\pi)$について次の問いに答えよ。
(1)$f(x)$を微分せよ。
(2)$f(x)$の最大値と最小値、およびそのときの$x$の値を求めよ。
【数Ⅰ】区間が動く2次関数の最大最小【丁寧に場合分け】

単元:
#数Ⅰ#2次関数#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$ aを定数とする.a \leqq x \leqq a+2における関数f(x)=x^2-2x+4の最大値および最小値を求めよ.$
この動画を見る
$ aを定数とする.a \leqq x \leqq a+2における関数f(x)=x^2-2x+4の最大値および最小値を求めよ.$
福田の数学〜明治大学2021年全学部統一入試Ⅲ第1問〜関数の増減と面積

単元:
#微分とその応用#積分とその応用#微分法#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#数学(高校生)#大学入試解答速報#数学#明治大学#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$関数$f(x)=\frac{1}{2}(x+\sqrt{2-3x^2})$の定義域は$-\frac{\sqrt{\boxed{\ \ ア\ \ }}}{\boxed{\ \ イ\ \ }} \leqq x \leqq \frac{\sqrt{\boxed{\ \ ウ\ \ }}}{\boxed{\ \ エ\ \ }}$であり、
$f(x)$は$x=\frac{\sqrt{\boxed{\ \ オ\ \ }}}{\boxed{\ \ カ\ \ }}$のとき、
最大値$\frac{\sqrt{\boxed{\ \ キ\ \ }}}{\boxed{\ \ ク\ \ }}$をとる。曲線$y=f(x)$、
直線$y=2x$およびy軸で囲まれた図形の面積は$\boxed{\ \ ケ\ \ }$となる。
$\boxed{\ \ ケ\ \ }$の解答群
$⓪\frac{\sqrt3}{18}\pi ①\frac{\sqrt3}{36}\pi ②\frac{\sqrt3}{72}\pi ③\frac{1}{6}+\frac{\sqrt3}{36}\pi ④\frac{1}{24}+\frac{\sqrt3}{36}\pi$
$⑤\frac{5}{24}+\frac{\sqrt3}{36}\pi ⑥\frac{1}{3}+\frac{\sqrt3}{18}\pi ⑦\frac{1}{6}+\frac{\sqrt3}{18}\pi ⑧\frac{1}{8}+\frac{\sqrt3}{18}\pi ⑨\frac{7}{24}+\frac{\sqrt3}{18}\pi$
この動画を見る
${\Large\boxed{1}}$関数$f(x)=\frac{1}{2}(x+\sqrt{2-3x^2})$の定義域は$-\frac{\sqrt{\boxed{\ \ ア\ \ }}}{\boxed{\ \ イ\ \ }} \leqq x \leqq \frac{\sqrt{\boxed{\ \ ウ\ \ }}}{\boxed{\ \ エ\ \ }}$であり、
$f(x)$は$x=\frac{\sqrt{\boxed{\ \ オ\ \ }}}{\boxed{\ \ カ\ \ }}$のとき、
最大値$\frac{\sqrt{\boxed{\ \ キ\ \ }}}{\boxed{\ \ ク\ \ }}$をとる。曲線$y=f(x)$、
直線$y=2x$およびy軸で囲まれた図形の面積は$\boxed{\ \ ケ\ \ }$となる。
$\boxed{\ \ ケ\ \ }$の解答群
$⓪\frac{\sqrt3}{18}\pi ①\frac{\sqrt3}{36}\pi ②\frac{\sqrt3}{72}\pi ③\frac{1}{6}+\frac{\sqrt3}{36}\pi ④\frac{1}{24}+\frac{\sqrt3}{36}\pi$
$⑤\frac{5}{24}+\frac{\sqrt3}{36}\pi ⑥\frac{1}{3}+\frac{\sqrt3}{18}\pi ⑦\frac{1}{6}+\frac{\sqrt3}{18}\pi ⑧\frac{1}{8}+\frac{\sqrt3}{18}\pi ⑨\frac{7}{24}+\frac{\sqrt3}{18}\pi$
福田のわかった数学〜高校3年生理系076〜平均値の定理(4)数列の極限の問題

単元:
#数列#漸化式#関数と極限#微分とその応用#数列の極限#接線と法線・平均値の定理#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$平均値の定理(4)
微分可能な関数$f(x)$が$f(1)=1, 0 \lt f'(x) \leqq \frac{1}{2}$を満たしている。
$a_{n+1}=f(a_n)$で定義される数列$\left\{a_n\right\}$について、
$\lim_{n \to \infty}a_n=1$であることを示せ。
この動画を見る
数学$\textrm{III}$平均値の定理(4)
微分可能な関数$f(x)$が$f(1)=1, 0 \lt f'(x) \leqq \frac{1}{2}$を満たしている。
$a_{n+1}=f(a_n)$で定義される数列$\left\{a_n\right\}$について、
$\lim_{n \to \infty}a_n=1$であることを示せ。
大学入試問題#13 自治医科大学(2021) 対数と整数問題

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$x,y:$自然数
$1+log_x(y-2)=4\ log_{x^2}2+3\ log_{x^3}(y+6)$が成り立つとき$|x-y|$の最小値を求めよ。
出典:2021年自治医科大学 入試問題
この動画を見る
$x,y:$自然数
$1+log_x(y-2)=4\ log_{x^2}2+3\ log_{x^3}(y+6)$が成り立つとき$|x-y|$の最小値を求めよ。
出典:2021年自治医科大学 入試問題
