 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
【数C】【空間ベクトル】平行六面体ABCD-EFGHにおいて、次の等式が成り立つことを示せ。(1) AG-BH=DF-CE(2) 3BH+2DF=2AG+3CE+2BC

単元:
#空間ベクトル#空間ベクトル#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#空間ベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
平行六面体ABCD-EFGHにおいて、次の等式が成り立つことを示せ。
(1) AG-BH=DF-CE
(2) 3BH+2DF=2AG+3CE+2BC
この動画を見る
平行六面体ABCD-EFGHにおいて、次の等式が成り立つことを示せ。
(1) AG-BH=DF-CE
(2) 3BH+2DF=2AG+3CE+2BC
【数B】【数列】1から8までの数字のさいころを繰り返し投げ、n回目までに出た数字の合計をX (n) とする。X (n) を3で割ったあまりが0,1,2をそれぞれ数列で置くとき、それぞれの一般項を求めよ

単元:
#数列#漸化式#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#中高教材#数列
指導講師:
理数個別チャンネル
問題文全文(内容文):
各面に1から8までの数字が1つずつ書かれた正八面体のさいころを繰り返し投げ、
n回目までに出た数字の合計をX (n) とする。
X (n) を3で割り切れる確率を $a_n$、X (n) を3で割った時1余る確率を$b_n$、
X(n)を3で割った時2余る確率を$c_n$とする。
ただし1から8までの数字の出る確率はどれも同じとする。
1) $a_1$,$b_1$, $c_1$を求めよ。
2)$a_{n+1}$、$b_{n+1}$、$c_{n+1}$を$a_n$、$b_n$、$c_n$を用いて表せ。
3)$a_{n+1}$を$a_n$を用いて表せ。
4) $a_n$、$b_n$、$c_n$を求めよ。
この動画を見る
各面に1から8までの数字が1つずつ書かれた正八面体のさいころを繰り返し投げ、
n回目までに出た数字の合計をX (n) とする。
X (n) を3で割り切れる確率を $a_n$、X (n) を3で割った時1余る確率を$b_n$、
X(n)を3で割った時2余る確率を$c_n$とする。
ただし1から8までの数字の出る確率はどれも同じとする。
1) $a_1$,$b_1$, $c_1$を求めよ。
2)$a_{n+1}$、$b_{n+1}$、$c_{n+1}$を$a_n$、$b_n$、$c_n$を用いて表せ。
3)$a_{n+1}$を$a_n$を用いて表せ。
4) $a_n$、$b_n$、$c_n$を求めよ。
【数B】【数列】数列{an}の一般項を求めよ。(1)a1=1, a2=2, an+2+3an+1-4an=0(2)a1=0, a2=1, an+2+5an+1+6an=0他1問

単元:
#数列#漸化式#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#中高教材#数列
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の条件によって定められる数列$a_n$の一般項を求めよ。
$a_1 = 1$,$a_2 = 2$
$a_{n+2} + 3a_{n+1} - 4a_n = 0$
$a_1 = 0$,$a_2 = 1$
$a_{n+2} + 5a_{n+1} + 6a_n = 0$
$a_1 = 1$, $a_2 = 4$
$a_{n+2} - 6a_{n+1} + 9a_n = 0$
この動画を見る
次の条件によって定められる数列$a_n$の一般項を求めよ。
$a_1 = 1$,$a_2 = 2$
$a_{n+2} + 3a_{n+1} - 4a_n = 0$
$a_1 = 0$,$a_2 = 1$
$a_{n+2} + 5a_{n+1} + 6a_n = 0$
$a_1 = 1$, $a_2 = 4$
$a_{n+2} - 6a_{n+1} + 9a_n = 0$
【数B】【数列】条件a1=4, an+1=4an+8/an+6によって定められる数列{an}に対して、bn=an-2/an+4とおくと、数列{bn}は等比数列である。数列{an}の一般項を求めよ。

単元:
#数列#漸化式#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#中高教材#数列
指導講師:
理数個別チャンネル
問題文全文(内容文):
$a_{1}=4$
$a_{n+1} = \dfrac{4a_n + 8}{a_n + 6}$
によって定められる数列$a_n$に対して、
$b_n = \dfrac{a_n - 2}{a_n + 4}$
とおくと、数列 $b_n$は等比数列である。
数列$a_n$の一般項を求めよ。
この動画を見る
$a_{1}=4$
$a_{n+1} = \dfrac{4a_n + 8}{a_n + 6}$
によって定められる数列$a_n$に対して、
$b_n = \dfrac{a_n - 2}{a_n + 4}$
とおくと、数列 $b_n$は等比数列である。
数列$a_n$の一般項を求めよ。
【数Ⅰ】【図形と計量】0°≦θ≦180°とする。次の不等式を満たすもの値の範囲を求めよ。-1<√3 tanθ <3 (他8問)

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$0^\circ \leq \theta \leq 180^\circ$とする。
次の不等式を満たす$\theta$ の値の範囲を求めよ。
$\sin\theta > \dfrac{1}{\sqrt{2}}$
$\sin\theta \leq \dfrac{1}{2}$
$\cos\theta \leq -\dfrac{\sqrt{3}}{2}$
$\cos\theta < -\dfrac{1}{\sqrt{2}}$
$0 < \tan\theta \leq 1$
$\tan\theta \geq \sqrt{3}$
$1 < 2\sin\theta \leq \sqrt{3}$
$1 \leq -2\cos\theta < \sqrt{3}$
$-1 < \sqrt{3}\tan\theta < 3$
この動画を見る
$0^\circ \leq \theta \leq 180^\circ$とする。
次の不等式を満たす$\theta$ の値の範囲を求めよ。
$\sin\theta > \dfrac{1}{\sqrt{2}}$
$\sin\theta \leq \dfrac{1}{2}$
$\cos\theta \leq -\dfrac{\sqrt{3}}{2}$
$\cos\theta < -\dfrac{1}{\sqrt{2}}$
$0 < \tan\theta \leq 1$
$\tan\theta \geq \sqrt{3}$
$1 < 2\sin\theta \leq \sqrt{3}$
$1 \leq -2\cos\theta < \sqrt{3}$
$-1 < \sqrt{3}\tan\theta < 3$
【数Ⅰ】【図形と計量】sinθ+cosθ=1/3のとき(1) sinθcosθの値(2) sin³θ+cos³θの値(3) sinθ-cosθの値

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
sinθ+cosθ=1/3のとき
(1) sinθcosθの値
(2) sin³θ+cos³θの値
(3) sinθ-cosθの値
この動画を見る
sinθ+cosθ=1/3のとき
(1) sinθcosθの値
(2) sin³θ+cos³θの値
(3) sinθ-cosθの値
【高校数学】隣接三項間の漸化式の特性方程式の意味~分かりやすく丁寧に~ 3-19.5【数学B】

【数Ⅰ】【図形と計量】(1)cos36°を求めよ(2)正五角形の対角線の長さを求めよ。

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1)cos36°を求めよ
(2)正五角形の対角線の長さを求めよ。
この動画を見る
(1)cos36°を求めよ
(2)正五角形の対角線の長さを求めよ。
【数B】【数列】nは自然数とする。連立不等式0≦x≦n, y≧0, y≦n²-x²の表す領域に含まれる格子点の個数を求めよ。

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#中高教材#数列
指導講師:
理数個別チャンネル
問題文全文(内容文):
nは自然数とする。連立不等式0≦x≦n, y≧0, y≦n²-x²の表す領域に含まれる格子点の個数を求めよ。
この動画を見る
nは自然数とする。連立不等式0≦x≦n, y≧0, y≦n²-x²の表す領域に含まれる格子点の個数を求めよ。
【数B】【数列】nは自然数とする。座標平面上の3点(0,0),(3n,0)(0,n)を頂点とする三角形の周および内部にある格子点の個数を求めよ。

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#中高教材#数列
指導講師:
理数個別チャンネル
問題文全文(内容文):
nは自然数とする。座標平面上の3点(0,0),(3n,0)(0,n)を頂点とする三角形の周および内部にある格子点の個数を求めよ。
この動画を見る
nは自然数とする。座標平面上の3点(0,0),(3n,0)(0,n)を頂点とする三角形の周および内部にある格子点の個数を求めよ。
【数B】【数列】(x+1)(x+2)(x+3)……(x+n)の展開式において、次の係数を求めよ。(1)xのn-1乗の係数(2)xのn-2乗の係数(n≧2)

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#中高教材#数列
指導講師:
理数個別チャンネル
問題文全文(内容文):
(x+1)(x+2)(x+3)……(x+n)の展開式において、次の係数を求めよ。
(1)xのn-1乗の係数
(2)xのn-2乗の係数(n≧2)
この動画を見る
(x+1)(x+2)(x+3)……(x+n)の展開式において、次の係数を求めよ。
(1)xのn-1乗の係数
(2)xのn-2乗の係数(n≧2)
【高校数学】隣接3項間の漸化式~解き方を覚えよう~ 3-19【数学B】

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
問題1 数列$\{an\}$の一般項を求めよ。
$a_{1} = 0, a_{2} = 1 ,a_{n+2}-5a_{n+1}+6a_n=0$
問題2 次のように定義される$\{an\}$の一般項$a_n$を求めよ。
$a_1=1,a_2=2,a_{n+2}-2a_{n+1}-15a_n=0$
この動画を見る
問題1 数列$\{an\}$の一般項を求めよ。
$a_{1} = 0, a_{2} = 1 ,a_{n+2}-5a_{n+1}+6a_n=0$
問題2 次のように定義される$\{an\}$の一般項$a_n$を求めよ。
$a_1=1,a_2=2,a_{n+2}-2a_{n+1}-15a_n=0$
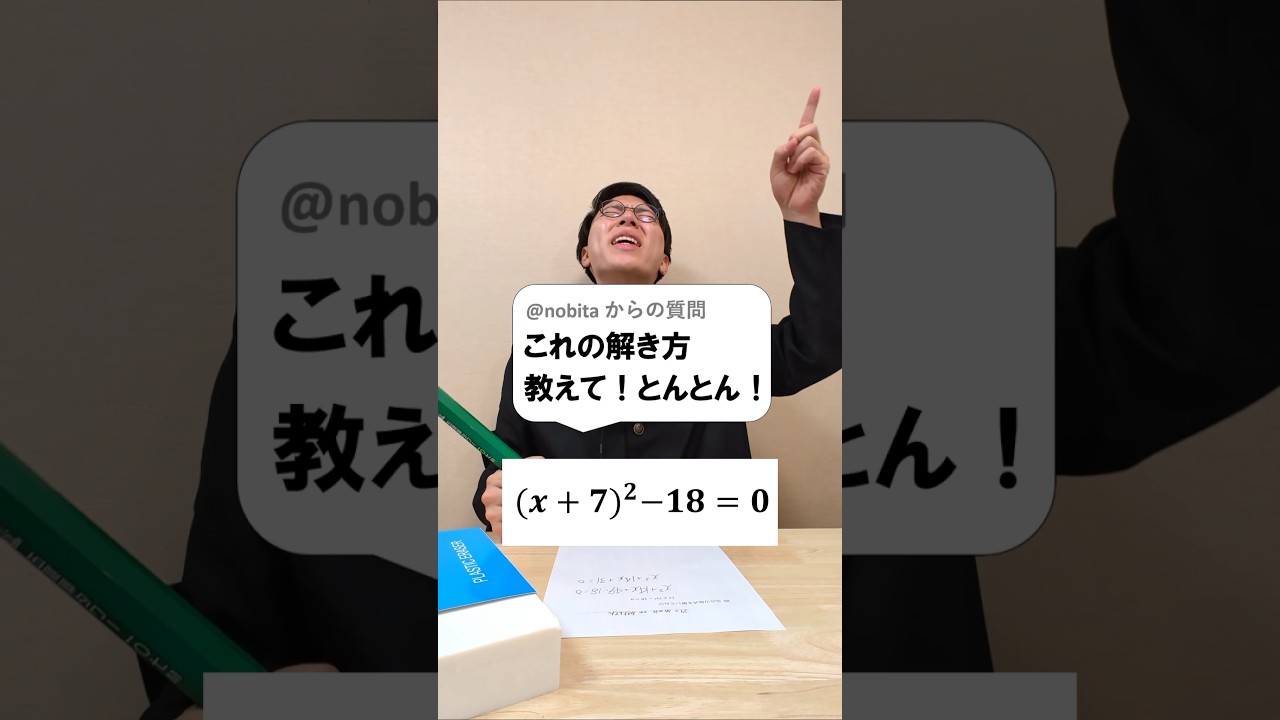
このタイプの2次方程式の解き方は?
【数Ⅰ】【2次関数】不等式 x²+9x+18<0 を満たすすべてのxが不等式 x²-4ax+3a<0 を満たすような定数a の値の範囲を求めよ。

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
不等式 x²+9x+18<0 を満たすすべてのxが不等式 x²-4ax+3a<0 を満たすような定数a の値の範囲を求めよ。
この動画を見る
不等式 x²+9x+18<0 を満たすすべてのxが不等式 x²-4ax+3a<0 を満たすような定数a の値の範囲を求めよ。
【数Ⅰ】【2次関数】aは正の定数とする。y=|x²-2x|(0≦x≦a)の最大値を求めよ。

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
aは正の定数とする。y=|x²-2x|(0≦x≦a)の最大値を求めよ。
この動画を見る
aは正の定数とする。y=|x²-2x|(0≦x≦a)の最大値を求めよ。
√5の小数部分は?

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$\sqrt5$の小数部分は?
この動画を見る
$\sqrt5$の小数部分は?
【高校数学】漸化式で特性方程式を使う理由 3-18.5【数学B】

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数列#漸化式#数学(高校生)#数B
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
【高校数学】漸化式で特性方程式を使う理由を解説していきます。
この動画を見る
【高校数学】漸化式で特性方程式を使う理由を解説していきます。
【数Ⅰ】【2次関数】(1) y=|x²+2x|のグラフを描け。(2) |x²+2x|=k の実数解の個数を求めよ。

三角って実はすごい図形?

単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
トラス構造などの解説をしていきます。
この動画を見る
トラス構造などの解説をしていきます。
これの何が間違い?

【数Ⅰ】【2次関数】グラフを利用して、次の不等式を解け。(1) |x+1|<2x (2) |x²-4| >-3x

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
グラフを利用して、次の不等式を解け。
(1) |x+1|<2x
(2) |x²-4| >-3x
この動画を見る
グラフを利用して、次の不等式を解け。
(1) |x+1|<2x
(2) |x²-4| >-3x
【数Ⅰ】【2次関数】x,yがお互いに関係なく変化するとき、Z=x²ー6xy+y²+2yの最小値を求めよ。

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
x,yがお互いに関係なく変化するとき、Z=x²ー6xy+y²+2yの最小値を求めよ。
この動画を見る
x,yがお互いに関係なく変化するとき、Z=x²ー6xy+y²+2yの最小値を求めよ。
【高校数学】特性方程式の漸化式~分かりやすく丁寧に~3-18【数学B】

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数列#漸化式#数学(高校生)#数B
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
特性方程式の漸化式
分かりやすく丁寧に解説していきます。
この動画を見る
特性方程式の漸化式
分かりやすく丁寧に解説していきます。
【数Ⅰ】【2次関数】x²+y²=1 のときx²ーy²+2xの最大値と最小値を求めよ。

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
x²+y²=1 のときx²ーy²+2xの最大値と最小値を求めよ。
この動画を見る
x²+y²=1 のときx²ーy²+2xの最大値と最小値を求めよ。
【数Ⅰ】【データの分析】672、693、644、665、630、644でc=7、x₀=644、u=(x-x₀)/c として新たな変量uを作る。変量uとxの平均値、分散、標準偏差を求めよ。

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#データの分析#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
変量xのデータが次のように与えられている。
672,693、644、665、630、644
c=7、x₀=644、u=(x-x₀)/c として新たな変量uを作る。
(1)変量uのデータの平均値、分散、標準偏差を求めよ。
(2)変量xのデータの平均値、分散、標準偏差を求めよ。
この動画を見る
変量xのデータが次のように与えられている。
672,693、644、665、630、644
c=7、x₀=644、u=(x-x₀)/c として新たな変量uを作る。
(1)変量uのデータの平均値、分散、標準偏差を求めよ。
(2)変量xのデータの平均値、分散、標準偏差を求めよ。
棒を動かして正方形からコインを出す問題

【数Ⅰ】【データの分析】あるクラスの生徒を対象に100点満点の試験を行ったところ、平均値は68点、分散は36であった。生徒全員の得点を2.5倍して、30点を加えたとき、平均値、分散、標準偏差を求めよ。

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#データの分析#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
あるクラスの生徒を対象に100点満点の試験を行ったところ、平均値は68点、分散は36であった。得点調整のため、生徒全員の得点を2.5倍して、更に30点を加えたとき、得点調整後の平均値、分散、標準偏差を求めよ。
この動画を見る
あるクラスの生徒を対象に100点満点の試験を行ったところ、平均値は68点、分散は36であった。得点調整のため、生徒全員の得点を2.5倍して、更に30点を加えたとき、得点調整後の平均値、分散、標準偏差を求めよ。
無限回したら0?∞?どっち?

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
箱に10個入れて、1個取り出す。
これを無限回すると、無限なのか0なのか解説します。
この動画を見る
箱に10個入れて、1個取り出す。
これを無限回すると、無限なのか0なのか解説します。
【高校数学】漸化式の問題演習~基本問題~ 3-17.5【数学B】

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
問1
次の条件によって定められる数列$\{an\}$の一般項を求めよ。
(1)$a_{1} = 0,a_{n+1}=a_n +2n+1$
(2)$a_{1}=1,a_{n+1} =a_n +3$
(3)$a_{1} = 2,a_{n+1}=-2a_n$
(4)$a_1=1, a_{n + 1}-a_n+2\cdot 3^{n-1}$
この動画を見る
問1
次の条件によって定められる数列$\{an\}$の一般項を求めよ。
(1)$a_{1} = 0,a_{n+1}=a_n +2n+1$
(2)$a_{1}=1,a_{n+1} =a_n +3$
(3)$a_{1} = 2,a_{n+1}=-2a_n$
(4)$a_1=1, a_{n + 1}-a_n+2\cdot 3^{n-1}$
【数Ⅰ】【データの分析】変量Xのデータの平均値xが35、分散Sx²が16で新しい変量Yのデータについて、平均値y、分散Sy²、標準偏差Syを求めよ(1)y=x-10(2)y=3x(3)y=-x/2+6

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#データの分析#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
変量Xのデータの平均値xが35、分散Sx²が16であるとする。
このとき、次の式によってえられる新しい変量Yのデータについて、平均値y、分散Sy²、標準偏差Syを求めよ。
(1)y=x-10
(2)y=3x
(3)y=-x/2+6
この動画を見る
変量Xのデータの平均値xが35、分散Sx²が16であるとする。
このとき、次の式によってえられる新しい変量Yのデータについて、平均値y、分散Sy²、標準偏差Syを求めよ。
(1)y=x-10
(2)y=3x
(3)y=-x/2+6
