 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
練習問題1(数検準1級、教員採用試験 レベル)
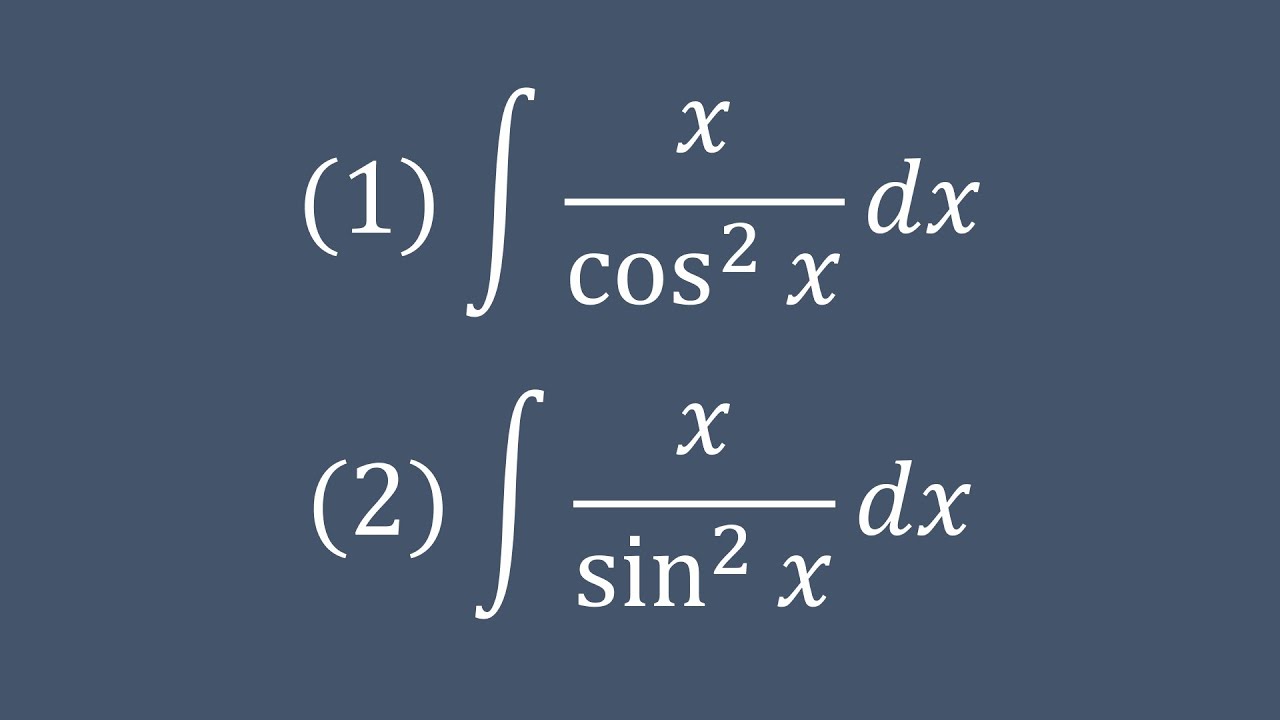
単元:
#数学検定・数学甲子園・数学オリンピック等#積分とその応用#不定積分#その他#数学検定#数学検定準1級#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
(1)$\int \frac{x}{cos^2x} dx$
(2)$\int \frac{x}{sin^2x} dx$
この動画を見る
(1)$\int \frac{x}{cos^2x} dx$
(2)$\int \frac{x}{sin^2x} dx$
横浜市立(医)3次方程式の実数解の個数

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^3+3ax^2+3ax+a^3=0$の実数解の個数を求めよ.
2004横浜市立(医)
この動画を見る
$x^3+3ax^2+3ax+a^3=0$の実数解の個数を求めよ.
2004横浜市立(医)
重積分⑩-3【曲面の面積】(高専数学 微積II,数検1級1次解析対応)
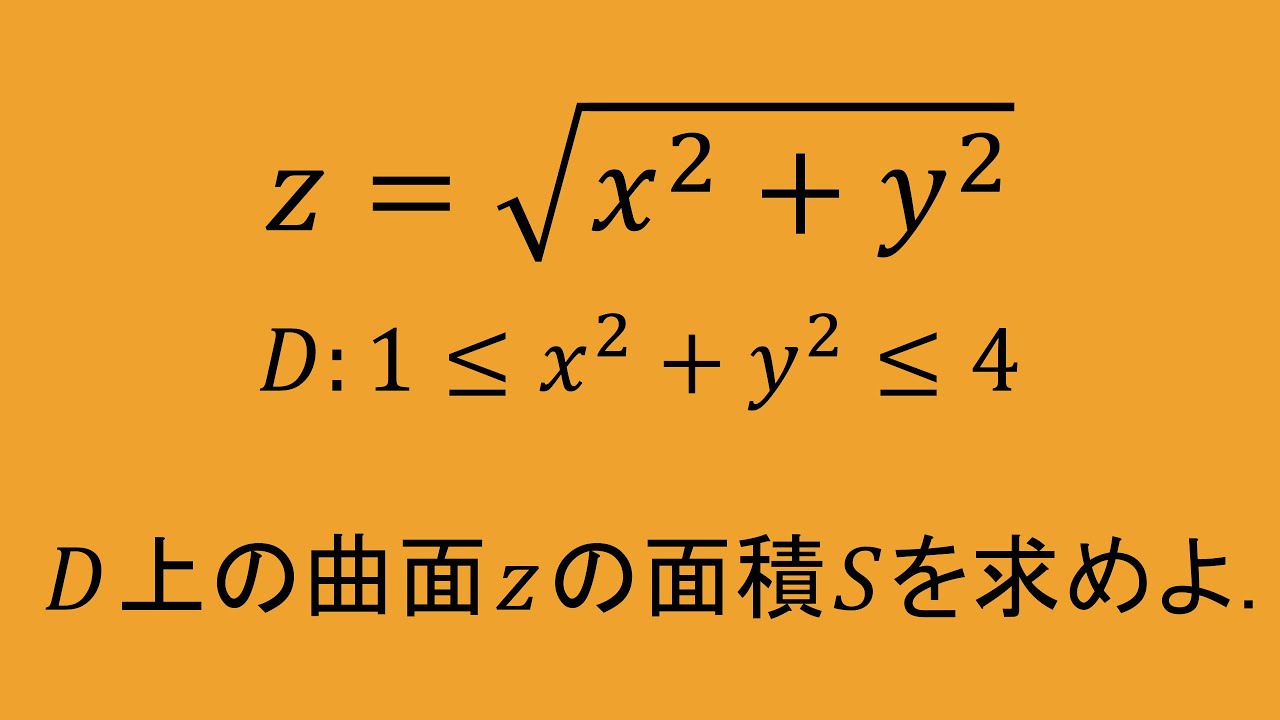
単元:
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$D:1 \leqq x^2+y^2 \leqq 4$
$Z= \sqrt{x^2+y^2}$
D上の曲面Zの面積Sを求めよ。
この動画を見る
$D:1 \leqq x^2+y^2 \leqq 4$
$Z= \sqrt{x^2+y^2}$
D上の曲面Zの面積Sを求めよ。
12愛知県教員採用試験(数学:3番 ひたすら積分)

単元:
#積分とその応用#面積・体積・長さ・速度#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
3⃣
$C_1:y=ax^3$と$C_2:y=logx$は接する。
$C_1,C_2$とx軸で囲まれた図形のx軸中心の回転体の体積Vを求めよ。
この動画を見る
3⃣
$C_1:y=ax^3$と$C_2:y=logx$は接する。
$C_1,C_2$とx軸で囲まれた図形のx軸中心の回転体の体積Vを求めよ。
三重大 対数と二次関数

単元:
#数Ⅰ#数Ⅱ#2次関数#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\alpha \gt 0$とする.
$f(x)=\log_3 \left(-\dfrac{1}{2}x^2+\dfrac{1}{2}\alpha x+9 \right)$
$f(x)$が整数となる$x$が$0\leqq x\leqq \alpha$の範囲でちょうど$6$個あるような$\alpha$の範囲を求めよ.
三重大過去問
この動画を見る
$\alpha \gt 0$とする.
$f(x)=\log_3 \left(-\dfrac{1}{2}x^2+\dfrac{1}{2}\alpha x+9 \right)$
$f(x)$が整数となる$x$が$0\leqq x\leqq \alpha$の範囲でちょうど$6$個あるような$\alpha$の範囲を求めよ.
三重大過去問
重積分⑩-2【曲面の面積】(高専数学 微積II,数検1級1次解析対応)
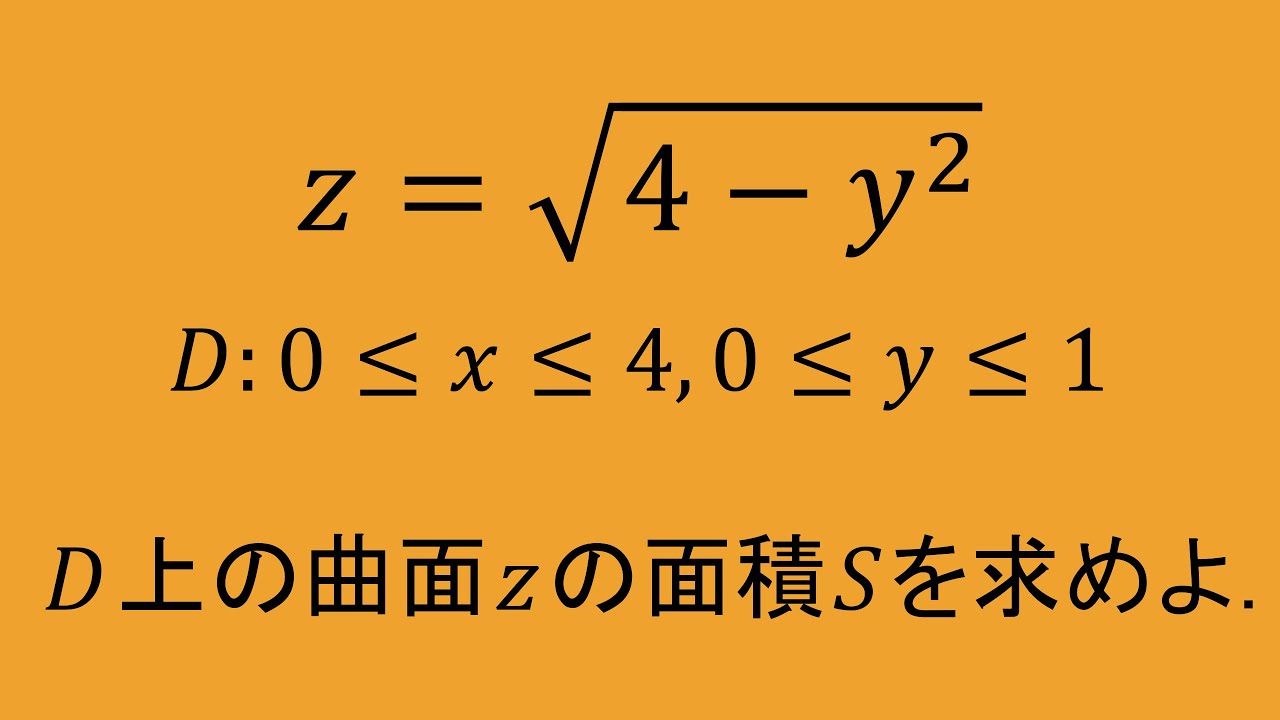
単元:
#数学検定・数学甲子園・数学オリンピック等#その他#数学検定#数学検定1級#その他#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$D:0 \leqq x \leqq 4 $ , $0 \leqq y \leqq 1$
$Z=\sqrt{4-y^2}$
D上の曲面Zの面積を求めよ
この動画を見る
$D:0 \leqq x \leqq 4 $ , $0 \leqq y \leqq 1$
$Z=\sqrt{4-y^2}$
D上の曲面Zの面積を求めよ
04神奈川県教員採用試験(数学:1番 整数問題)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣$x,y \in \mathbb{N}$ , $1 \leqq x, y \leqq 9$
$\frac{10+x}{10x+y} = \frac{1}{y}$
をみたす組(x,y)を全て求めよ。
この動画を見る
1⃣$x,y \in \mathbb{N}$ , $1 \leqq x, y \leqq 9$
$\frac{10+x}{10x+y} = \frac{1}{y}$
をみたす組(x,y)を全て求めよ。
東大 不定方程式

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x,y,z$は自然数とする.
①$x+y+z=xyz$を満たす$(x,y,z)$をすべて求めよ.$(x\leqq y\leqq z)$
②$x^3+y^3+z^3=xyz$を満たす$(x,y,z)$は存在しないことを示せ.
2006東大過去問
この動画を見る
$x,y,z$は自然数とする.
①$x+y+z=xyz$を満たす$(x,y,z)$をすべて求めよ.$(x\leqq y\leqq z)$
②$x^3+y^3+z^3=xyz$を満たす$(x,y,z)$は存在しないことを示せ.
2006東大過去問
「二次関数の最大最小 場合分け①】【高校数学ⅠA】を宇宙一わかりやすく

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
2次関数$f(x)=x^2-2ax+4(1 \leqq x \leqq 3)$について
(1)$f(x)$の最小値$m(a)$を求めよ。
2次関数$f(x)=x^2-2ax+4(1 \leqq x \leqq 3)$について
(2)$f(x)$の最大値$M(a)$を求めよ。
2次関数$f(x)=x^2-2ax+4(1 \leqq x \leqq 3)$について
(3)$y=m(a)$のグラフをかけ。
この動画を見る
2次関数$f(x)=x^2-2ax+4(1 \leqq x \leqq 3)$について
(1)$f(x)$の最小値$m(a)$を求めよ。
2次関数$f(x)=x^2-2ax+4(1 \leqq x \leqq 3)$について
(2)$f(x)$の最大値$M(a)$を求めよ。
2次関数$f(x)=x^2-2ax+4(1 \leqq x \leqq 3)$について
(3)$y=m(a)$のグラフをかけ。
重積分⑩-1【曲面の面積】(高専数学 微積II,数検1級1次解析対応)
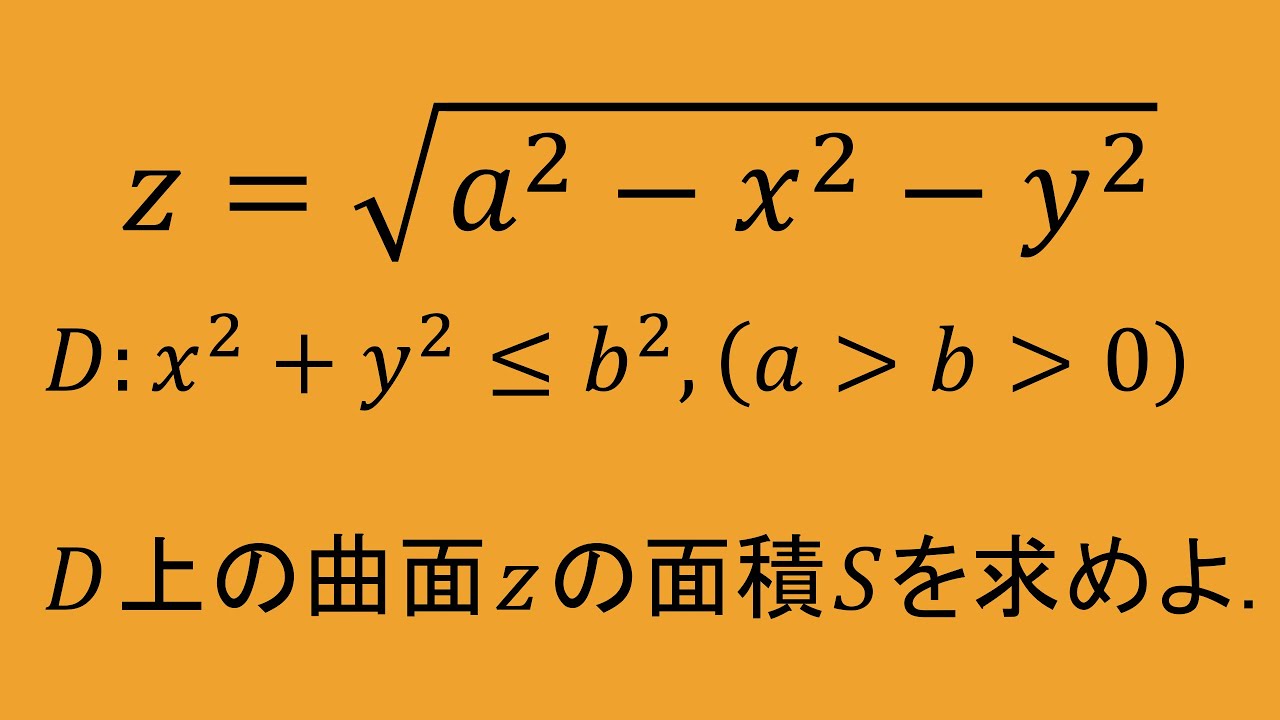
単元:
#数学検定・数学甲子園・数学オリンピック等#その他#数学検定#数学検定1級#その他#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$Z=\sqrt{a^2-x^2-y^2}$
$D:x^2+y^2=b^2$
(a>b>0)
D上の曲面Zの面積Sを求めよ。
この動画を見る
$Z=\sqrt{a^2-x^2-y^2}$
$D:x^2+y^2=b^2$
(a>b>0)
D上の曲面Zの面積Sを求めよ。
【高校数学】2次関数の最大最小例題~定義域の両方に文字~ 2-4.5【数学Ⅰ】

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
関数$y=-x^2+4x+5(a \leqq x \leqq a+2)$について、
(1) 最大値を求めよ
(2) 最小値を求めよ
この動画を見る
関数$y=-x^2+4x+5(a \leqq x \leqq a+2)$について、
(1) 最大値を求めよ
(2) 最小値を求めよ
09神奈川県教員採用試験(数学:4番 単なる積分)

単元:
#積分とその応用#定積分#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
4⃣$\pi \int_0^{\frac{\pi}{2}} sin(\pi cosx) sin2xdx$
この動画を見る
4⃣$\pi \int_0^{\frac{\pi}{2}} sin(\pi cosx) sin2xdx$
東邦大(医)三次方程式が自然数解を持つ条件

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a$は正の整数である.
$x^3-20x^2+(100-a)x+8a-23=0$が正の整数解をただ一つもつとする.
$a$の値を求めよ.
2016東邦大(医)過去問
この動画を見る
$a$は正の整数である.
$x^3-20x^2+(100-a)x+8a-23=0$が正の整数解をただ一つもつとする.
$a$の値を求めよ.
2016東邦大(医)過去問
【空間ベクトル】直線の方程式 発展分野

単元:
#空間ベクトル#空間ベクトル#数C
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
【空間ベクトル】直線の方程式 発展分野解説動画です
-----------------
点$A(3,2,1)$を通り、$\vec{ d }=(1,2,4)$に平行な直線の方程式は?
この動画を見る
【空間ベクトル】直線の方程式 発展分野解説動画です
-----------------
点$A(3,2,1)$を通り、$\vec{ d }=(1,2,4)$に平行な直線の方程式は?
重積分⑨-3【広義積分】(高専数学 微積II,数検1級1次解析対応)
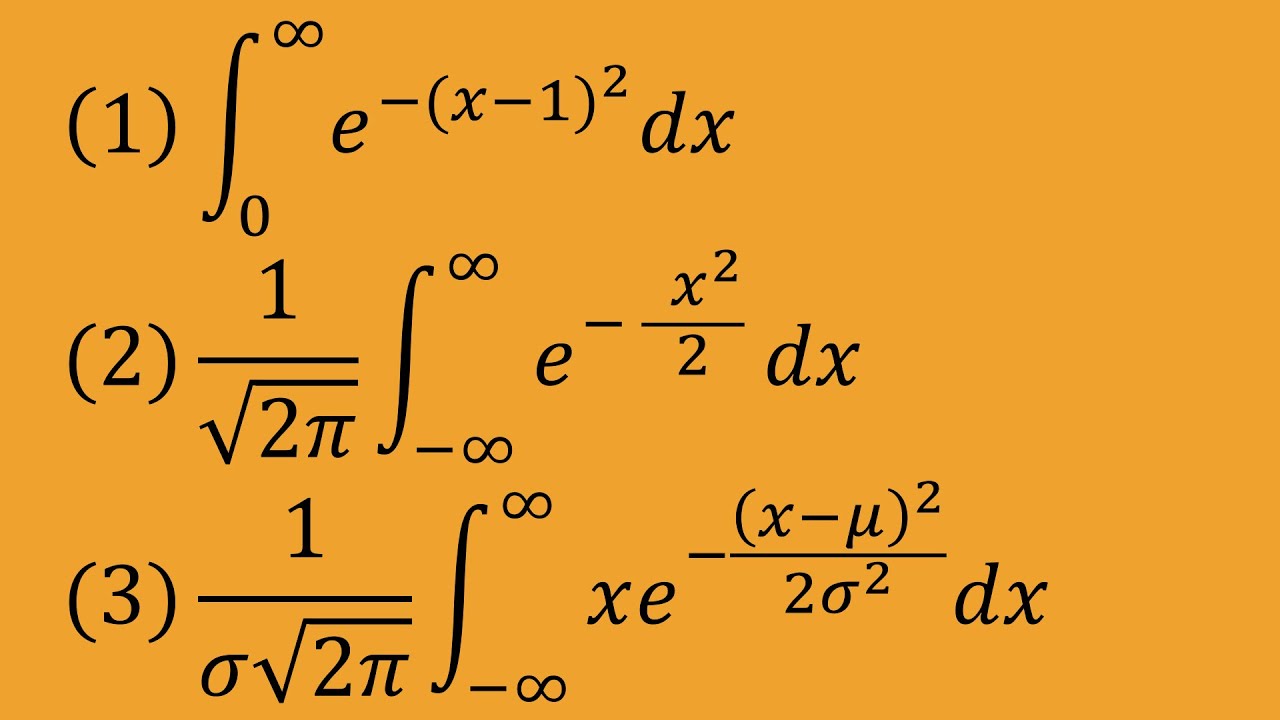
単元:
#数学検定・数学甲子園・数学オリンピック等#その他#数学検定#数学検定1級#その他#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\int_0^\infty e{-x^2}dx = \frac{\sqrt x}{2}$
(1)$\int_1^\infty e^{-(x-1)^2}dx$
(2)$\frac{1}{\sqrt{2x}} \int_{-\infty}^\infty e^{- \frac{x^2}{2}}dx$
(3)$\frac{1}{\sigma \sqrt{2x}} \int_{-\infty}^\infty xe^{-\frac{(x-\mu)^2}{2 \sigma^2}}dx$
この動画を見る
$\int_0^\infty e{-x^2}dx = \frac{\sqrt x}{2}$
(1)$\int_1^\infty e^{-(x-1)^2}dx$
(2)$\frac{1}{\sqrt{2x}} \int_{-\infty}^\infty e^{- \frac{x^2}{2}}dx$
(3)$\frac{1}{\sigma \sqrt{2x}} \int_{-\infty}^\infty xe^{-\frac{(x-\mu)^2}{2 \sigma^2}}dx$
06兵庫県教員採用試験(数学:5番類題 極限値)

単元:
#関数と極限#関数の極限#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
5⃣$\displaystyle \lim_{ x \to +0 } xlogx$
この動画を見る
5⃣$\displaystyle \lim_{ x \to +0 } xlogx$
北海道大 整数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x,y$を自然数とする.
(1)$\dfrac{3x}{x^2+2}$が自然数となる$x$を求めよ.
(2)$\dfrac{3x}{x^2+2}+\dfrac{1}{y}$が自然数となる$(x,y)$を求めよ.
2016北海道大過去問
この動画を見る
$x,y$を自然数とする.
(1)$\dfrac{3x}{x^2+2}$が自然数となる$x$を求めよ.
(2)$\dfrac{3x}{x^2+2}+\dfrac{1}{y}$が自然数となる$(x,y)$を求めよ.
2016北海道大過去問
「二次関数の最大最小②」【高校数学ⅠA】を宇宙一わかりやすく

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
(1)$y=(x^2-6x)^2+2(x^2-6x)-1$の最小値を求めよ。
(2)$y=(x^2-6x)^2+2(x^2-6x)-1(1 \leqq x \leqq 4)$の最大値と最小値を求めよ。
(3)$x \geqq 0,y \geqq 0x+y=1$のとき、$3x^2+y^2$の最大値と最小値を求めよ。
(4)実数$x,y$について$P=x^2+3y^2-2x+10y+4$の最小値を求めよ。
(5)実数$x,y$について$P=x^2-2xy+3y^2-2x+10y+4$の最小値を求めよ。
この動画を見る
(1)$y=(x^2-6x)^2+2(x^2-6x)-1$の最小値を求めよ。
(2)$y=(x^2-6x)^2+2(x^2-6x)-1(1 \leqq x \leqq 4)$の最大値と最小値を求めよ。
(3)$x \geqq 0,y \geqq 0x+y=1$のとき、$3x^2+y^2$の最大値と最小値を求めよ。
(4)実数$x,y$について$P=x^2+3y^2-2x+10y+4$の最小値を求めよ。
(5)実数$x,y$について$P=x^2-2xy+3y^2-2x+10y+4$の最小値を求めよ。
重積分⑨-2【広義積分】(高専数学 微積II,数検1級1次解析対応)
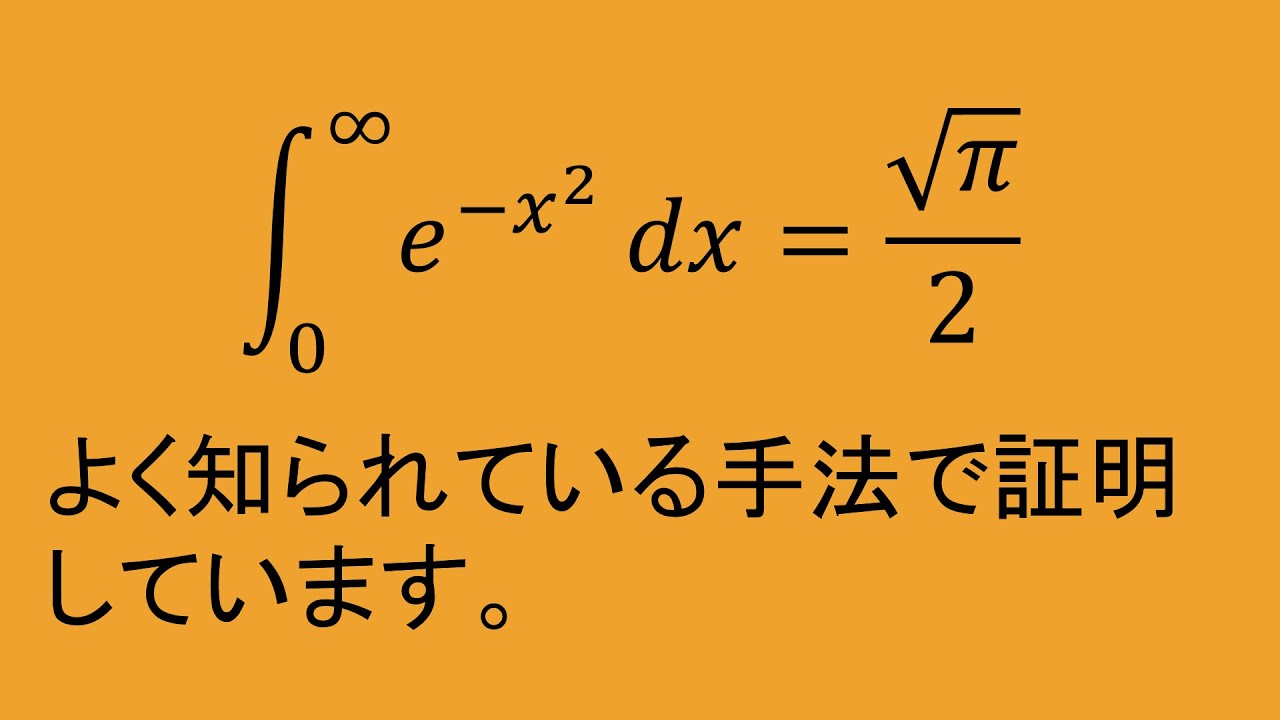
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#高専(高等専門学校)
指導講師:
ますただ
問題文全文(内容文):
目標$\int_0^\infty e^{-x^2}dx = \frac{\sqrt x}{2}$
準備$∬_{D_{a}}e^{-(x^2+y^2)}dxdy$
$D_a:x^2+y^2 \leqq a^2$
$x \geqq 0 , y \geqq 0$
この動画を見る
目標$\int_0^\infty e^{-x^2}dx = \frac{\sqrt x}{2}$
準備$∬_{D_{a}}e^{-(x^2+y^2)}dxdy$
$D_a:x^2+y^2 \leqq a^2$
$x \geqq 0 , y \geqq 0$
08兵庫県教員採用試験(数学:4番 微積・極限値)

単元:
#関数と極限#微分とその応用#関数の極限#関数の変化(グラフ・最大最小・方程式・不等式)#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
4⃣$f_n(x)=\frac{logx}{x^n}$
(1)$log x < x ( x > 1)$
を示し$\displaystyle \lim_{ x \to \infty } f_n(x)$を求めよ。
(2)$y=f_n(x)$のグラフをかけ
(3)$x=a_n$(極大値をとるx座標)
$y=f_n(x),$x軸で囲まれた面積を$S_n$とする。
$\displaystyle \lim_{ n \to \infty } n^2S_n$を求めよ。
この動画を見る
4⃣$f_n(x)=\frac{logx}{x^n}$
(1)$log x < x ( x > 1)$
を示し$\displaystyle \lim_{ x \to \infty } f_n(x)$を求めよ。
(2)$y=f_n(x)$のグラフをかけ
(3)$x=a_n$(極大値をとるx座標)
$y=f_n(x),$x軸で囲まれた面積を$S_n$とする。
$\displaystyle \lim_{ n \to \infty } n^2S_n$を求めよ。
素因数分解せよ

津田塾大 基本対称式

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a,b,c$は自然数である.
$abc,ab+bc+ca$,$a+b+c$がすべて3の倍数なら,$a,b,c$はすべて3の倍数であることを示せ.
2016津田塾大過去問
この動画を見る
$a,b,c$は自然数である.
$abc,ab+bc+ca$,$a+b+c$がすべて3の倍数なら,$a,b,c$はすべて3の倍数であることを示せ.
2016津田塾大過去問
重積分⑨-1【広義積分】(高専数学 微積II,数検1級1次解析対応)
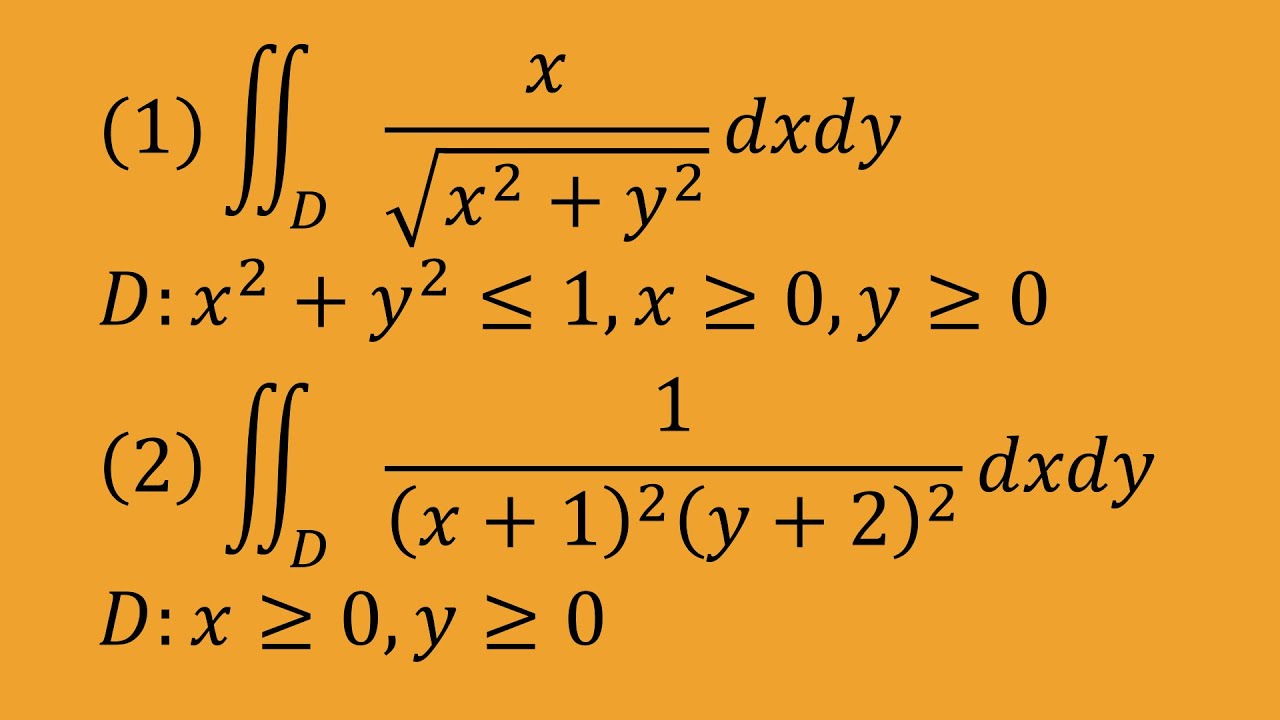
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#高専(高等専門学校)
指導講師:
ますただ
問題文全文(内容文):
広義積分(重積分)
(1)$∬_D\frac{x}{\sqrt{x^2+y^2}}dxdy$
$D:x^2+y^2 \leqq 1 , x \geqq 0 , y\geqq 0$
(2)$∬_D\frac{1}{(x+1)^2(y+2)^2}dxdy$
$D:x \geqq 0 , y \geqq 0$
この動画を見る
広義積分(重積分)
(1)$∬_D\frac{x}{\sqrt{x^2+y^2}}dxdy$
$D:x^2+y^2 \leqq 1 , x \geqq 0 , y\geqq 0$
(2)$∬_D\frac{1}{(x+1)^2(y+2)^2}dxdy$
$D:x \geqq 0 , y \geqq 0$
【意外と解けない?!?!】$y=3^{2x}$を微分せよ。

名古屋市立(医)不等式の証明

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a,b$は自然数である.
(1)$\sqrt2$は$\dfrac{b}{a}$と$\dfrac{2a+b}{a+b}$の間にある.
(2)$\sqrt2$は$\dfrac{b}{a}$と$\dfrac{2a+b}{a+b}$どちらに近いか.
1966名古屋市立(医)
この動画を見る
$a,b$は自然数である.
(1)$\sqrt2$は$\dfrac{b}{a}$と$\dfrac{2a+b}{a+b}$の間にある.
(2)$\sqrt2$は$\dfrac{b}{a}$と$\dfrac{2a+b}{a+b}$どちらに近いか.
1966名古屋市立(医)
「二次関数の最大最小①」全パターン【高校数学ⅠA】を宇宙一わかりやすく

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
次の問いに答えよ。
(1)関数$f(x)=2x^2-4x+c(-1 \leqq x \leqq 4)$の最大値が$7$となるような$c$の値を求めよ。
(2)関数$f(x)=ax^2-2ax+b(-1 \leqq x \leqq 2)$の最大値が$5$、最小値が$1$となるような$a,b$の値を求めよ。
2次関数$f(x)=x^2+2ax+2a-1(-2 \leqq x \leqq 3)$について、$a$の値が変化するときの最小値を$m(a)$とするとき、$m(a)$の最大値を求めよ。
この動画を見る
次の問いに答えよ。
(1)関数$f(x)=2x^2-4x+c(-1 \leqq x \leqq 4)$の最大値が$7$となるような$c$の値を求めよ。
(2)関数$f(x)=ax^2-2ax+b(-1 \leqq x \leqq 2)$の最大値が$5$、最小値が$1$となるような$a,b$の値を求めよ。
2次関数$f(x)=x^2+2ax+2a-1(-2 \leqq x \leqq 3)$について、$a$の値が変化するときの最小値を$m(a)$とするとき、$m(a)$の最大値を求めよ。
【数Ⅱ】微分法と積分法:定積分について基礎からめちゃめちゃ分かりやすく解説!用語や記号の解説からしますので初学者必見!

富山大(医) 無理数の証明

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$p,q$は異なる素数であり,$k,m,n$は整数である.
$k+m\sqrt p+n\sqrt q=0$なら,$k=m=n=0$を示せ.
(1)$\sqrt p$が無理数であることを示せ.
2016富山大(医)
この動画を見る
$p,q$は異なる素数であり,$k,m,n$は整数である.
$k+m\sqrt p+n\sqrt q=0$なら,$k=m=n=0$を示せ.
(1)$\sqrt p$が無理数であることを示せ.
2016富山大(医)
04兵庫県教員採用試験(数学:2番 数列と帰納法)

単元:
#数列#漸化式#数学的帰納法#その他#数学(高校生)#数B#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$a_1=\frac{1}{2}$ , $a_{n+1}=\frac{1}{2-a_n}$
一般項$a_n$を求めよ
この動画を見る
$a_1=\frac{1}{2}$ , $a_{n+1}=\frac{1}{2-a_n}$
一般項$a_n$を求めよ
「二次関数の決定」全パターン【高校数学ⅠA】を宇宙一わかりやすく

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
次の条件を満たす2次関数を求めよ。
(1)頂点が$(1,3)$で、点$(2,5)$を通る。
(2)軸が直線$x=2$で、2点$(0,-1),(-1,-6)$を通る。
(3)3点$(1,6),(-2,-9),(4,3)$を通る。
(4)3点$(-2,0),(3,0),(1,-12)$を通る。
(5)$y=2x^2$を平行移動したグラフで、点$(2,3)$を通り、頂点が直線$y=2x-1$上にある。
この動画を見る
次の条件を満たす2次関数を求めよ。
(1)頂点が$(1,3)$で、点$(2,5)$を通る。
(2)軸が直線$x=2$で、2点$(0,-1),(-1,-6)$を通る。
(3)3点$(1,6),(-2,-9),(4,3)$を通る。
(4)3点$(-2,0),(3,0),(1,-12)$を通る。
(5)$y=2x^2$を平行移動したグラフで、点$(2,3)$を通り、頂点が直線$y=2x-1$上にある。
