 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
聖マリアンナ医大 整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$p$は素数であり,$x,y,z$は整数である.
$x^3+py^3+p^2z^3-p^3xyz=0$ならば,$x=y=z=0$であることを示せ.
2016聖マリアンナ医大過去問
この動画を見る
$p$は素数であり,$x,y,z$は整数である.
$x^3+py^3+p^2z^3-p^3xyz=0$ならば,$x=y=z=0$であることを示せ.
2016聖マリアンナ医大過去問
【空間ベクトル】平面の方程式 3点を通る

単元:
#空間ベクトル#空間ベクトル#数学(高校生)#数C
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
【空間ベクトル】平面の方程式解説動画です
-----------------
3点$A(0,1,1),B(1,0,2),C(-3,2,3)$を通る平面の方程式は?
この動画を見る
【空間ベクトル】平面の方程式解説動画です
-----------------
3点$A(0,1,1),B(1,0,2),C(-3,2,3)$を通る平面の方程式は?
13愛知県教員採用試験(数学:7番 微積)

単元:
#積分とその応用#定積分#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
7⃣
$f(x)=\int_0^x 6t+2dt+\int_0^a f(t) dt$
$f(0)=a(>0)$
aの値を求めよ
この動画を見る
7⃣
$f(x)=\int_0^x 6t+2dt+\int_0^a f(t) dt$
$f(0)=a(>0)$
aの値を求めよ
重積分⑧-3【一般の変数変換】(高専数学 微積II,数検1級1次解析対応)
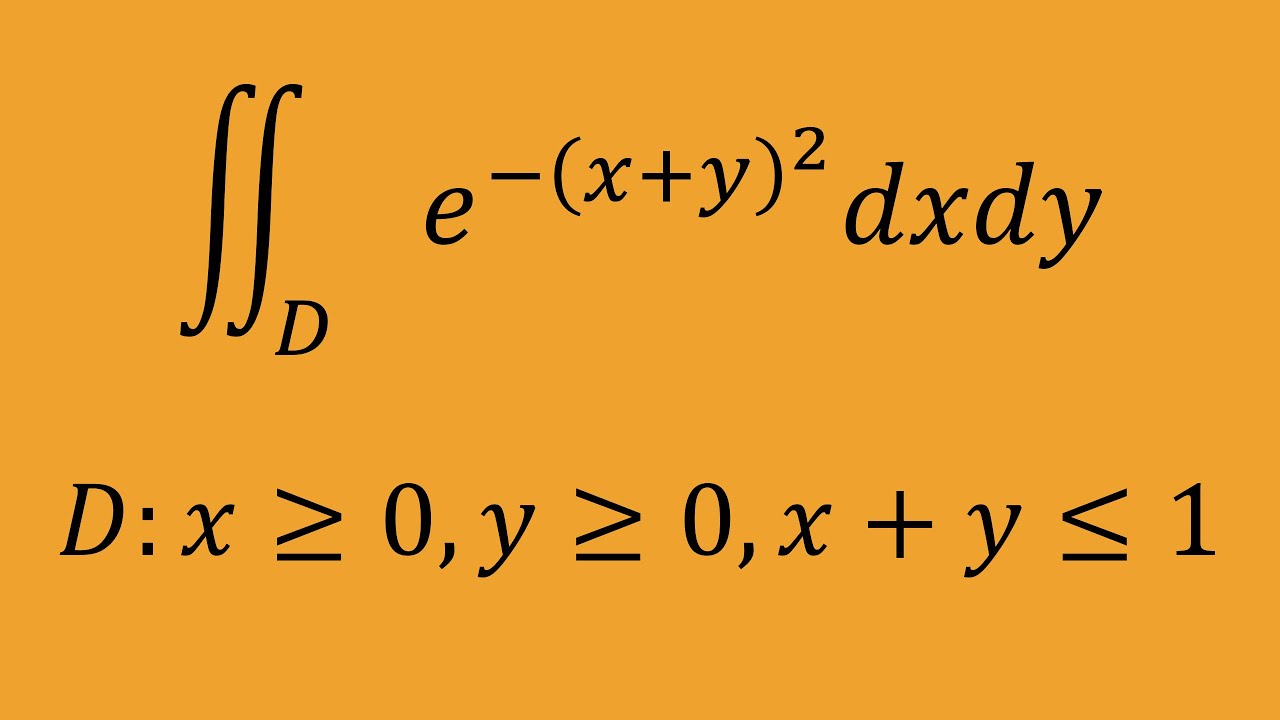
単元:
#大学入試過去問(数学)#数学検定・数学甲子園・数学オリンピック等#積分とその応用#学校別大学入試過去問解説(数学)#数学検定#数学検定1級#数学(高校生)#数Ⅲ#高専(高等専門学校)
指導講師:
ますただ
問題文全文(内容文):
$∬_De^{-(x+y)^2}dxdy$
$D:x \geqq 0 , y \geqq 0 , x+y \leqq 1$
この動画を見る
$∬_De^{-(x+y)^2}dxdy$
$D:x \geqq 0 , y \geqq 0 , x+y \leqq 1$
「二次関数の平行移動・対称移動」全パターン【高校数学ⅠA】を宇宙一わかりやすく

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
2次関数$y=2x^2-4x+5$ ・・・①について
$y=2x^2-4x+5$
$\ =2(x^2-2x)+5$
$\ 2\{(x-1)^2-1\}+5$
$\ 2(x-1)^2+3$
であるから、頂点$(1,3)$となる。 ・・・②
(1)
①を$x$軸方向に$3,y$軸方向に$-4$平行移動して得られるグラフの方程式を求めよ。
(2)
①のグラフを$x$軸に関して対称移動させた関数の方程式を求めよ。
(3)
①のグラフを$y$軸に関して対称移動させた関数の方程式を求めよ。
(4)
①のグラフを原点に関して対称移動させた関数の方程式を求めよ。
(5)
$x$軸方向に$1,y$軸方向に$-2$平行移動して、$x$軸に関して対称移動させたグラフの方程式が①になるようなグラフの方程式を求めよ。
(6)
任意の実数$k$について2次関数$y=3x^2+kx-2k+1$のグラフは、ある定点を通る。
その定点の座標を求めよ。
この動画を見る
2次関数$y=2x^2-4x+5$ ・・・①について
$y=2x^2-4x+5$
$\ =2(x^2-2x)+5$
$\ 2\{(x-1)^2-1\}+5$
$\ 2(x-1)^2+3$
であるから、頂点$(1,3)$となる。 ・・・②
(1)
①を$x$軸方向に$3,y$軸方向に$-4$平行移動して得られるグラフの方程式を求めよ。
(2)
①のグラフを$x$軸に関して対称移動させた関数の方程式を求めよ。
(3)
①のグラフを$y$軸に関して対称移動させた関数の方程式を求めよ。
(4)
①のグラフを原点に関して対称移動させた関数の方程式を求めよ。
(5)
$x$軸方向に$1,y$軸方向に$-2$平行移動して、$x$軸に関して対称移動させたグラフの方程式が①になるようなグラフの方程式を求めよ。
(6)
任意の実数$k$について2次関数$y=3x^2+kx-2k+1$のグラフは、ある定点を通る。
その定点の座標を求めよ。
重積分⑧-2【一般の変数変換】(高専数学 微積II,数検1級1次解析対応)
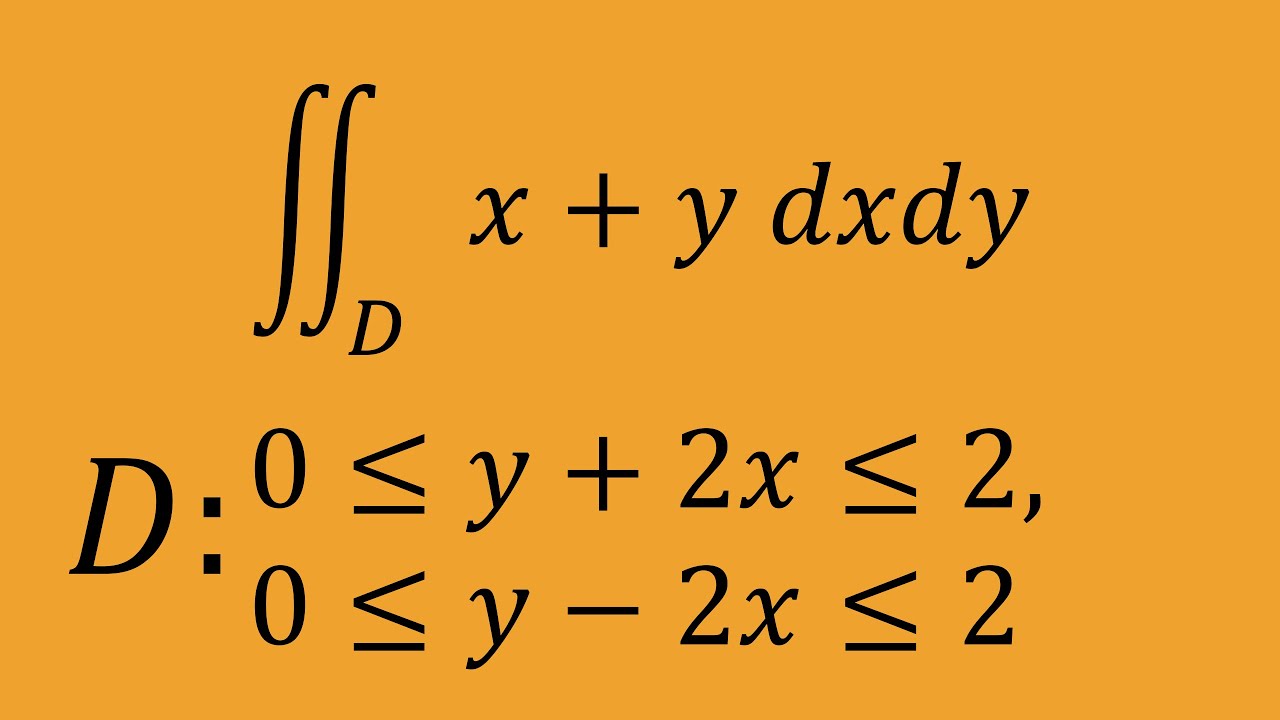
単元:
#大学入試過去問(数学)#数学検定・数学甲子園・数学オリンピック等#積分とその応用#学校別大学入試過去問解説(数学)#数学検定#数学検定1級#数学(高校生)#数Ⅲ#高専(高等専門学校)
指導講師:
ますただ
問題文全文(内容文):
$∬_D(x+y)dxdy$
$D : 0 \leqq y+2x \leqq 2 $,
$0 \leqq y-2x \leqq 2$
*図は動画内参照
この動画を見る
$∬_D(x+y)dxdy$
$D : 0 \leqq y+2x \leqq 2 $,
$0 \leqq y-2x \leqq 2$
*図は動画内参照
00兵庫県教員採用試験(数学:4番 対数)

単元:
#数Ⅱ#式と証明#図形と方程式#指数関数と対数関数#恒等式・等式・不等式の証明#軌跡と領域#対数関数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
4⃣$log_xy+2log_yx \leqq 3$
をみたす(x,y)の存在する領域を図示せよ
この動画を見る
4⃣$log_xy+2log_yx \leqq 3$
をみたす(x,y)の存在する領域を図示せよ
整数問題2021

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$2021^{2021^{2021}}$の下3桁を求めよ.
この動画を見る
$2021^{2021^{2021}}$の下3桁を求めよ.
重積分⑧-1【一般の変数変換】(高専数学 微積II,数検1級1次解析対応)
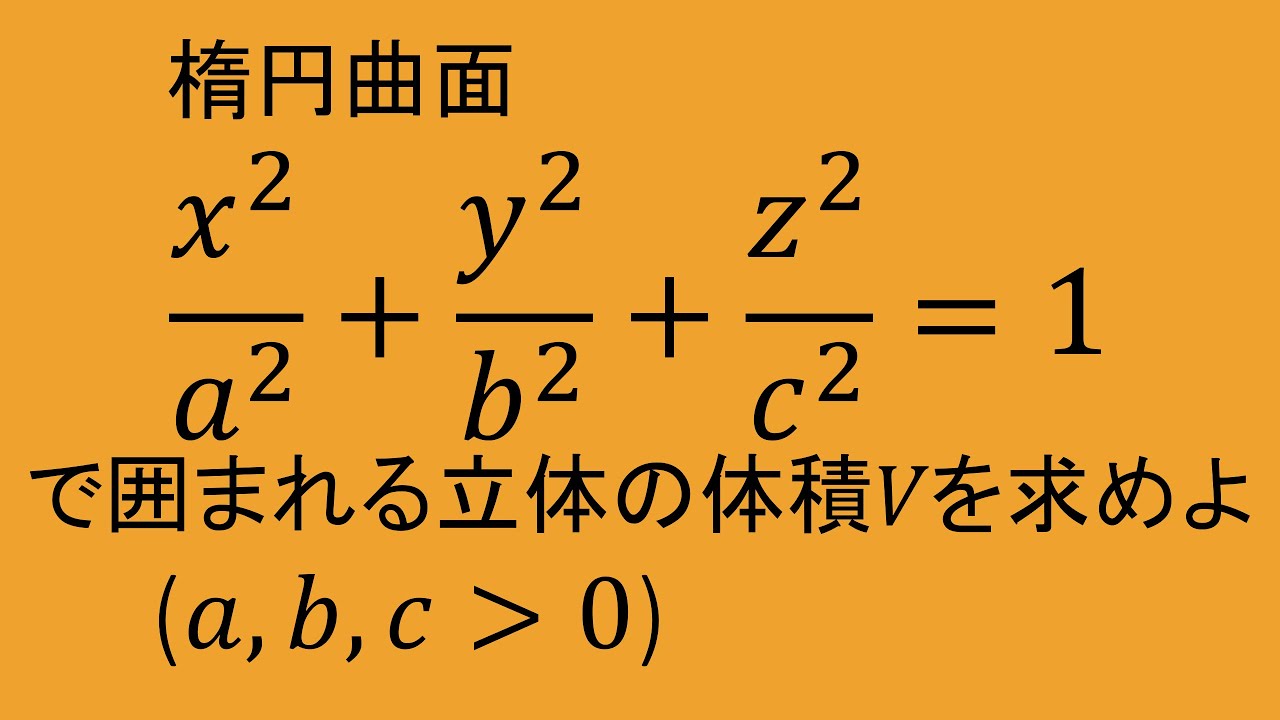
単元:
#数Ⅱ#大学入試過去問(数学)#数学検定・数学甲子園・数学オリンピック等#図形と方程式#円と方程式#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学検定#数学検定1級#数学(高校生)#数Ⅲ#高専(高等専門学校)
指導講師:
ますただ
問題文全文(内容文):
楕円面$\frac{x^2}{a^2}+ \frac{y^2}{b^2}+\frac{z^2}{c^2}=1$
で囲まれる立体の体積Vを求めよ $(a,b,c > 0)$
この動画を見る
楕円面$\frac{x^2}{a^2}+ \frac{y^2}{b^2}+\frac{z^2}{c^2}=1$
で囲まれる立体の体積Vを求めよ $(a,b,c > 0)$
16兵庫県教員採用試験(数学:3番 微積)

単元:
#積分とその応用#定積分#面積・体積・長さ・速度#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
3⃣直線$l_1:y=kx+2k$が曲線$C:y=x^3-3x+2$の変曲点を通るとき、$l_1$とCで囲まれた面積を求めよ。
この動画を見る
3⃣直線$l_1:y=kx+2k$が曲線$C:y=x^3-3x+2$の変曲点を通るとき、$l_1$とCで囲まれた面積を求めよ。
2021!を5の504乗で割ったあまり

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$2021!$を$5^{504}$で割った余りを求めよ.
この動画を見る
$2021!$を$5^{504}$で割った余りを求めよ.
【二次関数の平行移動・対称移動】を宇宙一わかりやすく【高校数学ⅠA】

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
【高校数学ⅠA】二次関数の平行移動・対称移動についての解説動画です
この動画を見る
【高校数学ⅠA】二次関数の平行移動・対称移動についての解説動画です
【高校数学】2次関数の最大最小例題~放物線の軸に文字~ 2-4.5【数学Ⅰ】

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
関数$y=x^2-2ax+4(0 \leqq x \leqq 3)$について
(1) 最小値を求めよ
(2) 最大値を求めよ
この動画を見る
関数$y=x^2-2ax+4(0 \leqq x \leqq 3)$について
(1) 最小値を求めよ
(2) 最大値を求めよ
13愛知県教員採用試験(数学:5番 微積)
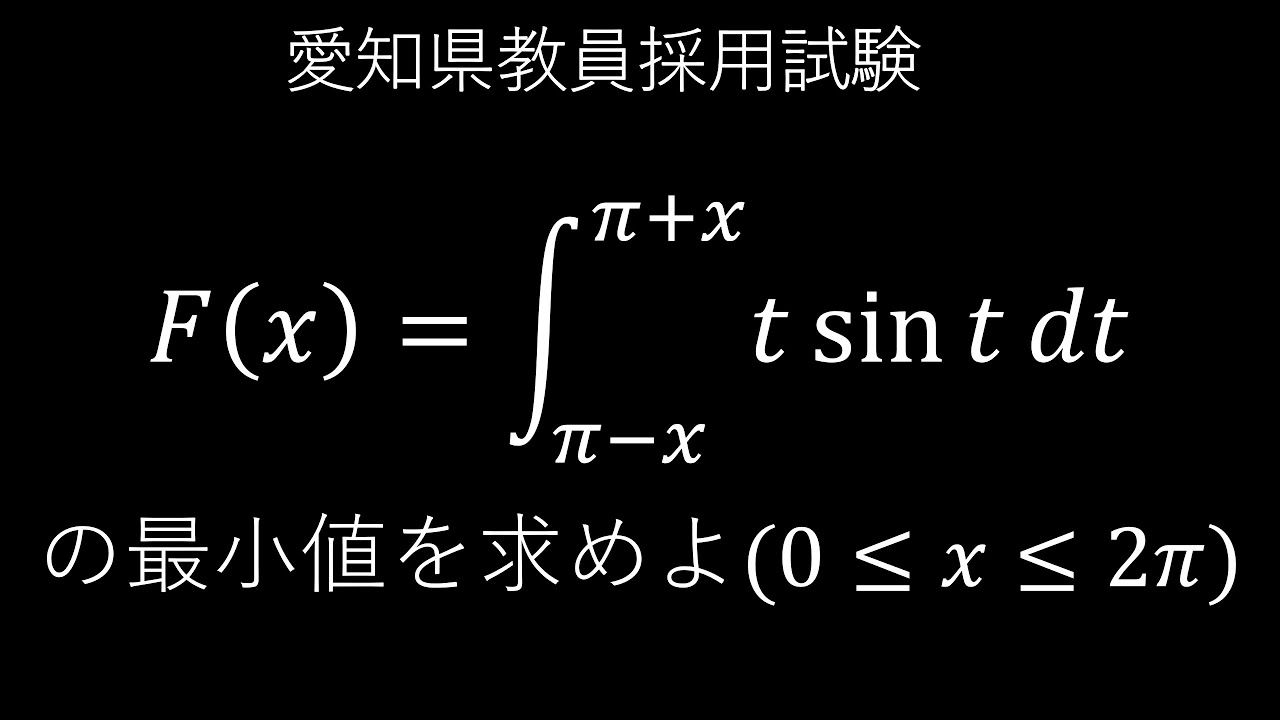
単元:
#微分とその応用#積分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
5⃣ $F(x)=\int_{\pi - x}^{\pi + x} t sint dt$
$(0 \leqq x \leqq 2\pi)$
F(x)の最小値を求めよ。
この動画を見る
5⃣ $F(x)=\int_{\pi - x}^{\pi + x} t sint dt$
$(0 \leqq x \leqq 2\pi)$
F(x)の最小値を求めよ。
京都大 整式の剰余

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x$は自然数とする.
整式$x^n$を整式$x^2-2x-1$sw割った余りを$ax+b$とする.
$a,b$は整数であり,$a,b$をともに割り切る素数は無いことを示せ.
2013京都大過去問
この動画を見る
$x$は自然数とする.
整式$x^n$を整式$x^2-2x-1$sw割った余りを$ax+b$とする.
$a,b$は整数であり,$a,b$をともに割り切る素数は無いことを示せ.
2013京都大過去問
10大阪府教員採用試験(数学:2番 微積)意外と沼にハマりがち

単元:
#数Ⅱ#指数関数と対数関数#対数関数#積分とその応用#定積分#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
2⃣ $f(x) = \frac{x}{1+x^2}$
f(α)=f(β) , 0 < α < β のとき$\int_α^β \frac{x}{1+x^2}dx= log_β$を示せ
この動画を見る
2⃣ $f(x) = \frac{x}{1+x^2}$
f(α)=f(β) , 0 < α < β のとき$\int_α^β \frac{x}{1+x^2}dx= log_β$を示せ
重積分⑦-4【極座標による変数変換】(高専数学 微積II,数検1級1次解析対応)
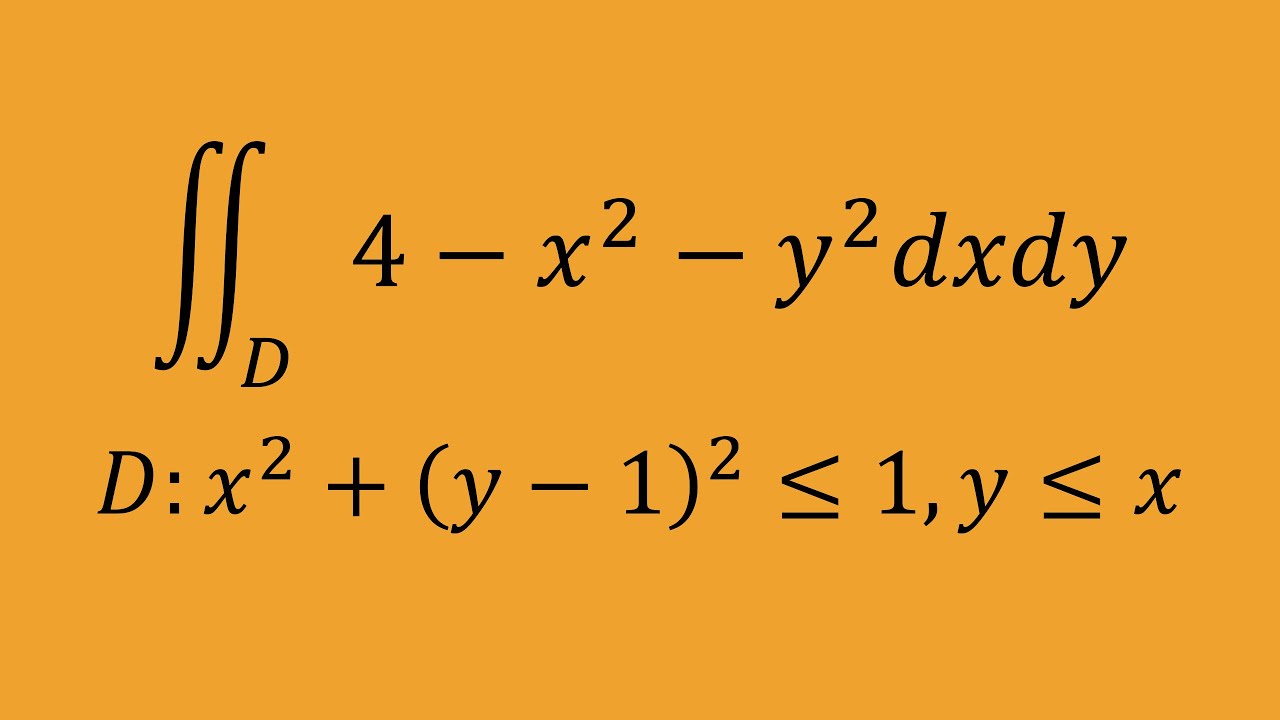
単元:
#大学入試過去問(数学)#数学検定・数学甲子園・数学オリンピック等#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学検定#数学検定1級#数学(高校生)#数Ⅲ#高専(高等専門学校)
指導講師:
ますただ
問題文全文(内容文):
$∬_D(4-x^2-y^2)dxdy$
$D:x^2+(y-1)^2 \leqq 1 $ , $y \leqq x$
この動画を見る
$∬_D(4-x^2-y^2)dxdy$
$D:x^2+(y-1)^2 \leqq 1 $ , $y \leqq x$
【数Ⅲ-175】曲線の長さ②(媒介変数表示編)

単元:
#微分とその応用#積分とその応用#微分法#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
数Ⅲ(曲線の長さ②・媒介変数表示編)
ポイント
曲線$x=f(t)$、$y=g(t) (a \leqq t \leqq b)$ の長さ$L$は $L=$①
②曲線$x=a\cos^3θ、y=a \sin^3θ (0 \leqq θ \leqq \frac{\pi}{2})$の長さを求めよ。
ただし$a \gt 0$とする。
この動画を見る
数Ⅲ(曲線の長さ②・媒介変数表示編)
ポイント
曲線$x=f(t)$、$y=g(t) (a \leqq t \leqq b)$ の長さ$L$は $L=$①
②曲線$x=a\cos^3θ、y=a \sin^3θ (0 \leqq θ \leqq \frac{\pi}{2})$の長さを求めよ。
ただし$a \gt 0$とする。
【数学B】平面の方程式(発展)【空間ベクトル】

単元:
#空間ベクトル#空間ベクトル#数C
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
【数学B】平面の方程式(発展)の解説動画です
-----------------
$A(1,2,2)$を通り、$\vec { n }(3,-2,4)$に垂直な平面の方程式は?
この動画を見る
【数学B】平面の方程式(発展)の解説動画です
-----------------
$A(1,2,2)$を通り、$\vec { n }(3,-2,4)$に垂直な平面の方程式は?
整式の剰余

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=x^{ab}+x^{a+b}+1$,$g(x)=x^2+x+1$
$a,b$は自然数とする.
$f(x)$が$g(x)$で割り切れるための$a,b$の条件を求めよ.
この動画を見る
$f(x)=x^{ab}+x^{a+b}+1$,$g(x)=x^2+x+1$
$a,b$は自然数とする.
$f(x)$が$g(x)$で割り切れるための$a,b$の条件を求めよ.
重積分⑦-3【極座標による変数変換】(高専数学 微積II,数検1級1次解析対応)
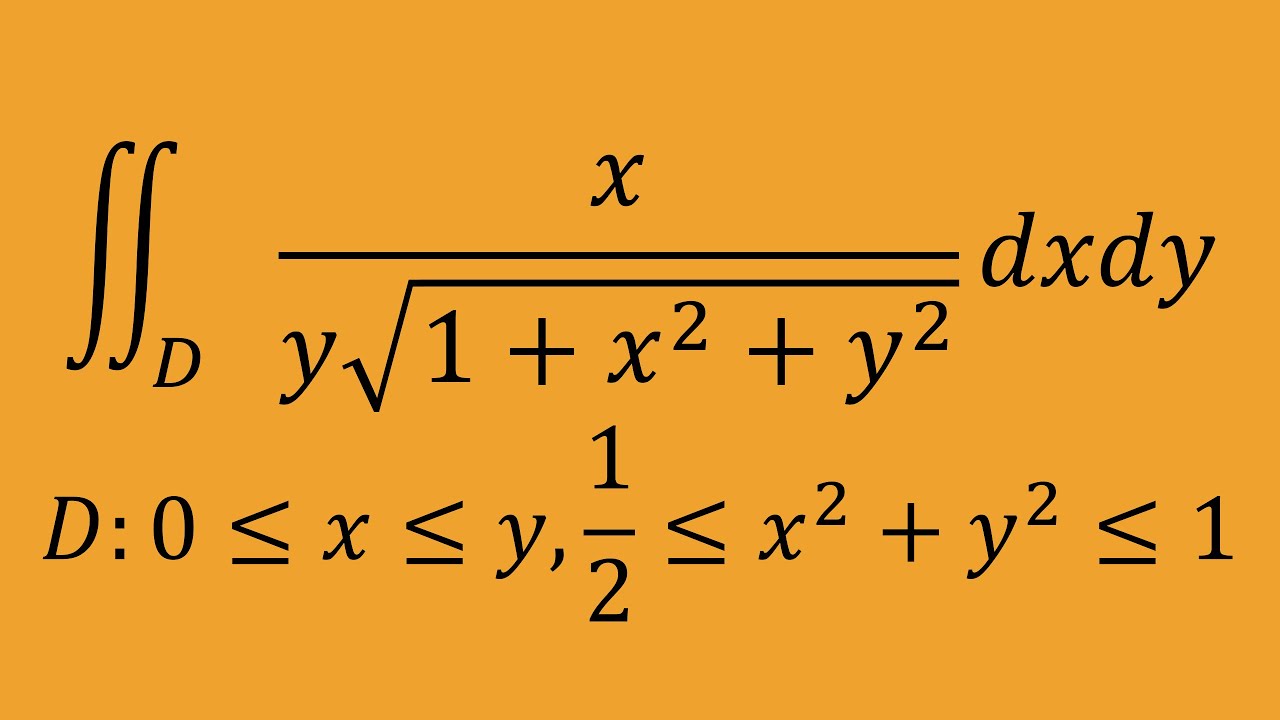
単元:
#大学入試過去問(数学)#数学検定・数学甲子園・数学オリンピック等#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学検定#数学検定1級#数学(高校生)#数Ⅲ#高専(高等専門学校)
指導講師:
ますただ
問題文全文(内容文):
$∬_D \frac{x}{y \sqrt{1+x^2+y^2}}dxdy$
$D: 0 \leqq x \leqq y $ , $\frac{1}{2} \leqq x^2+y^2 \leqq 1$
この動画を見る
$∬_D \frac{x}{y \sqrt{1+x^2+y^2}}dxdy$
$D: 0 \leqq x \leqq y $ , $\frac{1}{2} \leqq x^2+y^2 \leqq 1$
11神奈川県教員採用試験(数学:6番 指数)

単元:
#数Ⅱ#指数関数と対数関数#指数関数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
6⃣$4^x+9^y=a^2$
$2^{x+1}+3^{2y}$の最大値を求めよ。(a>1)
この動画を見る
6⃣$4^x+9^y=a^2$
$2^{x+1}+3^{2y}$の最大値を求めよ。(a>1)
東大 三角比と漸化式

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a=\sin^2\dfrac{\pi}{5}$であり,$b=\sin^2\dfrac{2\pi}{5}$である.
(1)$a+b,ab$は有理数であることを示せ.
(2)$(a^{-n}+b^{-n})(a+b)^n$は整数であることを示せ.($n$は自然数)
1994東大過去問
この動画を見る
$a=\sin^2\dfrac{\pi}{5}$であり,$b=\sin^2\dfrac{2\pi}{5}$である.
(1)$a+b,ab$は有理数であることを示せ.
(2)$(a^{-n}+b^{-n})(a+b)^n$は整数であることを示せ.($n$は自然数)
1994東大過去問
「対偶法と背理法の証明②」の全パターン【高校数学ⅠA】を宇宙一わかりやすく

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
(3)
$\sqrt{ 2 }$が無理数であることを用いて$3-\sqrt{ 2 }$が無理数であることを示せ。
(4)
$\sqrt{ 6 }$が無理数であることを用いて$\sqrt{ 3 }-\sqrt{ 2 }$が無理数であることを示せ。
(5)
(ⅰ)$n^2$が$3$の倍数ならば、$n$が$3$の倍数であることを示せ。
(ⅱ)$\sqrt{ 3 }$が無理数であることを示せ。
この動画を見る
(3)
$\sqrt{ 2 }$が無理数であることを用いて$3-\sqrt{ 2 }$が無理数であることを示せ。
(4)
$\sqrt{ 6 }$が無理数であることを用いて$\sqrt{ 3 }-\sqrt{ 2 }$が無理数であることを示せ。
(5)
(ⅰ)$n^2$が$3$の倍数ならば、$n$が$3$の倍数であることを示せ。
(ⅱ)$\sqrt{ 3 }$が無理数であることを示せ。
10神奈川県教員採用試験(数学:10番 複素数)

単元:
#複素数平面#複素数平面#その他#数学(高校生)#数C#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{10}$ $z=cosθ+isinθ$
$0 < θ \leqq \pi$
$w=\frac{1-z^3}{1-z}$ , $|w|=1$
のときθの値を求めよ。
この動画を見る
$\boxed{10}$ $z=cosθ+isinθ$
$0 < θ \leqq \pi$
$w=\frac{1-z^3}{1-z}$ , $|w|=1$
のときθの値を求めよ。
県立広島大 ガウス記号を含む二次方程式

重積分⑦-2【極座標による変数変換】(高専数学 微積II,数検1級1次解析対応)

単元:
#大学入試過去問(数学)#数学検定・数学甲子園・数学オリンピック等#平面上の曲線#積分とその応用#2次曲線#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#数学検定#数学検定1級#数学(高校生)#数C#数Ⅲ#高専(高等専門学校)
指導講師:
ますただ
問題文全文(内容文):
$x^2+y^2+z^2=4a^2$ , $z \geqq 0$
$(x-a)^2+y^2=a^2$ , $z \geqq 0$
xy平面 (a>0)で囲まれた体積Vを求めよ。
この動画を見る
$x^2+y^2+z^2=4a^2$ , $z \geqq 0$
$(x-a)^2+y^2=a^2$ , $z \geqq 0$
xy平面 (a>0)で囲まれた体積Vを求めよ。
旭川医科大 整数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
p^3-q^3-27r^3-9pqr=0 \\
p^2-10q-30r=11
\end{array}
\right.
\end{eqnarray}$
を満たす自然数$(p,q,r)$の組をすべて求めよ.
2015旭川医科大過去問
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
p^3-q^3-27r^3-9pqr=0 \\
p^2-10q-30r=11
\end{array}
\right.
\end{eqnarray}$
を満たす自然数$(p,q,r)$の組をすべて求めよ.
2015旭川医科大過去問
対偶法と背理法の証明の全パターン①【高校数学ⅠA】を宇宙一わかりやすく

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
次の問いに答えよ。
(1)
$mn$が偶数ならば、$m,n$のうち少なくとも1つは偶数であることを示せ。
ただし、$m,n$は整数とする。
(2)
$\sqrt{ 2 }$が無理数であることを示せ。
この動画を見る
次の問いに答えよ。
(1)
$mn$が偶数ならば、$m,n$のうち少なくとも1つは偶数であることを示せ。
ただし、$m,n$は整数とする。
(2)
$\sqrt{ 2 }$が無理数であることを示せ。
07神奈川県教員採用試験(数学:7番 数列の極限)

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#その他#数学(高校生)#数B#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
7⃣$a_1=\frac{1}{3}$ , $3^{n+1}a_{n+1}=3^na_n+1$
$\displaystyle \lim_{ n \to \infty } S_n$を求めよ
この動画を見る
7⃣$a_1=\frac{1}{3}$ , $3^{n+1}a_{n+1}=3^na_n+1$
$\displaystyle \lim_{ n \to \infty } S_n$を求めよ
