 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
九州大学 三倍角 高校数学 Japanese university entrance exam questions
単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
九州大学過去問題
(1)$\sin10^{\circ}$は3次方程式$8x^3-6x+1=0$の解であることを示せ。
(2)他の2解を求めよ。
この動画を見る
九州大学過去問題
(1)$\sin10^{\circ}$は3次方程式$8x^3-6x+1=0$の解であることを示せ。
(2)他の2解を求めよ。
福田の一夜漬け数学〜数列・漸化式(6)その他色々〜高校2年生

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
次の漸化式を解け。(すべて$a_1=1$とする)
①$a_{n+1}=\displaystyle \frac{a_n}{4a_n-1}$
②$a_{n+1}=2\displaystyle \sqrt{a_n}$
③$a_{n+1}=2(n+1)a_n$
④$a_{n+1}=\displaystyle \frac{4a_n+8}{a_n+6}$
この動画を見る
次の漸化式を解け。(すべて$a_1=1$とする)
①$a_{n+1}=\displaystyle \frac{a_n}{4a_n-1}$
②$a_{n+1}=2\displaystyle \sqrt{a_n}$
③$a_{n+1}=2(n+1)a_n$
④$a_{n+1}=\displaystyle \frac{4a_n+8}{a_n+6}$
東京海洋大学 漸化式 高校数学 Japanese university entrance exam questions

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
2013東京海洋大学過去問題
$a_1 = 1 \quad n=1,2,3\cdots$
$a_{n+1} = 27^{n^2-3n-9}a_n$
(1)一般項$a_n$を求めよ
(2)$a_n$が最小となるnの値
この動画を見る
2013東京海洋大学過去問題
$a_1 = 1 \quad n=1,2,3\cdots$
$a_{n+1} = 27^{n^2-3n-9}a_n$
(1)一般項$a_n$を求めよ
(2)$a_n$が最小となるnの値
福田の一夜漬け数学〜数列・漸化式(5)連立漸化式〜高校2年生

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
次の漸化式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_{n+1}=4a_n+b_n\\
b_{n+1}=a_n+4b_n\\
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_1=1\\
b_1=2\\
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_{n+1}=a_n+4b_n\\
b_{n+1}=a_n+b_n\\
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_1=1\\
b_1=1\\
\end{array}
\right.
\end{eqnarray}$
この動画を見る
次の漸化式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_{n+1}=4a_n+b_n\\
b_{n+1}=a_n+4b_n\\
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_1=1\\
b_1=2\\
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_{n+1}=a_n+4b_n\\
b_{n+1}=a_n+b_n\\
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_1=1\\
b_1=1\\
\end{array}
\right.
\end{eqnarray}$
【高校数学】数Ⅲ-97 三角関数の導関数②

単元:
#数Ⅱ#三角関数#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の関数を微分せよ。
①$y=\sin 2 x \cos x$
②$y=\sqrt{1+\sin x}$
③$y=\dfrac{x}{\sin x}$
④$y=\cos^3 2x$
⑤$y=\dfrac{\sin x}{\sin x+\cos x}$
⑥$y=\dfrac{1}{\sin x \cos x}$
この動画を見る
次の関数を微分せよ。
①$y=\sin 2 x \cos x$
②$y=\sqrt{1+\sin x}$
③$y=\dfrac{x}{\sin x}$
④$y=\cos^3 2x$
⑤$y=\dfrac{\sin x}{\sin x+\cos x}$
⑥$y=\dfrac{1}{\sin x \cos x}$
九州大学 整数問題 高校数学 Japanese university entrance exam questions

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
2014九州大学過去問題
(1)aは自然数$\quad$ $a^2$を3で割った余りは0か1を証明
(2)$a^2+b^2=3c^2$を満たすと仮定するとa,b,cはすべて3で割りきれなければならないことを証明せよ。
(3)$a^2+b^2=3c^2$を満たす自然数a,b,cは存在しないことを証明
この動画を見る
2014九州大学過去問題
(1)aは自然数$\quad$ $a^2$を3で割った余りは0か1を証明
(2)$a^2+b^2=3c^2$を満たすと仮定するとa,b,cはすべて3で割りきれなければならないことを証明せよ。
(3)$a^2+b^2=3c^2$を満たす自然数a,b,cは存在しないことを証明
【高校数学】数Ⅲ-96 三角関数の導関数①

単元:
#数Ⅱ#三角関数#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
$(\sin x)'= ①$
$(\cos x)'= ②$
$(\tan x)'= ③$
次の関数を微分せよ。
④$y=\sin 2x$
⑤$y=\cos (3x+2)$
⑥$y=\tan^2 x$
⑦$y=x \cos x$
⑧$y=\sin(x^2+3)$
⑨$y=\cos\dfrac{1}{x}$
この動画を見る
$(\sin x)'= ①$
$(\cos x)'= ②$
$(\tan x)'= ③$
次の関数を微分せよ。
④$y=\sin 2x$
⑤$y=\cos (3x+2)$
⑥$y=\tan^2 x$
⑦$y=x \cos x$
⑧$y=\sin(x^2+3)$
⑨$y=\cos\dfrac{1}{x}$
福田の一夜漬け数学〜数列・漸化式(4)3項間の漸化式〜高校2年生

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
次の漸化式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_1=1, a_2=5\\
a_{n+2}=5a_{n+1}-4a_n\\
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_1=1, a_2=5\\
a_{n+2}=4a_{n+1}-4a_n\\
\end{array}
\right.
\end{eqnarray}$
この動画を見る
次の漸化式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_1=1, a_2=5\\
a_{n+2}=5a_{n+1}-4a_n\\
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_1=1, a_2=5\\
a_{n+2}=4a_{n+1}-4a_n\\
\end{array}
\right.
\end{eqnarray}$
慶應(医)愛媛大 判別式 整数 高校数学 Japanese university entrance exam questions

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
愛媛大学過去問題
$3x^2+y^2+5z^2-2yz-12=0$
これを満たす整数(x,y,z)
慶応義塾大学過去問題
$\{ x^2+2(a+b)x+a^3 \}$ $\{ x^2+(a^2-ab+b^2)x+b^3 \} = 0$
が実根をもつことを証明。
この動画を見る
愛媛大学過去問題
$3x^2+y^2+5z^2-2yz-12=0$
これを満たす整数(x,y,z)
慶応義塾大学過去問題
$\{ x^2+2(a+b)x+a^3 \}$ $\{ x^2+(a^2-ab+b^2)x+b^3 \} = 0$
が実根をもつことを証明。
姪(高1)からの質問

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\frac{x+y}{3}=\frac{y+z}{6}=\frac{z+x}{7} \neq 0$
$\frac{x^3+y^3+z^3}{(x-y)(y-z)(z-x)}$
x,y,z正
$\frac{yz}{x}$=$\frac{zx}{4y}$=$\frac{xy}{9z}$
$\frac{x+y+z}{\sqrt{x^2+y^2+z^2}}$
この動画を見る
$\frac{x+y}{3}=\frac{y+z}{6}=\frac{z+x}{7} \neq 0$
$\frac{x^3+y^3+z^3}{(x-y)(y-z)(z-x)}$
x,y,z正
$\frac{yz}{x}$=$\frac{zx}{4y}$=$\frac{xy}{9z}$
$\frac{x+y+z}{\sqrt{x^2+y^2+z^2}}$
福田の一夜漬け数学〜数列・漸化式(3)〜高校2年生

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
次の漸化式を解け。(すべて、$a_1=1$とする)
①$(n+1)a_{n+1}=na_n+2$
②$na_{n+1}=(n+1)a_n+2$
③$(n+2)a_{n+1}=na_n+2$
④$na_{n+1}=(n+2)a_n+2$
この動画を見る
次の漸化式を解け。(すべて、$a_1=1$とする)
①$(n+1)a_{n+1}=na_n+2$
②$na_{n+1}=(n+1)a_n+2$
③$(n+2)a_{n+1}=na_n+2$
④$na_{n+1}=(n+2)a_n+2$
【高校数学】数Ⅲ-95 合成関数の微分法②

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の関数を微分せよ。
①$y=\sqrt{x^2-3x-1}$
②$y=\sqrt{(2x-3)^3}$
③$y=\left(\dfrac{2x}{x^2+1}\right)^4$
④$y=\sqrt{\dfrac{x+1}{x-3}}$
この動画を見る
次の関数を微分せよ。
①$y=\sqrt{x^2-3x-1}$
②$y=\sqrt{(2x-3)^3}$
③$y=\left(\dfrac{2x}{x^2+1}\right)^4$
④$y=\sqrt{\dfrac{x+1}{x-3}}$
早稲田(政経) 整数問題 高校数学 Japanese university entrance exam questions

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
2014早稲田大学過去問題
x,yは自然数、Pは3以上の素数
(1)$x^2-y^2 = P$が成り立つとき、x,yをPで表せ(答えのみ)
(2)$x^3-y^3 = P$が成り立つとき、Pを6で割った余りは1であることを証明せよ。
この動画を見る
2014早稲田大学過去問題
x,yは自然数、Pは3以上の素数
(1)$x^2-y^2 = P$が成り立つとき、x,yをPで表せ(答えのみ)
(2)$x^3-y^3 = P$が成り立つとき、Pを6で割った余りは1であることを証明せよ。
福田の一夜漬け数学〜数列・漸化式(2)〜高校2年生

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
次の漸化式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_1=1\\
a_{n+1}=3a_n+2^n\\
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_1=1\\
a_{n+1}=2a_n+n^2+2n\\
\end{array}
\right.
\end{eqnarray}$
この動画を見る
次の漸化式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_1=1\\
a_{n+1}=3a_n+2^n\\
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_1=1\\
a_{n+1}=2a_n+n^2+2n\\
\end{array}
\right.
\end{eqnarray}$
信州大学(医) 放物線への法線 高校数学 Japanese university entrance exam questions

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
2011信州大学過去問題
放物線$C:y=\frac{1}{2}x^2-1$上にない点P(a,b)をとる。C上の点Qに対し直線PQが点QでのCの接線と垂直に交わるとき、PQをPからCへの垂線(法線)という。
点P(a,b)からCへ3本の異なる垂線が引けるためのa,bの条件
この動画を見る
2011信州大学過去問題
放物線$C:y=\frac{1}{2}x^2-1$上にない点P(a,b)をとる。C上の点Qに対し直線PQが点QでのCの接線と垂直に交わるとき、PQをPからCへの垂線(法線)という。
点P(a,b)からCへ3本の異なる垂線が引けるためのa,bの条件
【高校数学】数Ⅲ-94 合成関数の微分法①

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の関数を微分せよ。
①$y=(x^2-5)^3$
②$y=(x^3+3x)^4$
③$y=(2x^3-3x+1)^5$
④$y=\dfrac{1}{(x^2-3)}^2$
⑤$y=\{(x-1)(x^2+4)\}^4$
この動画を見る
次の関数を微分せよ。
①$y=(x^2-5)^3$
②$y=(x^3+3x)^4$
③$y=(2x^3-3x+1)^5$
④$y=\dfrac{1}{(x^2-3)}^2$
⑤$y=\{(x-1)(x^2+4)\}^4$
福田の一夜漬け数学〜数列・漸化式(1)〜高校2年生

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
次の漸化式を解け。(すべて、$a_1=1$とする)
①$a_{n+1}=a_n+2$
②$a_{n+1}=2a_n$
③$a_{n+1}=2a_n+2$
④$a_{n+1}=a_n+2n$
⑤$a_{n+1}=2a_n+2^n$
⑥$a_{n+1}=2a_n+2n$
この動画を見る
次の漸化式を解け。(すべて、$a_1=1$とする)
①$a_{n+1}=a_n+2$
②$a_{n+1}=2a_n$
③$a_{n+1}=2a_n+2$
④$a_{n+1}=a_n+2n$
⑤$a_{n+1}=2a_n+2^n$
⑥$a_{n+1}=2a_n+2n$
山形大(医)整式の剰余 積の微分の導出 高校数学 Japanese university entrance exam questions

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
2006山形大学過去問題
整式P(x)を$(x+1)^2$で割ると余りが9、$(x-1)^2$で割ると余りは1
P(x)を$(x+1)^2(x-1)^2$で割った余りを求めよ。
この動画を見る
2006山形大学過去問題
整式P(x)を$(x+1)^2$で割ると余りが9、$(x-1)^2$で割ると余りは1
P(x)を$(x+1)^2(x-1)^2$で割った余りを求めよ。
【高校数学】数Ⅲ-93 商の微分法

単元:
#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の関数を微分せよ。
①$y=\dfrac{2x}{x^2+1}$
②$y=\dfrac{1+x^2}{1-x^2}$
③$y=\dfrac{x^2+x^2-5x+2}{x^2}$
④$y=\dfrac{x^2-4x+3}{\sqrt x}$
この動画を見る
次の関数を微分せよ。
①$y=\dfrac{2x}{x^2+1}$
②$y=\dfrac{1+x^2}{1-x^2}$
③$y=\dfrac{x^2+x^2-5x+2}{x^2}$
④$y=\dfrac{x^2-4x+3}{\sqrt x}$
秋田大(医) 因数分解 整式の剰余 高校数学 Japanese university entrance exam questions

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
2007秋田大学過去問題
因数分解せよ
(1) $x(x+1)(x+2)-y(y+1)(y+2)+xy(x-y)$
(2) $f(x)$を$x^2-4x+3$で割ったときの余りは$x+1$,$x^2-3x+2$で割ったときの余りは$3x-1$である。
$f(x)$を$x^3-6x^2+11x-6$で割ったときの余り。
この動画を見る
2007秋田大学過去問題
因数分解せよ
(1) $x(x+1)(x+2)-y(y+1)(y+2)+xy(x-y)$
(2) $f(x)$を$x^2-4x+3$で割ったときの余りは$x+1$,$x^2-3x+2$で割ったときの余りは$3x-1$である。
$f(x)$を$x^3-6x^2+11x-6$で割ったときの余り。
福田の一夜漬け数学〜数列・群数列(3)〜高校2年生
単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
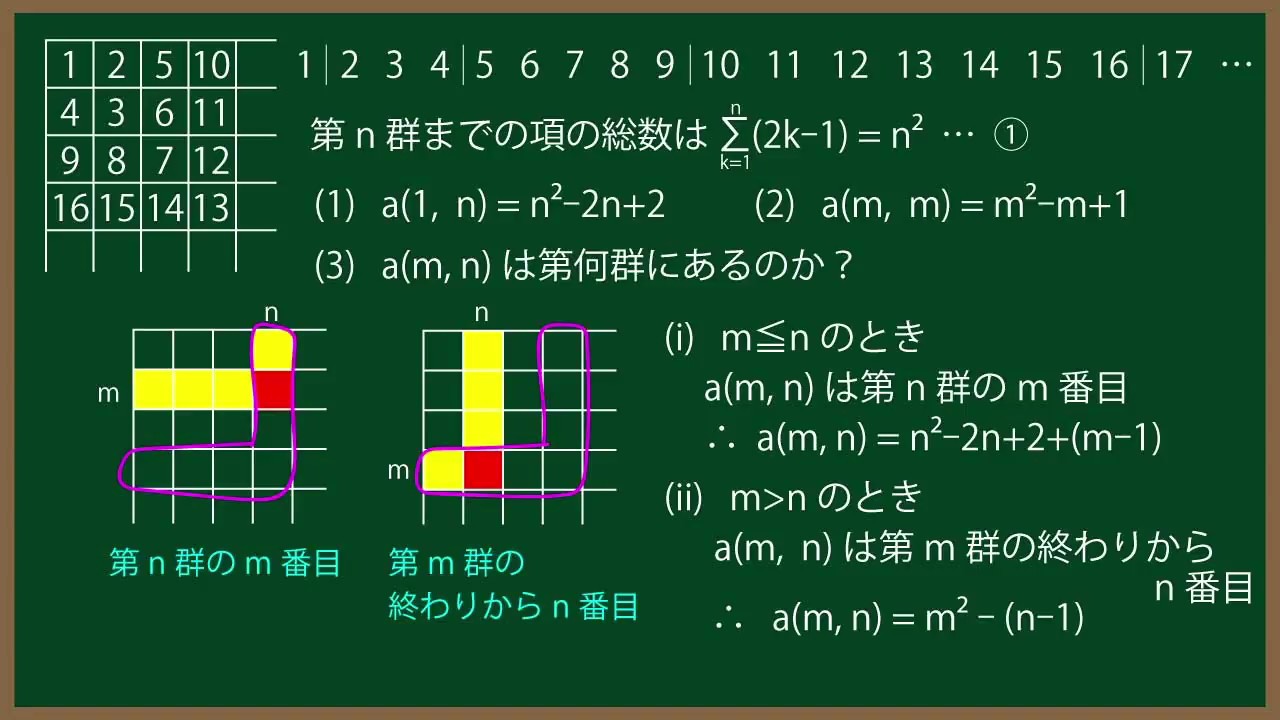
\begin{array}{|c|c|c|c|c}
\hline 1 & 2 & 5 & 10 & \\
\hline 4 & 3 &6 & 11 & \\
\hline 9 & 8 & 7 & 12 & \\
\hline 16 & 15 & 14 & 13 & \\
\hline \\
\end{array}
上図のように自然数を配置していく。
$m$行目、$n$列目にある数を$a(m,n)$と
表すことにする。
例えば、$a(3,2)=8$ である。
次の問いに答えよ。
(1)$a(1,n)$
(2)$a(m,m)$
(3)$a(m,n)$
(4)150は何行目の何列目に出てくるか。
この動画を見る
\begin{array}{|c|c|c|c|c}
\hline 1 & 2 & 5 & 10 & \\
\hline 4 & 3 &6 & 11 & \\
\hline 9 & 8 & 7 & 12 & \\
\hline 16 & 15 & 14 & 13 & \\
\hline \\
\end{array}
上図のように自然数を配置していく。
$m$行目、$n$列目にある数を$a(m,n)$と
表すことにする。
例えば、$a(3,2)=8$ である。
次の問いに答えよ。
(1)$a(1,n)$
(2)$a(m,m)$
(3)$a(m,n)$
(4)150は何行目の何列目に出てくるか。
【高校数学】数Ⅲ-92 積の微分法

単元:
#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の関数を微分せよ。
①$y=(x^2+2x)(x+3)$
②$y=(5x^2-3x-4)(2x+1)$
③$y=(x^2-3x+2)(x^2+1)$
④$y=(x+1)(x+2)(x+3)$
この動画を見る
次の関数を微分せよ。
①$y=(x^2+2x)(x+3)$
②$y=(5x^2-3x-4)(2x+1)$
③$y=(x^2-3x+2)(x^2+1)$
④$y=(x+1)(x+2)(x+3)$
山形大 漸化式 高校数学 Japanese university entrance exam questions

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
山形大学過去問題
$a_1 = -1$ $\quad$ $n=1,2,3\cdots$
$2\displaystyle \sum_{k=1}^{n}a_k=3a_{n+1}-2a_n-1$
一般項$a_n$を求めよ。
この動画を見る
山形大学過去問題
$a_1 = -1$ $\quad$ $n=1,2,3\cdots$
$2\displaystyle \sum_{k=1}^{n}a_k=3a_{n+1}-2a_n-1$
一般項$a_n$を求めよ。
福田の一夜漬け数学〜数列・群数列(2)〜高校2年生

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
数列 $1 2 1 3 2 $$1 4 $$3 $$2 $$1 $$5\cdots$について次を求めよ。
(1)第100項
(2)初項から第100項までの和
数列 $ \dfrac{2}{3} \dfrac{2}{5} \dfrac{4}{5} \dfrac{2}{7} \dfrac{4}{7} \dfrac{6}{7} \dfrac{2}{9}$$ \dfrac{4}{9}$$ \dfrac{6}{9}$$ \dfrac{8}{9}$$ \dfrac{2}{11}\cdots$について
次の問いに答えよ。
(1)$\displaystyle \frac{4}{15}$は第何項か。
(2)第100項は何か。
この動画を見る
数列 $1 2 1 3 2 $$1 4 $$3 $$2 $$1 $$5\cdots$について次を求めよ。
(1)第100項
(2)初項から第100項までの和
数列 $ \dfrac{2}{3} \dfrac{2}{5} \dfrac{4}{5} \dfrac{2}{7} \dfrac{4}{7} \dfrac{6}{7} \dfrac{2}{9}$$ \dfrac{4}{9}$$ \dfrac{6}{9}$$ \dfrac{8}{9}$$ \dfrac{2}{11}\cdots$について
次の問いに答えよ。
(1)$\displaystyle \frac{4}{15}$は第何項か。
(2)第100項は何か。
【高校数学】数Ⅲ-91 微分(復習編)

単元:
#微分とその応用#微分法#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の関数を微分せよ。
①$y=x^4+x^3+x^2+x+1$
②$y=-2x^3+7x+4$
③$y=-\dfrac{3}{2}x^4+\dfrac{1}{3}x^3-5x$
④$y=(x^3-1)^2$
⑤関数$f(x)=\vert x(x-2) \vert $が$x=2$で
微分可能であるかどうかを調べよ。
この動画を見る
次の関数を微分せよ。
①$y=x^4+x^3+x^2+x+1$
②$y=-2x^3+7x+4$
③$y=-\dfrac{3}{2}x^4+\dfrac{1}{3}x^3-5x$
④$y=(x^3-1)^2$
⑤関数$f(x)=\vert x(x-2) \vert $が$x=2$で
微分可能であるかどうかを調べよ。
横浜市立(医) 正二十面体 面のなす角 高校数学 Japanese university entrance exam questions

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
'94横浜市立大学過去問題
(1)正五角形ABCDEの一辺を1としたときのAD=ACの長さ
(2)正二十面体のとなり合う面のなす角をθとしたときのcosθの値
この動画を見る
'94横浜市立大学過去問題
(1)正五角形ABCDEの一辺を1としたときのAD=ACの長さ
(2)正二十面体のとなり合う面のなす角をθとしたときのcosθの値
【高校数学】数Ⅲ-90 微分とは?

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
関数$f(x)$の①を求めることを微分という。
導関数の定義に従って、次の関数を微分せよ。
②$f(x)=\dfrac{2}{x}$
③$f(x)=\sqrt{x+2}$
この動画を見る
関数$f(x)$の①を求めることを微分という。
導関数の定義に従って、次の関数を微分せよ。
②$f(x)=\dfrac{2}{x}$
③$f(x)=\sqrt{x+2}$
福田の一夜漬け数学〜数列・群数列(1)〜高校2年生

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
群数列 $1\ | \ 3 5 \ |\ 7 9 11$$ \ |\ 13 15 17 19$$ \ | \ 21 \cdots$について次を求めよ。
(1)第$n$群の初項
(2)第$n$群の総和
(3)301は第何群の何番目か
正の奇数の列$\left\{a_n\right\}$を次のように第$k$群に$2^{k-1}$個の項を含むように分ける。
$1\ | \ 3 5 \ |\ 7 9 11 13 $$\ | \ 15 17 19 21 $$23 25 27 29 $$\ | \ 31 \cdots$
(1)第$n$群の初項を求めよ。
(2)777は第何群の何番目か。
この動画を見る
群数列 $1\ | \ 3 5 \ |\ 7 9 11$$ \ |\ 13 15 17 19$$ \ | \ 21 \cdots$について次を求めよ。
(1)第$n$群の初項
(2)第$n$群の総和
(3)301は第何群の何番目か
正の奇数の列$\left\{a_n\right\}$を次のように第$k$群に$2^{k-1}$個の項を含むように分ける。
$1\ | \ 3 5 \ |\ 7 9 11 13 $$\ | \ 15 17 19 21 $$23 25 27 29 $$\ | \ 31 \cdots$
(1)第$n$群の初項を求めよ。
(2)777は第何群の何番目か。
東北大学 三次方程式 解と係数の関係 高校数学 Japanese university entrance exam questions

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
2013東北大学過去問題
$f(x)=x^3-kx^2-1$
f(x)=0の3解をα,β,γとする。
g(x)は$x^3$の係数が1である3次式で、g(x)=0の3解は、αβ,βγ,γαである。
(1)g(x)をkを用いて表せ。
(2)f(x)=0,とg(x)=0が共通解をもつkの値。
この動画を見る
2013東北大学過去問題
$f(x)=x^3-kx^2-1$
f(x)=0の3解をα,β,γとする。
g(x)は$x^3$の係数が1である3次式で、g(x)=0の3解は、αβ,βγ,γαである。
(1)g(x)をkを用いて表せ。
(2)f(x)=0,とg(x)=0が共通解をもつkの値。
福田の一夜漬け数学〜数列・和Snの問題〜高校2年生

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
数列$\left\{a_n\right\}$の初項から第$n$項までの和$S_n$が次のときの一般項$a_n$を求めよ。
(1)$S_n=n^2-2n+3$
(2)$S_n=2^n+3^n-2$
数列$\left\{a_n\right\}$の初項から第$n$項までの和$S_n$が$S_n=2a_n-n$であるとき、
$a_n$を求めよ。
この動画を見る
数列$\left\{a_n\right\}$の初項から第$n$項までの和$S_n$が次のときの一般項$a_n$を求めよ。
(1)$S_n=n^2-2n+3$
(2)$S_n=2^n+3^n-2$
数列$\left\{a_n\right\}$の初項から第$n$項までの和$S_n$が$S_n=2a_n-n$であるとき、
$a_n$を求めよ。
