 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
【数学】3分で和積公式が馬鹿でもわかる考え方

【数学】4分で積和公式が馬鹿でもわかる考え方

2点を通る直線の方程式を求めるのに連立方程式を使うのは卒業しましょう

放物線上の2点を通る直線の式を「3秒」で出だす方法

因数分解 「失敗しない」たすきがけ

ネイピア数 自然対数の底e とは

【センター試験】ズルい選択肢の選び方!分からなくても答えが出る【9割獲った勉強法】

単元:
#大学入試過去問(数学)#物理#化学#生物#センター試験・共通テスト関連#共通テスト#大学入試過去問(物理)#大学入試過去問(化学)#英語(高校生)#国語(高校生)#社会(高校生)#日本史#世界史#大学入試過去問(英語)#大学入試過去問(国語)#共通テスト#共通テスト(現代文)#その他#大学入試過去問(生物)#共通テスト・センター試験#共通テスト(古文)#共通テスト#論理思考#大学入試過去問・共通テスト・模試関連#大学入試過去問・共通テスト・模試関連#数学(高校生)#理科(高校生)#共通テスト
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
センター試験!分からなくても答えが出る!
「選択肢のズルい選び方」についてお話しています。
この動画を見る
センター試験!分からなくても答えが出る!
「選択肢のズルい選び方」についてお話しています。
【センター試験2018年】出題予想!今年はコレが出る?!~当たればラッキー?!的中を出してきたシノハラの「ココ」がヤバい!~京大模試全国一位の勉強法【篠原好】

単元:
#大学入試過去問(数学)#物理#化学#生物#センター試験・共通テスト関連#共通テスト#大学入試過去問(物理)#大学入試過去問(化学)#英語(高校生)#国語(高校生)#社会(高校生)#日本史#世界史#大学入試過去問(英語)#大学入試過去問(国語)#共通テスト#共通テスト(現代文)#大学入試過去問(生物)#共通テスト・センター試験#共通テスト(古文)#共通テスト#大学入試過去問・共通テスト・模試関連#大学入試過去問・共通テスト・模試関連#数学(高校生)#理科(高校生)#共通テスト
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
今年はコレが出る?!
「センター試験2018年」の出題予想です。
この動画を見る
今年はコレが出る?!
「センター試験2018年」の出題予想です。
積の微分、合成関数の微分、商の微分の導出

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
積の微分,合成関数の微分,商の微分の導出に関して解説していきます.
この動画を見る
積の微分,合成関数の微分,商の微分の導出に関して解説していきます.
積分で面積が出る理由

なぜ、マイナス×マイナスはプラスなのか? 負✕負=正 虚数(複素数)を使って説明します

素数が連続して出現しない区間はどれくらい?素数砂漠のお話

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
素数が連続して出現しない区間がどのくらいか解説します.
この動画を見る
素数が連続して出現しない区間がどのくらいか解説します.
弧度法を使う理由

単元:
#数Ⅱ#三角関数#微分法と積分法#三角関数とグラフ#平均変化率・極限・導関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
弧度法を使う理由を解説していきます.
この動画を見る
弧度法を使う理由を解説していきます.
指数法則 0乗はなぜ1か
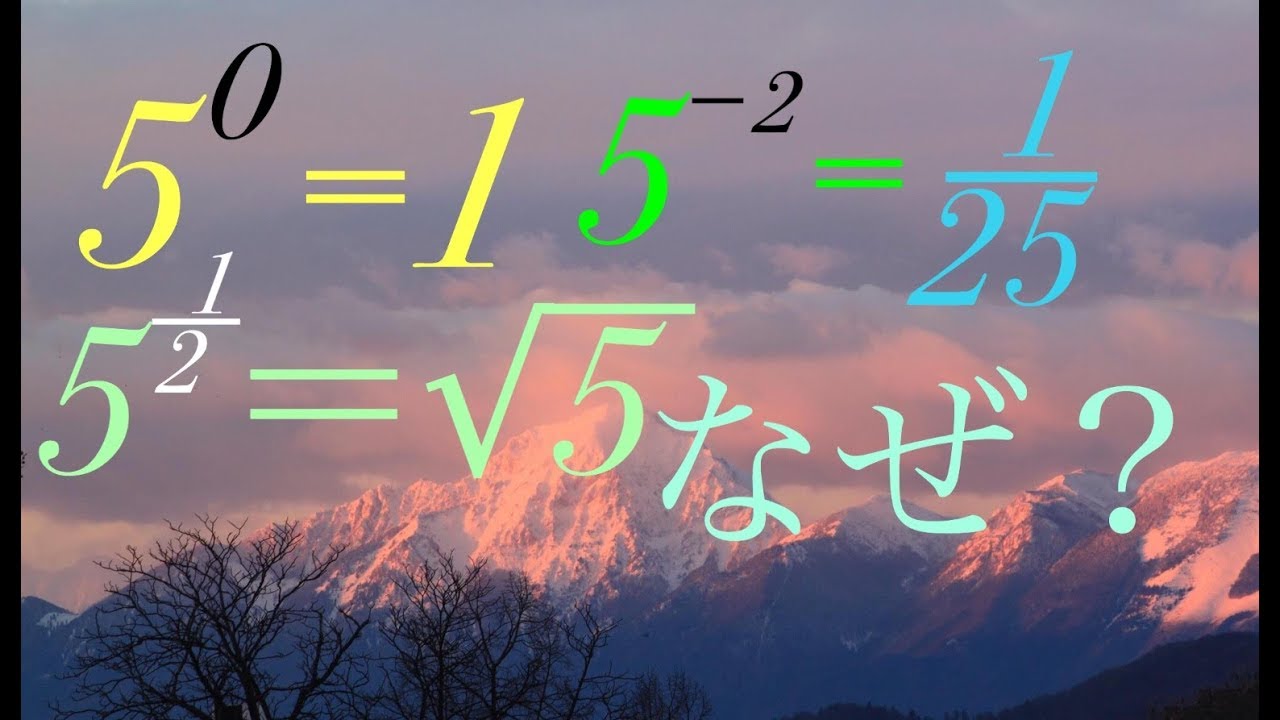
なぜ、0!=1 0の階乗がなぜ1?

【センター試験】センター利用の使い方!国立・私立別、受験生のセンター試験対策~京大模試全国一位・早稲田政経合格の勉強法【篠原好】

単元:
#その他#その他
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
国立・私立別、受験生のセンター試験対策
「センター利用の使い方」についてお話しています。
この動画を見る
国立・私立別、受験生のセンター試験対策
「センター利用の使い方」についてお話しています。
【高校数学】数Ⅲ-64 合成関数③

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①2つの関数$f(x)=ax-3,g(x)=-x+a$について、
$(fog)(x)$がつねに成り立つように、定数$a$の値を定めよ。
②関数$f(x)=\dfrac{x+1}{-2x+3},g(x)=\dfrac{ax-1}{bx+c}$について、
$(gof)(x)=x$が成り立つとき、定数$a,b,c$を求めよ。
この動画を見る
①2つの関数$f(x)=ax-3,g(x)=-x+a$について、
$(fog)(x)$がつねに成り立つように、定数$a$の値を定めよ。
②関数$f(x)=\dfrac{x+1}{-2x+3},g(x)=\dfrac{ax-1}{bx+c}$について、
$(gof)(x)=x$が成り立つとき、定数$a,b,c$を求めよ。
【高校数学】数Ⅲ-63 合成関数②

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$f(x)=5^x,g(x)=\log_5 x$であるとき、
合成関数$(gof)(x),(fog)(x)$を求めよ。
②$f(x)=x^2,g(x)=4x-3,h(x)=\sqrt{x^2+1}$であるとき、
合成関数$(ho(gof))(x),((hog)of)(x)$を求めよ。
この動画を見る
①$f(x)=5^x,g(x)=\log_5 x$であるとき、
合成関数$(gof)(x),(fog)(x)$を求めよ。
②$f(x)=x^2,g(x)=4x-3,h(x)=\sqrt{x^2+1}$であるとき、
合成関数$(ho(gof))(x),((hog)of)(x)$を求めよ。
【高校数学】数Ⅲ-62 合成関数①

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
$y$が$u$の関数で$y=g(u)$と表され、$u$が$x$の関数で$u=f(x)$と表されるとき、
$y$は$x$の関数で$y=g(f(x))$と表され、これを$f$と$g$の合成関数という。
また、$y=g(f(x))$を$y=①$と表す。
②$f(x)= 4x ^ 2 、g(x) = -\dfrac{1}{2} (x + 1)$であるとき、
合成関数$(gof)(x)、(fog)(x)$をそれぞれ求めなさい。
この動画を見る
$y$が$u$の関数で$y=g(u)$と表され、$u$が$x$の関数で$u=f(x)$と表されるとき、
$y$は$x$の関数で$y=g(f(x))$と表され、これを$f$と$g$の合成関数という。
また、$y=g(f(x))$を$y=①$と表す。
②$f(x)= 4x ^ 2 、g(x) = -\dfrac{1}{2} (x + 1)$であるとき、
合成関数$(gof)(x)、(fog)(x)$をそれぞれ求めなさい。
【高校数学】数Ⅲ-61 逆関数④

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の関数の逆関数を求めよ。
①$y=x^2-9 \quad (x \geqq 0)$
②$y=\dfrac{1}{2}x^2-3 \quad (x \leqq 0)$
③$y=-x^2+2x \quad (x \geqq 1)$
この動画を見る
次の関数の逆関数を求めよ。
①$y=x^2-9 \quad (x \geqq 0)$
②$y=\dfrac{1}{2}x^2-3 \quad (x \leqq 0)$
③$y=-x^2+2x \quad (x \geqq 1)$
【高校数学】数Ⅲ-60 逆関数③

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の関数の逆関数を求めよ。
①$y=\dfrac{3x-5}{x-2} \quad (x \gt 2)$
②$y=\dfrac{2x-1}{x+1} \quad (x \gt -1)$
この動画を見る
次の関数の逆関数を求めよ。
①$y=\dfrac{3x-5}{x-2} \quad (x \gt 2)$
②$y=\dfrac{2x-1}{x+1} \quad (x \gt -1)$
【高校数学】数Ⅲ-59 逆関数②

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の関数の逆関数を求めよ。
①$y=\log_{\frac{1}{2}} x$
②$y=2^{x+1}$
③$y=log_2 (x-1)$
④$y=-3^x$
この動画を見る
次の関数の逆関数を求めよ。
①$y=\log_{\frac{1}{2}} x$
②$y=2^{x+1}$
③$y=log_2 (x-1)$
④$y=-3^x$
【高校数学】数Ⅲ-58 逆関数①

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
関数$y=f(x)$の$x$と$y$を入れかえて得られる関数$y=g(x)$を$y=f(x)$の逆関数といい、
$y=①$で表す。
一般に、関数と逆関数では、定義域と②が入れかわり、
そのグラフは$y=③$に関して対称である。
次の関数の逆関数を求め、その定義域と値域を求めよ。
④$y = - 2x + 6\quad (- 1 \leqq x \leqq 4)$
⑤$y = - \sqrt{2 - x}$
この動画を見る
関数$y=f(x)$の$x$と$y$を入れかえて得られる関数$y=g(x)$を$y=f(x)$の逆関数といい、
$y=①$で表す。
一般に、関数と逆関数では、定義域と②が入れかわり、
そのグラフは$y=③$に関して対称である。
次の関数の逆関数を求め、その定義域と値域を求めよ。
④$y = - 2x + 6\quad (- 1 \leqq x \leqq 4)$
⑤$y = - \sqrt{2 - x}$
【高校数学】数Ⅲ-57 無理方程式の解の個数

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①方程式$\sqrt{x+1}=x+k$が異なる2つの実数解をもつように、
実数$k$の値の範囲を求めよ。
この動画を見る
①方程式$\sqrt{x+1}=x+k$が異なる2つの実数解をもつように、
実数$k$の値の範囲を求めよ。
【高校数学】数Ⅲ-56 無理不等式とグラフ

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の不等式を解け。
①$\sqrt{x-1} \gt x-3$
②$\sqrt{-2x+7} \leqq -x+2$
この動画を見る
次の不等式を解け。
①$\sqrt{x-1} \gt x-3$
②$\sqrt{-2x+7} \leqq -x+2$
【高校数学】数Ⅲ-55 無理関数とそのグラフ②

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の無理関数のグラフをかけ。
①$y=\sqrt{2-x}$
②$y=-\sqrt{2x-4}$
③$y=-\sqrt{-3x-5}$
図は動画内参照
この動画を見る
次の無理関数のグラフをかけ。
①$y=\sqrt{2-x}$
②$y=-\sqrt{2x-4}$
③$y=-\sqrt{-3x-5}$
図は動画内参照
【高校数学】数Ⅲ-54 無理関数とそのグラフ①

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の無理関数のグラフをかけ。
①$y=\sqrt{3x}$
②$y=-\sqrt3$
③$y=\sqrt{-3x}$
④$y=\sqrt{3x+6}$
この動画を見る
次の無理関数のグラフをかけ。
①$y=\sqrt{3x}$
②$y=-\sqrt3$
③$y=\sqrt{-3x}$
④$y=\sqrt{3x+6}$
【高校数学】 数Ⅲ-53 分数関数の決定

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$y=\dfrac{ax+b}{x+c}$のグラフが点$(2,1)$を通り、
2直線$x=3,y=-2$を漸近線とするとき、定数$a,b,c$の値を求めよ。
この動画を見る
①$y=\dfrac{ax+b}{x+c}$のグラフが点$(2,1)$を通り、
2直線$x=3,y=-2$を漸近線とするとき、定数$a,b,c$の値を求めよ。
【高校数学】数Ⅲ-52 分数不等式とグラフ

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の不等式を解け。
①$\dfrac{3x+1}{x-1} \gt x+2$
②$\dfrac{3x}{x+2} \geqq 2x-1$
この動画を見る
次の不等式を解け。
①$\dfrac{3x+1}{x-1} \gt x+2$
②$\dfrac{3x}{x+2} \geqq 2x-1$
【数学】十分条件と必要条件の覚え方~暗記のコツは「十必」だ!~偏差値84.9の数学対策【篠原好】

単元:
#その他#数学(高校生)
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
暗記のコツは「十必」だ!
数学の「十分条件と必要条件の違い」についてお話しています。
この動画を見る
暗記のコツは「十必」だ!
数学の「十分条件と必要条件の違い」についてお話しています。
