 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
【11月勉強法】共通テスト数学爆伸びのために〇〇をやれ

単元:
#大学入試過去問(数学)#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
共通テスト数学 勉強法
この動画を見る
共通テスト数学 勉強法
福田のおもしろ数学306〜5次方程式の5つの解がすべて実数にはなれない条件

単元:
#数Ⅱ#式と証明#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
実数係数の5次方程式
$z^5+az^4+bz^3+cz^2+dz+e=0$
について$2a^2\lt 5b$のときはすべての解が実数にはなれないことを示してください。
この動画を見る
実数係数の5次方程式
$z^5+az^4+bz^3+cz^2+dz+e=0$
について$2a^2\lt 5b$のときはすべての解が実数にはなれないことを示してください。
福田の数学〜早稲田大学2024商学部第1問(3)〜漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$C$を$1$でない正の実数とする。正の実数の数列$\{a_n\}$が次の条件を満たしている。
$a_1=C,$${a_n}^{n+1}{a_{n+1}}^n=C^{-(2n+1)}$
このとき、一般項$a_n$を$C$を用いて表せ。
この動画を見る
$C$を$1$でない正の実数とする。正の実数の数列$\{a_n\}$が次の条件を満たしている。
$a_1=C,$${a_n}^{n+1}{a_{n+1}}^n=C^{-(2n+1)}$
このとき、一般項$a_n$を$C$を用いて表せ。
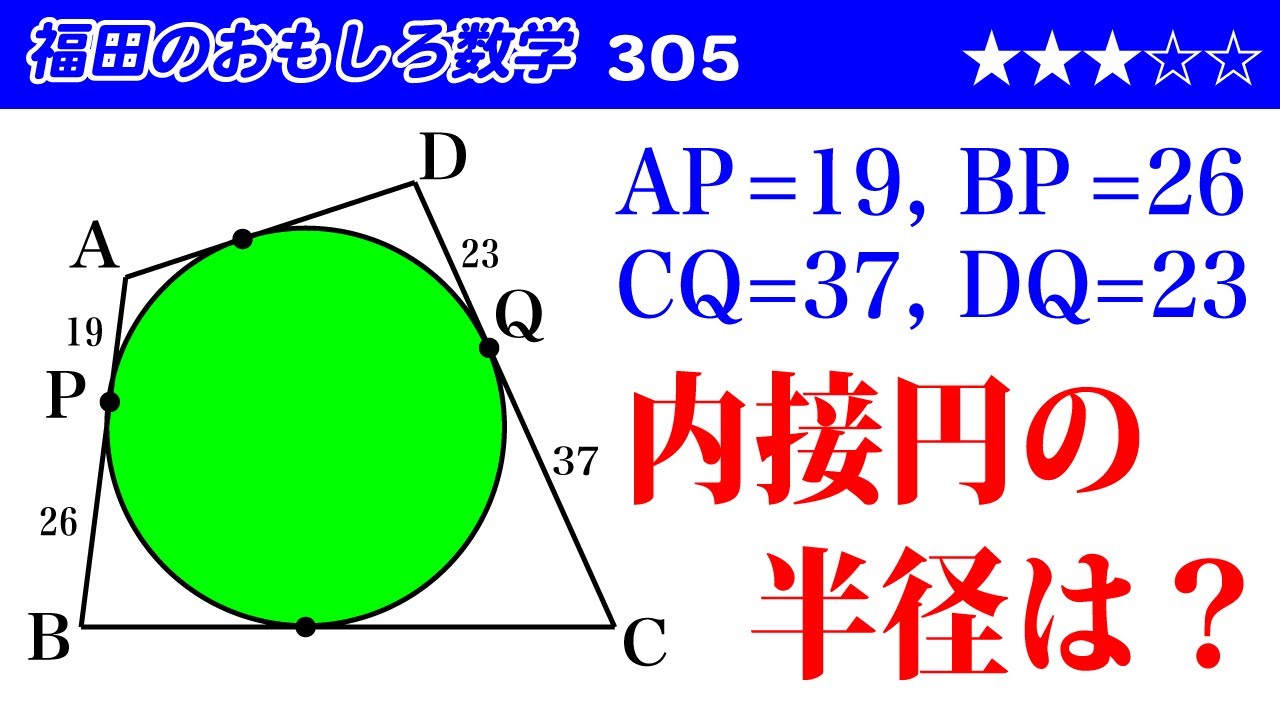
福田のおもしろ数学305〜四角形に内接する円の半径
単元:
#数Ⅰ#数A#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
図は動画参照
$AP=19,BP=26,CQ=37,DQ=23$
内接円の半径は?
この動画を見る
図は動画参照
$AP=19,BP=26,CQ=37,DQ=23$
内接円の半径は?
各大学で頻出の典型的な問題!基本的でありながらどの大学でも出題されます【大阪大学】【数学 入試問題】

単元:
#大学入試過去問(数学)#微分とその応用#接線と法線・平均値の定理#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数Ⅲ
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
aを実数とする。曲線y=e^x上の各点における法線のうちで、点p(a,3)を通るものの個数をn(a)とする。n(a)を求めよ。
この動画を見る
aを実数とする。曲線y=e^x上の各点における法線のうちで、点p(a,3)を通るものの個数をn(a)とする。n(a)を求めよ。
福田の数学〜早稲田大学2024商学部第1問(2)〜不等式で決定される自然数の列

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$n$を$2$以上の整数とし、$a_1,a_2,a_3,・・・,a_n$を正の整数とする。
$a_1=1,{a_{i+3}}^3\lt 27{a_i}^4(i=1,2,3,・・・,n-1)$
$\displaystyle \sum_{i=1}^{n-1}\frac{a_i}{a_{i+1}}=\frac{a_1}{a_{2}}+\frac{a_2}{a_{3}}+\frac{a_3}{a_{4}}+・・・+\frac{a_{n-1}}{a_{n}}\lt 1$
であるとき、$a_n$のとりうる値の最大値は?
この動画を見る
$n$を$2$以上の整数とし、$a_1,a_2,a_3,・・・,a_n$を正の整数とする。
$a_1=1,{a_{i+3}}^3\lt 27{a_i}^4(i=1,2,3,・・・,n-1)$
$\displaystyle \sum_{i=1}^{n-1}\frac{a_i}{a_{i+1}}=\frac{a_1}{a_{2}}+\frac{a_2}{a_{3}}+\frac{a_3}{a_{4}}+・・・+\frac{a_{n-1}}{a_{n}}\lt 1$
であるとき、$a_n$のとりうる値の最大値は?
福田のおもしろ数学304〜複素数の実部の最大値

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
複素数 $z$ が $|z|=4$ を満たすとき $\displaystyle (75+117i) z + \frac{96 + 144i}{z}$ の実部の最大値を求めよ。
この動画を見る
複素数 $z$ が $|z|=4$ を満たすとき $\displaystyle (75+117i) z + \frac{96 + 144i}{z}$ の実部の最大値を求めよ。
#高専 #定積分_71

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-1}^{0} \dfrac{dx}{\sqrt{x^2+2x+2}}$を解け.
高専定期試験
この動画を見る
$\displaystyle \int_{-1}^{0} \dfrac{dx}{\sqrt{x^2+2x+2}}$を解け.
高専定期試験
福田の数学〜早稲田大学2024商学部第1問(1)〜絶対値の付いた式の不等式を解く

単元:
#数Ⅰ#数と式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
不等式 $\displaystyle |\frac{2024n}{1 - 46n} + 44| < \frac{1}{2025}$ を満たす正の整数 $n$ の最小値を求めよ。
この動画を見る
不等式 $\displaystyle |\frac{2024n}{1 - 46n} + 44| < \frac{1}{2025}$ を満たす正の整数 $n$ の最小値を求めよ。
福田のおもしろ数学303〜階乗のたくさんある分数の和

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle \frac{1}{2! 17!} $$\displaystyle + \frac{1}{3! 16!} $$\displaystyle + \frac{1}{4! 15!}$$+ \cdots $$\displaystyle + \frac{1}{9! 10!} $$\displaystyle = \frac{N}{1! 18!}$ を満たす $N$ を求めよ。
この動画を見る
$\displaystyle \frac{1}{2! 17!} $$\displaystyle + \frac{1}{3! 16!} $$\displaystyle + \frac{1}{4! 15!}$$+ \cdots $$\displaystyle + \frac{1}{9! 10!} $$\displaystyle = \frac{N}{1! 18!}$ を満たす $N$ を求めよ。
福田の数学〜早稲田大学2024教育学部第4問〜媒介変数表示で表された曲線の対称性と面積体積の計算

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$xy$ 平面上の原点 $\mathrm{O}$ を中心とする単位円を考える。この円周上に点 $\mathrm{P}$ をとり、 $\mathrm{O}$ を極、 $x$ 軸の正の部分を始線とする点 $\mathrm{P}$ の偏角を $\theta$ とする。さらに、偏角が $3 \theta$ となる点 $\mathrm{Q}$ をこの円周上にとる。点 $\mathrm{P}$ を通る $x$ 軸に垂直な直線と点 $\mathrm{Q}$ を通る $y$ 軸に垂直な直線の交点を $\mathrm{R}$ とする。次の問いに答えよ。
$(1)$ $\theta$ が $0$ から $2 \pi$ まで変化するとき、点 $\mathrm{R}$ の軌跡の概形をかけ。
$(2)$ $(1)$ の点 $\mathrm{R}$ の軌跡によって囲まれた部分の面積を求めよ。
$(3)$ $(1)$ の点 $\mathrm{R}$ の軌跡によって囲まれた部分を、 $x$ 軸の周りに $1$ 回転させてできる立体の体積を求めよ。
この動画を見る
$xy$ 平面上の原点 $\mathrm{O}$ を中心とする単位円を考える。この円周上に点 $\mathrm{P}$ をとり、 $\mathrm{O}$ を極、 $x$ 軸の正の部分を始線とする点 $\mathrm{P}$ の偏角を $\theta$ とする。さらに、偏角が $3 \theta$ となる点 $\mathrm{Q}$ をこの円周上にとる。点 $\mathrm{P}$ を通る $x$ 軸に垂直な直線と点 $\mathrm{Q}$ を通る $y$ 軸に垂直な直線の交点を $\mathrm{R}$ とする。次の問いに答えよ。
$(1)$ $\theta$ が $0$ から $2 \pi$ まで変化するとき、点 $\mathrm{R}$ の軌跡の概形をかけ。
$(2)$ $(1)$ の点 $\mathrm{R}$ の軌跡によって囲まれた部分の面積を求めよ。
$(3)$ $(1)$ の点 $\mathrm{R}$ の軌跡によって囲まれた部分を、 $x$ 軸の周りに $1$ 回転させてできる立体の体積を求めよ。
これなんでか分かる?

福田のおもしろ数学302〜ベルトランの仮説を利用したn!の約数に関する性質

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$n$を3以上の整数とし、$n!$の正の約数を小さい方から$1=d_1\lt d_2\lt \cdots \lt d_k = n!$とする。$d_2-d_1\leqq d_3-d_2 \leqq \cdots \leqq d_k-d_{k-1}$が成り立つような$n$をすべて求めよ。
この動画を見る
$n$を3以上の整数とし、$n!$の正の約数を小さい方から$1=d_1\lt d_2\lt \cdots \lt d_k = n!$とする。$d_2-d_1\leqq d_3-d_2 \leqq \cdots \leqq d_k-d_{k-1}$が成り立つような$n$をすべて求めよ。
福田の数学〜早稲田大学2024教育学部第3問〜法線上の点の座標と最小値

単元:
#大学入試過去問(数学)#微分とその応用#微分法#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
放物線 $C : y = x ^ 2$ 上に点$P(t, t²)$をとる。$C$の点$P$における法線上に点$Q$を、$PQ=1$ であり、点$Q$の$y$座標が点$P$の$y$座標よりも大きくなるようにとる。 点$Q$の$x$座標を$f(t)$ とおく。次の問いに答えよ。
(1) $f(t)$ を求めよ。
(2) $t$が$0\leqq t$の範囲を動くときの$f(t)$の最小値を求めよ。
この動画を見る
放物線 $C : y = x ^ 2$ 上に点$P(t, t²)$をとる。$C$の点$P$における法線上に点$Q$を、$PQ=1$ であり、点$Q$の$y$座標が点$P$の$y$座標よりも大きくなるようにとる。 点$Q$の$x$座標を$f(t)$ とおく。次の問いに答えよ。
(1) $f(t)$ を求めよ。
(2) $t$が$0\leqq t$の範囲を動くときの$f(t)$の最小値を求めよ。
テストでランダムと同じやつ正答率高いのは?

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
マークシートのテストにおいて、ランダムに選ぶのと同じものを選び続けるのとではどちらの方が正答率が高いのかについて解説する動画です
この動画を見る
マークシートのテストにおいて、ランダムに選ぶのと同じものを選び続けるのとではどちらの方が正答率が高いのかについて解説する動画です
π=4の証明は本当なのか?

割って余る問題 整数問題 西大和学園

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#西大和学園高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
ある自然数nについて
n+5は9の倍数
n+9は5の倍数
nを45で割った余りは?
この動画を見る
ある自然数nについて
n+5は9の倍数
n+9は5の倍数
nを45で割った余りは?
福田のおもしろ数学301〜4次方程式の解と係数の関係

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$x ^ 4 - 18x ^ 3 + k x ^ 2 + 200x - 1984 = 0 $の2つの解の積が$-32$のとき、実数$k$の値は?
この動画を見る
$x ^ 4 - 18x ^ 3 + k x ^ 2 + 200x - 1984 = 0 $の2つの解の積が$-32$のとき、実数$k$の値は?
福田の数学〜早稲田大学2024教育学部第2問〜複素数の集合に関する論証

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$3$つの複素数 $z_1, z_2, z_3$に関する条件$P$を次のように定める。
P: 「$z_1, z_2, z_3$はどれも0ではなく、互いに異なり、かつ$ \{{z_1}^n | n は整数\} = \{{z_2}^n | nは整数\} = \{{z_3}^n |n は整数\}$
である。」
次の問いに答えよ。
(1) $3$つの複素数 $z_1,z_2,z_3$が条件$P$を満たしているとする。このとき$ |z_1| = 1$ であることを示せ。また集合$ \{{z_1}^n | n は整数\}$の要素の個数は有限であることを示せ。
(2) 条件$P$を満たす3つの複素数 $z_1,z_2,z_3$のうち、集合$ \{{z_1}^n | n は整数\}$の要素の個数が最小となるものを考える。このとき集合$ \{{z_1}^n | n は整数\}$を求めよ。
この動画を見る
$3$つの複素数 $z_1, z_2, z_3$に関する条件$P$を次のように定める。
P: 「$z_1, z_2, z_3$はどれも0ではなく、互いに異なり、かつ$ \{{z_1}^n | n は整数\} = \{{z_2}^n | nは整数\} = \{{z_3}^n |n は整数\}$
である。」
次の問いに答えよ。
(1) $3$つの複素数 $z_1,z_2,z_3$が条件$P$を満たしているとする。このとき$ |z_1| = 1$ であることを示せ。また集合$ \{{z_1}^n | n は整数\}$の要素の個数は有限であることを示せ。
(2) 条件$P$を満たす3つの複素数 $z_1,z_2,z_3$のうち、集合$ \{{z_1}^n | n は整数\}$の要素の個数が最小となるものを考える。このとき集合$ \{{z_1}^n | n は整数\}$を求めよ。
みんなは何番?
単元:
#その他#その他#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
チャンネル登録はこれ✅
/ @akitonton
#勉強 #授業 #あきとんとん #教育系YouTuber #shorts
分かりやすかった,面白かったと思ったら高評価チャンネル登録お願いします.
質問等ございましたら,コメント,SNSでお寄せ下さい.
~~~~~~~~~~~~~~~~~~~~~~~
Instagram: / akitonton5
TikTok: / akitonton
twitter: / akitonton5
LINE:https://lin.ee/xg8a0Pu
https://timeline.line.me/user/_dabZdm...
自習室: https://akitonton.com
~~~~~~~~~~~~~~~~~~~~~~~
この動画を見る
チャンネル登録はこれ✅
/ @akitonton
#勉強 #授業 #あきとんとん #教育系YouTuber #shorts
分かりやすかった,面白かったと思ったら高評価チャンネル登録お願いします.
質問等ございましたら,コメント,SNSでお寄せ下さい.
~~~~~~~~~~~~~~~~~~~~~~~
Instagram: / akitonton5
TikTok: / akitonton
twitter: / akitonton5
LINE:https://lin.ee/xg8a0Pu
https://timeline.line.me/user/_dabZdm...
自習室: https://akitonton.com
~~~~~~~~~~~~~~~~~~~~~~~
福田のおもしろ数学300〜絶対値の付いた式の定積分

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$
\displaystyle \int_{0}^{ \pi } |a \sin \ nx + b \cos nx| dx
\quad
$
(nは自然数)を求めよ
この動画を見る
$
\displaystyle \int_{0}^{ \pi } |a \sin \ nx + b \cos nx| dx
\quad
$
(nは自然数)を求めよ
福田の数学〜早稲田大学2024教育学部第1問(4)〜領域と奇跡

単元:
#数Ⅰ#数Ⅱ#2次関数#図形と方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$
\begin{eqnarray}
\fcolorbox{#000}{ #fff }{$1$} \ (4) \\
\end{eqnarray}
$
$xy$平面上に3点$O(0,0),A(1,0),B(1,1)$をとる。点$(x,y)$が三角形$OAB$の周および内部を動くときに点$(x+y,xy)$が動く範囲の面積を求めよ。
この動画を見る
$
\begin{eqnarray}
\fcolorbox{#000}{ #fff }{$1$} \ (4) \\
\end{eqnarray}
$
$xy$平面上に3点$O(0,0),A(1,0),B(1,1)$をとる。点$(x,y)$が三角形$OAB$の周および内部を動くときに点$(x+y,xy)$が動く範囲の面積を求めよ。
π=4って証明見たけど本当?

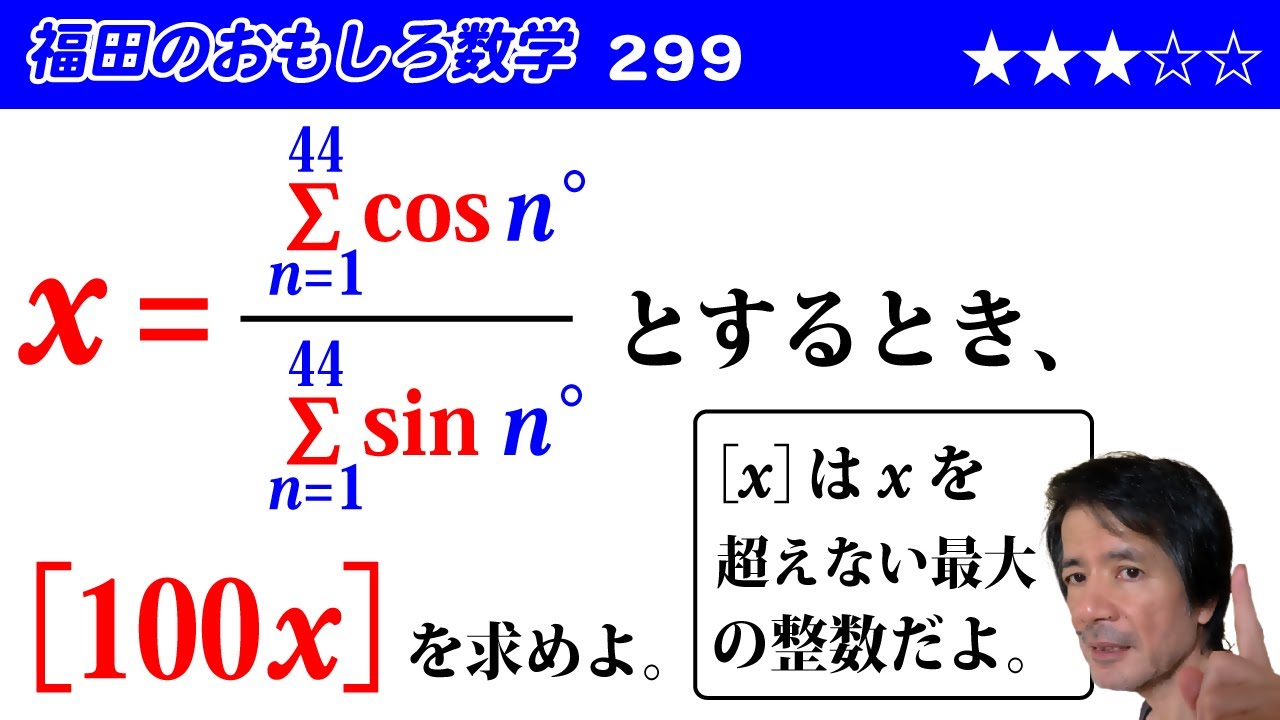
福田のおもしろ数学299〜三角関数で表された式の値
単元:
#数Ⅱ#三角関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$x = \frac{\displaystyle \sum_{i=1}^{44} cos \ n^{ \circ }}{\displaystyle \sum_{i=1}^{44} sin \ n^{ \circ }}$とするとき、$[100x]$を求めよ。
この動画を見る
$x = \frac{\displaystyle \sum_{i=1}^{44} cos \ n^{ \circ }}{\displaystyle \sum_{i=1}^{44} sin \ n^{ \circ }}$とするとき、$[100x]$を求めよ。
福田の数学〜早稲田大学2024教育学部第1問(3)〜対称軸を2本もつ多角形

単元:
#数A#図形の性質#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$xy$ 平面上の多角形で、$x$ 軸はこの多角形の対称軸であり、直線 $y=\frac{\sqrt{3}}{3} x$ もこの多角形の対称軸であるものを考える。このような多角形の辺の数の最小値を求めよ。
この動画を見る
$xy$ 平面上の多角形で、$x$ 軸はこの多角形の対称軸であり、直線 $y=\frac{\sqrt{3}}{3} x$ もこの多角形の対称軸であるものを考える。このような多角形の辺の数の最小値を求めよ。
福田のおもしろ数学298〜幾何の問題2つの長方形

単元:
#数A#図形の性質#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\mathrm{A,D,H,G}$ が同一円周上にあるとき、$\mathrm{CE}$ の長さを求めよ。(図は動画内参照)
この動画を見る
$\mathrm{A,D,H,G}$ が同一円周上にあるとき、$\mathrm{CE}$ の長さを求めよ。(図は動画内参照)
福田の数学〜早稲田大学2024教育学部第1問(2)〜空間で格子点を頂点とする正六角形の一辺の長さの最小値

単元:
#数A#図形の性質#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$x$ 座標、$y$ 座標、$z$ 座標がすべて整数であるような $xyz$ 空間の点を格子点と呼ぶ。頂点がすべて格子点であるような $xyz$ 空間内の正 $6$ 角形の $1$ 辺の長さの最小値を求めよ。
この動画を見る
$x$ 座標、$y$ 座標、$z$ 座標がすべて整数であるような $xyz$ 空間の点を格子点と呼ぶ。頂点がすべて格子点であるような $xyz$ 空間内の正 $6$ 角形の $1$ 辺の長さの最小値を求めよ。
和と積が等しくなるような自然数の組?シンプルだけど難しい!どう解く?

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
相違なるn個の自然数の和と積が等しいとき、nの値とそれらn個の自然数の組をすべて求めよ。ただし、n≧2とする。
この動画を見る
相違なるn個の自然数の和と積が等しいとき、nの値とそれらn個の自然数の組をすべて求めよ。ただし、n≧2とする。
この出し方知ってる?

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
二次関数$y=\frac{1}{2}x^2$上の2点A(-4, 8), B(2, 2)と原点Oを結んでできる三角形の面積を求めよ
この動画を見る
二次関数$y=\frac{1}{2}x^2$上の2点A(-4, 8), B(2, 2)と原点Oを結んでできる三角形の面積を求めよ
福田のおもしろ数学297〜1分チャレンジ! 魔方陣

