 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
不等式 順天堂大

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x$についての不等式
$ax+5>4a+1$の解が$x=3$を含むとき、定数$a$の値の範囲を求めよ
順天堂大学
この動画を見る
$x$についての不等式
$ax+5>4a+1$の解が$x=3$を含むとき、定数$a$の値の範囲を求めよ
順天堂大学
福田の数学〜早稲田大学2024年人間科学部第4問〜関数の増減と接線の傾きの長さ

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ $f(x)$=$x^3$+$ax^2$+$bx$+$\displaystyle\frac{1}{4}a^2$ が$x$=-2 で極値をとり、その値が1であるとき、定数$a$, $b$の値は$a$=$\boxed{\ \ ソ\ \ }$, $b$=$\boxed{\ \ タ\ \ }$ である。このとき、曲線$y$=$f(x)$上の点$(t, f(t))$における接線の傾きは$t$=$\displaystyle\frac{\boxed{チ}}{\boxed{ツ}}$ のとき、最小値$\displaystyle\frac{\boxed{テ}}{\boxed{ト}}$ をとる。
この動画を見る
$\Large\boxed{4}$ $f(x)$=$x^3$+$ax^2$+$bx$+$\displaystyle\frac{1}{4}a^2$ が$x$=-2 で極値をとり、その値が1であるとき、定数$a$, $b$の値は$a$=$\boxed{\ \ ソ\ \ }$, $b$=$\boxed{\ \ タ\ \ }$ である。このとき、曲線$y$=$f(x)$上の点$(t, f(t))$における接線の傾きは$t$=$\displaystyle\frac{\boxed{チ}}{\boxed{ツ}}$ のとき、最小値$\displaystyle\frac{\boxed{テ}}{\boxed{ト}}$ をとる。
大学入試問題#809「関数の相性が良さそうではない。」 #福島県立医科大学(2023) #極限

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#福島県立医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{\sin\ 2x}{log_2(x+2)-1}$
出典:2023年福島県立医科大学 入試問題
この動画を見る
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{\sin\ 2x}{log_2(x+2)-1}$
出典:2023年福島県立医科大学 入試問題
【統計分野、演習編】確率密度関数と面積の関係の確認【数学b】

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
指導講師:
3rd School
問題文全文(内容文):
確率変数$X$の確率密度関数$f(x)$が次の式で表されるとき、確率$P(0 \leqq x \leqq 2)$を求めよ
$f(x)=\displaystyle \frac{1}{8}x(0 \leqq x \leqq 4)$
この動画を見る
確率変数$X$の確率密度関数$f(x)$が次の式で表されるとき、確率$P(0 \leqq x \leqq 2)$を求めよ
$f(x)=\displaystyle \frac{1}{8}x(0 \leqq x \leqq 4)$
福田の数学〜早稲田大学2024年人間科学部第3問〜平面へ下ろした垂線の長さ
単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
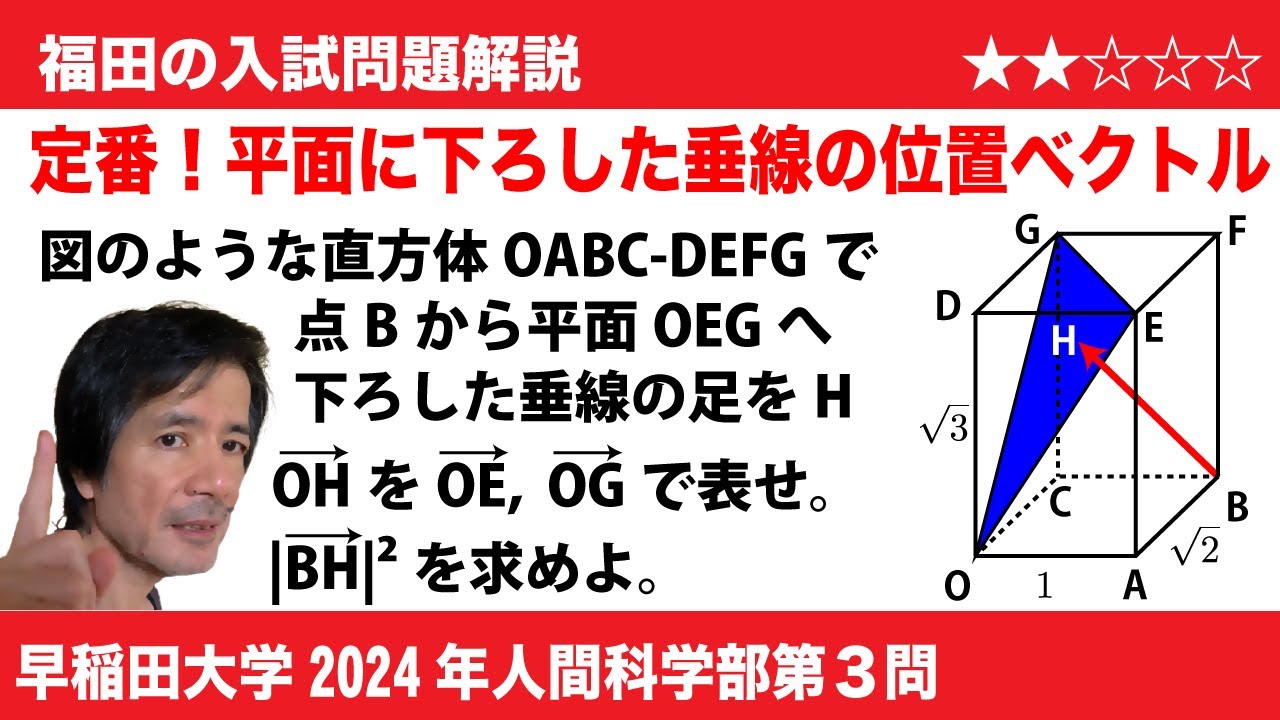
$\Large\boxed{3}$ 直方体OABC-DEFGにおける各辺の長さは
OA=CB=DE=GF=1
AB=OC=EF=DG=$\sqrt 2$
OD=AE=BF=CG=$\sqrt 3$
である。点Bから3点O, E, Gを含む平面に下ろした垂線の足をHとする。このとき、$\overrightarrow{\textrm{OH}}$=$\displaystyle\frac{\boxed{ケ}}{\boxed{コ}}\overrightarrow{\textrm{OE}}$+$\displaystyle\frac{\boxed{サ}}{\boxed{シ}}\overrightarrow{\textrm{OG}}$ と表すことができ、$|\overrightarrow{\textrm{BH}}|^2$=$\displaystyle\frac{\boxed{ス}}{\boxed{セ}}$ である。
この動画を見る
$\Large\boxed{3}$ 直方体OABC-DEFGにおける各辺の長さは
OA=CB=DE=GF=1
AB=OC=EF=DG=$\sqrt 2$
OD=AE=BF=CG=$\sqrt 3$
である。点Bから3点O, E, Gを含む平面に下ろした垂線の足をHとする。このとき、$\overrightarrow{\textrm{OH}}$=$\displaystyle\frac{\boxed{ケ}}{\boxed{コ}}\overrightarrow{\textrm{OE}}$+$\displaystyle\frac{\boxed{サ}}{\boxed{シ}}\overrightarrow{\textrm{OG}}$ と表すことができ、$|\overrightarrow{\textrm{BH}}|^2$=$\displaystyle\frac{\boxed{ス}}{\boxed{セ}}$ である。
福田のおもしろ数学130〜合成関数の性質

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$f(x)$=$ax$+$b$, $g(x)$=$cx$+$d$ ($a$≠0, $c$≠0)とする。このとき次の条件を満たす関数$h(x)$, $k(x)$を求めよ。
(1)$g(h(x))$=$f(x)$ (2)$k(g(x))$=$f(x)$
この動画を見る
$f(x)$=$ax$+$b$, $g(x)$=$cx$+$d$ ($a$≠0, $c$≠0)とする。このとき次の条件を満たす関数$h(x)$, $k(x)$を求めよ。
(1)$g(h(x))$=$f(x)$ (2)$k(g(x))$=$f(x)$
大学入試問題#808「難しすぎない良問」 #東京医科大学(2009) #整数問題

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#東京医科大学
指導講師:
ますただ
問題文全文(内容文):
不等式$\sqrt{ n+1 }-\sqrt{ n } \gt \displaystyle \frac{1}{100}$を満たす正の整数$n$の最大値を求めよ。
出典:2009年東京医科大学 入試問題
この動画を見る
不等式$\sqrt{ n+1 }-\sqrt{ n } \gt \displaystyle \frac{1}{100}$を満たす正の整数$n$の最大値を求めよ。
出典:2009年東京医科大学 入試問題
福田の数学〜早稲田大学2024年人間科学部第2問〜反復試行と条件付き確率

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ $n$を2以上の自然数とする。1から$n$までの番号が1つずつつけられた$n$個の玉が中身の見えない袋に入っている。袋の中から1個の玉を選んで番号を確認して袋に戻すという操作を$n$回繰り返す。この$n$回の操作の中で、1から$n$-1までのいずれの番号の玉も選ばれているとき、番号が$n$の玉も選ばれている条件付き確率を$P(n)$とするとき、$P(3)$=$\frac{\boxed{オ}}{\boxed{カ}}$, $P(50)$=$\frac{\boxed{キ}}{\boxed{ク}}$ である。
この動画を見る
$\Large\boxed{2}$ $n$を2以上の自然数とする。1から$n$までの番号が1つずつつけられた$n$個の玉が中身の見えない袋に入っている。袋の中から1個の玉を選んで番号を確認して袋に戻すという操作を$n$回繰り返す。この$n$回の操作の中で、1から$n$-1までのいずれの番号の玉も選ばれているとき、番号が$n$の玉も選ばれている条件付き確率を$P(n)$とするとき、$P(3)$=$\frac{\boxed{オ}}{\boxed{カ}}$, $P(50)$=$\frac{\boxed{キ}}{\boxed{ク}}$ である。
福田のおもしろ数学129〜三角関数の最大問題
単元:
#数Ⅱ#三角関数#三角関数とグラフ
指導講師:
福田次郎
問題文全文(内容文):
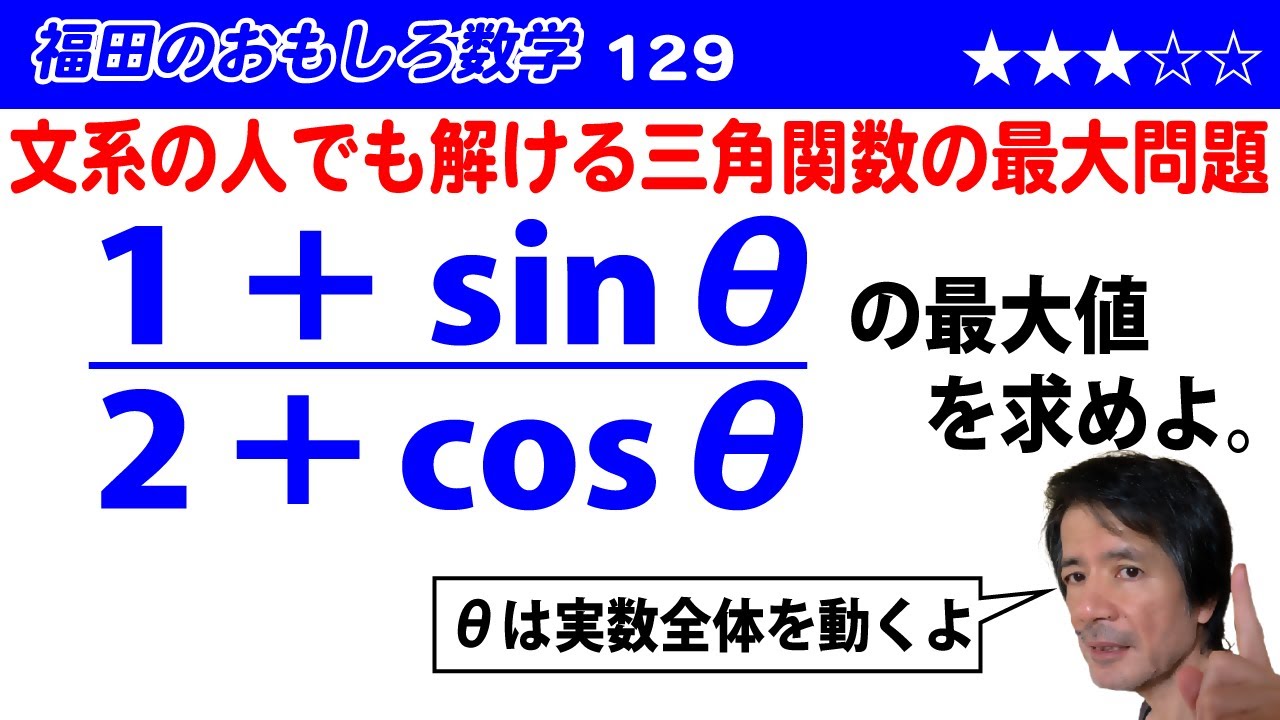
$\displaystyle\frac{1+\sin\theta}{2+\cos\theta}$($\theta$は実数)の最大値を求めよ。
この動画を見る
$\displaystyle\frac{1+\sin\theta}{2+\cos\theta}$($\theta$は実数)の最大値を求めよ。
整数問題 城北高校

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
20以下の自然数nのうち
$(n+1)^2+(n+3)^2+(n+5)^2$が7の倍数となるものは何個?
城北高等学校
この動画を見る
20以下の自然数nのうち
$(n+1)^2+(n+3)^2+(n+5)^2$が7の倍数となるものは何個?
城北高等学校
大学入試問題#807「落ち着いて解く!」 #福島県立医科大学(2019) #積分方程式

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#福島県立医科大学
指導講師:
ますただ
問題文全文(内容文):
実数$x$についての関数の列$\{f_n(x\})$が
$f_n(x)=\displaystyle \sum_{k=1}^n \displaystyle \frac{x^k}{k}-2\displaystyle \int_{0}^{1} f_n(t)dt$を満たしている。
$\displaystyle \lim_{ n \to \infty } f_n(0)$を求めよ。
出典:2019年福島県立医科大学 入試問題
この動画を見る
実数$x$についての関数の列$\{f_n(x\})$が
$f_n(x)=\displaystyle \sum_{k=1}^n \displaystyle \frac{x^k}{k}-2\displaystyle \int_{0}^{1} f_n(t)dt$を満たしている。
$\displaystyle \lim_{ n \to \infty } f_n(0)$を求めよ。
出典:2019年福島県立医科大学 入試問題
福田の数学〜早稲田大学2024年人間科学部第1問(3)〜指数法則と式の値

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (3)$10^x$=25, $100^y$=400 のとき、$3x$+$6y$-2=$\boxed{エ}$ である。
この動画を見る
$\Large\boxed{1}$ (3)$10^x$=25, $100^y$=400 のとき、$3x$+$6y$-2=$\boxed{エ}$ である。
東大生のワイヤレスイヤホンの見付け方が凄すぎた
単元:
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
ワイヤレスイヤホンを落としたときの見つけ方
三角形の外心の話です
この動画を見る
ワイヤレスイヤホンを落としたときの見つけ方
三角形の外心の話です
【短時間でポイントチェック!!】ベクトルの平行〔現役講師解説、数学〕

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師:
3rd School
問題文全文(内容文):
ベクトルの平行を短時間で解くポイント解説動画です
----------------------------------------
次の2つのベクトル$\vec{ a },\vec{ b }$が平行になるように$x$の値を求めよ。
①
$\vec{ a }=(x,-2),\vec{ b }=(2,1)$
②
$\vec{ a }=(-9,x),\vec{ b }=(x,-1)$
この動画を見る
ベクトルの平行を短時間で解くポイント解説動画です
----------------------------------------
次の2つのベクトル$\vec{ a },\vec{ b }$が平行になるように$x$の値を求めよ。
①
$\vec{ a }=(x,-2),\vec{ b }=(2,1)$
②
$\vec{ a }=(-9,x),\vec{ b }=(x,-1)$
大学入試問題#806「The 良問!」 兵庫県立大学中期(2014) #微積の応用

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#兵庫県立大学
指導講師:
ますただ
問題文全文(内容文):
微分可能な関数$f(x)$が
$f(x)=\displaystyle \int_{0}^{x} \sqrt{ f(t)^2+1 }\ dt$を満たすとする。
このとき以下の問いに答えよ。
1.$f'(x)$と$f''(x)$を$f(x)$で表せ。
2.関数$log(f(x)+f'(x))$を求めよ。
3.$f(x)$を求めよ。
出典:2014年兵庫県立大学中期 入試問題
この動画を見る
微分可能な関数$f(x)$が
$f(x)=\displaystyle \int_{0}^{x} \sqrt{ f(t)^2+1 }\ dt$を満たすとする。
このとき以下の問いに答えよ。
1.$f'(x)$と$f''(x)$を$f(x)$で表せ。
2.関数$log(f(x)+f'(x))$を求めよ。
3.$f(x)$を求めよ。
出典:2014年兵庫県立大学中期 入試問題
平方根 法政大学高校

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(a-2 \sqrt 2)(4+3 \sqrt 2) = \sqrt 2b$となる整数$a,b$を求めよ
法政大学高等学校
この動画を見る
$(a-2 \sqrt 2)(4+3 \sqrt 2) = \sqrt 2b$となる整数$a,b$を求めよ
法政大学高等学校
福田の数学〜早稲田大学2024年人間科学部第1問(2)〜不等式の表す領域の面積

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (2)次の連立不等式で表される領域の面積は$\boxed{イ}$+$\boxed{ウ}\pi$ である。
$\left\{\begin{array}{1}
x^2+y^2≦4|x|+4|y|\\
x^2≦y^2\\
\end{array}\right.$
この動画を見る
$\Large\boxed{1}$ (2)次の連立不等式で表される領域の面積は$\boxed{イ}$+$\boxed{ウ}\pi$ である。
$\left\{\begin{array}{1}
x^2+y^2≦4|x|+4|y|\\
x^2≦y^2\\
\end{array}\right.$
みんな何問できた?

単元:
#算数(中学受験)#その他#その他#その他#その他#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
①$e^{i \pi}+1=0$
②$\displaystyle \frac{a^2u}{at^2}=v^2 \frac{a^2u}{ax^2}$
③底辺$\times$高さ$\div 2$
④$x=\frac{-b \pm \sqrt{ b^2-4ac }}{2a}$
⑤$E=mc^2$
⑥$2 \pi r$
⑦$\displaystyle \frac{av}{at}+(v・\triangledown)v=-\frac{1}{p}\triangledown p+v \triangledown ^2v+f(x,t)$
⑧$\frac{4\pi r^3}{3}$
この動画を見る
①$e^{i \pi}+1=0$
②$\displaystyle \frac{a^2u}{at^2}=v^2 \frac{a^2u}{ax^2}$
③底辺$\times$高さ$\div 2$
④$x=\frac{-b \pm \sqrt{ b^2-4ac }}{2a}$
⑤$E=mc^2$
⑥$2 \pi r$
⑦$\displaystyle \frac{av}{at}+(v・\triangledown)v=-\frac{1}{p}\triangledown p+v \triangledown ^2v+f(x,t)$
⑧$\frac{4\pi r^3}{3}$
何問できた?

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
展開の問題
①$(x+2)(x+3)$
②$(3x+5)(3x-2)$
③$(x-2)^2$
④$\require{physics} \qty( 3x+\frac{1}{5} ) \require{physics} \qty( 3x-\frac{1}{5} )$
⑤$(t+3)^2$
この動画を見る
展開の問題
①$(x+2)(x+3)$
②$(3x+5)(3x-2)$
③$(x-2)^2$
④$\require{physics} \qty( 3x+\frac{1}{5} ) \require{physics} \qty( 3x-\frac{1}{5} )$
⑤$(t+3)^2$
福田のおもしろ数学127〜こんな漸化式解けるの?〜難しい漸化式の解き方

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$a_1$=$\displaystyle\frac{1}{2}$, $a_{n+1}$=$\sqrt{\displaystyle\frac{a_n+1}{2}}$ を満たす数列$\left\{a_n\right\}$の一般項$a_n$を求めよ。
この動画を見る
$a_1$=$\displaystyle\frac{1}{2}$, $a_{n+1}$=$\sqrt{\displaystyle\frac{a_n+1}{2}}$ を満たす数列$\left\{a_n\right\}$の一般項$a_n$を求めよ。
大学入試問題#805「特に言うことないよねーw」 #東邦大学医学部(2004) #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#東邦大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{ \pi } (\sin2x\cos\ x+\sin\ x \cos2x) dx$
出典:2004年東邦大学医学部
この動画を見る
$\displaystyle \int_{0}^{ \pi } (\sin2x\cos\ x+\sin\ x \cos2x) dx$
出典:2004年東邦大学医学部
福田の数学〜早稲田大学2024年人間科学部第1問(1)〜4次式の最小値

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (1)$x$が実数であるとき、$x(x+1)(x+2)(x+3)$ の最小値は$\boxed{\ \ ア\ \ }$である。
この動画を見る
$\Large\boxed{1}$ (1)$x$が実数であるとき、$x(x+1)(x+2)(x+3)$ の最小値は$\boxed{\ \ ア\ \ }$である。
因数分解の裏技

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
たすき掛けの因数分解の裏技説明動画です
$5x^2-11x+2=??$
この動画を見る
たすき掛けの因数分解の裏技説明動画です
$5x^2-11x+2=??$
福田のおもしろ数学126〜条件付き最大値の問題

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
正の数$x$, $y$が$x^2$-$2x$+$4y^2$=0 を満たして変わるとき、$xy$の最大値を求めよ。
この動画を見る
正の数$x$, $y$が$x^2$-$2x$+$4y^2$=0 を満たして変わるとき、$xy$の最大値を求めよ。
大学入試問題#804「このタイプは定期的に出題」 #兵庫県立大学中期(2014) #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#兵庫県立大学
指導講師:
ますただ
問題文全文(内容文):
$f(x)=2\sin2x-\sin\ x$とする。
定積分$\displaystyle \int_{0}^{\pi} |f(x)| dx$の値を求めよ。
出典:2014年兵庫県立大学中期 入試問題
この動画を見る
$f(x)=2\sin2x-\sin\ x$とする。
定積分$\displaystyle \int_{0}^{\pi} |f(x)| dx$の値を求めよ。
出典:2014年兵庫県立大学中期 入試問題
すべて〇〇しなくていい。千葉工大

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(x+1)(x+3)(x+5)(x+7)$を展開したときの$x^2$の係数は?
千葉工業大学
この動画を見る
$(x+1)(x+3)(x+5)(x+7)$を展開したときの$x^2$の係数は?
千葉工業大学
福田の数学〜一橋大学2024年文系第5問〜円の中心を含む三角形になる確率
単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
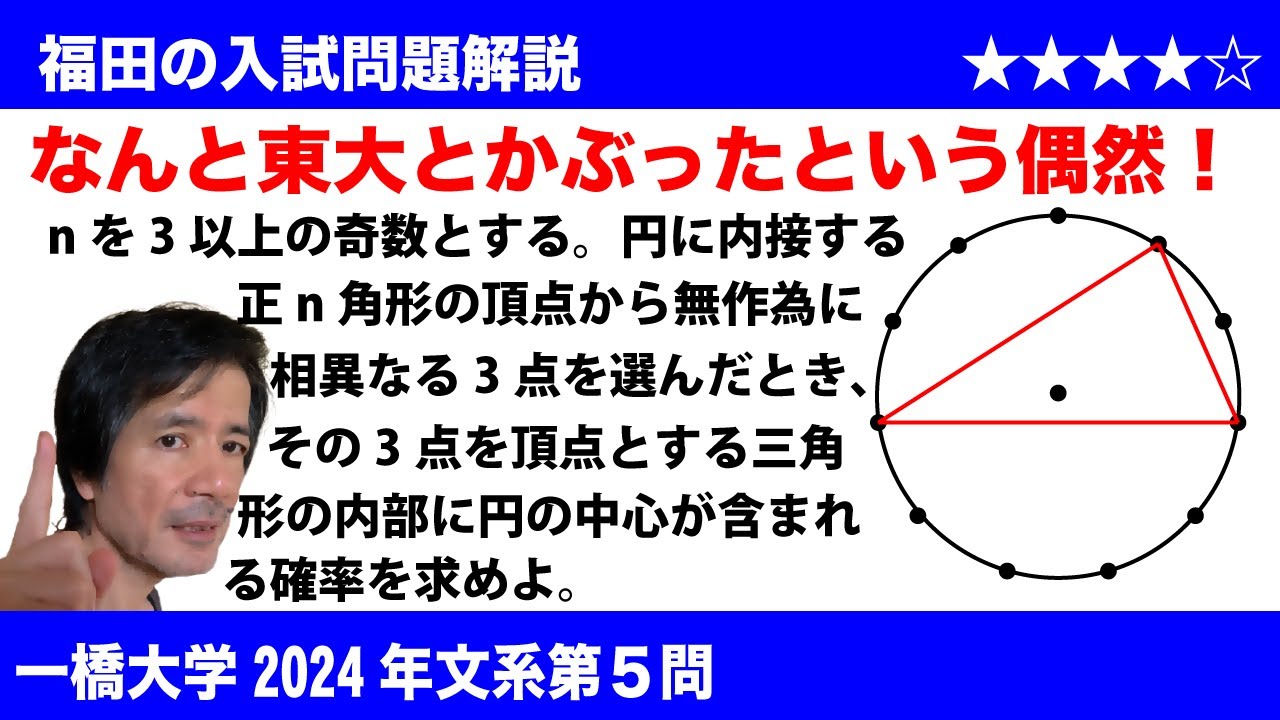
$\Large\boxed{5}$ $n$を3以上の奇数とする。円に内接する正$n$角形の頂点から無作為に相異なる3点を選んだ時、その3点を頂点とする三角形の内部に円の中心が含まれる確率$p_n$を求めよ。
この動画を見る
$\Large\boxed{5}$ $n$を3以上の奇数とする。円に内接する正$n$角形の頂点から無作為に相異なる3点を選んだ時、その3点を頂点とする三角形の内部に円の中心が含まれる確率$p_n$を求めよ。
一手間加えるだけで美味しい方程式

福田の数学〜一橋大学2024年文系第4問〜ひし形になる条件と面積の最小

単元:
#数Ⅰ#図形と計量#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 実数$a$,$b$は-1<$a$<1, -1<$b$<1 を満たす。座標空間内に4点A($a$, -1, -1), B(-1, $b$, -1), C($-a$, 1, 1), D(1, $-b$, 1)をとる。
(1)A, B, C, Dがひし形の頂点となるとき、$a$と$b$の会計を表す等式を求めよ。
(2)$a$, $b$が(1)の等式を満たすとき、A, B, C, Dを頂点とする四角形の面積の最小値を求めよ。
この動画を見る
$\Large\boxed{4}$ 実数$a$,$b$は-1<$a$<1, -1<$b$<1 を満たす。座標空間内に4点A($a$, -1, -1), B(-1, $b$, -1), C($-a$, 1, 1), D(1, $-b$, 1)をとる。
(1)A, B, C, Dがひし形の頂点となるとき、$a$と$b$の会計を表す等式を求めよ。
(2)$a$, $b$が(1)の等式を満たすとき、A, B, C, Dを頂点とする四角形の面積の最小値を求めよ。
これ全部わかる?

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
①$1^0$
②$\sqrt[ 3 ]{ 27 }$
③$2^2$
④$7-1$
⑤$\sqrt{ 49 }$
⑥$2^3$
⑦$\sqrt{ 81 }$
⑧$5+5$
⑨$\sqrt{ 144 }$
この動画を見る
①$1^0$
②$\sqrt[ 3 ]{ 27 }$
③$2^2$
④$7-1$
⑤$\sqrt{ 49 }$
⑥$2^3$
⑦$\sqrt{ 81 }$
⑧$5+5$
⑨$\sqrt{ 144 }$
