 空間図形
空間図形
 空間図形
空間図形
円錐 香川誠陵 2022入試問題解説21問目
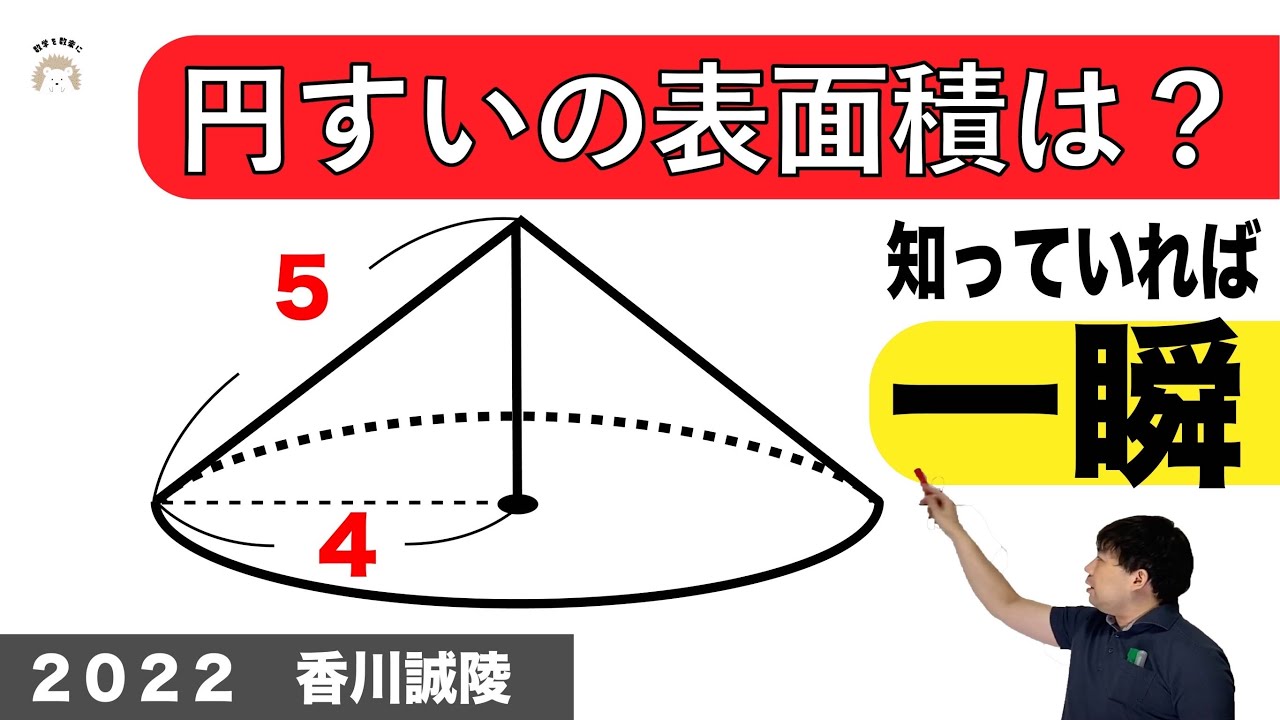
【高校受験対策/数学】死守-97

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#方程式#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#平方根#2次方程式#空間図形#相似な図形#円#文字と式#平面図形#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守97
①$5-(-7)$を計算しなさい。
➁$\sqrt{ 27 }+\sqrt{ 12 }$を計算しなさい。
③$(\sqrt{ 2 }-1)^2$を計算しなさい。
④連立方程式を解きなさい。
$2x-3y=-4$
$x+2y=5$
⑤二次方程式$3x^2+7x+1=0$を解きなさい。
⑥相似な2つの立体$F,G$がある。
$F$と$G$の相似比が$3:5$であり、$F$の体積が$81\pi$$cm^3$のとき、$G$の体積を求めなさい。
⑦右の図のように、4点$A,B,C,D$が線分$BC$を直径とする 同じ円周上にあるとき、
$\angle ADB$の大きさを求めなさい。
⑧右下の図のような線分$OA$がある。
$\angle AOB=30°,OA=OB$となる二等辺三角形$OAB$を作図しなさい。
また点$B$の位置を示す文字$B$も図の中に書き入れなさい。
ただし、作図には定規とコンパスを用い、作図に用いた線は消えずに残しておくこと。
この動画を見る
高校受験対策・死守97
①$5-(-7)$を計算しなさい。
➁$\sqrt{ 27 }+\sqrt{ 12 }$を計算しなさい。
③$(\sqrt{ 2 }-1)^2$を計算しなさい。
④連立方程式を解きなさい。
$2x-3y=-4$
$x+2y=5$
⑤二次方程式$3x^2+7x+1=0$を解きなさい。
⑥相似な2つの立体$F,G$がある。
$F$と$G$の相似比が$3:5$であり、$F$の体積が$81\pi$$cm^3$のとき、$G$の体積を求めなさい。
⑦右の図のように、4点$A,B,C,D$が線分$BC$を直径とする 同じ円周上にあるとき、
$\angle ADB$の大きさを求めなさい。
⑧右下の図のような線分$OA$がある。
$\angle AOB=30°,OA=OB$となる二等辺三角形$OAB$を作図しなさい。
また点$B$の位置を示す文字$B$も図の中に書き入れなさい。
ただし、作図には定規とコンパスを用い、作図に用いた線は消えずに残しておくこと。
【高校受験対策/数学】死守-94

単元:
#数学(中学生)#中1数学#正の数・負の数#式の計算(展開、因数分解)#平方根#空間図形#文字と式#標本調査
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守94
①$(-3)×5$を計算せよ。
②$\frac{x}{2}-2+(\frac{x}{5}-1)$を計算せよ。
③$24xy^2÷(-8xy)×2x$を計算せよ。
④$(\sqrt{3}+\sqrt{2})(2\sqrt{3}+\sqrt{2})+\frac{6}{\sqrt{6}}$を計算せよ。
⑤$(x-3)^2-(x+4)(x-4)$を計算せよ。
⑥$x^2-8x+12$を因数分解せよ。
⑦右の図のように、底面が正方形BCDEである正四角すいABCDEがある。
このとき、直線BCとねじれの位置にある直線をすべて書きなさい。
⑧気温は、高度が100$m$増すごとに0.6℃ずつ低くなる。
地上の気温が7.6℃のとき、地上から2000m上空の気温は何℃か求めよ。
⑨下の表は、あるクラスの13人のハンドボール投げの記録を、大きさの順に並べたものである。
この13人と太郎さんを合わせた14人の記録の中央値は、太郎さんを合わせる前の13人の記録の中央値と比べて、1$m$大きい。
このとき太郎さんの記録は何$m$か求めよ。
この動画を見る
高校受験対策・死守94
①$(-3)×5$を計算せよ。
②$\frac{x}{2}-2+(\frac{x}{5}-1)$を計算せよ。
③$24xy^2÷(-8xy)×2x$を計算せよ。
④$(\sqrt{3}+\sqrt{2})(2\sqrt{3}+\sqrt{2})+\frac{6}{\sqrt{6}}$を計算せよ。
⑤$(x-3)^2-(x+4)(x-4)$を計算せよ。
⑥$x^2-8x+12$を因数分解せよ。
⑦右の図のように、底面が正方形BCDEである正四角すいABCDEがある。
このとき、直線BCとねじれの位置にある直線をすべて書きなさい。
⑧気温は、高度が100$m$増すごとに0.6℃ずつ低くなる。
地上の気温が7.6℃のとき、地上から2000m上空の気温は何℃か求めよ。
⑨下の表は、あるクラスの13人のハンドボール投げの記録を、大きさの順に並べたものである。
この13人と太郎さんを合わせた14人の記録の中央値は、太郎さんを合わせる前の13人の記録の中央値と比べて、1$m$大きい。
このとき太郎さんの記録は何$m$か求めよ。
【高校受験対策/数学】死守-91

単元:
#数学(中学生)#中1数学#正の数・負の数#平方根#比例・反比例#空間図形#2次関数#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守91
①$-7+9$を計算しなさい。
②$\frac{15}{2}×(-\frac{4}{5})$を計算しなさい。
③$3(2x-y)+4(x+3y)$を 計算しなさい。
④$y$は$x$に反比例し、$x=3$のとき$y=2$である。
$y$を$x$の式で表しなさい。
⑤14の平方根うち、正数の数であるものを答えなさい。
⑥底面が1辺$6cm$の正方形で、体積が$96cm^3$である四角すいの高さを求めなさい。
⑦2つの整数$m,n$について、計算の結果がいつも整数になるとは限らないものを、
次のア~エから1つ選び、記号で答えなさい。
ア $m+n$
イ $m-n$
ウ $m×n$
エ $m÷n$
⑧関数$y=-\frac{3}{4}x^2$について、
次のア~エのうち、正しいものを2つ選び記号で 答えなさい。
ア 変化の割合は一定ではない。
イ $x$の値がどのように変化しても、その値が増加することはない。
ウ $x$がどのような値でも、$y$の値は負の数である。
エ グラフの開き方は関数$y=x^2$のグラフより大きい。
この動画を見る
高校受験対策・死守91
①$-7+9$を計算しなさい。
②$\frac{15}{2}×(-\frac{4}{5})$を計算しなさい。
③$3(2x-y)+4(x+3y)$を 計算しなさい。
④$y$は$x$に反比例し、$x=3$のとき$y=2$である。
$y$を$x$の式で表しなさい。
⑤14の平方根うち、正数の数であるものを答えなさい。
⑥底面が1辺$6cm$の正方形で、体積が$96cm^3$である四角すいの高さを求めなさい。
⑦2つの整数$m,n$について、計算の結果がいつも整数になるとは限らないものを、
次のア~エから1つ選び、記号で答えなさい。
ア $m+n$
イ $m-n$
ウ $m×n$
エ $m÷n$
⑧関数$y=-\frac{3}{4}x^2$について、
次のア~エのうち、正しいものを2つ選び記号で 答えなさい。
ア 変化の割合は一定ではない。
イ $x$の値がどのように変化しても、その値が増加することはない。
ウ $x$がどのような値でも、$y$の値は負の数である。
エ グラフの開き方は関数$y=x^2$のグラフより大きい。
【裏技】知らないと損

【高校受験対策/数学】死守-89

単元:
#数学(中学生)#中1数学#正の数・負の数#式の計算(展開、因数分解)#平方根#空間図形#確率#2次関数#円#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守89
①$-3-(-7)$を計算しなさい。
②$8-(-3)^2$を計算しなさい。
③$(-9ab^2)×2a÷(-3ab)$を計算しなさい。
④$(\sqrt{7}+\sqrt{5})(\sqrt{7}-\sqrt{5})$を計算しなさい。
⑤$x^2-3x-18$を因数分解しなさい。
⑥絶対値が$4$より小さい整数の個数を求めなさい。
⑦右の図のア~ウは、関数$y=-2x^2、y=x^2$および$y=\frac{1}{2}x^2$のグラフを同じ座標軸を使ってかいたものです。
$y=x^2$のグラフをア~ウから一つ選びなさい。
⑧右の図のような、半径$5cm$、中心角$90°$のおうぎ形$OAB$があります。
このおうぎ形を直線$OA$を回転の軸として1回転させてできる立体の体積を求めなさい。
⑨大小2つのさいころを同時に投げるとき、出る目の数の和がちょうど$5$以下となる確率を求めなさい。
ただしさいころの$1$から$6$までの目の出方は同様に確からしいものとします。
この動画を見る
高校受験対策・死守89
①$-3-(-7)$を計算しなさい。
②$8-(-3)^2$を計算しなさい。
③$(-9ab^2)×2a÷(-3ab)$を計算しなさい。
④$(\sqrt{7}+\sqrt{5})(\sqrt{7}-\sqrt{5})$を計算しなさい。
⑤$x^2-3x-18$を因数分解しなさい。
⑥絶対値が$4$より小さい整数の個数を求めなさい。
⑦右の図のア~ウは、関数$y=-2x^2、y=x^2$および$y=\frac{1}{2}x^2$のグラフを同じ座標軸を使ってかいたものです。
$y=x^2$のグラフをア~ウから一つ選びなさい。
⑧右の図のような、半径$5cm$、中心角$90°$のおうぎ形$OAB$があります。
このおうぎ形を直線$OA$を回転の軸として1回転させてできる立体の体積を求めなさい。
⑨大小2つのさいころを同時に投げるとき、出る目の数の和がちょうど$5$以下となる確率を求めなさい。
ただしさいころの$1$から$6$までの目の出方は同様に確からしいものとします。
【数学】立体図形:サンタの帽子の体積を求めよう! ~クリスマススペシャル~
これみんな知ってた?

正四角錐の表面積...

【高校受験対策/数学】死守-86

単元:
#数学(中学生)#中1数学#正の数・負の数#方程式#平方根#比例・反比例#空間図形#2次関数#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守86 @1:57
①$3×(-8)$を計算しなさい。
➁$\frac{1}{2}-\frac{5}{6}$を計算しなさい。
③$-8x^3÷4x^2×(-x)$を計算しなさい。
④$\sqrt{50}+\sqrt{2}$を計算しなさい。
⑤六角形の内角の和を求めなさい。
⑥関数$y=ax^2$について、$x$の値が$2$から$6$まで増加するときの変化の割合が$-4$である。
このとき$a$の値を求めなさい。
⑦右の図は立方体の展開図である。
この立方体において、面$A$と平行になる面を、ア~オの中から1つ選び記号で答えなさい。
⑧$-3$と$-2\sqrt{2}$の大小を、不等号を使って表しなさい。
⑨ある中学校の生徒の人数は126人で、126人全員が徒歩通学か自転車通学のいずれか一方で通学しており、
徒歩通学をしている生徒と自転車通学をしている生徒の人数の比は$5:2$である。
このとき、自転車通学をしている生徒の人数を求めなさい。
この動画を見る
高校受験対策・死守86 @1:57
①$3×(-8)$を計算しなさい。
➁$\frac{1}{2}-\frac{5}{6}$を計算しなさい。
③$-8x^3÷4x^2×(-x)$を計算しなさい。
④$\sqrt{50}+\sqrt{2}$を計算しなさい。
⑤六角形の内角の和を求めなさい。
⑥関数$y=ax^2$について、$x$の値が$2$から$6$まで増加するときの変化の割合が$-4$である。
このとき$a$の値を求めなさい。
⑦右の図は立方体の展開図である。
この立方体において、面$A$と平行になる面を、ア~オの中から1つ選び記号で答えなさい。
⑧$-3$と$-2\sqrt{2}$の大小を、不等号を使って表しなさい。
⑨ある中学校の生徒の人数は126人で、126人全員が徒歩通学か自転車通学のいずれか一方で通学しており、
徒歩通学をしている生徒と自転車通学をしている生徒の人数の比は$5:2$である。
このとき、自転車通学をしている生徒の人数を求めなさい。
【高校受験対策/数学】死守-85

単元:
#数学(中学生)#中1数学#中3数学#正の数・負の数#方程式#平方根#2次方程式#空間図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守85 @4:15
①$2-(3-8)$を計算しなさい。
②$(\frac{1}{3}-\frac{3}{4})÷\frac{5}{6}$を計算しなさい。
③$(-4x)^2÷12xy×9xy^2$を計算しなさい。
④$\sqrt{18}-\frac{10}{\sqrt{ 2 }}$を計算しなさい。
⑤2次方程式$(x-4)(3x+2)=8x-5$を解きなさい。
⑥右の図のように、底面が直角三角形で、側面がすべて長方形の三角柱があり、$AB=6cm$、$BE=4cm$、$\angle ABC=30°$、$\angle ACB=90°$である。
この三角柱の体積を求めなさい。
⑦空間内にある平面$P$と、異なる2直線$l,m$の位置関係について、
つねに正しいものを、次のア~エから1つ選び記号で答えなさい。
ア 直線$l$と直線$m$が、それぞれ平面$P$と交わるならば、直線$l$と直線$m$は交わる。
イ 直線$l$と直線$m$が、それぞれ平面$P$と平行ならば、直線$l$と直線$m$は平行である。
ウ 平面$P$と交わる直線$l$が、平面$P$上にある直線$m$と垂直であるならば、平面$P$と直線$l$は垂直である。
エ 平面$P$と交わる直線$l$が、平面$P$上にある直線$m$と交わらないならば、直線$l$と直線$m$はねじれの位置にある。
この動画を見る
高校受験対策・死守85 @4:15
①$2-(3-8)$を計算しなさい。
②$(\frac{1}{3}-\frac{3}{4})÷\frac{5}{6}$を計算しなさい。
③$(-4x)^2÷12xy×9xy^2$を計算しなさい。
④$\sqrt{18}-\frac{10}{\sqrt{ 2 }}$を計算しなさい。
⑤2次方程式$(x-4)(3x+2)=8x-5$を解きなさい。
⑥右の図のように、底面が直角三角形で、側面がすべて長方形の三角柱があり、$AB=6cm$、$BE=4cm$、$\angle ABC=30°$、$\angle ACB=90°$である。
この三角柱の体積を求めなさい。
⑦空間内にある平面$P$と、異なる2直線$l,m$の位置関係について、
つねに正しいものを、次のア~エから1つ選び記号で答えなさい。
ア 直線$l$と直線$m$が、それぞれ平面$P$と交わるならば、直線$l$と直線$m$は交わる。
イ 直線$l$と直線$m$が、それぞれ平面$P$と平行ならば、直線$l$と直線$m$は平行である。
ウ 平面$P$と交わる直線$l$が、平面$P$上にある直線$m$と垂直であるならば、平面$P$と直線$l$は垂直である。
エ 平面$P$と交わる直線$l$が、平面$P$上にある直線$m$と交わらないならば、直線$l$と直線$m$はねじれの位置にある。
【裏技】これで求まる理由分かる?
単元:
#数学(中学生)#中1数学#空間図形
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
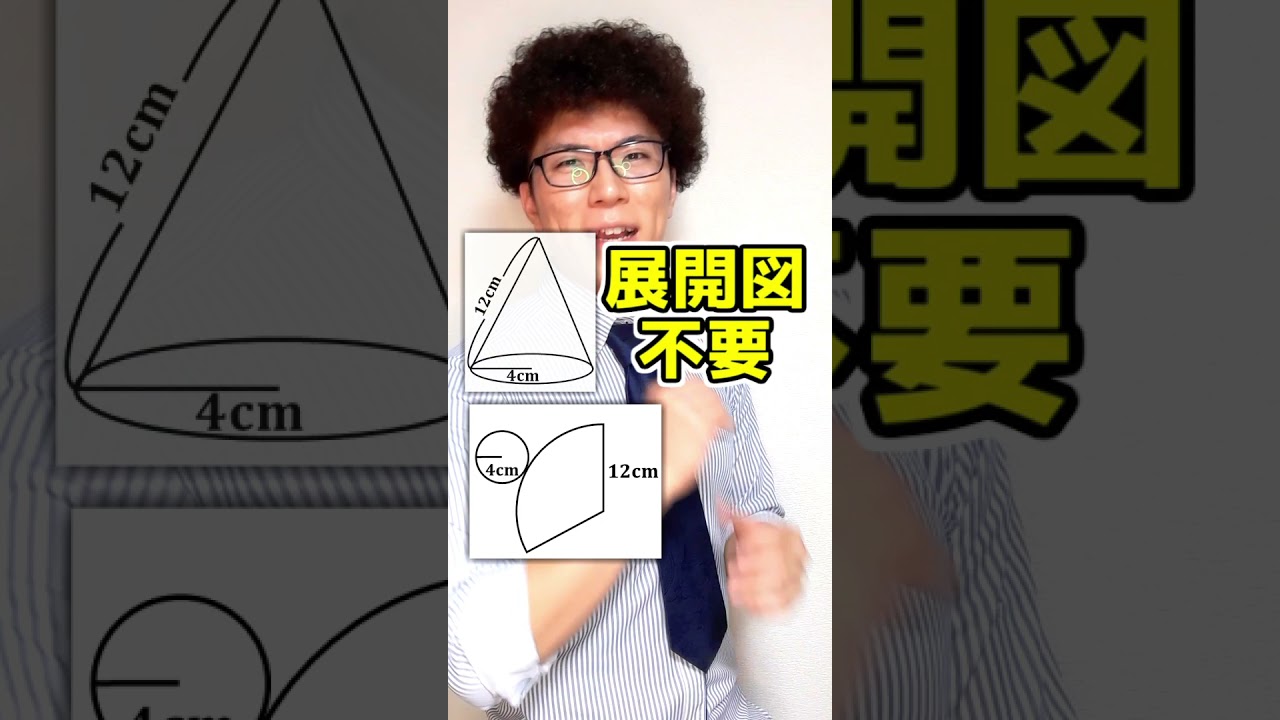
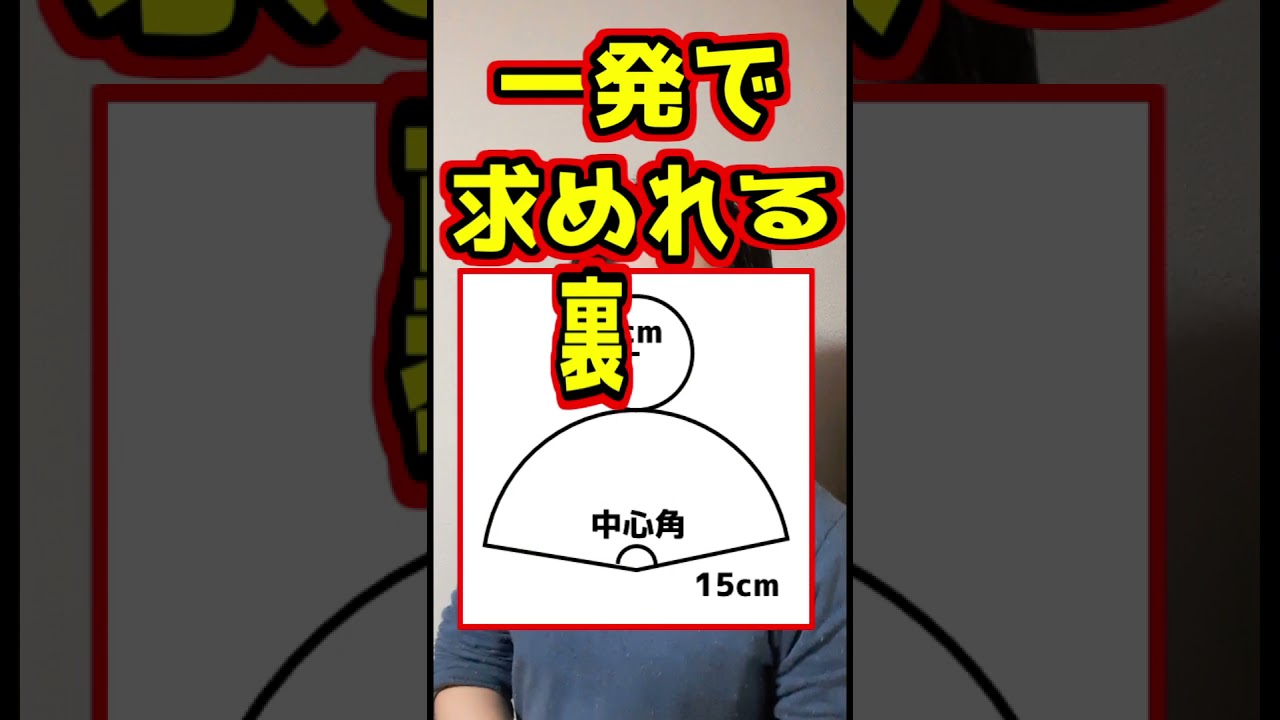
【中1数学】円錐の裏技集の証明 中心角・側面積・表面積についての動画です
この動画を見る
【中1数学】円錐の裏技集の証明 中心角・側面積・表面積についての動画です
【高校受験対策/数学】死守83

単元:
#数学(中学生)#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#平方根#2次方程式#比例・反比例#空間図形#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守83
①$-1-5$を計算しなさい。
②$(-3)^2+4×(-2)$を計算しなさい。
③$10xy^2÷ (-5y)×3x$を計算しなさい。
④$2x-y-\frac{5x+y}{3}$を計算しなさい。
⑤$(\sqrt{5}+3)(\sqrt{5}-2)$を計算しなさい。
⑥次の方程式を解きなさい。
$x^2=9x$
⑦$l=2\pi r$を$r$について解きなさい。
⑧正$n$角形の1つの内角が$140°$であるとき、$n$の値を求めなさい。
⑨$y$は$x$に比例し、$x=-3$のとき、$y=18$である。
$x=\frac{1}{2}$のときの$y$の値を求めなさい。
➉空間内の平面について述べた文として適切でないものを、次のア~エの中から1つ選びその記号を書きなさい。
ア 一直線上にある3点をふくむ平面は1つに決まる。
イ 交わる2直線をふくむ平面は1つに決まる。
ウ 平行な2直線をふくむ平面は1つに決まる。
エ 1つの直線とその直線上にない1点をふくむ平面は1つに決まる。
この動画を見る
高校受験対策・死守83
①$-1-5$を計算しなさい。
②$(-3)^2+4×(-2)$を計算しなさい。
③$10xy^2÷ (-5y)×3x$を計算しなさい。
④$2x-y-\frac{5x+y}{3}$を計算しなさい。
⑤$(\sqrt{5}+3)(\sqrt{5}-2)$を計算しなさい。
⑥次の方程式を解きなさい。
$x^2=9x$
⑦$l=2\pi r$を$r$について解きなさい。
⑧正$n$角形の1つの内角が$140°$であるとき、$n$の値を求めなさい。
⑨$y$は$x$に比例し、$x=-3$のとき、$y=18$である。
$x=\frac{1}{2}$のときの$y$の値を求めなさい。
➉空間内の平面について述べた文として適切でないものを、次のア~エの中から1つ選びその記号を書きなさい。
ア 一直線上にある3点をふくむ平面は1つに決まる。
イ 交わる2直線をふくむ平面は1つに決まる。
ウ 平行な2直線をふくむ平面は1つに決まる。
エ 1つの直線とその直線上にない1点をふくむ平面は1つに決まる。
空間上の2点間の距離 香川県
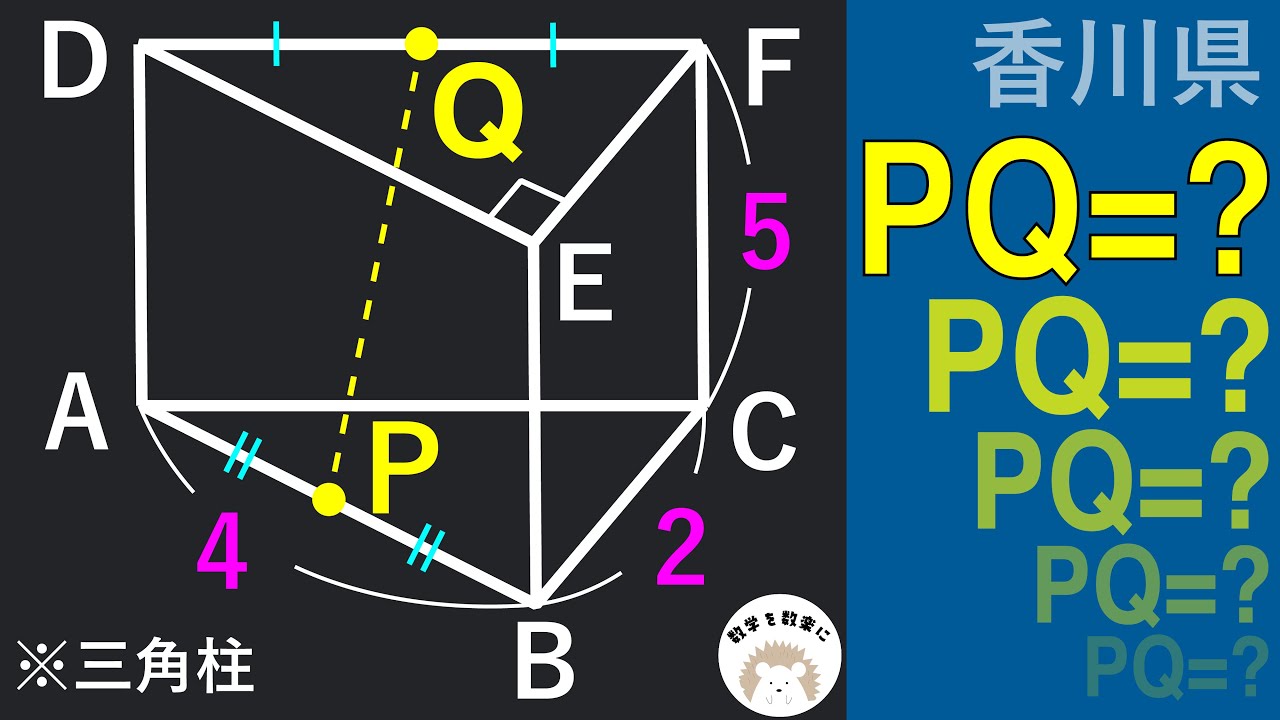
【高校受験対策/数学】死守-80

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#方程式#式の計算(単項式・多項式・式の四則計算)#連立方程式#2次方程式#空間図形#1次関数#確率#2次関数#文字と式#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守80
①$-3+(-4)×5$を計算しなさい。
②$4xy÷8x×6y$を計算しなさい。
③$\frac{4x-y}{2}-(2x-3y)$を計算しなさい。
④連立方程式を解きなさい。
$5x-4y=9$
$2x-3y=5$
③下の図で、$\angle x$の大きさを求めなさい。
④地球の直径は約$12700km$です。
有効数字が$1,2,7$であるとして、この距離を整数部分が1けたの数と、10の何乗かの積の形で表すと右のようになります。
アとイにあてはまる数を書きなさい。
⑦半径が$2cm$の球の体積と表面積を求めなさい。ただし円周率は$\pi$とする。
⑧赤玉3個と白玉2個が入っている袋があります。
この袋から玉を1個取り出して色を確認して、それを袋に戻してから、もう一度玉を1個取り出して色を確認します。
このとき、2回とも同じ色の玉が出る確率を求めなさい。
ただし、袋の中は見えないものとし、どの玉が出ることも同様に確からしいものとする。
⑨関数$y=ax^2$について、$x$の変域が$-2 \leqq x \leqq 3$のとき、$y$の変域は$-3b \leqq y \leqq 0$となりました。
このとき$a$の値を求めなさい。
この動画を見る
高校受験対策・死守80
①$-3+(-4)×5$を計算しなさい。
②$4xy÷8x×6y$を計算しなさい。
③$\frac{4x-y}{2}-(2x-3y)$を計算しなさい。
④連立方程式を解きなさい。
$5x-4y=9$
$2x-3y=5$
③下の図で、$\angle x$の大きさを求めなさい。
④地球の直径は約$12700km$です。
有効数字が$1,2,7$であるとして、この距離を整数部分が1けたの数と、10の何乗かの積の形で表すと右のようになります。
アとイにあてはまる数を書きなさい。
⑦半径が$2cm$の球の体積と表面積を求めなさい。ただし円周率は$\pi$とする。
⑧赤玉3個と白玉2個が入っている袋があります。
この袋から玉を1個取り出して色を確認して、それを袋に戻してから、もう一度玉を1個取り出して色を確認します。
このとき、2回とも同じ色の玉が出る確率を求めなさい。
ただし、袋の中は見えないものとし、どの玉が出ることも同様に確からしいものとする。
⑨関数$y=ax^2$について、$x$の変域が$-2 \leqq x \leqq 3$のとき、$y$の変域は$-3b \leqq y \leqq 0$となりました。
このとき$a$の値を求めなさい。
【高校受験対策/数学】死守76

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根#比例・反比例#空間図形#確率#文字と式#標本調査
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守76
①$2-(-5)$を計算しなさい。
②$4x-2x×\frac{1}{2}$を計算しなさい。
③$-6a^3b^2÷(-4ab)$を計算しなさい。
④$x=-2$、$y=3$のとき$(2x-y-6)+3(x+y+2)$の値を求めなさい。
③下の図の三角柱$ABC-DEF$において、 辺$AB$とねじれの位置にある辺をすべて答えなさい。
⑥$n$を自然数とする。$\sqrt{24n}$が自然数となるような$n$のうち、最も小さい数を求めなさい。
⑦2つの容器A、Bに牛乳が入っており、容器Bに入っている牛乳の量は、容器Aに入っている牛乳の量の2倍である。
容器Aに$140ml$の牛乳を加えたところ、 容器Aと容器Bの牛乳の量の比が$5:3$となった。
はじめに容器Aに入って いた牛乳の量は何$ml$であったか、求めなさい。
⑧あるクラスの女子生徒20人が体カテストで反復横とびを行い、
その記録を整理したところ、20人の記録の中央値は50回であった。
この20人の記録について、次のア~エのうち、必ず正しいといえるものを1つ選びなさい。
ア 20人の記録の合計は1000回である。
イ 20人のうち、記録が50回であった生徒が最も多い。
ウ 20人のうち、記録が60回以上であった生徒は1人もいない。
エ 20人のうち、記録が50回以上であった生徒が少なくとも10人いる。
この動画を見る
高校受験対策・死守76
①$2-(-5)$を計算しなさい。
②$4x-2x×\frac{1}{2}$を計算しなさい。
③$-6a^3b^2÷(-4ab)$を計算しなさい。
④$x=-2$、$y=3$のとき$(2x-y-6)+3(x+y+2)$の値を求めなさい。
③下の図の三角柱$ABC-DEF$において、 辺$AB$とねじれの位置にある辺をすべて答えなさい。
⑥$n$を自然数とする。$\sqrt{24n}$が自然数となるような$n$のうち、最も小さい数を求めなさい。
⑦2つの容器A、Bに牛乳が入っており、容器Bに入っている牛乳の量は、容器Aに入っている牛乳の量の2倍である。
容器Aに$140ml$の牛乳を加えたところ、 容器Aと容器Bの牛乳の量の比が$5:3$となった。
はじめに容器Aに入って いた牛乳の量は何$ml$であったか、求めなさい。
⑧あるクラスの女子生徒20人が体カテストで反復横とびを行い、
その記録を整理したところ、20人の記録の中央値は50回であった。
この20人の記録について、次のア~エのうち、必ず正しいといえるものを1つ選びなさい。
ア 20人の記録の合計は1000回である。
イ 20人のうち、記録が50回であった生徒が最も多い。
ウ 20人のうち、記録が60回以上であった生徒は1人もいない。
エ 20人のうち、記録が50回以上であった生徒が少なくとも10人いる。
【高校受験対策/数学】死守74

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根#空間図形#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守74
①$6-17$を計算しなさい。
②$6÷(-\frac{2}{3})$を計算しなさい。
③$2x+3y-(\frac{x+5y}{2})$を計算しなさい。
④$(\sqrt{3}+1)(\sqrt{3}-3)$を計算しなさい。
⑤ 下の図のような、平行四辺形$ABCD$がある。このとき$\angle x$の大きさを求めなさい。
⑥右の図のように、1辺の長さが$4cm$の立方体にちょうど入る大きさの球がある。
この球の体積を求めなさい。
⑦$am$のリボンから$bm$切り取ると、残りのリボンの長さは$2m$より短い。
この数量の関係を不等式で表しなさい。
⑧ある小学校で、工場の見学に行くために電車を利用することになった。
通常は児童15人と先生2人が支払う運賃の合計が9100円になる。
しかし、児童が10人以上いるとき児童の運賃のみが4割引きになる。
このため、児童15人と先生2人の運賃との合計は6100円になった。
このとき、割引きされた後の児童1人分の運賃を求めなさい。
この動画を見る
高校受験対策・死守74
①$6-17$を計算しなさい。
②$6÷(-\frac{2}{3})$を計算しなさい。
③$2x+3y-(\frac{x+5y}{2})$を計算しなさい。
④$(\sqrt{3}+1)(\sqrt{3}-3)$を計算しなさい。
⑤ 下の図のような、平行四辺形$ABCD$がある。このとき$\angle x$の大きさを求めなさい。
⑥右の図のように、1辺の長さが$4cm$の立方体にちょうど入る大きさの球がある。
この球の体積を求めなさい。
⑦$am$のリボンから$bm$切り取ると、残りのリボンの長さは$2m$より短い。
この数量の関係を不等式で表しなさい。
⑧ある小学校で、工場の見学に行くために電車を利用することになった。
通常は児童15人と先生2人が支払う運賃の合計が9100円になる。
しかし、児童が10人以上いるとき児童の運賃のみが4割引きになる。
このため、児童15人と先生2人の運賃との合計は6100円になった。
このとき、割引きされた後の児童1人分の運賃を求めなさい。
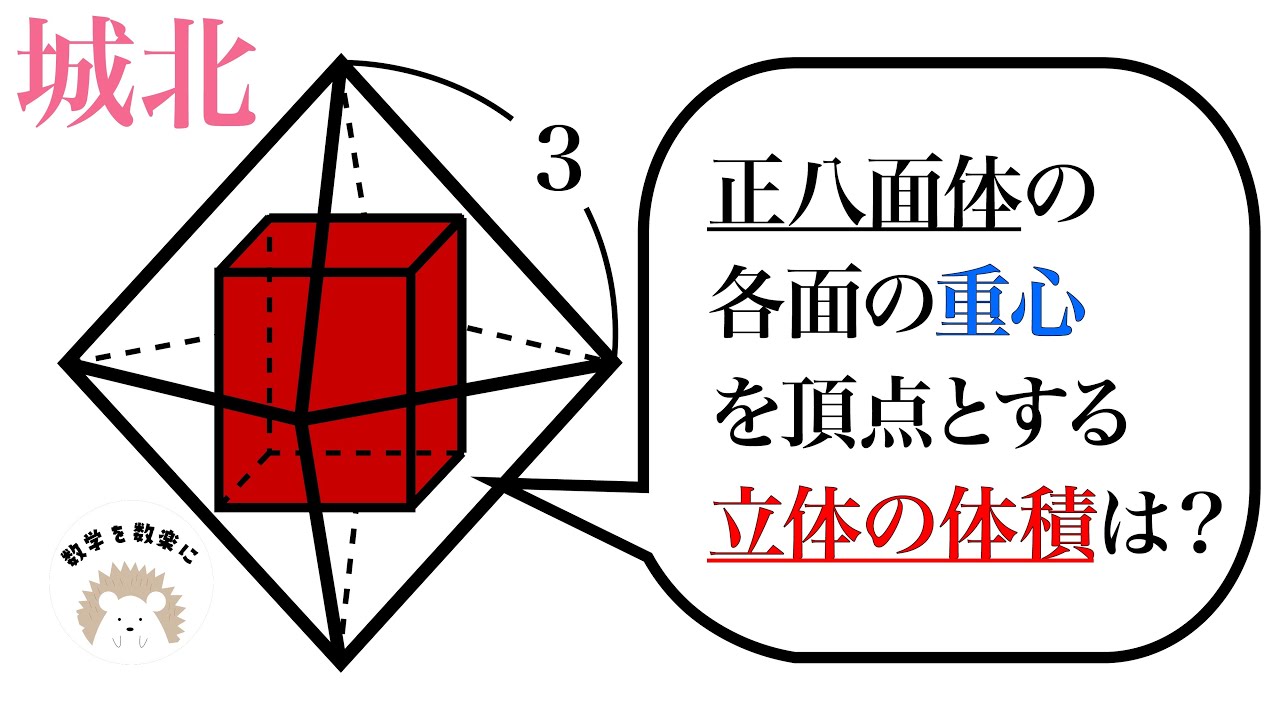
立体図形は再生されないってわかっているけど、受験生が1人でも必要とするのなら動画を撮らないといけないとは思ってはいるが、それでも再生されないと悲しい気持ちにはなるが、でも受験生のためと思って動画作った
単元:
#数学(中学生)#中1数学#空間図形#立体図形#立体図形その他#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
正八面体の各面を重心を頂点とする立体の体積は?
*図は動画内参照
城北高等学校
この動画を見る
正八面体の各面を重心を頂点とする立体の体積は?
*図は動画内参照
城北高等学校
【高校受験対策/数学】死守72

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根#2次方程式#空間図形#平行と合同#確率#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守72
①$2-6$を計算しなさい。
➁$-3×(-2^2)$を計算しなさい。
③$\frac{2a+b}{ 3 }+\frac{a-b}{ 2 }$を計算しなさい。
④$xy^2×x^2÷xy$を計算しなさい。
⑤$\frac{6}{\sqrt{3}}+\sqrt{15}×\sqrt{5}$を計算しなさい。
⑥2次方程式$x^2+7x-18=0$ を解きなさい。
⑦$a=\sqrt{5}+3$のとき、$a^2-6a+9$の値を求めなさい。
⑧500円、100円、50円の硬貨が1枚ずつある。
この3枚を同時に1回投げるとき、表が出た硬貨の合計金額が500円以下になる確率を求めなさい。
ただし3枚の硬貨のそれぞれについて、表と裏の出方は同様に確からしいとする。
⑨右の図は底面の半径が$3cm$、側面になるおうぎ形の半径が$5cm$の円錐の展開図である。
これを組み立ててできる円錐の体積を求めなさい。
この動画を見る
高校受験対策・死守72
①$2-6$を計算しなさい。
➁$-3×(-2^2)$を計算しなさい。
③$\frac{2a+b}{ 3 }+\frac{a-b}{ 2 }$を計算しなさい。
④$xy^2×x^2÷xy$を計算しなさい。
⑤$\frac{6}{\sqrt{3}}+\sqrt{15}×\sqrt{5}$を計算しなさい。
⑥2次方程式$x^2+7x-18=0$ を解きなさい。
⑦$a=\sqrt{5}+3$のとき、$a^2-6a+9$の値を求めなさい。
⑧500円、100円、50円の硬貨が1枚ずつある。
この3枚を同時に1回投げるとき、表が出た硬貨の合計金額が500円以下になる確率を求めなさい。
ただし3枚の硬貨のそれぞれについて、表と裏の出方は同様に確からしいとする。
⑨右の図は底面の半径が$3cm$、側面になるおうぎ形の半径が$5cm$の円錐の展開図である。
これを組み立ててできる円錐の体積を求めなさい。
浦和学院のラスボス
単元:
#数学(中学生)#中1数学#空間図形#立体図形#体積・表面積・回転体・水量・変化のグラフ#立体図形その他#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
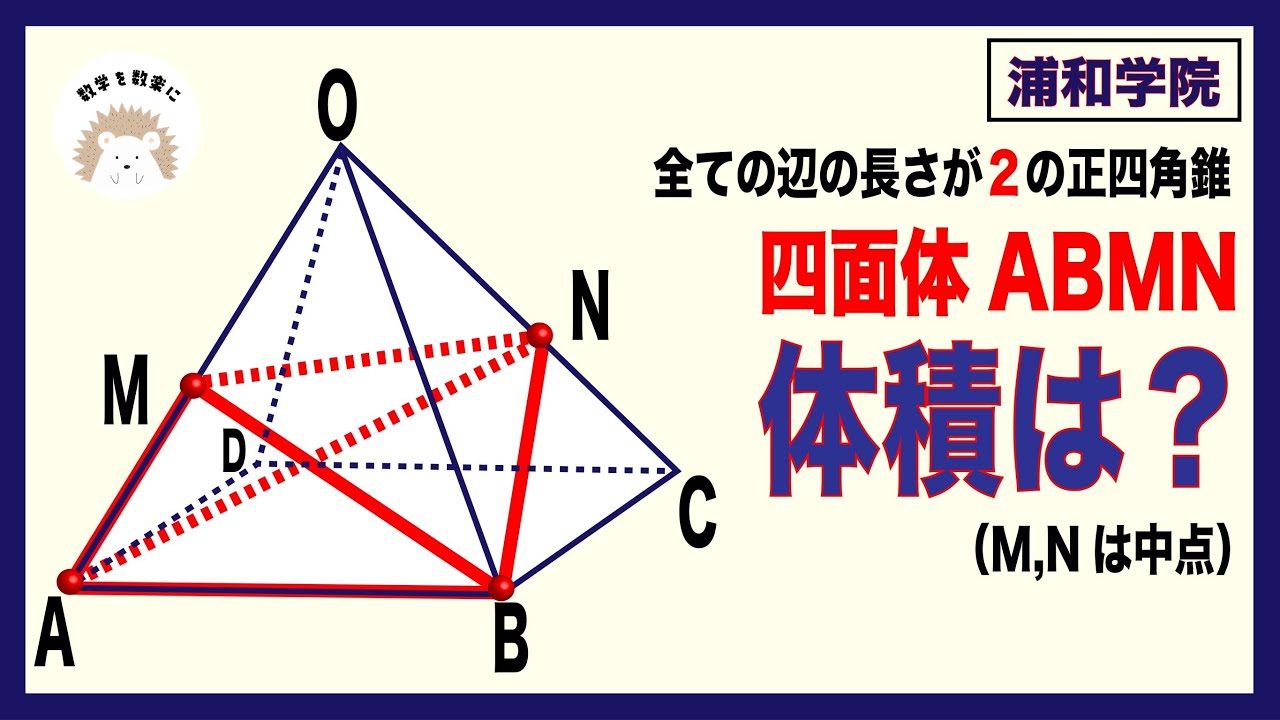
すべての辺の長さが2の正四角錐
四面体ABMNの体積=?
浦和学院高等学校
この動画を見る
すべての辺の長さが2の正四角錐
四面体ABMNの体積=?
浦和学院高等学校
【裏技】円錐の表面積を一瞬で出す

単元:
#算数(中学受験)#数学(中学生)#中1数学#空間図形#立体図形#立体図形その他
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
円錐の表面積を一瞬で計算するための解説動画です
この動画を見る
円錐の表面積を一瞬で計算するための解説動画です
【3分で数学の知識が1 up!】図形:佐賀県公立高等学校~全国入試問題解法
単元:
#数学(中学生)#空間図形#平面図形#高校入試過去問(数学)#佐賀県立高校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 佐賀県の公立高校
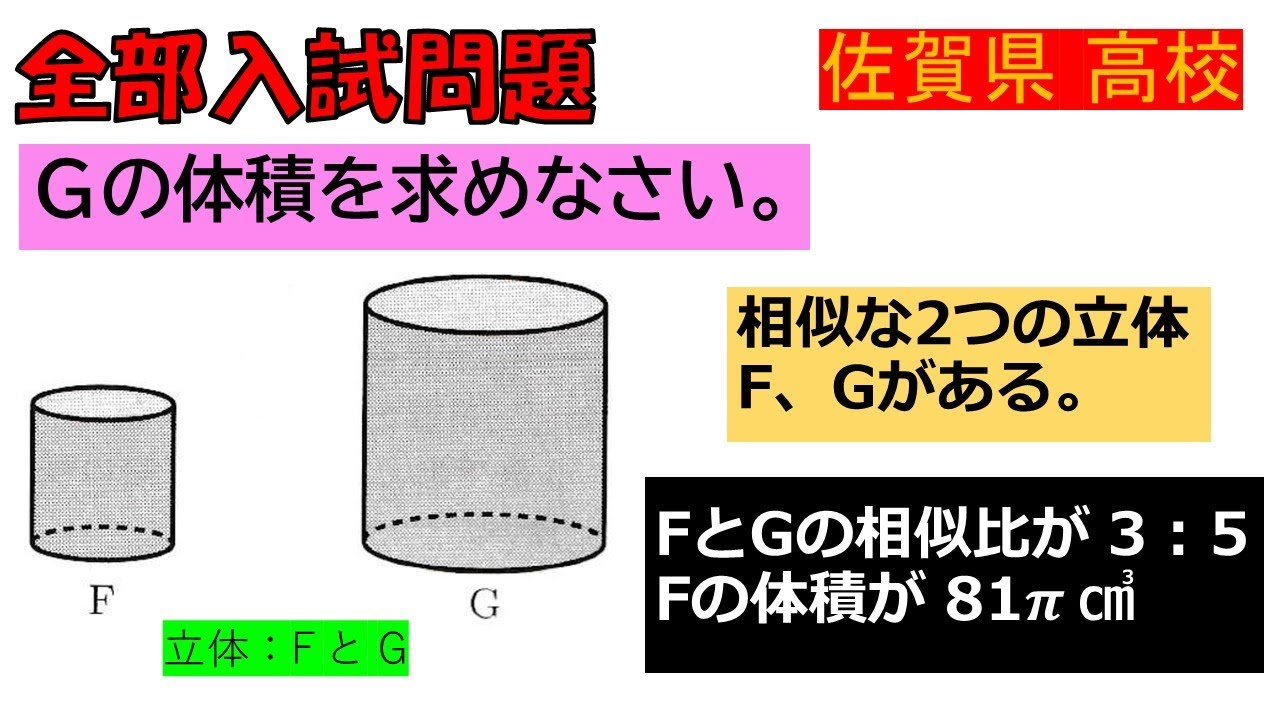
$G$の体積を求めなさい。
相似な2つの立体 $F$、$G$がある。
$F$と$G$の相似比が$3:5$
Fの体積が $81πcm^3$
※図は動画内参照
この動画を見る
入試問題 佐賀県の公立高校
$G$の体積を求めなさい。
相似な2つの立体 $F$、$G$がある。
$F$と$G$の相似比が$3:5$
Fの体積が $81πcm^3$
※図は動画内参照
【良問で身に付く数学の応用力!】空間図形:茨城県公立高等学校~全国入試問題解法【とんとん♪】
単元:
#数学(中学生)#空間図形#高校入試過去問(数学)#茨城県公立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 茨城県の公立高等学校
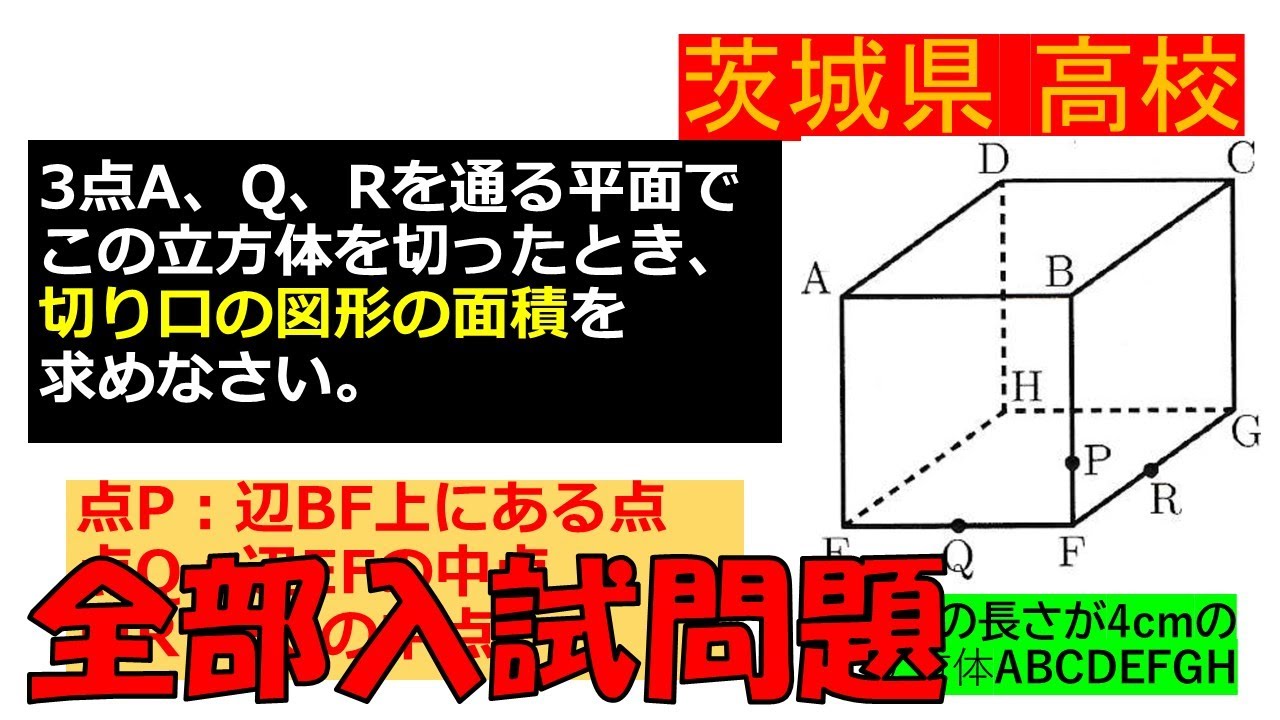
3点A、Q、Rを通る平面で この立方体を切ったとき、
切り口の図形の面積を求めなさい。
点P:辺BF上にある点
点Q:辺EFの中点
点R: FGの中点
※図は動画内参照
この動画を見る
入試問題 茨城県の公立高等学校
3点A、Q、Rを通る平面で この立方体を切ったとき、
切り口の図形の面積を求めなさい。
点P:辺BF上にある点
点Q:辺EFの中点
点R: FGの中点
※図は動画内参照
【5分で完全理解!】空間図形:山形県公立高等学校~全国入試問題解法
単元:
#数学(中学生)#空間図形#山形県公立高等学校#山形県立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 山形県の公立高等学校
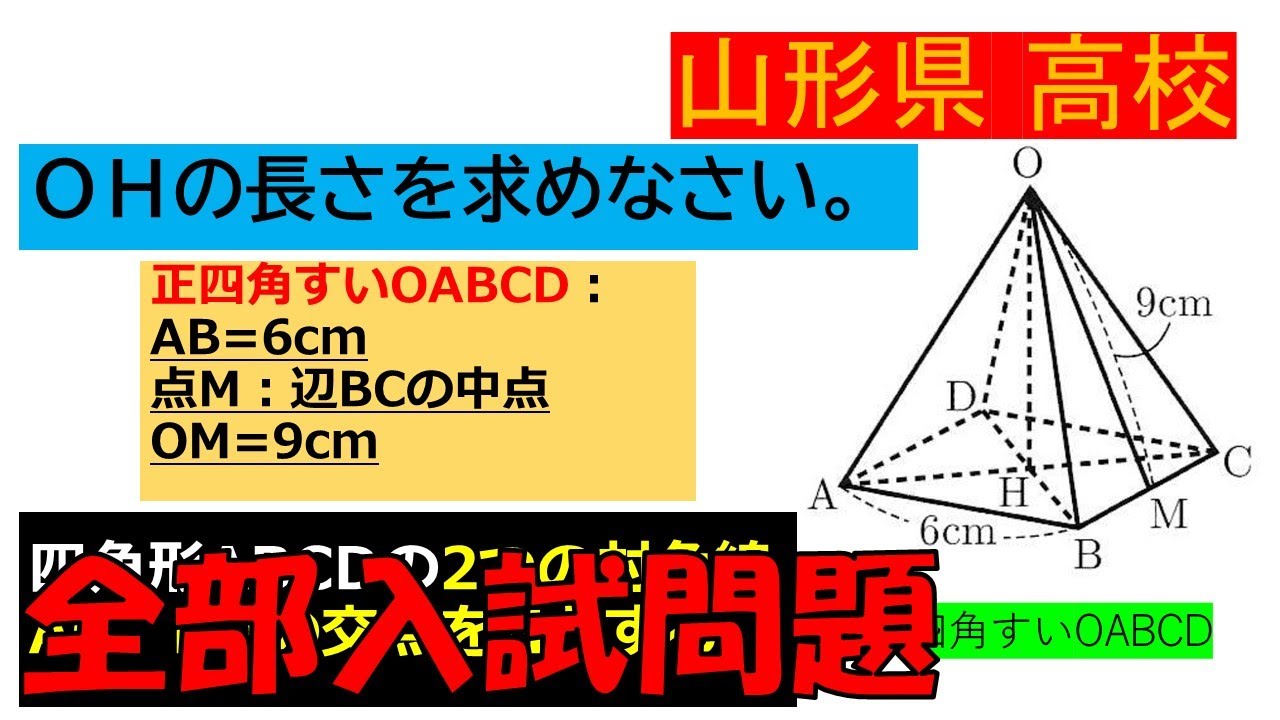
$OH$の長さを求めなさい。
正四角すい$OABCD :$
$AB=6cm$
点$M$:辺$BC$の中点
$OM=9cm$
四角形$ABCD$の$2$つの対角線 $AC$、$BD$の交点を$H$とする。
※図は動画内参照
この動画を見る
入試問題 山形県の公立高等学校
$OH$の長さを求めなさい。
正四角すい$OABCD :$
$AB=6cm$
点$M$:辺$BC$の中点
$OM=9cm$
四角形$ABCD$の$2$つの対角線 $AC$、$BD$の交点を$H$とする。
※図は動画内参照
【TikTok】円柱の表面積の裏技

【TikTok】円錐の中心角の裏技
立方体の角 A

【5分で完答 !?】空間図形:函館ラ・サール高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#空間図形#高校入試過去問(数学)#函館ラ・サール高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
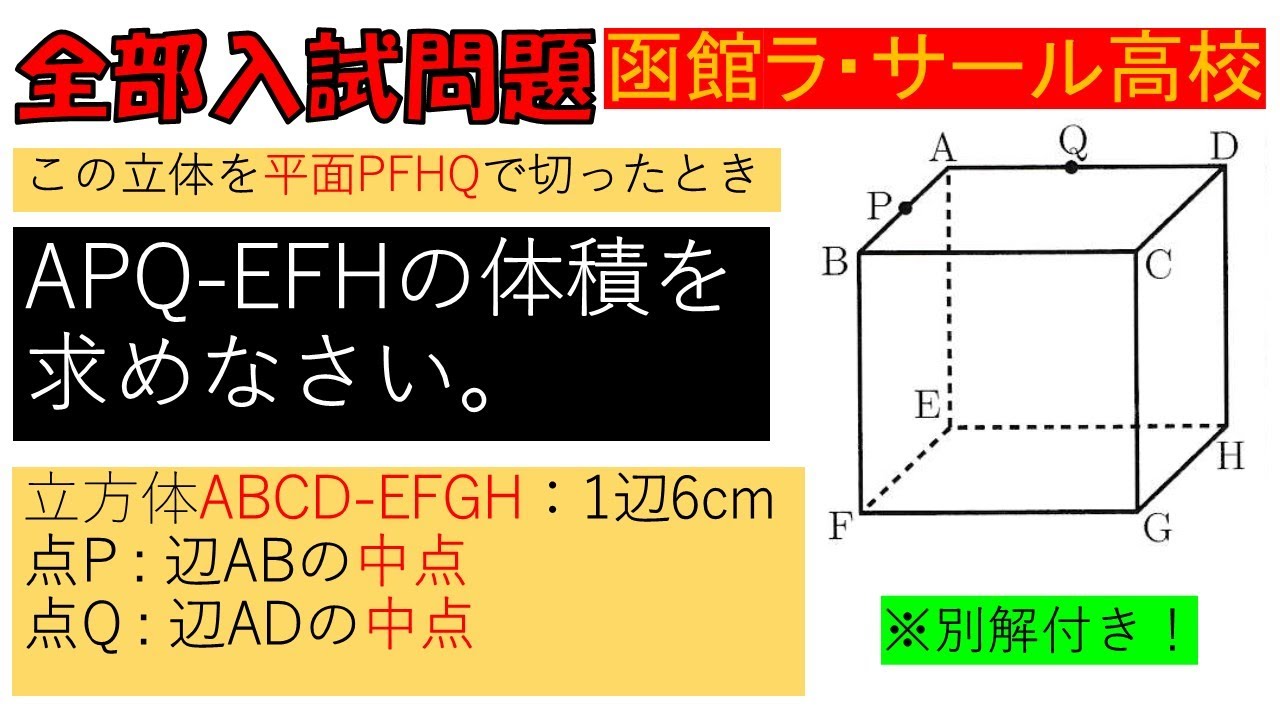
入試問題 函館ラ・サール高等学校
この立体を平面$PFHQ$で切ったとき
$APQ-EFH$の体積を 求めなさい。
立方体$ABCD-EFGH$:1辺6cm
点$P$:辺$AB$の中点
点$Q$:辺$AD$の中点
※図は動画内参照
この動画を見る
入試問題 函館ラ・サール高等学校
この立体を平面$PFHQ$で切ったとき
$APQ-EFH$の体積を 求めなさい。
立方体$ABCD-EFGH$:1辺6cm
点$P$:辺$AB$の中点
点$Q$:辺$AD$の中点
※図は動画内参照
【中学数学】中学数学で球の体積と表面積の公式の証明

【中学数学】球の公式まとめ~半球とかの裏技も紹介~【中1数学】

