 連立方程式
連立方程式
 連立方程式
連立方程式
【コロンブスの卵!】2元2次連立方程式:中学からの連立方程式~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
x + y = 3 \\
x^2+y^2=5
\end{array}
\right.
\end{eqnarray}$
を解け.
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
x + y = 3 \\
x^2+y^2=5
\end{array}
\right.
\end{eqnarray}$
を解け.
気付けば爽快!!ルートの入った連立方程式
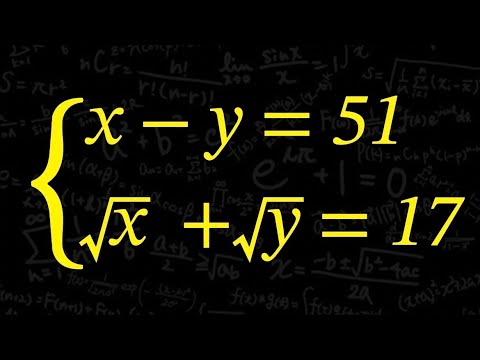
単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
数学を数楽に
問題文全文(内容文):
\begin{eqnarray}
\left\{
\begin{array}{l}
x - y = 51 \\
\sqrt x + \sqrt y = 17
\end{array}
\right.
\end{eqnarray}
この動画を見る
\begin{eqnarray}
\left\{
\begin{array}{l}
x - y = 51 \\
\sqrt x + \sqrt y = 17
\end{array}
\right.
\end{eqnarray}
【これも連立方程式?】3元1次連立方程式③:中学からの連立方程式~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
連立方程式
$ x+y=3...①$
$ y+z=5...②$
$ z+x=4...③$ を解け.
この動画を見る
連立方程式
$ x+y=3...①$
$ y+z=5...②$
$ z+x=4...③$ を解け.
2次の連立方程式 明大明治2023

単元:
#数学(中学生)#連立方程式#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
\begin{eqnarray}
\left\{
\begin{array}{l}
x^2 -4y^2 -10x +25 = 0 \\
x^2 + x -6 -2xy + 4y = 0
\end{array}
\right.
\end{eqnarray}
(x,y)の組をすべて求めよ。
2023明治大学付属明治高等学校(改)
この動画を見る
\begin{eqnarray}
\left\{
\begin{array}{l}
x^2 -4y^2 -10x +25 = 0 \\
x^2 + x -6 -2xy + 4y = 0
\end{array}
\right.
\end{eqnarray}
(x,y)の組をすべて求めよ。
2023明治大学付属明治高等学校(改)
【中学数学】数学用語チェック絵本 act2 vol.2連立方程式

【かなり便利!】3元1次連立方程式:中学からの連立方程式~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ x+2y+3z=14 $
$ 2x+y+z=7 $
$ x+3y+z=10 $ を解け.
この動画を見る
$ x+2y+3z=14 $
$ 2x+y+z=7 $
$ x+3y+z=10 $ を解け.
工夫して解こう!!連立方程式 共立女子第二

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
y - (3x - 1) = 0 \\
2(3x - 1) + 7y = 18
\end{array}
\right.
\end{eqnarray}
共立女子第二高等学校
この動画を見る
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
y - (3x - 1) = 0 \\
2(3x - 1) + 7y = 18
\end{array}
\right.
\end{eqnarray}
共立女子第二高等学校
【方法を徹底するために】2元1次連立方程式:中学からの連立方程式~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の連立方程式を解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x+2y=7 \\
2x+y=4
\end{array}
\right.
\end{eqnarray}$
この動画を見る
次の連立方程式を解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x+2y=7 \\
2x+y=4
\end{array}
\right.
\end{eqnarray}$
ちょっと変わった連立方程式

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
数学を数楽に
問題文全文(内容文):
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
\frac{1}{x+y} -x = 2 \\
\frac{1}{x+y} + y =4
\end{array}
\right.
\end{eqnarray}
2023中央大学付属高等学校
この動画を見る
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
\frac{1}{x+y} -x = 2 \\
\frac{1}{x+y} + y =4
\end{array}
\right.
\end{eqnarray}
2023中央大学付属高等学校
【ひと工夫で簡単に解ける…!】連立方程式:東京工業大学附属科学技術高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の連立方程式を解きなさい.
$\begin{eqnarray}
\left\{
\begin{array}{l}
1001x+999y=1007 \\
999x+1001y=993
\end{array}
\right.
\end{eqnarray}$
東工大科技高校過去問
この動画を見る
次の連立方程式を解きなさい.
$\begin{eqnarray}
\left\{
\begin{array}{l}
1001x+999y=1007 \\
999x+1001y=993
\end{array}
\right.
\end{eqnarray}$
東工大科技高校過去問
式の値 ラ・サール 2023
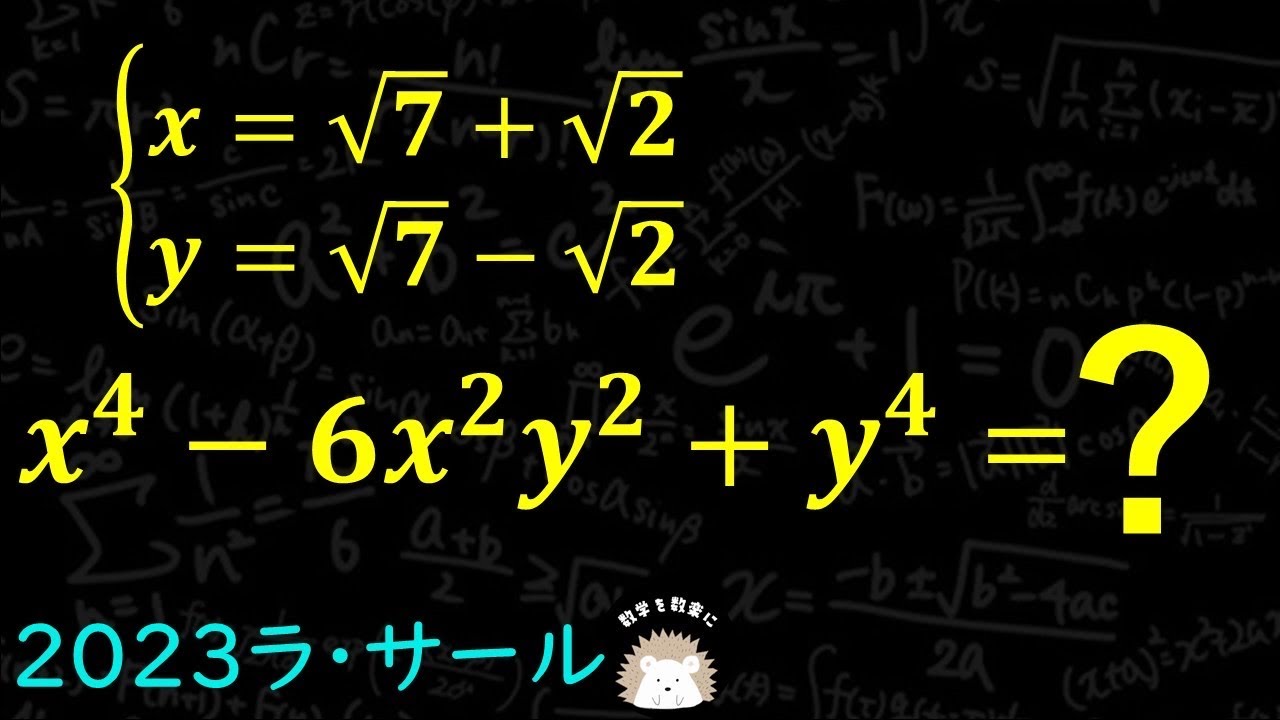
単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#連立方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
\begin{eqnarray}
\left\{
\begin{array}{l}
x = \sqrt 7 + \sqrt 2 \\
y = \sqrt 7 - \sqrt 2
\end{array}
\right.
\end{eqnarray}
$x^4 - 6x^2y^2 +y^4 = ?$
2023ラ・サール学園
この動画を見る
\begin{eqnarray}
\left\{
\begin{array}{l}
x = \sqrt 7 + \sqrt 2 \\
y = \sqrt 7 - \sqrt 2
\end{array}
\right.
\end{eqnarray}
$x^4 - 6x^2y^2 +y^4 = ?$
2023ラ・サール学園
【分かっていても手間はかかる】連立方程式:東大寺学園高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
x,yについての連立方程式
$ \begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{3}{3x+4y}-\dfrac{4}{4x-3y}=10 \\
\dfrac{4}{3x+4y}+\dfrac{3}{4x-3y}=5
\end{array}
\right.
\end{eqnarray}$
を解け.
東大寺学園高校過去問
この動画を見る
x,yについての連立方程式
$ \begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{3}{3x+4y}-\dfrac{4}{4x-3y}=10 \\
\dfrac{4}{3x+4y}+\dfrac{3}{4x-3y}=5
\end{array}
\right.
\end{eqnarray}$
を解け.
東大寺学園高校過去問
高等学校入学試験予想問題:鳥取県公立高等学校~全部入試問題
単元:
#数学(中学生)#中1数学#中2数学#中3数学#方程式#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#2次方程式#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#平面図形#三角形と四角形
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \boxed{1}$
(1)$ 10xy^2\div(-5y)\times 3x$
(2)$ 2x-y-\dfrac{5x+y}{3}$
(3)$ \begin{eqnarray}
\left\{
\begin{array}{l}
2x-3y=2 \\
x+2y=8
\end{array}
\right.
\end{eqnarray}$
$ x=?,y=? $
(4)$ 2x^2+3x-1=0 $
$ x=? $
$ \boxed{2}$
$\dfrac{3a-5}{2}=b ・・・・①$
$ 3a-5=2b・・・・②$
$ 3a=2b+5・・・・③$
$ a=\dfrac{2b+5}{3}・・・・④$
「等式の両辺に同じ数を足しても等式が成り立つ」に導く式変形か?
$\boxed{3}$
$ AD\parallel BC,BC=2AD,AD \lt CD,\angle ADC=90°$
$ 台形ABCD,\angle CAE=90°$である.
①$ \triangle ACD \backsim \triangle ECA $の証明をせよ.
②(1)$ DE=? $
(2)$ \triangle EHD=?$
(3)$ FH:GH=?$
この動画を見る
$ \boxed{1}$
(1)$ 10xy^2\div(-5y)\times 3x$
(2)$ 2x-y-\dfrac{5x+y}{3}$
(3)$ \begin{eqnarray}
\left\{
\begin{array}{l}
2x-3y=2 \\
x+2y=8
\end{array}
\right.
\end{eqnarray}$
$ x=?,y=? $
(4)$ 2x^2+3x-1=0 $
$ x=? $
$ \boxed{2}$
$\dfrac{3a-5}{2}=b ・・・・①$
$ 3a-5=2b・・・・②$
$ 3a=2b+5・・・・③$
$ a=\dfrac{2b+5}{3}・・・・④$
「等式の両辺に同じ数を足しても等式が成り立つ」に導く式変形か?
$\boxed{3}$
$ AD\parallel BC,BC=2AD,AD \lt CD,\angle ADC=90°$
$ 台形ABCD,\angle CAE=90°$である.
①$ \triangle ACD \backsim \triangle ECA $の証明をせよ.
②(1)$ DE=? $
(2)$ \triangle EHD=?$
(3)$ FH:GH=?$
2023高校入試数学解説63問目 分母が文字の連立方程式 城北高校
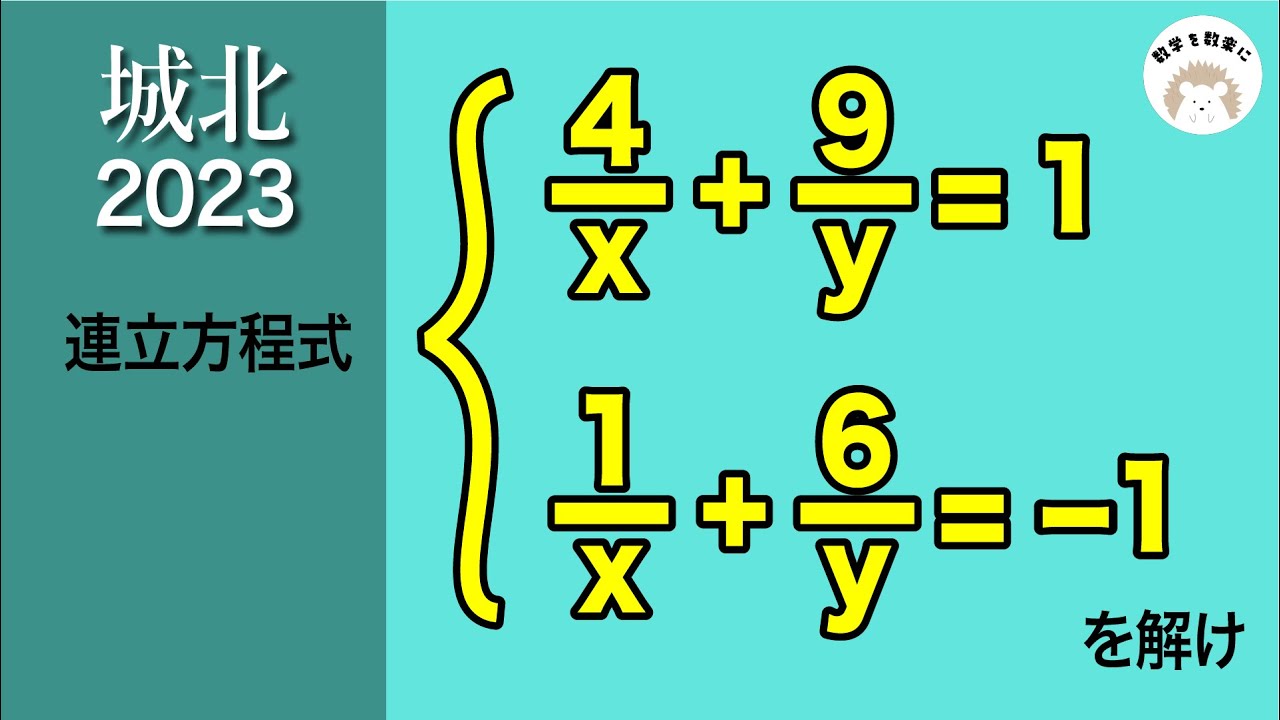
単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
\frac{4}{x} + \frac{9}{y} = 1 \\
\frac{1}{x} + \frac{6}{y} = -1
\end{array}
\right.
\end{eqnarray}
2023城北学園高等学校
この動画を見る
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
\frac{4}{x} + \frac{9}{y} = 1 \\
\frac{1}{x} + \frac{6}{y} = -1
\end{array}
\right.
\end{eqnarray}
2023城北学園高等学校
連立方程式の応用問題を難なく解く動画~全国入試問題解法 #shorts #数学 #高校受験 #過去問

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \begin{eqnarray}
\left\{
\begin{array}{l}
3x+2y=14 \\
ax+by=3
\end{array}
\right.
\end{eqnarray}$
$ \begin{eqnarray}
\left\{
\begin{array}{l}
bx-ay=-5 \\
4x-5y=11
\end{array}
\right.
\end{eqnarray}$
の解が一致するとき,$ a,b $の値をそれぞれ求めなさい.
巣鴨高校過去問
この動画を見る
$ \begin{eqnarray}
\left\{
\begin{array}{l}
3x+2y=14 \\
ax+by=3
\end{array}
\right.
\end{eqnarray}$
$ \begin{eqnarray}
\left\{
\begin{array}{l}
bx-ay=-5 \\
4x-5y=11
\end{array}
\right.
\end{eqnarray}$
の解が一致するとき,$ a,b $の値をそれぞれ求めなさい.
巣鴨高校過去問
佐賀県立高校入試2021年2⃣連立方程式
単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#佐賀県立高校
指導講師:
重吉
問題文全文(内容文):
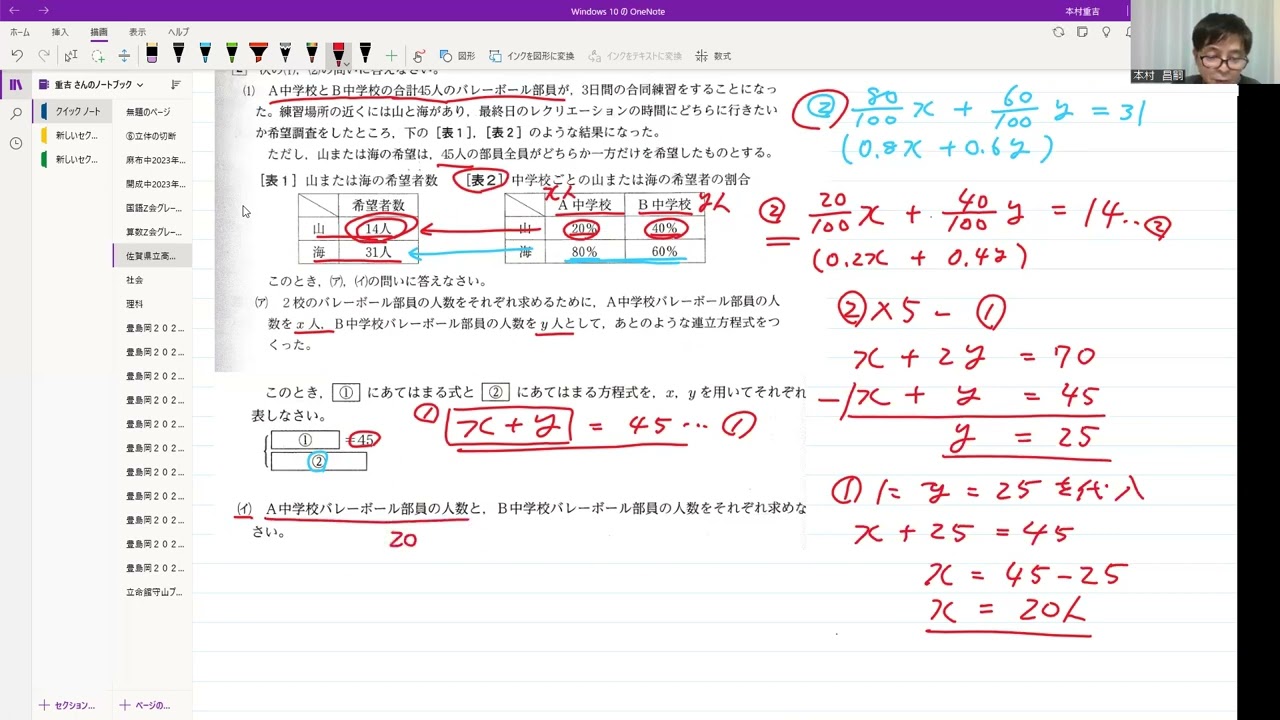
佐賀県立高校入試2021年2⃣連立方程式
-----------------
A中学校とB中学校の合計45人のバレーボール部員が、3日間の合同練習をすることになった。
練習場所の近くには山と海があり、最終日のレクリエーションの時間にどちらに行きたいか希望調査をしたところ、動画内の表のような結果になった。
ただし、山または海の希望は、45人の部員全員がどちらか一方だけを希望したものとする。
(ア)
2校のバレーボール部員の人数をそれぞれ求めるために、A中学校バレーボール部員の人数を$x$人、B中学校バレーボール部員の人数を$y$人として、あとのような連立方程式をつくった。
このとき、①にあてはまる式と②にあてはまる方程式を、$x,y$を用いてそれぞれ表しなさい。
$\begin{eqnarray}
\left\{
\begin{array}{l}
① = 45 \\
②
\end{array}
\right.
\end{eqnarray}$
(イ)
A中学校バレーボール部員の人数と、B中学校バレーボール部員の人数をそれぞれ求めなさい。
この動画を見る
佐賀県立高校入試2021年2⃣連立方程式
-----------------
A中学校とB中学校の合計45人のバレーボール部員が、3日間の合同練習をすることになった。
練習場所の近くには山と海があり、最終日のレクリエーションの時間にどちらに行きたいか希望調査をしたところ、動画内の表のような結果になった。
ただし、山または海の希望は、45人の部員全員がどちらか一方だけを希望したものとする。
(ア)
2校のバレーボール部員の人数をそれぞれ求めるために、A中学校バレーボール部員の人数を$x$人、B中学校バレーボール部員の人数を$y$人として、あとのような連立方程式をつくった。
このとき、①にあてはまる式と②にあてはまる方程式を、$x,y$を用いてそれぞれ表しなさい。
$\begin{eqnarray}
\left\{
\begin{array}{l}
① = 45 \\
②
\end{array}
\right.
\end{eqnarray}$
(イ)
A中学校バレーボール部員の人数と、B中学校バレーボール部員の人数をそれぞれ求めなさい。
高等学校入学試験予想問題:明治学院高等学校~全部入試問題
単元:
#数学(中学生)#中1数学#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#空間図形#1次関数#2次関数#円#平面図形
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \boxed{1}$
(1)$ 9xy^2\div \left(-\dfrac{3}{2}xy\right)^3\times \dfrac{3}{4}x^4y$を計算せよ.
(2)$ \begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{3}{4}x+\dfrac{y}{2}=1 \\
2x-3y=1
\end{array}
\right.
\end{eqnarray}$ を解け.
(3)図の円$ O $において,$ \angle x $の大きさを求めよ.
$ \boxed{2}$
放物線$ y=x^2 $上に5点$ A,B,C,D,E $があり,それぞれのx座標は,$ a,-5,-2,2,4 $である.(ただし,$ a\lt -5 $)
さらに,線分$ CE $の中点$ F $は直線$ AD $上にあるとき,あとの問いに答えよ.
(1)点$ F $の座標を求めよ.
(2)$ a $の値を求めよ.
(3)$ \triangle ABD $と$ \triangle AED $の面積の比の最も簡単な整数の比で表せ.
$ \boxed{3}$
図のように,直方体$ ABCD-EFGH $があり,$ AB=3,AD=6,AE=2$である.
点$G$からこの直方体の対角線$CE$に垂線を引き,その交点を$P$とする.
このとき,次の各問いに答えよ.
(1)線分$ GP $の長さを求めよ.
(2)三角錐$ P-GEF$の体積を求めよ.
(3)辺$ AD $の中点を$Q$とし,辺$FG$上に$FR=2$となる点$R$をとる.
3点$B,Q,R $を通る平面と線分$EG$の交点を$S$とするとき,三角錐$P-GSR $の体積を求めよ.
この動画を見る
$ \boxed{1}$
(1)$ 9xy^2\div \left(-\dfrac{3}{2}xy\right)^3\times \dfrac{3}{4}x^4y$を計算せよ.
(2)$ \begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{3}{4}x+\dfrac{y}{2}=1 \\
2x-3y=1
\end{array}
\right.
\end{eqnarray}$ を解け.
(3)図の円$ O $において,$ \angle x $の大きさを求めよ.
$ \boxed{2}$
放物線$ y=x^2 $上に5点$ A,B,C,D,E $があり,それぞれのx座標は,$ a,-5,-2,2,4 $である.(ただし,$ a\lt -5 $)
さらに,線分$ CE $の中点$ F $は直線$ AD $上にあるとき,あとの問いに答えよ.
(1)点$ F $の座標を求めよ.
(2)$ a $の値を求めよ.
(3)$ \triangle ABD $と$ \triangle AED $の面積の比の最も簡単な整数の比で表せ.
$ \boxed{3}$
図のように,直方体$ ABCD-EFGH $があり,$ AB=3,AD=6,AE=2$である.
点$G$からこの直方体の対角線$CE$に垂線を引き,その交点を$P$とする.
このとき,次の各問いに答えよ.
(1)線分$ GP $の長さを求めよ.
(2)三角錐$ P-GEF$の体積を求めよ.
(3)辺$ AD $の中点を$Q$とし,辺$FG$上に$FR=2$となる点$R$をとる.
3点$B,Q,R $を通る平面と線分$EG$の交点を$S$とするとき,三角錐$P-GSR $の体積を求めよ.
高等学校入学試験予想問題:近畿大学附属高等学校~全部入試問題

単元:
#数学(中学生)#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#1次関数#2次関数#円
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \boxed{1}$
(1)$ \dfrac{4x-y}{9}-\dfrac{5x-4y}{12}$を計算せよ.
(2)$ xy-3y-3x+9 $を因数分解せよ.
(3)
$ \begin{eqnarray}
\left\{
\begin{array}{l}
2x-y=1 \\
2ax+by=16
\end{array}
\right.
\end{eqnarray}$
$ \begin{eqnarray}
\left\{
\begin{array}{l}
ax+2y=8 \\
-3x+2y=3
\end{array}
\right.
\end{eqnarray}$
が同じ解をもつとき,$ a,b $の値を求めよ.
$ \boxed{2}$
図のように,関数$ y=x^2 $のグラフと直線$ y=-2x+8 $との交点を$ A,B,$直線$AB $の中点を$M$とするとき,次の問いに答えよ.
ただし,点$A$のx座標は負とする.
(1)点$A$の座標を求めよ.
(2)直線$OM$の式を求めよ.
(3)$ \triangle OCM $をx軸のまわりに1回転させてできる立体の体積を求めよ.
$ \boxed{3}$
図のように,点$O$を中心とし,線分$AB$を直径とする半径6の円があり,点$C$は線分$OB$の中点である,2点$D,E$は直径$AB$に対して同じ側の円周上にあり,$AB$と$CD$は直角,$AB$と$OE$は直角となっている.
また,線分$AD$と線分$OE$の交点を点$F$とする.
このとき,次の問いに答えよ.
(1)$CD$の長さを求めよ.
(2)$ \triangle AEF$の面積を求めよ.
(3)$ AF:AD$の比を求めよ.また,$\triangle DEF $の面積を求めよ.
この動画を見る
$ \boxed{1}$
(1)$ \dfrac{4x-y}{9}-\dfrac{5x-4y}{12}$を計算せよ.
(2)$ xy-3y-3x+9 $を因数分解せよ.
(3)
$ \begin{eqnarray}
\left\{
\begin{array}{l}
2x-y=1 \\
2ax+by=16
\end{array}
\right.
\end{eqnarray}$
$ \begin{eqnarray}
\left\{
\begin{array}{l}
ax+2y=8 \\
-3x+2y=3
\end{array}
\right.
\end{eqnarray}$
が同じ解をもつとき,$ a,b $の値を求めよ.
$ \boxed{2}$
図のように,関数$ y=x^2 $のグラフと直線$ y=-2x+8 $との交点を$ A,B,$直線$AB $の中点を$M$とするとき,次の問いに答えよ.
ただし,点$A$のx座標は負とする.
(1)点$A$の座標を求めよ.
(2)直線$OM$の式を求めよ.
(3)$ \triangle OCM $をx軸のまわりに1回転させてできる立体の体積を求めよ.
$ \boxed{3}$
図のように,点$O$を中心とし,線分$AB$を直径とする半径6の円があり,点$C$は線分$OB$の中点である,2点$D,E$は直径$AB$に対して同じ側の円周上にあり,$AB$と$CD$は直角,$AB$と$OE$は直角となっている.
また,線分$AD$と線分$OE$の交点を点$F$とする.
このとき,次の問いに答えよ.
(1)$CD$の長さを求めよ.
(2)$ \triangle AEF$の面積を求めよ.
(3)$ AF:AD$の比を求めよ.また,$\triangle DEF $の面積を求めよ.
佐賀県立高校入試2022年数学2⃣連立方程式
単元:
#数学(中学生)#中2数学#連立方程式#佐賀県立高校
指導講師:
重吉
問題文全文(内容文):
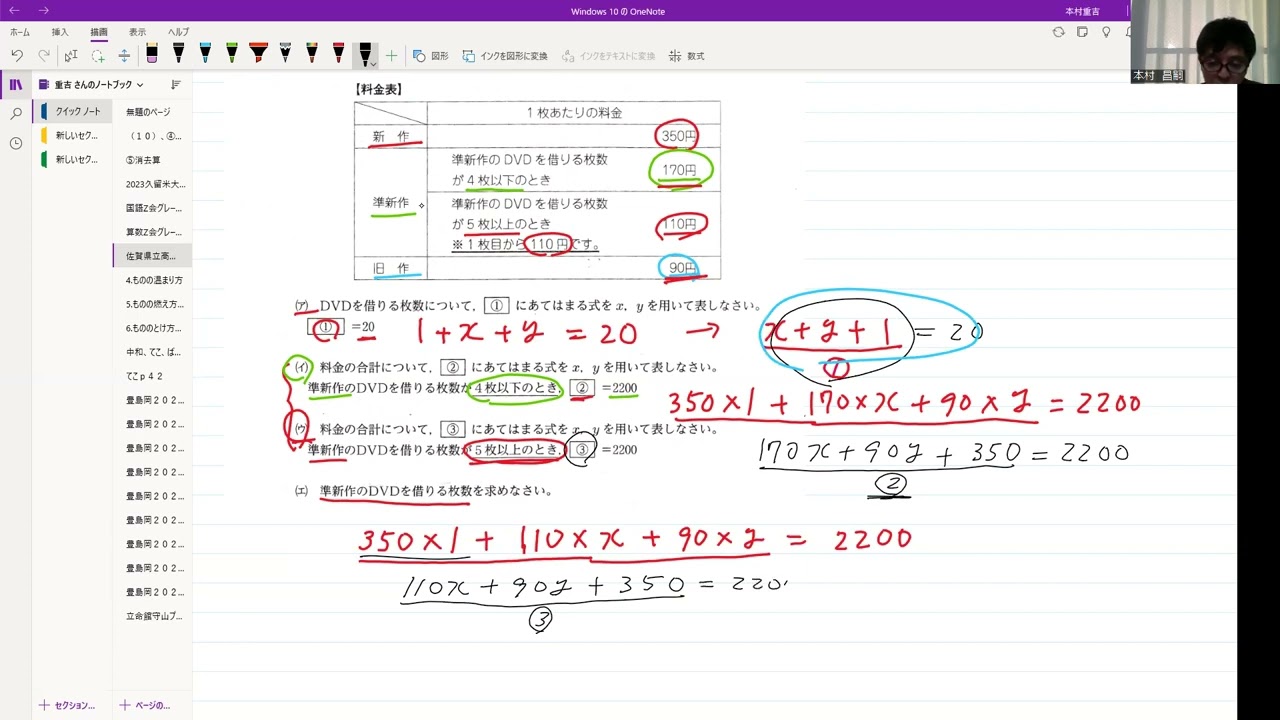
佐賀県立高校入試2022年数学2⃣連立方程式
-----------------
(ア)
DVDを借りる枚数について、①にあてはまる式を$x$、$y$を用いて表しなさい。
①=20
(イ)
料金の合計について、②にあてはまる式を$x$、$y$を用いて表しなさい。
準新作のDVDを借りる枚数が4枚以下のとき、②=2200
(ウ)
料金の合計について、③にあてはまる式を$x$、$y$を用いて表しなさい。
準新作のDVDを借りる枚数が5枚以上のとき。③=2200
(エ)
準新作のDVDを借りる枚数を求めなさい。
この動画を見る
佐賀県立高校入試2022年数学2⃣連立方程式
-----------------
(ア)
DVDを借りる枚数について、①にあてはまる式を$x$、$y$を用いて表しなさい。
①=20
(イ)
料金の合計について、②にあてはまる式を$x$、$y$を用いて表しなさい。
準新作のDVDを借りる枚数が4枚以下のとき、②=2200
(ウ)
料金の合計について、③にあてはまる式を$x$、$y$を用いて表しなさい。
準新作のDVDを借りる枚数が5枚以上のとき。③=2200
(エ)
準新作のDVDを借りる枚数を求めなさい。
【見た目以上に難しい!?】連立方程式:ラ・サール高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{3}{4}x-\dfrac{1}{2}(y+1)=1 \\
\dfrac{1}{3}(x+1)+\dfrac{3}{4}(y-1)=9
\end{array}
\right.
\end{eqnarray}$
この連立方程式を解け.
ラサール高校過去問
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{3}{4}x-\dfrac{1}{2}(y+1)=1 \\
\dfrac{1}{3}(x+1)+\dfrac{3}{4}(y-1)=9
\end{array}
\right.
\end{eqnarray}$
この連立方程式を解け.
ラサール高校過去問
東海高校 ただの連立方程式だけど‥‥

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
鈴木貫太郎
問題文全文(内容文):
連立方程式を解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
(\sqrt5-1)x+y=\sqrt5-1 \\
x+(\sqrt5+1)y=\sqrt5+1
\end{array}
\right.
\end{eqnarray}$
東海高校過去問
この動画を見る
連立方程式を解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
(\sqrt5-1)x+y=\sqrt5-1 \\
x+(\sqrt5+1)y=\sqrt5+1
\end{array}
\right.
\end{eqnarray}$
東海高校過去問
福田の1.5倍速演習〜合格する重要問題050〜一橋大学2017年度文系第2問〜連立方程式の整数解

単元:
#連立方程式#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{2}}$ 連立方程式$\\$
$\left\{\begin{array}{1}
x^2=yz+7\\
y^2=zx+7\\
z^2=xy+7\\
\end{array}\right.\\$
を満たす整数の組(x,y,z)でx $\leqq$ y $\leqq$ zとなるものを求めよ。
2017一橋大学文系過去問
この動画を見る
$\Large{\boxed{2}}$ 連立方程式$\\$
$\left\{\begin{array}{1}
x^2=yz+7\\
y^2=zx+7\\
z^2=xy+7\\
\end{array}\right.\\$
を満たす整数の組(x,y,z)でx $\leqq$ y $\leqq$ zとなるものを求めよ。
2017一橋大学文系過去問
【一本道が見えますか】連立方程式:巣鴨高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2つの連立方程式
$ \begin{eqnarray}
\left\{
\begin{array}{l}
3x + 2y = 14 \\
ax + by = 3
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
bx -ay = -5 \\
4x-5y = 11
\end{array}
\right.
\end{eqnarray}$
の解が一致するとき$a,b$の値をそれぞれ求めなさい.
巣鴨高校過去問
この動画を見る
2つの連立方程式
$ \begin{eqnarray}
\left\{
\begin{array}{l}
3x + 2y = 14 \\
ax + by = 3
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
bx -ay = -5 \\
4x-5y = 11
\end{array}
\right.
\end{eqnarray}$
の解が一致するとき$a,b$の値をそれぞれ求めなさい.
巣鴨高校過去問
連立方程式なんだけど解を直接求めようとすると自滅する問題~全国入試問題解法 #Shorts #数学 #高校入試

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
の比$ x:y$を最も簡単な整数の比で答えなさい.
連立方程式$\begin{eqnarray}
\left\{
\begin{array}{l}
37x-53y=2 \\
17x-19y=1
\end{array}
\right.
\end{eqnarray}$
法政第二高校過去問
この動画を見る
の比$ x:y$を最も簡単な整数の比で答えなさい.
連立方程式$\begin{eqnarray}
\left\{
\begin{array}{l}
37x-53y=2 \\
17x-19y=1
\end{array}
\right.
\end{eqnarray}$
法政第二高校過去問
連立方程式だけど。。 筑波大附属
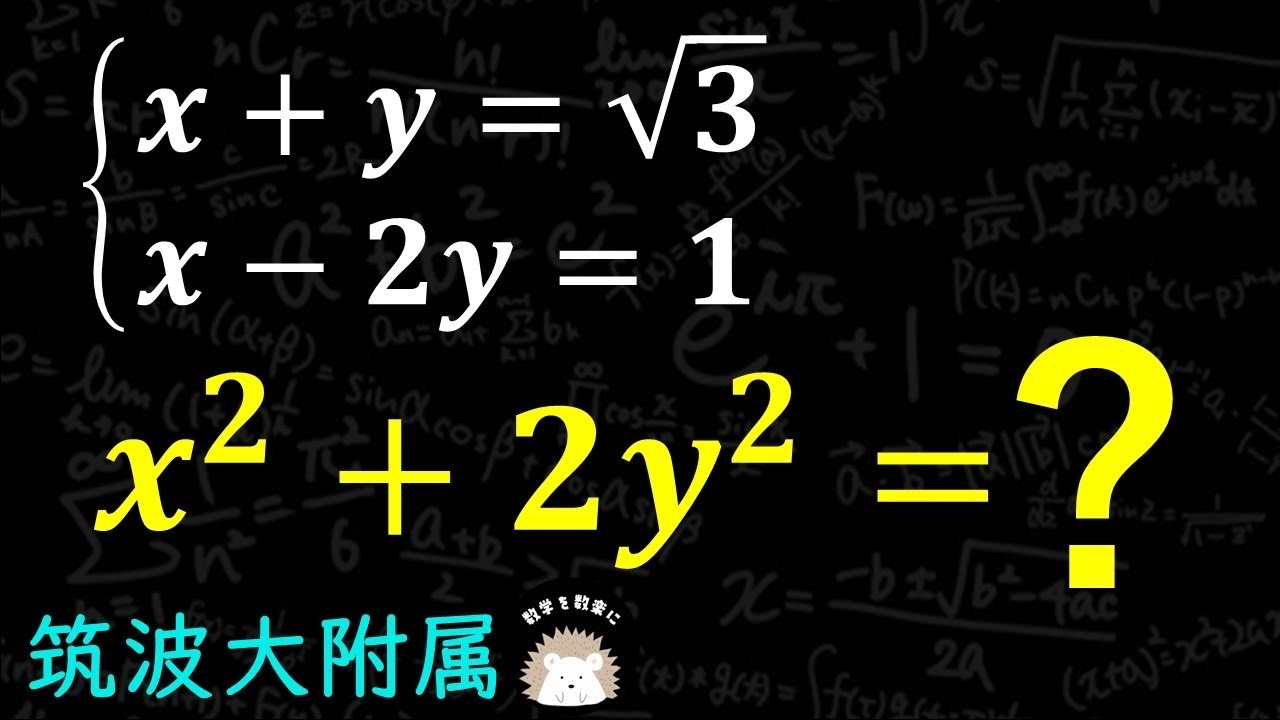
単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$
\begin{eqnarray}
\left\{
\begin{array}{l}
x + y = \sqrt 3 \\
x - 2y = 1
\end{array}
\right.
\end{eqnarray}
$
$x^2+2y^2 =?$
筑波大学付属高等学校
この動画を見る
$
\begin{eqnarray}
\left\{
\begin{array}{l}
x + y = \sqrt 3 \\
x - 2y = 1
\end{array}
\right.
\end{eqnarray}
$
$x^2+2y^2 =?$
筑波大学付属高等学校
2次式 連立方程式 国学院高校
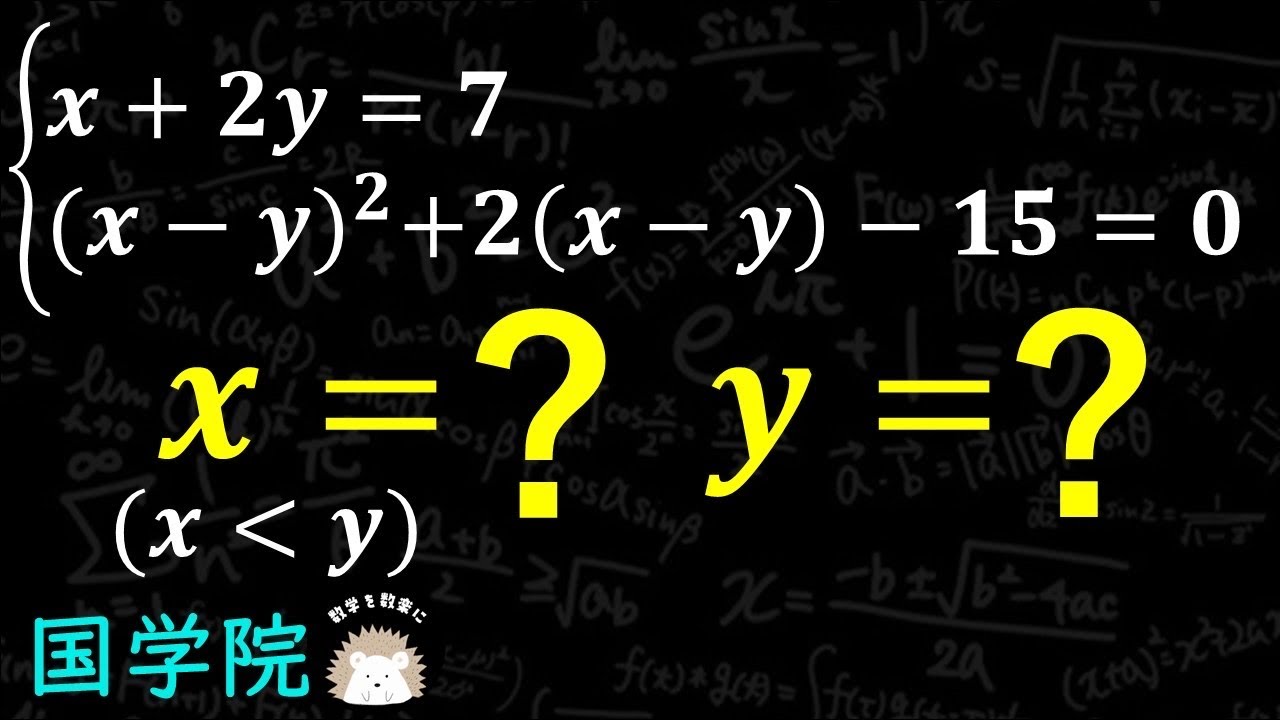
単元:
#数学(中学生)#中2数学#連立方程式#数Ⅰ#2次関数#2次方程式と2次不等式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
\begin{eqnarray}
\left\{
\begin{array}{l}
x + 2y = 7 \\
(x-y)^2+2(x-y)-15 = 0
\end{array}
\right.
\end{eqnarray}
x=? y=?
(x<y)
國學院高等学校
この動画を見る
\begin{eqnarray}
\left\{
\begin{array}{l}
x + 2y = 7 \\
(x-y)^2+2(x-y)-15 = 0
\end{array}
\right.
\end{eqnarray}
x=? y=?
(x<y)
國學院高等学校
【分数…同じ部分…!】連立方程式:日本大学第三高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
連立方程式$\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{2x+4}{3}+\dfrac{y+1}{2}=1 \\
2x+4-\dfrac{y+1}{6}=-\dfrac{1}{3}
\end{array}
\right.
\end{eqnarray}$
を解きなさい.
日大第三高校過去問
この動画を見る
連立方程式$\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{2x+4}{3}+\dfrac{y+1}{2}=1 \\
2x+4-\dfrac{y+1}{6}=-\dfrac{1}{3}
\end{array}
\right.
\end{eqnarray}$
を解きなさい.
日大第三高校過去問
指数の連立方程式
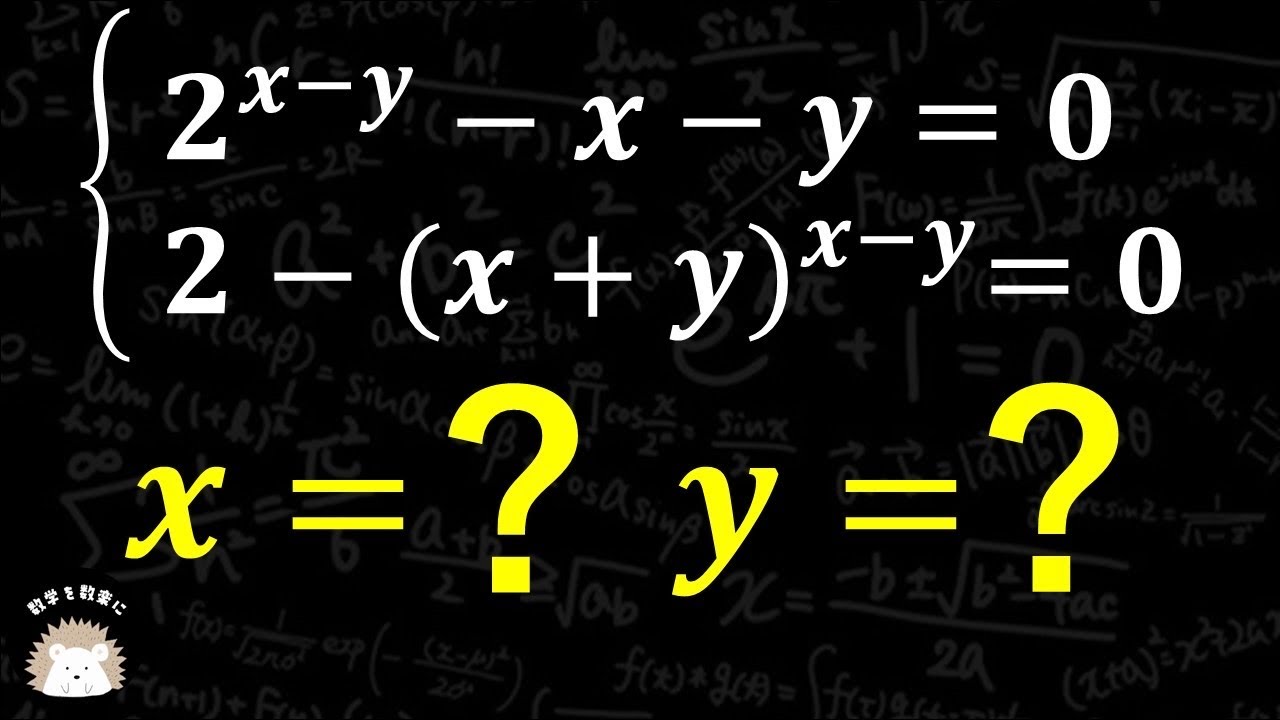
単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
数学を数楽に
問題文全文(内容文):
\begin{eqnarray}
\left\{
\begin{array}{l}
2^{x-y}-x-y = 0 \\
2-(x+y)^{x-y}=0
\end{array}
\right.
\end{eqnarray}
x=? y=?
この動画を見る
\begin{eqnarray}
\left\{
\begin{array}{l}
2^{x-y}-x-y = 0 \\
2-(x+y)^{x-y}=0
\end{array}
\right.
\end{eqnarray}
x=? y=?
【当たって砕けろ!】連立方程式:法政大学第二高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
解の比$x:y$を最も簡単な整数の比で答えなさい.
連立方程式$\begin{eqnarray}
\left\{
\begin{array}{l}
37x-53y=2 \\
17x-19y=1
\end{array}
\right.
\end{eqnarray}$
法政大第二高校過去問
この動画を見る
解の比$x:y$を最も簡単な整数の比で答えなさい.
連立方程式$\begin{eqnarray}
\left\{
\begin{array}{l}
37x-53y=2 \\
17x-19y=1
\end{array}
\right.
\end{eqnarray}$
法政大第二高校過去問
分母に文字がある連立方程式 東邦大附属東邦

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
x + \frac{1}{y} = 1 \\
\frac{1}{x} + y = 4
\end{array}
\right.
\end{eqnarray}
東邦大学付属東邦高等学校
この動画を見る
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
x + \frac{1}{y} = 1 \\
\frac{1}{x} + y = 4
\end{array}
\right.
\end{eqnarray}
東邦大学付属東邦高等学校
