 平行と合同
平行と合同
 平行と合同
平行と合同
【中学数学】平行線と角の問題演習~補助線の引き方~ 4-1.5【中2数学】

【中学数学】平行線と角の問題演習・基礎 4-1.5【中2数学】
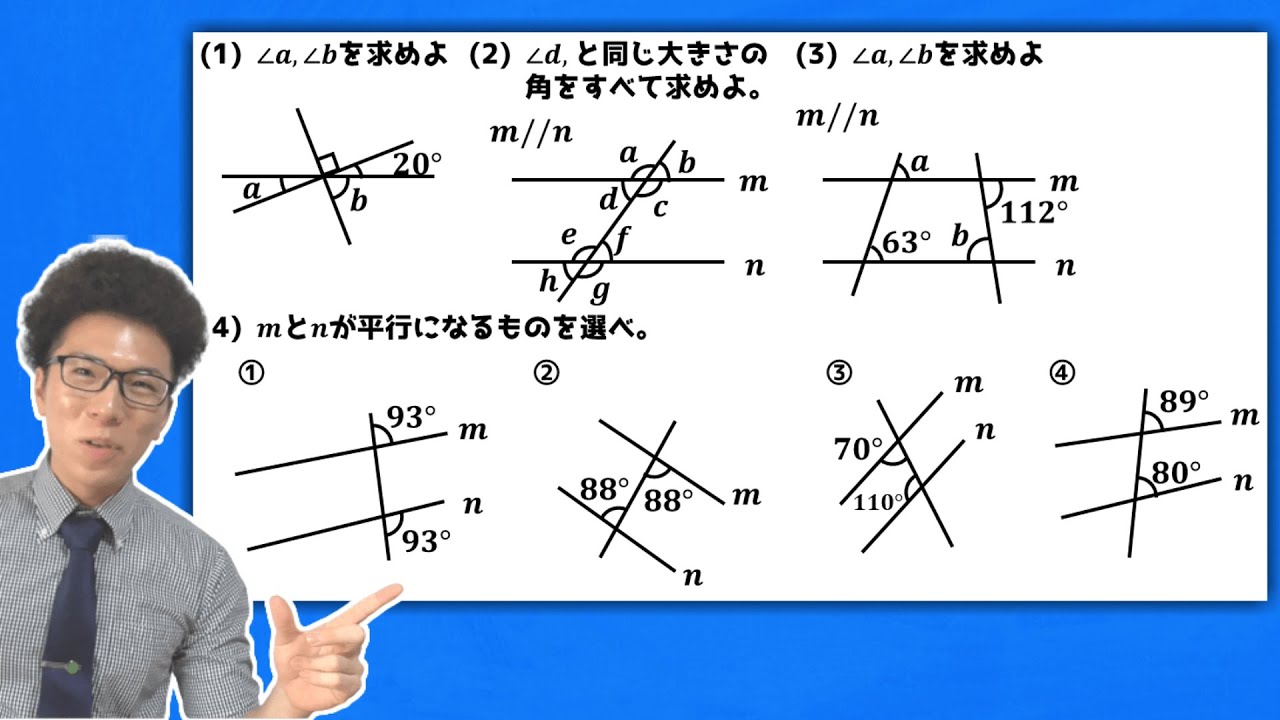
【中学数学】平行線と角を丁寧に~対頂角・同位角・錯角~ 4-1【中2数学】

【中学数学】四角形の面積を2等分する直線のまとめ【中2数学】
単元:
#数学(中学生)#中1数学#中2数学#平行と合同#平面図形#三角形と四角形
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
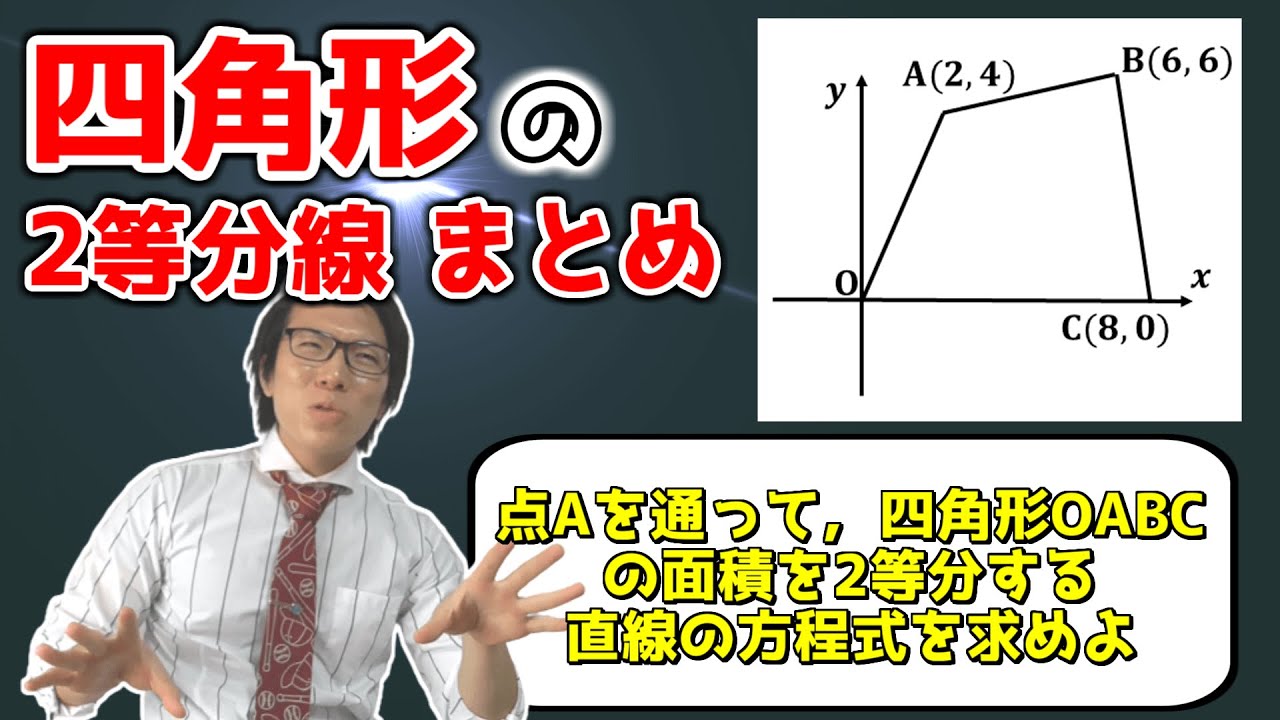
動画内の図、点Aを通て、四角形OABCを二等分する直線の式を求めよ。
この動画を見る
動画内の図、点Aを通て、四角形OABCを二等分する直線の式を求めよ。
【裏技】〇●の二等分線の図形の問題

【高校受験対策/数学】死守75

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根#2次方程式#1次関数#平行と合同#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守75
①$-8+5$を計算しなさい。
②$1+3×-(\frac{2}{7})$を計算しなさい。
③$2(a+4b)+3(a-2b)$を計算しなさい。
④$\sqrt{27}-\frac{6}{\sqrt{3}}$を計算しなさい。
⑤$(x+1)^2+(x-4)(x+2)$を計算しなさい。
⑥次の式を因数分解しなさい。
$9x^2-4y^2$
⑦右の図のように、長方形$ABCD$を対角線$AC$を折り目として折り返し、
頂点$B$が移った点を$E$とする。
$\angle ACE=20°$のとき、$\angle x$の大きさを求めなさい。
⑧右の図のように、2点$A(2,6)$、$B(8,2)$がある。
次の文中の(ア)、(イ)にあてはまる数を求めなさい。
直線$y=ax$のグラフが、線分$AB$上の点を通るとき、$a$の値の範囲は、(ア) $ \leqq a\leqq$ (イ)である。
この動画を見る
高校受験対策・死守75
①$-8+5$を計算しなさい。
②$1+3×-(\frac{2}{7})$を計算しなさい。
③$2(a+4b)+3(a-2b)$を計算しなさい。
④$\sqrt{27}-\frac{6}{\sqrt{3}}$を計算しなさい。
⑤$(x+1)^2+(x-4)(x+2)$を計算しなさい。
⑥次の式を因数分解しなさい。
$9x^2-4y^2$
⑦右の図のように、長方形$ABCD$を対角線$AC$を折り目として折り返し、
頂点$B$が移った点を$E$とする。
$\angle ACE=20°$のとき、$\angle x$の大きさを求めなさい。
⑧右の図のように、2点$A(2,6)$、$B(8,2)$がある。
次の文中の(ア)、(イ)にあてはまる数を求めなさい。
直線$y=ax$のグラフが、線分$AB$上の点を通るとき、$a$の値の範囲は、(ア) $ \leqq a\leqq$ (イ)である。
気づけば一瞬!!気づけば爽快!!

単元:
#数学(中学生)#中2数学#平行と合同#三角形と四角形
指導講師:
数学を数楽に
問題文全文(内容文):
2つの合同な長方形
長方形の面積は10
ABEFの面積=?
*図は動画内参照
この動画を見る
2つの合同な長方形
長方形の面積は10
ABEFの面積=?
*図は動画内参照
【高校受験対策/数学】死守72

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根#2次方程式#空間図形#平行と合同#確率#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守72
①$2-6$を計算しなさい。
➁$-3×(-2^2)$を計算しなさい。
③$\frac{2a+b}{ 3 }+\frac{a-b}{ 2 }$を計算しなさい。
④$xy^2×x^2÷xy$を計算しなさい。
⑤$\frac{6}{\sqrt{3}}+\sqrt{15}×\sqrt{5}$を計算しなさい。
⑥2次方程式$x^2+7x-18=0$ を解きなさい。
⑦$a=\sqrt{5}+3$のとき、$a^2-6a+9$の値を求めなさい。
⑧500円、100円、50円の硬貨が1枚ずつある。
この3枚を同時に1回投げるとき、表が出た硬貨の合計金額が500円以下になる確率を求めなさい。
ただし3枚の硬貨のそれぞれについて、表と裏の出方は同様に確からしいとする。
⑨右の図は底面の半径が$3cm$、側面になるおうぎ形の半径が$5cm$の円錐の展開図である。
これを組み立ててできる円錐の体積を求めなさい。
この動画を見る
高校受験対策・死守72
①$2-6$を計算しなさい。
➁$-3×(-2^2)$を計算しなさい。
③$\frac{2a+b}{ 3 }+\frac{a-b}{ 2 }$を計算しなさい。
④$xy^2×x^2÷xy$を計算しなさい。
⑤$\frac{6}{\sqrt{3}}+\sqrt{15}×\sqrt{5}$を計算しなさい。
⑥2次方程式$x^2+7x-18=0$ を解きなさい。
⑦$a=\sqrt{5}+3$のとき、$a^2-6a+9$の値を求めなさい。
⑧500円、100円、50円の硬貨が1枚ずつある。
この3枚を同時に1回投げるとき、表が出た硬貨の合計金額が500円以下になる確率を求めなさい。
ただし3枚の硬貨のそれぞれについて、表と裏の出方は同様に確からしいとする。
⑨右の図は底面の半径が$3cm$、側面になるおうぎ形の半径が$5cm$の円錐の展開図である。
これを組み立ててできる円錐の体積を求めなさい。
【中学数学】平行線と面積の基礎~等積変形~【中2数学】

証明:沖縄県高校入試~全国入試問題解法
単元:
#数学(中学生)#平行と合同#相似な図形#平面図形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
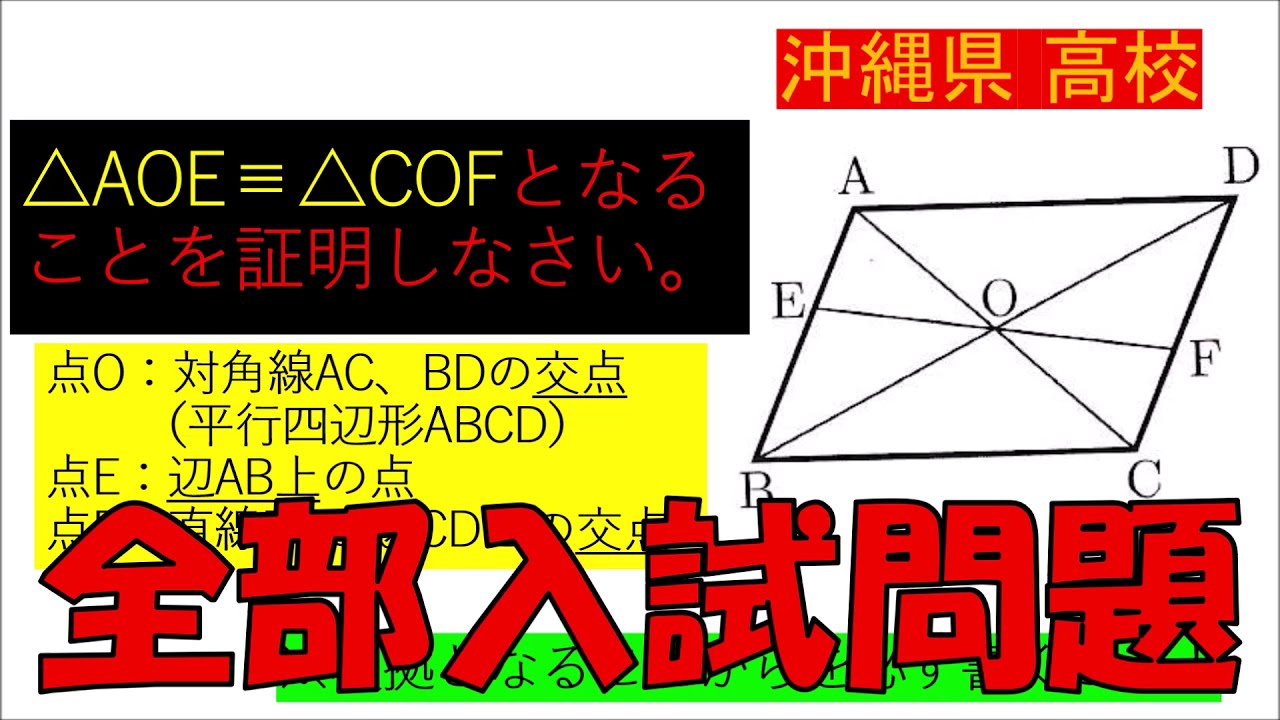
入試問題 沖縄県の高校
$\triangle AOE \equiv \triangle COF$となる
ことを証明しなさい。
点O:対角線$AC$、$BD$の交点 (平行四辺形$ABCD$)
点E:辺$AB$上の点
点F:直線$EO$と辺$CD$との交点
※根拠となることがらを必ず書くこと!
※図は動画内参照
この動画を見る
入試問題 沖縄県の高校
$\triangle AOE \equiv \triangle COF$となる
ことを証明しなさい。
点O:対角線$AC$、$BD$の交点 (平行四辺形$ABCD$)
点E:辺$AB$上の点
点F:直線$EO$と辺$CD$との交点
※根拠となることがらを必ず書くこと!
※図は動画内参照
【中学数学】三角形の合同・相似の部分点の取り方~最後の悪あがき~

単元:
#数学(中学生)#中2数学#中3数学#平行と合同#相似な図形#高校入試過去問(数学)#大阪府公立高等学校#北海道公立高等学校
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
三角形の合同・相似の部分点の取り方についての説明動画です
この動画を見る
三角形の合同・相似の部分点の取り方についての説明動画です
【高校受験対策/数学】死守67

単元:
#数学(中学生)#中2数学#中3数学#方程式#式の計算(単項式・多項式・式の四則計算)#平方根#2次方程式#比例・反比例#平行と合同#確率#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守67
① 2次方程式を$x^3+3x-1=0$を解きなさい。
②$\sqrt{24}\div\sqrt{3}-\sqrt{2}$を計算しなさい。
③関数$y=\frac{3}{x}$について、$x$の変域が$1 \leqq x \leqq 6$のとき、$y$の変域を答えなさい。
④
$x$枚の空の封筒と$y$本の鉛筆がある。
封筒の中に鉛筆を4本ずつ入れると8本足りず、3本ずつ入れると12本余る。
このとき$x$と$y$の値を求めなさい。
⑤
右の図のような、$AD=2cm$、$BC=5cm$、$AD/\!/BC$である台形$ABCD$があり、対角線$AC$、$BD$の交点を$E$とする。
点$E$から辺$DC$上に辺$BC$と線分$EF$が平行となる点$F$をとるとき、線分$EF$の長さを答えなさい。
⑥
1から6までの目のついた大、小2つのさいころを同時に投げたとき、大きいさいころの出た目の数を$a$、小さいさいころの出た目の数を$b$とする。
このとき、出た目の数の積$a×b$の値が25以下となる確率を求めなさい。
⑦
右の図のように直線$l$と2つの点$A$、$B$がある。
直線$l$上にあって、2つの点$A$、$B$を通る円の中心$P$を、定規とコンパスを用いて作図しなさい。
ただし作図に使った線は消さずに残しておくこと。
この動画を見る
高校受験対策・死守67
① 2次方程式を$x^3+3x-1=0$を解きなさい。
②$\sqrt{24}\div\sqrt{3}-\sqrt{2}$を計算しなさい。
③関数$y=\frac{3}{x}$について、$x$の変域が$1 \leqq x \leqq 6$のとき、$y$の変域を答えなさい。
④
$x$枚の空の封筒と$y$本の鉛筆がある。
封筒の中に鉛筆を4本ずつ入れると8本足りず、3本ずつ入れると12本余る。
このとき$x$と$y$の値を求めなさい。
⑤
右の図のような、$AD=2cm$、$BC=5cm$、$AD/\!/BC$である台形$ABCD$があり、対角線$AC$、$BD$の交点を$E$とする。
点$E$から辺$DC$上に辺$BC$と線分$EF$が平行となる点$F$をとるとき、線分$EF$の長さを答えなさい。
⑥
1から6までの目のついた大、小2つのさいころを同時に投げたとき、大きいさいころの出た目の数を$a$、小さいさいころの出た目の数を$b$とする。
このとき、出た目の数の積$a×b$の値が25以下となる確率を求めなさい。
⑦
右の図のように直線$l$と2つの点$A$、$B$がある。
直線$l$上にあって、2つの点$A$、$B$を通る円の中心$P$を、定規とコンパスを用いて作図しなさい。
ただし作図に使った線は消さずに残しておくこと。
【高校受験対策/数学】死守65

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(展開、因数分解)#2次方程式#比例・反比例#平行と合同#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守65
①右の図のように、直線$l$、直線$m$と2つの直線が交わっている。
$\angle a,\angle b,\angle c,\angle d,\angle e$のうち、どの角とどの角が等しければ、直線$l$と直線$m$が平行であるといえるか、その2つの角を答えなさい。
②$x^2-10x+25$を因数分解しなさい。
③2次方程式$(2x-5)^2=18$を解きなさい。
④右のア~オのうち、絶対値が最も大きい数を選び、記号で答えなさい。
ア $3.2$
イ $-\frac{7}{2}$
ウ $2\sqrt{2}$
エ $\frac{10}{3}$
オ $-3$
⑤右のア~オのうち、$y$が$x$に比例するものをすべて選び、記号で答えなさい。
ア 自然数$x$の約数の個数は$y$ 個である。
イ $x$ 円の商品を1000円支払って買うとき、おつりは$y$ 円である。
ウ 1200mの道のりを分速$x$ mの速さで進むとき、かかる時間は$y$ 分である。
エ 15%の食塩水が$x$ gあるとき、この食塩水に含まれる食塩の量は$y$ gである。
オ 何も入っていない容器に水を毎分2Lずつ$x$ 分間入れるとき、たまる水の量は$y$ Lである。
⑥右のア~オのうち、関数$y=2x^2$ついて述べた文として正しいものをすべて選び、記号で答えなさい。
ア この関数のグラフは、原点を通る。
イ $x \gt 0$のとき、$x$が増加すると$y$は減少する。
ウ この関数のグラフは$x$ 軸について対称である。
エ $x$の変域が$-1 \leqq x \leqq 2$のとき、$y$の変域は$0 \leqq y \leqq 8$である。
オ $x$の値がどの値からどの値まで増加するかに関わらず、変化の割合は常に2である。
この動画を見る
高校受験対策・死守65
①右の図のように、直線$l$、直線$m$と2つの直線が交わっている。
$\angle a,\angle b,\angle c,\angle d,\angle e$のうち、どの角とどの角が等しければ、直線$l$と直線$m$が平行であるといえるか、その2つの角を答えなさい。
②$x^2-10x+25$を因数分解しなさい。
③2次方程式$(2x-5)^2=18$を解きなさい。
④右のア~オのうち、絶対値が最も大きい数を選び、記号で答えなさい。
ア $3.2$
イ $-\frac{7}{2}$
ウ $2\sqrt{2}$
エ $\frac{10}{3}$
オ $-3$
⑤右のア~オのうち、$y$が$x$に比例するものをすべて選び、記号で答えなさい。
ア 自然数$x$の約数の個数は$y$ 個である。
イ $x$ 円の商品を1000円支払って買うとき、おつりは$y$ 円である。
ウ 1200mの道のりを分速$x$ mの速さで進むとき、かかる時間は$y$ 分である。
エ 15%の食塩水が$x$ gあるとき、この食塩水に含まれる食塩の量は$y$ gである。
オ 何も入っていない容器に水を毎分2Lずつ$x$ 分間入れるとき、たまる水の量は$y$ Lである。
⑥右のア~オのうち、関数$y=2x^2$ついて述べた文として正しいものをすべて選び、記号で答えなさい。
ア この関数のグラフは、原点を通る。
イ $x \gt 0$のとき、$x$が増加すると$y$は減少する。
ウ この関数のグラフは$x$ 軸について対称である。
エ $x$の変域が$-1 \leqq x \leqq 2$のとき、$y$の変域は$0 \leqq y \leqq 8$である。
オ $x$の値がどの値からどの値まで増加するかに関わらず、変化の割合は常に2である。
【高校受験対策/数学】図形-37

単元:
#数学(中学生)#中2数学#平行と合同#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・図形37
Q
右の図は、$AB=$$\sqrt{3}$ cm、$BC=3$ cmの平行四辺形$ABCD$である。
辺$AD$上に$AE=1$ cmとなる点$E$をとり、線分$BD$と線分$CE$の交点を$F$とするとき、次の各問いに答えなさい。
問1
$△ABE$と$△CBD$が相似になることを次のように証明した。
(あ)には角、(い)には数、(う)には辺、(え)にはことばをそれぞれ入れなさい。
【証明】
$△ABE$と$△CBD$について
仮定より$\angle BAE=$ (あ) ・・・①
また$AE:CD=1:$ (い) ・・・➁
$AB:$ (う) $=\sqrt{3}:3$
$=1:$ (い) ・・・③
➁、③から
$AE:CD=AB:$ (う) ・・・④
①、④から、2組の辺の(え)とその間の角がそれぞれ等しいので
$\triangle ABE \backsim \triangle CBD$
問2
$△BCF$の面積は$△ABE$の面積の何倍か求めなさい。
この動画を見る
高校受験対策・図形37
Q
右の図は、$AB=$$\sqrt{3}$ cm、$BC=3$ cmの平行四辺形$ABCD$である。
辺$AD$上に$AE=1$ cmとなる点$E$をとり、線分$BD$と線分$CE$の交点を$F$とするとき、次の各問いに答えなさい。
問1
$△ABE$と$△CBD$が相似になることを次のように証明した。
(あ)には角、(い)には数、(う)には辺、(え)にはことばをそれぞれ入れなさい。
【証明】
$△ABE$と$△CBD$について
仮定より$\angle BAE=$ (あ) ・・・①
また$AE:CD=1:$ (い) ・・・➁
$AB:$ (う) $=\sqrt{3}:3$
$=1:$ (い) ・・・③
➁、③から
$AE:CD=AB:$ (う) ・・・④
①、④から、2組の辺の(え)とその間の角がそれぞれ等しいので
$\triangle ABE \backsim \triangle CBD$
問2
$△BCF$の面積は$△ABE$の面積の何倍か求めなさい。
【大切だから解いて欲しい!】図形:岐阜県高校入試~全国入試問題解法
単元:
#数学(中学生)#中2数学#平行と合同#高校入試過去問(数学)#岐阜県公立高校入試
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
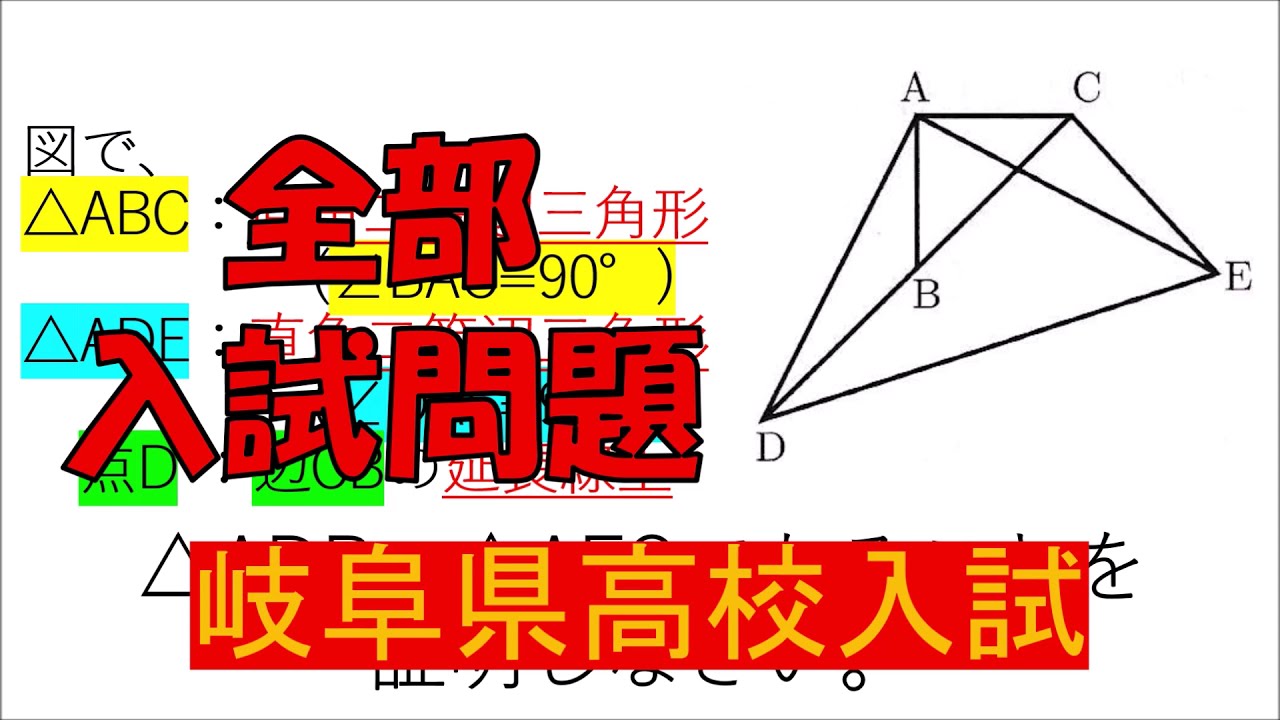
入試問題 岐阜県の高校
図で、
$\triangle ABC$:直角二等辺三角形
$(\angle BAC=90°)$
$\triangle AED$:直角二等辺三角形
$(\angle DAE=90°)$
点$D$:辺$CB$の延長線上
$\triangle ADB = \triangle AEC$であることを
証明しなさい。
※図は動画内参照
この動画を見る
入試問題 岐阜県の高校
図で、
$\triangle ABC$:直角二等辺三角形
$(\angle BAC=90°)$
$\triangle AED$:直角二等辺三角形
$(\angle DAE=90°)$
点$D$:辺$CB$の延長線上
$\triangle ADB = \triangle AEC$であることを
証明しなさい。
※図は動画内参照
【高校受験対策/数学】死守60

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#平方根#空間図形#1次関数#平行と合同#確率#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守605-41
①$-5-(-7)$を計算しなさい。
➁$(\frac{1}{4}-\frac{2}{3})\times 12$を計算しなさい。
③$4x \times\frac{2}{5}xy \div 2x^2$を計算しなさい。
④$(-2a+3)(2a+3)+9$を計算しなさい。
⑤$\sqrt{24} \div \sqrt{8}-\sqrt{12}$を計算しなさい。
⑥$150$を素因数分解しなさい。
⑦次の連立方程式を解きなさい。
$y=4(x+2)$
$6x-y=-10$
⑧次の数量の関係を等式で表しなさい。
100円硬貨が$a$ 枚、50円硬貨が$b$ 枚あり、これらをすべて10円硬貨に両替すると$c$ 枚になる。
⑨箱の中に同じ大きさの白玉がたくさん入っている。
そこに同じ大きさの黒玉100個入れてよくかき混ぜた後、その中から34個の玉を無作為に取りだしたところ、黒玉が4個入っていた。
この結果から、箱の中にはおよそ何個の白玉が入っていると考えられるか求めなさい。
➉半径6cmの球を中心$o$を通る平面で切った半球の表面積を求めなさい。
⑪右の図で$l /\!/ m$、$AB=AC$のとき、$\angle x$ の大きさを求めなさい。
この動画を見る
高校受験対策・死守605-41
①$-5-(-7)$を計算しなさい。
➁$(\frac{1}{4}-\frac{2}{3})\times 12$を計算しなさい。
③$4x \times\frac{2}{5}xy \div 2x^2$を計算しなさい。
④$(-2a+3)(2a+3)+9$を計算しなさい。
⑤$\sqrt{24} \div \sqrt{8}-\sqrt{12}$を計算しなさい。
⑥$150$を素因数分解しなさい。
⑦次の連立方程式を解きなさい。
$y=4(x+2)$
$6x-y=-10$
⑧次の数量の関係を等式で表しなさい。
100円硬貨が$a$ 枚、50円硬貨が$b$ 枚あり、これらをすべて10円硬貨に両替すると$c$ 枚になる。
⑨箱の中に同じ大きさの白玉がたくさん入っている。
そこに同じ大きさの黒玉100個入れてよくかき混ぜた後、その中から34個の玉を無作為に取りだしたところ、黒玉が4個入っていた。
この結果から、箱の中にはおよそ何個の白玉が入っていると考えられるか求めなさい。
➉半径6cmの球を中心$o$を通る平面で切った半球の表面積を求めなさい。
⑪右の図で$l /\!/ m$、$AB=AC$のとき、$\angle x$ の大きさを求めなさい。
【中学数学】平行と合同:多角形と角 星形五角形の内角の和☆

【中学数学】合同の証明の演習~北海道公立高校入試標準2019~【高校受験】
単元:
#数学(中学生)#中2数学#平行と合同#高校入試過去問(数学)#北海道公立高校入試
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
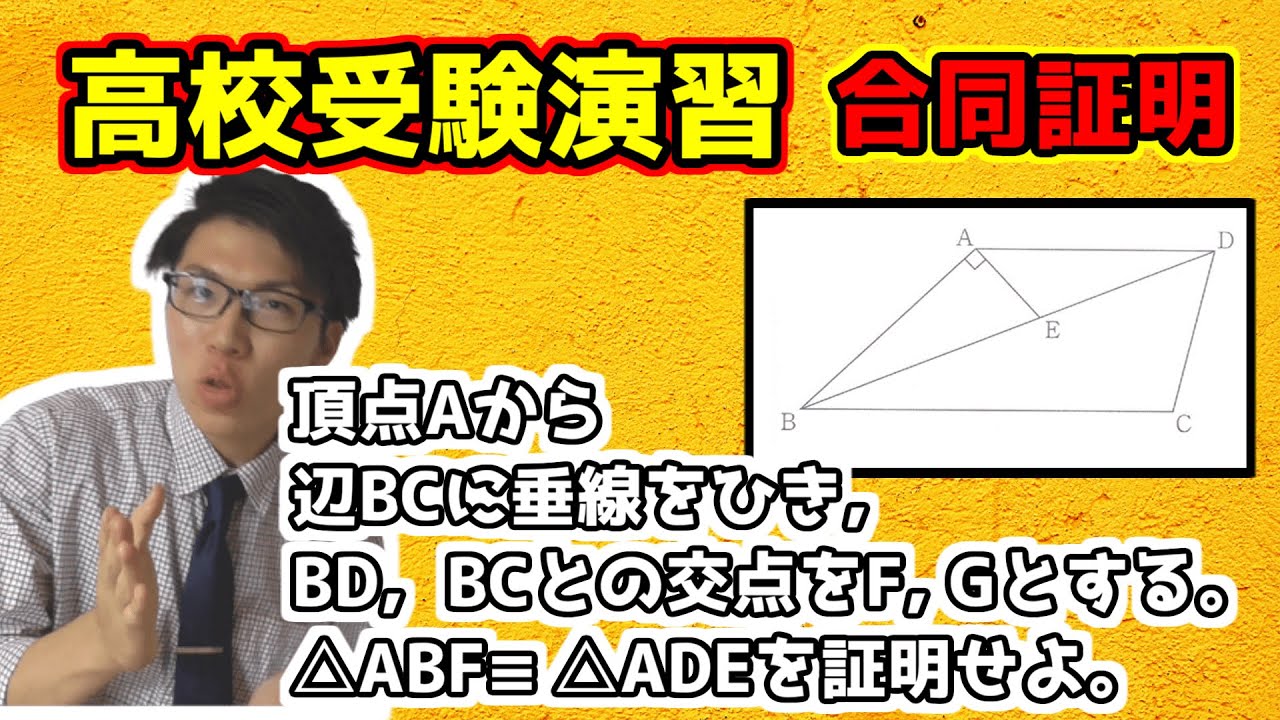
動画内の図のように、AB=AD、AD//BC、$\angle$ABCが鋭角である台形がある。
対角線BD上に点Eを、$\angle$BAE=90°となるようにとる。
1⃣
$\angle$ADB=20°、$\angle$BCD=100°のとき、$\angle$BDCの大きさを求めよ。
2⃣
頂点Aから辺BCに垂線をひき、対角線BD、辺BCとの交点をそれぞれF,Gとする。
このとき、$\triangle$ABF$\equiv$ADEを証明せよ。
この動画を見る
動画内の図のように、AB=AD、AD//BC、$\angle$ABCが鋭角である台形がある。
対角線BD上に点Eを、$\angle$BAE=90°となるようにとる。
1⃣
$\angle$ADB=20°、$\angle$BCD=100°のとき、$\angle$BDCの大きさを求めよ。
2⃣
頂点Aから辺BCに垂線をひき、対角線BD、辺BCとの交点をそれぞれF,Gとする。
このとき、$\triangle$ABF$\equiv$ADEを証明せよ。
【中学数学】三角形の合同の証明問題が誰でもできるようになる方法~数学苦手はみないと損です~

灘高校の小問 その3
単元:
#数学(中学生)#中2数学#平行と合同#高校入試過去問(数学)#灘高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
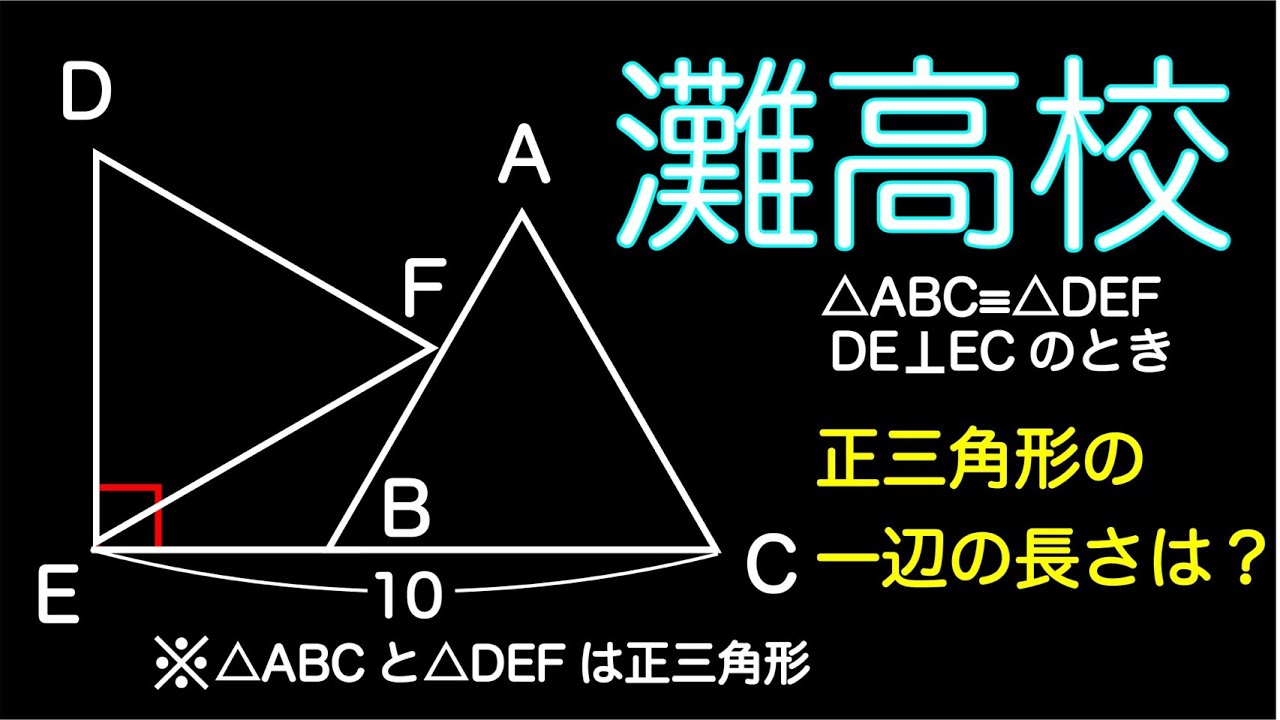
$\triangle \textrm{ABC} \equiv \triangle \textrm{FDE}$
正三角形の一辺の長さは?
この動画を見る
$\triangle \textrm{ABC} \equiv \triangle \textrm{FDE}$
正三角形の一辺の長さは?
角の二等分線+平行、垂直=?
単元:
#数学(中学生)#中2数学#平行と合同#三角形と四角形#高校入試過去問(数学)#江戸川学園取手高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
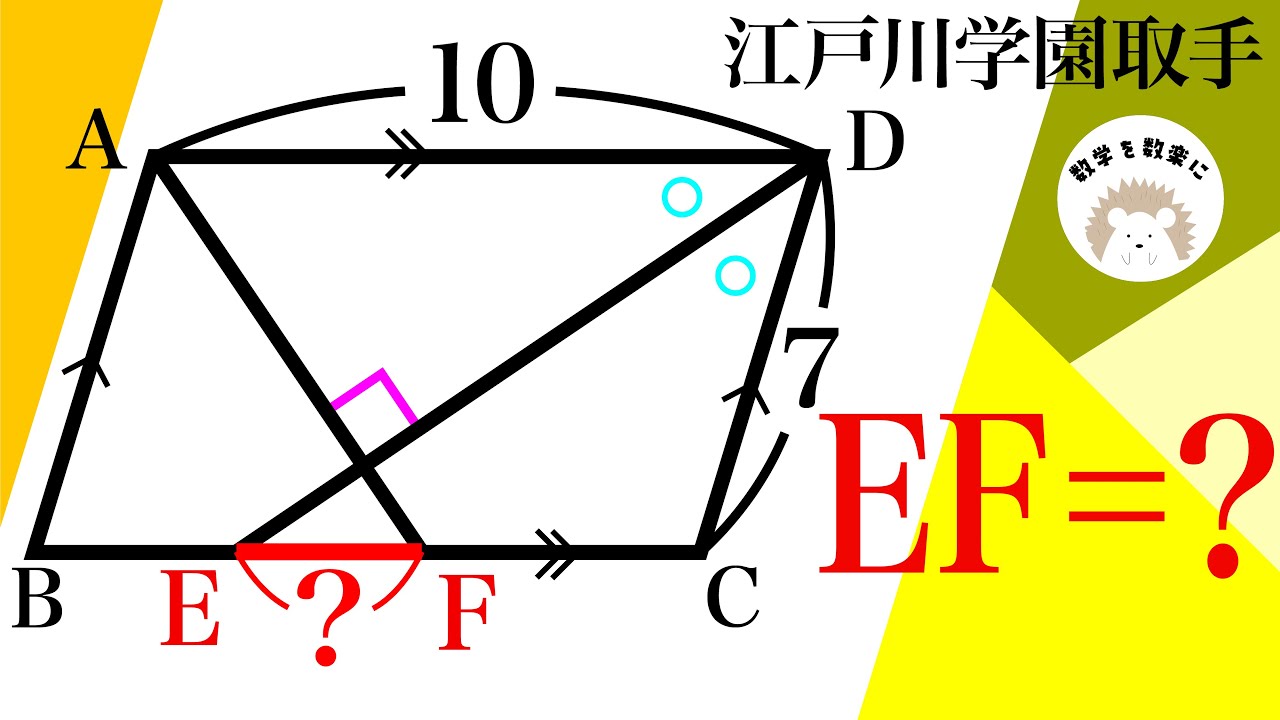
動画内の図を参照し、$\textrm{EF}$の長さを求めよ。
出典:2017年江戸川学園取手
この動画を見る
動画内の図を参照し、$\textrm{EF}$の長さを求めよ。
出典:2017年江戸川学園取手
【高校受験対策】数学-図形23

単元:
#数学(中学生)#中2数学#中3数学#平行と合同#相似な図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・図形23
右の図において、$△ABC$は$AB=AC$の二等辺三角形であり、 点$D$、$E$はそれぞれ辺$AB$、$AC$の中点である。
また、点$F$は直線DE上の点であり、$EF=DE$である。 このとき次の問1、問2に答えなさい。
問1
$AF=BE$であることを証明しなさい。
問2
線分$BF$と線分$CE$との交点を$G$とする。
$△AEF$において辺AFを底辺とするときの高さを$x$、$△BGE$において辺$BE$を底辺とするときの高さを$y$とするとき、$x:y$を求めなさい。
この動画を見る
高校受験対策・図形23
右の図において、$△ABC$は$AB=AC$の二等辺三角形であり、 点$D$、$E$はそれぞれ辺$AB$、$AC$の中点である。
また、点$F$は直線DE上の点であり、$EF=DE$である。 このとき次の問1、問2に答えなさい。
問1
$AF=BE$であることを証明しなさい。
問2
線分$BF$と線分$CE$との交点を$G$とする。
$△AEF$において辺AFを底辺とするときの高さを$x$、$△BGE$において辺$BE$を底辺とするときの高さを$y$とするとき、$x:y$を求めなさい。
【高校受験対策】数学-死守35

単元:
#数学(中学生)#中1数学#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#平方根#1次関数#平行と合同#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守35
①$6a \div -(\frac{3}{2})$
➁$9-(-15)\div3$
③$\sqrt{54}+4\sqrt{6}$
④$4x^2 \times -\frac{5}{6}xy$
⑤$\sqrt{18}-\frac{4}{\sqrt{2}}$
⑥
$2x+5y=3$
$x-3y=7$
⑦$x=19$のとき、$x^2-10x+9$の値を求めなさい。
⑧2次方程式$x^2+3x-0$を解きなさい
⑨直線$y=-x+7$に平行で、点$(4,-1)$を通る直線の式を求めなさい。
⑩右の図のような五角柱ABCDEFGHIJにおいて、 辺AFとねじれの位置にある辺の数を求めなさい。
⑪半径が$6cm$、中心角が$40°$のおうぎ形の面積を求めなさい。 ただし円周率は$\pi$とする。
⑫$8\leqq \sqrt{n} \leqq9$にあてはまる自然数$n$は、全部で何個あるか求めなさい。
⑬
袋の中に赤玉が3個、白玉が2個入っています。
この袋の中から2個の玉を同時に取り出すとき、取り出した2個の玉が同じ色である確率を求めなさい。ただし、どの玉の取り出し方も同様に確からしいものとします。
⑭
底面の半径が$4cm$で、表面積が$84\pi cm^2$の円柱がある。
この円柱の体積を求めなさい。ただし円周率は$\pi$とする。
この動画を見る
高校受験対策・死守35
①$6a \div -(\frac{3}{2})$
➁$9-(-15)\div3$
③$\sqrt{54}+4\sqrt{6}$
④$4x^2 \times -\frac{5}{6}xy$
⑤$\sqrt{18}-\frac{4}{\sqrt{2}}$
⑥
$2x+5y=3$
$x-3y=7$
⑦$x=19$のとき、$x^2-10x+9$の値を求めなさい。
⑧2次方程式$x^2+3x-0$を解きなさい
⑨直線$y=-x+7$に平行で、点$(4,-1)$を通る直線の式を求めなさい。
⑩右の図のような五角柱ABCDEFGHIJにおいて、 辺AFとねじれの位置にある辺の数を求めなさい。
⑪半径が$6cm$、中心角が$40°$のおうぎ形の面積を求めなさい。 ただし円周率は$\pi$とする。
⑫$8\leqq \sqrt{n} \leqq9$にあてはまる自然数$n$は、全部で何個あるか求めなさい。
⑬
袋の中に赤玉が3個、白玉が2個入っています。
この袋の中から2個の玉を同時に取り出すとき、取り出した2個の玉が同じ色である確率を求めなさい。ただし、どの玉の取り出し方も同様に確からしいものとします。
⑭
底面の半径が$4cm$で、表面積が$84\pi cm^2$の円柱がある。
この円柱の体積を求めなさい。ただし円周率は$\pi$とする。
【高校受験対策】数学-関数38
単元:
#数学(中学生)#中2数学#1次関数#平行と合同
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・関数38
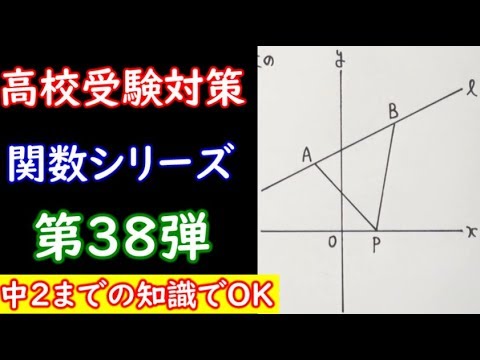
Q.
右の図で、直線$l$は関数$y=\frac{1}{2}x+6$のグラフです。点$A$・点$B$は直線$l$上の点で、点$A$の座標は$(-2,5)$、点$B$の座標は$(4,8)$です。 このとき次の各問に答えなさい。
①2点、$o,A$を通る直線の傾きを求めなさい。
点$P$は$x$軸上の$x>0$の部分にあり、$△APB$の面積は$26cm^2$です。
②点$P$の座標を求めなさい。
③点$P$を通り、$△APB$の面積を2等分する直線の式を求めなさい。
この動画を見る
高校受験対策・関数38
Q.
右の図で、直線$l$は関数$y=\frac{1}{2}x+6$のグラフです。点$A$・点$B$は直線$l$上の点で、点$A$の座標は$(-2,5)$、点$B$の座標は$(4,8)$です。 このとき次の各問に答えなさい。
①2点、$o,A$を通る直線の傾きを求めなさい。
点$P$は$x$軸上の$x>0$の部分にあり、$△APB$の面積は$26cm^2$です。
②点$P$の座標を求めなさい。
③点$P$を通り、$△APB$の面積を2等分する直線の式を求めなさい。
【高校受験対策】数学-図形21/後編
単元:
#数学(中学生)#中2数学#平行と合同
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・図形21
Q.
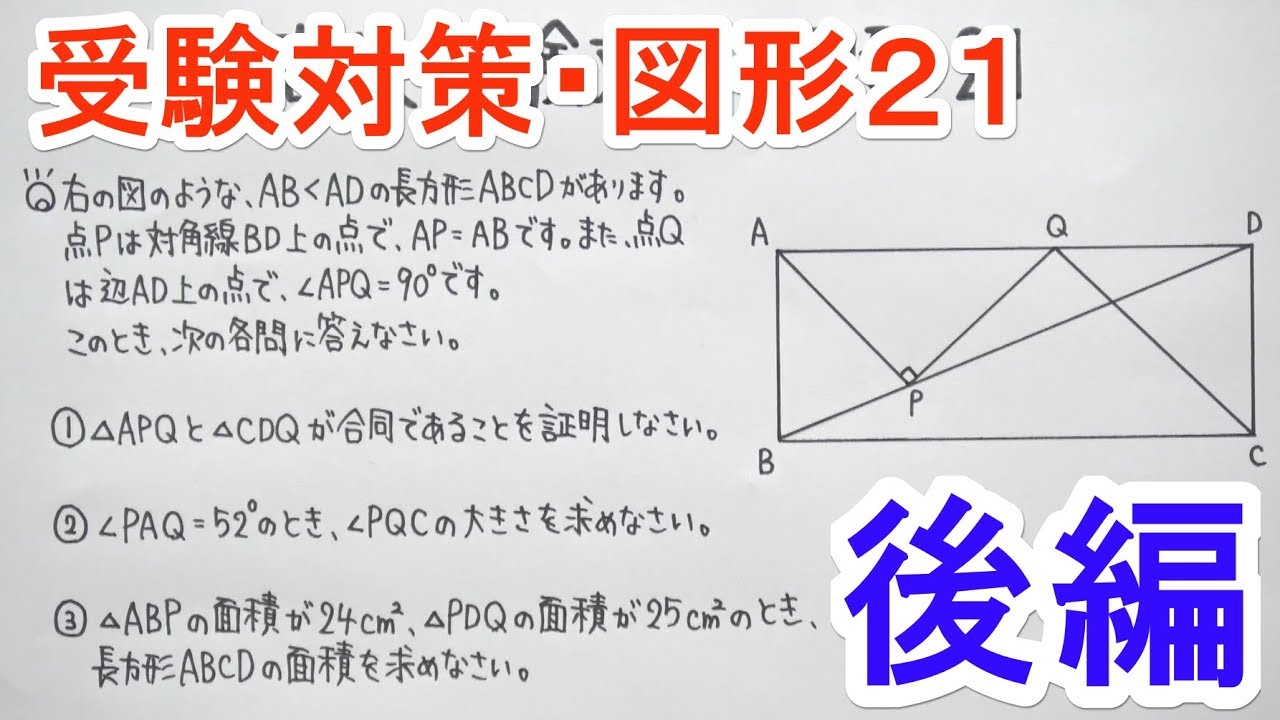
右の図のような、$AB<AD$の長方形$ABCD$があります。 点$P$は対角線$BD$上の点で、$AP=AB$です。また点$Q$は辺$AD$上の点で、$\angle APQ=90°$です。
このとき、次の各問に答えなさい。
①$△APQ$と$△CDQ$が合同であることを証明しなさい。
②$\angle PAQ=52°$のとき、$\angle PQC$の大きさを求めなさい。
③$△ABP$の面積が$24cm^2$、$△PDQ$の面積が$25cm^2$のとき、 長方形$ABCD$の面積を求めなさい。
この動画を見る
高校受験対策・図形21
Q.
右の図のような、$AB<AD$の長方形$ABCD$があります。 点$P$は対角線$BD$上の点で、$AP=AB$です。また点$Q$は辺$AD$上の点で、$\angle APQ=90°$です。
このとき、次の各問に答えなさい。
①$△APQ$と$△CDQ$が合同であることを証明しなさい。
②$\angle PAQ=52°$のとき、$\angle PQC$の大きさを求めなさい。
③$△ABP$の面積が$24cm^2$、$△PDQ$の面積が$25cm^2$のとき、 長方形$ABCD$の面積を求めなさい。
【高校受験対策】数学-図形21/前編
単元:
#数学(中学生)#中2数学#平行と合同
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・図形21
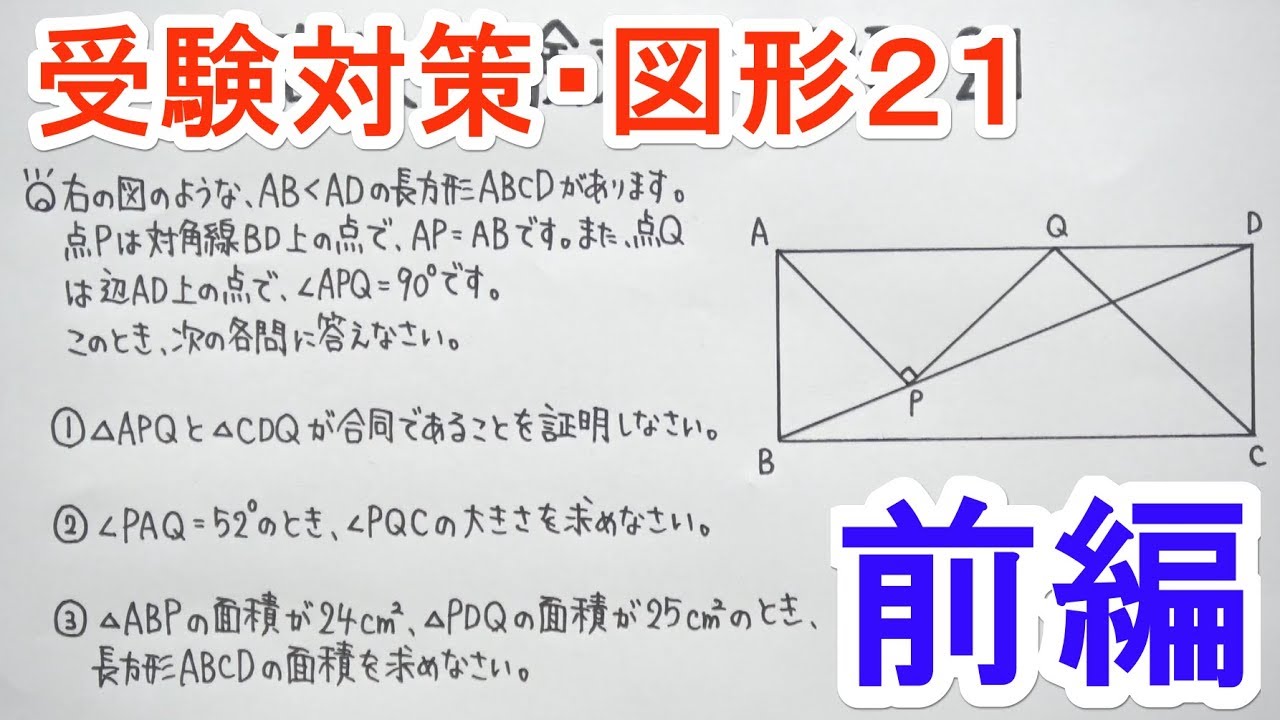
Q.
右の図のような、$AB<AD$の長方形$ABCD$があります。 点$P$は対角線$BD$上の点で、$AP=AB$です。また点$Q$は辺$AD$上の点で、$∠APQ=90°$です。
このとき、次の各問に答えなさい。
①$△APQ$と$△CDQ$が合同であることを証明しなさい。
②$\angle PAQ=52°$のとき$\angle PQC$の大きさを求めなさい。
③$△ABP$の面積が$24cm^2$、$△PDQ$の面積が$25cm^2$のとき、 長方形$ABCD$の面積を求めなさい。
この動画を見る
高校受験対策・図形21
Q.
右の図のような、$AB<AD$の長方形$ABCD$があります。 点$P$は対角線$BD$上の点で、$AP=AB$です。また点$Q$は辺$AD$上の点で、$∠APQ=90°$です。
このとき、次の各問に答えなさい。
①$△APQ$と$△CDQ$が合同であることを証明しなさい。
②$\angle PAQ=52°$のとき$\angle PQC$の大きさを求めなさい。
③$△ABP$の面積が$24cm^2$、$△PDQ$の面積が$25cm^2$のとき、 長方形$ABCD$の面積を求めなさい。
【高校受験対策】数学-死守32

単元:
#数学(中学生)#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#2次方程式#平行と合同#確率#速さ#速さその他#表とグラフ#表とグラフ・集合
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$-2+5$を計算しなさい。
②$3 + 3 ^ 4 \div (- 9)$を計算しなさい。
③$4(2a - 3) - 2(3a - 5)$を計算しなさい。
④$\dfrac{x-y}{6}-\dfrac{x+y}{8}$を計算しなさい。
⑤$3\sqrt8 - \sqrt{50} + sqrt{18}$を計算しなさい。
⑥2次方程式$(x + 2)(x - 2) = 2(3x - 2)$を解きなさい。
⑦かずよしくんは、自宅から1800mはなれた学校に登校するため、
午前7時30分に家を出発した。
最初は毎分60mの速さで歩いていたが、遅刻しそうになったので、
途中から毎分100mの速さで走ったところ、午前7時56分に学校に着いた。
かずよしくんが走った道のりは何mか、求めなさい。
⑧赤球3個と白球3個が入っている袋がある。
この袋の中から、同時に2個の球を取り出すとき、
赤球と白球が1個ずつである確率を求めなさい。
ただし、どの球を取り出すことも、同様に確からしいものとする。
⑨左下の図1で、正六角形$ABCDEF$に、2つの平行な直線$\ell、m$が交わっており、
交点はそれぞれ$G、H、I、J$である。
$\angle GHF=78°$のとき、$\angle IJE$の大きさを求めなさい。
⑩ある中学校の1年A組25人と1年B組25人の休日の学習時間を調べた。
下の図2、 図3は、それぞれの結果をヒストグラムに表したもので、
2つの図から「1年A組は1年B組 より、$\Box$」と読みとることができた。
$\Box$にあてはまるものとして適切なものを、 下のア~エから1つ選び、記号で書きなさい。
ア→学習時間の分布の範囲が小さい
イ→最頻値を含む階級の度数が多い
ウ→中央値を含む、階級の度数が少ない
エ→学習時間が150分以上の人数が多い
図は動画内参照
この動画を見る
①$-2+5$を計算しなさい。
②$3 + 3 ^ 4 \div (- 9)$を計算しなさい。
③$4(2a - 3) - 2(3a - 5)$を計算しなさい。
④$\dfrac{x-y}{6}-\dfrac{x+y}{8}$を計算しなさい。
⑤$3\sqrt8 - \sqrt{50} + sqrt{18}$を計算しなさい。
⑥2次方程式$(x + 2)(x - 2) = 2(3x - 2)$を解きなさい。
⑦かずよしくんは、自宅から1800mはなれた学校に登校するため、
午前7時30分に家を出発した。
最初は毎分60mの速さで歩いていたが、遅刻しそうになったので、
途中から毎分100mの速さで走ったところ、午前7時56分に学校に着いた。
かずよしくんが走った道のりは何mか、求めなさい。
⑧赤球3個と白球3個が入っている袋がある。
この袋の中から、同時に2個の球を取り出すとき、
赤球と白球が1個ずつである確率を求めなさい。
ただし、どの球を取り出すことも、同様に確からしいものとする。
⑨左下の図1で、正六角形$ABCDEF$に、2つの平行な直線$\ell、m$が交わっており、
交点はそれぞれ$G、H、I、J$である。
$\angle GHF=78°$のとき、$\angle IJE$の大きさを求めなさい。
⑩ある中学校の1年A組25人と1年B組25人の休日の学習時間を調べた。
下の図2、 図3は、それぞれの結果をヒストグラムに表したもので、
2つの図から「1年A組は1年B組 より、$\Box$」と読みとることができた。
$\Box$にあてはまるものとして適切なものを、 下のア~エから1つ選び、記号で書きなさい。
ア→学習時間の分布の範囲が小さい
イ→最頻値を含む階級の度数が多い
ウ→中央値を含む、階級の度数が少ない
エ→学習時間が150分以上の人数が多い
図は動画内参照
【テスト対策 中1】6章-1

単元:
#数学(中学生)#中1数学#平行と合同#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎次のことがらのうち、つねに成り立つものをすべて選びなさい。
ただし、$\ell、m、n$は直線、$A、B、C$は平面とする。
①$ℓ//m、m\perp n$ならば$\ell \perp n$
②$ℓ//m、m//n$ならば$ℓ//n$
③$\ell \perp m、m\perp n$ならば$\ell //n$
④$ℓ//A、m//A$ならば$ℓ//m$
⑤$\ell \perp A、m\perp A$ならば$ℓ//m$
⑥$A//C、B//C$ならば$A//B$
⑦$A\perp C、B\perp C$ならば$A//B$
⑧$A//B、\ell \perp A$ならば$\ell \perp B$
この動画を見る
◎次のことがらのうち、つねに成り立つものをすべて選びなさい。
ただし、$\ell、m、n$は直線、$A、B、C$は平面とする。
①$ℓ//m、m\perp n$ならば$\ell \perp n$
②$ℓ//m、m//n$ならば$ℓ//n$
③$\ell \perp m、m\perp n$ならば$\ell //n$
④$ℓ//A、m//A$ならば$ℓ//m$
⑤$\ell \perp A、m\perp A$ならば$ℓ//m$
⑥$A//C、B//C$ならば$A//B$
⑦$A\perp C、B\perp C$ならば$A//B$
⑧$A//B、\ell \perp A$ならば$\ell \perp B$
【テスト対策 中2】5章-2

単元:
#数学(中学生)#中2数学#平行と合同
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右の図において、$AB=CD,AB /\!/ CD$のとき、
$AO=CO$であることを証明しなさい。
図は動画内参照
この動画を見る
右の図において、$AB=CD,AB /\!/ CD$のとき、
$AO=CO$であることを証明しなさい。
図は動画内参照
【受験対策】数学-証明4

単元:
#数学(中学生)#中2数学#中3数学#平行と合同#円#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右図のように,円$O$に正三角形$ABC$が内接している.
点$C$をふくまない側にある孤$AB$上に点$D$をとり,
$△ADB$をつくる.
線分$CD$をひき,線分$AB$との交点を$E$とし,
線分$CD$上に$AD=CF$となる点$F$をとる.
線分$BF$を延長した直線と線分$AC$,円$O$との交点を
それぞれ$G,H$とする.
このとき,次の各問いに答えなさい.
ただし,点$H$は点$B$と異なる点とする .
①$△ADB\equiv △CFB$を証明しなさい.
②$\triangle BFE \sim \triangle CHG$を証明しなさい.
図は動画内参照
この動画を見る
右図のように,円$O$に正三角形$ABC$が内接している.
点$C$をふくまない側にある孤$AB$上に点$D$をとり,
$△ADB$をつくる.
線分$CD$をひき,線分$AB$との交点を$E$とし,
線分$CD$上に$AD=CF$となる点$F$をとる.
線分$BF$を延長した直線と線分$AC$,円$O$との交点を
それぞれ$G,H$とする.
このとき,次の各問いに答えなさい.
ただし,点$H$は点$B$と異なる点とする .
①$△ADB\equiv △CFB$を証明しなさい.
②$\triangle BFE \sim \triangle CHG$を証明しなさい.
図は動画内参照
