 中2数学
中2数学
 中2数学
中2数学
文章題にみえて実は。。。広陵

5で割った余り 法政大学高校

単元:
#数学(中学生)#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)#法政大学高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
$2023^3+2024^4$
を5で割ったときの余りは?
この動画を見る
$2023^3+2024^4$
を5で割ったときの余りは?
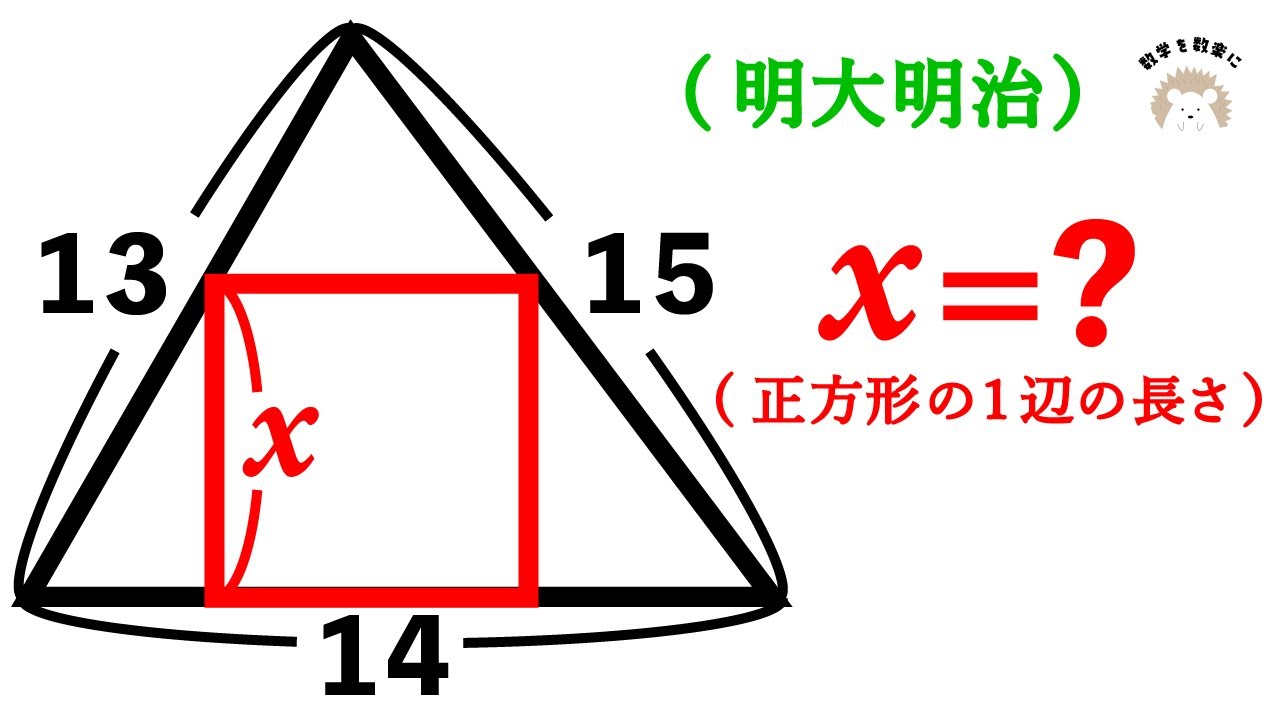
円と接線 2通りで解説 埼玉県
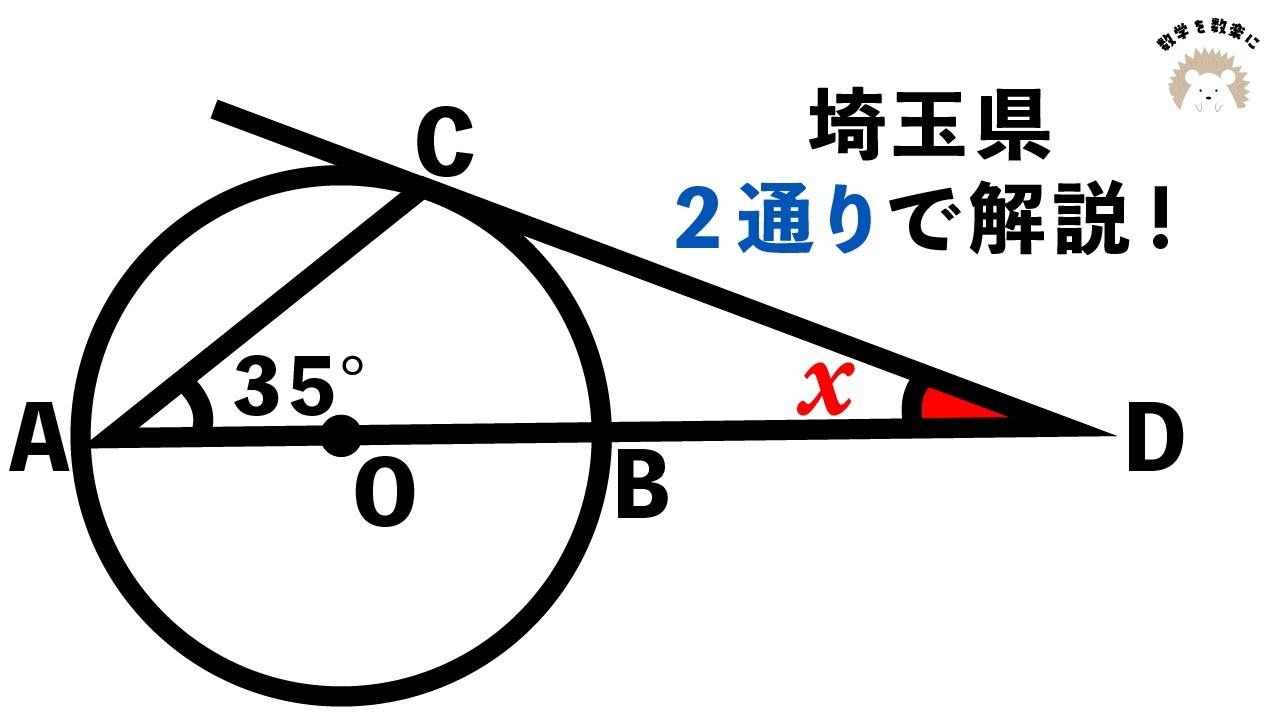
三角形に内接する正方形 明大明治
単元:
#数学(中学生)#中1数学#中2数学#中3数学#相似な図形#平面図形#三角形と四角形#高校入試過去問(数学)#明治大学付属明治高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
x=?(正方形の1辺の長さ)
この動画を見る
x=?(正方形の1辺の長さ)
【そう考えるか…!】連立方程式:東京都立国立高等学校~全国入試問題解法
単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#東京都立国立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
連立方程式
$\begin{equation}
\left\{ \,
\begin{aligned}
& \frac{3}{2}x-\frac{2}{3}y = 20 \\
& -\frac{2}{3}x+\frac{3}{2}y = 20
\end{aligned}
\right.
\end{equation}\;$を解け。
この動画を見る
連立方程式
$\begin{equation}
\left\{ \,
\begin{aligned}
& \frac{3}{2}x-\frac{2}{3}y = 20 \\
& -\frac{2}{3}x+\frac{3}{2}y = 20
\end{aligned}
\right.
\end{equation}\;$を解け。
【他の解き方は…!】連立方程式:洛南高等学校~全国入試問題解法
単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#洛南高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
連立方程式
$\begin{equation}
\left\{ \,
\begin{aligned}
& \frac{3}{x}+\frac{2}{y}=7 \\
& \frac{5}{x}-\frac{4}{y}=8
\end{aligned}
\right.
\end{equation}\;$を解きなさい。
この動画を見る
連立方程式
$\begin{equation}
\left\{ \,
\begin{aligned}
& \frac{3}{x}+\frac{2}{y}=7 \\
& \frac{5}{x}-\frac{4}{y}=8
\end{aligned}
\right.
\end{equation}\;$を解きなさい。
もう一人が男の子である確率は?

単元:
#数学(中学生)#中2数学#確率
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
ある家庭に2人の子どもがいる。子どものうち1人が男の子の時、もう1人の子が男の子である確率はいくらか?
この動画を見る
ある家庭に2人の子どもがいる。子どものうち1人が男の子の時、もう1人の子が男の子である確率はいくらか?
三角形の相似 日大二
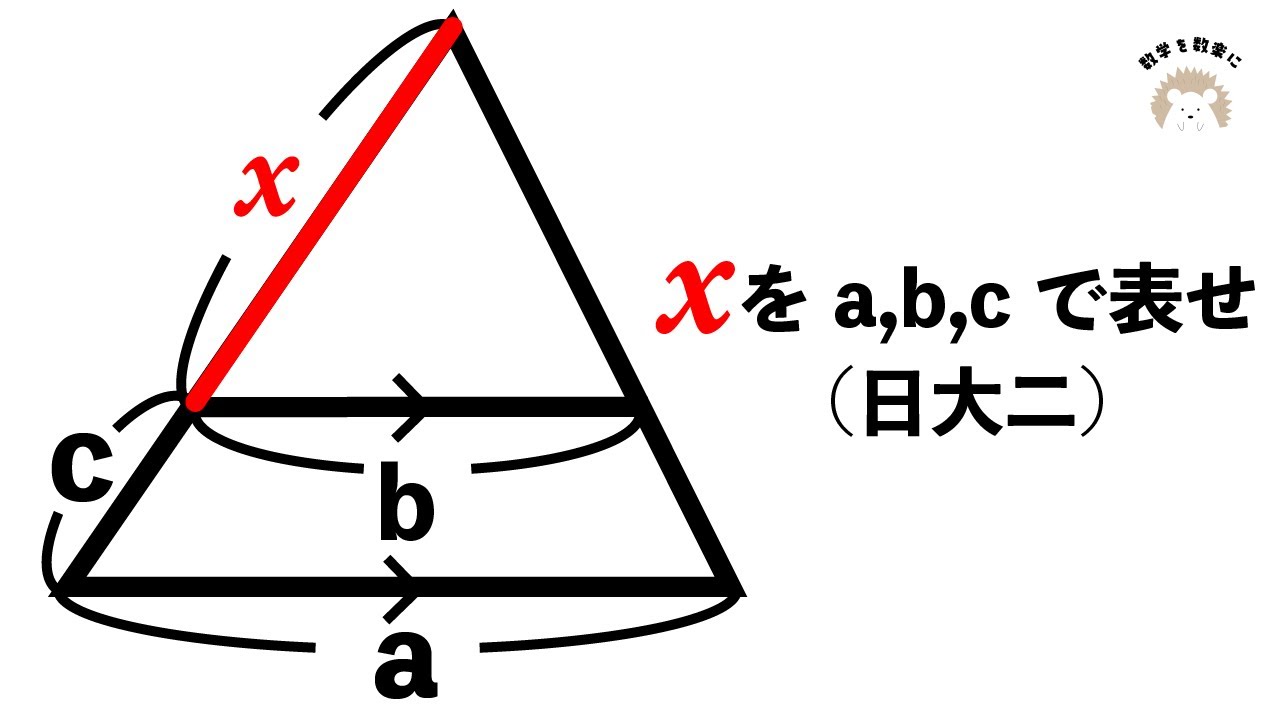
単元:
#数学(中学生)#中2数学#三角形と四角形#高校入試過去問(数学)#日本大学第二高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
次の図のxをa,b,cで表せ。(図は動画参照)
この動画を見る
次の図のxをa,b,cで表せ。(図は動画参照)
【理解度が試される…!】有理数:大阪府~全国入試問題解法
単元:
#数学(中学生)#中1数学#中2数学#式の計算(単項式・多項式・式の四則計算)#文字と式#高校入試過去問(数学)#大阪府高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$x\;$を有理数とする。$\displaystyle\frac{35}{12}x\;$と$\displaystyle\frac{21}{20}x\;$の値がともに自然数となる最も小さい$x\;$の値を求めなさい。
この動画を見る
$x\;$を有理数とする。$\displaystyle\frac{35}{12}x\;$と$\displaystyle\frac{21}{20}x\;$の値がともに自然数となる最も小さい$x\;$の値を求めなさい。
3点が一直線上 明星

3点が一直線上 明星

単元:
#数学(中学生)#中2数学#1次関数
指導講師:
数学を数楽に
問題文全文(内容文):
3点$(0,8),(1,t),(4,1-t)$が
一直線上にあるとき、
定数$t$の値を求めよ
この動画を見る
3点$(0,8),(1,t),(4,1-t)$が
一直線上にあるとき、
定数$t$の値を求めよ
一次関数であるものを選べ 愛知県

一次関数であるものを選べ 愛知県

単元:
#数学(中学生)#中2数学#1次関数#高校入試過去問(数学)#愛知県公立高校入試
指導講師:
数学を数楽に
問題文全文(内容文):
$yがxの1次関数となるものを選べ。$
ア 面積100cm$^2$でたての長さが$x$cmである長方形の横の長さ$y$cm
イ 1辺の長さ$x$cmである正三角形の周の長さ$y$cm
ウ 半径が$x$cmである円の面積$y$cm$^2$
エ 1辺の長さが$x$cmである立方体の体積$y$cm$^3$
この動画を見る
$yがxの1次関数となるものを選べ。$
ア 面積100cm$^2$でたての長さが$x$cmである長方形の横の長さ$y$cm
イ 1辺の長さ$x$cmである正三角形の周の長さ$y$cm
ウ 半径が$x$cmである円の面積$y$cm$^2$
エ 1辺の長さが$x$cmである立方体の体積$y$cm$^3$
絶対答えが37になる計算

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
「絶対答えが37になる計算」について解説しています。
この動画を見る
「絶対答えが37になる計算」について解説しています。
直角三角形の中に直角

平行線と比
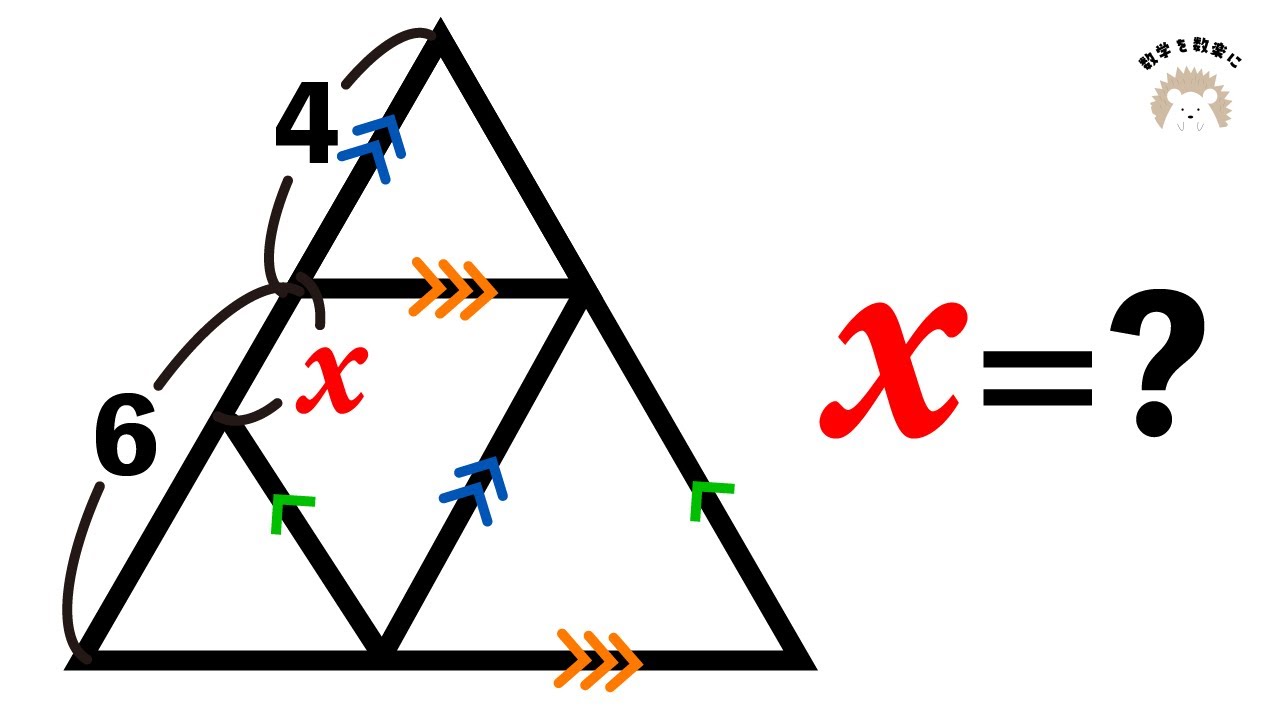
【少しでも上手く…!】連立方程式:慶応義塾高等学校~全国入試問題解法
単元:
#連立方程式#高校入試過去問(数学)#慶應義塾高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$a,b$を定数とする。$x,y$の連立方程式、
\begin{eqnarray}
\left\{
\begin{array}{l}
(a+2)x - (b-1)y = 33 \\
(a-1)x + (2b+1)y = 9
\end{array}
\right.
\end{eqnarray}
の解が$x = 3,y = 1$であるとき、$a,b$の値を求めよ。
この動画を見る
$a,b$を定数とする。$x,y$の連立方程式、
\begin{eqnarray}
\left\{
\begin{array}{l}
(a+2)x - (b-1)y = 33 \\
(a-1)x + (2b+1)y = 9
\end{array}
\right.
\end{eqnarray}
の解が$x = 3,y = 1$であるとき、$a,b$の値を求めよ。
【少しでも上手く…!】連立方程式:慶応義塾高等学校~全国入試問題解法

単元:
#数学(中学生)#連立方程式#高校入試過去問(数学)#慶應義塾高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$
\left\{
\begin{array}{l}
(a+2)x + (b-1)y = 33 \\
(a-1)x + (2b+1)y = 9
\end{array}
\right.
$
$の解が x = 3,y = 1であるとき、a = \boxed{ } , b = \boxed{ }である$
この動画を見る
$
\left\{
\begin{array}{l}
(a+2)x + (b-1)y = 33 \\
(a-1)x + (2b+1)y = 9
\end{array}
\right.
$
$の解が x = 3,y = 1であるとき、a = \boxed{ } , b = \boxed{ }である$
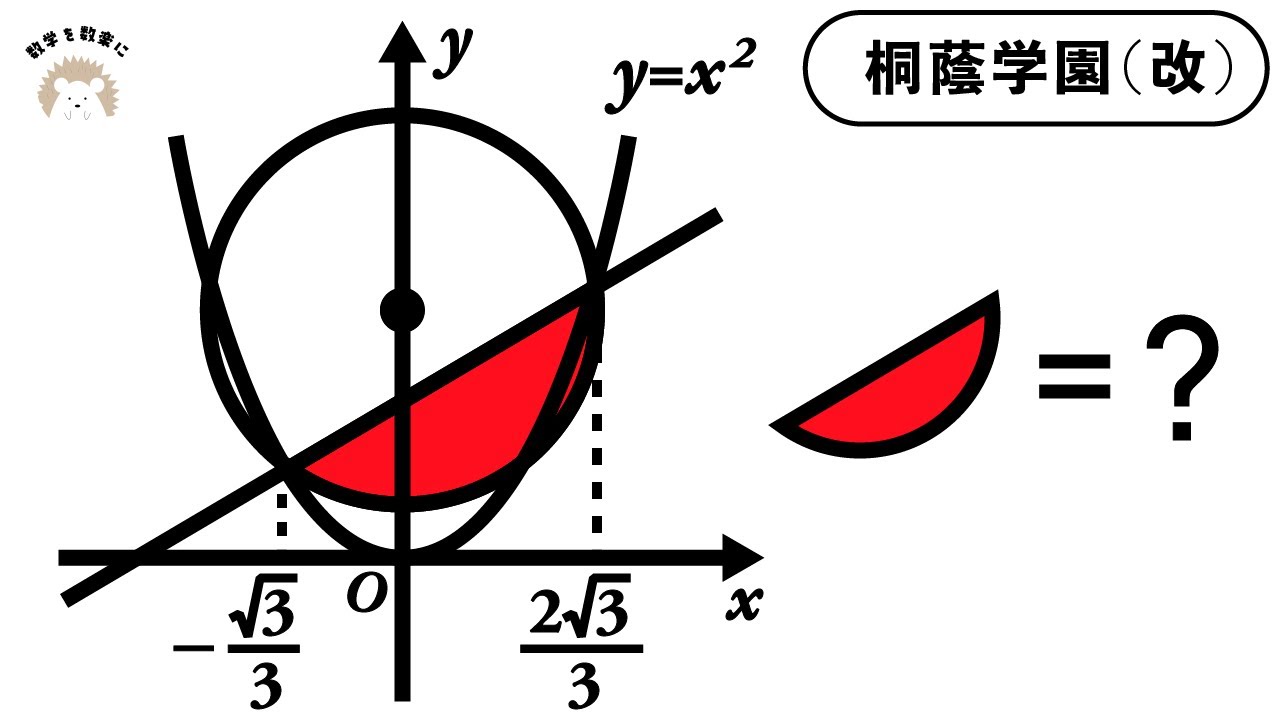
座標平面 円 面積 桐蔭学園
単元:
#数学(中学生)#中1数学#中2数学#平面図形#三角形と四角形#高校入試過去問(数学)#桐蔭学園高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
図の赤い部分の面積は?
この動画を見る
図の赤い部分の面積は?
分母の有理化のタイミング 桃山学院

単元:
#数学(中学生)#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#平方根
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{41}{\sqrt{42}}-(\frac{\sqrt{6}}{\sqrt{7}}-\frac{\sqrt{7}}{\sqrt{6}})$
この動画を見る
$\frac{41}{\sqrt{42}}-(\frac{\sqrt{6}}{\sqrt{7}}-\frac{\sqrt{7}}{\sqrt{6}})$
動点P

高校入試だけど多項定理 江戸川学園取手

単元:
#数学(中学生)#中1数学#中2数学#中3数学#方程式#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#高校入試過去問(数学)#江戸川学園取手高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
$(x^{2}+x+1)^{3}$を展開して整理した時の $x^{2}$ の係数を答えよ
この動画を見る
$(x^{2}+x+1)^{3}$を展開して整理した時の $x^{2}$ の係数を答えよ
【情報を合わせて…!】図形:活水高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#平行と合同#相似な図形#三角形と四角形#高校入試過去問(数学)#活水高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
lとmが平行であり、AB=BC であるとき、xの角度を求めよ
この動画を見る
lとmが平行であり、AB=BC であるとき、xの角度を求めよ
場合の数 中学生の解き方 高校生の解き方
単元:
#数学(中学生)#確率#高校入試過去問(数学)#東海大学付属浦安高等学校
指導講師:
数学を数楽に
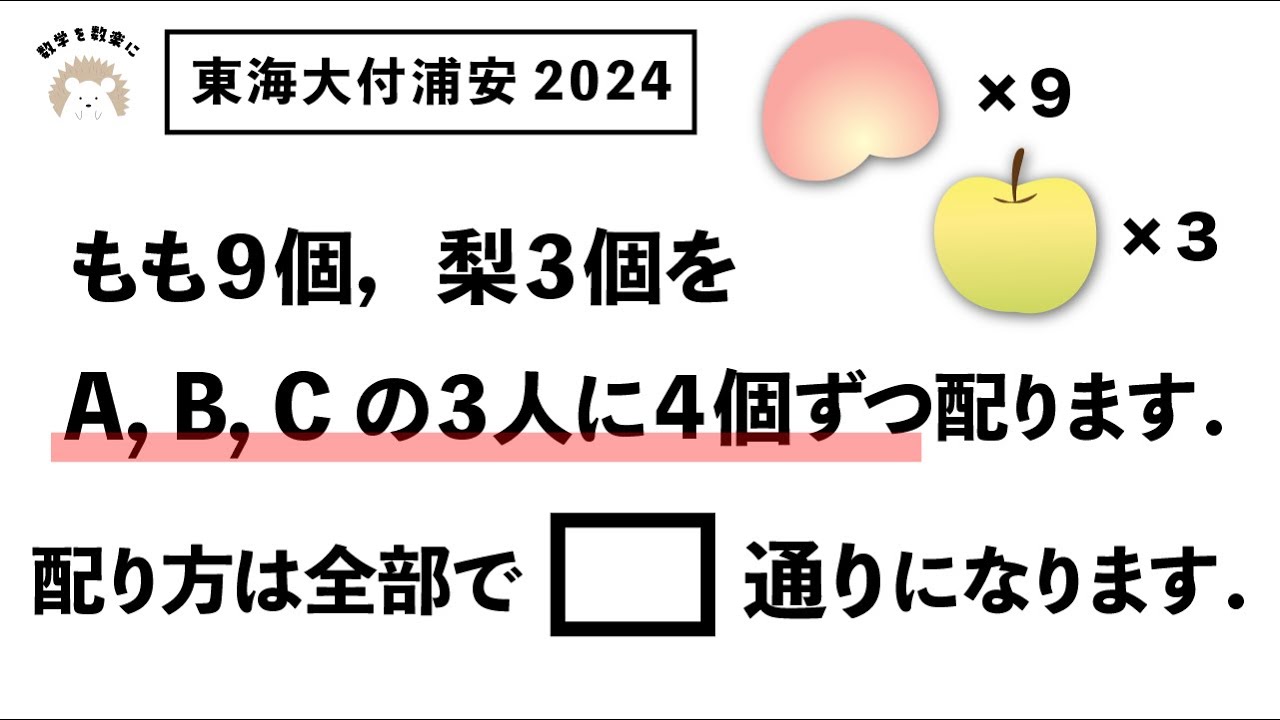
問題文全文(内容文):
もも9個、梨3個をA,B,Cの3人に4個ずつ配ります。配り方は全部で▢通りになります。
この動画を見る
もも9個、梨3個をA,B,Cの3人に4個ずつ配ります。配り方は全部で▢通りになります。
【少しでも考えやすく…!】文章題:名古屋国際高等学校~全国入試問題解法
単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)#名古屋国際高等学校
指導講師:
問題文全文(内容文):
$今年のある会社の入社人数は、昨年に比べて男性は2割減少、女性は1割増加し、全体では1割減少した。$
$昨年の男性の入社者人数は、昨年の男女合わせた全体の入社人数の何倍であったかを求めなさい$
この動画を見る
$今年のある会社の入社人数は、昨年に比べて男性は2割減少、女性は1割増加し、全体では1割減少した。$
$昨年の男性の入社者人数は、昨年の男女合わせた全体の入社人数の何倍であったかを求めなさい$
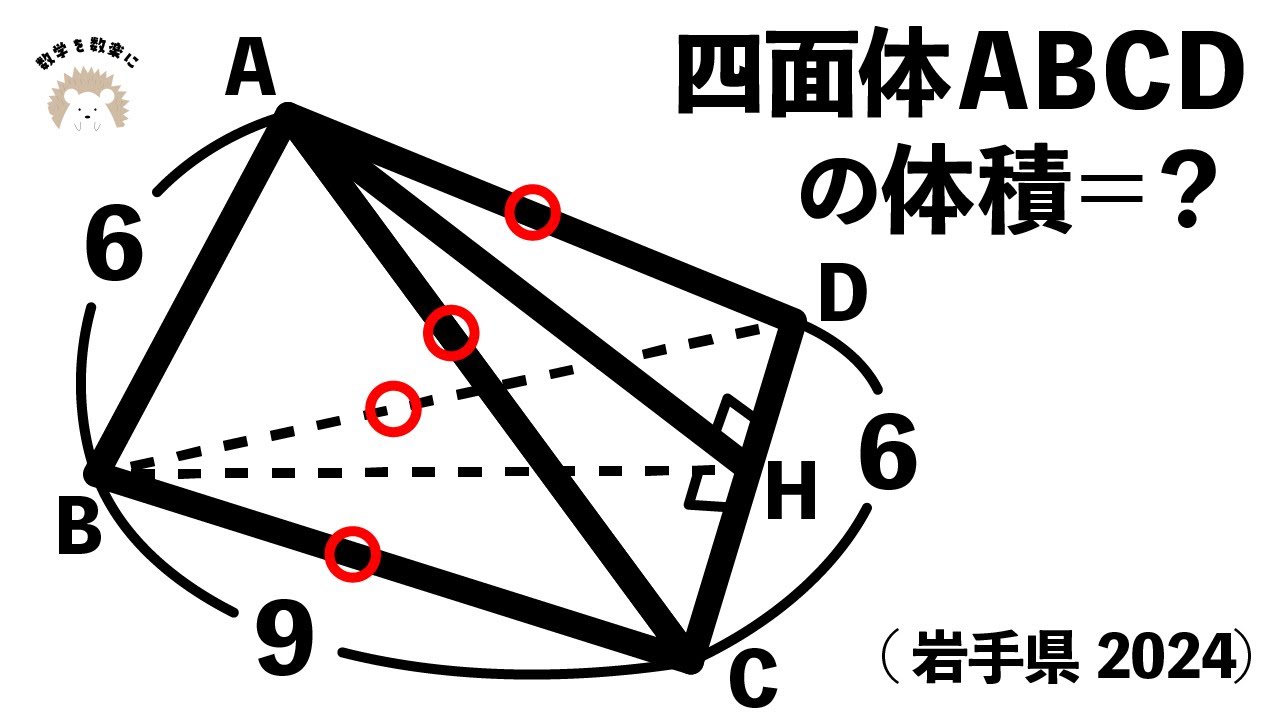
2024年岩手県のラスボス 四面体の体積
斜めの正方形

斜めの正方形

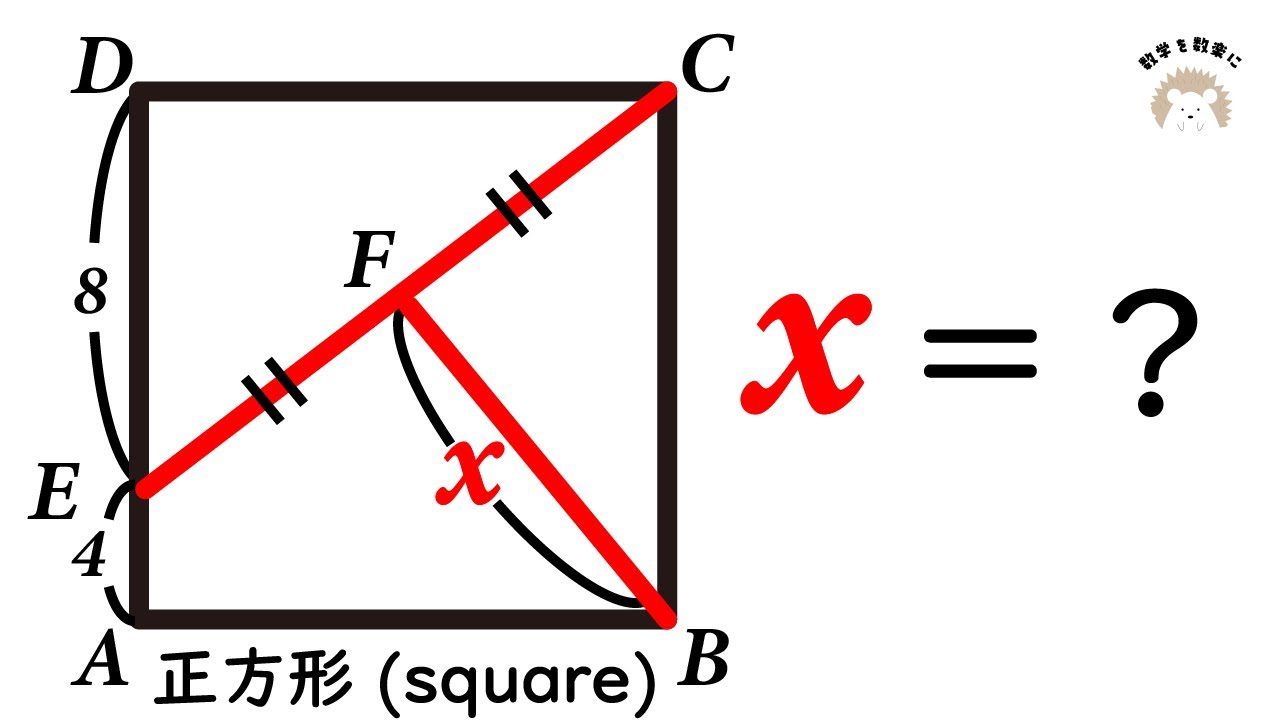
図形の問題に見えて〇〇の問題 2通りで解説 正方形
三角形の重心 一点で交わるのはなぜ?

