 式の計算(展開、因数分解)
式の計算(展開、因数分解)
 式の計算(展開、因数分解)
式の計算(展開、因数分解)
999 マークシートです B

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$999^2-1+999^2+4 \times 999 +3 = ▢ \times 10^▢$
日本大学櫻丘高等学校
この動画を見る
$999^2-1+999^2+4 \times 999 +3 = ▢ \times 10^▢$
日本大学櫻丘高等学校
【みんな好き好き】因数分解:中部~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
全国の入試 中部
$x^2-2(m-1)x-2m+1$
因数分解せよ。
この動画を見る
全国の入試 中部
$x^2-2(m-1)x-2m+1$
因数分解せよ。
【みんな大好き】因数分解:明治薬科~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 明治薬科
$x^2+4xy+3y^2+2x+4y+1$
因数分解せよ。
この動画を見る
入試問題 明治薬科
$x^2+4xy+3y^2+2x+4y+1$
因数分解せよ。
2021 素因数分解

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
2021を素因数分解せよ(ただし$45^2=2025$とする)
2021就実高等学校
この動画を見る
2021を素因数分解せよ(ただし$45^2=2025$とする)
2021就実高等学校
困ったら解の公式!? C 2021 明大明治

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$(\sqrt 2 + \sqrt 3 + \sqrt 6)(2\sqrt 2 - \sqrt 3 - \sqrt 6)=?$
$x^2+(\sqrt 2 - 2\sqrt 3 - 2\sqrt 6)x + (5+6\sqrt 2 -2\sqrt 3 -\sqrt 6 ) = 0$を解け
2021明治大学付属明治高等学校
この動画を見る
$(\sqrt 2 + \sqrt 3 + \sqrt 6)(2\sqrt 2 - \sqrt 3 - \sqrt 6)=?$
$x^2+(\sqrt 2 - 2\sqrt 3 - 2\sqrt 6)x + (5+6\sqrt 2 -2\sqrt 3 -\sqrt 6 ) = 0$を解け
2021明治大学付属明治高等学校
【みんな大好き】因数分解:長崎総合科学~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#長崎総合科学大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 長崎総合科学
$x^3+4x^2+x-6$
因数分解せよ。
この動画を見る
入試問題 長崎総合科学
$x^3+4x^2+x-6$
因数分解せよ。
2021慶應義塾最初の一問 B

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$(a^2-2a-6)(a^2-2a-17)+18$を因数分解せよ。
2021慶應義塾高等学校
この動画を見る
$(a^2-2a-6)(a^2-2a-17)+18$を因数分解せよ。
2021慶應義塾高等学校
慶應義塾 B 2021最初の一問

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$(a^2-2a-6)(a^2-2a-17)+18$を因数分解せよ。
2021慶應義塾高等学校
この動画を見る
$(a^2-2a-6)(a^2-2a-17)+18$を因数分解せよ。
2021慶應義塾高等学校
因数分解 A 中大横浜 2021

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$a^2(x-1)-x+1$を因数分解せよ。
中央大学附属横浜高等学校
この動画を見る
$a^2(x-1)-x+1$を因数分解せよ。
中央大学附属横浜高等学校
2021 慶應志木高校 最初の一題

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
a+b+c=0,abc=2021のとき
(ab+ca)(ca+bc)(bc+ab)=
2021慶應義塾志木高等学校
この動画を見る
a+b+c=0,abc=2021のとき
(ab+ca)(ca+bc)(bc+ab)=
2021慶應義塾志木高等学校
誘導に従って因数分解!! 2021中央大学附属 B

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$S=n^4-5n^3-10n^2+35n+49$
(1)$(n-\frac{7}{n})^2$を展開せよ。
(2)$t=n-\frac{7}{n}$とするとき$\frac{S}{n^2}$をtで表せ。
(3)Sを因数分解せよ。
2021中央大学附属高等学校
この動画を見る
$S=n^4-5n^3-10n^2+35n+49$
(1)$(n-\frac{7}{n})^2$を展開せよ。
(2)$t=n-\frac{7}{n}$とするとき$\frac{S}{n^2}$をtで表せ。
(3)Sを因数分解せよ。
2021中央大学附属高等学校
因数分解 B 2021 城北
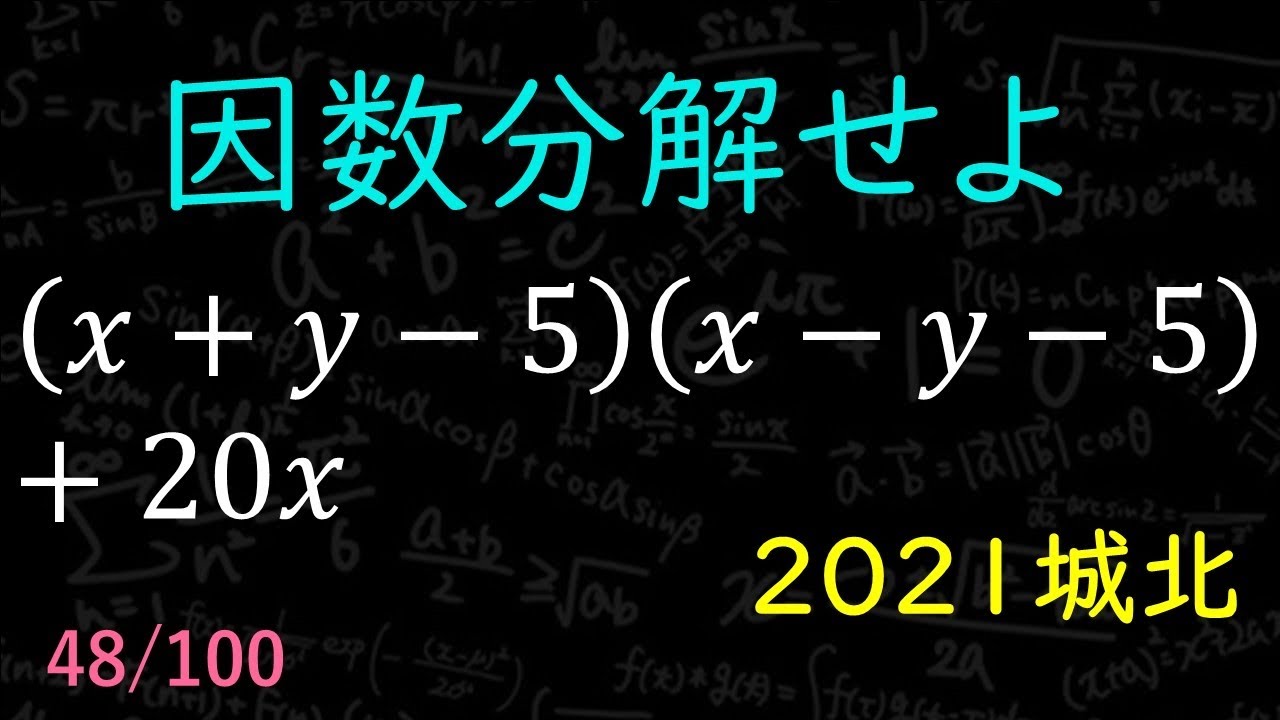
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
(x+y-5)(x-y-5)+20xを因数分解せよ。
2021城北高等学校
この動画を見る
(x+y-5)(x-y-5)+20xを因数分解せよ。
2021城北高等学校
因数分解 B 明大明治 2021

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$4a^2-b^2+16c^2-16ac$を因数分解せよ。
2021明治大学付属明治高等学校
この動画を見る
$4a^2-b^2+16c^2-16ac$を因数分解せよ。
2021明治大学付属明治高等学校
【みんな大好き】因数分解:明治大学付属明治高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#明治大学付属明治高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 明治大学付属明治高等学校
$(x-6y+3z)(x+2y-z)+5z(4y-z)-20y^2$
を因数分解すると▭である。
この動画を見る
入試問題 明治大学付属明治高等学校
$(x-6y+3z)(x+2y-z)+5z(4y-z)-20y^2$
を因数分解すると▭である。
そのまま代入すると大変!❓ 2021 城北

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x^2-x-1= 0 $の解のうち大きい方の解をaとする。
$3a^2-a-3=?$
2021城北高等学校
この動画を見る
$x^2-x-1= 0 $の解のうち大きい方の解をaとする。
$3a^2-a-3=?$
2021城北高等学校
2021 東大寺学園 因数分解 B

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
(3a+2c)(3a-2c)-b(b-4c)-(6a-1)を因数分解せよ。
2021東大寺学園高等学校
この動画を見る
(3a+2c)(3a-2c)-b(b-4c)-(6a-1)を因数分解せよ。
2021東大寺学園高等学校
2021 早稲田本庄最初の一問

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$4(x^2+2xy+y^2) - (2x+y+1)^2$を因数分解せよ。
2021早稲田大学 本庄高等学院
この動画を見る
$4(x^2+2xy+y^2) - (2x+y+1)^2$を因数分解せよ。
2021早稲田大学 本庄高等学院
因数分解:福岡大学附属大濠高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#福岡大学附属大濠高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 福岡大学附属大濠高等学校
次の問いに答えよ。
$x^2y^2-4x^2-9y^2+36$
を因数分解すると▭である。
この動画を見る
入試問題 福岡大学附属大濠高等学校
次の問いに答えよ。
$x^2y^2-4x^2-9y^2+36$
を因数分解すると▭である。
式の値の最大 最小 2021 ラ・サール C

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$-1 \leqq x \leqq 2$ , $3 \leqq y \leqq 4$のとき
$x^2y-y$の最大値,最小値は?
2021ラ・サール高等学校
この動画を見る
$-1 \leqq x \leqq 2$ , $3 \leqq y \leqq 4$のとき
$x^2y-y$の最大値,最小値は?
2021ラ・サール高等学校
2021 平方根と因数分解 A 昭和学院秀英
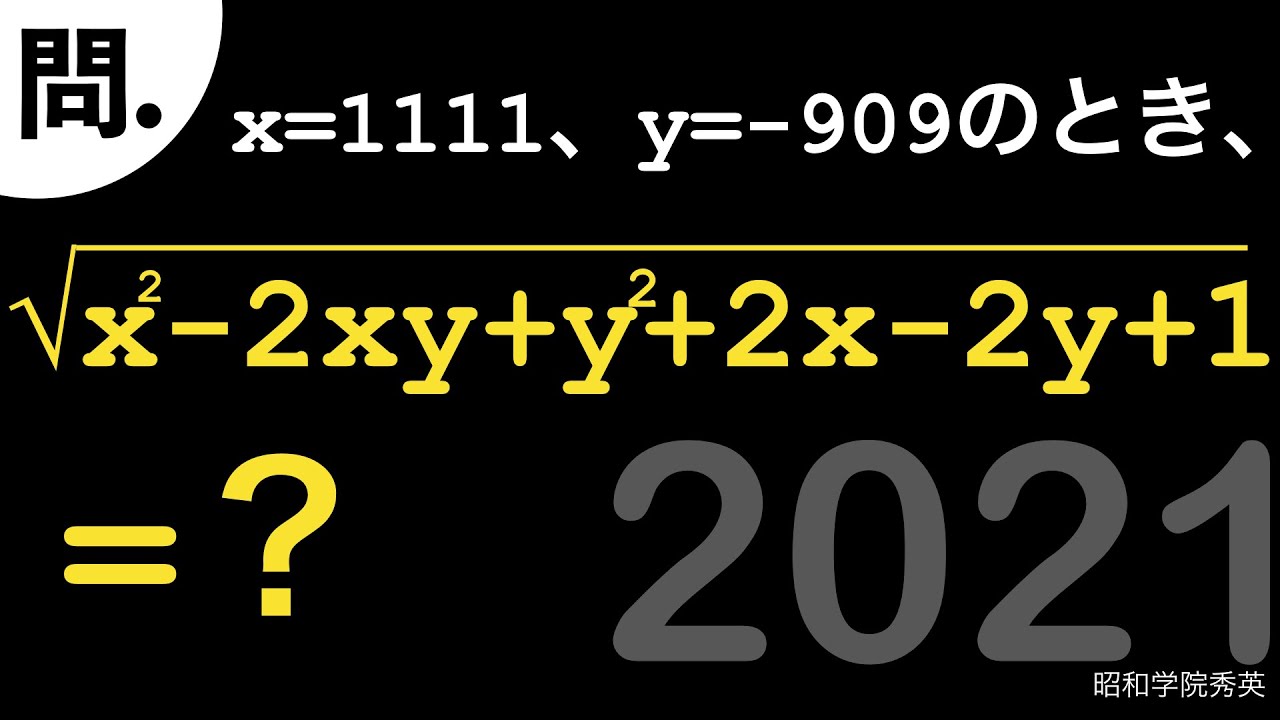
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#平方根#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
x=1111,y=-909のとき
$\sqrt{x^2-2xy+y^2+2x-2y+1} =?$
2021昭和学院秀英高等学校
この動画を見る
x=1111,y=-909のとき
$\sqrt{x^2-2xy+y^2+2x-2y+1} =?$
2021昭和学院秀英高等学校
【高校受験対策/数学】死守66

単元:
#数学(中学生)#中1数学#中2数学#中3数学#方程式#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根#2次方程式#空間図形#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守66
①$6x\times2xy\div3y$を計算しなさい。
②$\sqrt{18}-6\sqrt{2}$を計算しなさい。
③$x^2+4x-12$を因数分解しなさい。
④2次方程式$3x^2-5x+1=0$を解きなさい。
⑤方程式$5x+3=2x+6$を解きなさい。
⑥$\frac{1}{2}(3x-y)-\frac{4x-y}{3}$を計算しなさい。
⑦2次方程式$2(x-2)^2-3(x-2)+1=0$を解きなさい。
⑧$x=2+\sqrt{3}$、$y=2-\sqrt{3}$のとき、$(1+\frac{1}{x})(1+\frac{1}{y})$の値を求めなさい。
⑨右の図のような、底面の半径が3cm、高さが4cmの円錐があります。この円錐の表面積を求めなさい。ただし円周率は$\pi$とします。
➉右の図のように、円Oとこの円の外部の点Pがあります。
点Pを通る円の接線をコンパスと定規を使って1つ作図しなさい。
ただし、作するためにかいた線は消さないでおきなさい。
この動画を見る
高校受験対策・死守66
①$6x\times2xy\div3y$を計算しなさい。
②$\sqrt{18}-6\sqrt{2}$を計算しなさい。
③$x^2+4x-12$を因数分解しなさい。
④2次方程式$3x^2-5x+1=0$を解きなさい。
⑤方程式$5x+3=2x+6$を解きなさい。
⑥$\frac{1}{2}(3x-y)-\frac{4x-y}{3}$を計算しなさい。
⑦2次方程式$2(x-2)^2-3(x-2)+1=0$を解きなさい。
⑧$x=2+\sqrt{3}$、$y=2-\sqrt{3}$のとき、$(1+\frac{1}{x})(1+\frac{1}{y})$の値を求めなさい。
⑨右の図のような、底面の半径が3cm、高さが4cmの円錐があります。この円錐の表面積を求めなさい。ただし円周率は$\pi$とします。
➉右の図のように、円Oとこの円の外部の点Pがあります。
点Pを通る円の接線をコンパスと定規を使って1つ作図しなさい。
ただし、作するためにかいた線は消さないでおきなさい。
【高校受験対策/数学】死守65

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(展開、因数分解)#2次方程式#比例・反比例#平行と合同#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守65
①右の図のように、直線$l$、直線$m$と2つの直線が交わっている。
$\angle a,\angle b,\angle c,\angle d,\angle e$のうち、どの角とどの角が等しければ、直線$l$と直線$m$が平行であるといえるか、その2つの角を答えなさい。
②$x^2-10x+25$を因数分解しなさい。
③2次方程式$(2x-5)^2=18$を解きなさい。
④右のア~オのうち、絶対値が最も大きい数を選び、記号で答えなさい。
ア $3.2$
イ $-\frac{7}{2}$
ウ $2\sqrt{2}$
エ $\frac{10}{3}$
オ $-3$
⑤右のア~オのうち、$y$が$x$に比例するものをすべて選び、記号で答えなさい。
ア 自然数$x$の約数の個数は$y$ 個である。
イ $x$ 円の商品を1000円支払って買うとき、おつりは$y$ 円である。
ウ 1200mの道のりを分速$x$ mの速さで進むとき、かかる時間は$y$ 分である。
エ 15%の食塩水が$x$ gあるとき、この食塩水に含まれる食塩の量は$y$ gである。
オ 何も入っていない容器に水を毎分2Lずつ$x$ 分間入れるとき、たまる水の量は$y$ Lである。
⑥右のア~オのうち、関数$y=2x^2$ついて述べた文として正しいものをすべて選び、記号で答えなさい。
ア この関数のグラフは、原点を通る。
イ $x \gt 0$のとき、$x$が増加すると$y$は減少する。
ウ この関数のグラフは$x$ 軸について対称である。
エ $x$の変域が$-1 \leqq x \leqq 2$のとき、$y$の変域は$0 \leqq y \leqq 8$である。
オ $x$の値がどの値からどの値まで増加するかに関わらず、変化の割合は常に2である。
この動画を見る
高校受験対策・死守65
①右の図のように、直線$l$、直線$m$と2つの直線が交わっている。
$\angle a,\angle b,\angle c,\angle d,\angle e$のうち、どの角とどの角が等しければ、直線$l$と直線$m$が平行であるといえるか、その2つの角を答えなさい。
②$x^2-10x+25$を因数分解しなさい。
③2次方程式$(2x-5)^2=18$を解きなさい。
④右のア~オのうち、絶対値が最も大きい数を選び、記号で答えなさい。
ア $3.2$
イ $-\frac{7}{2}$
ウ $2\sqrt{2}$
エ $\frac{10}{3}$
オ $-3$
⑤右のア~オのうち、$y$が$x$に比例するものをすべて選び、記号で答えなさい。
ア 自然数$x$の約数の個数は$y$ 個である。
イ $x$ 円の商品を1000円支払って買うとき、おつりは$y$ 円である。
ウ 1200mの道のりを分速$x$ mの速さで進むとき、かかる時間は$y$ 分である。
エ 15%の食塩水が$x$ gあるとき、この食塩水に含まれる食塩の量は$y$ gである。
オ 何も入っていない容器に水を毎分2Lずつ$x$ 分間入れるとき、たまる水の量は$y$ Lである。
⑥右のア~オのうち、関数$y=2x^2$ついて述べた文として正しいものをすべて選び、記号で答えなさい。
ア この関数のグラフは、原点を通る。
イ $x \gt 0$のとき、$x$が増加すると$y$は減少する。
ウ この関数のグラフは$x$ 軸について対称である。
エ $x$の変域が$-1 \leqq x \leqq 2$のとき、$y$の変域は$0 \leqq y \leqq 8$である。
オ $x$の値がどの値からどの値まで増加するかに関わらず、変化の割合は常に2である。
2021入試予想問題~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2021入試予想問題~全国入試問題解法
以下の問いに答えなさい。
$2001 + 2002 + 2003 + … + 2021$
を計算せよ。
この動画を見る
2021入試予想問題~全国入試問題解法
以下の問いに答えなさい。
$2001 + 2002 + 2003 + … + 2021$
を計算せよ。
2021入試予想問題~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2021入試予想問題~全国入試問題解法
次の入試問題を解け。
$2021 = 43 × 47$
①$2025=45^2$であることを
利用して $2021$の約数を求めよ。
②$2025=45^2$であることを
利用して $2021$の約数を求めよ。
③以下の式を計算せよ
$2025^2+2020 \times 2021-4041 \times 2025$
④$2001+2002+2003+....+2021$
を計算せよ。
⑤$a,ℓ$:自然数、$a$を$ℓ$で割った余り$R_{ℓ}(a)$
(1)$R_{40} (2021), R_{40} (2021^2)$を求めよ。
(2)$R_{40} (2021^{2021})$を求めよ。
⑥ある整数$x$を$12$で割ると、
余りろとなりました。
このとき、$x$を$2021$倍した
$2021x$を$12$で割った余りを求めよ。
⑦ $3^{2021}$の一の位の数を求めなさい。
この動画を見る
2021入試予想問題~全国入試問題解法
次の入試問題を解け。
$2021 = 43 × 47$
①$2025=45^2$であることを
利用して $2021$の約数を求めよ。
②$2025=45^2$であることを
利用して $2021$の約数を求めよ。
③以下の式を計算せよ
$2025^2+2020 \times 2021-4041 \times 2025$
④$2001+2002+2003+....+2021$
を計算せよ。
⑤$a,ℓ$:自然数、$a$を$ℓ$で割った余り$R_{ℓ}(a)$
(1)$R_{40} (2021), R_{40} (2021^2)$を求めよ。
(2)$R_{40} (2021^{2021})$を求めよ。
⑥ある整数$x$を$12$で割ると、
余りろとなりました。
このとき、$x$を$2021$倍した
$2021x$を$12$で割った余りを求めよ。
⑦ $3^{2021}$の一の位の数を求めなさい。
因数分解:日本大学第二高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#日本大学第二高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 日本大学第二高等学校
$(x^2+3)^2-16x^2$
を因数分解せよ。
この動画を見る
入試問題 日本大学第二高等学校
$(x^2+3)^2-16x^2$
を因数分解せよ。
2001を素因数分解せよ 土佐高校

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{676} = ?$
2001を素因数分解せよ。
2011土佐高等学校
この動画を見る
$\sqrt{676} = ?$
2001を素因数分解せよ。
2011土佐高等学校
因数分解:函館ラ・サール高等学校~全国入試問題解法【メリクリ!】

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#函館ラ・サール高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 函館ラ・サール高等学校
$a^2 – 9b^2 – 4a + 4$
を因数分解しなさい。
この動画を見る
入試問題 函館ラ・サール高等学校
$a^2 – 9b^2 – 4a + 4$
を因数分解しなさい。
【高校受験対策/数学】死守60

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#平方根#空間図形#1次関数#平行と合同#確率#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守605-41
①$-5-(-7)$を計算しなさい。
➁$(\frac{1}{4}-\frac{2}{3})\times 12$を計算しなさい。
③$4x \times\frac{2}{5}xy \div 2x^2$を計算しなさい。
④$(-2a+3)(2a+3)+9$を計算しなさい。
⑤$\sqrt{24} \div \sqrt{8}-\sqrt{12}$を計算しなさい。
⑥$150$を素因数分解しなさい。
⑦次の連立方程式を解きなさい。
$y=4(x+2)$
$6x-y=-10$
⑧次の数量の関係を等式で表しなさい。
100円硬貨が$a$ 枚、50円硬貨が$b$ 枚あり、これらをすべて10円硬貨に両替すると$c$ 枚になる。
⑨箱の中に同じ大きさの白玉がたくさん入っている。
そこに同じ大きさの黒玉100個入れてよくかき混ぜた後、その中から34個の玉を無作為に取りだしたところ、黒玉が4個入っていた。
この結果から、箱の中にはおよそ何個の白玉が入っていると考えられるか求めなさい。
➉半径6cmの球を中心$o$を通る平面で切った半球の表面積を求めなさい。
⑪右の図で$l /\!/ m$、$AB=AC$のとき、$\angle x$ の大きさを求めなさい。
この動画を見る
高校受験対策・死守605-41
①$-5-(-7)$を計算しなさい。
➁$(\frac{1}{4}-\frac{2}{3})\times 12$を計算しなさい。
③$4x \times\frac{2}{5}xy \div 2x^2$を計算しなさい。
④$(-2a+3)(2a+3)+9$を計算しなさい。
⑤$\sqrt{24} \div \sqrt{8}-\sqrt{12}$を計算しなさい。
⑥$150$を素因数分解しなさい。
⑦次の連立方程式を解きなさい。
$y=4(x+2)$
$6x-y=-10$
⑧次の数量の関係を等式で表しなさい。
100円硬貨が$a$ 枚、50円硬貨が$b$ 枚あり、これらをすべて10円硬貨に両替すると$c$ 枚になる。
⑨箱の中に同じ大きさの白玉がたくさん入っている。
そこに同じ大きさの黒玉100個入れてよくかき混ぜた後、その中から34個の玉を無作為に取りだしたところ、黒玉が4個入っていた。
この結果から、箱の中にはおよそ何個の白玉が入っていると考えられるか求めなさい。
➉半径6cmの球を中心$o$を通る平面で切った半球の表面積を求めなさい。
⑪右の図で$l /\!/ m$、$AB=AC$のとき、$\angle x$ の大きさを求めなさい。
【中学数学】多項式:25x²-100y²の因数分解、あなたは引っ掛からずに解けますか??

【やり方をマスターしよう!】因数分解:東大寺学園入試~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#東大寺学園高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東大寺学園の高校
次の問いに答えよ。
$4(a+b)(a-b)+c(ac-c)$
この動画を見る
入試問題 東大寺学園の高校
次の問いに答えよ。
$4(a+b)(a-b)+c(ac-c)$
