 2次関数
2次関数
 2次関数
2次関数
2次関数を通る直線の式の求め方

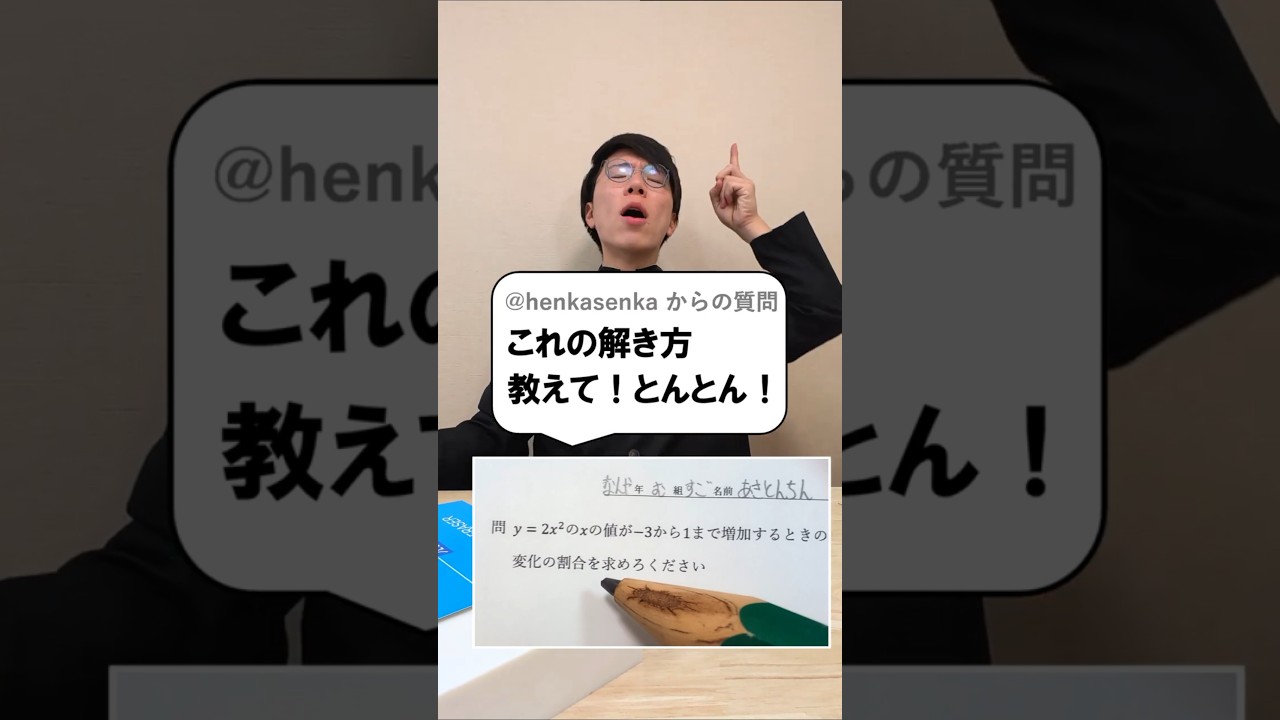
これどうやって解く?
単元:
#数学(中学生)#中3数学#2次関数
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$y=2x^2$の4$x$の値が$-3$から$1$まで増加するときの
変化の割合を求めなさい。
この動画を見る
$y=2x^2$の4$x$の値が$-3$から$1$まで増加するときの
変化の割合を求めなさい。
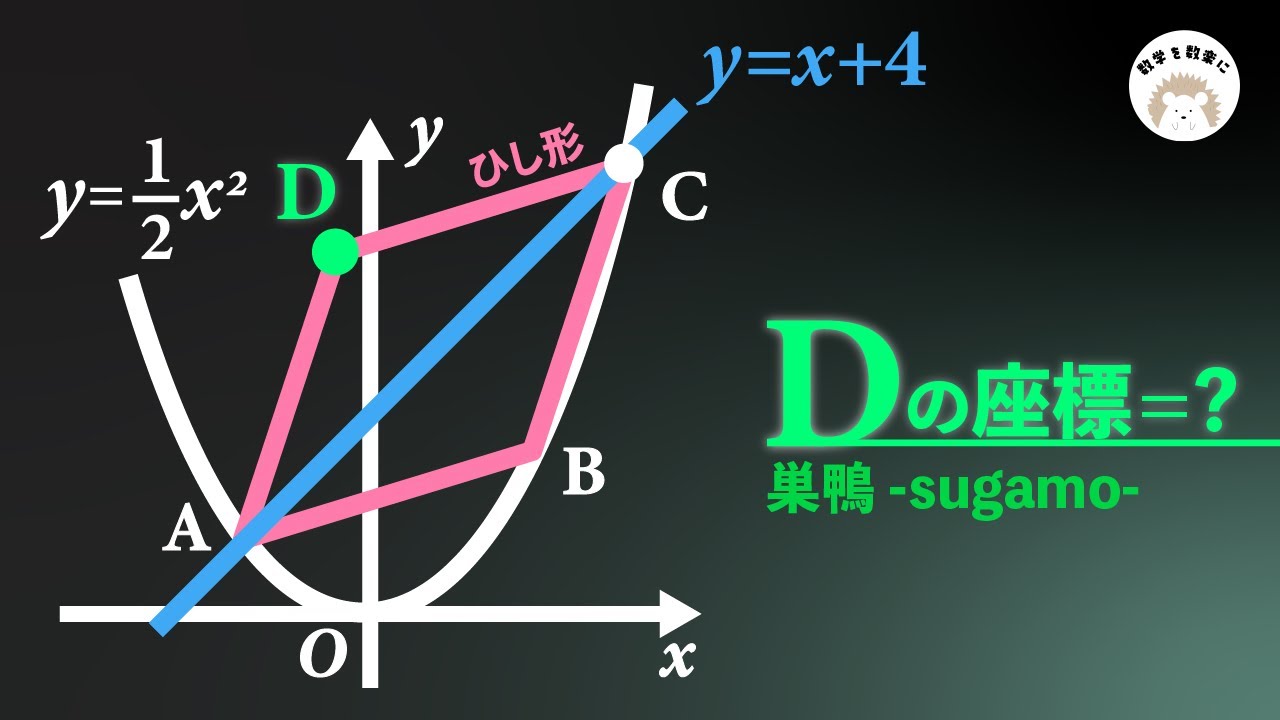
バリバリの高校入試問題 巣鴨高校 座標平面上のひし形
2次関数(放物線)折ることできる?

何を折っているでしょう?

【中学数学】2次関数の問題~2024年度北海道公立高校入試大問3~【高校受験】
単元:
#数学(中学生)#中3数学#数Ⅰ#2次関数#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
ユキさんたちのクラスでは、数学の授業で関数のグラフについてコンピュータを使って学習しています。次の問いに答えなさい。
問1 先生が提示した画面1には、関数$y=x^{ 2 }$のグラフと、このグラフ上の2点A、Bを通る直線が表示されています。点Aの$x$座標は3、点Bの$x$座標は-2です。点Oは原点とします。
ユキさんは、画面1を見て、2点A、Bを通る直線の式を求めたいと考え、求め方について、次のような見通しを立てています。
ユキさんの見通し
2点A、Bを通る直線の式を求めるには、2点A、Bの座標がわかれば良い。
次の(1)、(2)に答えなさい。
(1)点Aの$y$座標を求めなさい。
(2)ユキさんの見通しを用いて、2点A、Bを通る直線の式を求めなさい。
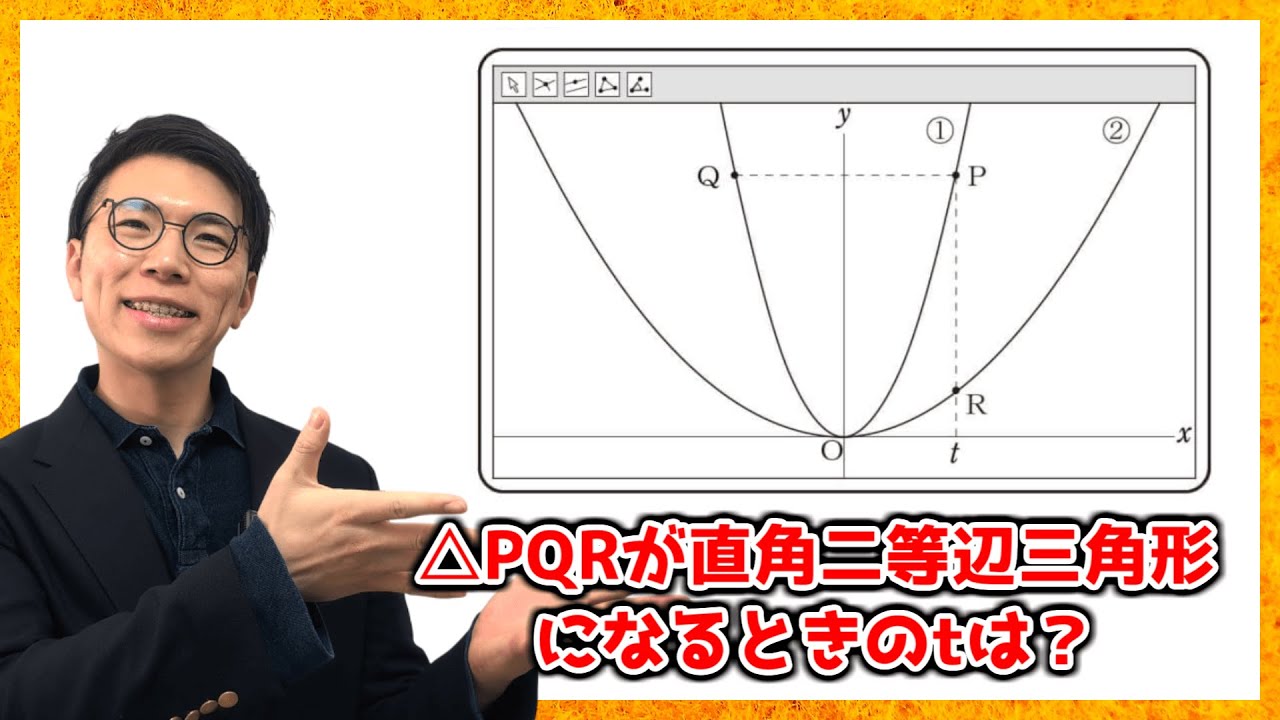
問2 △PQRが直角二等辺三角形になる時の$t$の値を求めなさい。
先生が提示した画面2には2つの関数$y=2x^{ 2 }$・・・①,$y=\frac{1}{2}x^{ 2 }$・・・②のグラフが表示されています。①のグラフ上に点Pがあり、点Pの$x$座標は$t$です。点Qは、点Pと$y$軸について対称な点です。また、点Rは、点Pを通り、$y$軸に平行な直線と②のグラフとの交点です。点Oは原点とし、$t$>0とします。
ユキさんたちは、点Pを①のグラフ上で動かすことで、△PQRがどのように変化するかについて、話し合っています。
ユキさん「点Pを動かすと、点Qと点Rも同時に動くね。」
ルイさん「このとき、△PQRはいつでも直角三角形になるね。」
ユキさん「・・・あれ?△PQRが直角に等辺三角形に見えるときがあるよ?」
ルイさん「本当に直角二等辺三角形になるときがあるのかな。」
ユキさん「じゃあ、△PQRが直角二等辺三角形になるときの点Pの座標を求めてみようか。」
ルイさん「点Pの座標を求めるには、$t$の値がわかればいいね。」
△PQRが直角二等辺三角形になるときの$t$の値を求めなさい。
この動画を見る
ユキさんたちのクラスでは、数学の授業で関数のグラフについてコンピュータを使って学習しています。次の問いに答えなさい。
問1 先生が提示した画面1には、関数$y=x^{ 2 }$のグラフと、このグラフ上の2点A、Bを通る直線が表示されています。点Aの$x$座標は3、点Bの$x$座標は-2です。点Oは原点とします。
ユキさんは、画面1を見て、2点A、Bを通る直線の式を求めたいと考え、求め方について、次のような見通しを立てています。
ユキさんの見通し
2点A、Bを通る直線の式を求めるには、2点A、Bの座標がわかれば良い。
次の(1)、(2)に答えなさい。
(1)点Aの$y$座標を求めなさい。
(2)ユキさんの見通しを用いて、2点A、Bを通る直線の式を求めなさい。
問2 △PQRが直角二等辺三角形になる時の$t$の値を求めなさい。
先生が提示した画面2には2つの関数$y=2x^{ 2 }$・・・①,$y=\frac{1}{2}x^{ 2 }$・・・②のグラフが表示されています。①のグラフ上に点Pがあり、点Pの$x$座標は$t$です。点Qは、点Pと$y$軸について対称な点です。また、点Rは、点Pを通り、$y$軸に平行な直線と②のグラフとの交点です。点Oは原点とし、$t$>0とします。
ユキさんたちは、点Pを①のグラフ上で動かすことで、△PQRがどのように変化するかについて、話し合っています。
ユキさん「点Pを動かすと、点Qと点Rも同時に動くね。」
ルイさん「このとき、△PQRはいつでも直角三角形になるね。」
ユキさん「・・・あれ?△PQRが直角に等辺三角形に見えるときがあるよ?」
ルイさん「本当に直角二等辺三角形になるときがあるのかな。」
ユキさん「じゃあ、△PQRが直角二等辺三角形になるときの点Pの座標を求めてみようか。」
ルイさん「点Pの座標を求めるには、$t$の値がわかればいいね。」
△PQRが直角二等辺三角形になるときの$t$の値を求めなさい。
【定義に従え…!】平方根:江戸川学園取手高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#平方根#2次関数#高校入試過去問(数学)#江戸川学園取手高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
関数$y=\sqrt{x}\;$について、$x\;$の値が4から9まで増加するときの変化の割合を求めなさい。
この動画を見る
関数$y=\sqrt{x}\;$について、$x\;$の値が4から9まで増加するときの変化の割合を求めなさい。
【とても大切な問題…!】二次関数:京都府~全国入試問題解法
単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)#京都府公立高校入試
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
関数$y=\displaystyle\frac{1}{4}x^2\;$について、$a\leqq x \leqq 3,\;\; b\leqq y \leqq 9\;$のとき、$a,b\;$の値をそれぞれ求めよ。
この動画を見る
関数$y=\displaystyle\frac{1}{4}x^2\;$について、$a\leqq x \leqq 3,\;\; b\leqq y \leqq 9\;$のとき、$a,b\;$の値をそれぞれ求めよ。
【一度は解きたい…!】二次関数:ノートルダム女学院高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#2次関数
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
放物線$y=a^2x^2\;$と直線$y=ax+2\;$が異なる2点$A,B\;$で交わっている。ただし、$a \gt 0$
$\triangle OAB\;$の面積が15となる$a$の値を求めよ。
この動画を見る
放物線$y=a^2x^2\;$と直線$y=ax+2\;$が異なる2点$A,B\;$で交わっている。ただし、$a \gt 0$
$\triangle OAB\;$の面積が15となる$a$の値を求めよ。
バリバリの高校入試問題 巣鴨高校 座標平面上のひし形

バリバリの高校入試問題 巣鴨高校 座標平面上のひし形

2024開成高校最初の1問

単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)#開成高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
動画内の図を参照し、$Z$の座標を求めなさい。
出典:2024開成高等学校
この動画を見る
動画内の図を参照し、$Z$の座標を求めなさい。
出典:2024開成高等学校
放物線と正三角形 開成高校

単元:
#中3数学#2次関数#高校入試過去問(数学)#開成高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
動画内の図を参照し、正三角形$\rm{ABC}$の1辺の長さを求めよ。
出典:開成高校
この動画を見る
動画内の図を参照し、正三角形$\rm{ABC}$の1辺の長さを求めよ。
出典:開成高校
この問題一瞬で解ける?
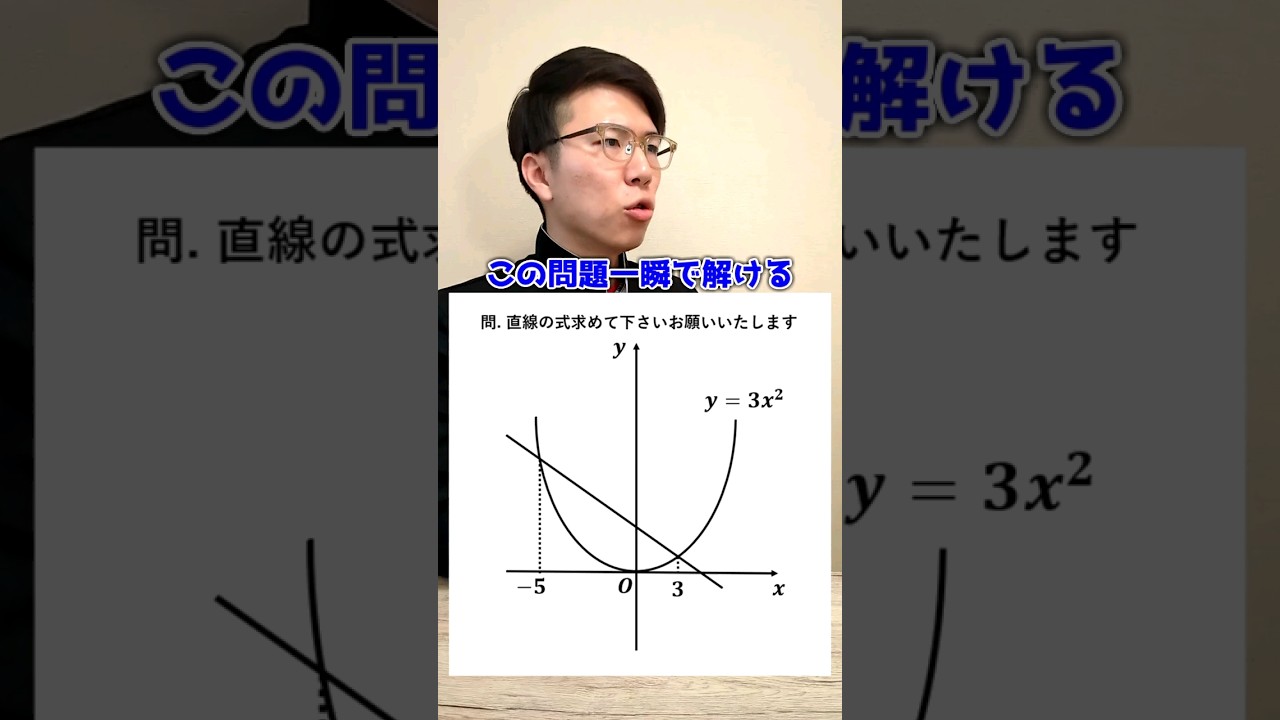
【イメージできるか…!】法政大学第二高等学校:二次関数~全国入試問題解法
単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)#法政大学第二高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
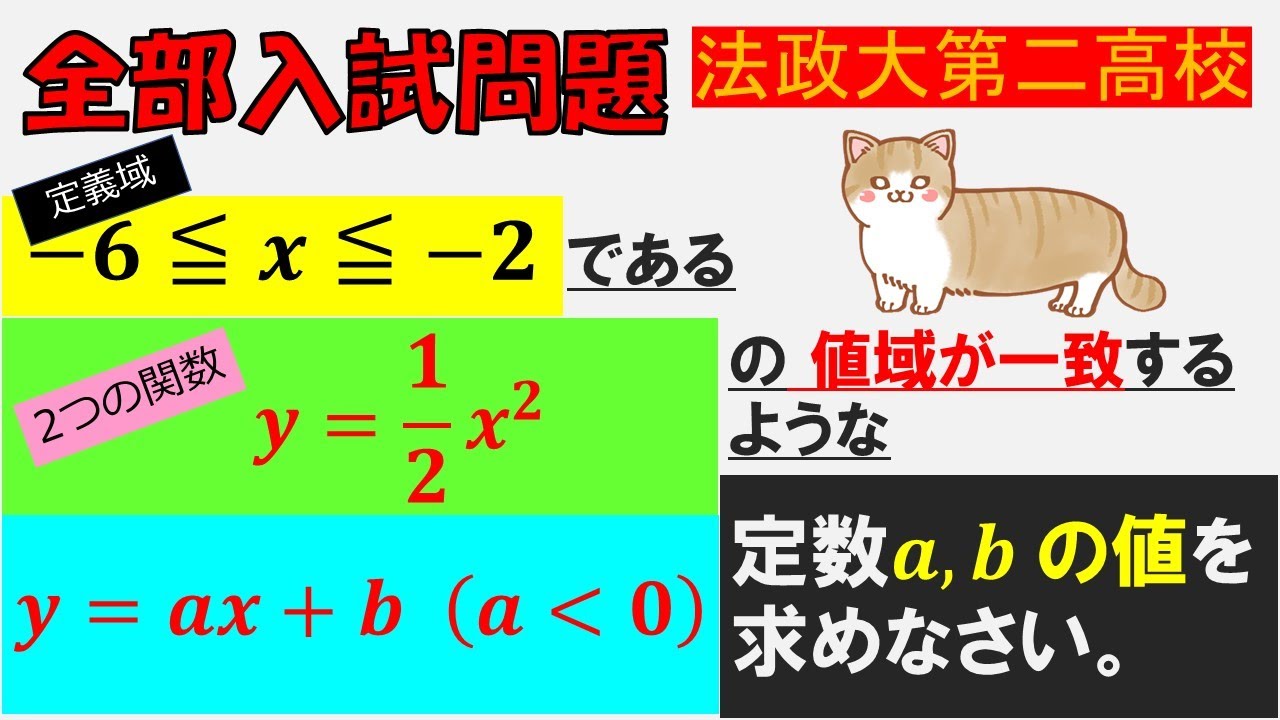
定義域$ -6 \leqq x \leqq -2 $である2つの関数
$ y=\dfrac{1}{2}x^2, y=ax+b(a \lt 0)$の値域が一致するような
定数$ a,b $の値を求めなさい.
法政大第二高校過去問
この動画を見る
定義域$ -6 \leqq x \leqq -2 $である2つの関数
$ y=\dfrac{1}{2}x^2, y=ax+b(a \lt 0)$の値域が一致するような
定数$ a,b $の値を求めなさい.
法政大第二高校過去問
【よく出題される…!】二次関数:和洋国府台女子高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#2次関数
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
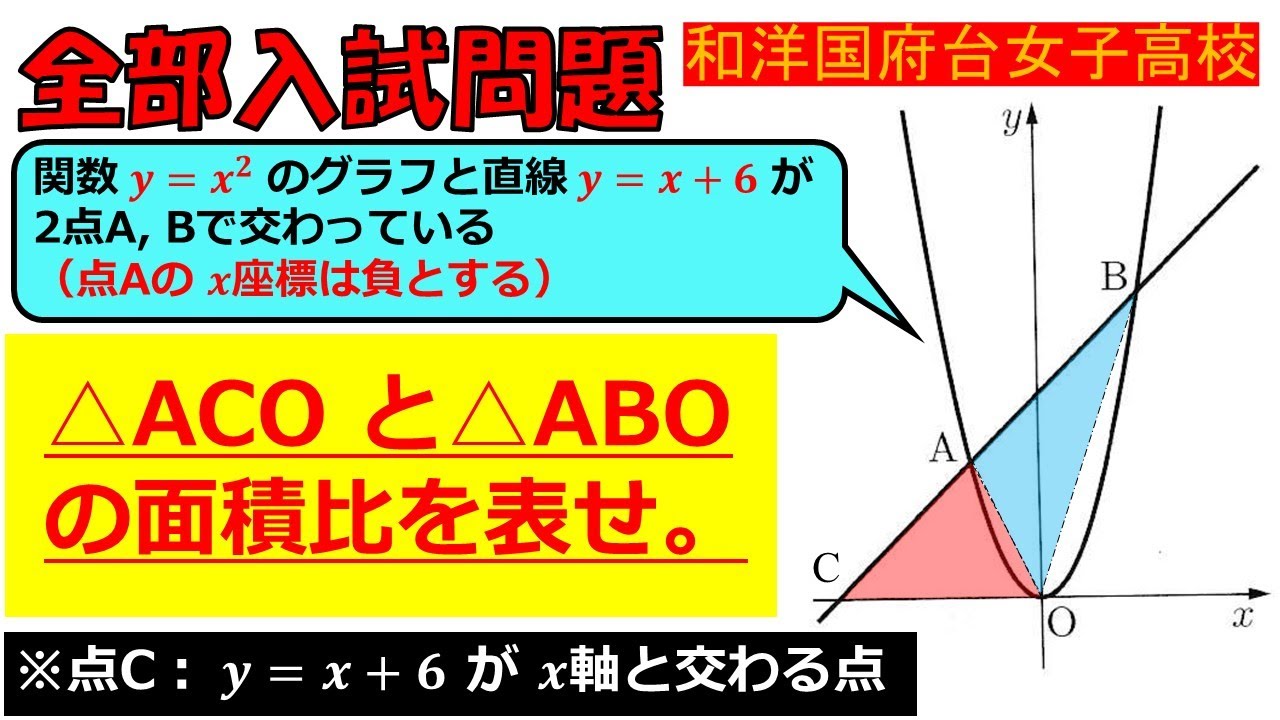
関数$ y=x^2 $のグラフと直線$ y=x+6 $が2点$ A,B $で交わっている.
(点Aのx座標は負とする)
$ \triangle ACO$ と$ \triangle ABO $の面積比を表せ.
和洋国府台女子高校過去問
この動画を見る
関数$ y=x^2 $のグラフと直線$ y=x+6 $が2点$ A,B $で交わっている.
(点Aのx座標は負とする)
$ \triangle ACO$ と$ \triangle ABO $の面積比を表せ.
和洋国府台女子高校過去問
数学好きな皆さまへ。解いてみて下さい

彼は何をしているのか?

グラフをかけ。

二次関数と三角形には簡単に面積を導ける裏ワザがある~全国入試問題解法 #shorts #数学 #高校入試 #sound #裏ワザ

単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
関数$ y=x^2 $のグラフ上に2点A,Bがある.
点A:x=-2,点B:x=1
(1)点Aのy座標を求めよ.
(2)直線ABの式を求めよ.
(3)$ \triangle OAB $の面積を求めよ.
長崎県高校過去問
この動画を見る
関数$ y=x^2 $のグラフ上に2点A,Bがある.
点A:x=-2,点B:x=1
(1)点Aのy座標を求めよ.
(2)直線ABの式を求めよ.
(3)$ \triangle OAB $の面積を求めよ.
長崎県高校過去問
【「変化の割合」のガイネンは今後も大切!】二次関数:法政大学第二高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ a \gt 0 $とする.
$ y=ax+2$と$ y-ax^2 $において
xが-1からaまで増加するときの変化の割合が等しいとき,
aの値を求めなさい.
法大第二高校過去問
この動画を見る
$ a \gt 0 $とする.
$ y=ax+2$と$ y-ax^2 $において
xが-1からaまで増加するときの変化の割合が等しいとき,
aの値を求めなさい.
法大第二高校過去問
【3分で勝負するには!】二次関数:長崎県公立高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
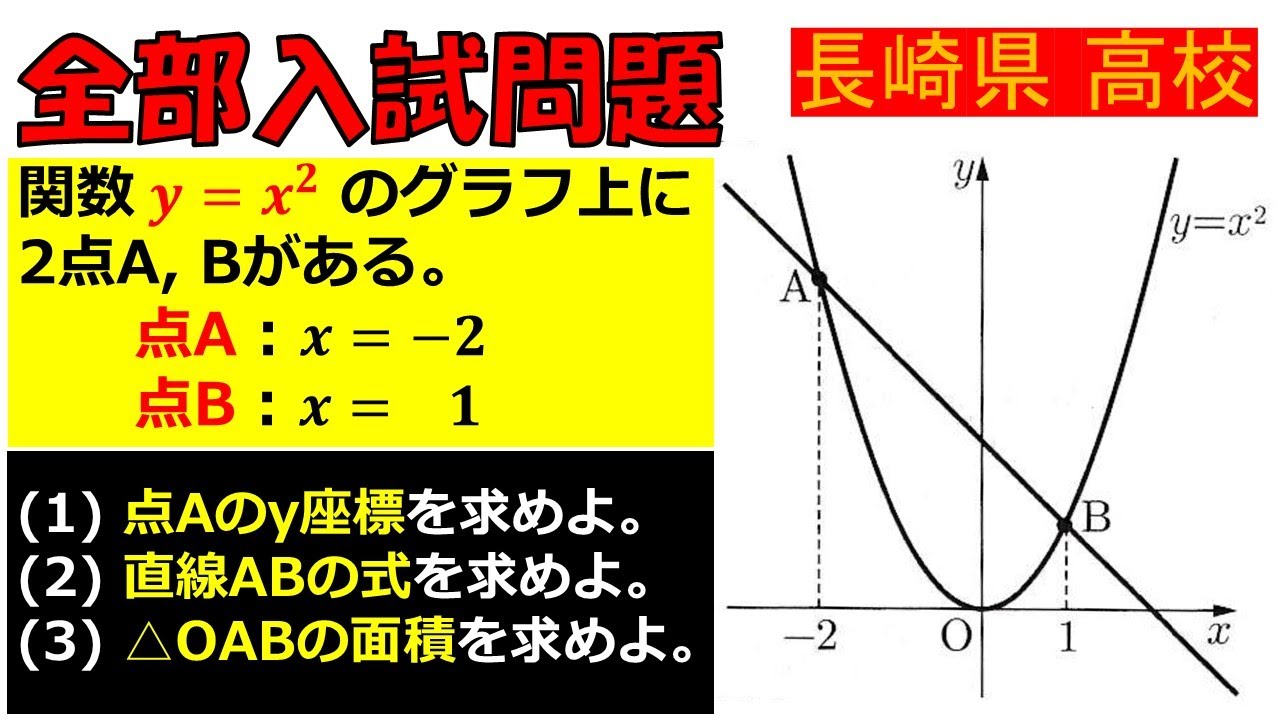
関数$ y=x^2 $のグラフ上に2点A,Bがある.
点A:x=-2,点B:x=1
(1)点Aのy座標を求めよ.
(2)直線ABの式を求めよ.
(3)$ \triangle OAB $の面積を求めよ.
長崎県高校過去問
この動画を見る
関数$ y=x^2 $のグラフ上に2点A,Bがある.
点A:x=-2,点B:x=1
(1)点Aのy座標を求めよ.
(2)直線ABの式を求めよ.
(3)$ \triangle OAB $の面積を求めよ.
長崎県高校過去問
高等学校入学試験予想問題:三重県公立高等学校~全部入試問題

単元:
#数学(中学生)#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#1次関数#2次関数#円
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \boxed{1}$
(1)$ -1+4\div \dfrac{2}{3}$
(2)$ 3(2a+5b)-(a+2b)$
(3)$ (x-2)(x+2)+(x-1)(x+4)$
(4)$ x^2+5x+3=0 $
$ \boxed{2}$
(1)点Pの座標は?
(2)y軸上に点Q,Qのy座標をt($ t \gt 4 $)とする.
Qを通り,x軸に平行な直線とb,mの交点をR,Sとする.
①t=6のとき,$ \triangle PRS $は?
②$ \triangle PRS $の面積が$ \triangle ABP $の5倍であるとき,tは?
$ \boxed{3}$
円周上にA,B,C,D,Eがある.
$AC=AE$,$\stackrel{\huge\frown}{BC}$=$\stackrel{\huge\frown}{DE}$であり,交点$ F,G$である.
(1)$ \triangle ABC \equiv \triangle AGE $を証明せよ.
(2)$ AB=4 $cm,$ AE=6$cm,$ DG=3 $cmのとき,
①$ AF=? $
②$ \triangle ABG $と$ \triangle CEF $の面積比を求めよ.
この動画を見る
$ \boxed{1}$
(1)$ -1+4\div \dfrac{2}{3}$
(2)$ 3(2a+5b)-(a+2b)$
(3)$ (x-2)(x+2)+(x-1)(x+4)$
(4)$ x^2+5x+3=0 $
$ \boxed{2}$
(1)点Pの座標は?
(2)y軸上に点Q,Qのy座標をt($ t \gt 4 $)とする.
Qを通り,x軸に平行な直線とb,mの交点をR,Sとする.
①t=6のとき,$ \triangle PRS $は?
②$ \triangle PRS $の面積が$ \triangle ABP $の5倍であるとき,tは?
$ \boxed{3}$
円周上にA,B,C,D,Eがある.
$AC=AE$,$\stackrel{\huge\frown}{BC}$=$\stackrel{\huge\frown}{DE}$であり,交点$ F,G$である.
(1)$ \triangle ABC \equiv \triangle AGE $を証明せよ.
(2)$ AB=4 $cm,$ AE=6$cm,$ DG=3 $cmのとき,
①$ AF=? $
②$ \triangle ABG $と$ \triangle CEF $の面積比を求めよ.
2023高校入試数学解説86問目 二次関数と変域の応用 埼玉県学校選択問題(改)

単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$y=2x^2$についてxの変域が$a \leqq x \leqq a+4$のときyの変域は$0 \leqq y \leqq 18$となった。
aの値をすべて求めよ。
2023埼玉県
この動画を見る
$y=2x^2$についてxの変域が$a \leqq x \leqq a+4$のときyの変域は$0 \leqq y \leqq 18$となった。
aの値をすべて求めよ。
2023埼玉県
2023高校入試数学解説84問目 一次関数と二次関数 埼玉県学校選択問題
単元:
#数学(中学生)#中2数学#中3数学#1次関数#2次関数#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
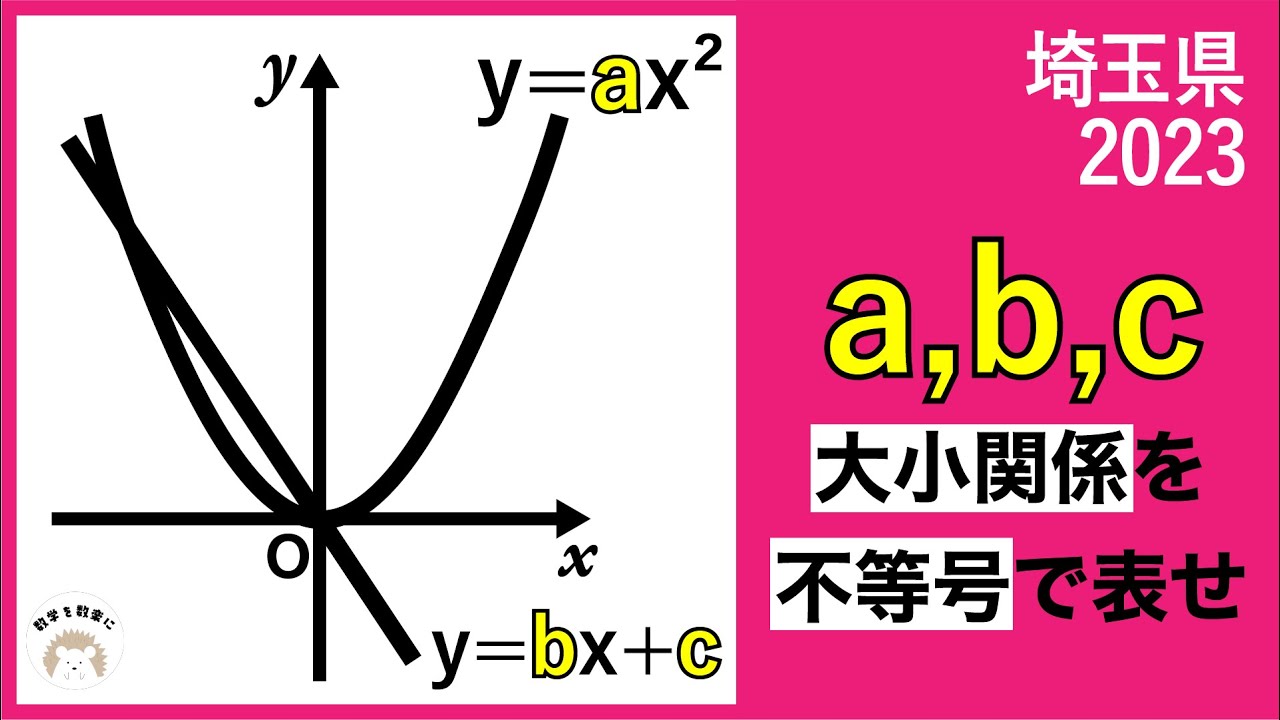
$y=ax^2$
$y=bx+c$
a,b,c大小関係を不等号で表せ
*図は動画内参照
2023埼玉県
この動画を見る
$y=ax^2$
$y=bx+c$
a,b,c大小関係を不等号で表せ
*図は動画内参照
2023埼玉県
2023高校入試数学解説81問目 二次関数の変域 埼玉県

単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$y=2x^2$において
xの変域は$a \leqq x \leqq 1$
yの変域は$0 \leqq y \leqq 18$
aの値を求めよ
2023埼玉県
この動画を見る
$y=2x^2$において
xの変域は$a \leqq x \leqq 1$
yの変域は$0 \leqq y \leqq 18$
aの値を求めよ
2023埼玉県
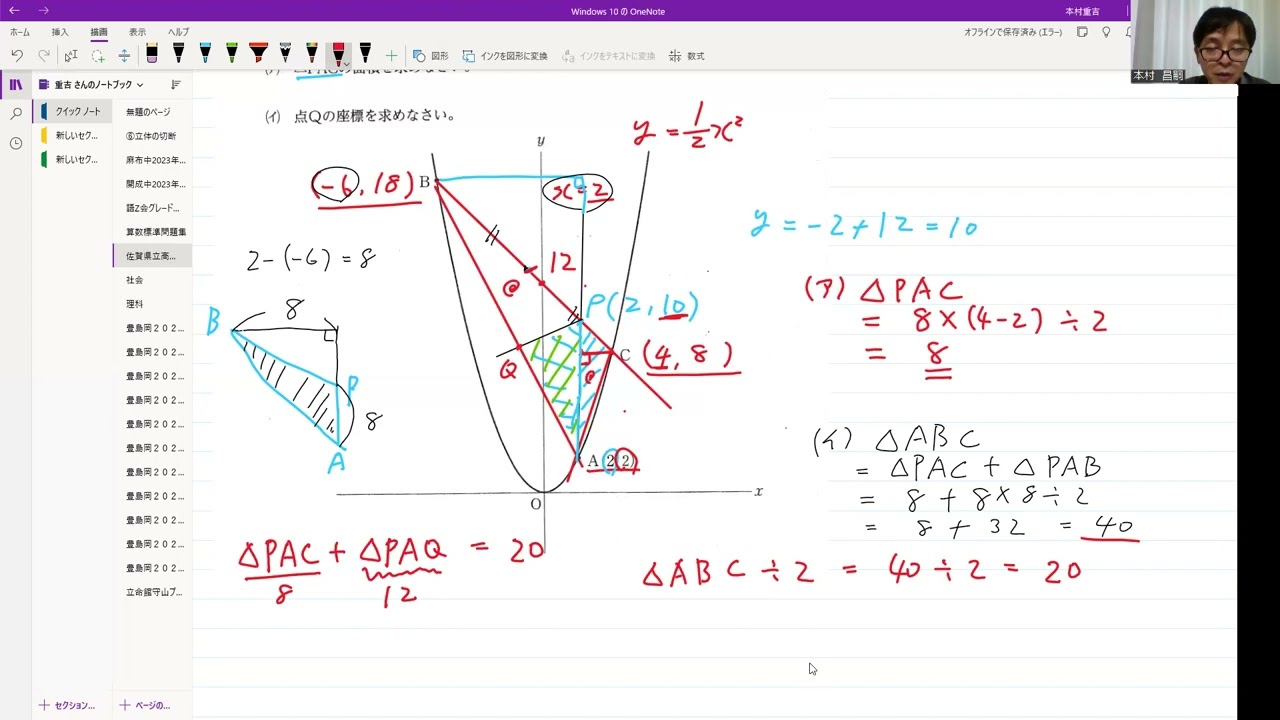
佐賀県立高校入試2021年4⃣(5)「二次関数、一次関数」
単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)#佐賀県立高校
指導講師:
重吉
問題文全文(内容文):
佐賀県立高校入試2021年4⃣(5)「二次関数、一次関数」
-----------------
動画内の図のように、関数 $y = ax^2$のグラフ上に3点A、B、Cがある。
点の座標は A(2, 2) 、点Bのx座標は-6、点Cのx座標は4である。
点Aを通りy軸に平行な直線と、2点B、Cを通る直線との交点をPとする。
また、点Pを通り△ABCの面積を2等分する直線と、2点A、Bを通る直線との交点をQとする。
このとき(ア)、(イ)の問いに答えなさい。
(ア) △PACの面積を求めなさい。
(イ) 点Qの座標を求めなさい。
この動画を見る
佐賀県立高校入試2021年4⃣(5)「二次関数、一次関数」
-----------------
動画内の図のように、関数 $y = ax^2$のグラフ上に3点A、B、Cがある。
点の座標は A(2, 2) 、点Bのx座標は-6、点Cのx座標は4である。
点Aを通りy軸に平行な直線と、2点B、Cを通る直線との交点をPとする。
また、点Pを通り△ABCの面積を2等分する直線と、2点A、Bを通る直線との交点をQとする。
このとき(ア)、(イ)の問いに答えなさい。
(ア) △PACの面積を求めなさい。
(イ) 点Qの座標を求めなさい。
2023高校入試数学解説71問目 2次関数の変域 千葉県

単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$y= \frac{1}{3}x^2$において
xの変域は$-3 \leqq x \leqq a$
yの変域は$0 \leqq y \leqq 3$
整数aの値をすべて求めよ
2023千葉県
この動画を見る
$y= \frac{1}{3}x^2$において
xの変域は$-3 \leqq x \leqq a$
yの変域は$0 \leqq y \leqq 3$
整数aの値をすべて求めよ
2023千葉県
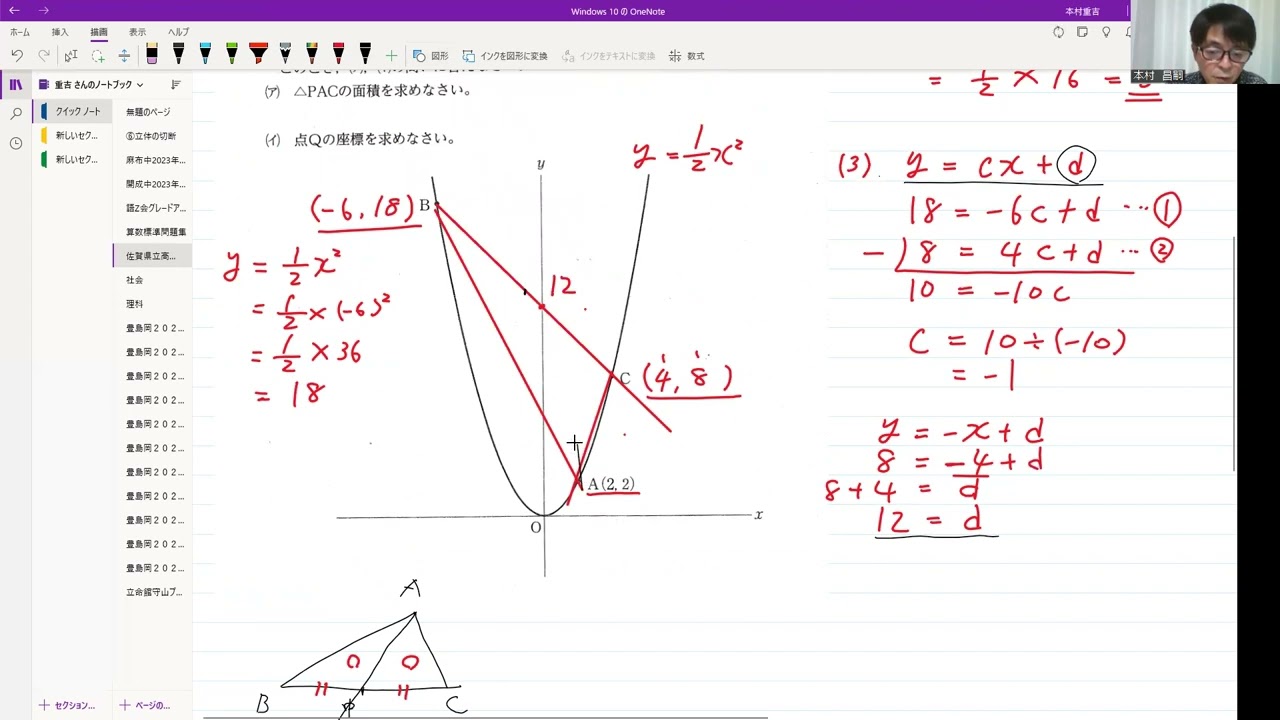
賀県立高校入試2021年4⃣(1)~(4)「二次関数、一次関数」
単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)#佐賀県立高校
指導講師:
重吉
問題文全文(内容文):
賀県立高校入試2021年4⃣(1)~(4)「二次関数、一次関数」
-----------------
動画内の図のように、関数$y=ax^2$のグラフ上に3点A、B、Cがある。
点Aの座標はA(2.2)、点Bの$x$座標は-6、点Cの$x$座標は4である。
(1)aの値を求めなさい。
(2)点Cの$y$座標を求めなさい。
(3)2点B、Cを通る直線の切片を求めなさい。
(4)点Aを通り△ABCの面積を2等分する直線と、2点B、Cを通る直線との交点の座標を求めなさい。
この動画を見る
賀県立高校入試2021年4⃣(1)~(4)「二次関数、一次関数」
-----------------
動画内の図のように、関数$y=ax^2$のグラフ上に3点A、B、Cがある。
点Aの座標はA(2.2)、点Bの$x$座標は-6、点Cの$x$座標は4である。
(1)aの値を求めなさい。
(2)点Cの$y$座標を求めなさい。
(3)2点B、Cを通る直線の切片を求めなさい。
(4)点Aを通り△ABCの面積を2等分する直線と、2点B、Cを通る直線との交点の座標を求めなさい。
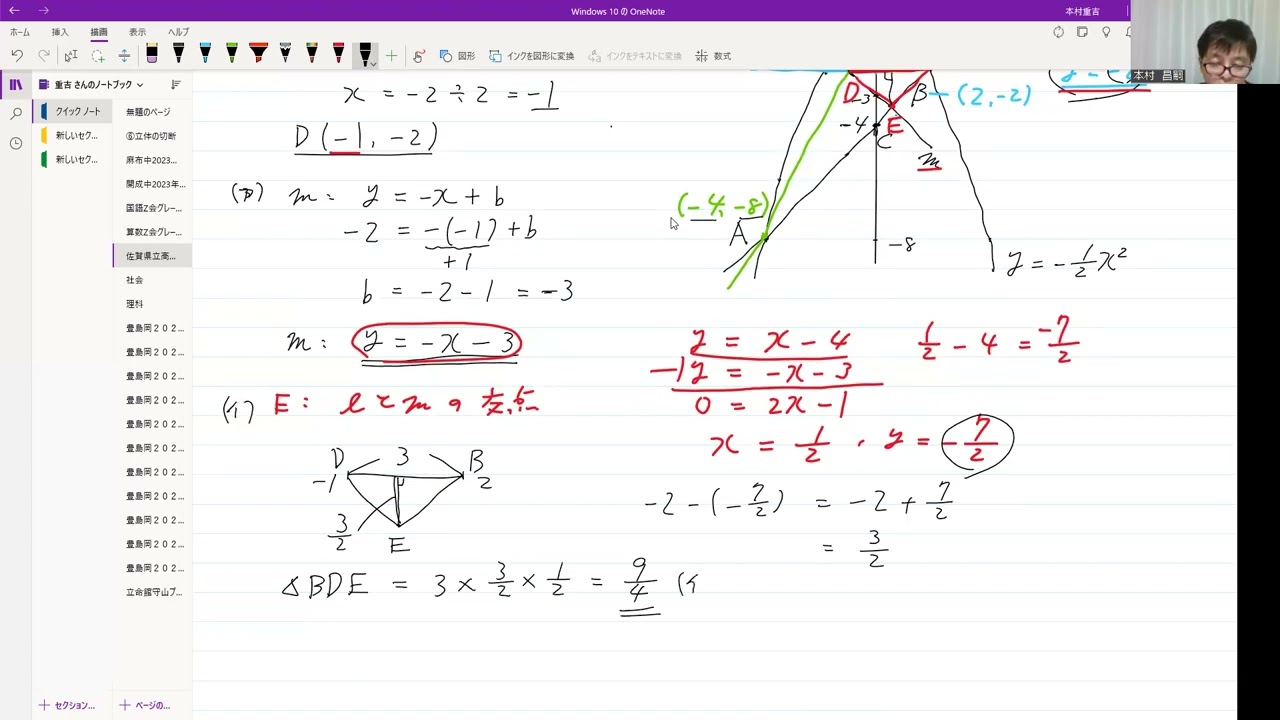
佐賀県立高校入試2022年4⃣関数(5)
単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)#佐賀県立高校
指導講師:
重吉
問題文全文(内容文):
佐賀県立高校入試2022年4⃣関数(5)
-----------------
点Bを通り$x$軸に平行な直線と、原点と点Aを通る直線との交点をDとする。
また、点Dを通り、傾き-1の直線を$m$とし、直線$l$と直線$m$との交点をEとする。
このとき、(ア)~(ウ)の各問いに答えなさい。
(ア)直線$m$の式を求めなさい。
(イ)△BDEの面積を求めなさい。
(ウ)△ACDの面積を$S$.△BDEの面積を$T$とするとき、$S:T$を最も簡単な整数の比で表しなさい。
この動画を見る
佐賀県立高校入試2022年4⃣関数(5)
-----------------
点Bを通り$x$軸に平行な直線と、原点と点Aを通る直線との交点をDとする。
また、点Dを通り、傾き-1の直線を$m$とし、直線$l$と直線$m$との交点をEとする。
このとき、(ア)~(ウ)の各問いに答えなさい。
(ア)直線$m$の式を求めなさい。
(イ)△BDEの面積を求めなさい。
(ウ)△ACDの面積を$S$.△BDEの面積を$T$とするとき、$S:T$を最も簡単な整数の比で表しなさい。
