 数学(中学生)
数学(中学生)
 数学(中学生)
数学(中学生)
補助せえん(城北2012改題)

120° 135° 150° (高校入試数学)

単元:
#数学(中学生)#中2数学#三角形と四角形
指導講師:
数学を数楽に
問題文全文(内容文):
1つの角が$150^{ \circ },135^{ \circ },120^{ \circ }$の三角形についての説明動画です
この動画を見る
1つの角が$150^{ \circ },135^{ \circ },120^{ \circ }$の三角形についての説明動画です
【高校受験対策】数学-図形28

単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・図形28
Q
右の図1で、四角形$ABCD$は平行四辺形である。
点$P$は辺$CD$上にある点で、頂点$C$,頂点$D$のいずれにも一致しない。頂点$A$と点$P$を結ぶ。
問1
図1において、$\angle ABC=50°$、$\angle DAP$の大きさを$a°$とするとき、
$\angle APC$の大きさを$a$を用いて表しなさい。
問2
右の図2は、図1において頂点$B$と点$P$を結び、頂点$D$を通り線分$BP$に平行な直線を引き、
辺$AB$との交点を$Q$、線分$AP$との交点を$R$とする。 次の(1)、(2)に答えよ。
(1) $\triangle ABP \backsim \triangle PDR$であることを証明せよ。
(2) 図2において頂点$C$と点$R$を結び、線分$BP$と線分$CR$の交点を$S$とする。
$CP:PD=2:1$のとき、四角に$QBSR$の面積は$△AQR$の面積の何倍であるが求めなさい。
この動画を見る
高校受験対策・図形28
Q
右の図1で、四角形$ABCD$は平行四辺形である。
点$P$は辺$CD$上にある点で、頂点$C$,頂点$D$のいずれにも一致しない。頂点$A$と点$P$を結ぶ。
問1
図1において、$\angle ABC=50°$、$\angle DAP$の大きさを$a°$とするとき、
$\angle APC$の大きさを$a$を用いて表しなさい。
問2
右の図2は、図1において頂点$B$と点$P$を結び、頂点$D$を通り線分$BP$に平行な直線を引き、
辺$AB$との交点を$Q$、線分$AP$との交点を$R$とする。 次の(1)、(2)に答えよ。
(1) $\triangle ABP \backsim \triangle PDR$であることを証明せよ。
(2) 図2において頂点$C$と点$R$を結び、線分$BP$と線分$CR$の交点を$S$とする。
$CP:PD=2:1$のとき、四角に$QBSR$の面積は$△AQR$の面積の何倍であるが求めなさい。
【高校受験対策】数学-死守42

単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守42
Q.次の計算をしなさい。
①$13-4^2$
②$\sqrt{50}-3\sqrt{2}$
③$18xy^3 \div (-3y)^2$
④$3x+7+3(x-2)$
⑤$(\sqrt{7}+2\sqrt{5})(\sqrt{7}-2\sqrt{5})$
⑥方程式$x-y+1=3x+7=-2y$を解きなさい。
⑦$a,b$を負の数とするとき、次のア~エの式のうちその値がつねに負になるものはどれですか。
一つ選び記号を書きなさい。
ア $ab$
イ $a+b$
ウ $-(a+b)$
エ $(a-b)^2$
⑧1辺の長さが$xcm$の正方形がある。
この正方形の縦の長さを4cm長くし、横の長さを5cm長くして長方形をつくったところ、
できた長方形の面積は210$cm^2$であった。 $x$の値を求めなさい。
⑨$x=5-2\sqrt{3}$のとき$x^2-10x+2$の値を求めなさい。
⑩右の表は、ある果樹園で収穫された50個のみかんの重さを度数分布表にまとめたものである。
この度数分布表から、50個のみかんの重さの最頻値を求めなさい。
この動画を見る
高校受験対策・死守42
Q.次の計算をしなさい。
①$13-4^2$
②$\sqrt{50}-3\sqrt{2}$
③$18xy^3 \div (-3y)^2$
④$3x+7+3(x-2)$
⑤$(\sqrt{7}+2\sqrt{5})(\sqrt{7}-2\sqrt{5})$
⑥方程式$x-y+1=3x+7=-2y$を解きなさい。
⑦$a,b$を負の数とするとき、次のア~エの式のうちその値がつねに負になるものはどれですか。
一つ選び記号を書きなさい。
ア $ab$
イ $a+b$
ウ $-(a+b)$
エ $(a-b)^2$
⑧1辺の長さが$xcm$の正方形がある。
この正方形の縦の長さを4cm長くし、横の長さを5cm長くして長方形をつくったところ、
できた長方形の面積は210$cm^2$であった。 $x$の値を求めなさい。
⑨$x=5-2\sqrt{3}$のとき$x^2-10x+2$の値を求めなさい。
⑩右の表は、ある果樹園で収穫された50個のみかんの重さを度数分布表にまとめたものである。
この度数分布表から、50個のみかんの重さの最頻値を求めなさい。
【中学数学】平面図形と角度~〇●の二等分線の裏技教えます~前半 4-6【中2数学】

【高校受験対策】数学-規則性8

単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・規則性8
Q.
形も大きさも同じ半径1cmの円盤がたくさんある。
これらを図1のように、縦m枚、横n枚(m,nは3以上の整数)の長形状に並べる。
このとき4つの角にある円盤の中心を結んでできる図形は長方形である。
さらに図2のように、それぞれの円盤は$x$で示した、点で他の円盤と接しており、ある円盤が接している円盤の枚数をその円盤に書く。
例えば、図2はm=3、n=4の長方形状に円盤を並べたものであり、
円盤Aは2枚の円盤と接しているので、円盤Aに書かれる数は2となる。
同様に円盤Bに 書かれる数は3、円盤Cに書かれる数は4となる。
また、m=3、n=4の長方形状に円盤を並べた とき、すべての円盤に他の円盤と押している枚数をそれぞれ書くと、図3のようになる。
①m=4、n=5のとき、3が書かれた円盤の枚数を求めなさい。
②m=5、n=6のとき、円盤に書かれた数の合計を求めなさい。
③m=$x$、n=$x$のとき、円盤に書かれた数の合計は440であった。
このとき$x$の値を求めなさい。
④の文のⅠ、Ⅱ、Ⅲに当てはまる数を求めなさい。ただしa,bは20以上の整数で、a \lt bとする。
m=a+1、n=b+1として、円盤を図1のように並べる。
4つの角にある円盤の中心を結んでできる長方形の面積が780$cm^2$となるとき、
4が書かれた円盤の枚数はa=(Ⅰ)、b=(Ⅱ)のとき最も多くなり、その枚数は(Ⅲ)枚である。
この動画を見る
高校受験対策・規則性8
Q.
形も大きさも同じ半径1cmの円盤がたくさんある。
これらを図1のように、縦m枚、横n枚(m,nは3以上の整数)の長形状に並べる。
このとき4つの角にある円盤の中心を結んでできる図形は長方形である。
さらに図2のように、それぞれの円盤は$x$で示した、点で他の円盤と接しており、ある円盤が接している円盤の枚数をその円盤に書く。
例えば、図2はm=3、n=4の長方形状に円盤を並べたものであり、
円盤Aは2枚の円盤と接しているので、円盤Aに書かれる数は2となる。
同様に円盤Bに 書かれる数は3、円盤Cに書かれる数は4となる。
また、m=3、n=4の長方形状に円盤を並べた とき、すべての円盤に他の円盤と押している枚数をそれぞれ書くと、図3のようになる。
①m=4、n=5のとき、3が書かれた円盤の枚数を求めなさい。
②m=5、n=6のとき、円盤に書かれた数の合計を求めなさい。
③m=$x$、n=$x$のとき、円盤に書かれた数の合計は440であった。
このとき$x$の値を求めなさい。
④の文のⅠ、Ⅱ、Ⅲに当てはまる数を求めなさい。ただしa,bは20以上の整数で、a \lt bとする。
m=a+1、n=b+1として、円盤を図1のように並べる。
4つの角にある円盤の中心を結んでできる長方形の面積が780$cm^2$となるとき、
4が書かれた円盤の枚数はa=(Ⅰ)、b=(Ⅱ)のとき最も多くなり、その枚数は(Ⅲ)枚である。
三角形と内接円(高校入試数学 数I)

ブーメランの角と円周角(高校入試数学)

直角三角形の性質(高校入試数学)

単元:
#数学(中学生)#中2数学#中3数学#数A#図形の性質#円#周角と円に内接する四角形・円と接線・接弦定理#三角形と四角形#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
直角三角形の性質についての説明動画です
この動画を見る
直角三角形の性質についての説明動画です
【高校受験対策】数学-死守41

単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守41
①$5 \div\frac{1}{2} \times (-8)$を計算しなさい。
②$(\sqrt{7}-1)^2$を計算しなさい。
③$a=3$、$b=-4$のとき、 $(-ab)^3 \div ab^2$の値を求めなさい。
④2次方程式で$x^2=6x$を解きなさい。
⑤次の連立方程式を解きなさい。
$-x+2y=8$
$3x-y=6$
⑥4枚の硬貨を同時に投げたとき、表と裏が2枚ずつ出る確率を求めなさい。
⑦底面の半径が3cm、高さが4cmである円柱の表面積を求めなさい。
ただし円周率は$\pi$とする。
⑧右の図の円$o$において、$\angle x$の大きさを求めなさい。
⑨左の表はとある市における、7月の日ごとの最高気温を 度数分布表にまとめたものである。
次のア~エのうち、この表から読み取れることとして正しいものをすべて選び、記号で答えなさい。
ア 最高気温が37.0℃の日は5日あった。
イ 最高気温が40.0℃以上の日は1日もなかった
ウ 28,0℃以上 30.0℃未満の階級の相対度数は1である。
エ 中央値が含まれるのは34.0℃以上36.0℃未満の階級である。
この動画を見る
高校受験対策・死守41
①$5 \div\frac{1}{2} \times (-8)$を計算しなさい。
②$(\sqrt{7}-1)^2$を計算しなさい。
③$a=3$、$b=-4$のとき、 $(-ab)^3 \div ab^2$の値を求めなさい。
④2次方程式で$x^2=6x$を解きなさい。
⑤次の連立方程式を解きなさい。
$-x+2y=8$
$3x-y=6$
⑥4枚の硬貨を同時に投げたとき、表と裏が2枚ずつ出る確率を求めなさい。
⑦底面の半径が3cm、高さが4cmである円柱の表面積を求めなさい。
ただし円周率は$\pi$とする。
⑧右の図の円$o$において、$\angle x$の大きさを求めなさい。
⑨左の表はとある市における、7月の日ごとの最高気温を 度数分布表にまとめたものである。
次のア~エのうち、この表から読み取れることとして正しいものをすべて選び、記号で答えなさい。
ア 最高気温が37.0℃の日は5日あった。
イ 最高気温が40.0℃以上の日は1日もなかった
ウ 28,0℃以上 30.0℃未満の階級の相対度数は1である。
エ 中央値が含まれるのは34.0℃以上36.0℃未満の階級である。
正八角形と正十二角形(高校入試数学)

単元:
#数学(中学生)#中3数学#三平方の定理
指導講師:
数学を数楽に
問題文全文(内容文):
円と正多角形についての解説動画です
①円の半径が4、内側に接している正八角形の面積を求めよ。
②円の半径が4、内側に接している正十二角形の面積を求めよ。
この動画を見る
円と正多角形についての解説動画です
①円の半径が4、内側に接している正八角形の面積を求めよ。
②円の半径が4、内側に接している正十二角形の面積を求めよ。
円に内接する四角形(数A 高校入試数学)

単元:
#数学(中学生)#中3数学#数A#図形の性質#円#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係
指導講師:
数学を数楽に
問題文全文(内容文):
円に内接する四角形の性質について説明動画です
この動画を見る
円に内接する四角形の性質について説明動画です
正五角形の対角線の長さ(高校入試数学、大学入試数学)

正三角形と正六角形(高校受験数学)

直角三角形の垂線の長さ(高校受験数学)

【高校受験対策】数学-文章題7

単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・文章題7
Q
ガス会社Aとガス会社Bでは、定額の基本料金と使用したガス1$m^3$当たりにかかる料金を会社ごとに定めており、
契約している世帯の1か月のガス料金は次の計算式によって決まる。
(1か月のガス料金)=(基本料金)+(1$m^3$当たりにかかる料金)×(1か月の使用量($m^3$))
①
ガス会社Aと契約しているある世帯において、使用量が2.2$m^3$であった月の料金は2822円であり、
使用量が3.1$m^3$であった月の料金は3281円であった。
ガス会社Aが定めている基本料金と1$m^3$当たりにかかる料金をそれぞれ求めなさい。
②
ガス会社Bでは、ガス会社Aよりも基本料金を90円安く定めている。
1か月の使用量が4.5$m^3$の とき、ガス会社A、ガス会社Bのいずれの会社と契約している場合でも、
この月のガス料金は同じ額になるという。
ガス会社Bが定めている1$m^3$当たりにかかる料金を求めなさい。
この動画を見る
高校受験対策・文章題7
Q
ガス会社Aとガス会社Bでは、定額の基本料金と使用したガス1$m^3$当たりにかかる料金を会社ごとに定めており、
契約している世帯の1か月のガス料金は次の計算式によって決まる。
(1か月のガス料金)=(基本料金)+(1$m^3$当たりにかかる料金)×(1か月の使用量($m^3$))
①
ガス会社Aと契約しているある世帯において、使用量が2.2$m^3$であった月の料金は2822円であり、
使用量が3.1$m^3$であった月の料金は3281円であった。
ガス会社Aが定めている基本料金と1$m^3$当たりにかかる料金をそれぞれ求めなさい。
②
ガス会社Bでは、ガス会社Aよりも基本料金を90円安く定めている。
1か月の使用量が4.5$m^3$の とき、ガス会社A、ガス会社Bのいずれの会社と契約している場合でも、
この月のガス料金は同じ額になるという。
ガス会社Bが定めている1$m^3$当たりにかかる料金を求めなさい。
【高校受験対策】数学-死守40

単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守40
Q.次の①~③の計算をしなさい。
①$-7+3$
➁$5x^2x$
③$8 \times \frac{3a-1}{4}$
④$4x+5y-(x+3y)$
⑤$4a^3b \div 2ab$
⑥$\sqrt{50}-\sqrt{8}$
⑦$\frac{x+y}{2}+\frac{x-y}{4}$
⑧$(x+3)(2x-1)$を展開しなさい。
⑨$x^2-9y^2$を因数分解しなさい。
⑩$2<\sqrt{a}<3$を満たす自然数$a$を小さい順にすべて書きなさい。
⑪「1個$a$gのおもり2個と、1個$b$gのおもり3個の合計の重さは500gである。」
という数量の関係を等式で表しなさい。
⑫2次方程式$(x-1)^2=x+4$を解きなさい。
⑬関数$y=x^2$について、$x$の変域が$-1 \leqq x \leqq 3$のとき、$y$の変域を求めなさい。
⑭右の図の直方体ABCD-EFGHにおいて、 AB=6cm.、AD=4cm、AE=4cmのとき、 四面体ABCFの体積を求めなさい。
この動画を見る
高校受験対策・死守40
Q.次の①~③の計算をしなさい。
①$-7+3$
➁$5x^2x$
③$8 \times \frac{3a-1}{4}$
④$4x+5y-(x+3y)$
⑤$4a^3b \div 2ab$
⑥$\sqrt{50}-\sqrt{8}$
⑦$\frac{x+y}{2}+\frac{x-y}{4}$
⑧$(x+3)(2x-1)$を展開しなさい。
⑨$x^2-9y^2$を因数分解しなさい。
⑩$2<\sqrt{a}<3$を満たす自然数$a$を小さい順にすべて書きなさい。
⑪「1個$a$gのおもり2個と、1個$b$gのおもり3個の合計の重さは500gである。」
という数量の関係を等式で表しなさい。
⑫2次方程式$(x-1)^2=x+4$を解きなさい。
⑬関数$y=x^2$について、$x$の変域が$-1 \leqq x \leqq 3$のとき、$y$の変域を求めなさい。
⑭右の図の直方体ABCD-EFGHにおいて、 AB=6cm.、AD=4cm、AE=4cmのとき、 四面体ABCFの体積を求めなさい。
【高校受験対策】数学-図形27

単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・図形27
Q.
右の図のように、1辺の長さが4cmの立方体$ABCDEFGH$がある。
辺$BF$上に点$P$をとり、辺$EF$、$FG$の中点をそれぞれ$Q,R$とする。
このとき次の問いに答えなさい
①辺$AG$の長さを求めなさい。
②$AP+PG$の長さを最も短くしたとき、$AP+PG$の長さを求めなさい。
③3点、$A,Q,R$を通る平面でこの立方体を切ったとき、切り口の図形の面積を求めなさい。
この動画を見る
高校受験対策・図形27
Q.
右の図のように、1辺の長さが4cmの立方体$ABCDEFGH$がある。
辺$BF$上に点$P$をとり、辺$EF$、$FG$の中点をそれぞれ$Q,R$とする。
このとき次の問いに答えなさい
①辺$AG$の長さを求めなさい。
②$AP+PG$の長さを最も短くしたとき、$AP+PG$の長さを求めなさい。
③3点、$A,Q,R$を通る平面でこの立方体を切ったとき、切り口の図形の面積を求めなさい。
【中学受験算数】ピラミッド相似、リボン相似、色々な相似問題はこう解け! ゼロから始める中学受験算数41
単元:
#算数(中学受験)#数学(中学生)#中3数学#相似な図形#平面図形#相似と相似を利用した問題
指導講師:
こばちゃん塾
問題文全文(内容文):
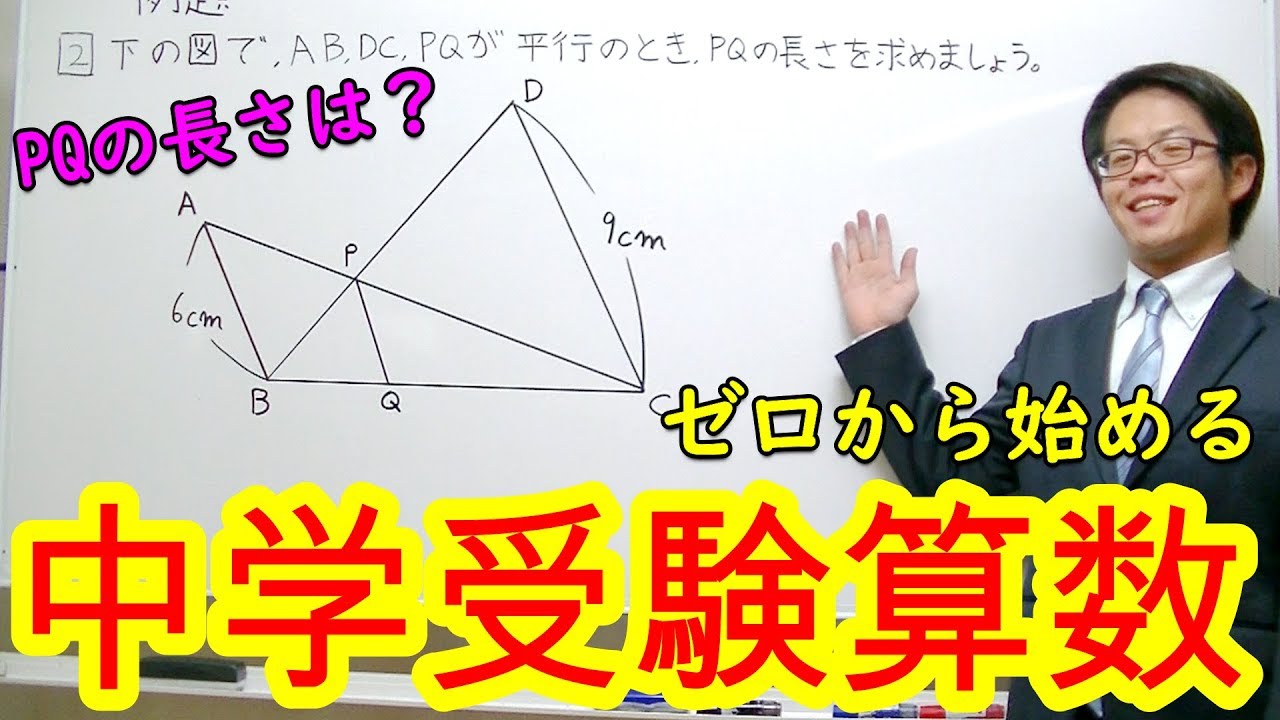
1⃣下の図で、BCとDEが平行のとき、XYの値を求めましょう。
2⃣下の図で、AB、DC、PQが平行のとき、PQの長さを求めましょう。
*図は動画内参照
この動画を見る
1⃣下の図で、BCとDEが平行のとき、XYの値を求めましょう。
2⃣下の図で、AB、DC、PQが平行のとき、PQの長さを求めましょう。
*図は動画内参照
【高校受験対策】数学-死守39

単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守39
①$-7+5$
➁$(-3) \times4-(-6)×4$
③$\frac{2}{3}\div -\frac{8}{3}+\frac{1}{2}$
④$4(-x+3y)-5(x+2y)$
⑤$\frac{14}{\sqrt{7}}+\sqrt{3}\times\sqrt{21}$
⑥$x^2+5x-36$を因数分解しなさい。
⑦2次方程式$3x^2+3x-1=0$を解きなさい。
⑧$x$についての方程式$3x-4=x-2a$の解が$5$であるとき、$a$の値を求めなさい。
⑨$n$を自然数とするとき、$4 \lt \sqrt{n}\lt 10$をみたす$n$の値は何個あるか求めなさい。
➉下の図のように$△ABC$がある。
このとき、$△ABC$を点$o$を中心として点対称移動させた図形をかきなさい。
この動画を見る
高校受験対策・死守39
①$-7+5$
➁$(-3) \times4-(-6)×4$
③$\frac{2}{3}\div -\frac{8}{3}+\frac{1}{2}$
④$4(-x+3y)-5(x+2y)$
⑤$\frac{14}{\sqrt{7}}+\sqrt{3}\times\sqrt{21}$
⑥$x^2+5x-36$を因数分解しなさい。
⑦2次方程式$3x^2+3x-1=0$を解きなさい。
⑧$x$についての方程式$3x-4=x-2a$の解が$5$であるとき、$a$の値を求めなさい。
⑨$n$を自然数とするとき、$4 \lt \sqrt{n}\lt 10$をみたす$n$の値は何個あるか求めなさい。
➉下の図のように$△ABC$がある。
このとき、$△ABC$を点$o$を中心として点対称移動させた図形をかきなさい。
【中1数学】元大手塾講師が教える!中学数学基礎講座10 実は難関?四則の範囲、正負の数の利用!

単元:
#数学(中学生)#中1数学#正の数・負の数
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣次の質問に答えましょう。
(1)2つの自然数で、加法、減法、乗法、除法の計算をすると、答えが常に自然数となるのは?
(2)2つの整数で、加法、減法、乗法、除法の計算をすると、答えが常に整数となるのは?
2⃣次の平均を求めましょう
A君・・・157㎝
B君・・・153㎝
C君・・・158㎝
D君・・・154㎝
この動画を見る
1⃣次の質問に答えましょう。
(1)2つの自然数で、加法、減法、乗法、除法の計算をすると、答えが常に自然数となるのは?
(2)2つの整数で、加法、減法、乗法、除法の計算をすると、答えが常に整数となるのは?
2⃣次の平均を求めましょう
A君・・・157㎝
B君・・・153㎝
C君・・・158㎝
D君・・・154㎝
【中1数学】元大手塾講師が教える!中学数学基礎講座9 間違う人続出!指数!

単元:
#数学(中学生)#中1数学#正の数・負の数
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣
(1)$2^2×3^2=$
(2)$(-6)^2÷(-3^2)=$
2⃣
(1)$18-(-4)×(-7)=$
(2)$(-4)× \{ -5-(-2) \} +9=$
3⃣
(1)$(\frac{2}{3} + \frac{3}{4})×(-12)=$
(2)$18×(- \frac{1}{6} + \frac{1}{2})=$
この動画を見る
1⃣
(1)$2^2×3^2=$
(2)$(-6)^2÷(-3^2)=$
2⃣
(1)$18-(-4)×(-7)=$
(2)$(-4)× \{ -5-(-2) \} +9=$
3⃣
(1)$(\frac{2}{3} + \frac{3}{4})×(-12)=$
(2)$18×(- \frac{1}{6} + \frac{1}{2})=$
【中1数学】元大手塾講師が教える!中学数学基礎講座8 基本!乗法・除法の混じった計算!!

単元:
#数学(中学生)#中1数学#正の数・負の数
指導講師:
こばちゃん塾
問題文全文(内容文):
(1)$(-\frac{5}{8})×\frac{4}{5}$ =
(2)$\frac{2}{3} ÷ (-\frac{3}{5})$ =
(3)(-5)×13×(-20)=
(4)$3×(-\frac{2}{3})×\frac{1}{5}=$
(5)$\frac{2}{7}÷(-2)×(-14)=$
この動画を見る
(1)$(-\frac{5}{8})×\frac{4}{5}$ =
(2)$\frac{2}{3} ÷ (-\frac{3}{5})$ =
(3)(-5)×13×(-20)=
(4)$3×(-\frac{2}{3})×\frac{1}{5}=$
(5)$\frac{2}{7}÷(-2)×(-14)=$
中学数学 作図4 共通外接線

【高校受験対策】数学-関数43

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・関数43
Q.
右の図において、曲線アは関数$y=\frac{1}{2}x^2$のグラフである。
曲線ア上の点で$x$座標が$4$である点を$A$、$y$軸上の点で$y$座標が$10,6$である点をそれぞれ$B,C$とし、線分$OB$の中点を$D$とする。
また、線分$OA$上に点$E$をとる。ただし$O$は原点とする。
①2点$A,D$を通る直線の式を求めなさい。
②$△OAB$の面積を求めなさい。
③四角形$ABCE$の面積が$△OAB$の面積の$\frac{1}{2}$であるとき、 点$E$の座標を求めなさい。
この動画を見る
高校受験対策・関数43
Q.
右の図において、曲線アは関数$y=\frac{1}{2}x^2$のグラフである。
曲線ア上の点で$x$座標が$4$である点を$A$、$y$軸上の点で$y$座標が$10,6$である点をそれぞれ$B,C$とし、線分$OB$の中点を$D$とする。
また、線分$OA$上に点$E$をとる。ただし$O$は原点とする。
①2点$A,D$を通る直線の式を求めなさい。
②$△OAB$の面積を求めなさい。
③四角形$ABCE$の面積が$△OAB$の面積の$\frac{1}{2}$であるとき、 点$E$の座標を求めなさい。
高校入試 作図有名問題3
高校入試 有名作図問題 四角形の面積を二等分
単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
鈴木貫太郎
問題文全文(内容文):
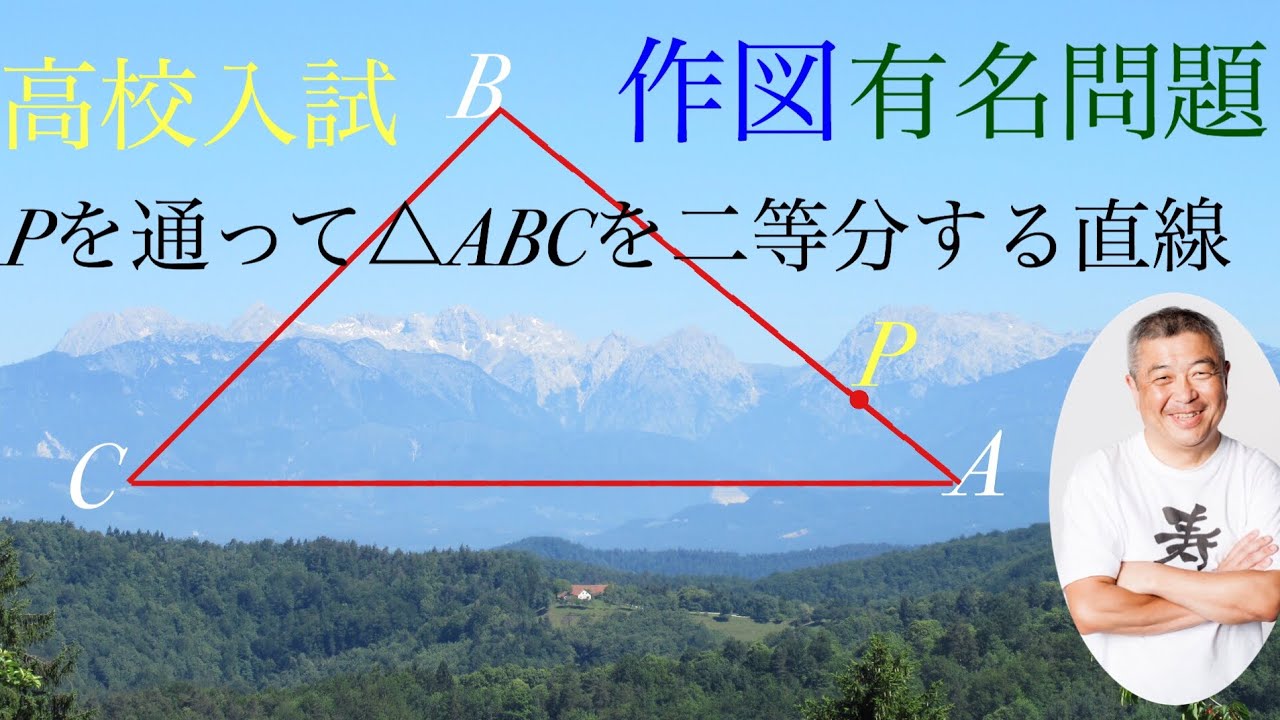
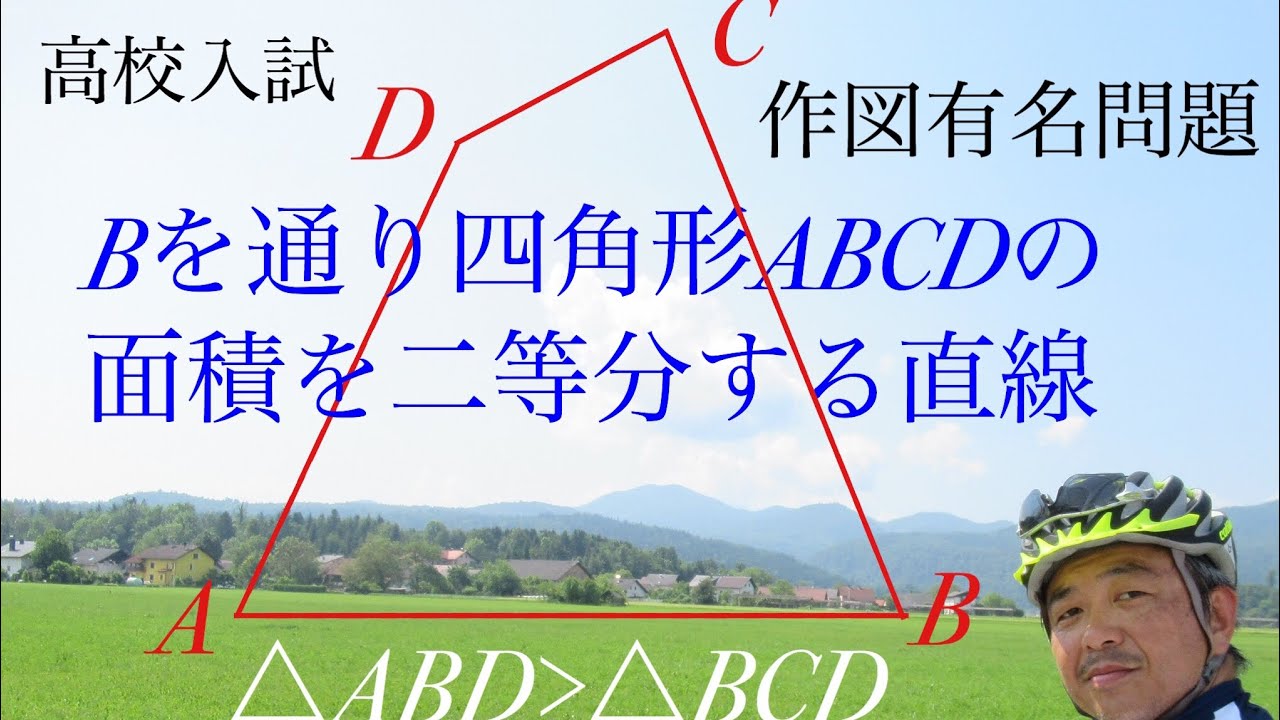
$B$を通り四角形$ABCD$の面積を2等分する直線
$\triangle ABD \gt \triangle BCD$
作図せよ
この動画を見る
$B$を通り四角形$ABCD$の面積を2等分する直線
$\triangle ABD \gt \triangle BCD$
作図せよ
【高校受験対策】数学-死守38

単元:
#数学(中学生)#中1数学#中2数学#中3数学#方程式#連立方程式#2次方程式#1次関数#確率#2次関数#円
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守38
①$-7+5$を計算しなさい。
➁$\frac{3x-2}{5} \times10$を計算しなさい。
③$5ab^2 \div\frac{a}{3}$を計算しなさい。
④$(x+8)(x-6)$を計算しなさい。
⑤$25$の平方根を求めなさい。
⑥関数$y=\frac{a}{x}$のグラフが点$(6,-2)$を通るとき、$a$の値をを求めなさい。
⑦連立方程式を解きなさい。
$3x+y=-5$
$2x+3y=6$
⑧二次方程式を解きなさい。
$x^2+7x+1=0$
⑨右の図1で$\angle x$大きさを求めなさい。
⑩大小2つのさいころを同時に投げるとき、 2つとも同じ目が出る確率を求めなさい。
⑪右の図2において、点$A,B,C$は円$O$の周上の点である。
$\angle x$の大きさを求めなさい。
⑫左の図3のように、$y=ax^2(a\gt0)$のグラフ上 に2点$A,B$があり、$x$座標はそれぞれ$-6,4$である。
直線$AB$の傾きがであるとき、$a$の値を求めなさい。
この動画を見る
高校受験対策・死守38
①$-7+5$を計算しなさい。
➁$\frac{3x-2}{5} \times10$を計算しなさい。
③$5ab^2 \div\frac{a}{3}$を計算しなさい。
④$(x+8)(x-6)$を計算しなさい。
⑤$25$の平方根を求めなさい。
⑥関数$y=\frac{a}{x}$のグラフが点$(6,-2)$を通るとき、$a$の値をを求めなさい。
⑦連立方程式を解きなさい。
$3x+y=-5$
$2x+3y=6$
⑧二次方程式を解きなさい。
$x^2+7x+1=0$
⑨右の図1で$\angle x$大きさを求めなさい。
⑩大小2つのさいころを同時に投げるとき、 2つとも同じ目が出る確率を求めなさい。
⑪右の図2において、点$A,B,C$は円$O$の周上の点である。
$\angle x$の大きさを求めなさい。
⑫左の図3のように、$y=ax^2(a\gt0)$のグラフ上 に2点$A,B$があり、$x$座標はそれぞれ$-6,4$である。
直線$AB$の傾きがであるとき、$a$の値を求めなさい。
高校入試 作図問題 円外の1点から円に接線を引け

【中1数学】元大手塾講師が教える!中学数学基礎講座 第7回 超簡単!正負の数の乗法・除法

単元:
#数学(中学生)#中1数学#正の数・負の数
指導講師:
こばちゃん塾
問題文全文(内容文):
(1)(-7)×3=
(2)6×(-9)=
(3)(-8)×(-4)=
(4)(-15)÷3=
(5)16÷(-4)=
(6)(-24)÷(-6)=
(7)(-2.4)×(-0.3)=
(8)(-3.6)÷9=
この動画を見る
(1)(-7)×3=
(2)6×(-9)=
(3)(-8)×(-4)=
(4)(-15)÷3=
(5)16÷(-4)=
(6)(-24)÷(-6)=
(7)(-2.4)×(-0.3)=
(8)(-3.6)÷9=
