 数学(中学生)
数学(中学生)
 数学(中学生)
数学(中学生)
【正体見たり…!】平方根:慶応義塾高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#慶應義塾高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
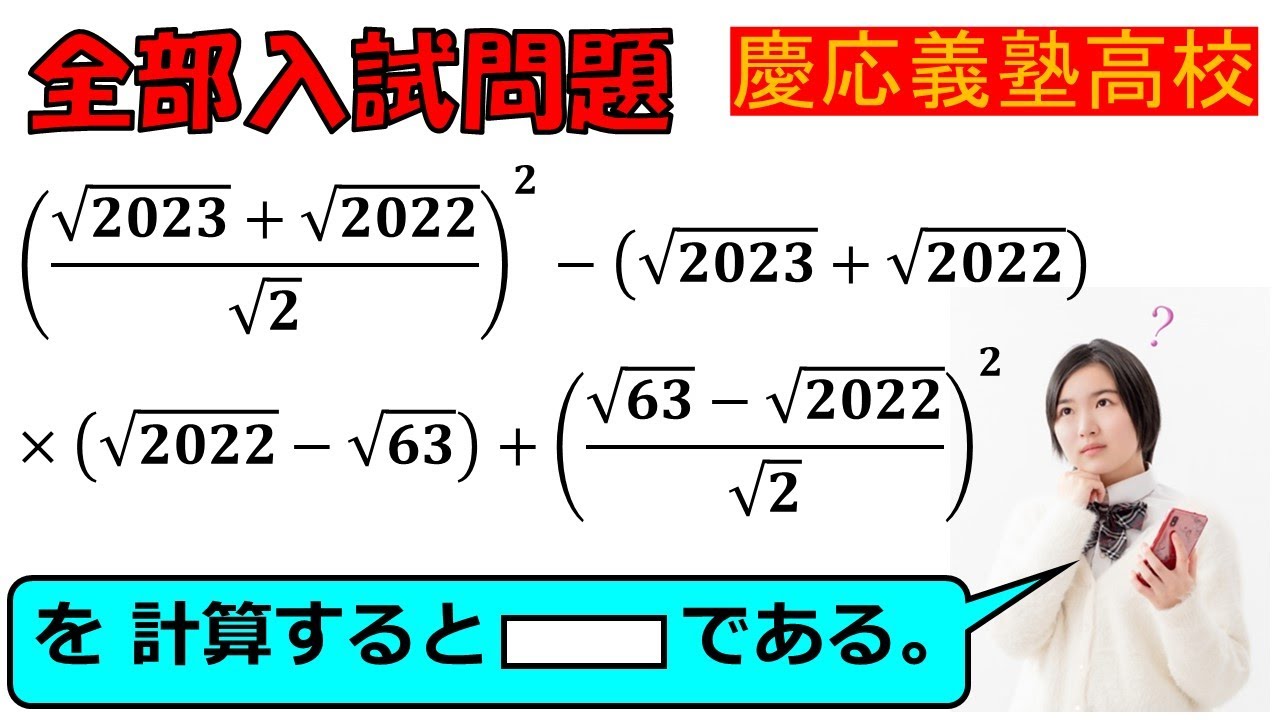
入試問題 慶応義塾高等学校
$(\displaystyle \frac{\sqrt{ 2023 }+\sqrt{ 2022 }}{\sqrt{ 2 }})^2-(\sqrt{ 2023 }+\sqrt{ 2022 }) \times (\sqrt{ 2022 }-\sqrt{ 63 })+(\displaystyle \frac{\sqrt{ 63 }-\sqrt{ 2022 }}{\sqrt{ 2 }})^2$
を計算すると▭である。
この動画を見る
入試問題 慶応義塾高等学校
$(\displaystyle \frac{\sqrt{ 2023 }+\sqrt{ 2022 }}{\sqrt{ 2 }})^2-(\sqrt{ 2023 }+\sqrt{ 2022 }) \times (\sqrt{ 2022 }-\sqrt{ 63 })+(\displaystyle \frac{\sqrt{ 63 }-\sqrt{ 2022 }}{\sqrt{ 2 }})^2$
を計算すると▭である。
2次方程式を解け

中学生も解ける!?5次方程式を解け

乗法公式を面積図で

【脳活性化…!】確率:明治学院東村山高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#明治学院東村山高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 明治学院東村山高等学校
サイズが異なるさいころを同時に投げ
さいころの目の積が100に
なる場合は何通りあるか。
この動画を見る
入試問題 明治学院東村山高等学校
サイズが異なるさいころを同時に投げ
さいころの目の積が100に
なる場合は何通りあるか。
分母に文字がある連立方程式 洛南

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#洛南高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
連立方程式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
2a+\displaystyle \frac{1}{b}=7 \\
7a-\displaystyle \frac{3}{b}=5
\end{array}
\right.
\end{eqnarray}$
出典:洛南高等学校
この動画を見る
連立方程式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
2a+\displaystyle \frac{1}{b}=7 \\
7a-\displaystyle \frac{3}{b}=5
\end{array}
\right.
\end{eqnarray}$
出典:洛南高等学校
ルートの計算
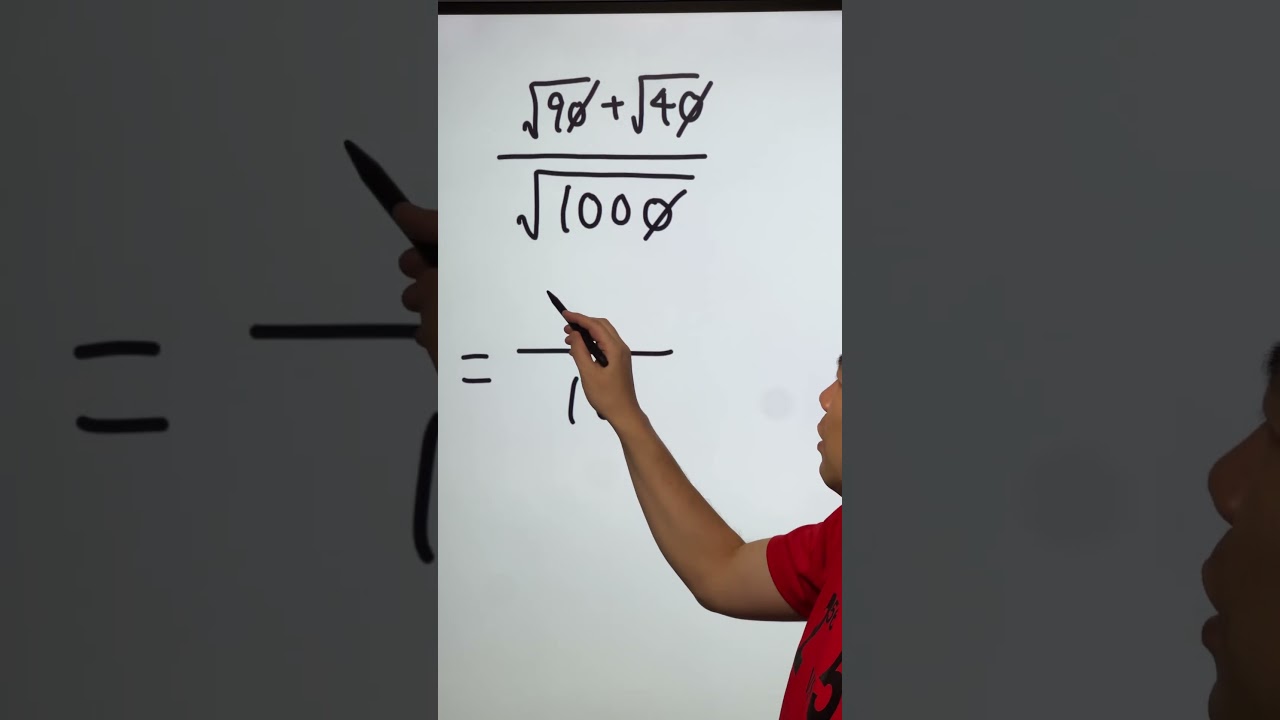
単元:
#数学(中学生)#中3数学#平方根
指導講師:
数学を数楽に
問題文全文(内容文):
$\displaystyle \frac{\sqrt{ 90 }+\sqrt{ 40 }}{{ \sqrt{ 1000 } }}=??$
この動画を見る
$\displaystyle \frac{\sqrt{ 90 }+\sqrt{ 40 }}{{ \sqrt{ 1000 } }}=??$
正方形の面積🟰❓

【数学】中高一貫校問題集2幾何176:三平方の定理:平面図形 共通接線の長さ1

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1)図1で、2つの円O,O´は外接しており、A,Bは共通接線の接点である。O,O´の半径がそれぞれ5cm,2cmであるとき、線分ABの長さを求めなさい。
(2)図2で、A,Bは、2つの円O,O´の共通接線の接点である。O,O´の半径がそれぞれ5cm,3cmで、2つの円の中心間の距離が10cmであるとき、線分ABの長さを求めなさい。
この動画を見る
(1)図1で、2つの円O,O´は外接しており、A,Bは共通接線の接点である。O,O´の半径がそれぞれ5cm,2cmであるとき、線分ABの長さを求めなさい。
(2)図2で、A,Bは、2つの円O,O´の共通接線の接点である。O,O´の半径がそれぞれ5cm,3cmで、2つの円の中心間の距離が10cmであるとき、線分ABの長さを求めなさい。
ルートの計算 2024洛南

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#洛南高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
以下を求めよ。
$(1+\sqrt{ 2 }+\sqrt{ 4 }+\sqrt{ 8 }+\sqrt{ 16 }+\sqrt{ 32 })\times(1-\sqrt{ 2 }+\sqrt{ 4 }-\sqrt{ 8 }+\sqrt{ 16 }-\sqrt{ 32 })$
この動画を見る
以下を求めよ。
$(1+\sqrt{ 2 }+\sqrt{ 4 }+\sqrt{ 8 }+\sqrt{ 16 }+\sqrt{ 32 })\times(1-\sqrt{ 2 }+\sqrt{ 4 }-\sqrt{ 8 }+\sqrt{ 16 }-\sqrt{ 32 })$
【数学】中高一貫校問題集2幾何175:三平方の定理:平面図形 四角形の面積

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(代数編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の四角形ABCDの面積を求めなさい。ただし、(1)で、AD//BCである。
この動画を見る
次の四角形ABCDの面積を求めなさい。ただし、(1)で、AD//BCである。
【思ったより上手く…!】文字式:共立女子第二高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#共立女子第二高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 共立女子第二高等学校
$x=\sqrt{ 3 }-5$のとき
$x^2+3x-10$ の値を求めなさい。
この動画を見る
入試問題 共立女子第二高等学校
$x=\sqrt{ 3 }-5$のとき
$x^2+3x-10$ の値を求めなさい。
【中学数学】平面が1つに決まる条件・2直線,直線と平面,平面と平面の位置関係【中1数学】

単元:
#数学(中学生)#中1数学#平面図形
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
【中学数学】平面が1つに決まる条件・2直線,直線と平面,平面と平面の位置関係についての解説動画です
この動画を見る
【中学数学】平面が1つに決まる条件・2直線,直線と平面,平面と平面の位置関係についての解説動画です
気付けば一瞬!!長方形の中にある三角形
単元:
#数学(中学生)#中2数学#平行と合同#三角形と四角形
指導講師:
数学を数楽に
問題文全文(内容文):
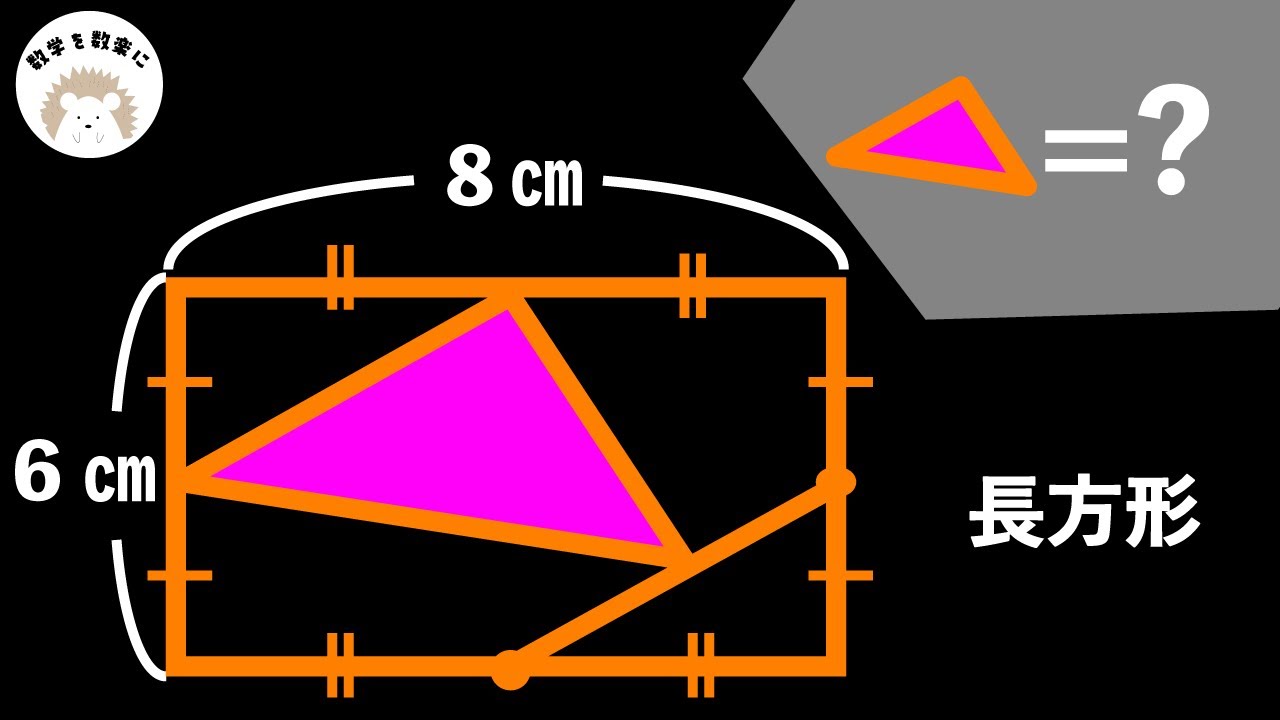
動画内の図において、$\triangle \textrm{EHI}$を求めよ。
この動画を見る
動画内の図において、$\triangle \textrm{EHI}$を求めよ。
こんな解き方知ってる?

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
5x+2y=-9 \\
-2x+9y=-16
\end{array}
\right.
\end{eqnarray}$
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
5x+2y=-9 \\
-2x+9y=-16
\end{array}
\right.
\end{eqnarray}$
【大切な考え方…!】整数:帝京高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#帝京高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 帝京高等学校
元の$2$桁の自然数は▭です。
$2$桁の自然数があり、十の位と一の位の数の和は$9$です
また、十の位の数と一の位の数を 入れ替えてできる数は、元の数の$2$倍より$9$小さくなる
▭部分を求めよ。
この動画を見る
入試問題 帝京高等学校
元の$2$桁の自然数は▭です。
$2$桁の自然数があり、十の位と一の位の数の和は$9$です
また、十の位の数と一の位の数を 入れ替えてできる数は、元の数の$2$倍より$9$小さくなる
▭部分を求めよ。
割り算

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
数学を数楽に
問題文全文(内容文):
$3\div7=??$
$2024\div2025=??$
$2y\div3x=??$
この動画を見る
$3\div7=??$
$2024\div2025=??$
$2y\div3x=??$
【数学】中高一貫校問題集2幾何174:三平方の定理:平面図形 三角形の面積+ヘロンの公式
単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の△ABCの面積を求めなさい。(3辺の長さが2cm、3cm、4cmの三角形の面積を求めよ)
この動画を見る
次の△ABCの面積を求めなさい。(3辺の長さが2cm、3cm、4cmの三角形の面積を求めよ)
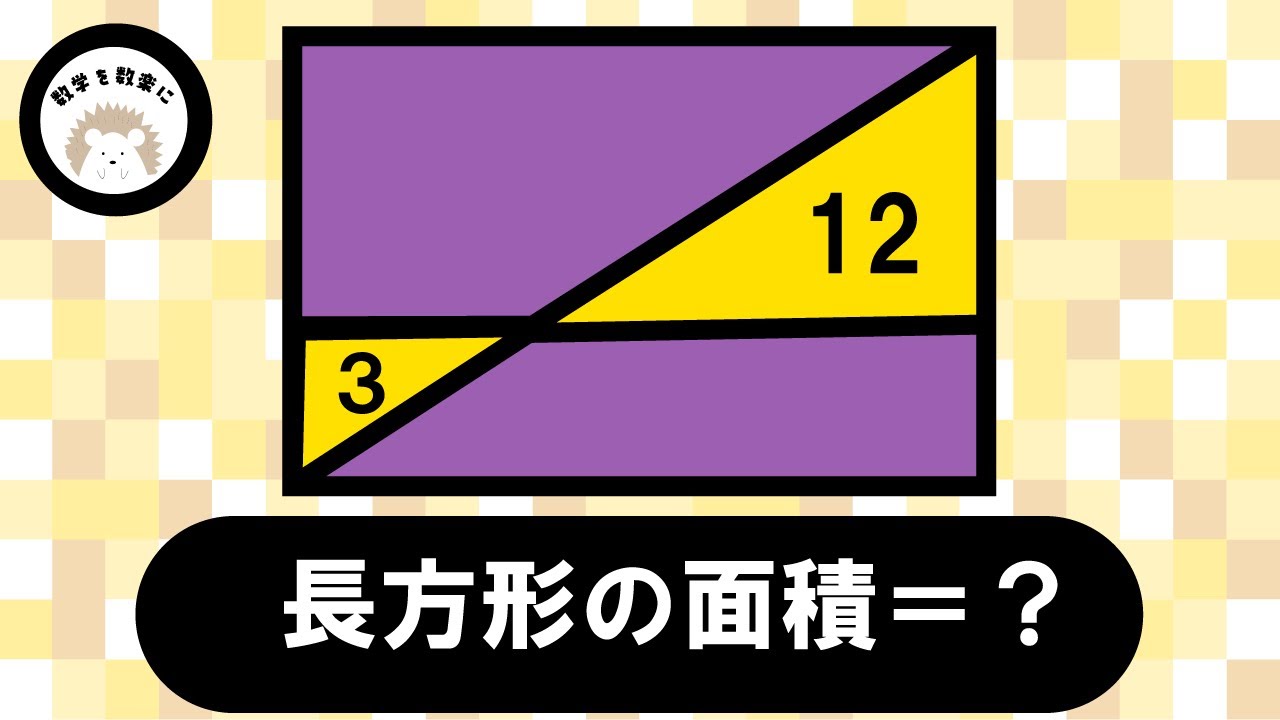
長方形の面積🟰❓
【重要!!】式の活用(式の変形の仕方)[現役講師解説、中学2年、数学〕

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
3rd School
問題文全文(内容文):
[ ]の中を=にしてください
①$2x+y=5[x]$
②$7xy+5=0[y]$
この動画を見る
[ ]の中を=にしてください
①$2x+y=5[x]$
②$7xy+5=0[y]$
【基本を制する者が…!】因数分解:明治学院東村山高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#明治学院東村山高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 明治学院東村山高等学校
$2ax - bx - 6ay + 3by$
を因数分解しなさい。
この動画を見る
入試問題 明治学院東村山高等学校
$2ax - bx - 6ay + 3by$
を因数分解しなさい。
平方根と式の値 2024駒込
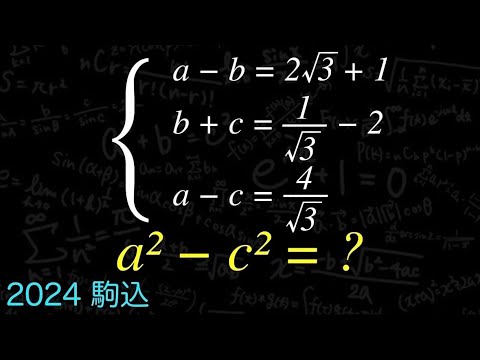
単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
数学を数楽に
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
a-b=2\sqrt{ 3 }+1 \\
b+c=\displaystyle \frac{1}{\sqrt{ 3 }}-2 \\
a-c=\displaystyle \frac{4}{\sqrt{ 3 }}
\end{array}
\right.
\end{eqnarray}$
$a^2-c^2=?$
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
a-b=2\sqrt{ 3 }+1 \\
b+c=\displaystyle \frac{1}{\sqrt{ 3 }}-2 \\
a-c=\displaystyle \frac{4}{\sqrt{ 3 }}
\end{array}
\right.
\end{eqnarray}$
$a^2-c^2=?$
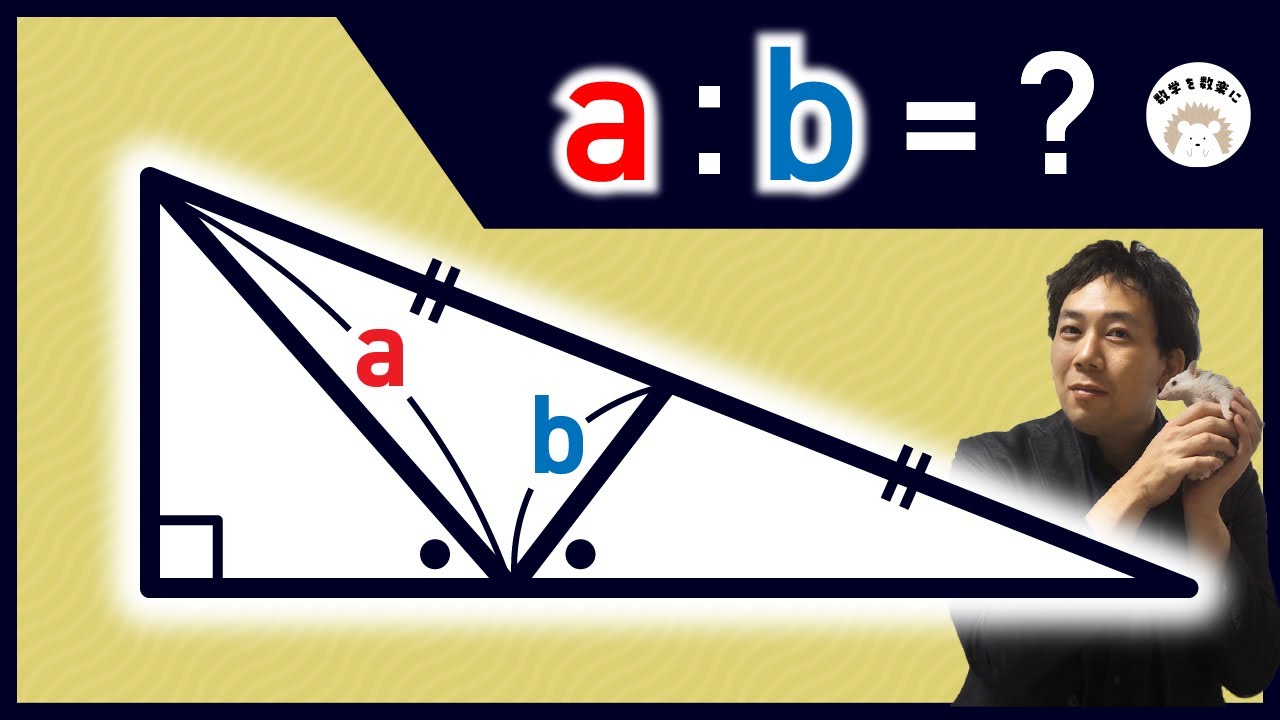
気付けば一瞬!!2通りで解説
【それって、つまり…!】整数:立命館高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#立命館高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 立命館高等学校
1から30までのすべての整数の積は・・・
一の位から何個連続で0が並ぶか。
[つまり、 1×2×3×…×28×29×30 ということ!]
この動画を見る
入試問題 立命館高等学校
1から30までのすべての整数の積は・・・
一の位から何個連続で0が並ぶか。
[つまり、 1×2×3×…×28×29×30 ということ!]
円と角の和

単元:
#算数(中学受験)#数学(中学生)#中1数学#平面図形#角度と面積#平面図形
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle x+ \angle y= ?$
*図は動画内参照
この動画を見る
$\angle x+ \angle y= ?$
*図は動画内参照
この手があったか!分母の有理化

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{21}{\sqrt 7}=$
この動画を見る
$\frac{21}{\sqrt 7}=$
文字式のイメージはどう?

単元:
#数学(中学生)#中1数学#文字と式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
下記質問の解説動画です
文字式の計算が分からないです
$a+b+c=?$
この動画を見る
下記質問の解説動画です
文字式の計算が分からないです
$a+b+c=?$
【規則性は…!】数列:明治学院東村山高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#明治学院東村山高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 明治学院東山高等学校
以下のように分数が 規則的に並んでいる。
$\displaystyle \frac{1}{2},\displaystyle \frac{1}{3},\displaystyle \frac{2}{3},\displaystyle \frac{1}{4},\displaystyle \frac{2}{4},\displaystyle \frac{3}{4},\displaystyle \frac{1}{5},・・・$
39番目の分数を答えなさい。
この動画を見る
入試問題 明治学院東山高等学校
以下のように分数が 規則的に並んでいる。
$\displaystyle \frac{1}{2},\displaystyle \frac{1}{3},\displaystyle \frac{2}{3},\displaystyle \frac{1}{4},\displaystyle \frac{2}{4},\displaystyle \frac{3}{4},\displaystyle \frac{1}{5},・・・$
39番目の分数を答えなさい。
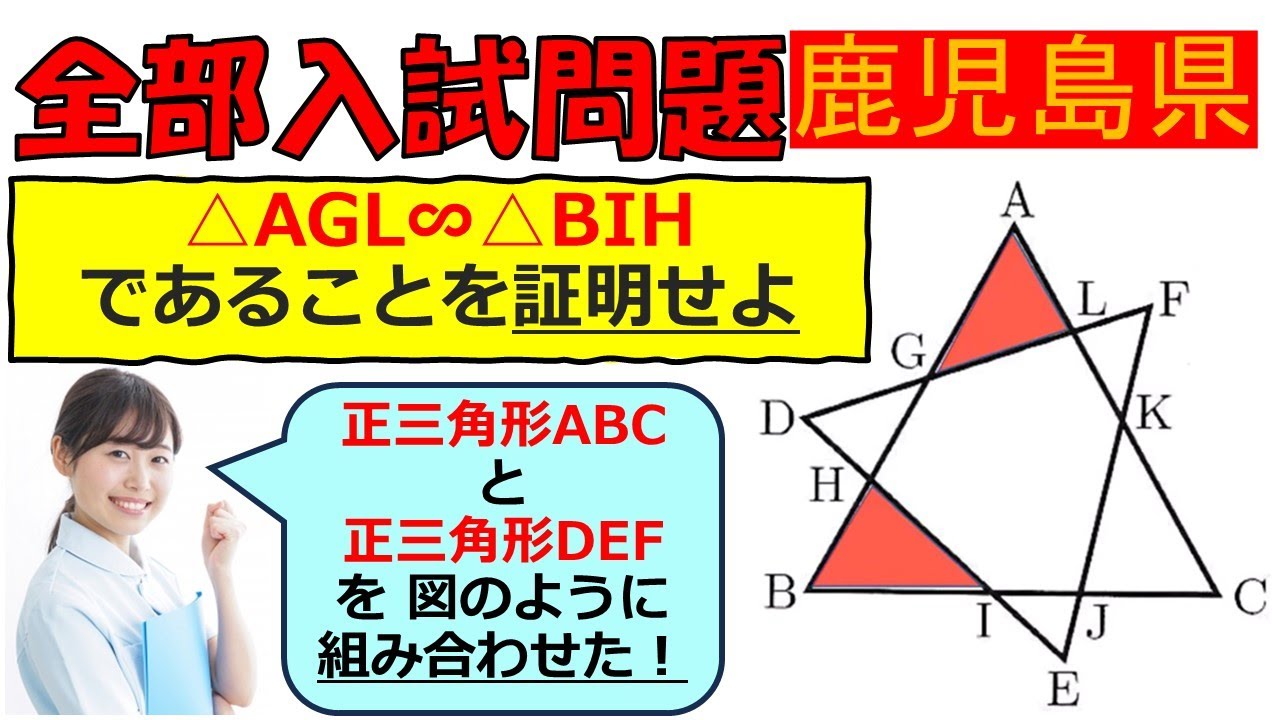
【必要なトコロは…!】図形:鹿児島県~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#鹿児島県公立高校入試
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \triangle AGL \backsim \triangle BIH$であることを証明せよ.
鹿児島県公立高等学校過去問
この動画を見る
$ \triangle AGL \backsim \triangle BIH$であることを証明せよ.
鹿児島県公立高等学校過去問
福田のおもしろ数学143〜斜面の勾配

単元:
#数学(中学生)#中3数学#大学入試過去問(数学)#三平方の定理#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
傾いた平面上で、もっとも急な方向の勾配(傾き)が$\frac{1}{3}$であるという。いま南北方向の勾配を測ったところ$\frac{1}{5}$であった。
東西方向の勾配はどれだけか。
この動画を見る
傾いた平面上で、もっとも急な方向の勾配(傾き)が$\frac{1}{3}$であるという。いま南北方向の勾配を測ったところ$\frac{1}{5}$であった。
東西方向の勾配はどれだけか。
