 数学(中学生)
数学(中学生)
 数学(中学生)
数学(中学生)
半円 愛光高校
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
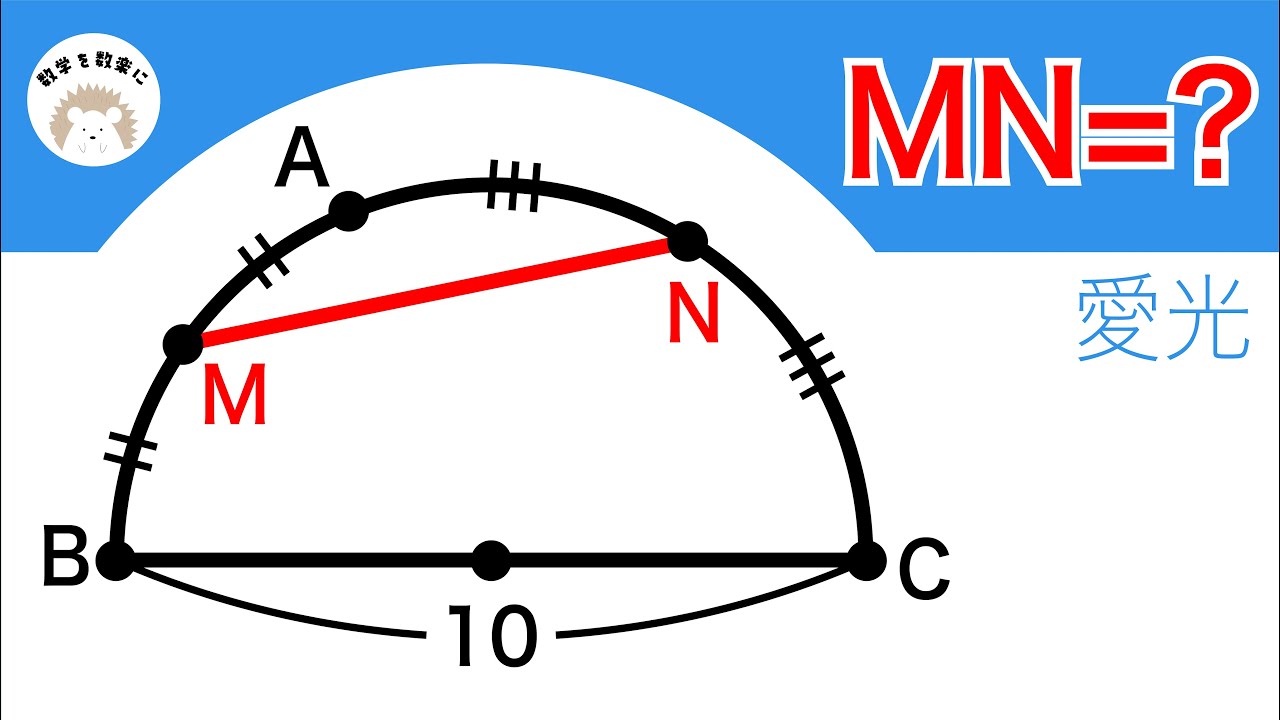
MN=?
*図は動画内参照
愛光学園
この動画を見る
MN=?
*図は動画内参照
愛光学園
【困難は分解せよ!】平方根:桐朋高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\dfrac{(\sqrt{14}-\sqrt6)(\sqrt7+\sqrt3)}{2}-(\sqrt2+1)^2$を計算せよ.
桐朋高校過去問
この動画を見る
$\dfrac{(\sqrt{14}-\sqrt6)(\sqrt7+\sqrt3)}{2}-(\sqrt2+1)^2$を計算せよ.
桐朋高校過去問
平面と直線との交点 正四面体
【中学数学】2次関数の変域をどこよりも丁寧に 4-2【中3数学】

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
問1. $y=\frac{1}{3}x^2$について、$x$の変域が次のとき$y$の変域を求めよ。
(1) $1\leqq x \leqq 6$ (2)$-3 \leqq x \leqq 5$ (3) $-3< x \leqq 1$
問2. $y=-2x^2$について、$x$の変域が次のとき$y$の変域を求めよ。
(1) $-1 < x < 5$(2)$-8 \leqq x \leqq -2$
この動画を見る
問1. $y=\frac{1}{3}x^2$について、$x$の変域が次のとき$y$の変域を求めよ。
(1) $1\leqq x \leqq 6$ (2)$-3 \leqq x \leqq 5$ (3) $-3< x \leqq 1$
問2. $y=-2x^2$について、$x$の変域が次のとき$y$の変域を求めよ。
(1) $-1 < x < 5$(2)$-8 \leqq x \leqq -2$
【一度解けば忘れない解法!】空間図形:東海大学附属浦安高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#空間図形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
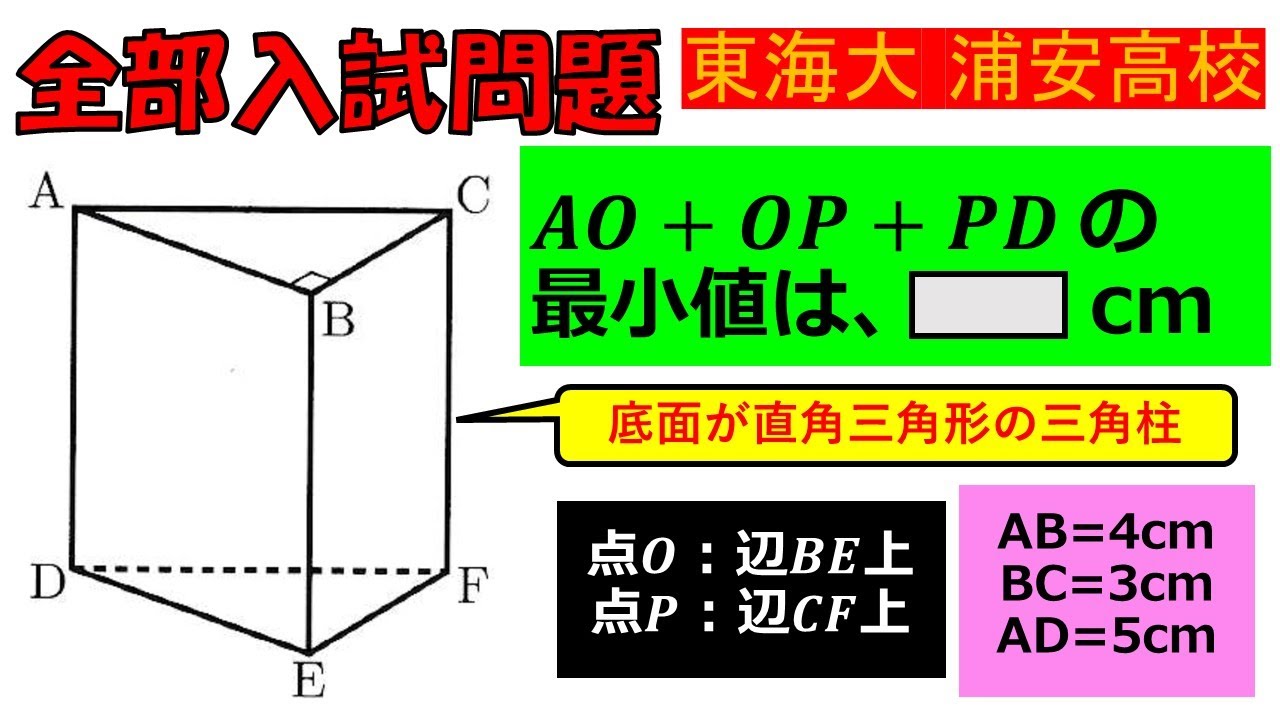
底面が直角三角形の三角柱の$AO+OP+PD$の最小値は,$\Box$cmである.
東海大浦安高校過去問
この動画を見る
底面が直角三角形の三角柱の$AO+OP+PD$の最小値は,$\Box$cmである.
東海大浦安高校過去問
これでも高校入試 因数分解 久留米大附設

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$x^2+(a+7)x -6(a-2)(a+1)$
久留米大学附設高等学校
この動画を見る
因数分解せよ
$x^2+(a+7)x -6(a-2)(a+1)$
久留米大学附設高等学校
n度目の正直🙇♂️ 式の展開 東海高校

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$(x^3-\frac{1}{2}x+1)(\frac{1}{3}x^3 -x^2 +5)$を展開したときの$x^3$の係数は?
東海高等学校
この動画を見る
$(x^3-\frac{1}{2}x+1)(\frac{1}{3}x^3 -x^2 +5)$を展開したときの$x^3$の係数は?
東海高等学校
【中学数学】1次関数の決定をどこよりも丁寧に 3-2【中2数学】

単元:
#数学(中学生)#中2数学#1次関数
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
問 対木の直線の式を求めよ
(1) 2点(1, 6) (-3, -2)を通る直線
(2)傾きが$\frac{1}{2}$で点(4, 3)を通る直線
(3)切片が5で点(2, $\frac{1}{3}$)を通る直線
(4)直線$y=3x+7$に平行で点(-1, 1)を通る直線
この動画を見る
問 対木の直線の式を求めよ
(1) 2点(1, 6) (-3, -2)を通る直線
(2)傾きが$\frac{1}{2}$で点(4, 3)を通る直線
(3)切片が5で点(2, $\frac{1}{3}$)を通る直線
(4)直線$y=3x+7$に平行で点(-1, 1)を通る直線
【手がかりを順番に探れ!】二次方程式:日本大学第二高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$x^2-ax+3=0$の解の1つは$x^2-4x+12=0$の小さい方の解に1を加えたものと等しい.
$a$の値を求めよ.
日大第二高校過去問
この動画を見る
$x^2-ax+3=0$の解の1つは$x^2-4x+12=0$の小さい方の解に1を加えたものと等しい.
$a$の値を求めよ.
日大第二高校過去問
福田の数学〜上智大学2022年理工学部第3問〜複素数平面上の点列と三角形の相似

単元:
#大学入試過去問(数学)#複素数平面#相似な図形#数列#漸化式#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数B#数C
指導講師:
福田次郎
問題文全文(内容文):
複素数からなる数列${z_n}$を、次の条件で定める。
$z_1=0,\ \ \ z_{n+1}=(1+i)z_n-i \ \ \ (i=1,2,3, \ \ ...)$
正の整数nに対し、z_nに対応する負素数平面上の点をA_nとおく。
(1)$z_2=\boxed{ツ }+\boxed{ツ }\ i, \ \ \ z_3=\boxed{ト}+$
$\boxed{ナ}\ i,\ \ \ z_4=\boxed{二}+\boxed{ヌ}\ i $である。
(2)$r \gt 0,\ 0 \leqq θ \lt 2\pi$ を用いて、$1+i=r(\cos θ+i\sin θ)$のように$1+i$を極形式で
表すとき、$r=\sqrt{\boxed{ネ}},\ θ=\frac{\boxed{ノ }}{\boxed{ハ}}\pi$である。
(3)すべての正の整数nに対する$\triangle PA_nA_{n+1}$が互いに相似になる点Pに対応する
複素数は、$\boxed{ヒ}+\boxed{フ }\ i$である。
(4)$|z_n| \gt 1000$となる最小のnは$n=\boxed{へ}$である。
(5)$A_{2022+k}$が実軸上にある最小の正の整数kは$k=\boxed{ホ}$である。
2022上智大学理工学部過去問
この動画を見る
複素数からなる数列${z_n}$を、次の条件で定める。
$z_1=0,\ \ \ z_{n+1}=(1+i)z_n-i \ \ \ (i=1,2,3, \ \ ...)$
正の整数nに対し、z_nに対応する負素数平面上の点をA_nとおく。
(1)$z_2=\boxed{ツ }+\boxed{ツ }\ i, \ \ \ z_3=\boxed{ト}+$
$\boxed{ナ}\ i,\ \ \ z_4=\boxed{二}+\boxed{ヌ}\ i $である。
(2)$r \gt 0,\ 0 \leqq θ \lt 2\pi$ を用いて、$1+i=r(\cos θ+i\sin θ)$のように$1+i$を極形式で
表すとき、$r=\sqrt{\boxed{ネ}},\ θ=\frac{\boxed{ノ }}{\boxed{ハ}}\pi$である。
(3)すべての正の整数nに対する$\triangle PA_nA_{n+1}$が互いに相似になる点Pに対応する
複素数は、$\boxed{ヒ}+\boxed{フ }\ i$である。
(4)$|z_n| \gt 1000$となる最小のnは$n=\boxed{へ}$である。
(5)$A_{2022+k}$が実軸上にある最小の正の整数kは$k=\boxed{ホ}$である。
2022上智大学理工学部過去問
関数の問題にみえて実は○形の問題 中央大杉並

単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
a=?
*図は動画内参照
中央大学杉並高等学校
この動画を見る
a=?
*図は動画内参照
中央大学杉並高等学校
√と二乗は打ち消し合う?? 熊本マリスト学園

単元:
#数学(中学生)#数Ⅰ#数A#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$9+\sqrt {a^2} = 25$
整数aを求めよ
熊本マリスト学園高等学校
この動画を見る
$9+\sqrt {a^2} = 25$
整数aを求めよ
熊本マリスト学園高等学校
【考えて解くか、解きながら考えるか…】計算:大阪教育大学附属高等学校平野校舎~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の計算をし,$\Box$に当てはまる数を答えなさい.
$340^2-337^2-3^2=\Box$
大教大付属高校平野過去問
この動画を見る
次の計算をし,$\Box$に当てはまる数を答えなさい.
$340^2-337^2-3^2=\Box$
大教大付属高校平野過去問
【直前にもう一度見なおしたい!】文章題:専修大学附属高等学校~全国入試問題解法
単元:
#数学(中学生)#文章題#売買損益と食塩水#文章題その他#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
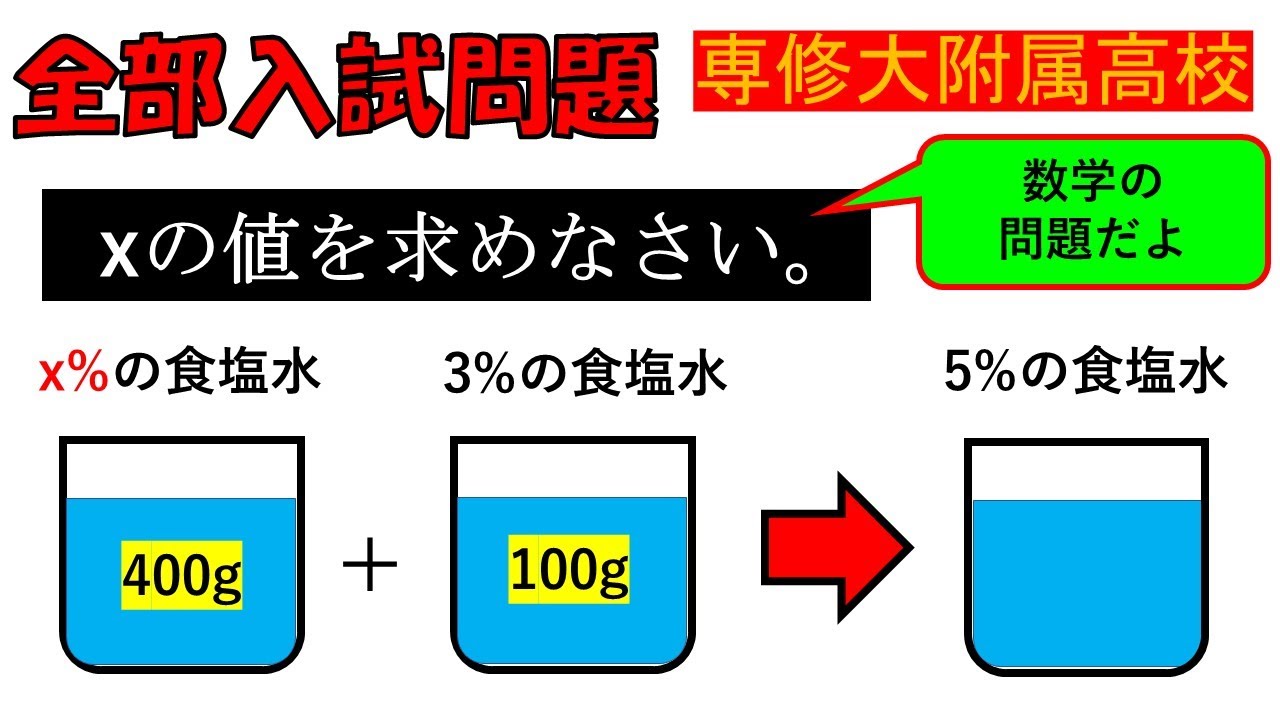
$A$の容器に$x$%の食塩水が400g入っている.
$A$の容器に$3$%の食塩水を100g加え,よくかき混ぜたところ,
$A$の容器の食塩水は$5$%となった.
$x$の値を求めなさい.
専修大学附属高等学校過去問
この動画を見る
$A$の容器に$x$%の食塩水が400g入っている.
$A$の容器に$3$%の食塩水を100g加え,よくかき混ぜたところ,
$A$の容器の食塩水は$5$%となった.
$x$の値を求めなさい.
専修大学附属高等学校過去問
左右が異なる回転体 市川高校

単元:
#数学(中学生)#立体図形#体積・表面積・回転体・水量・変化のグラフ#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
AB=4
回転体の体積=?
*図は動画内参照
市川高等学校
この動画を見る
AB=4
回転体の体積=?
*図は動画内参照
市川高等学校
分母に文字がある連立方程式 東邦大附属東邦

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
x + \frac{1}{y} = 1 \\
\frac{1}{x} + y = 4
\end{array}
\right.
\end{eqnarray}
東邦大学付属東邦高等学校
この動画を見る
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
x + \frac{1}{y} = 1 \\
\frac{1}{x} + y = 4
\end{array}
\right.
\end{eqnarray}
東邦大学付属東邦高等学校
【中学数学】方程式の基礎をどこよりも丁寧に 3-1【中1数学】

単元:
#数学(中学生)#中1数学#方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
(1)次の方程式のうち3が解であるものをすべて選べ
①$3x+2=11$ ②$\frac{1}{3}x+4=7$ ③$-2x+1=10$ ④$\frac{1}{6}x+\frac{1}{2}=1$
(2)次の方程式を解け
①$x-5=-7$ ②$2x=4$ ③$3x+4=-8$
この動画を見る
(1)次の方程式のうち3が解であるものをすべて選べ
①$3x+2=11$ ②$\frac{1}{3}x+4=7$ ③$-2x+1=10$ ④$\frac{1}{6}x+\frac{1}{2}=1$
(2)次の方程式を解け
①$x-5=-7$ ②$2x=4$ ③$3x+4=-8$
【数学】二次方程式の活用:みんなが嫌いな動く点Pを得意に!

単元:
#数学(中学生)#中3数学#2次方程式
教材:
#KEYワーク#KEYワーク(数学)中2#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
みんなの苦手な動点Pの問題を克服しよう!
この動画を見る
みんなの苦手な動点Pの問題を克服しよう!
難しい空間図形を解きながら音楽を聞く動画~全国入試問題解法 #Shorts #数学 #高校入試
単元:
#数学(中学生)#中1数学#空間図形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
立方体$ABCD-EFGH$は1辺6cmであり,
点$P$は辺$AB$の中点であり,点$O$は辺$AD$の中点である.
この立体を平面$TPHQ$で切ったとき,
$APQ-EFH$の体積を求めなさい.
函館ラサール高校過去問
この動画を見る
立方体$ABCD-EFGH$は1辺6cmであり,
点$P$は辺$AB$の中点であり,点$O$は辺$AD$の中点である.
この立体を平面$TPHQ$で切ったとき,
$APQ-EFH$の体積を求めなさい.
函館ラサール高校過去問
【中学数学】方程式の基礎をどこよりも丁寧に 3-1【中1数学】

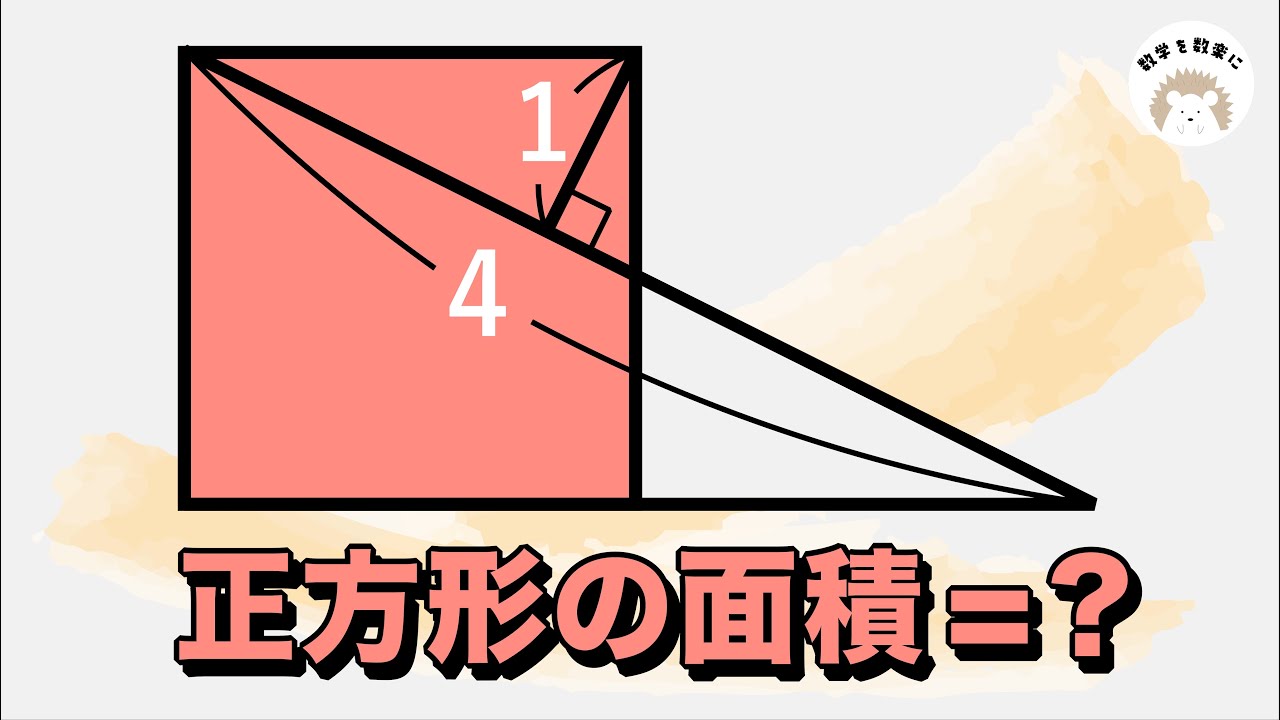
気付けば一瞬!!正方形の面積
【3分で問題との付き合い方を学ぶ】:中央大学杉並高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$(x+a)(x+b)$を展開すると$x^2+cx+12$となる.
$c$のとりうる値は何通りあるか.
中大杉並高校過去問
この動画を見る
$(x+a)(x+b)$を展開すると$x^2+cx+12$となる.
$c$のとりうる値は何通りあるか.
中大杉並高校過去問
整数問題 東京学芸大学附属

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$2^a \times 3^b \times 7^c$(a,b,cは正の整数)の形で表される3ケタの数の中で最小の数と最大の数を求めよ。
東京学芸大学附属高校
この動画を見る
$2^a \times 3^b \times 7^c$(a,b,cは正の整数)の形で表される3ケタの数の中で最小の数と最大の数を求めよ。
東京学芸大学附属高校
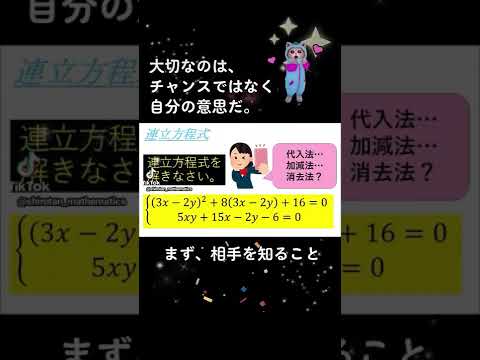
難しい連立方程式だけど音楽が気になる動画~全国入試問題解法 #Shorts #数学 #sound
単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
(3x-2y)^2+8(3x-2y)+16=0 \\
5xy+15x-2y-6=0
\end{array}
\right.
\end{eqnarray}$
連立方程式を解きなさい.
渋谷教育幕張高校過去問
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
(3x-2y)^2+8(3x-2y)+16=0 \\
5xy+15x-2y-6=0
\end{array}
\right.
\end{eqnarray}$
連立方程式を解きなさい.
渋谷教育幕張高校過去問
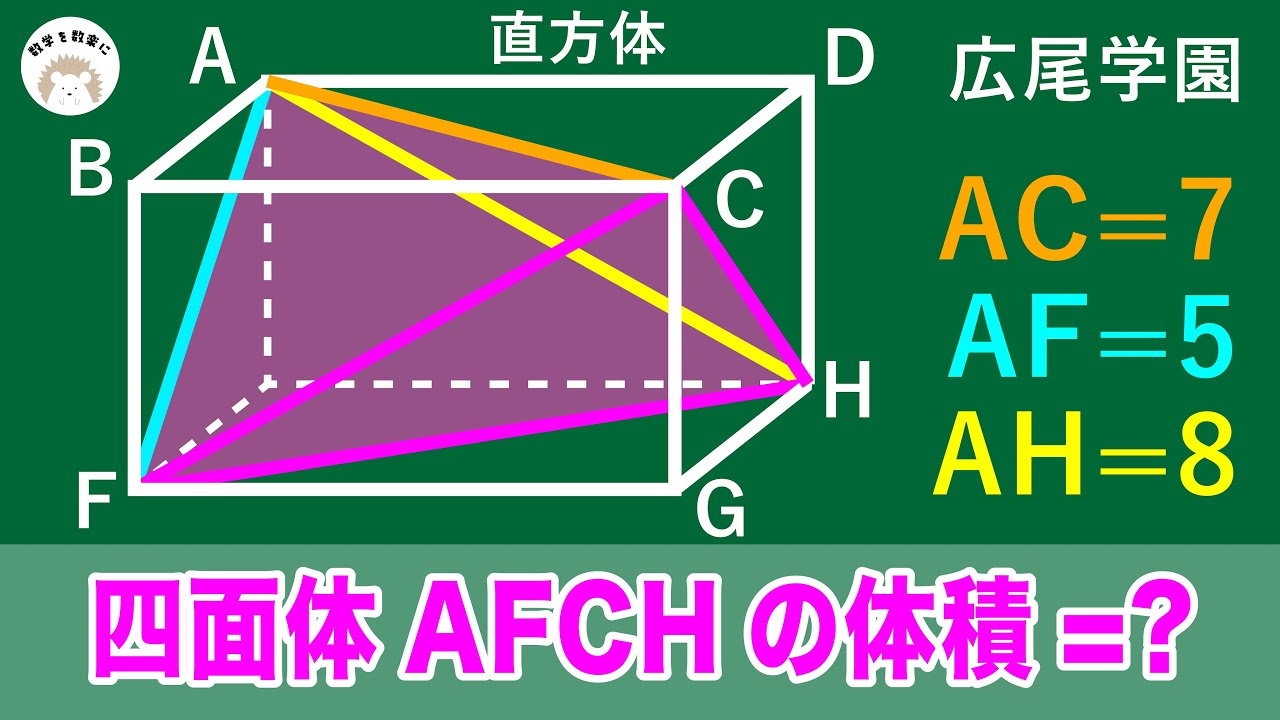
直方体の中の等面四面体の体積 広尾学園
単元:
#数学(中学生)#立体図形#体積・表面積・回転体・水量・変化のグラフ#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
AC=7
AF=5
AH=8
四面体AFCHの体積=?
*図は動画内参照
広尾学園高等学校
この動画を見る
AC=7
AF=5
AH=8
四面体AFCHの体積=?
*図は動画内参照
広尾学園高等学校
【数検3級】数学検定3級2次 問題8

単元:
#数学(中学生)#中3数学#数学検定・数学甲子園・数学オリンピック等#相似な図形#数学検定#数学検定3級
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題8.右の図のような、∠A=90°の直角三角形ABCについて、次の問いに答えなさい。
(18) 辺BC上にあり、△ABC∽△PBAとなる点Pを、下の<注>にしたがって作図しなさい。作図をする代わりに、作図の方法を言葉で説明してもかまいません。
<注> a コンパスとものさしを使って作図してください。ただし、ものさしは直線を引くことだけに用いてください。
b コンパスの線は、はっきりと見えるようにかいてください。コンパスの針をさした位置に、・の印をつけてください。
c 作図に用いた線は消さないで残しておき、線を引いた順に①、②、③、・・・の番号を書いてください。
この動画を見る
問題8.右の図のような、∠A=90°の直角三角形ABCについて、次の問いに答えなさい。
(18) 辺BC上にあり、△ABC∽△PBAとなる点Pを、下の<注>にしたがって作図しなさい。作図をする代わりに、作図の方法を言葉で説明してもかまいません。
<注> a コンパスとものさしを使って作図してください。ただし、ものさしは直線を引くことだけに用いてください。
b コンパスの線は、はっきりと見えるようにかいてください。コンパスの針をさした位置に、・の印をつけてください。
c 作図に用いた線は消さないで残しておき、線を引いた順に①、②、③、・・・の番号を書いてください。
確率の問題は解法が複数存在する30秒~全国入試問題解法 #Shorts #数学 #確率
単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
この箱から玉を1個取り出し,それを箱に戻さずに,もう1個取り出す.
取り出した2個の玉の色が異なる確率を求めない.
山形県高校過去問
この動画を見る
この箱から玉を1個取り出し,それを箱に戻さずに,もう1個取り出す.
取り出した2個の玉の色が異なる確率を求めない.
山形県高校過去問
平方根の計算 関西学院

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{\sqrt {0.52^2 - 0.2^2}}{0.4^2}$
関西学院
この動画を見る
$\frac{\sqrt {0.52^2 - 0.2^2}}{0.4^2}$
関西学院
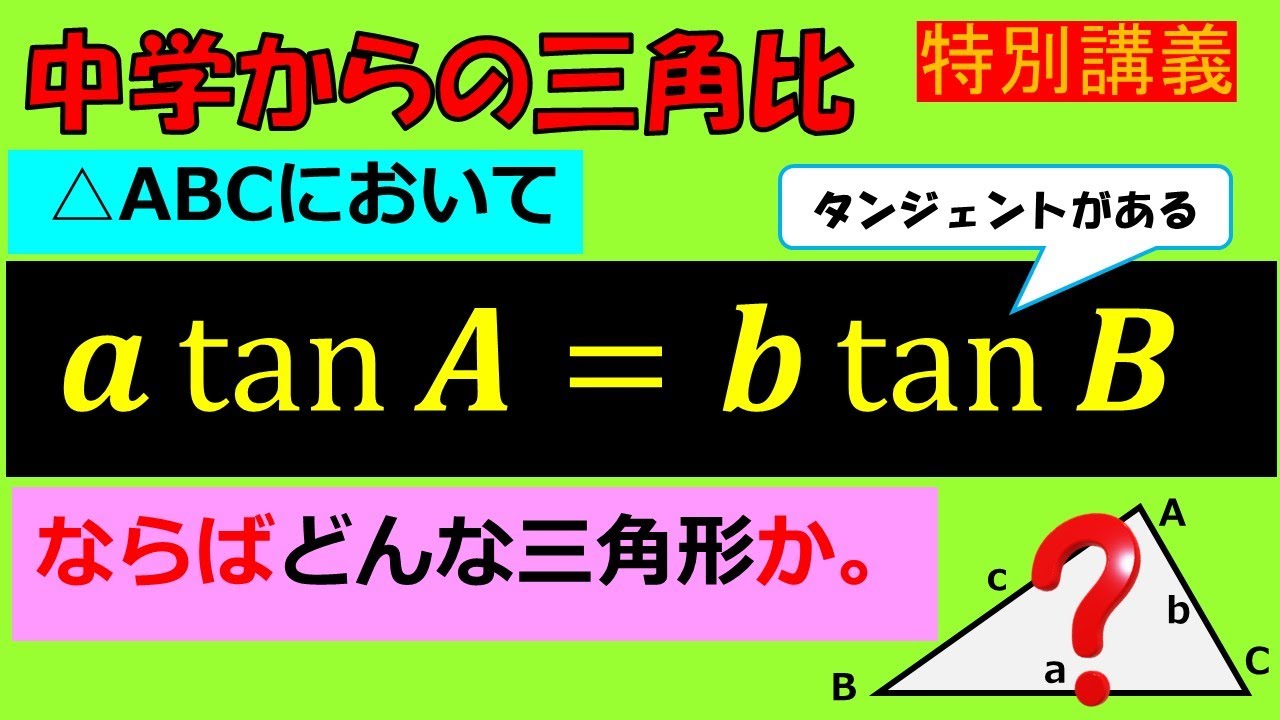
【中学からの!】タンジェントを含む計算:三角比~全国入試問題解法
単元:
#数学(中学生)#図形と計量#三角比(三角比・拡張・相互関係・単位円)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\triangle ABC$において
$a \tan A=b \tan B$ならばどんな三角形か.
この動画を見る
$\triangle ABC$において
$a \tan A=b \tan B$ならばどんな三角形か.
因数分解 解き方3通り!! 慶應義塾高校

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ。
$(2x+11)^2 - (x+9)^2 -2(x+2)^2$
慶應義塾高等学校
この動画を見る
因数分解せよ。
$(2x+11)^2 - (x+9)^2 -2(x+2)^2$
慶應義塾高等学校
