 数学(中学生)
数学(中学生)
 数学(中学生)
数学(中学生)
高等学校入学試験問題予想:日本大学第二高等学校~全部入試問題

単元:
#数学(中学生)#高校入試過去問(数学)#日本大学第二高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試予想問題~日大第二高校
・$\displaystyle \frac{3}{2} \div (-\displaystyle \frac{1}{2})^2+(-3)^2 \times (-\displaystyle \frac{1}{4})^3 \div 0.75^2+(0.5-1)^2$
を計算せよ。
・$a^2+aℓ-3ac-2ℓ^2+3ℓc $を因数分解せよ。
・$\sqrt{ \displaystyle \frac{72}{n} } $が自然数となるような自然数$n$の個数を求めよ。
・2人でじゃんけんをしたとき、2人の出した 手の指の本数の合計が奇数になる確率 を求めよ。
(グー:0,チョキ:2、パー:5)
1辺の長さが4の立方体 点P:辺EFを1:3
点Q:辺BCの中点
(1)~(3)を求めよ。
(1)PからEGに引いた垂線の長さ?
(2)QからEGに引いた重線の長さ?
(3)線分EGの中点をMとする
線分PMと線分QMの長さの和?
※図は動画内参照
この動画を見る
入試予想問題~日大第二高校
・$\displaystyle \frac{3}{2} \div (-\displaystyle \frac{1}{2})^2+(-3)^2 \times (-\displaystyle \frac{1}{4})^3 \div 0.75^2+(0.5-1)^2$
を計算せよ。
・$a^2+aℓ-3ac-2ℓ^2+3ℓc $を因数分解せよ。
・$\sqrt{ \displaystyle \frac{72}{n} } $が自然数となるような自然数$n$の個数を求めよ。
・2人でじゃんけんをしたとき、2人の出した 手の指の本数の合計が奇数になる確率 を求めよ。
(グー:0,チョキ:2、パー:5)
1辺の長さが4の立方体 点P:辺EFを1:3
点Q:辺BCの中点
(1)~(3)を求めよ。
(1)PからEGに引いた垂線の長さ?
(2)QからEGに引いた重線の長さ?
(3)線分EGの中点をMとする
線分PMと線分QMの長さの和?
※図は動画内参照
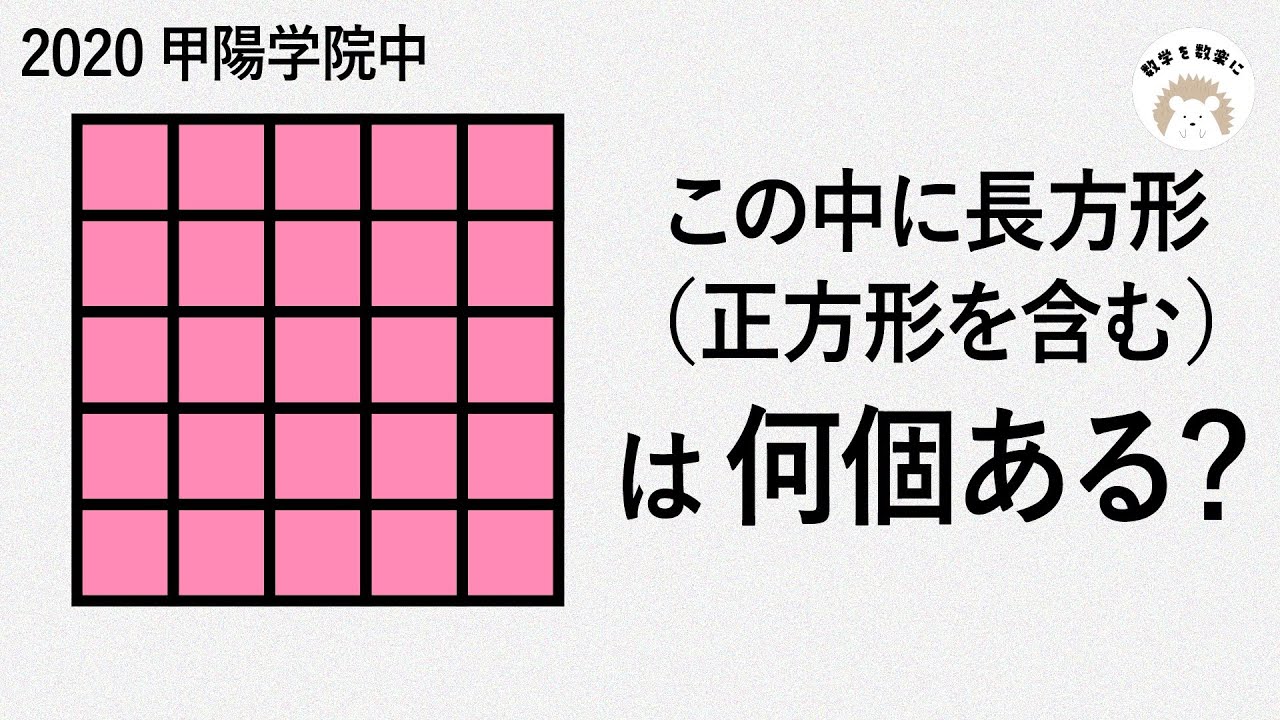
長方形何個? 甲陽学院中
単元:
#算数(中学受験)#中1数学#過去問解説(学校別)#平面図形#角度と面積#平面図形
指導講師:
数学を数楽に
問題文全文(内容文):
この中に長方形(正方形を含む)は何個ある?
*図は動画内参照
2020甲陽学院中学校
この動画を見る
この中に長方形(正方形を含む)は何個ある?
*図は動画内参照
2020甲陽学院中学校
食塩水の濃度の必勝法

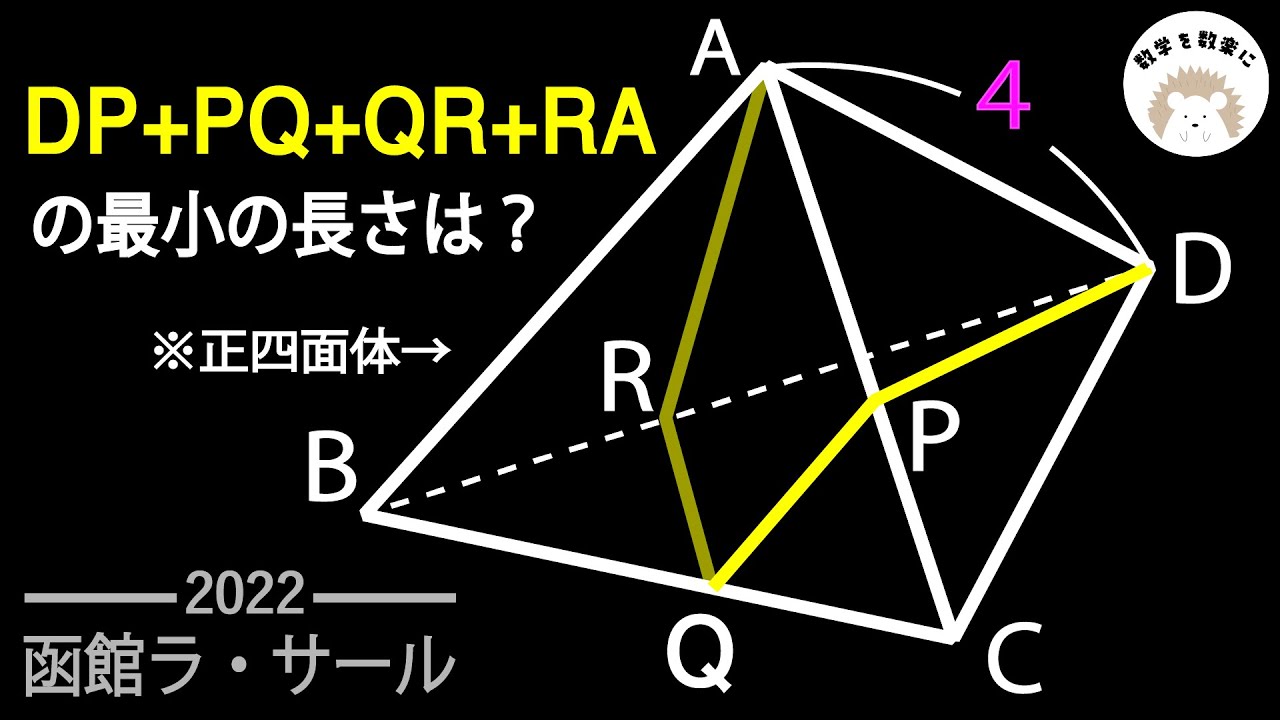
最短距離 正四面体 函館ラ・サール2022入試問題解説32問目
単元:
#数学(中学生)#中1数学#空間図形#立体図形#立体図形その他#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
正四面体
DP+PQ+QR+RAの最小の長さは?
*図は動画内参照
2022函館ラ・サール高等学校
この動画を見る
正四面体
DP+PQ+QR+RAの最小の長さは?
*図は動画内参照
2022函館ラ・サール高等学校
サクッと解こう!高校入試レベル
高等学校入学試験問題予想:近畿大学附属高等学校~全部入試問題

単元:
#数学(中学生)#高校入試過去問(数学)#近畿大学付属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試予想問題~近畿大学附属高等学校 2022年
・$\displaystyle \frac{3a-7}{4}-\displaystyle \frac{2a-5}{3}$
・$(\sqrt{ 32 }-\sqrt{ 6 }-2)(\sqrt{ 18 }+\displaystyle \frac{2\sqrt{ 6 }}{3}+\sqrt{ \displaystyle \frac{ 2 }{ 3 }})$
$3x+2y=4$
$6x-7y=3a$
の解の比が$x:y=2:3$
定数aの値を求めよ。
$y=\displaystyle \frac{a}{x}(a \gt o)$と
$y=\displaystyle \frac{1}{4}x^2$点aで交わる。
($X$座標が4)
点Aからx軸に下ろした垂線とx軸の交点Bとし、
$y=\displaystyle \frac{a}{x}$上に点C,$y=\displaystyle \frac{1}{4}x^2$上にD点
(1)aの値?
(2)△ABCの面積が8のとき点Cの座標?
(3) (2) のとき、△ABC=△BCDとなる点D?
但し、A,Dは異なる。
この動画を見る
入試予想問題~近畿大学附属高等学校 2022年
・$\displaystyle \frac{3a-7}{4}-\displaystyle \frac{2a-5}{3}$
・$(\sqrt{ 32 }-\sqrt{ 6 }-2)(\sqrt{ 18 }+\displaystyle \frac{2\sqrt{ 6 }}{3}+\sqrt{ \displaystyle \frac{ 2 }{ 3 }})$
$3x+2y=4$
$6x-7y=3a$
の解の比が$x:y=2:3$
定数aの値を求めよ。
$y=\displaystyle \frac{a}{x}(a \gt o)$と
$y=\displaystyle \frac{1}{4}x^2$点aで交わる。
($X$座標が4)
点Aからx軸に下ろした垂線とx軸の交点Bとし、
$y=\displaystyle \frac{a}{x}$上に点C,$y=\displaystyle \frac{1}{4}x^2$上にD点
(1)aの値?
(2)△ABCの面積が8のとき点Cの座標?
(3) (2) のとき、△ABC=△BCDとなる点D?
但し、A,Dは異なる。
なんで円の面積は半径×半径×π?

2022年2月2日 名城大学附属2022入試問題解説30問目

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$(2022 - 2) \div 2022 \times \frac{3 \times (333 + 4)}{5 \times (200+2)}=?$
2022名城大学附属高等学校
この動画を見る
$(2022 - 2) \div 2022 \times \frac{3 \times (333 + 4)}{5 \times (200+2)}=?$
2022名城大学附属高等学校
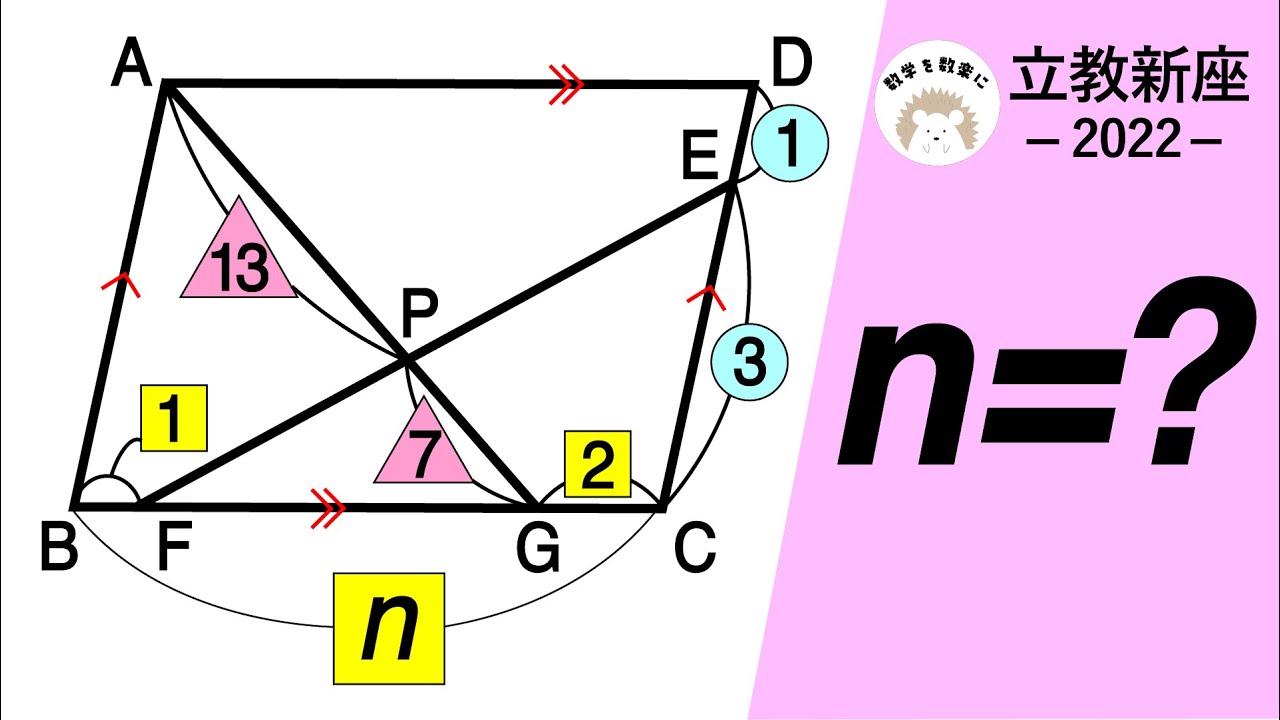
図形 比 立教新座 2022 入試問題解説 29問目
単元:
#数学(中学生)#中1数学#中2数学#平面図形#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
n=?
*図は動画内参照
2022立教新座高等学校(改)
この動画を見る
n=?
*図は動画内参照
2022立教新座高等学校(改)
池を反対方向に回る問題

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1周960mの池をA、Bが池に沿って反対方向に進む。
Aは70m/分、Bは50m/分のとき何分後に出会うか?
この動画を見る
1周960mの池をA、Bが池に沿って反対方向に進む。
Aは70m/分、Bは50m/分のとき何分後に出会うか?
小数部分 立教新座 2022 入試問題解説 28問目 西大和学園も全く同じ問題でした。
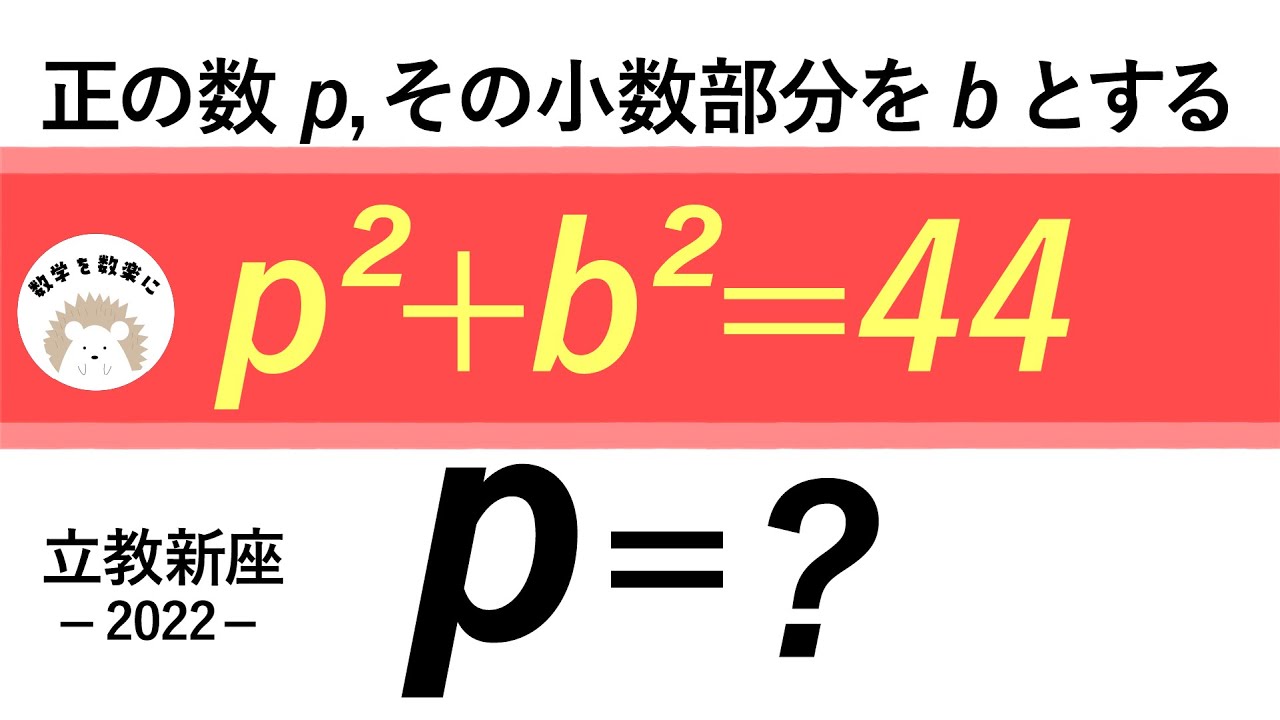
単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
正の数p、その小数部分をbとする
$p^2+b^2 = 44$
p=?
2022立教新座高等学校
この動画を見る
正の数p、その小数部分をbとする
$p^2+b^2 = 44$
p=?
2022立教新座高等学校
二等辺三角形と正方形3つ 四天王寺中
単元:
#算数(中学受験)#中2数学#過去問解説(学校別)#三角形と四角形
指導講師:
数学を数楽に
問題文全文(内容文):
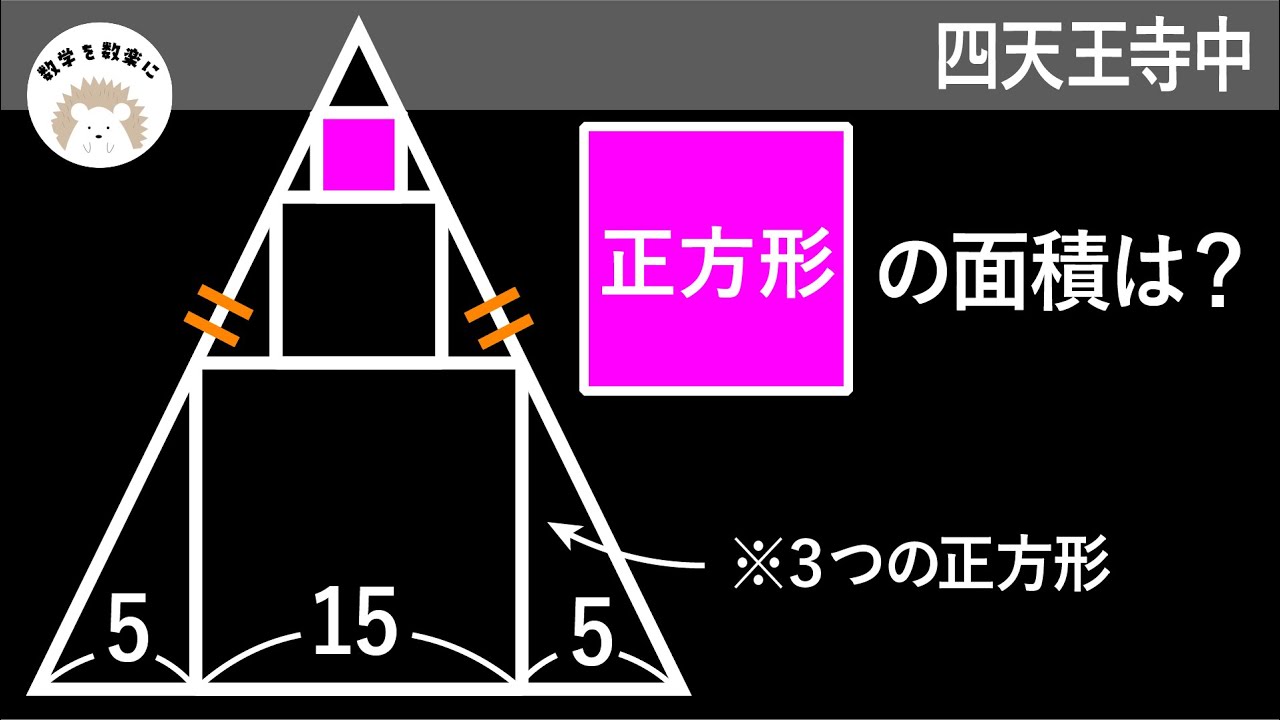
二等辺三角形と3つの正方形
正方形HIGFの面積は?
*図は動画内参照
2020四天王寺中学校
この動画を見る
二等辺三角形と3つの正方形
正方形HIGFの面積は?
*図は動画内参照
2020四天王寺中学校
円周角 中央大杉並 推薦 2022入試問題解説27問目

単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle MBN = ?$
*図は動画内参照
2022中央大学杉並高等学校
この動画を見る
$\angle MBN = ?$
*図は動画内参照
2022中央大学杉並高等学校
【裏技】これ知ってる?

受験生よ。ここで差がつきますよ。芝浦工大柏 2022入試問題解説26問目
単元:
#数学(中学生)#中1数学#空間図形#立体図形#体積・表面積・回転体・水量・変化のグラフ#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
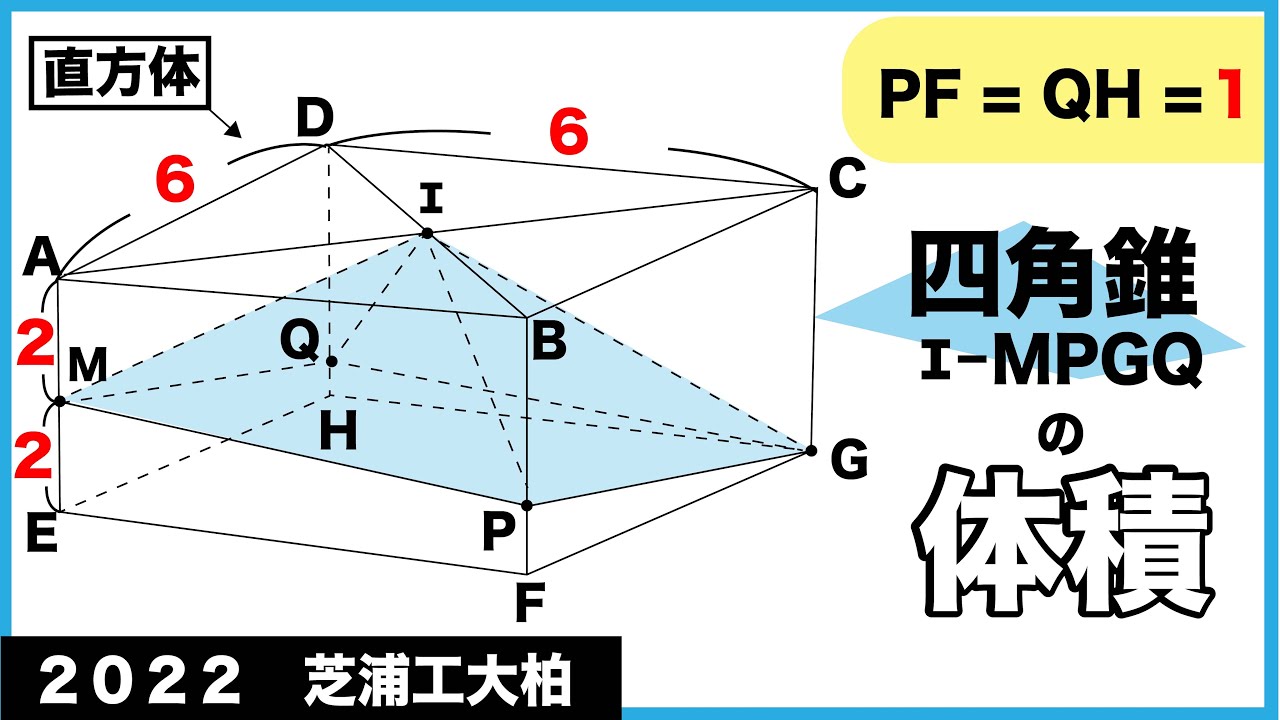
直方体
PF=QH=1
四角形I-MPGQの体積=?
2022芝浦工業大学柏高等学校
この動画を見る
直方体
PF=QH=1
四角形I-MPGQの体積=?
2022芝浦工業大学柏高等学校
【中学数学】円周角の定理のまとめ~基礎固め~【中3数学】

単元:
#数学(中学生)#中3数学#円
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1つの弧に対する円周角は中心角の半分の大きさ $\angle APB=\frac{1}{2}2\angle AOB~\angle AOB=2\angle APB$
1つの弧に対する円周角の大きさは等しい$\angle APB=\angle AQB$
弧の長さが等しい⇔円周角が等しい$\stackrel{\frown}{AB}=\stackrel{\frown}{AB}~\angle APB=\angle CQD$
線分$AB$が直径$\angle APB=90°$
この動画を見る
1つの弧に対する円周角は中心角の半分の大きさ $\angle APB=\frac{1}{2}2\angle AOB~\angle AOB=2\angle APB$
1つの弧に対する円周角の大きさは等しい$\angle APB=\angle AQB$
弧の長さが等しい⇔円周角が等しい$\stackrel{\frown}{AB}=\stackrel{\frown}{AB}~\angle APB=\angle CQD$
線分$AB$が直径$\angle APB=90°$
これは知らないと損すぎる

【中学数学】因数分解のテクニックまとめ 3-4【中3数学】

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$\displaystyle
(1)\,6x^2y-15xy^2+27xy$
$\displaystyle
(2)\,x^2+x-56$
$\displaystyle
(3)\,x^2-18x+81$
$\displaystyle
(4)\,4x^2+20x+25$
$\displaystyle
(5)\,4x^2-81$
$\displaystyle
(6)\,9(a+B)^2-30(a+b)+16$
$\displaystyle
(7)\,6x^2+12x-48$
$\displaystyle
(8)\,ax+ay-5x-5y$
$\displaystyle
(9)\,x^2+6xy+9y^2-4a^2$
$\displaystyle
(10)\,1-x^2+8xy-16y^2$
この動画を見る
$\displaystyle
(1)\,6x^2y-15xy^2+27xy$
$\displaystyle
(2)\,x^2+x-56$
$\displaystyle
(3)\,x^2-18x+81$
$\displaystyle
(4)\,4x^2+20x+25$
$\displaystyle
(5)\,4x^2-81$
$\displaystyle
(6)\,9(a+B)^2-30(a+b)+16$
$\displaystyle
(7)\,6x^2+12x-48$
$\displaystyle
(8)\,ax+ay-5x-5y$
$\displaystyle
(9)\,x^2+6xy+9y^2-4a^2$
$\displaystyle
(10)\,1-x^2+8xy-16y^2$
球の表面積ってなんで4πr^2?

単元:
#数学(中学生)#中1数学#空間図形
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
球の表面積が$4 \pi r ^ 2$になるのはなぜか、理由解説動画です
この動画を見る
球の表面積が$4 \pi r ^ 2$になるのはなぜか、理由解説動画です
2次方程式の応用 明大明治 2022入試問題解説 25問目

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
xについての2次方程式
$x^2-K^2x + 2(K^2 -2 )= 0$(K> 0)
一方の解がもう一方の解の2倍になる時、
Kの値を全て求めよ
2022明治大学付属明治高等学校
この動画を見る
xについての2次方程式
$x^2-K^2x + 2(K^2 -2 )= 0$(K> 0)
一方の解がもう一方の解の2倍になる時、
Kの値を全て求めよ
2022明治大学付属明治高等学校
面積比 三重高校のラスト問題2022入試問題解説 24問目
単元:
#数学(中学生)#中1数学#平面図形#角度と面積#平面図形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
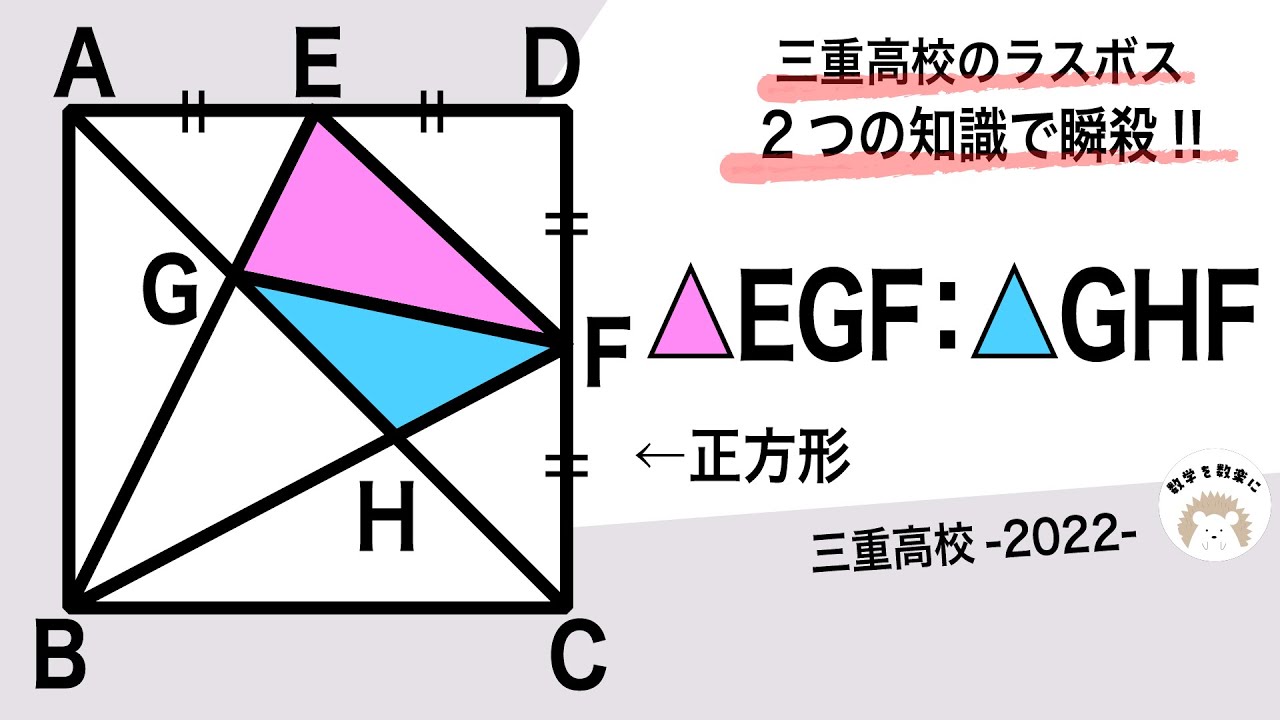
△EGF:△GHF
*図は動画内参照
2022三重高等学校
この動画を見る
△EGF:△GHF
*図は動画内参照
2022三重高等学校
【中学数学】相似な図形:線分比と面積比の巧みな利用
単元:
#数学(中学生)#中3数学#相似な図形
指導講師:
理数個別チャンネル
問題文全文(内容文):
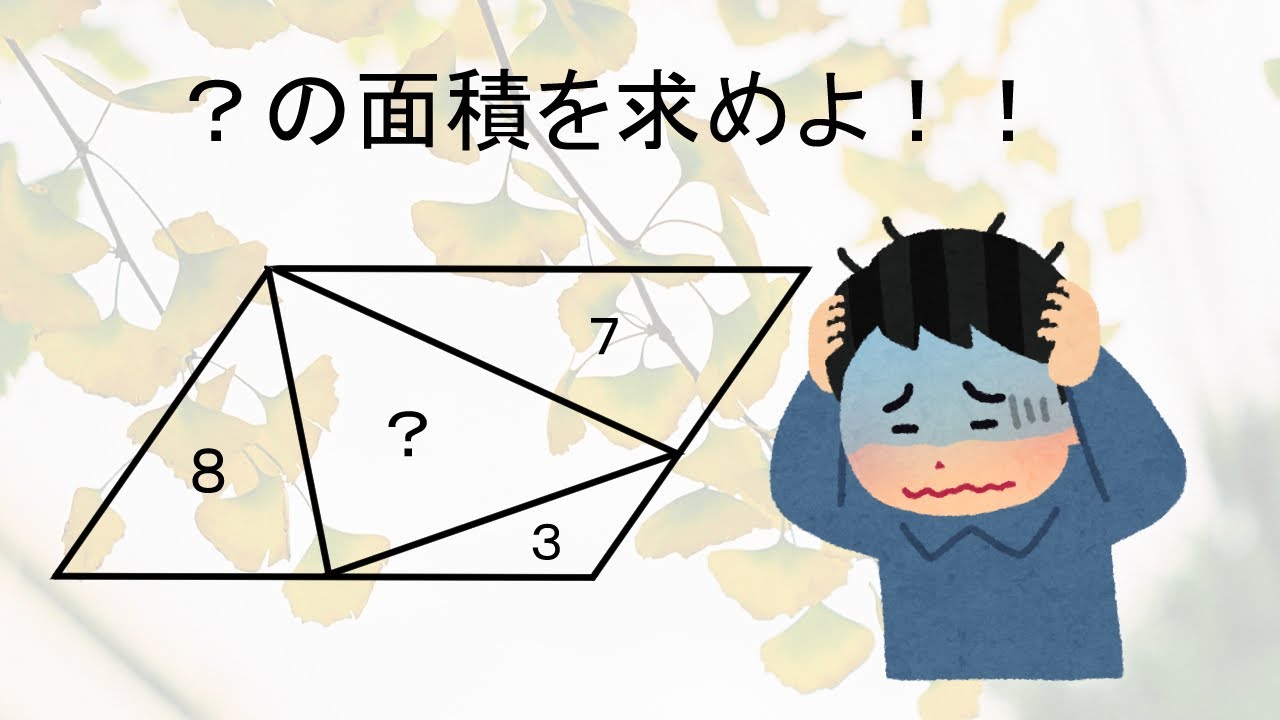
【中学数学 相似な図形】
平行四辺形ABCDにおいて、△ABE=8、△ADF=7、△CEF=3のとき、△AEFの面積を求めよ。
この動画を見る
【中学数学 相似な図形】
平行四辺形ABCDにおいて、△ABE=8、△ADF=7、△CEF=3のとき、△AEFの面積を求めよ。
高校入試レベルだよ
【まずは完答、それから本質をつかむこと!】図形:慶応義塾高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#慶應義塾高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
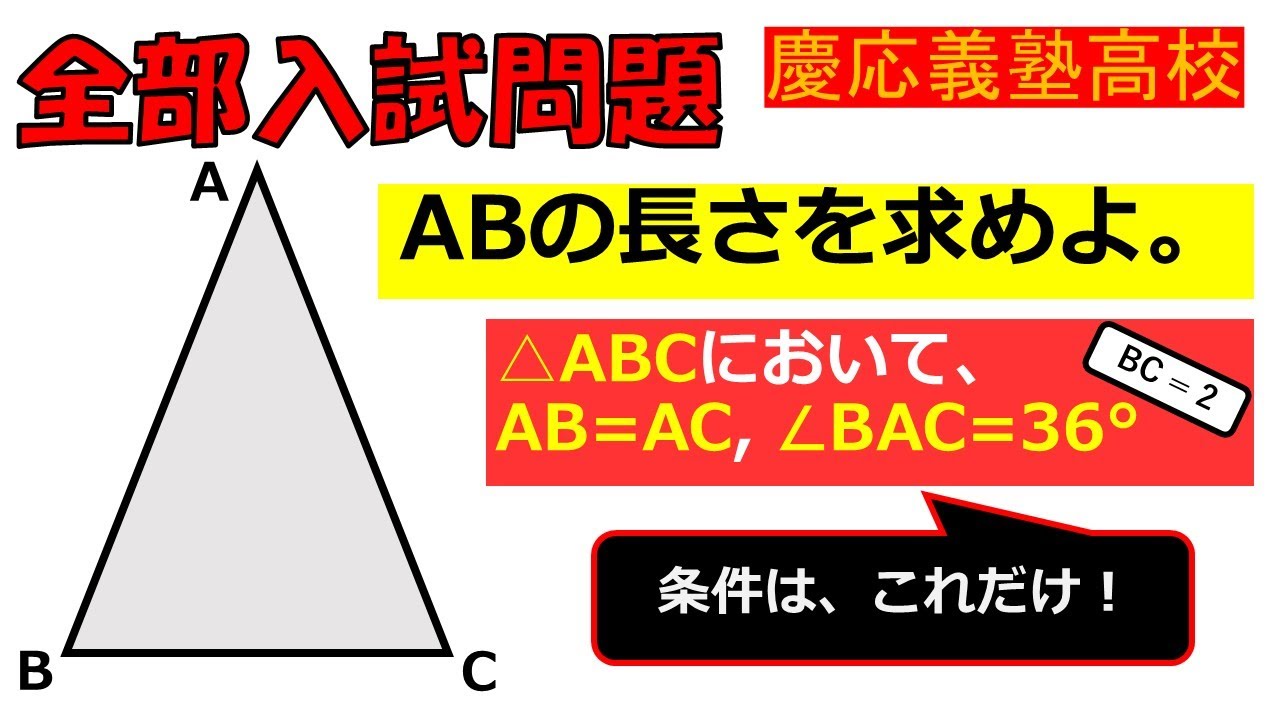
$ \triangle ABC$において,$\angle BAC=36^{ \circ }$
$BC=2$
条件はこれだけ!
※図は動画内参照
この動画を見る
$ \triangle ABC$において,$\angle BAC=36^{ \circ }$
$BC=2$
条件はこれだけ!
※図は動画内参照
チェバの定理使わずに解ける? 香川誠陵 2022入試問題解説23問目
単元:
#数学(中学生)#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
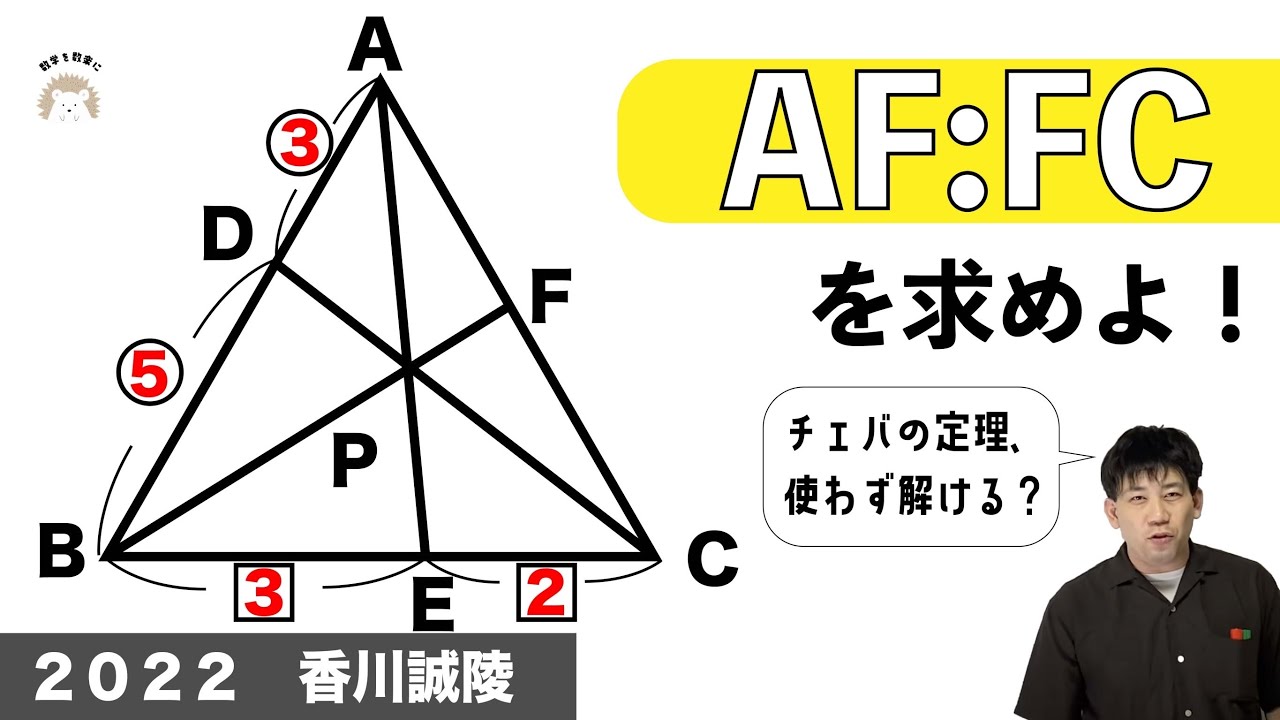
チェバの定理は使わない
AF:FCを求めよ
*図は動画内参照
2022香川誠陵高等学校
この動画を見る
チェバの定理は使わない
AF:FCを求めよ
*図は動画内参照
2022香川誠陵高等学校
【裏技】暗算で円錐の表面積

平方根の計算 香川誠陵 2022入試問題解説 22問目

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
計算せよ
$(\frac{2}{\sqrt 2} + \frac{3}{\sqrt 3}) \times (\sqrt {18} - \sqrt {12})$
2022香川誠陵高等学校
この動画を見る
計算せよ
$(\frac{2}{\sqrt 2} + \frac{3}{\sqrt 3}) \times (\sqrt {18} - \sqrt {12})$
2022香川誠陵高等学校
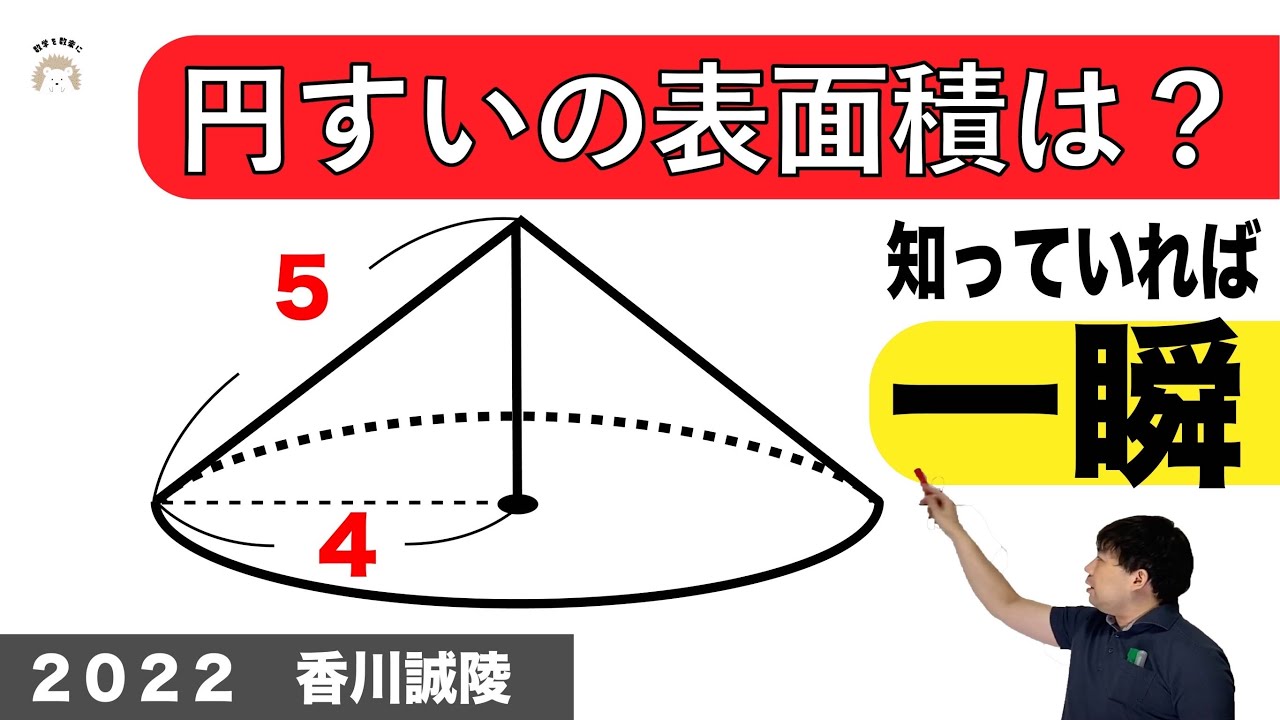
円錐 香川誠陵 2022入試問題解説21問目
【図形の奥義⁈実は追加の問題も大切!】図形:岐阜県立高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#岐阜県公立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
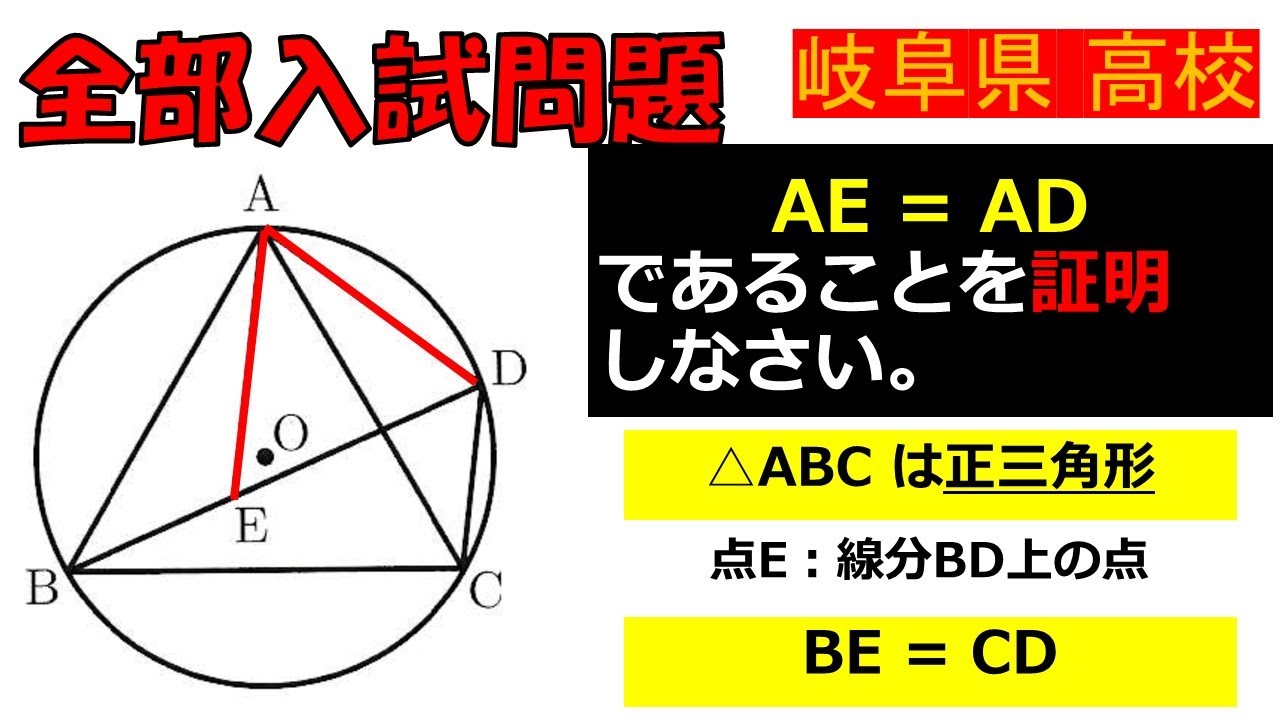
全国入試問題~岐阜県立高等学校
AE = ADであることを証明 しなさい。
△ABC は正三角形
点E:線分BD上の点
BE = CDは等しい
※図は動画内参照
この動画を見る
全国入試問題~岐阜県立高等学校
AE = ADであることを証明 しなさい。
△ABC は正三角形
点E:線分BD上の点
BE = CDは等しい
※図は動画内参照
【中学数学】食塩水の濃度~この動画1つで完璧に~【中1数学】

単元:
#数学(中学生)#中1数学#方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
(1) 食塩10gが水40gに溶けている食塩水の濃度を求めよ
(2) 5%の食塩水100gに吹く前れる食塩の量を求めよ
(3) 12%の食塩水200gと7%の食塩水300gを混ぜたとき何%の食塩水になりますか
(4) 10%の食塩水300gとx%の食塩水450gを混ぜたとき、7%の食塩水になる。xを求めよ
(5) 6%の食塩水100gから水何gを蒸発させると8%の食塩水になるか
(6) 6%の食塩水100gに水何gを混ぜると5%の食塩水になるか
この動画を見る
(1) 食塩10gが水40gに溶けている食塩水の濃度を求めよ
(2) 5%の食塩水100gに吹く前れる食塩の量を求めよ
(3) 12%の食塩水200gと7%の食塩水300gを混ぜたとき何%の食塩水になりますか
(4) 10%の食塩水300gとx%の食塩水450gを混ぜたとき、7%の食塩水になる。xを求めよ
(5) 6%の食塩水100gから水何gを蒸発させると8%の食塩水になるか
(6) 6%の食塩水100gに水何gを混ぜると5%の食塩水になるか
