 福田次郎
福田次郎
 福田次郎
福田次郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
福田のおもしろ数学235〜無限級数の収束・発散の判定

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
無限級数 $1-1+1-1+1-1+1-1+ \cdots$ の収束・発散を判定せよ。
この動画を見る
無限級数 $1-1+1-1+1-1+1-1+ \cdots$ の収束・発散を判定せよ。
福田のおもしろ数学233〜区分求積の公式の変形

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{1}{n}\displaystyle \sum_{k=1}^n f\left( \frac{k}{n} \right) = \int_0^1 f(x) dx$である。では$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{1}{n}\displaystyle \sum_{k=3}^{n+5} f\left( \frac{k}{n} \right)$はどうなる?
この動画を見る
$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{1}{n}\displaystyle \sum_{k=1}^n f\left( \frac{k}{n} \right) = \int_0^1 f(x) dx$である。では$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{1}{n}\displaystyle \sum_{k=3}^{n+5} f\left( \frac{k}{n} \right)$はどうなる?
福田の数学〜浜松医科大学2024医学部第2問〜日本シリーズ形式の確率とシグマに関する等式の証明

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
以下の問いに答えよ。なお、${}_n \mathrm{ C }_r$は二項係数を表す。
(1) AさんとBさんが将棋の対局を繰り返し行い、先に3回勝った方が優勝するものとする。AさんがBさんに1回の対局で勝つ確率は$p$であるとする。また各対局において引き分けはないものとする。このとき、Aさんが優勝する確率を$p$の式として表せ。
(2) (1) において $p = 0.75$ であるときに、Aさんが優勝する確率を、小数第3位を四捨五入して小数第2位まで求めよ。
(3) (1) において「先に3回」を「先に$N$回」 ($N$は2以上の自然数)にしたときの Aさんが優勝する確率を$p$と$N$の式として表せ。必要ならば和の記号$\sum$や二項係数${}_n \mathrm{ C }_r$を用いてもよい。
(4) すべての自然数$m$について
$\displaystyle \sum_{k=1}^m \displaystyle \frac{{}_{m+k} \mathrm{ C }_k}{2^k} = 2^m-1$
であることを証明せよ。
この動画を見る
以下の問いに答えよ。なお、${}_n \mathrm{ C }_r$は二項係数を表す。
(1) AさんとBさんが将棋の対局を繰り返し行い、先に3回勝った方が優勝するものとする。AさんがBさんに1回の対局で勝つ確率は$p$であるとする。また各対局において引き分けはないものとする。このとき、Aさんが優勝する確率を$p$の式として表せ。
(2) (1) において $p = 0.75$ であるときに、Aさんが優勝する確率を、小数第3位を四捨五入して小数第2位まで求めよ。
(3) (1) において「先に3回」を「先に$N$回」 ($N$は2以上の自然数)にしたときの Aさんが優勝する確率を$p$と$N$の式として表せ。必要ならば和の記号$\sum$や二項係数${}_n \mathrm{ C }_r$を用いてもよい。
(4) すべての自然数$m$について
$\displaystyle \sum_{k=1}^m \displaystyle \frac{{}_{m+k} \mathrm{ C }_k}{2^k} = 2^m-1$
であることを証明せよ。
福田のおもしろ数学232〜1980で割り切れる証明

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$2450^n-1370^n+1150^n-250^n$が$1980$で割り切れることを示せ。
この動画を見る
$2450^n-1370^n+1150^n-250^n$が$1980$で割り切れることを示せ。
福田の数学〜浜松医科大学2024医学部第1問〜等式と不等式の証明とタンジェントの加法定理

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#三角関数#恒等式・等式・不等式の証明#加法定理とその応用#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
以下の問いに答えよ。
(1) $a$, $b$, $c$ を正の実数とする。このとき、不等式
$a^2b^2+b^2c^2+c^2a^2 \geqq abc(a+b+c)$
を証明せよ。また、等号が成り立つときの$a$, $b$, $c$ の条件を求めよ。
(2) 鋭角三角形の3つの内角を$A$, $B$, $C$とおく。以下の問いに答えよ。
(a)等式
$\tan A+\tan B+\tan C=\tan A\tan B\tan C$
を証明せよ。
(b)不等式
$\displaystyle \frac{1}{\tan A}+\displaystyle \frac{1}{\tan B}+\displaystyle \frac{1}{\tan C} \geqq\sqrt{ 3 }$
を証明せよ。また、等号が成り立つときの鋭角三角形の条件を求めよ。
この動画を見る
以下の問いに答えよ。
(1) $a$, $b$, $c$ を正の実数とする。このとき、不等式
$a^2b^2+b^2c^2+c^2a^2 \geqq abc(a+b+c)$
を証明せよ。また、等号が成り立つときの$a$, $b$, $c$ の条件を求めよ。
(2) 鋭角三角形の3つの内角を$A$, $B$, $C$とおく。以下の問いに答えよ。
(a)等式
$\tan A+\tan B+\tan C=\tan A\tan B\tan C$
を証明せよ。
(b)不等式
$\displaystyle \frac{1}{\tan A}+\displaystyle \frac{1}{\tan B}+\displaystyle \frac{1}{\tan C} \geqq\sqrt{ 3 }$
を証明せよ。また、等号が成り立つときの鋭角三角形の条件を求めよ。
福田のおもしろ数学231〜交代級数の収束発散

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
交代級数$1-\displaystyle \frac{1}{2}+\displaystyle \frac{1}{3}-\displaystyle \frac{1}{4}+\displaystyle \frac{1}{5}-\cdots$が収束することを示し、その和を求めよ。
この動画を見る
交代級数$1-\displaystyle \frac{1}{2}+\displaystyle \frac{1}{3}-\displaystyle \frac{1}{4}+\displaystyle \frac{1}{5}-\cdots$が収束することを示し、その和を求めよ。
福田の数学〜東京医科歯科大学2024医学部第3問〜定積分の性質と置換積分の計算の解

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京医科歯科大学
指導講師:
福田次郎
問題文全文(内容文):
$\fbox{3} f(x)$を連続関数とするとき、次の各問いに答えよ。
(1)次の等式を示せ。$\displaystyle \int_{0}^{ \frac{\pi}{2} } f(\sin 2x)\sin x dx=\displaystyle \int_{0}^{ \frac{\pi}{2} } f(\sin 2x)\cos x dx$
(2)次の等式を示せ。$\displaystyle \int_{0}^{ \frac{\pi}{2} } f(\sin 2x)(\sin x+\cos x) dx=\displaystyle \int_{-1}^{1} f(1-t^2)dt$
(3)次の定積分の値を求めよ。$\displaystyle \int_{0}^{ \frac{\pi}{2} } \frac{\sin x}{1+\sqrt{\sin 2x}} dx$
この動画を見る
$\fbox{3} f(x)$を連続関数とするとき、次の各問いに答えよ。
(1)次の等式を示せ。$\displaystyle \int_{0}^{ \frac{\pi}{2} } f(\sin 2x)\sin x dx=\displaystyle \int_{0}^{ \frac{\pi}{2} } f(\sin 2x)\cos x dx$
(2)次の等式を示せ。$\displaystyle \int_{0}^{ \frac{\pi}{2} } f(\sin 2x)(\sin x+\cos x) dx=\displaystyle \int_{-1}^{1} f(1-t^2)dt$
(3)次の定積分の値を求めよ。$\displaystyle \int_{0}^{ \frac{\pi}{2} } \frac{\sin x}{1+\sqrt{\sin 2x}} dx$
福田のおもしろ数学230〜調和級数の収束発散

単元:
#数列の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
調和級数$1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots$が発散することを証明して下さい。
この動画を見る
調和級数$1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots$が発散することを証明して下さい。
福田の数学〜東京医科歯科大学2024医学部第2問〜ベクトルの勾配と無理不等式の解

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#数学(高校生)#数C#東京医科歯科大学
指導講師:
福田次郎
問題文全文(内容文):
$\fbox{2} xyz$ 空間において、点$\mathrm{ A }( 1, 0, 0 )$, $\mathrm{ B }(0, 1, 0)$, $\mathrm{ C }(-1, 0, 0)$, $\mathrm{ D }(0, 0, 1)$ をとり、線分 $\mathrm{ CD }$の中点を$\mathrm{ M }$とする。さらに、$\mathrm{ N }$を線分$\mathrm{ BD }$上の点とする。また、$z$軸と平行でない直線上の異なる2点$\mathrm{ P }(x, y, z), \mathrm{ Q }(x', y', z')$ に対して
$\frac{z' - z}{\sqrt{(x' - x) ^ 2 + (y' - y) ^ 2}}$をベクトル$\overrightarrow{ \mathrm{ PQ } }$の勾配と呼ぶ。$\overrightarrow{ \mathrm{ AN } }$の勾配を$t_1$、$\overrightarrow{ \mathrm{ NM } }$の勾配を$t_2$とするとき、
以下の各問いに答えよ。
(1) $t_2 = 0$ となるように$\mathrm{ N }$をとったとき、$t_1$の値を求めよ。
(2) $l = |\overrightarrow{ \mathrm{ AN } }|+|\overrightarrow{ \mathrm{ NM } }|$とし、$l$が最小となるように$\mathrm{ N }$をとったとき、$l$の値を求めよ。
(3) $0 \leqq t_{2} \leqq t_{1}$ となるように$\mathrm{ N }$をとったとき、$\mathrm{ N }$の$y$座標を$s$とする。$s$がとりうる値の範囲を求めよ。
この動画を見る
$\fbox{2} xyz$ 空間において、点$\mathrm{ A }( 1, 0, 0 )$, $\mathrm{ B }(0, 1, 0)$, $\mathrm{ C }(-1, 0, 0)$, $\mathrm{ D }(0, 0, 1)$ をとり、線分 $\mathrm{ CD }$の中点を$\mathrm{ M }$とする。さらに、$\mathrm{ N }$を線分$\mathrm{ BD }$上の点とする。また、$z$軸と平行でない直線上の異なる2点$\mathrm{ P }(x, y, z), \mathrm{ Q }(x', y', z')$ に対して
$\frac{z' - z}{\sqrt{(x' - x) ^ 2 + (y' - y) ^ 2}}$をベクトル$\overrightarrow{ \mathrm{ PQ } }$の勾配と呼ぶ。$\overrightarrow{ \mathrm{ AN } }$の勾配を$t_1$、$\overrightarrow{ \mathrm{ NM } }$の勾配を$t_2$とするとき、
以下の各問いに答えよ。
(1) $t_2 = 0$ となるように$\mathrm{ N }$をとったとき、$t_1$の値を求めよ。
(2) $l = |\overrightarrow{ \mathrm{ AN } }|+|\overrightarrow{ \mathrm{ NM } }|$とし、$l$が最小となるように$\mathrm{ N }$をとったとき、$l$の値を求めよ。
(3) $0 \leqq t_{2} \leqq t_{1}$ となるように$\mathrm{ N }$をとったとき、$\mathrm{ N }$の$y$座標を$s$とする。$s$がとりうる値の範囲を求めよ。
福田のおもしろ数学229〜置換積分の計算

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle \int^3_2\dfrac{1}{1+x^2}dx$の値を求めよ。
この動画を見る
$\displaystyle \int^3_2\dfrac{1}{1+x^2}dx$の値を求めよ。
福田のおもしろ数学239〜定積分と不等式の関係

単元:
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$k>0$ のとき、
$\displaystyle
\frac{1}{2(k+1)}<\int^{1}_{0}\frac{1-x}{k+x}dx<\frac{1}{2k}
$
を示して下さい。
この動画を見る
$k>0$ のとき、
$\displaystyle
\frac{1}{2(k+1)}<\int^{1}_{0}\frac{1-x}{k+x}dx<\frac{1}{2k}
$
を示して下さい。
福田の数学〜東京医科歯科大学2024医学部第1問〜n変数の不定方程式の解

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#数学(高校生)#東京医科歯科大学
指導講師:
福田次郎
問題文全文(内容文):
$n$を$2$以上の自然数とする。自然数の組$(a_1,a_2,\cdots,a_n)$を解とする方程式
$(*)~a_1+a_2+\cdots+a_n=a_1 \times a_2 \times \cdots \times a_n$を考える。
(1) $n=3$のとき、$(*)$の解$(a_1,a_2,a_3)$のうち、$a_1\leqq a_2 \leqq a_3$を満たすものをすべて求めよ。
(2) $n\geqq 3$のとき、$(*)$の任意の解$(a_1,a_2,\cdots,a_n)$において、$a_i=1$となる$i$が少なくとも1つ存在することを示せ。
(3) $(*)$のある解$(a_1,a_2,\cdots,a_n)$において、$a_i=1$となる$i$がちょうど2個存在しているとする。このとき、$n$のとりうる値を全て求めよ。
この動画を見る
$n$を$2$以上の自然数とする。自然数の組$(a_1,a_2,\cdots,a_n)$を解とする方程式
$(*)~a_1+a_2+\cdots+a_n=a_1 \times a_2 \times \cdots \times a_n$を考える。
(1) $n=3$のとき、$(*)$の解$(a_1,a_2,a_3)$のうち、$a_1\leqq a_2 \leqq a_3$を満たすものをすべて求めよ。
(2) $n\geqq 3$のとき、$(*)$の任意の解$(a_1,a_2,\cdots,a_n)$において、$a_i=1$となる$i$が少なくとも1つ存在することを示せ。
(3) $(*)$のある解$(a_1,a_2,\cdots,a_n)$において、$a_i=1$となる$i$がちょうど2個存在しているとする。このとき、$n$のとりうる値を全て求めよ。
福田のおもしろ数学228〜合成関数の定義からf(0)を求める

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$f(f(x))=x^2-x+1$のとき、$f(0)$を求めよ。
この動画を見る
$f(f(x))=x^2-x+1$のとき、$f(0)$を求めよ。
福田の数学〜中央大学202理工学部第4問〜sin(x)のn乗の定積分と極限

単元:
#関数と極限#積分とその応用#関数の極限#定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$n=1,2,3,\cdots$に対し、$\displaystyle I_n=\int_0^{\frac{\pi}{2}}\sin^nxdx$とおく。また、$\displaystyle I_0=\int_0^{\frac{\pi}{2}}1dx$とする。
(1) $(n+1)I_{n+1}=nI_{n-1}$を示せ。
(2) $nI_nI_{n-1}$を求めよ。
(3) $I_{n+1} < I_n$を示せ。
(4) 極限$\displaystyle \lim_{n \to\infty}nI_n^2$を求めよ。
この動画を見る
$n=1,2,3,\cdots$に対し、$\displaystyle I_n=\int_0^{\frac{\pi}{2}}\sin^nxdx$とおく。また、$\displaystyle I_0=\int_0^{\frac{\pi}{2}}1dx$とする。
(1) $(n+1)I_{n+1}=nI_{n-1}$を示せ。
(2) $nI_nI_{n-1}$を求めよ。
(3) $I_{n+1} < I_n$を示せ。
(4) 極限$\displaystyle \lim_{n \to\infty}nI_n^2$を求めよ。
福田のおもしろ数学227〜極限と区分求積法

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle \lim_{n\to\infty}\dfrac1n\sqrt[n]{_{2n}\mathrm{P}_n}$を求めよ
この動画を見る
$\displaystyle \lim_{n\to\infty}\dfrac1n\sqrt[n]{_{2n}\mathrm{P}_n}$を求めよ
福田の数学〜中央大学202理工学部第3問〜関数の列と漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#微分とその応用#色々な関数の導関数#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
関数$f(x),g(x)$に対し、$s_n(x)=f(x)^n+g(x)^n$とおき、さらに$s_1(x)=x, s_2(x)=x^2+2$が成り立つとする。
(1) $f(x)+g(x)$と$s_3(x)$を求めよ。
(2) $s_{n+2}(x)$を$s_n(x)$と$s_{n+1}(x)$を用いて表せ。
(3) $s_n(x)$の$x=0$における値$s_n(0)$と微分係数$s_n'(0)$を求めよ。
この動画を見る
関数$f(x),g(x)$に対し、$s_n(x)=f(x)^n+g(x)^n$とおき、さらに$s_1(x)=x, s_2(x)=x^2+2$が成り立つとする。
(1) $f(x)+g(x)$と$s_3(x)$を求めよ。
(2) $s_{n+2}(x)$を$s_n(x)$と$s_{n+1}(x)$を用いて表せ。
(3) $s_n(x)$の$x=0$における値$s_n(0)$と微分係数$s_n'(0)$を求めよ。
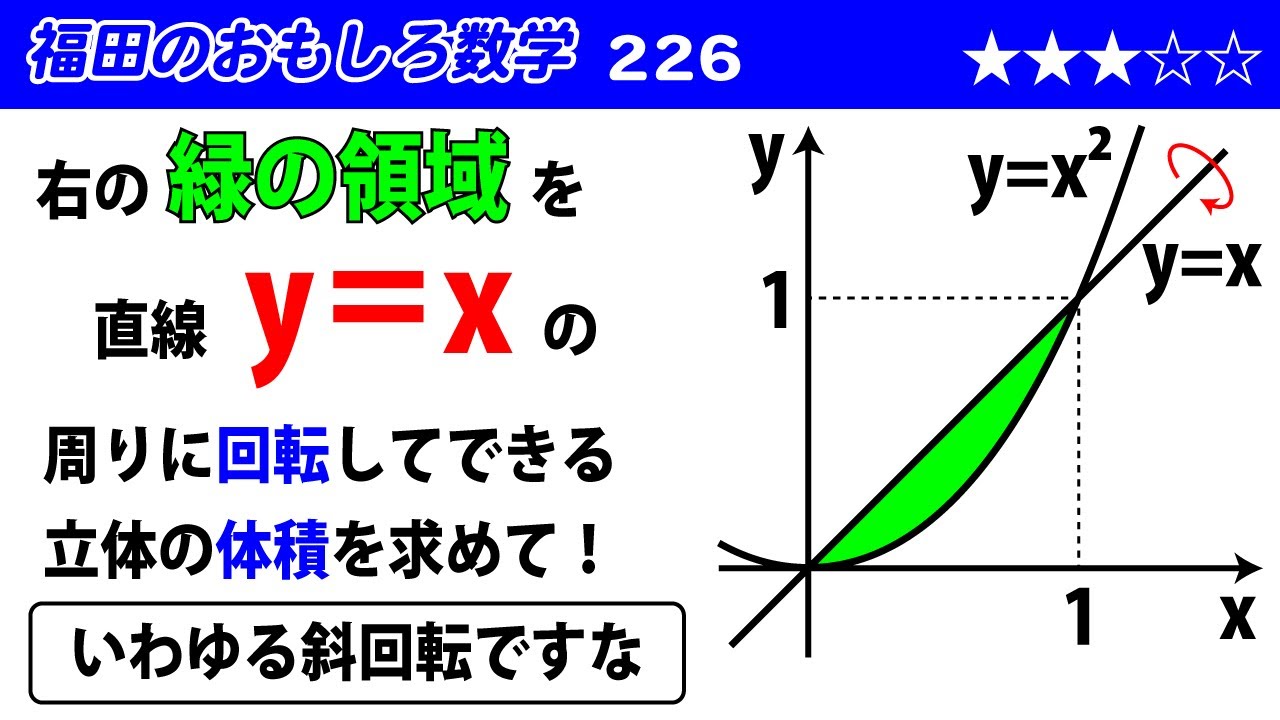
福田のおもしろ数学226〜回転体の体積と斜回転
単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
領域を直線$y=x$の周りに1回転させてできる立体の体積を求めよ。(図は動画参照)
この動画を見る
領域を直線$y=x$の周りに1回転させてできる立体の体積を求めよ。(図は動画参照)
福田の数学〜中央大学2024理工学部第2問〜確率の基本性質と3で割ったときの剰余類

単元:
#数A#場合の数と確率#整数の性質#確率#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$n$ を $3$ 以上の整数とする。$1, \, 2, \, \ldots, \, n$ の数が1つずつ書かれた $n$ 枚のカードがある。これらをよく混ぜて1枚のカードを引き、そこに書かれた数を $X$ とする。そのカードを元に戻し、よく混ぜてからもう一度1枚のカードを引き、そこに書かれた数を $Y$ とする。このとき $X-Y$ が $3$ の倍数である確率を $p(n)$、$X-Y-1$ が $3$ の倍数である確率を $q(n)$、$X-Y+1$ が $3$ の倍数である確率を $r(n)$ とする。
$(1)$ $q(3)=\fbox{ク}$ である。
$(2)$ $r(n)$ は $q(n)$ を用いて $r(n)=\fbox{ケ}$ と表せる。
$(3)$ $n$ が $3$ の倍数であるとき、$p(n)=\frac{\fbox{コ}}{\fbox{サ}}$ が成り立つ。
$(4)$ $n-1$ が $3$ の倍数であるとき、$p(n)=\frac{\fbox{シ}}{\fbox{ス}}$ が成り立つ。
$(5)$ $n-2$ が $3$ の倍数であるとき、$p(n)=\frac{\fbox{セ}}{\fbox{ソ}}$ が成り立つ。
この動画を見る
$n$ を $3$ 以上の整数とする。$1, \, 2, \, \ldots, \, n$ の数が1つずつ書かれた $n$ 枚のカードがある。これらをよく混ぜて1枚のカードを引き、そこに書かれた数を $X$ とする。そのカードを元に戻し、よく混ぜてからもう一度1枚のカードを引き、そこに書かれた数を $Y$ とする。このとき $X-Y$ が $3$ の倍数である確率を $p(n)$、$X-Y-1$ が $3$ の倍数である確率を $q(n)$、$X-Y+1$ が $3$ の倍数である確率を $r(n)$ とする。
$(1)$ $q(3)=\fbox{ク}$ である。
$(2)$ $r(n)$ は $q(n)$ を用いて $r(n)=\fbox{ケ}$ と表せる。
$(3)$ $n$ が $3$ の倍数であるとき、$p(n)=\frac{\fbox{コ}}{\fbox{サ}}$ が成り立つ。
$(4)$ $n-1$ が $3$ の倍数であるとき、$p(n)=\frac{\fbox{シ}}{\fbox{ス}}$ が成り立つ。
$(5)$ $n-2$ が $3$ の倍数であるとき、$p(n)=\frac{\fbox{セ}}{\fbox{ソ}}$ が成り立つ。
福田のおもしろ数学225〜楕円と直線の交点を使った線分の長さの積の最小値

単元:
#数A#図形の性質#平面上の曲線#方べきの定理と2つの円の関係#2次曲線#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
点 $\mathrm{P}(2,1)$ を通る直線が楕円 $\displaystyle \frac{x^2}{2}+\frac{y^2}{3}=1$ と異なる2点 $\mathrm{Q}, \, \mathrm{R}$ で交わっている。$\mathrm{PQ} \cdot \mathrm{PR}$ の最小値を求めよ。
この動画を見る
点 $\mathrm{P}(2,1)$ を通る直線が楕円 $\displaystyle \frac{x^2}{2}+\frac{y^2}{3}=1$ と異なる2点 $\mathrm{Q}, \, \mathrm{R}$ で交わっている。$\mathrm{PQ} \cdot \mathrm{PR}$ の最小値を求めよ。
福田の数学〜中央大学2024理工学部第1問〜3つの関数の大小関係と絶対不等式

単元:
#数Ⅰ#2次関数#2次関数とグラフ#微分とその応用#積分とその応用#接線と法線・平均値の定理#関数の変化(グラフ・最大最小・方程式・不等式)#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$a$ を $1$ 以上の実数、$b$ を実数とし、関数 $f(x), \, g(x), \, h(x)$ を以下で定める。
$\displaystyle f(x)=-|2|x|-1|, \quad g(x)=ax+b, \quad h(x)=e^x$
$(1)$ すべての実数 $x$ に対して $f(x) \leq g(x)$ が成り立つ。$(a, \, b)$ の範囲は、条件 $a \geq 1$ の下では、$b \geq 1$ のとき $a \leq \fbox{ア}$ であり、$\frac{1}{2} \leq b \leq 1$ のとき $a \leq \fbox{イ}$ である。$b < \frac{1}{2}$ のとき条件を満たす $a$ は存在しない。
$(2)$ 実数$p$ に対し、$x=p$ における $y=h(x)$ の接線の方程式は $y=\fbox{ウ}$ である。したがって $a=e^p$ のとき、すべての実数 $x$ に対して $g(x) \leq h(x)$ が成り立つのは $b \leq \fbox{エ}$ のときであり、これは $a$ と $b$ の関係式として $b \leq \fbox{オ}$
$(3)$ すべての実数 $x$ に対し、$f(x) \leq g(x) \leq h(x)$ が成り立つような $(a, \, b)$ 全体のなす領域を $D$ とする。$D$ における $a$ の最大値は $\fbox{カ}$ である。また、$D$ の面積は $\fbox{キ}$ である。
この動画を見る
$a$ を $1$ 以上の実数、$b$ を実数とし、関数 $f(x), \, g(x), \, h(x)$ を以下で定める。
$\displaystyle f(x)=-|2|x|-1|, \quad g(x)=ax+b, \quad h(x)=e^x$
$(1)$ すべての実数 $x$ に対して $f(x) \leq g(x)$ が成り立つ。$(a, \, b)$ の範囲は、条件 $a \geq 1$ の下では、$b \geq 1$ のとき $a \leq \fbox{ア}$ であり、$\frac{1}{2} \leq b \leq 1$ のとき $a \leq \fbox{イ}$ である。$b < \frac{1}{2}$ のとき条件を満たす $a$ は存在しない。
$(2)$ 実数$p$ に対し、$x=p$ における $y=h(x)$ の接線の方程式は $y=\fbox{ウ}$ である。したがって $a=e^p$ のとき、すべての実数 $x$ に対して $g(x) \leq h(x)$ が成り立つのは $b \leq \fbox{エ}$ のときであり、これは $a$ と $b$ の関係式として $b \leq \fbox{オ}$
$(3)$ すべての実数 $x$ に対し、$f(x) \leq g(x) \leq h(x)$ が成り立つような $(a, \, b)$ 全体のなす領域を $D$ とする。$D$ における $a$ の最大値は $\fbox{カ}$ である。また、$D$ の面積は $\fbox{キ}$ である。
福田のおもしろ数学224〜3次式が素数となる整数nを求める

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$n^3-7n+9$が素数となるような整数$n$をすべて求めよ。
この動画を見る
$n^3-7n+9$が素数となるような整数$n$をすべて求めよ。
福田の数学〜中央大学2024経済学部第3問〜数列と漸化式
単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
3.
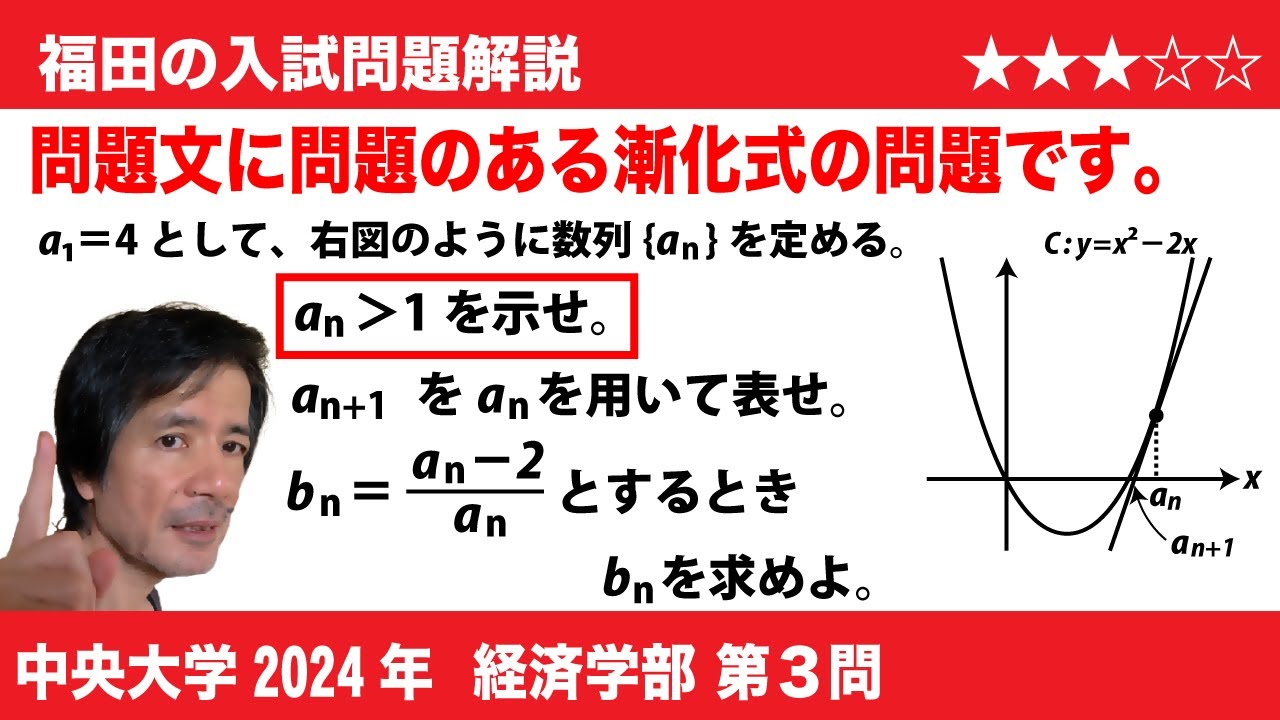
座標平面上に曲線 $C$ : $y = x ^ 2 - 2x$ がある。$C$上の点$P_n (a_n, a_n²-2a_n) \ ( n = 1 , 2, 3, ・・・) $について、 $a_{1} = 4$ とし、 $a_{n + 1}$ は$C$の$P_n$における接線と$x$軸との交点の$x$座標であるとする。このとき、$a_n$は$1$より大きいことが分かっている。以下の設問に答えよ。
(1) $a_{n+ 1}$を$a_n$を用いて表せ。
(2) $b_{n}= \dfrac{a_n-2}{a_n}$とするとき、 $b_{n+ 1}$ を$b_n$を用いて表せ。
(3) $b_n$を$n$を用いて表せ。
この動画を見る
3.
座標平面上に曲線 $C$ : $y = x ^ 2 - 2x$ がある。$C$上の点$P_n (a_n, a_n²-2a_n) \ ( n = 1 , 2, 3, ・・・) $について、 $a_{1} = 4$ とし、 $a_{n + 1}$ は$C$の$P_n$における接線と$x$軸との交点の$x$座標であるとする。このとき、$a_n$は$1$より大きいことが分かっている。以下の設問に答えよ。
(1) $a_{n+ 1}$を$a_n$を用いて表せ。
(2) $b_{n}= \dfrac{a_n-2}{a_n}$とするとき、 $b_{n+ 1}$ を$b_n$を用いて表せ。
(3) $b_n$を$n$を用いて表せ。
福田のおもしろ数学223〜合成関数でできた方程式の解と不動点

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$f(x)=|x-1|$のとき、$f(f(x))=f(f(f(x)))$を満たす$x$をすべて求めよ。
この動画を見る
$f(x)=|x-1|$のとき、$f(f(x))=f(f(f(x)))$を満たす$x$をすべて求めよ。
福田の数学〜中央大学2024経済学部第2問〜2つの国のGDPの比較と常用対数

単元:
#数Ⅱ#指数関数と対数関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
2.
今年A国のGDP(国内総生産)はB国のGDPの$2$倍である。いま、A国の GDPは1年ごとに$4$%減少し、B国のGDPは$8$%増加すると仮定するとき、以下の問いに答えよ。ただし、 $\log_{10}2 = 0.301$, $\log_{10}3 = 0.4771$ とする。
(1) 今年のA国のGDPを$x$とするとき、n年後のA国とB国のGDPをそれぞれ、$x$と$n$を用いて表せ。
(2) B国のGDPが始めてA国のGDPより大きくなるのは今年から何年後か。答は整数で求めよ。
この動画を見る
2.
今年A国のGDP(国内総生産)はB国のGDPの$2$倍である。いま、A国の GDPは1年ごとに$4$%減少し、B国のGDPは$8$%増加すると仮定するとき、以下の問いに答えよ。ただし、 $\log_{10}2 = 0.301$, $\log_{10}3 = 0.4771$ とする。
(1) 今年のA国のGDPを$x$とするとき、n年後のA国とB国のGDPをそれぞれ、$x$と$n$を用いて表せ。
(2) B国のGDPが始めてA国のGDPより大きくなるのは今年から何年後か。答は整数で求めよ。
福田のおもしろ数学222〜条件付きの不等式の証明

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$a \geq b \geq c, \, x \geq y \geq z, \, x+y+z=0$ のとき、$ax+by+cz \geq 0$ を示せ。
この動画を見る
$a \geq b \geq c, \, x \geq y \geq z, \, x+y+z=0$ のとき、$ax+by+cz \geq 0$ を示せ。
福田の数学〜中央大学2024経済学部第1問(6)〜定積分で表された関数

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
関数 $f(x)$ は
$\displaystyle f(x)=x^2 \int^{2}_{0} f'(t) dt +Ax, \quad f(1)=1$
を満たしている。ただし、$A$ は定数である。このとき、$f(x)$ が最大になる $x$ を求めよ。
この動画を見る
関数 $f(x)$ は
$\displaystyle f(x)=x^2 \int^{2}_{0} f'(t) dt +Ax, \quad f(1)=1$
を満たしている。ただし、$A$ は定数である。このとき、$f(x)$ が最大になる $x$ を求めよ。
福田のおもしろ数学221〜x^y=y^xを解こう

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$x^y=y^x \, (x>0, \, y>0)$ を満たす $(x, \, y)$ を求めて下さい。
この動画を見る
$x^y=y^x \, (x>0, \, y>0)$ を満たす $(x, \, y)$ を求めて下さい。
福田の数学〜中央大学2024経済学部第1問(5)〜ベクトルの基本的な演算

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\bigtriangleup \mathrm{ABC}$ と点 $\mathrm{P}$ があり、$2\vec{\mathrm{AP}}+3\vec{\mathrm{BP}}+5\vec{\mathrm{CP}}=\vec{0}$ を満たしている。このとき、$\vec{\mathrm{AB}}=\vec{b}, \, \vec{\mathrm{AC}}=\vec{c}$ として、$\vec{\mathrm{AP}}$ を $\vec{b}$ と $\vec{c}$ で表せ。
この動画を見る
$\bigtriangleup \mathrm{ABC}$ と点 $\mathrm{P}$ があり、$2\vec{\mathrm{AP}}+3\vec{\mathrm{BP}}+5\vec{\mathrm{CP}}=\vec{0}$ を満たしている。このとき、$\vec{\mathrm{AB}}=\vec{b}, \, \vec{\mathrm{AC}}=\vec{c}$ として、$\vec{\mathrm{AP}}$ を $\vec{b}$ と $\vec{c}$ で表せ。
福田のおもしろ数学220〜二項係数のシグマ計算

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle\sum^{20}_{k=5} {}_{k}\mathrm{C}_{4}$ を計算して下さい。
この動画を見る
$\displaystyle\sum^{20}_{k=5} {}_{k}\mathrm{C}_{4}$ を計算して下さい。
福田の数学〜中央大学2024経済学部第1問(4)〜タンジェントの加法定理

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
・ $\tan\alpha=2,\tan\beta=3$のとき$\alpha+\beta$を求めよ。ただし、$0 < \alpha < \dfrac\pi2,0 < \beta < \dfrac\pi2$とする。
・ $\tan\alpha=2,\tan\beta=5,\tan\gamma=8$のとき$\alpha+\beta+\gamma$を求めよ。ただし、$\alpha,\beta,\gamma$は鋭角とする。
この動画を見る
・ $\tan\alpha=2,\tan\beta=3$のとき$\alpha+\beta$を求めよ。ただし、$0 < \alpha < \dfrac\pi2,0 < \beta < \dfrac\pi2$とする。
・ $\tan\alpha=2,\tan\beta=5,\tan\gamma=8$のとき$\alpha+\beta+\gamma$を求めよ。ただし、$\alpha,\beta,\gamma$は鋭角とする。



