数学・算数の楽しさを思い出した / Ken
数学・算数の楽しさを思い出した / Ken
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
高校の時に唯一好きだった教科の数学。 その延長で、大学は某大学の数学科に進学。
社会人になり、数学から離れていたが、仕事で数学に触れる機会があり、再度その面白さに魅了されました。
数学・算数の成績が上がるような動画や数学・算数が好きになるような動画配信をしています。
本職はエンジニア。
数学成績アップのための問題解説 ・面白い算数・数学の問題解説 ・入試問題の問題解説 ・高校数学・中学数学の解説を配信中！
難易度表記のあるレベルのわかりやすい動画内容が魅力。難関大学の過去問を中心に数学解説動画を展開中。
2023年京大数学！整式の割り算！２通りで解説します【京都大学】【数学 入試問題】
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
整式$x^{2023}-1$を整式$x^{4}+x^{3}+x^{2}+x+1$で割ったときの余りを求めよ。
京都大過去問
この動画を見る
整式$x^{2023}-1$を整式$x^{4}+x^{3}+x^{2}+x+1$で割ったときの余りを求めよ。
京都大過去問
【重要】三角形の外心！特徴をまとめてみた #Shorts
単元：
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
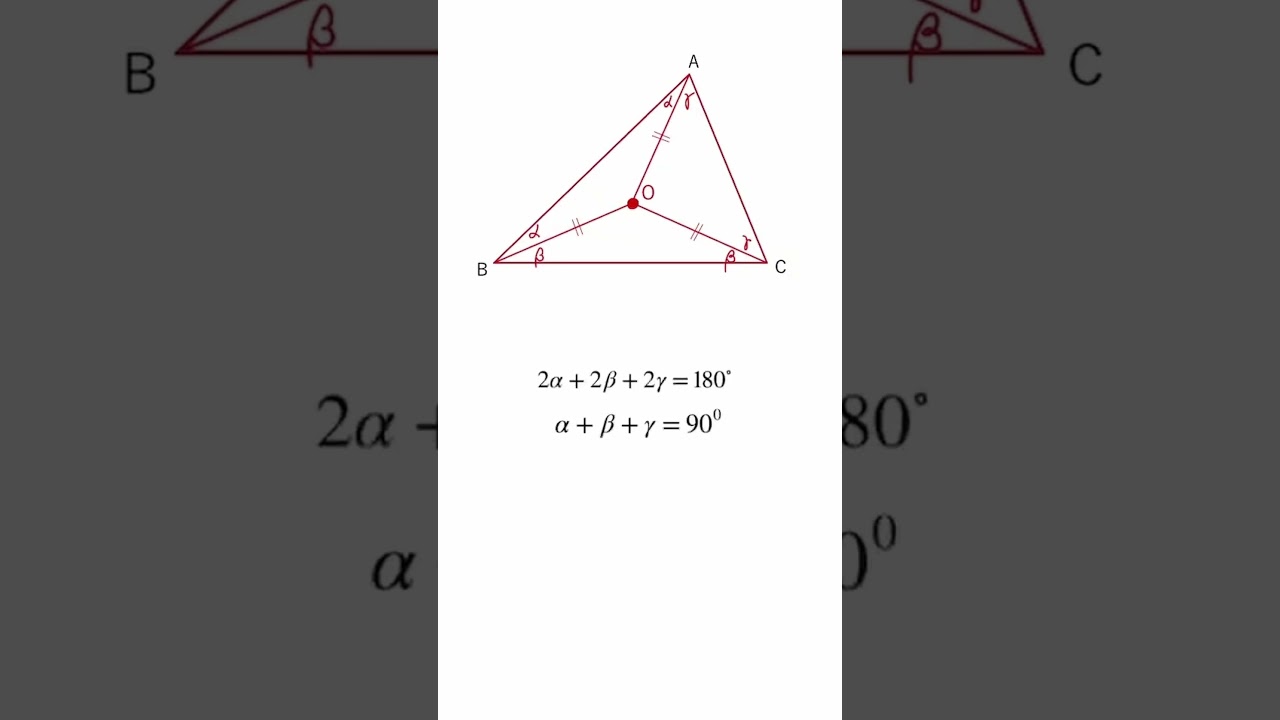
三角形の外心の特徴について解説していきます。
この動画を見る
三角形の外心の特徴について解説していきます。
2023年京大の数学！最大値・最小値【京都大学】【数学 入試問題】
単元：
#大学入試過去問(数学)#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
次の関数$f(x)$の最大値と最小値を求めよ。
$f(x)=e^{-x^{2}}+\dfrac{1}{4}x^{2}+1+\dfrac{1}{e^{-x^{2}}+\dfrac{1}{4}x^{2}+1}$ $(-1≦x≦1)$
ただし、$e$は自然対数の底であり、その値は$e=2.71･･･$である。
2023京都大過去問
この動画を見る
次の関数$f(x)$の最大値と最小値を求めよ。
$f(x)=e^{-x^{2}}+\dfrac{1}{4}x^{2}+1+\dfrac{1}{e^{-x^{2}}+\dfrac{1}{4}x^{2}+1}$ $(-1≦x≦1)$
ただし、$e$は自然対数の底であり、その値は$e=2.71･･･$である。
2023京都大過去問
【数学】三角形の五心！特徴をまとめてみた（重心 編） #Shorts
単元：
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
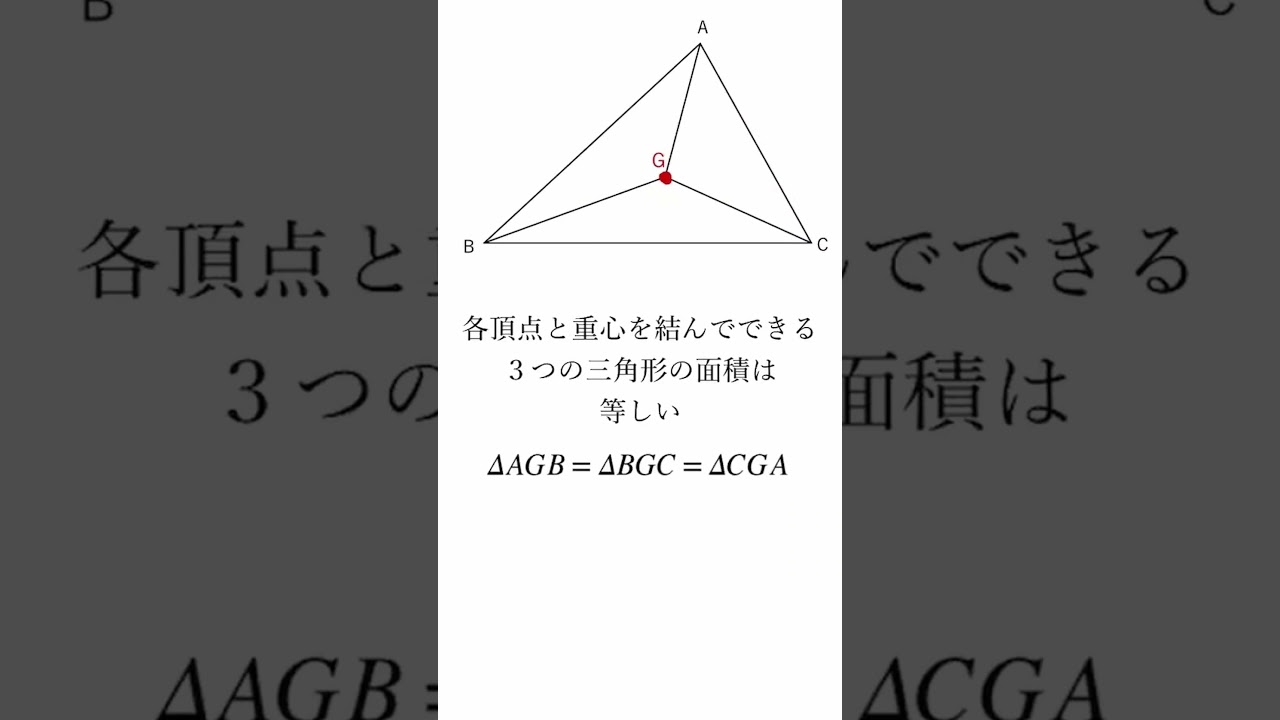
三角形の五心(重心)に関して解説していきます。
この動画を見る
三角形の五心(重心)に関して解説していきます。
気持ちいい別解あり！これ解ける？【京都大学】【数学 入試問題】
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$a,b,c$を正の数とするとき、不等式
$2\left( -\frac{a+b}{2}-\sqrt{ab}\right)≦3\left(\frac{a+b+c}{2}-\sqrt[3]{abc}\right)$
を証明せよ。
また、等号が成立するのはどんな場合か。
京都大過去問
この動画を見る
$a,b,c$を正の数とするとき、不等式
$2\left( -\frac{a+b}{2}-\sqrt{ab}\right)≦3\left(\frac{a+b+c}{2}-\sqrt[3]{abc}\right)$
を証明せよ。
また、等号が成立するのはどんな場合か。
京都大過去問
【高校数学】むやみに代入するな！因数定理のちょっとした裏技！ #Shorts
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
因数分解せよ。
$x^3+6x^2-6x+7$
この動画を見る
因数分解せよ。
$x^3+6x^2-6x+7$
極限の難問！答えは予測できるが・・・【一橋大学】【数学 入試問題】
単元：
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数Ⅲ
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$\displaystyle \lim_{ x \to \infty }(\cos^2 \sqrt{x+1}+\sin^2\sqrt{x})$を求めよ。
一橋大過去問
この動画を見る
$\displaystyle \lim_{ x \to \infty }(\cos^2 \sqrt{x+1}+\sin^2\sqrt{x})$を求めよ。
一橋大過去問
【高校数学】これが京大の入試問題！？中学生でも解けます #Shorts
単元：
#数学(中学生)#中２数学#三角形と四角形
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
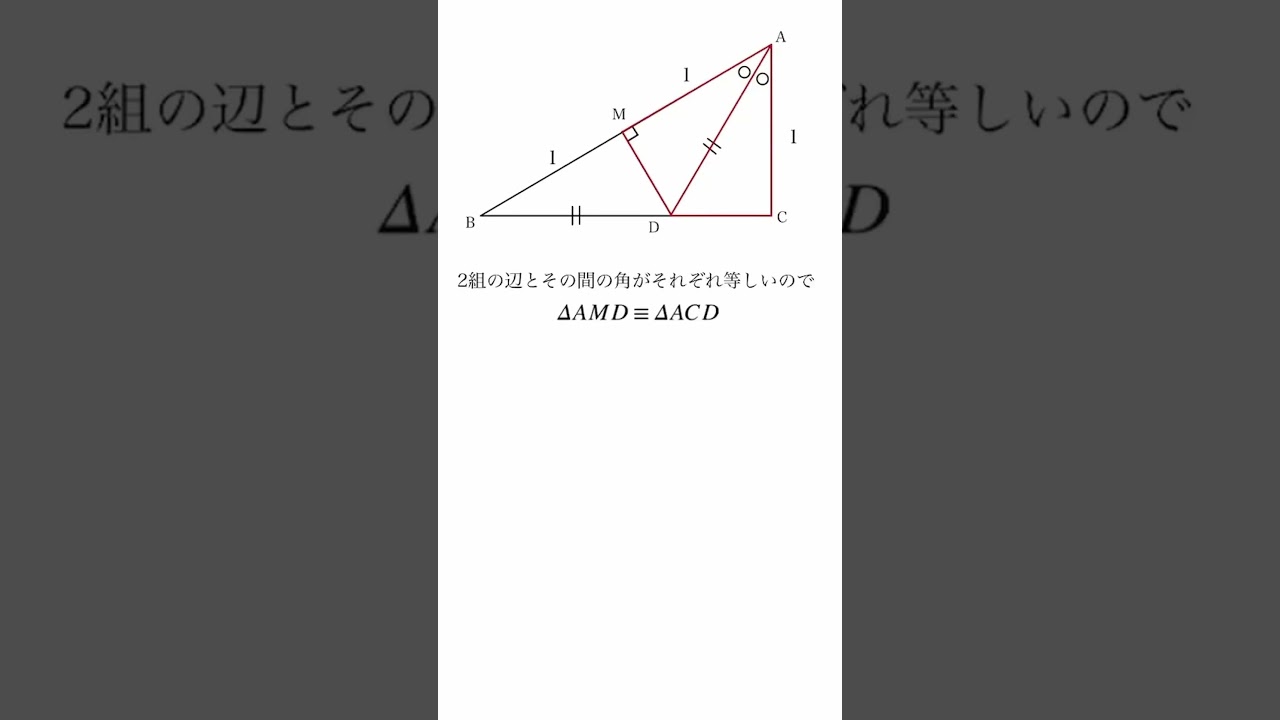
$\triangle ABC$において、$AB=2,AC=1$とする。
$\angle BAC$の二等分線と辺$BC$の交点を$D$とする。
$AD=BD$となるとき、$\triangle ABC$の面積を求めよ。
この動画を見る
$\triangle ABC$において、$AB=2,AC=1$とする。
$\angle BAC$の二等分線と辺$BC$の交点を$D$とする。
$AD=BD$となるとき、$\triangle ABC$の面積を求めよ。
多くの単元が絡んだ問題！解けますか？【一橋大学】【数学 入試問題】
単元：
#数A#数Ⅱ#大学入試過去問(数学)#整数の性質#三角関数#指数関数と対数関数#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$0≦θ≦2\pi$とする。$\log_{ 2 }(4\sin^2θ+3\cosθ-4),$
$\log_{ 2 }(-4\cos^3θ+3\cosθ+1)$がともに整数となるような$θ$の値をすべて求めよ。
一橋大過去問
この動画を見る
$0≦θ≦2\pi$とする。$\log_{ 2 }(4\sin^2θ+3\cosθ-4),$
$\log_{ 2 }(-4\cos^3θ+3\cosθ+1)$がともに整数となるような$θ$の値をすべて求めよ。
一橋大過去問
【数学雑学】無限に続く円周率。その羅列した数字の中には。。。 #shorts
単元：
#算数(中学受験)#その他#その他#その他#その他#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
円周率の中にある数学の不思議を解説していきます。
この動画を見る
円周率の中にある数学の不思議を解説していきます。
指数・対数 × 整数問題！落としたくない問題です【大阪大学】【数学 入試問題】
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
連立方程式$\begin{eqnarray}
\left\{
\begin{array}{l}
2^x+3^y=43 \\
\log_{ 2 } x-\log_{ 3 } y=1
\end{array}
\right.
\end{eqnarray}$を考える。
(1)この連立方程式を満たす自然数$x,y$の組を求めよ。
(2)この連立方程式を満たす正の実数$x,y$は、(1)で求めた自然数の組以外に存在しないことを示せ。
大阪大過去問
この動画を見る
連立方程式$\begin{eqnarray}
\left\{
\begin{array}{l}
2^x+3^y=43 \\
\log_{ 2 } x-\log_{ 3 } y=1
\end{array}
\right.
\end{eqnarray}$を考える。
(1)この連立方程式を満たす自然数$x,y$の組を求めよ。
(2)この連立方程式を満たす正の実数$x,y$は、(1)で求めた自然数の組以外に存在しないことを示せ。
大阪大過去問
【高校数学】裏技！円に内接する四角形の面積の求め方！ #Shorts
単元：
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
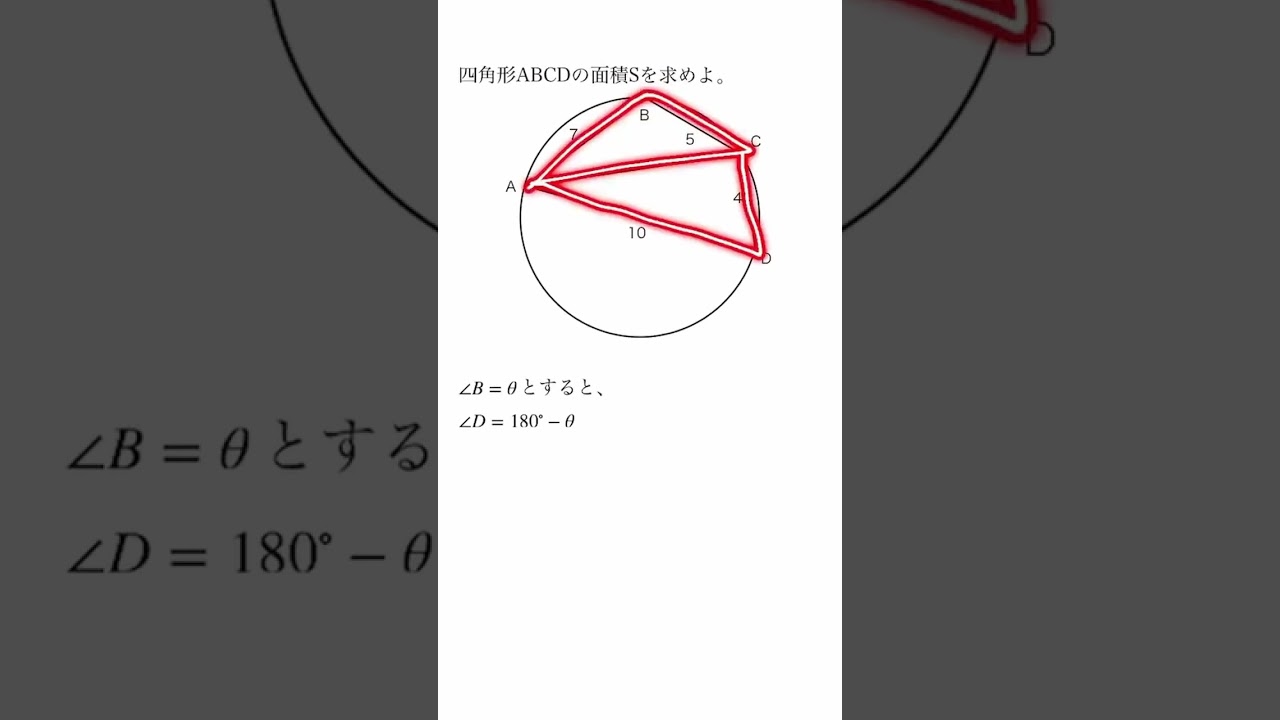
四角形$ABCD$の面積$S$を求めよ。
この動画を見る
四角形$ABCD$の面積$S$を求めよ。
満点は激ムズ！？常用対数の難問です【お茶の水女子大学】【数学 入試問題】
単元：
#数Ⅱ#指数関数と対数関数#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
以下の問いに答えよ。ただし、必要があれば、
$0.3010<\log_{10} 2<0.3011$
$0.4771<\log_{10} 3<0.4772$であることを用いてもよい。
(1)$3^{53}$の桁数を求めよ。
(2)$3^{53}$の最高位の数と1の位の数をそれぞれ求めよ。
(3)$|3^{53}-2^m|$が最小となる整数$m$を求めよ。
お茶の水女子大過去問
この動画を見る
以下の問いに答えよ。ただし、必要があれば、
$0.3010<\log_{10} 2<0.3011$
$0.4771<\log_{10} 3<0.4772$であることを用いてもよい。
(1)$3^{53}$の桁数を求めよ。
(2)$3^{53}$の最高位の数と1の位の数をそれぞれ求めよ。
(3)$|3^{53}-2^m|$が最小となる整数$m$を求めよ。
お茶の水女子大過去問
【工夫あり】二次方程式の解を四捨五入！？【一橋大学】【数学 入試問題】
単元：
#数Ⅰ#大学入試過去問(数学)#２次関数#2次関数とグラフ#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$m,n$を正の整数とする。$x$についての二次方程式$12x^2-mx+n=0$の二つの実数解を小数第2位で四捨五入して0.3および0.7を得た。$m,n$を求めよ。
一橋大過去問
この動画を見る
$m,n$を正の整数とする。$x$についての二次方程式$12x^2-mx+n=0$の二つの実数解を小数第2位で四捨五入して0.3および0.7を得た。$m,n$を求めよ。
一橋大過去問
図形×整数問題！差がつく問題です【一橋大学】【数学 入試問題】
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
直角三角形の3辺の長さがすべて整数のとき、面積は2の整数倍であることを示せ。
一橋大過去問
この動画を見る
直角三角形の3辺の長さがすべて整数のとき、面積は2の整数倍であることを示せ。
一橋大過去問
中学生でも解ける大学入試問題！【早稲田大学】【数学 入試問題】
単元：
#数Ⅰ#大学入試過去問(数学)#２次関数#2次関数とグラフ#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$x$の二次関数$y=ax^2+bx+c$のグラフが相違なる3点$(a,b),(b,c),(c,a)$を通るものとする。
ただし,$abc≠0$とする。このとき,次の問いに答えよ。
(1)$a$の値を求めよ。
(2)$b,c$の値を求めよ。
早稲田大過去問
この動画を見る
$x$の二次関数$y=ax^2+bx+c$のグラフが相違なる3点$(a,b),(b,c),(c,a)$を通るものとする。
ただし,$abc≠0$とする。このとき,次の問いに答えよ。
(1)$a$の値を求めよ。
(2)$b,c$の値を求めよ。
早稲田大過去問
【数列】超基本的な問題です！解けますか？【甲南大学】
単元：
#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
9を分母とする正の既約分数で,100より小さいものの総和を求めよ。
甲南大過去問
この動画を見る
9を分母とする正の既約分数で,100より小さいものの総和を求めよ。
甲南大過去問
4次方程式が2つの実数解しか持たないということは・・・【早稲田大学】【数学 入試問題】
単元：
#数Ⅰ#大学入試過去問(数学)#２次関数#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$a,b,c$は整数とする。四次方程式$x^4+ax^3+bx^2+cx+3=0$の実数解が1と3となるような$a$の最大値？で最小値は？である。
早稲田大過去問
この動画を見る
$a,b,c$は整数とする。四次方程式$x^4+ax^3+bx^2+cx+3=0$の実数解が1と3となるような$a$の最大値？で最小値は？である。
早稲田大過去問
二次関数の難問！大事な考え方【神戸大学】【数学 入試問題】
単元：
#数Ⅰ#大学入試過去問(数学)#２次関数#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$a$を実数とし,$f(x)=-x^2-2x+2,g(x)=-x^2+ax+a$とする。以下の問いに答えよ。
(1)すべての実数$s,t$に対して$f(x)≧g(t)$が成り立つような,$a$の値の範囲を求めよ。
(2)$0≦x≦1を満たすすべての$x$に対して,$f(x)≧g(x)が成り立つような$a$の範囲を求めよ。
神戸大過去問
この動画を見る
$a$を実数とし,$f(x)=-x^2-2x+2,g(x)=-x^2+ax+a$とする。以下の問いに答えよ。
(1)すべての実数$s,t$に対して$f(x)≧g(t)$が成り立つような,$a$の値の範囲を求めよ。
(2)$0≦x≦1を満たすすべての$x$に対して,$f(x)≧g(x)が成り立つような$a$の範囲を求めよ。
神戸大過去問
2次方程式の入試問題！絶対に落としたくない問題です【島根大学】【数学 入試問題】
単元：
#数Ⅰ#大学入試過去問(数学)#２次関数#2次関数とグラフ#学校別大学入試過去問解説(数学)#数学(高校生)#島根大学
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$a$を実数とする。２次方程式$x^2+2ax+(a-1)=0$の解を$\alpha,\beta$とする。
(1)$\alpha$と$\beta$は異なる実数であることを示せ。
(2)$\alpha$と$\beta$のうち,少なくとも1つは負であることを示せ。
(3)$\alpha≦0,\beta≦0$であるとき,$\alpha^2+\beta^2$の最小値を求めよ。
島根大過去問
この動画を見る
$a$を実数とする。２次方程式$x^2+2ax+(a-1)=0$の解を$\alpha,\beta$とする。
(1)$\alpha$と$\beta$は異なる実数であることを示せ。
(2)$\alpha$と$\beta$のうち,少なくとも1つは負であることを示せ。
(3)$\alpha≦0,\beta≦0$であるとき,$\alpha^2+\beta^2$の最小値を求めよ。
島根大過去問
あの東大の問題の類題！「あれ」で一発で解けます【数学 入試問題】
単元：
#数学検定・数学甲子園・数学オリンピック等#数学甲子園
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
x⁶+y⁶+z⁶=3xyzを満たす整数(x,y,z)をすべて求めよ
2013数学甲子園予選
この動画を見る
x⁶+y⁶+z⁶=3xyzを満たす整数(x,y,z)をすべて求めよ
2013数学甲子園予選
あの東大の問題の類題！「あれ」で一発で解けます【数学 入試問題】
単元：
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
次の等式を満たす整数$x,y,z$の組$(x,y,z)$をすべて求めなさい。
$x^6+y^6+z^6=3xyz$
この動画を見る
次の等式を満たす整数$x,y,z$の組$(x,y,z)$をすべて求めなさい。
$x^6+y^6+z^6=3xyz$
あの公式で一撃！これ因数分解できる？ #Shorts
単元：
#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$(a-b)^3+(b-c)^3-3(a-b)(b-c)(c-a)$
因数分解せよ。
この動画を見る
$(a-b)^3+(b-c)^3-3(a-b)(b-c)(c-a)$
因数分解せよ。
工夫が大事！3次関数の決定【一橋大学】【数学 入試問題】
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
次の4つの条件を満たす3次関数を求めよ
(i)f(0)=0,f(2)=1
(ii)0.2
(iv)f(x)=0の解はすべて整数
一橋2020
この動画を見る
次の4つの条件を満たす3次関数を求めよ
(i)f(0)=0,f(2)=1
(ii)0.2
(iv)f(x)=0の解はすべて整数
一橋2020
工夫が大事！3次関数の決定【一橋大学】【数学 入試問題】
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
以下の4つの条件を満たす3次関数$f(x)$を求めよ。
( i )$f(0)=0,f(2)=1$
( ii )$0.2<f(1)<0.3$
( iii )$f(x)は極限値0をもつ$
(iv)$f(x)=0の解はすべて整数$
この動画を見る
以下の4つの条件を満たす3次関数$f(x)$を求めよ。
( i )$f(0)=0,f(2)=1$
( ii )$0.2<f(1)<0.3$
( iii )$f(x)は極限値0をもつ$
(iv)$f(x)=0の解はすべて整数$
３通りで解説！xとyを「あれ」に・・・【大阪大学】【数学 入試問題】
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
実数$x,y$が$|x|≦1$と$|y|≦1$を満たすとき,不等式
$0≦x^2+y^2-2x^2y^2+2xy\sqrt{1-x^2}\sqrt{1-y^2}$
$≦1$
が成り立つことを示せ。
大阪大過去問
この動画を見る
実数$x,y$が$|x|≦1$と$|y|≦1$を満たすとき,不等式
$0≦x^2+y^2-2x^2y^2+2xy\sqrt{1-x^2}\sqrt{1-y^2}$
$≦1$
が成り立つことを示せ。
大阪大過去問
【高校数学】いろんな方法で因数分解してみた #Shorts
単元：
#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$x^5+x^4+x^3+x^2+x+1$
因数分解せよ。
この動画を見る
$x^5+x^4+x^3+x^2+x+1$
因数分解せよ。
複素数平面！円が１と−１を通るということは・・・【京都大学】【数学 入試問題】
単元：
#大学入試過去問(数学)#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数C
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
複素数$a$に対してその共役な複素数$\bar{ a }$で表す。
$a$を実数でない複素数とする。複素数平面内の円$C$が$1,-1,a$を通るならば,$C$は-$\displaystyle \frac{1}{\bar{ a }}$も通ることを示せ。
京都大過去問
この動画を見る
複素数$a$に対してその共役な複素数$\bar{ a }$で表す。
$a$を実数でない複素数とする。複素数平面内の円$C$が$1,-1,a$を通るならば,$C$は-$\displaystyle \frac{1}{\bar{ a }}$も通ることを示せ。
京都大過去問
大小比較！この形は超頻出なので絶対に抑えておきたい問題【一橋大学】【数学 入試問題】
単元：
#大学入試過去問(数学)#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数Ⅲ
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$e^\pi$と$\pi^e$の大小を比較せよ。
一橋大過去問
この動画を見る
$e^\pi$と$\pi^e$の大小を比較せよ。
一橋大過去問
頻出！微分のよく見るような問題【京都大学】【数学 入試問題】
単元：
#大学入試過去問(数学)#微分とその応用#接線と法線・平均値の定理#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師：
数学・算数の楽しさを思い出した / Ken
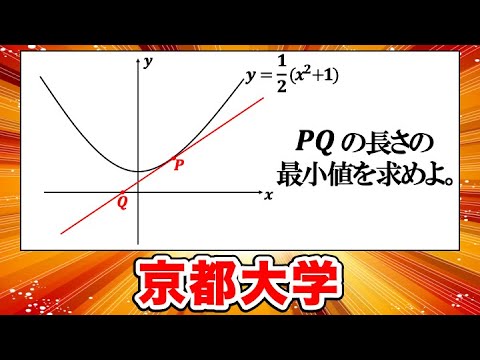
問題文全文(内容文)：
曲線$y=\displaystyle \frac{1}{2}(x^2+1)$上の点$P$における接線は$x$軸と交わるとし,その交点を$\varrho$とおく。線分$P\varrho$の長さを$L$とするとき,$L$が取りうる値の最小値を求めよ。
京都大過去問
この動画を見る
曲線$y=\displaystyle \frac{1}{2}(x^2+1)$上の点$P$における接線は$x$軸と交わるとし,その交点を$\varrho$とおく。線分$P\varrho$の長さを$L$とするとき,$L$が取りうる値の最小値を求めよ。
京都大過去問