 ますただ
ますただ
 ますただ
ますただ
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
大学入試問題#818「なんてことはない問題」 #京都大学(1979)

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \frac{2^n}{n} \gt n$を満たす自然数$n$の範囲を求めよ。
出典:1979年京都大学 入試問題
この動画を見る
$\displaystyle \frac{2^n}{n} \gt n$を満たす自然数$n$の範囲を求めよ。
出典:1979年京都大学 入試問題
#筑波大学(2019) #定積分 #Shorts

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#筑波大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} xe^{2x} dx$
出典:2019年筑波大学
この動画を見る
$\displaystyle \int_{0}^{1} xe^{2x} dx$
出典:2019年筑波大学
#奈良教育大学(2014) #定積分 #Shorts
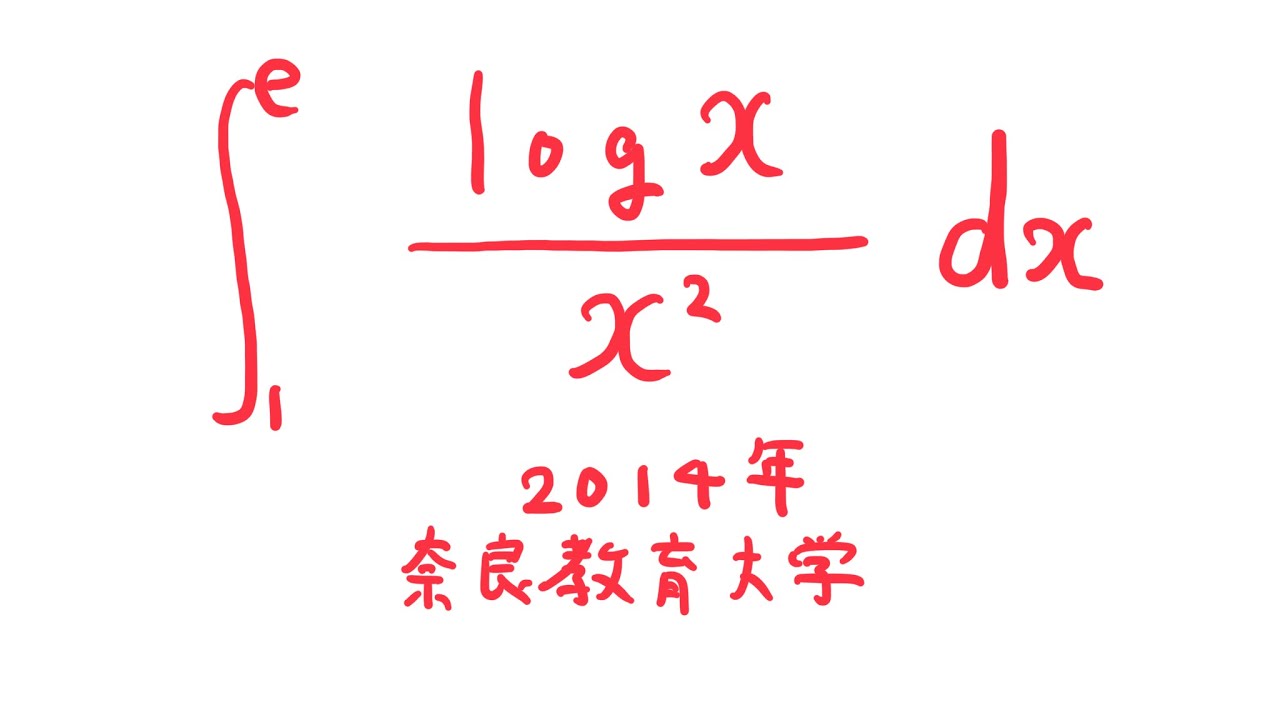
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#奈良教育大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{e} \displaystyle \frac{log\ x}{x^2} dx$
出典:2014年奈良教育大学
この動画を見る
$\displaystyle \int_{1}^{e} \displaystyle \frac{log\ x}{x^2} dx$
出典:2014年奈良教育大学
大学入試問題#817「難易度の高い詰将棋!大局観が大事!」 #東京医科歯科大学(2024)

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#東京医科歯科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{\sin\ x}{1+\sqrt{ \sin\ 2x }} dx$
出典:2024年東京医科歯科大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{\sin\ x}{1+\sqrt{ \sin\ 2x }} dx$
出典:2024年東京医科歯科大学
#上智大学(2016) #ウォリス積分 #定積分 #Shorts
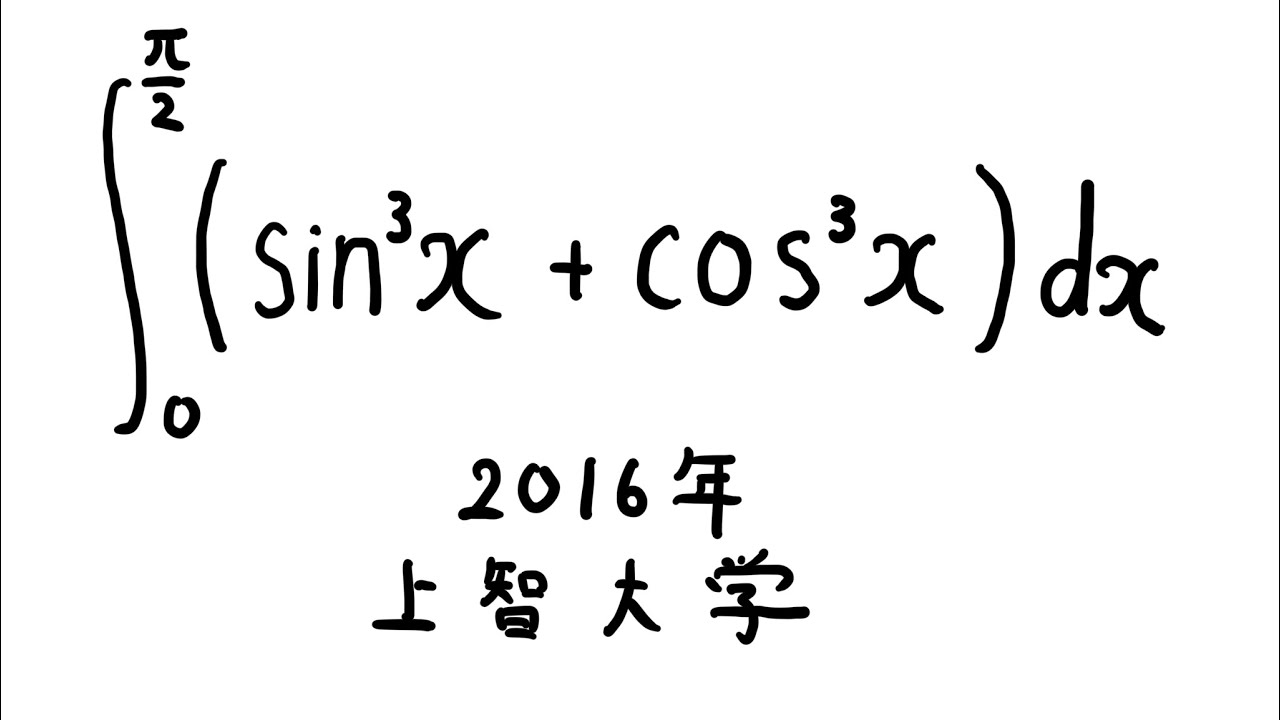
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#上智大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}} (\sin^3x+\cos^3x) dx$
出典:2016年上智大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} (\sin^3x+\cos^3x) dx$
出典:2016年上智大学
#筑波大学(2018) #定積分 #Shorts
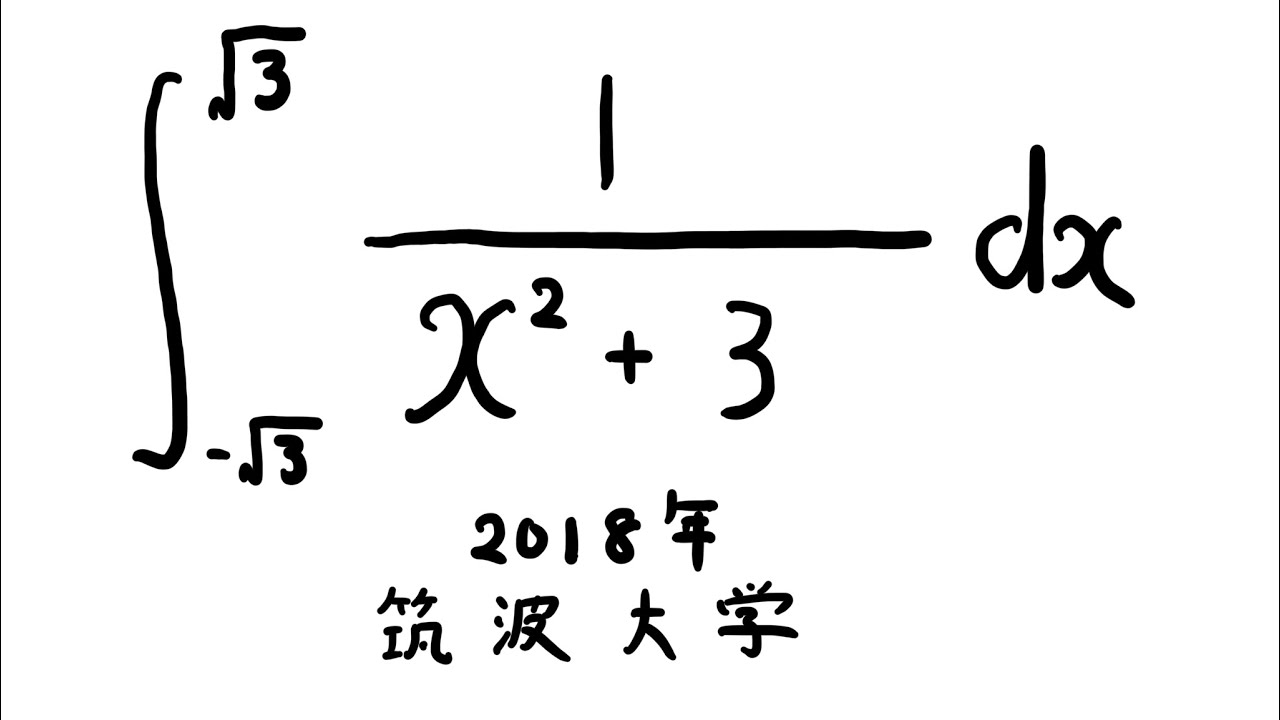
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#筑波大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\sqrt{ 3 }}^{\sqrt{ 3 }} \displaystyle \frac{1}{x^2+3} dx$
出典:2018年筑波大学
この動画を見る
$\displaystyle \int_{-\sqrt{ 3 }}^{\sqrt{ 3 }} \displaystyle \frac{1}{x^2+3} dx$
出典:2018年筑波大学
大学入試問題#816「ほぼ直感通り!」 #東京医科大学(2011)

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#東京医科大学
指導講師:
ますただ
問題文全文(内容文):
すべての正の数$x,y$に対して、不等式
$\displaystyle \frac{K}{x+y} \leq \displaystyle \frac{1}{x}+\displaystyle \frac{49}{y}$
が成り立つような定数$K$の最大値を求めよ。
出典:2011年東京医科大学
この動画を見る
すべての正の数$x,y$に対して、不等式
$\displaystyle \frac{K}{x+y} \leq \displaystyle \frac{1}{x}+\displaystyle \frac{49}{y}$
が成り立つような定数$K$の最大値を求めよ。
出典:2011年東京医科大学
#奈良教育大学(2008) #定積分 #Shorts

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#奈良教育大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \displaystyle \frac{x^2}{1+x^2} dx$
出典:2008年奈良教育大学
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{x^2}{1+x^2} dx$
出典:2008年奈良教育大学
#奈良教育大学(2008) #定積分 #Shorts
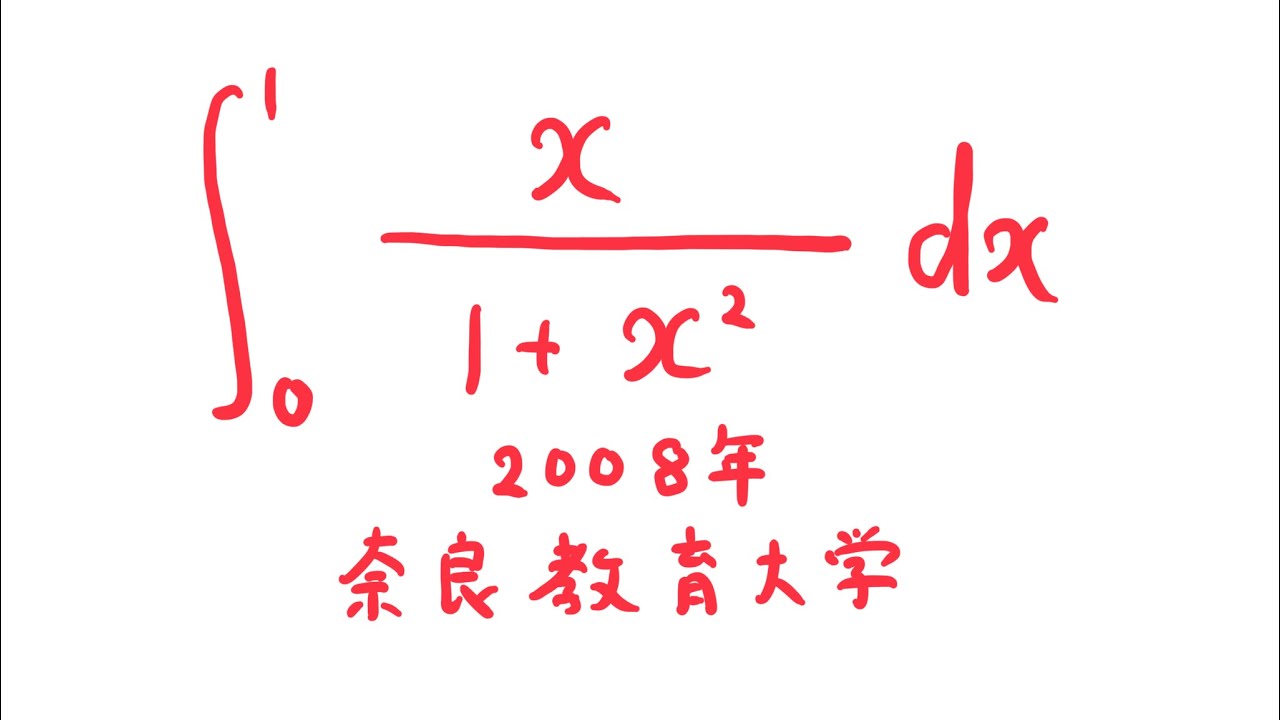
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#奈良教育大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \displaystyle \frac{x}{1+x^2} dx$
出典:2008年奈良教育大学
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{x}{1+x^2} dx$
出典:2008年奈良教育大学
大学入試問題#815「工夫は1回で大丈夫」 #京都大学(1970) #帰納法

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$(\displaystyle \frac{n+1}{2})^n \gt n!$を証明せよ。
ここに$n$は2以上の整数とする。
出典:1970年京都大学 入試問題
この動画を見る
$(\displaystyle \frac{n+1}{2})^n \gt n!$を証明せよ。
ここに$n$は2以上の整数とする。
出典:1970年京都大学 入試問題
大学入試問題#814「初手ミスると沼」 #島根大学(2024) #指数方程式

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#島根大学
指導講師:
ますただ
問題文全文(内容文):
方程式$25^x-15^x=9^x$を解け。
出典:2024年鳥取大学
この動画を見る
方程式$25^x-15^x=9^x$を解け。
出典:2024年鳥取大学
大学入試問題#813「見通しは立てやすい」 #京都大学(1972) #極限

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
次の式で定められる関数$F(x)$に対して、
$\displaystyle \lim_{ x \to \infty } [F(x) -log\ x]$を求めよ。
ただし、$x \gt 0$とする。
$F(x)=\displaystyle \int_{0}^{x} \displaystyle \frac{1}{(t+1)(t+3)}dt$
出典:1972年京都大学 入試問題
この動画を見る
次の式で定められる関数$F(x)$に対して、
$\displaystyle \lim_{ x \to \infty } [F(x) -log\ x]$を求めよ。
ただし、$x \gt 0$とする。
$F(x)=\displaystyle \int_{0}^{x} \displaystyle \frac{1}{(t+1)(t+3)}dt$
出典:1972年京都大学 入試問題
大学入試問題#812「怖いのは計算ミスのみ」 #福島県立医科大学(2016) #積分方程式

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#福島県立医科大学
指導講師:
ますただ
問題文全文(内容文):
$f(x)=\cos\ x+\displaystyle \int_{0}^{\pi} \sin(x-t)f(t)dt$を満たす関数$f(x)$を求めよ。
出典:2016年福島県立医科大学 入試問題
この動画を見る
$f(x)=\cos\ x+\displaystyle \int_{0}^{\pi} \sin(x-t)f(t)dt$を満たす関数$f(x)$を求めよ。
出典:2016年福島県立医科大学 入試問題
大学入試問題#811「方向性が見えれば、気合いで解ける」 #京都大学(1972) #式変形

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
実数または複素数の$x,y,z,a$について、
$x+y+z=a$
$x^3+y^3+z^3=a^3$
の2式が成立するとき、$x,y,z$のうちの少なくとも1つは$a$に等しいことを示せ。
出典:1972年京都大学
この動画を見る
実数または複素数の$x,y,z,a$について、
$x+y+z=a$
$x^3+y^3+z^3=a^3$
の2式が成立するとき、$x,y,z$のうちの少なくとも1つは$a$に等しいことを示せ。
出典:1972年京都大学
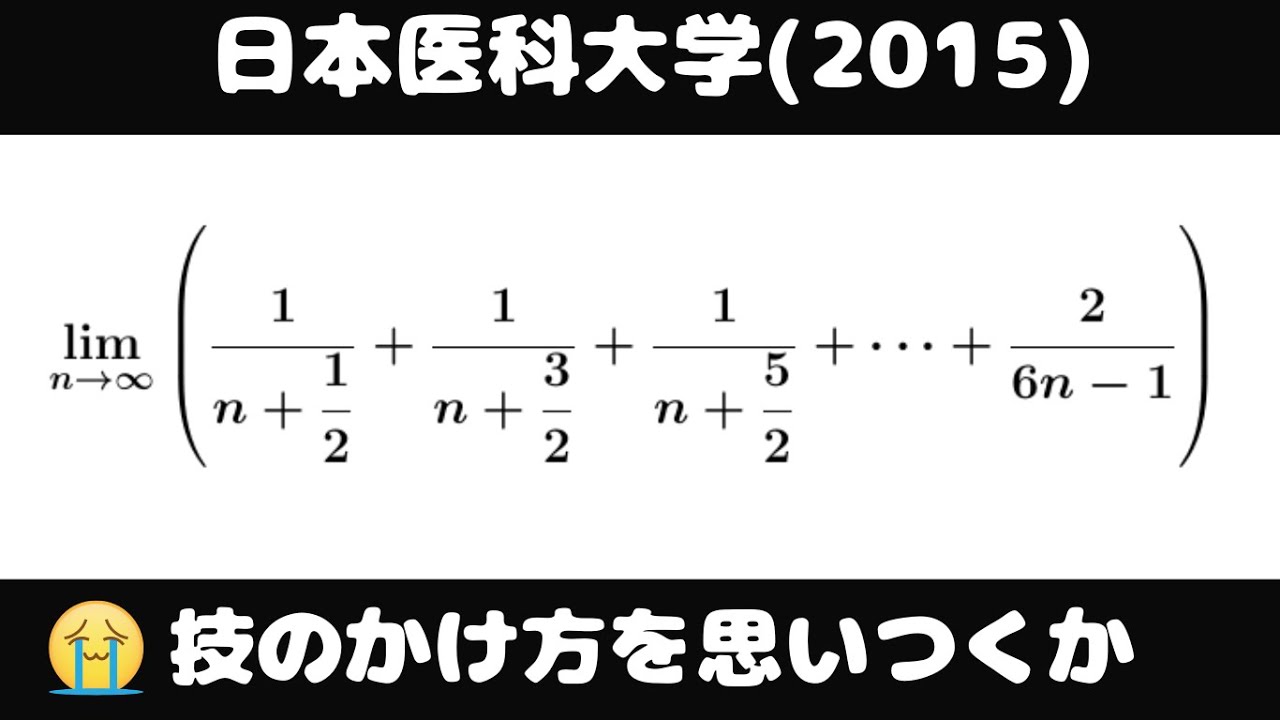
大学入試問題#810「難易度高めの良問」 #日本医科大学(2015) #区分求積法 僚太さんの紹介問題です
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#日本医科大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } (\displaystyle \frac{1}{n+\displaystyle \frac{1}{2}}+\displaystyle \frac{1}{n+\displaystyle \frac{3}{2}}+\displaystyle \frac{1}{n+\displaystyle \frac{5}{2}}+・・・+\displaystyle \frac{2}{6n-1})$
出典:2015年日本医科大学 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty } (\displaystyle \frac{1}{n+\displaystyle \frac{1}{2}}+\displaystyle \frac{1}{n+\displaystyle \frac{3}{2}}+\displaystyle \frac{1}{n+\displaystyle \frac{5}{2}}+・・・+\displaystyle \frac{2}{6n-1})$
出典:2015年日本医科大学 入試問題
大学入試問題#809「関数の相性が良さそうではない。」 #福島県立医科大学(2023) #極限

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#福島県立医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{\sin\ 2x}{log_2(x+2)-1}$
出典:2023年福島県立医科大学 入試問題
この動画を見る
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{\sin\ 2x}{log_2(x+2)-1}$
出典:2023年福島県立医科大学 入試問題
大学入試問題#808「難しすぎない良問」 #東京医科大学(2009) #整数問題

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#東京医科大学
指導講師:
ますただ
問題文全文(内容文):
不等式$\sqrt{ n+1 }-\sqrt{ n } \gt \displaystyle \frac{1}{100}$を満たす正の整数$n$の最大値を求めよ。
出典:2009年東京医科大学 入試問題
この動画を見る
不等式$\sqrt{ n+1 }-\sqrt{ n } \gt \displaystyle \frac{1}{100}$を満たす正の整数$n$の最大値を求めよ。
出典:2009年東京医科大学 入試問題
大学入試問題#807「落ち着いて解く!」 #福島県立医科大学(2019) #積分方程式

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#福島県立医科大学
指導講師:
ますただ
問題文全文(内容文):
実数$x$についての関数の列$\{f_n(x\})$が
$f_n(x)=\displaystyle \sum_{k=1}^n \displaystyle \frac{x^k}{k}-2\displaystyle \int_{0}^{1} f_n(t)dt$を満たしている。
$\displaystyle \lim_{ n \to \infty } f_n(0)$を求めよ。
出典:2019年福島県立医科大学 入試問題
この動画を見る
実数$x$についての関数の列$\{f_n(x\})$が
$f_n(x)=\displaystyle \sum_{k=1}^n \displaystyle \frac{x^k}{k}-2\displaystyle \int_{0}^{1} f_n(t)dt$を満たしている。
$\displaystyle \lim_{ n \to \infty } f_n(0)$を求めよ。
出典:2019年福島県立医科大学 入試問題
大学入試問題#806「The 良問!」 兵庫県立大学中期(2014) #微積の応用

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#兵庫県立大学
指導講師:
ますただ
問題文全文(内容文):
微分可能な関数$f(x)$が
$f(x)=\displaystyle \int_{0}^{x} \sqrt{ f(t)^2+1 }\ dt$を満たすとする。
このとき以下の問いに答えよ。
1.$f'(x)$と$f''(x)$を$f(x)$で表せ。
2.関数$log(f(x)+f'(x))$を求めよ。
3.$f(x)$を求めよ。
出典:2014年兵庫県立大学中期 入試問題
この動画を見る
微分可能な関数$f(x)$が
$f(x)=\displaystyle \int_{0}^{x} \sqrt{ f(t)^2+1 }\ dt$を満たすとする。
このとき以下の問いに答えよ。
1.$f'(x)$と$f''(x)$を$f(x)$で表せ。
2.関数$log(f(x)+f'(x))$を求めよ。
3.$f(x)$を求めよ。
出典:2014年兵庫県立大学中期 入試問題
大学入試問題#805「特に言うことないよねーw」 #東邦大学医学部(2004) #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#東邦大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{ \pi } (\sin2x\cos\ x+\sin\ x \cos2x) dx$
出典:2004年東邦大学医学部
この動画を見る
$\displaystyle \int_{0}^{ \pi } (\sin2x\cos\ x+\sin\ x \cos2x) dx$
出典:2004年東邦大学医学部
大学入試問題#804「このタイプは定期的に出題」 #兵庫県立大学中期(2014) #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#兵庫県立大学
指導講師:
ますただ
問題文全文(内容文):
$f(x)=2\sin2x-\sin\ x$とする。
定積分$\displaystyle \int_{0}^{\pi} |f(x)| dx$の値を求めよ。
出典:2014年兵庫県立大学中期 入試問題
この動画を見る
$f(x)=2\sin2x-\sin\ x$とする。
定積分$\displaystyle \int_{0}^{\pi} |f(x)| dx$の値を求めよ。
出典:2014年兵庫県立大学中期 入試問題
#64 #数検1級1次過去問 #高次方程式

単元:
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定1級
指導講師:
ますただ
問題文全文(内容文):
$4$次方程式
$x^4-4x-1=0$について、次の問いに答えよ。
1.上の方程式の実数解を求めよ。
2.上の方程式の虚数解を求めよ
出典:数検1級1次過去問
この動画を見る
$4$次方程式
$x^4-4x-1=0$について、次の問いに答えよ。
1.上の方程式の実数解を求めよ。
2.上の方程式の虚数解を求めよ
出典:数検1級1次過去問
大学入試問題#803「マジで気合い!」 #大阪市立大学(2000) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#大阪市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \displaystyle \frac{1}{(1+x^2)^4} dx$
出典:2000年大阪市立大学
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{1}{(1+x^2)^4} dx$
出典:2000年大阪市立大学
大学入試問題#802「ほんまに解いてほしい良問」 #岡山大学(2002) #通過領域

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#数学(高校生)#岡山大学
指導講師:
ますただ
問題文全文(内容文):
座標平面上に点$A(0,2)$と点$B(1,0)$があり線分$AB$上の点$P$から$x$軸、$y$軸におろした垂線の足をそれぞれ$Q,R$とする。
点$P$が$A$から$B$まで動くとき、線分$QR$の通過する部分の面積を求めよ。
出典:2002年岡山大学 入試問題
この動画を見る
座標平面上に点$A(0,2)$と点$B(1,0)$があり線分$AB$上の点$P$から$x$軸、$y$軸におろした垂線の足をそれぞれ$Q,R$とする。
点$P$が$A$から$B$まで動くとき、線分$QR$の通過する部分の面積を求めよ。
出典:2002年岡山大学 入試問題
大学入試問題#800「コメントが難しい」 #兵庫県立大学中期(2012) #極限

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#兵庫県立大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
実数$x$に対して
$f(x)=\displaystyle \lim_{ x \to \infty } n\{\sin(\displaystyle \frac{1+n}{n}x)+\sin(\displaystyle \frac{1-n}{n}x)\}$とおく。
次の問いに答えよ。
1.$f(x)$を求めよ。
2.定積分$\displaystyle \int_{0}^{\pi} f(x) dx$を求めよ。
出典:2012年兵庫県立大学中期 入試問題
この動画を見る
実数$x$に対して
$f(x)=\displaystyle \lim_{ x \to \infty } n\{\sin(\displaystyle \frac{1+n}{n}x)+\sin(\displaystyle \frac{1-n}{n}x)\}$とおく。
次の問いに答えよ。
1.$f(x)$を求めよ。
2.定積分$\displaystyle \int_{0}^{\pi} f(x) dx$を求めよ。
出典:2012年兵庫県立大学中期 入試問題
大学入試問題#799「もう詰んでます!」 #大阪公立大学(2024) #定積分 #King_property

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#大阪公立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\sqrt{ 3 }}^{\sqrt{ 3 }} \displaystyle \frac{log(1+x^2)}{1+e^x} dx$
出典:2024年大阪公立大学
この動画を見る
$\displaystyle \int_{-\sqrt{ 3 }}^{\sqrt{ 3 }} \displaystyle \frac{log(1+x^2)}{1+e^x} dx$
出典:2024年大阪公立大学
大学入試問題#798「微分方程式の基礎トレーニング」 横浜国立大学(2024) #微分方程式

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#兵庫県立大学
指導講師:
ますただ
問題文全文(内容文):
実数全体で定義された連続関数$f(x)$が、すべての実数$x$に対して$f(x) \gt 0,$かつ
$f(x)=\displaystyle \int_{0}^{ x } \displaystyle \frac{t}{(t^2+1)f(t)} dt+1$を満たすとき、$f(x)$を求めよ。
出典:2024年横浜国立大学
この動画を見る
実数全体で定義された連続関数$f(x)$が、すべての実数$x$に対して$f(x) \gt 0,$かつ
$f(x)=\displaystyle \int_{0}^{ x } \displaystyle \frac{t}{(t^2+1)f(t)} dt+1$を満たすとき、$f(x)$を求めよ。
出典:2024年横浜国立大学
大学入試問題#797「たぶん部分積分でもいけそう」 #名古屋工業大学(2014) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#名古屋工業大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{log\ 2}^{log\ 3} \displaystyle \frac{xe^x}{(e^x-1)^2} dx$
出典:2014年名古屋工業大学
この動画を見る
$\displaystyle \int_{log\ 2}^{log\ 3} \displaystyle \frac{xe^x}{(e^x-1)^2} dx$
出典:2014年名古屋工業大学
大学入試問題#796「解法は、ほぼ1択か」 #横浜国立大学(2024) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{log\sqrt{ 3 }} \displaystyle \frac{e^{3x}+4e^{2x}+e^x}{e^{4x}+2e^{2x}+1}dx$
出典:2024年横浜国立大学
この動画を見る
$\displaystyle \int_{0}^{log\sqrt{ 3 }} \displaystyle \frac{e^{3x}+4e^{2x}+e^x}{e^{4x}+2e^{2x}+1}dx$
出典:2024年横浜国立大学
#64 #数検1級1次過去問「久しぶりに重積分やってみよー」 #重積分 #高専

単元:
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定1級
指導講師:
ますただ
問題文全文(内容文):
領域$D$が次のように与えられている。
$D=\{(x,y)|0 \leq x \leq 1,0 \leq y \leq 1\}$
このとき、次の2重積分を計算せよ。
$\displaystyle \int\displaystyle \int_{D}|x-y|^{-\frac{2}{3}}dxdy$
出典:数検1級1次
この動画を見る
領域$D$が次のように与えられている。
$D=\{(x,y)|0 \leq x \leq 1,0 \leq y \leq 1\}$
このとき、次の2重積分を計算せよ。
$\displaystyle \int\displaystyle \int_{D}|x-y|^{-\frac{2}{3}}dxdy$
出典:数検1級1次



