ますただ
ますただ
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
大学入試問題をベースに数学の動画を作成しています。大学過去問を多数解説しています。
頻繁に更新していますので是非ご視聴ください！
職業：数学者
職歴：高校非常勤（院生時代）、高専、大学 准教授
趣味：
①将棋 棋力は将棋ウォーズ４段、将棋倶楽部２４はR２０００前後（小学校５，６年のころに頑張ってました）
②麻雀 アカウントは消えましたが、無課金で天鵬で７段まで上がりました。
③ソフトテニス 中学から大学まで、１０年間部活でやっていました。大学時代は４年になってもリーグにでていました。
大学入試問題#612「チャートにありそう」 慶応義塾大学(2011) #2次不等式
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
すべての実数$y$に対して$x^2+xy+y^2 \gt x+y$が成り立つ$x$の値の範囲を求めよ。
出典：2011年慶應義塾大学 入試問題
この動画を見る
すべての実数$y$に対して$x^2+xy+y^2 \gt x+y$が成り立つ$x$の値の範囲を求めよ。
出典：2011年慶應義塾大学 入試問題
大学入試問題#611「ストレートに解けそう」 千葉大学(2014) #定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} e^{\sin\ x}(\sin2x-2\cos\ x) dx$
出典：2014年千葉大学 入試問題
この動画を見る
$\displaystyle \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} e^{\sin\ x}(\sin2x-2\cos\ x) dx$
出典：2014年千葉大学 入試問題
福島県立医科大学(2005) #Shorts
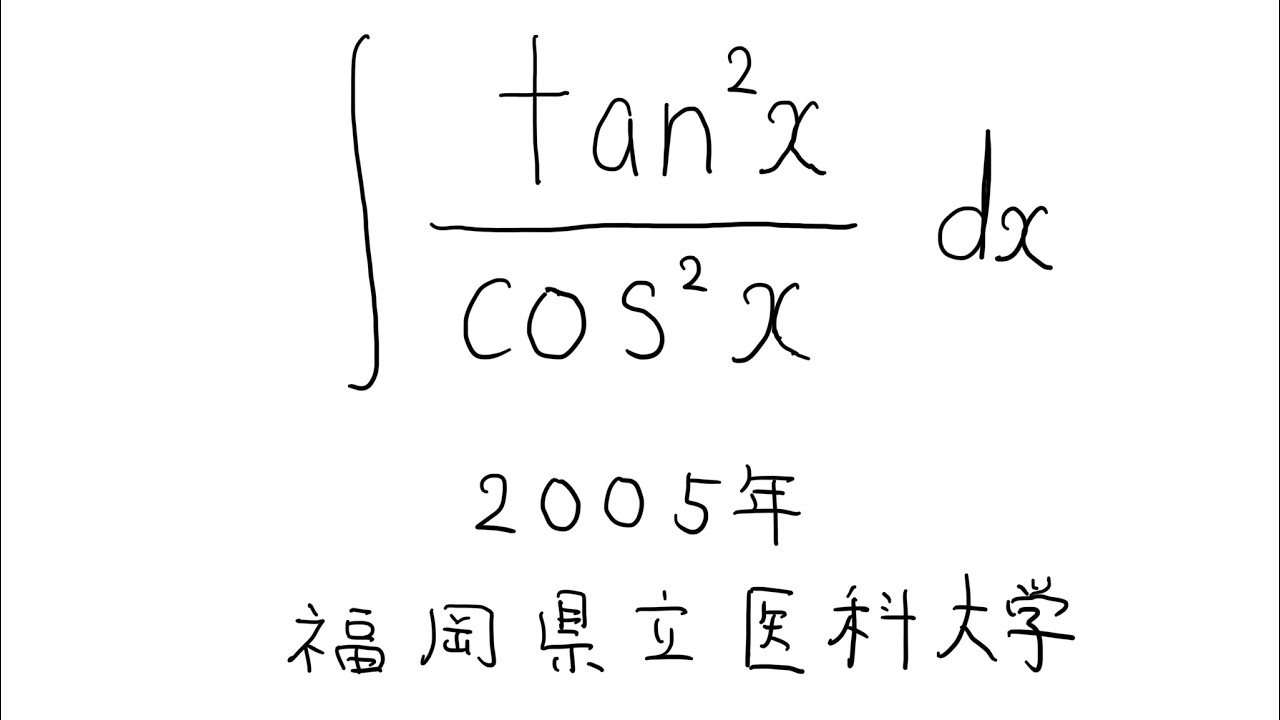
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#福島県立医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{\tan^2x}{\cos^2x} dx$
出典：2005年福岡県立医科大学
この動画を見る
$\displaystyle \int \displaystyle \frac{\tan^2x}{\cos^2x} dx$
出典：2005年福岡県立医科大学
大学入試問題#610「初見だと涙がでるかも」 産業医科大学(2022) #不定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#産業医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int (2\sqrt{ x^2+1 }-\displaystyle \frac{1}{\sqrt{ x^2+1 }})dx$
出典：2022年産業医科大学 入試問題
この動画を見る
$\displaystyle \int (2\sqrt{ x^2+1 }-\displaystyle \frac{1}{\sqrt{ x^2+1 }})dx$
出典：2022年産業医科大学 入試問題
大学入試問題#609「落とすと落ちる良問」 早稲田大学(2023) #整数問題
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$0 \lt x \leqq y \leqq z$
$xyz=x+y+z$を満たす整数$x,y,z$の組を求めよ
出典：2023年早稲田大学 入試問題
この動画を見る
$0 \lt x \leqq y \leqq z$
$xyz=x+y+z$を満たす整数$x,y,z$の組を求めよ
出典：2023年早稲田大学 入試問題
大学入試問題#608「絶対値・・・・」 横浜市立大学(2009) #定積分
単元：
#数Ⅰ#数Ⅱ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#三角関数#三角関数とグラフ#加法定理とその応用#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{-\frac{\pi}{6}}^{\frac{\pi}{2}} |\sin2\ x| \sin\ x\ dx$
出典：2009年横浜市立大学 入試問題
この動画を見る
$\displaystyle \int_{-\frac{\pi}{6}}^{\frac{\pi}{2}} |\sin2\ x| \sin\ x\ dx$
出典：2009年横浜市立大学 入試問題
大学入試問題#607「やばい、忙しすぎる」 青山学院大学(2007) #定積分
単元：
#数Ⅱ#三角関数#三角関数とグラフ#微分とその応用#積分とその応用#微分法#定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{\frac{\pi}{2}}^{\pi} x(\cos2x-\sin2x) dx$
出典：2007年青山学院大学 入試問題
この動画を見る
$\displaystyle \int_{\frac{\pi}{2}}^{\pi} x(\cos2x-\sin2x) dx$
出典：2007年青山学院大学 入試問題
大学入試問題#606「見るからに落とせない気がする」 福島大学(2012) #方程式
単元：
#数Ⅰ#２次関数#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#2次方程式と2次不等式#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$x=\sqrt{ 2+\sqrt{ x^2-2 } }$を満たす実数$x$を求めよ
出典：2012年福島大学 入試問題
この動画を見る
$x=\sqrt{ 2+\sqrt{ x^2-2 } }$を満たす実数$x$を求めよ
出典：2012年福島大学 入試問題
高校の範囲で解ける積分 By 英語orドイツ語シはBかHか さん #定積分
単元：
#複素数平面#積分とその応用#複素数平面#定積分#数学(高校生)#数C#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1} arg(1+\sqrt{ -x }) dx$
$-\pi \leqq arg(1+\sqrt{ -x }) \lt \pi$
この動画を見る
$\displaystyle \int_{0}^{1} arg(1+\sqrt{ -x }) dx$
$-\pi \leqq arg(1+\sqrt{ -x }) \lt \pi$
青山学院大学(2007年) #Shorts
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#青山学院大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{4} \displaystyle \frac{x^2+1}{x+1} dx$
出典：2007年青山学院大学
この動画を見る
$\displaystyle \int_{0}^{4} \displaystyle \frac{x^2+1}{x+1} dx$
出典：2007年青山学院大学
大学入試問題#昭和大#604「nの計算丁寧に」 昭和大学医学部(2014) #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#昭和大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1} x^2(1-x)^n dx$
$n$自然数
出典：2014年昭和大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} x^2(1-x)^n dx$
$n$自然数
出典：2014年昭和大学 入試問題
大学入試問題#603「もう飽きた？」 千葉大学(1989) #極限
単元：
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$P_n=\sqrt[ n ]{ \displaystyle \frac{(3n)!}{(2n)!} }$とおく
（1）$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{P_n}{n}$を求めよ
（2）$\displaystyle \lim_{ n \to \infty } (\displaystyle \frac{n+2}{n})^{P_n}$を求めよ
出典：1989年千葉大学 入試問題
この動画を見る
$P_n=\sqrt[ n ]{ \displaystyle \frac{(3n)!}{(2n)!} }$とおく
（1）$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{P_n}{n}$を求めよ
（2）$\displaystyle \lim_{ n \to \infty } (\displaystyle \frac{n+2}{n})^{P_n}$を求めよ
出典：1989年千葉大学 入試問題
大学入試問題#601「これは落としたくないかも」 広島大学後期(2014) #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#広島大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$f(x)=x\ log\ x$のとき
$(\displaystyle \frac{1}{e} \leqq x \leqq )$
$\displaystyle \int_{0}^{e} f^{-1}(x) dx$を求めよ
出典：2014年広島大学後期 入試問題
この動画を見る
$f(x)=x\ log\ x$のとき
$(\displaystyle \frac{1}{e} \leqq x \leqq )$
$\displaystyle \int_{0}^{e} f^{-1}(x) dx$を求めよ
出典：2014年広島大学後期 入試問題
大学入試問題#600「合同式使ってみた」 山梨大学医学部(2014) #整式
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#複素数と方程式#整式の除法・分数式・二項定理#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#山梨大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$x^{2014}$を$x^4+x^3+x^2+x+1$で割った余りを求めよ
出典：2014年山梨大学 入試問題
この動画を見る
$x^{2014}$を$x^4+x^3+x^2+x+1$で割った余りを求めよ
出典：2014年山梨大学 入試問題
大学入試問題#599「King-propertyは使ってません」 南山大学(2013) 定積分
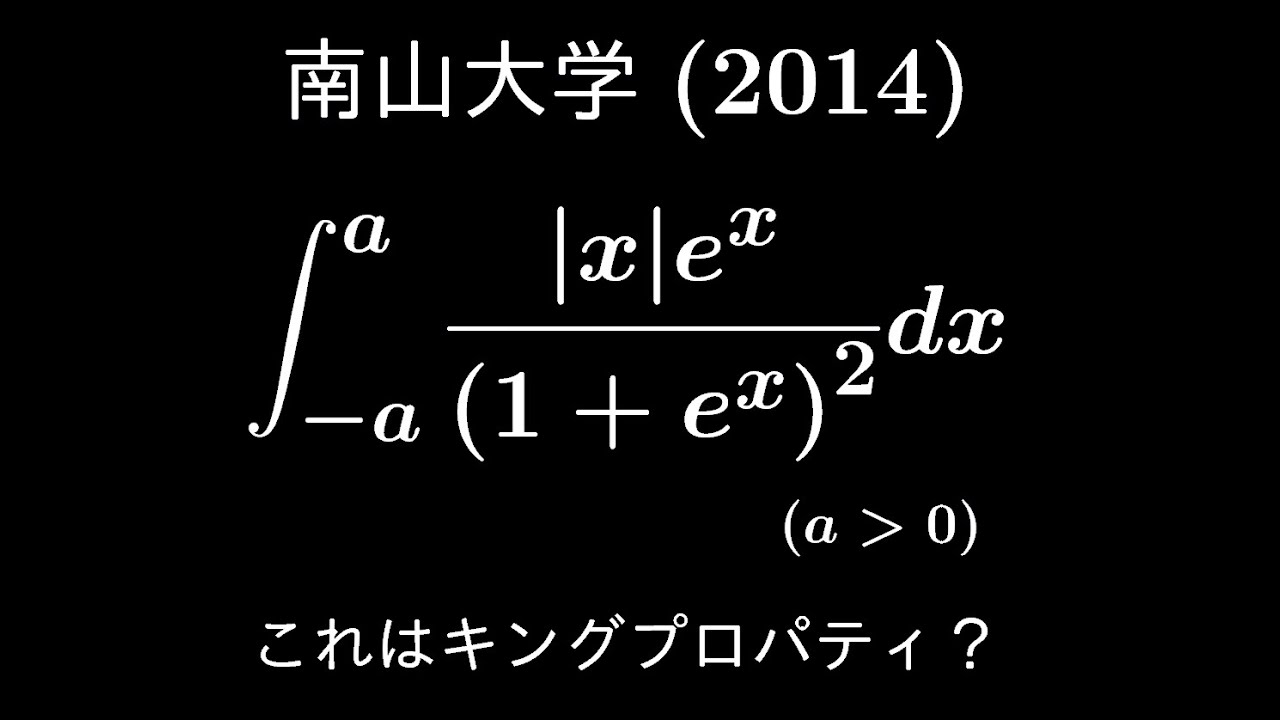
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#南山大学
指導講師：
ますただ
問題文全文(内容文)：
$a \gt 0$
$\displaystyle \int_{-a}^{a} \displaystyle \frac{|x|e^x}{(1+e^x)^2} dx$
出典：2013年南山大学 入試問題
この動画を見る
$a \gt 0$
$\displaystyle \int_{-a}^{a} \displaystyle \frac{|x|e^x}{(1+e^x)^2} dx$
出典：2013年南山大学 入試問題
大学入試問題#598「計算が大変でした」 関西大学(2009) #区分求積法
単元：
#大学入試過去問(数学)#関数と極限#積分とその応用#数列の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#関西大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n \displaystyle \frac{n-k}{n\sqrt{ 3n^2+k^2 }}$
出典：2009年関西大学 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n \displaystyle \frac{n-k}{n\sqrt{ 3n^2+k^2 }}$
出典：2009年関西大学 入試問題
大学入試問題#597「難しくはないと思う」 大阪教育大学(2014) #命題②
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題（集合・命題と条件・背理法）#学校別大学入試過去問解説(数学)#数学(高校生)#大阪教育大学
指導講師：
ますただ
問題文全文(内容文)：
$\alpha=\sqrt[ 3 ]{ 2 }$（が無理数は使用可）
$\alpha^2+p\alpha+q=0$を満たす有理数$p,q$が存在しなことを示せ
出典：2015年大阪教育大学 入試問題
この動画を見る
$\alpha=\sqrt[ 3 ]{ 2 }$（が無理数は使用可）
$\alpha^2+p\alpha+q=0$を満たす有理数$p,q$が存在しなことを示せ
出典：2015年大阪教育大学 入試問題
電気通信大学2014年 #定積分 #Shorts
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#電気通信大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1} x^2(1-x)^9 dx$
出典：2014年電気通信大学
この動画を見る
$\displaystyle \int_{0}^{1} x^2(1-x)^9 dx$
出典：2014年電気通信大学
大学入試問題#596「√２のいとこ」 大阪教育大学(2014) #命題①
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題（集合・命題と条件・背理法）#学校別大学入試過去問解説(数学)#数学(高校生)#大阪教育大学
指導講師：
ますただ
問題文全文(内容文)：
$\sqrt[ 3 ]{ 2 }$は無理数であることを示せ
出典：2015年大阪教育大学 入試問題
この動画を見る
$\sqrt[ 3 ]{ 2 }$は無理数であることを示せ
出典：2015年大阪教育大学 入試問題
電気通信大学2014年 #極限 #Shorts
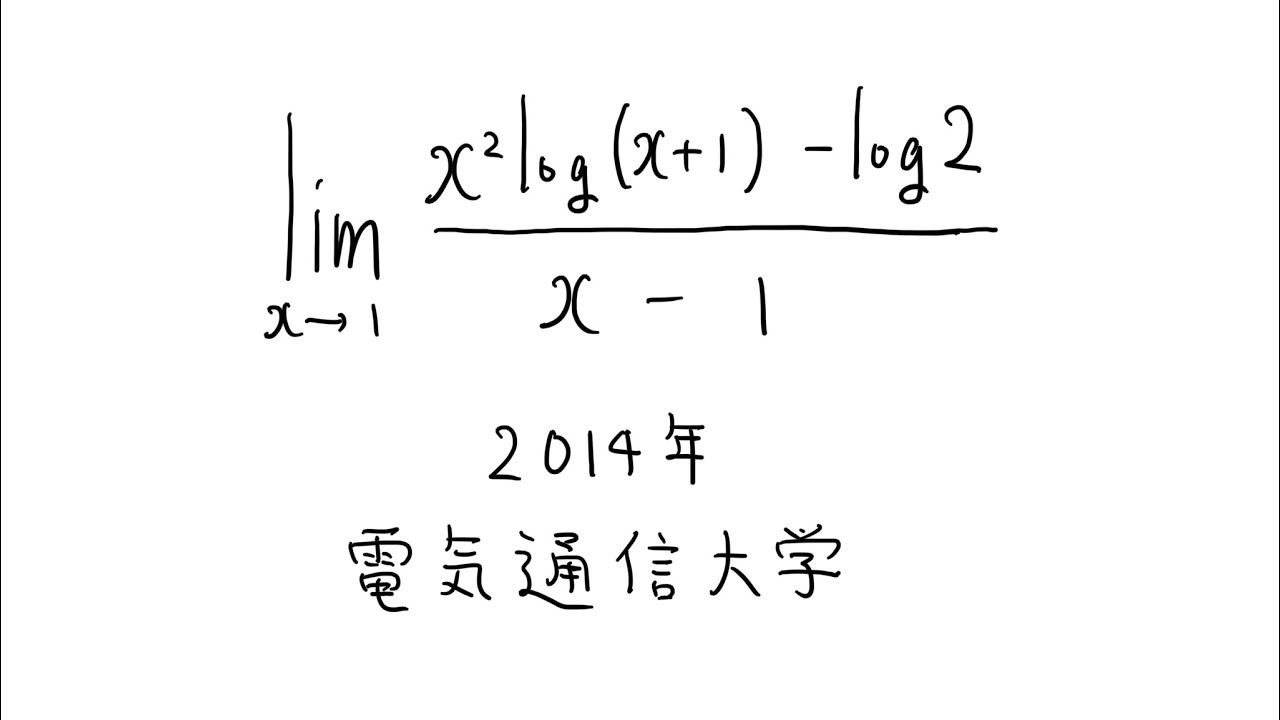
単元：
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#電気通信大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ x \to 1 } \displaystyle \frac{x^2log(x+1)-log\ 2}{x-1}$
出典：2014年電気通信大学
この動画を見る
$\displaystyle \lim_{ x \to 1 } \displaystyle \frac{x^2log(x+1)-log\ 2}{x-1}$
出典：2014年電気通信大学
大学入試問題#595「山口大学に初挑戦！」 山口大学(2014) #数列
単元：
#大学入試過去問(数学)#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#山口大学#数B#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$a_n=\tan\displaystyle \frac{\pi}{2^{n+1}}$のとき
$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{a_{n+1}}{a_n}$を求めよ
出典：2014年山口大学 入試問題
この動画を見る
$a_n=\tan\displaystyle \frac{\pi}{2^{n+1}}$のとき
$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{a_{n+1}}{a_n}$を求めよ
出典：2014年山口大学 入試問題
大学入試問題#594「やばいのは見た目だけ」 東京帝国大学(1926) #複素数
単元：
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C
指導講師：
ますただ
問題文全文(内容文)：
$\sqrt[ 3 ]{ i }$を求めよ。
$(i^2=-1)$
出典：1926年東京帝国大学医学部 入試問題
この動画を見る
$\sqrt[ 3 ]{ i }$を求めよ。
$(i^2=-1)$
出典：1926年東京帝国大学医学部 入試問題
大学入試問題#593「計算ミスに気をつける」 福島大学(1987) #極限
単元：
#大学入試過去問(数学)#積分とその応用#数列の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n \displaystyle \frac{n}{(2n+k)^2}log\displaystyle \frac{n+2k}{n}$
出典：1987年福島大学 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n \displaystyle \frac{n}{(2n+k)^2}log\displaystyle \frac{n+2k}{n}$
出典：1987年福島大学 入試問題
関西医科大学 #極限 #Shorts
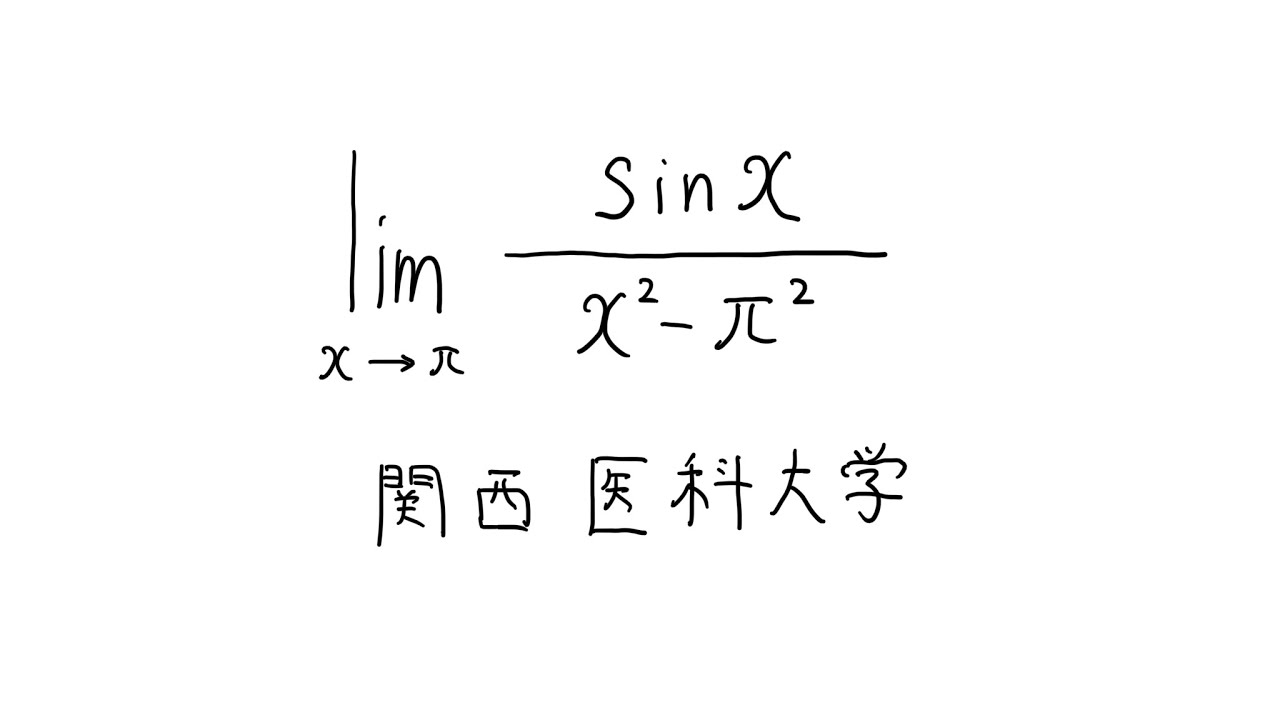
単元：
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#関西医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ x \to \pi } \displaystyle \frac{\sin\ x}{x^2-\pi^2}$を求めよ
出典：関西医科大学
この動画を見る
$\displaystyle \lim_{ x \to \pi } \displaystyle \frac{\sin\ x}{x^2-\pi^2}$を求めよ
出典：関西医科大学
大学入試問題#594「解法が見えると計算に萎えそう」 南山大学(2019) #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#南山大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{2}} (\cos^3\theta\sin\theta)e^{-\cos\theta}d\theta$
出典：2019年南山大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} (\cos^3\theta\sin\theta)e^{-\cos\theta}d\theta$
出典：2019年南山大学 入試問題
大学入試問題#593「カップラーメン食べながらでも解いて」 関西大学(2011) #三角関数
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#数学(高校生)#関西大学
指導講師：
ますただ
問題文全文(内容文)：
$x-y=\displaystyle \frac{\pi}{3}$のとき
$\displaystyle \frac{\sin\ x-\sin\ y}{\cos\ x+\cos\ y}$の値を求めよ
出典：2011年関西大学 入試問題
この動画を見る
$x-y=\displaystyle \frac{\pi}{3}$のとき
$\displaystyle \frac{\sin\ x-\sin\ y}{\cos\ x+\cos\ y}$の値を求めよ
出典：2011年関西大学 入試問題
大学入試問題#592「カップラーメンができる前には解きたい」 北海学園大学(2019) #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{4}} \tan^3x\ dx$
出典：2019年北海学園大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}} \tan^3x\ dx$
出典：2019年北海学園大学 入試問題
大学入試問題#591「技をかけたくなる積分」 茨城大学(2021) #定積分
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#茨城大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{-1}^{1} (1+x+x^2)^2 dx$
出典：2021年茨城大学 入試問題
この動画を見る
$\displaystyle \int_{-1}^{1} (1+x+x^2)^2 dx$
出典：2021年茨城大学 入試問題
大学入試問題#590「見た目以上に難しめ」 横浜市立大学(2020) #定積分
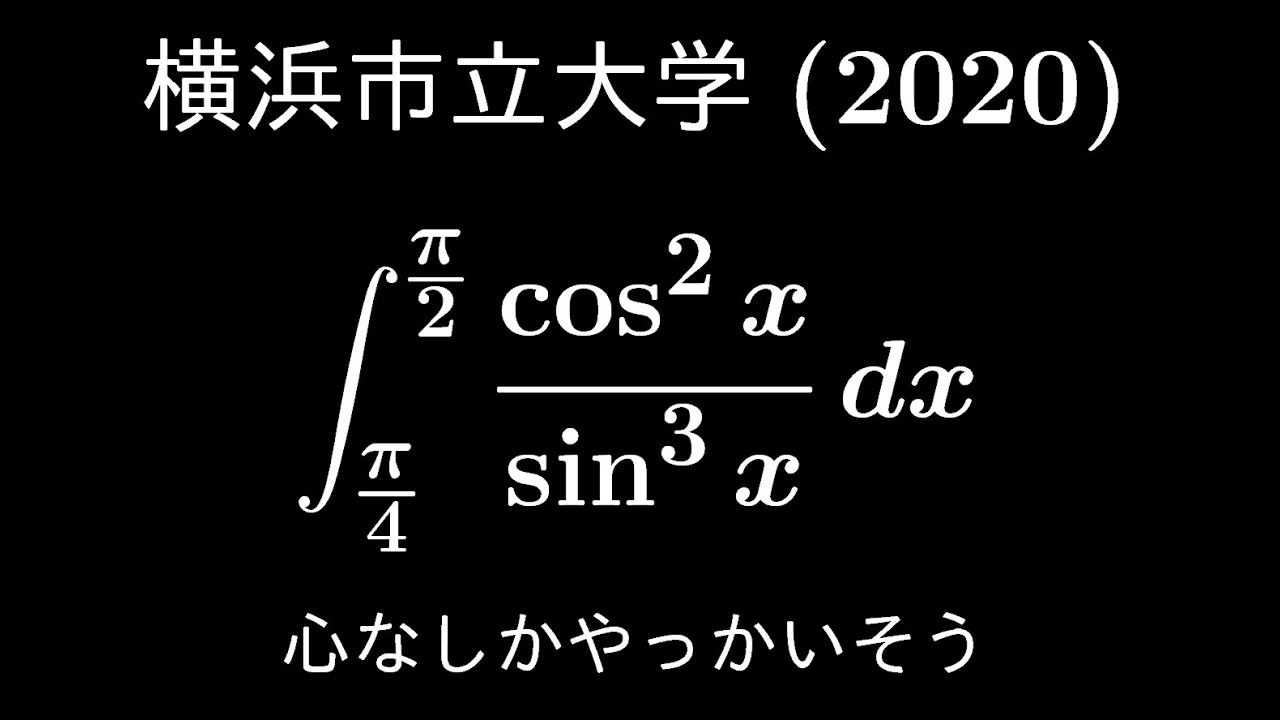
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#横浜市立大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \displaystyle \frac{\cos^2\ x}{\sin^3\ x} dx$
出典：2020年横浜市立大学医理学部 入試問題
この動画を見る
$\displaystyle \int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \displaystyle \frac{\cos^2\ x}{\sin^3\ x} dx$
出典：2020年横浜市立大学医理学部 入試問題
会津大学2014 #Shorts #不定積分
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{dx}{x(log\ x)^2}$
出典：2014年会津大学
この動画を見る
$\displaystyle \int \displaystyle \frac{dx}{x(log\ x)^2}$
出典：2014年会津大学