ますただ
ますただ
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
大学入試問題をベースに数学の動画を作成しています。大学過去問を多数解説しています。
頻繁に更新していますので是非ご視聴ください！
職業：数学者
職歴：高校非常勤（院生時代）、高専、大学 准教授
趣味：
①将棋 棋力は将棋ウォーズ４段、将棋倶楽部２４はR２０００前後（小学校５，６年のころに頑張ってました）
②麻雀 アカウントは消えましたが、無課金で天鵬で７段まで上がりました。
③ソフトテニス 中学から大学まで、１０年間部活でやっていました。大学時代は４年になってもリーグにでていました。
大学入試問題#567「定数aの処理の難しさ」 東京大学1938 #不定積分
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int x^2(x^2+a^2)^{\frac{1}{2}}\ dx$
出典：1938年東京帝国大学 入試問題
この動画を見る
$\displaystyle \int x^2(x^2+a^2)^{\frac{1}{2}}\ dx$
出典：1938年東京帝国大学 入試問題
大学入試問題#566「計算力勝負」 京都帝国大学(1936) #不定積分
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{x^3}{x^2-3x+2}\ dx$
出典：1936年京都帝国大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{x^3}{x^2-3x+2}\ dx$
出典：1936年京都帝国大学 入試問題
ハルハルさん作成問題 #極限の存在範囲
単元：
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ x \to \infty } \displaystyle \frac{\sqrt{ (1+\displaystyle \frac{a^2}{x})(1+\displaystyle \frac{a}{x})(1+\displaystyle \frac{b}{x}) }-1}{x^b}=\displaystyle \frac{b^2}{a}+1$
を満たす実数の組$(a,b)$を平面上に図示せよ
この動画を見る
$\displaystyle \lim_{ x \to \infty } \displaystyle \frac{\sqrt{ (1+\displaystyle \frac{a^2}{x})(1+\displaystyle \frac{a}{x})(1+\displaystyle \frac{b}{x}) }-1}{x^b}=\displaystyle \frac{b^2}{a}+1$
を満たす実数の組$(a,b)$を平面上に図示せよ
大学入試問題#565「これは落とせない」 京都帝国大学(1935) #不定積分
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{e^x-1}{e^x+1}\ dx$
出典：1935年京都帝国大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{e^x-1}{e^x+1}\ dx$
出典：1935年京都帝国大学 入試問題
大学入試問題#564「構想力が鍛えられる問題！」 東京帝国大学(1934) #不定積分
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{3x+4}{\sqrt{ x^2+2x+5 }}\ dx$
出典：1934年東京帝国大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{3x+4}{\sqrt{ x^2+2x+5 }}\ dx$
出典：1934年東京帝国大学 入試問題
大学入試問題#563「一度は解きたい問題」 東京帝国大学(1934) 曲線の長さ
単元：
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
曲線$y=\displaystyle \frac{e^x+e^{-x}}{2}$の$x=0$から$x=a$までの長さを求めよ。
出典：1934年東京帝国大学 入試問題
この動画を見る
曲線$y=\displaystyle \frac{e^x+e^{-x}}{2}$の$x=0$から$x=a$までの長さを求めよ。
出典：1934年東京帝国大学 入試問題
大学入試問題#562「証明問題じゃなきゃ解けるのか？」 東京帝国大学1937 #定積分
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#加法定理とその応用#数列#数学的帰納法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数B#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$n$：正の整数
$\displaystyle \int_{0}^{\pi} \displaystyle \frac{\sin(2n-1)x}{\sin\ x}\ dx=\pi$を示せ
出典：1937年東京帝国大学 入試問題
この動画を見る
$n$：正の整数
$\displaystyle \int_{0}^{\pi} \displaystyle \frac{\sin(2n-1)x}{\sin\ x}\ dx=\pi$を示せ
出典：1937年東京帝国大学 入試問題
大学入試問題#561「不定積分だと難易度爆上げ」 東京帝国大学(1930) #不定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{dx}{x\sqrt{ 1-x^2 }}$
出典：1930年東京帝国大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{dx}{x\sqrt{ 1-x^2 }}$
出典：1930年東京帝国大学 入試問題
大学入試問題#560「初手が大事」 同志社大学(2016) #不定積分
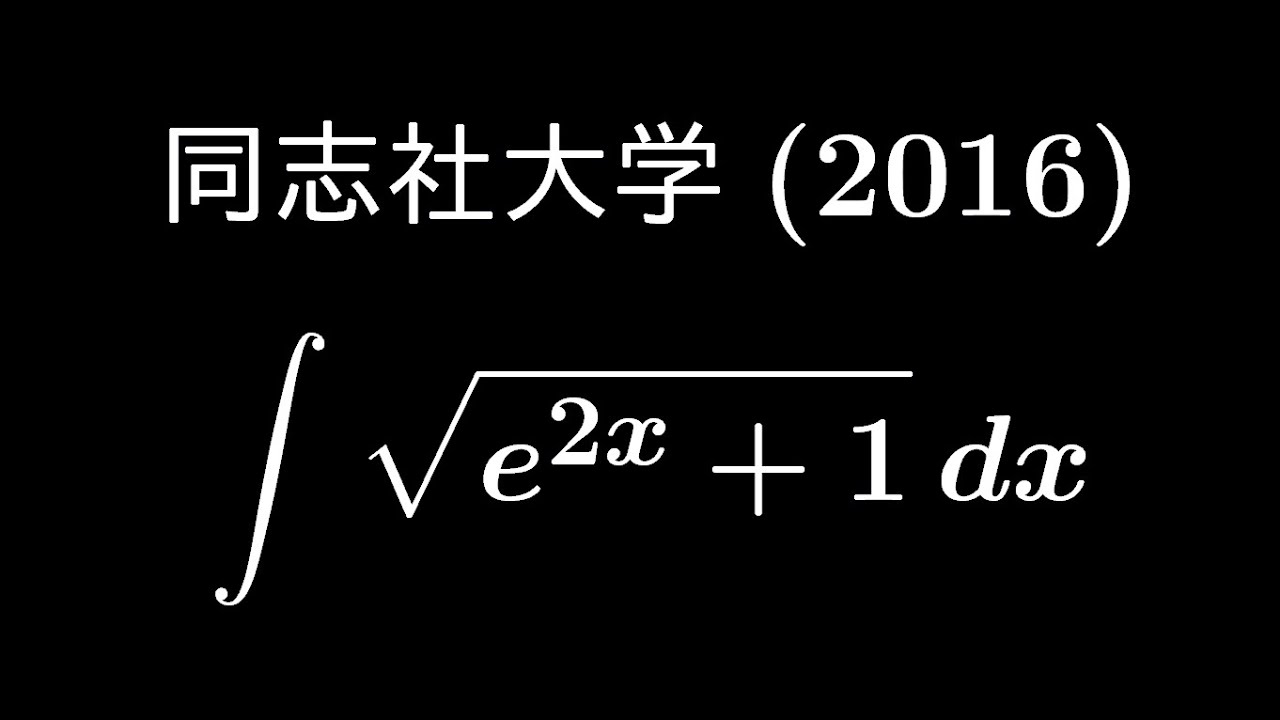
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#同志社大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \sqrt{ e^{2x}+1 }\ dx$
出典：2016年同志社大学 入試問題
この動画を見る
$\displaystyle \int \sqrt{ e^{2x}+1 }\ dx$
出典：2016年同志社大学 入試問題
大学入試問題#559「解法色々」 筑波大学(2020) #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{4}} \sin^2x\ \cos2x\ dx$
出典：2020年筑波大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}} \sin^2x\ \cos2x\ dx$
出典：2020年筑波大学 入試問題
大学入試問題#558 東京帝国大学(1933) #方程式
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \frac{\sqrt{ x+1 }+\sqrt{ x-1 }}{\sqrt{ x+1 }-\sqrt{ x-1 }}=\displaystyle \frac{4x-1}{2}$
出典：1933年東京帝国大学 入試問題
この動画を見る
$\displaystyle \frac{\sqrt{ x+1 }+\sqrt{ x-1 }}{\sqrt{ x+1 }-\sqrt{ x-1 }}=\displaystyle \frac{4x-1}{2}$
出典：1933年東京帝国大学 入試問題
大学入試問題#557「類題多数」 関西大学(2011) #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#関西大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1} \displaystyle \frac{dx}{e^x+2e^{-x}+3}$
出典：2011年関西大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{dx}{e^x+2e^{-x}+3}$
出典：2011年関西大学 入試問題
大学入試問題#556「技はかかりそうだけど、正面突破」 東京帝国大学大正14年 #定積分
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#定積分#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{x+\sin\ x}{1+\cos\ x} dx$
出典：大正14年東京大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{x+\sin\ x}{1+\cos\ x} dx$
出典：大正14年東京大学 入試問題
大学入試問題#555「不定積分だと難易度があがりがち」 東京帝国大学(1928) #不定積分
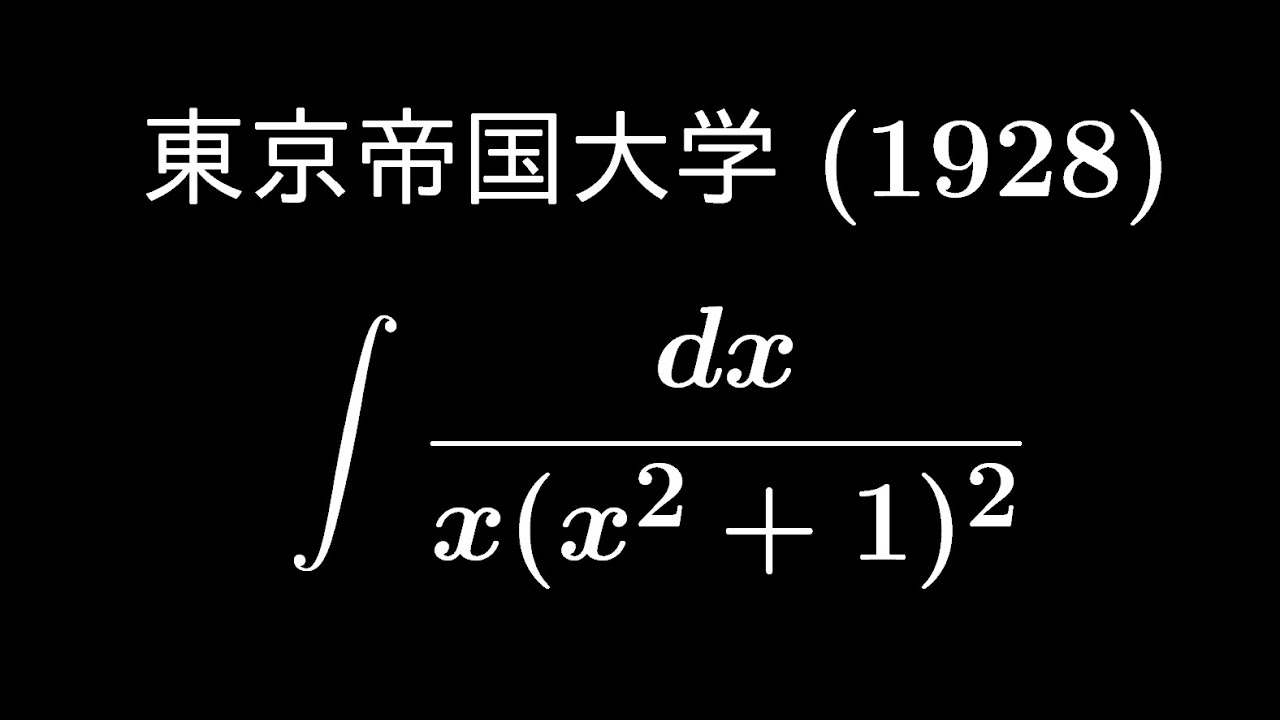
単元：
#大学入試過去問(数学)#積分とその応用#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{dx}{x(x^2+1)^2}$
出典：1928年東京帝国大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{dx}{x(x^2+1)^2}$
出典：1928年東京帝国大学 入試問題
大学入試問題#554「受験生の心を折にきてる。」 東邦大学医学部(2013) #定積分
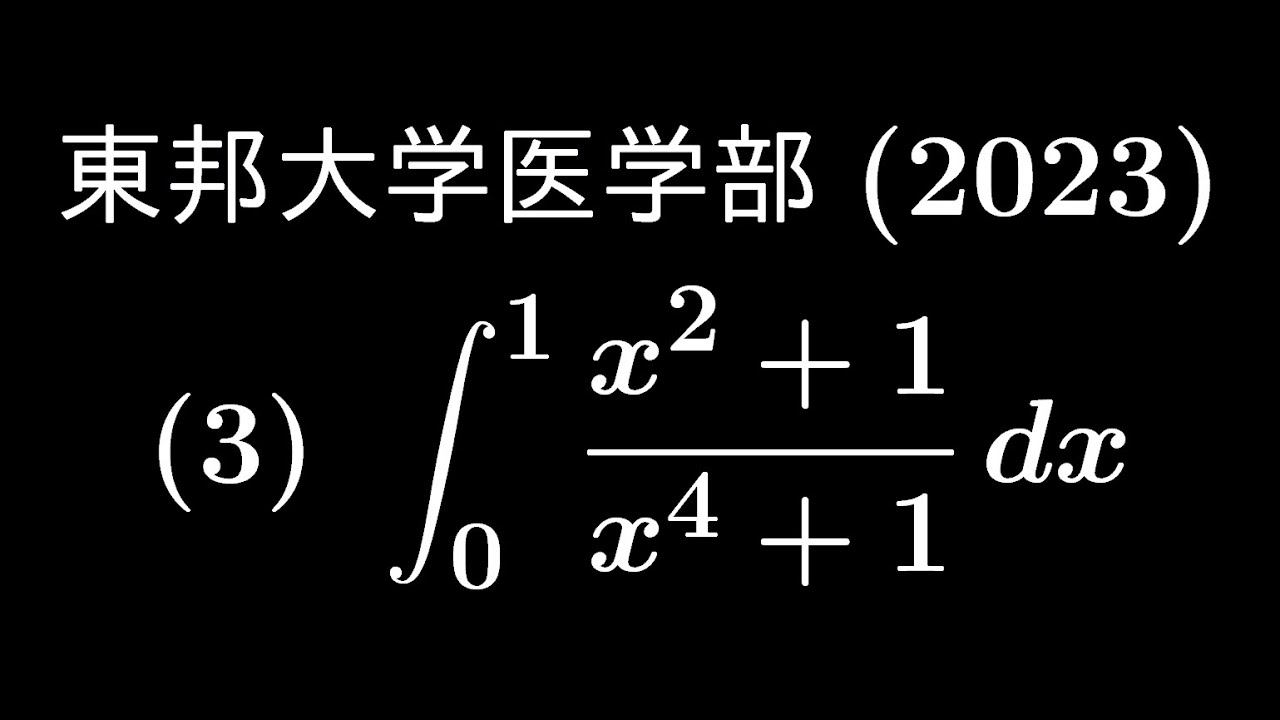
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東邦大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1} \displaystyle \frac{x^2+1}{x^4+1} dx$
出典：2013年東邦大学医学部 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{x^2+1}{x^4+1} dx$
出典：2013年東邦大学医学部 入試問題
大学入試問題#553「誘導なかったら、萎える」 東邦大学医学部(2013) #定積分
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東邦大学
指導講師：
ますただ
問題文全文(内容文)：
（1）
$\alpha=\displaystyle \frac{\pi}{4},\beta=\displaystyle \frac{3\pi}{4}$のとき
$\tan\displaystyle \frac{\alpha}{2}+\tan\displaystyle \frac{\beta}{2}$の値を求めよ
（2）
$\displaystyle \int_{0}^{1} \displaystyle \frac{dx}{x^2-\sqrt{ 2 }x+1}$
出典：2013年東邦大学医学部 入試問題
この動画を見る
（1）
$\alpha=\displaystyle \frac{\pi}{4},\beta=\displaystyle \frac{3\pi}{4}$のとき
$\tan\displaystyle \frac{\alpha}{2}+\tan\displaystyle \frac{\beta}{2}$の値を求めよ
（2）
$\displaystyle \int_{0}^{1} \displaystyle \frac{dx}{x^2-\sqrt{ 2 }x+1}$
出典：2013年東邦大学医学部 入試問題
大学入試問題#552「解き方いろいろ」 岡山県立大学(2023) #定積分
単元：
#数Ⅱ#大学入試過去問(数学)#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#岡山県立大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{1}{2}} \displaystyle \frac{x^3}{\sqrt{ 1-x^2 }} dx$
出典：2023年岡山県立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{1}{2}} \displaystyle \frac{x^3}{\sqrt{ 1-x^2 }} dx$
出典：2023年岡山県立大学 入試問題
大学入試問題#551「もはやオリジナル越えの芸術点高め！」 東京医科大学類題 By 英語orドイツ語シはBかHか さん #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} \displaystyle \frac{e^{\tan^2x+\sqrt{ \tan|x| }e^{\tan|x|}}}{1-\sin\ x} dx$
出典：2022年東京医科大学
この動画を見る
$\displaystyle \int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} \displaystyle \frac{e^{\tan^2x+\sqrt{ \tan|x| }e^{\tan|x|}}}{1-\sin\ x} dx$
出典：2022年東京医科大学
大学入試問題#550「これは難しい！！！」 By にっし～Diaryさん #定積分
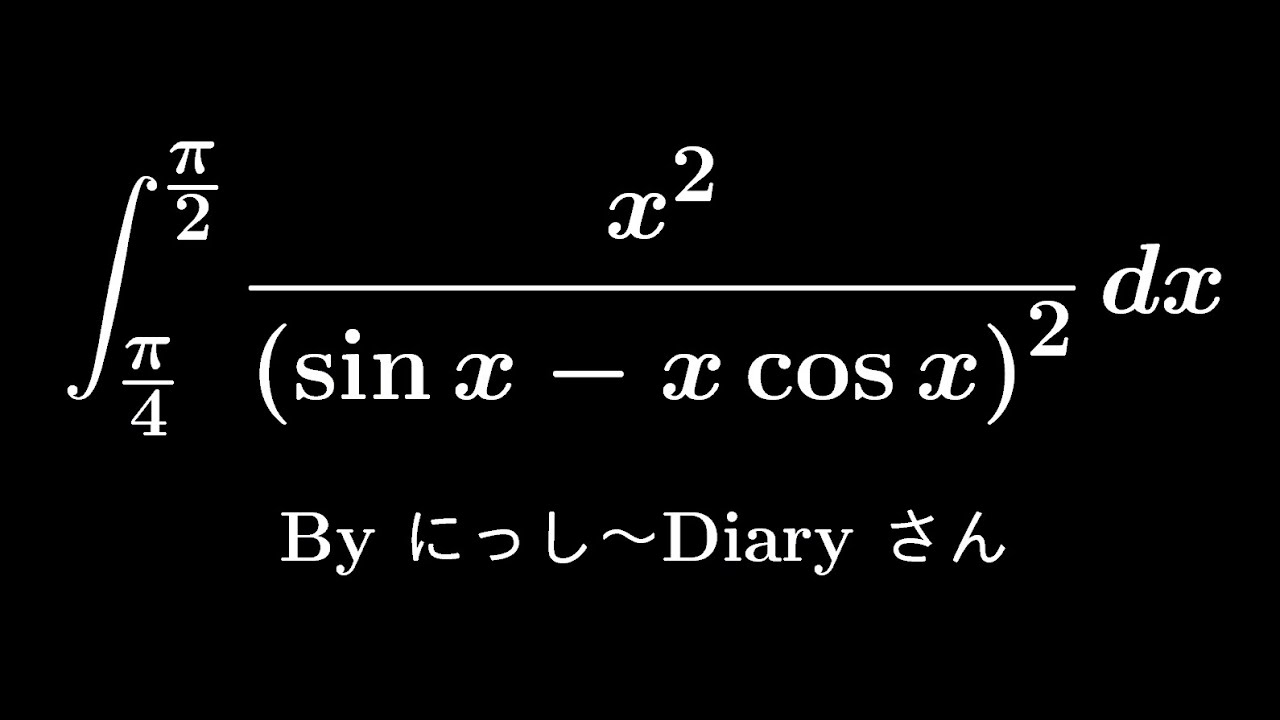
単元：
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \displaystyle \frac{x^2}{(\sin\ x-x\ \cos\ x)^2} dx$
この動画を見る
$\displaystyle \int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \displaystyle \frac{x^2}{(\sin\ x-x\ \cos\ x)^2} dx$
大学入試問題#549「解き方は色々」 島根大学(2023) #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#島根大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1} \displaystyle \frac{2x-2}{2x^2-2x+1}dx$
出典：2023年島根大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{2x-2}{2x^2-2x+1}dx$
出典：2023年島根大学 入試問題
大学入試問題#548「結局は定石通り」 広島大学AO(2022) #整数問題
単元：
#数A#大学入試過去問(数学)#整数の性質#学校別大学入試過去問解説(数学)#数学(高校生)#広島大学
指導講師：
ますただ
問題文全文(内容文)：
$\begin{eqnarray}
\left\{
\begin{array}{l}
0 \lt a \lt b \lt c \\
\displaystyle \frac{1}{ab}+\displaystyle \frac{1}{bc}+\displaystyle \frac{1}{ca}=\displaystyle \frac{1}{3}
\end{array}
\right.
\end{eqnarray}$
を満たす整数の組$(a,b,c)$をすべて求めよ。
出典：2022年広島大学AO入試
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
0 \lt a \lt b \lt c \\
\displaystyle \frac{1}{ab}+\displaystyle \frac{1}{bc}+\displaystyle \frac{1}{ca}=\displaystyle \frac{1}{3}
\end{array}
\right.
\end{eqnarray}$
を満たす整数の組$(a,b,c)$をすべて求めよ。
出典：2022年広島大学AO入試
大学入試問題#547「基本問題」 愛媛大学(2023) #整数問題
単元：
#数A#大学入試過去問(数学)#整数の性質#学校別大学入試過去問解説(数学)#数学(高校生)#愛媛大学#大阪市立大学
指導講師：
ますただ
問題文全文(内容文)：
$m^2-mn-2n^2=22$を満たす自然数の組$(m,n)$をすべて求めよ
出典：2023年愛媛大学
この動画を見る
$m^2-mn-2n^2=22$を満たす自然数の組$(m,n)$をすべて求めよ
出典：2023年愛媛大学
大学院入試問題#1「間違えてたらすみません」 岡山大学大学院 #微分方程式
単元：
#微分とその応用#微分法#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
（1）
$\displaystyle \frac{dy}{dx}=\displaystyle \frac{4y}{3x},\ x \gt 0$の一般項を求めよ
（2）
$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{dy}{dx}=\displaystyle \frac{2y}{3x}+\displaystyle \frac{2x}{y},\ x \gt 0 \\
y(1)=3
\end{array}
\right.
\end{eqnarray}$を満たす解を求めよ
出典：岡山大学大学院 入試問題
この動画を見る
（1）
$\displaystyle \frac{dy}{dx}=\displaystyle \frac{4y}{3x},\ x \gt 0$の一般項を求めよ
（2）
$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{dy}{dx}=\displaystyle \frac{2y}{3x}+\displaystyle \frac{2x}{y},\ x \gt 0 \\
y(1)=3
\end{array}
\right.
\end{eqnarray}$を満たす解を求めよ
出典：岡山大学大学院 入試問題
大学入試問題#546「もう飽きてると思います」 愛知教育大学(2023) #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#愛知教育大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{-1}^{1} \displaystyle \frac{x^2}{1+e^x} dx$
出典：2023年愛知教育大学 入試問題
この動画を見る
$\displaystyle \int_{-1}^{1} \displaystyle \frac{x^2}{1+e^x} dx$
出典：2023年愛知教育大学 入試問題
大学入試問題#545「作成時間がありませんでした」 会津大学(2023) #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1} (2x+1)log(x+1)\ dx$
出典：2023年会津大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} (2x+1)log(x+1)\ dx$
出典：2023年会津大学 入試問題
大学入試問題#544「これはさすがに合同式か・・・・」 京都大学(2023) #整式
単元：
#数A#数Ⅱ#大学入試過去問(数学)#複素数と方程式#整数の性質#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$x^{2023}-1$を$x^4+x^3+x^2+x+1$で割ったときの余りを求めよ
出典：2023年京都大学 入試問題
この動画を見る
$x^{2023}-1$を$x^4+x^3+x^2+x+1$で割ったときの余りを求めよ
出典：2023年京都大学 入試問題
大学入試問題#543「見た目は次数だけ」 前橋工科大学(2023) #定積分
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\sqrt[ 4 ]{ 3 }} (x^7-3x^3)e^{-\frac{x^4}{4}}\ dx$
出典：2023年前橋工科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\sqrt[ 4 ]{ 3 }} (x^7-3x^3)e^{-\frac{x^4}{4}}\ dx$
出典：2023年前橋工科大学 入試問題
大学入試問題#542「どこでも対称性が流行」 九州大学(2023) #高次方程式
単元：
#数Ⅱ#大学入試過去問(数学)#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師：
ますただ
問題文全文(内容文)：
$x^4-2x+3x^2-2x+1=0$を解け
出典：2023年九州大学 入試問題
この動画を見る
$x^4-2x+3x^2-2x+1=0$を解け
出典：2023年九州大学 入試問題
大学入試問題#541「初手が大事」長崎大学(2023)定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#長崎大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{2} \displaystyle \frac{x^2}{x^2+(3-x)^2} dx$
出典：2023年長崎大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{2} \displaystyle \frac{x^2}{x^2+(3-x)^2} dx$
出典：2023年長崎大学 入試問題
大学入試問題#540「これは平均点の調整すらならないような」 京都大学(2023) #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{4} \sqrt{ x }\ log(x^2)\ dx$
出典：2023年京都大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{4} \sqrt{ x }\ log(x^2)\ dx$
出典：2023年京都大学 入試問題