 ますただ
ますただ
 ますただ
ますただ
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
#広島市立大学2014#不定積分#ますただ
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#広島市立大学
指導講師:
ますただ
問題文全文(内容文):
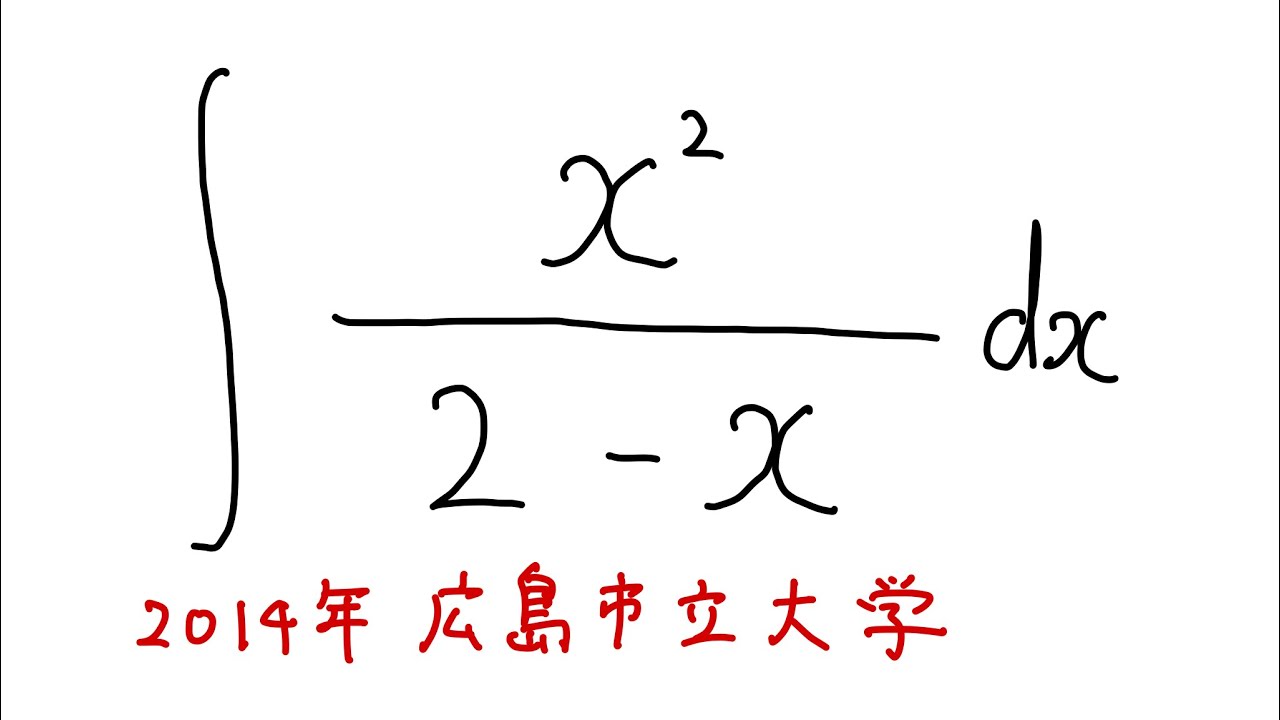
$\displaystyle \int \displaystyle \frac{x^2}{2-x} dx$
出典:2014年広島市立大学
この動画を見る
$\displaystyle \int \displaystyle \frac{x^2}{2-x} dx$
出典:2014年広島市立大学
#電気通信大学2015#定積分#ますただ
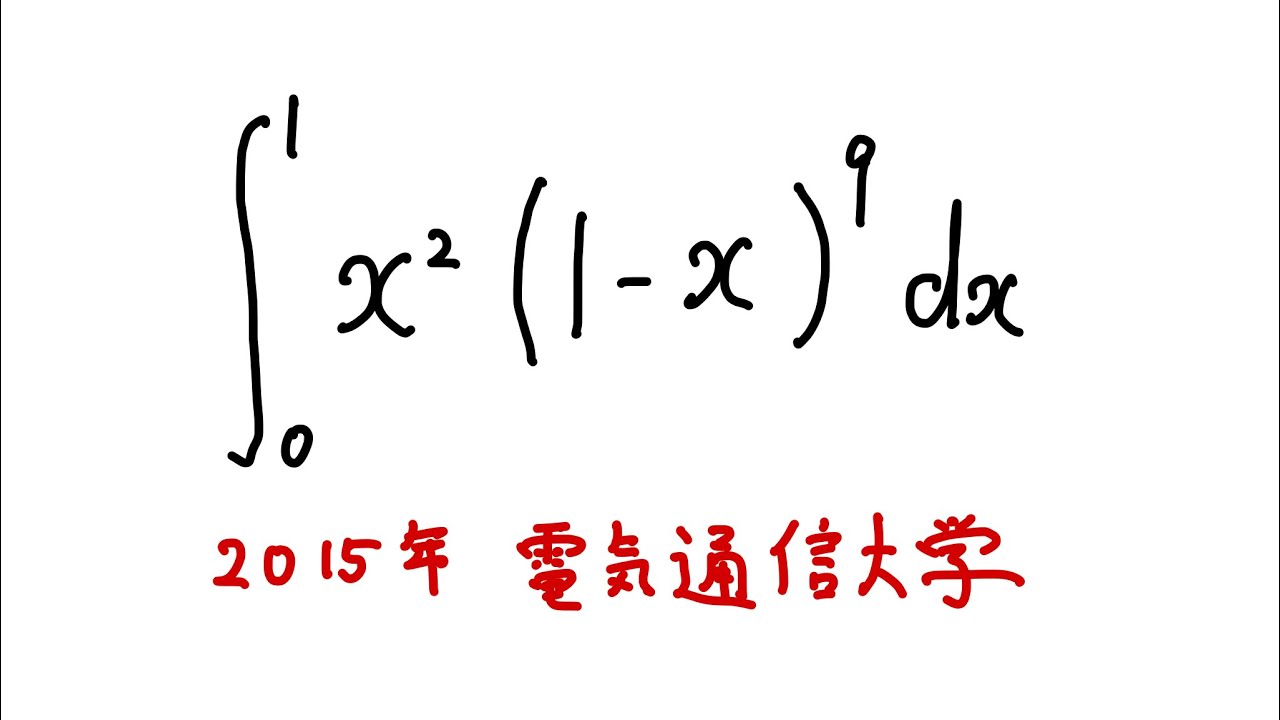
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} x^2(1-x)^9 dx$
出典:2015年電気通信大学
この動画を見る
$\displaystyle \int_{0}^{1} x^2(1-x)^9 dx$
出典:2015年電気通信大学
大学入試問題#891「まだこのタイプの問題残ってた」 #信州大学(2023) #キングプロパティ

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#信州大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\pi}^{ \pi } \displaystyle \frac{1}{1+e^{-2\sin x}} dx$
出典:2023年信州大学
この動画を見る
$\displaystyle \int_{-\pi}^{ \pi } \displaystyle \frac{1}{1+e^{-2\sin x}} dx$
出典:2023年信州大学
#富山大学薬学部2018#不定積分
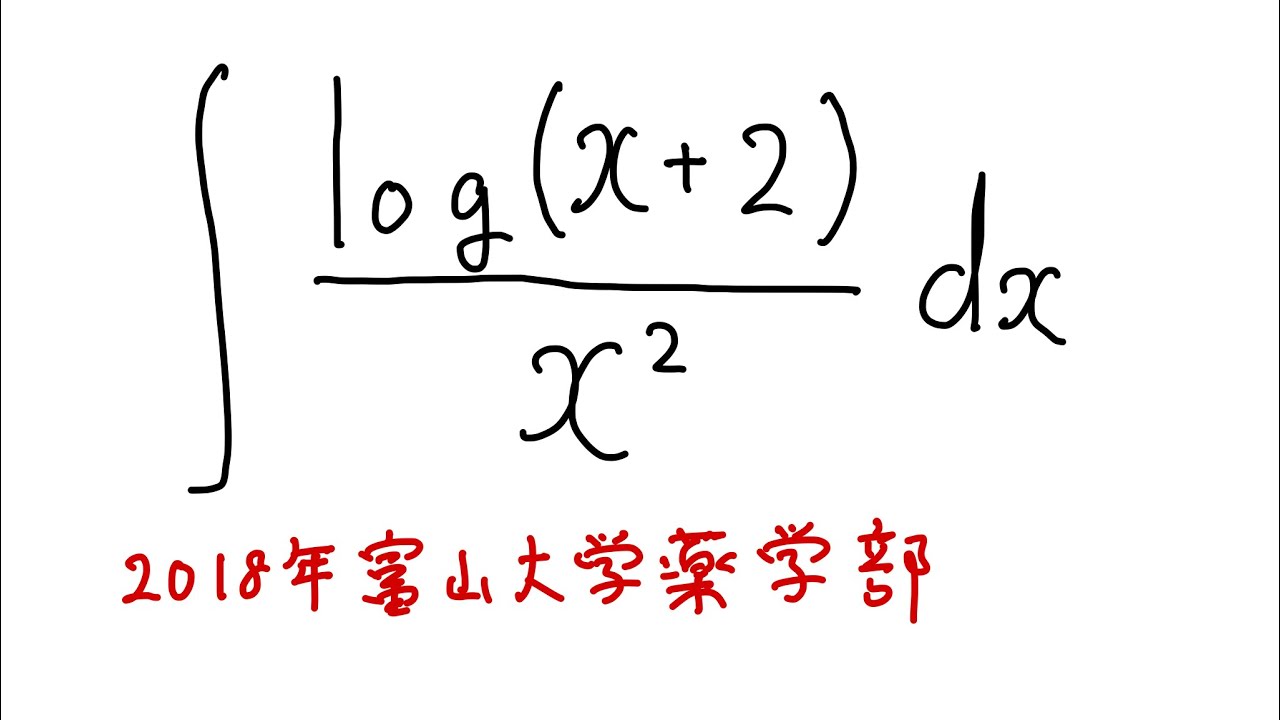
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#富山大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{log(x+2)}{x^2} dx$
出典:2018年富山大学薬学部
この動画を見る
$\displaystyle \int \displaystyle \frac{log(x+2)}{x^2} dx$
出典:2018年富山大学薬学部
#数検準1級1次_4#不定積分
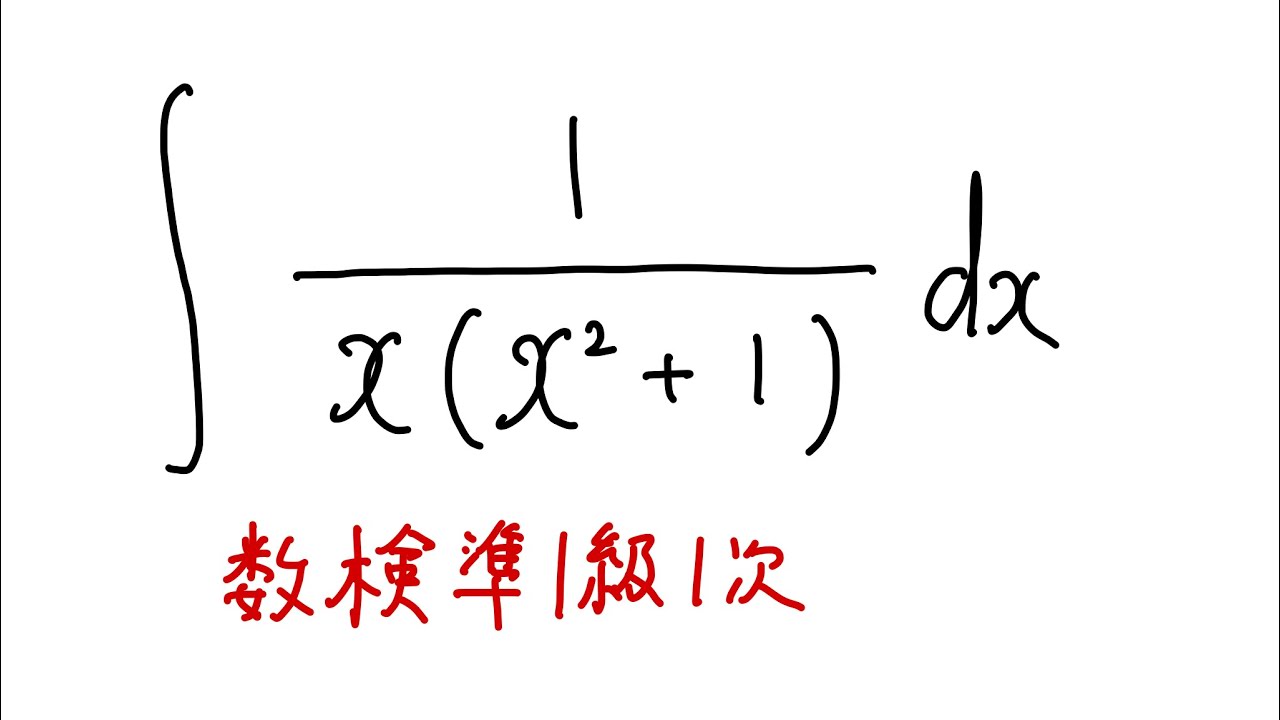
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{1}{x(x^2+1)} dx$
出典:数検準1級1次
この動画を見る
$\displaystyle \int \displaystyle \frac{1}{x(x^2+1)} dx$
出典:数検準1級1次
大学入試問題#890「苦手な受験生多そう」 #富山大学(2019)

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#富山大学
指導講師:
ますただ
問題文全文(内容文):
$f(x)=x\sqrt{ x+1 }$を導関数の定義に従って微分せよ。
出典:2019年富山大学推薦
この動画を見る
$f(x)=x\sqrt{ x+1 }$を導関数の定義に従って微分せよ。
出典:2019年富山大学推薦
#藤田医科大学2023#定積分
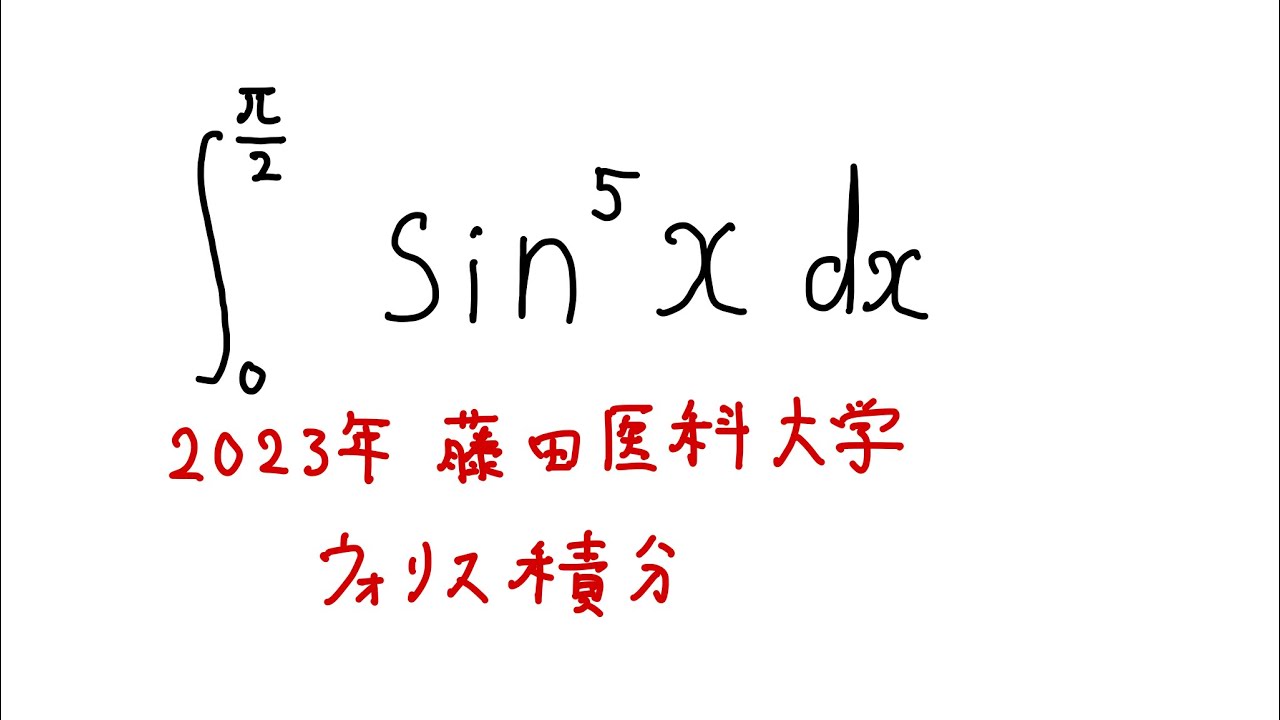
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#藤田医科大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sin^5x$ $dx$
出典:2023年藤田医科大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sin^5x$ $dx$
出典:2023年藤田医科大学
#数検準1級1次_2 #不定積分

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{e^x}{e^x+e^{-x}} dx$
出典:数検準1級1次
この動画を見る
$\displaystyle \int \displaystyle \frac{e^x}{e^x+e^{-x}} dx$
出典:数検準1級1次
大学入試問題#889「丁寧に計算するのみ」 #富山大学(2019)

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#富山大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{2\pi} (\cos^2x+x^2\sin^2x) dx$
出典:2019年富山大学推薦
この動画を見る
$\displaystyle \int_{0}^{2\pi} (\cos^2x+x^2\sin^2x) dx$
出典:2019年富山大学推薦
#数検準1級1次 #7
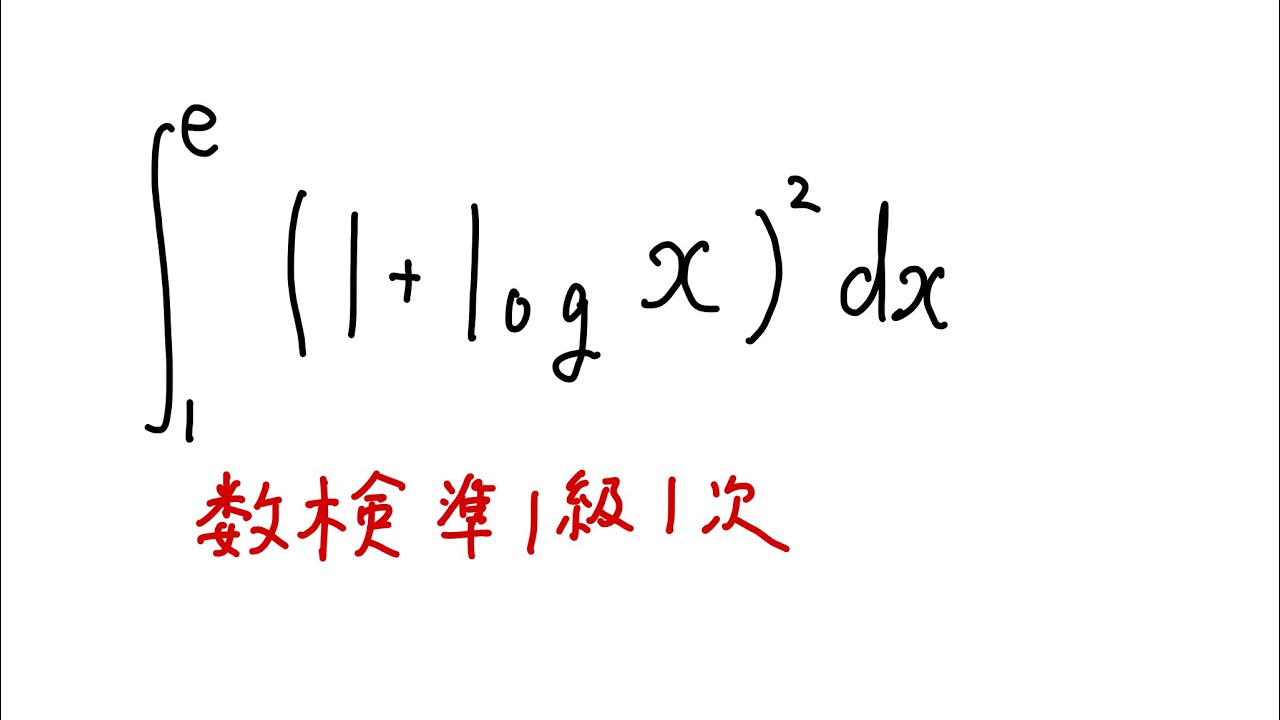
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{e} (1+log x)^2$ $dx$
出典:数検準1級1次
この動画を見る
$\displaystyle \int_{1}^{e} (1+log x)^2$ $dx$
出典:数検準1級1次
#数検準1級1次-1 #定積分

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の定積分を解け。
$\displaystyle \int_{0}^{1} \displaystyle \frac{x}{x^4+2x^2+1} dx$
出典:数検準1級1次
この動画を見る
以下の定積分を解け。
$\displaystyle \int_{0}^{1} \displaystyle \frac{x}{x^4+2x^2+1} dx$
出典:数検準1級1次
大学入試問題#888「絶対にチャートに載ってる」 #奈良県立医科大学(2014)

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#奈良県立医科大学
指導講師:
ますただ
問題文全文(内容文):
3次方程式
$x^3-6ax^2+9a^2x-4a=0$が相異なる3つの実数解をもつような$a$の範囲を求めよ。
出典:2014年奈良県立医科大学
この動画を見る
3次方程式
$x^3-6ax^2+9a^2x-4a=0$が相異なる3つの実数解をもつような$a$の範囲を求めよ。
出典:2014年奈良県立医科大学
#数検準1級1次#6#極限
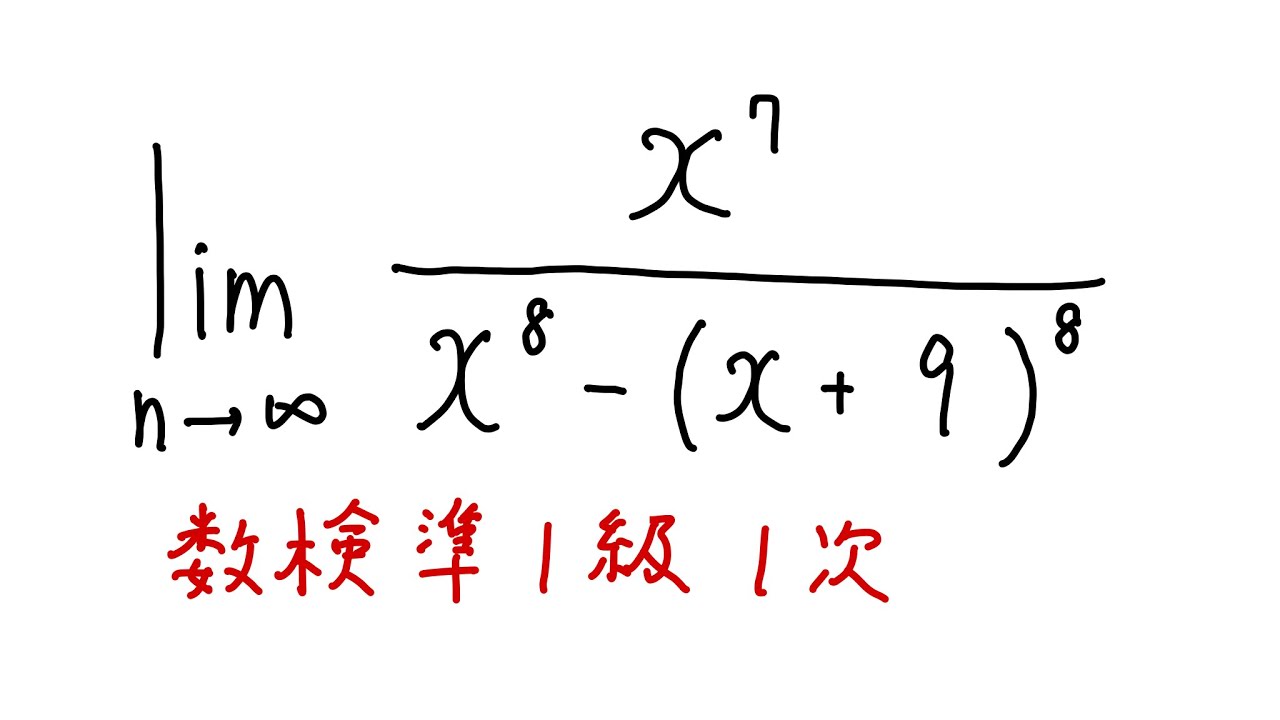
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#数学検定#数学検定準1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to \infty } \displaystyle \frac{x^7}{x^8-(x+9)^8}$
出典:数検準1級1次
この動画を見る
$\displaystyle \lim_{ x \to \infty } \displaystyle \frac{x^7}{x^8-(x+9)^8}$
出典:数検準1級1次
#数検準1級1次過去問#極限#ますただ

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#数学検定#数学検定準1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
以下の極限を解け。
$\displaystyle \lim_{ n \to \infty } \{2\sqrt{ n^2+4n }-\sqrt{ 4n^2+5n }\}$
出典:数検準1級1次
この動画を見る
以下の極限を解け。
$\displaystyle \lim_{ n \to \infty } \{2\sqrt{ n^2+4n }-\sqrt{ 4n^2+5n }\}$
出典:数検準1級1次
#数学検定準1級2次過去問#70「根性出すしかないんかなー」 #定積分

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \displaystyle \frac{x^4(1-x)^4}{1+x^2} dx$
出典:数検準1級2次
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{x^4(1-x)^4}{1+x^2} dx$
出典:数検準1級2次
#数検準1級1次#5#不定積分

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ x+1 }} dx$
出典:数検準1級
この動画を見る
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ x+1 }} dx$
出典:数検準1級
#東京理科大学2023#定積分#ますただ

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#東京理科大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\sqrt{ e }} \displaystyle \frac{e}{x^2+e} dx$
出典:2023年東京理科大学
この動画を見る
$\displaystyle \int_{0}^{\sqrt{ e }} \displaystyle \frac{e}{x^2+e} dx$
出典:2023年東京理科大学
大学入試問題#887「小問ではめんどいよー」 #兵庫医科大学(2010) #整式

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)#兵庫医科大学
指導講師:
ますただ
問題文全文(内容文):
$x^{2010}$を$x^4-1$で割った余りに$x=3$を代入した値を求めよ。
出典:2010年兵庫医科大学
この動画を見る
$x^{2010}$を$x^4-1$で割った余りに$x=3$を代入した値を求めよ。
出典:2010年兵庫医科大学
#数検準1級-1#定積分#ますただ
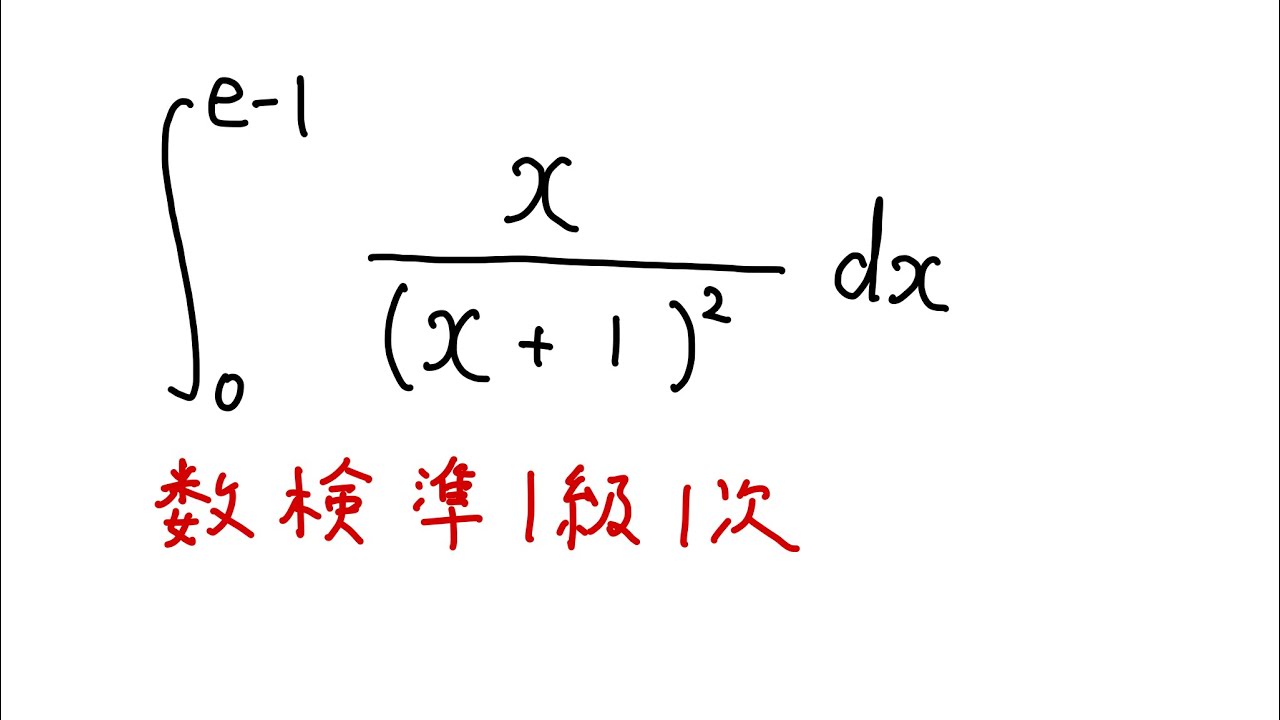
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{e-1} \displaystyle \frac{x}{(x+1)^2} dx$
出典:数検準1級1次
この動画を見る
$\displaystyle \int_{0}^{e-1} \displaystyle \frac{x}{(x+1)^2} dx$
出典:数検準1級1次
#数検準1級1次#極限#ますただ

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#数学検定#数学検定準1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to 3 } \displaystyle \frac{x-3}{\sqrt{ 3x+7 }-4}$
出典:数検準1級1次
この動画を見る
$\displaystyle \lim_{ x \to 3 } \displaystyle \frac{x-3}{\sqrt{ 3x+7 }-4}$
出典:数検準1級1次
#数学検定準1級2次過去問#69「展開が最短かも」 #定積分

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} x^4(1-x)^4$ $dx$
出典:数検準1級1次
この動画を見る
$\displaystyle \int_{0}^{1} x^4(1-x)^4$ $dx$
出典:数検準1級1次
#数検準1級1次#定積分#ますただ
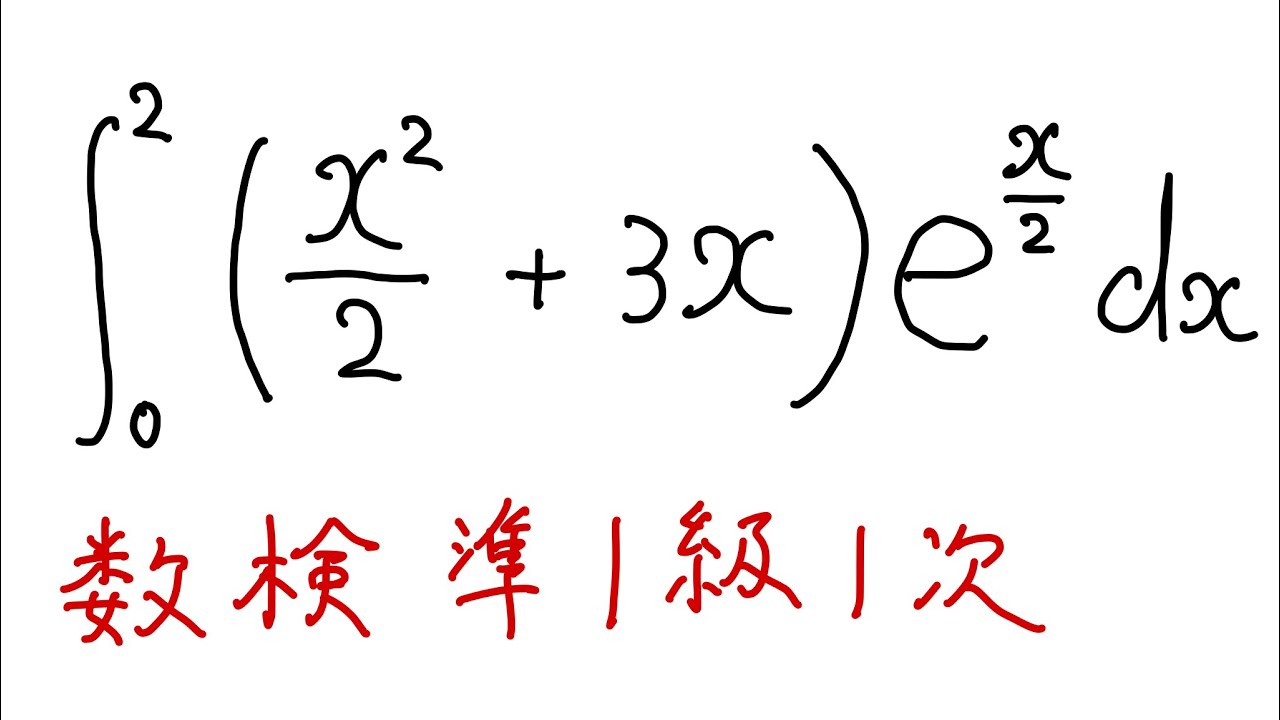
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{2} (\displaystyle \frac{x^2}{2}+3x)e^{\frac{x}{2}}dx$
出典:
この動画を見る
$\displaystyle \int_{0}^{2} (\displaystyle \frac{x^2}{2}+3x)e^{\frac{x}{2}}dx$
出典:
#山梨大学2013#定積分#ますただ

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#山梨大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-10}^{0} \displaystyle \frac{1}{(x+11)(x+12)}$ $dx$
出典:2013年山梨大学
この動画を見る
$\displaystyle \int_{-10}^{0} \displaystyle \frac{1}{(x+11)(x+12)}$ $dx$
出典:2013年山梨大学
#数検準1級1次過去問#定積分

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{e^2-1} log(x+1)$ $dx$
出典:数検準1級1次
この動画を見る
$\displaystyle \int_{0}^{e^2-1} log(x+1)$ $dx$
出典:数検準1級1次
大学入試問題#885「油断したら沼るかも」 #奈良県立医科大学(2014) 三角関数と整数問題
単元:
#数A#数Ⅱ#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#三角関数#学校別大学入試過去問解説(数学)#数学(高校生)#奈良県立医科大学
指導講師:
ますただ
問題文全文(内容文):
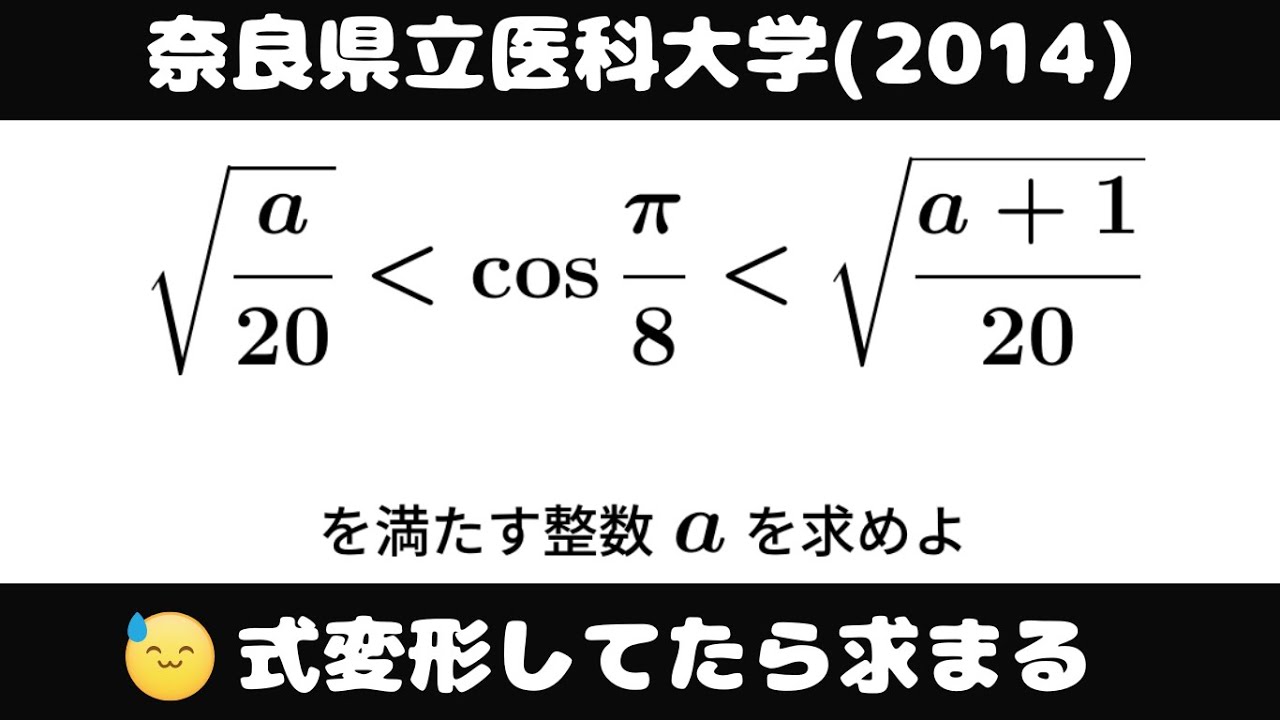
$\sqrt{ \displaystyle \frac{a}{20} } \lt \cos\displaystyle \frac{\pi}{8} \lt \sqrt{ \displaystyle \frac{a+1}{20} }$を満たす整数$a$を求めよ。
出典:2014年奈良県立医科大学
この動画を見る
$\sqrt{ \displaystyle \frac{a}{20} } \lt \cos\displaystyle \frac{\pi}{8} \lt \sqrt{ \displaystyle \frac{a+1}{20} }$を満たす整数$a$を求めよ。
出典:2014年奈良県立医科大学
#福岡大学#不定積分#ますただ

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#福岡大学
指導講師:
ますただ
問題文全文(内容文):
以下の不定積分を解け
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ 2x+1 }}$ $dx$
出典:福岡大学
この動画を見る
以下の不定積分を解け
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ 2x+1 }}$ $dx$
出典:福岡大学
#福島大学2013#定積分#ますただ
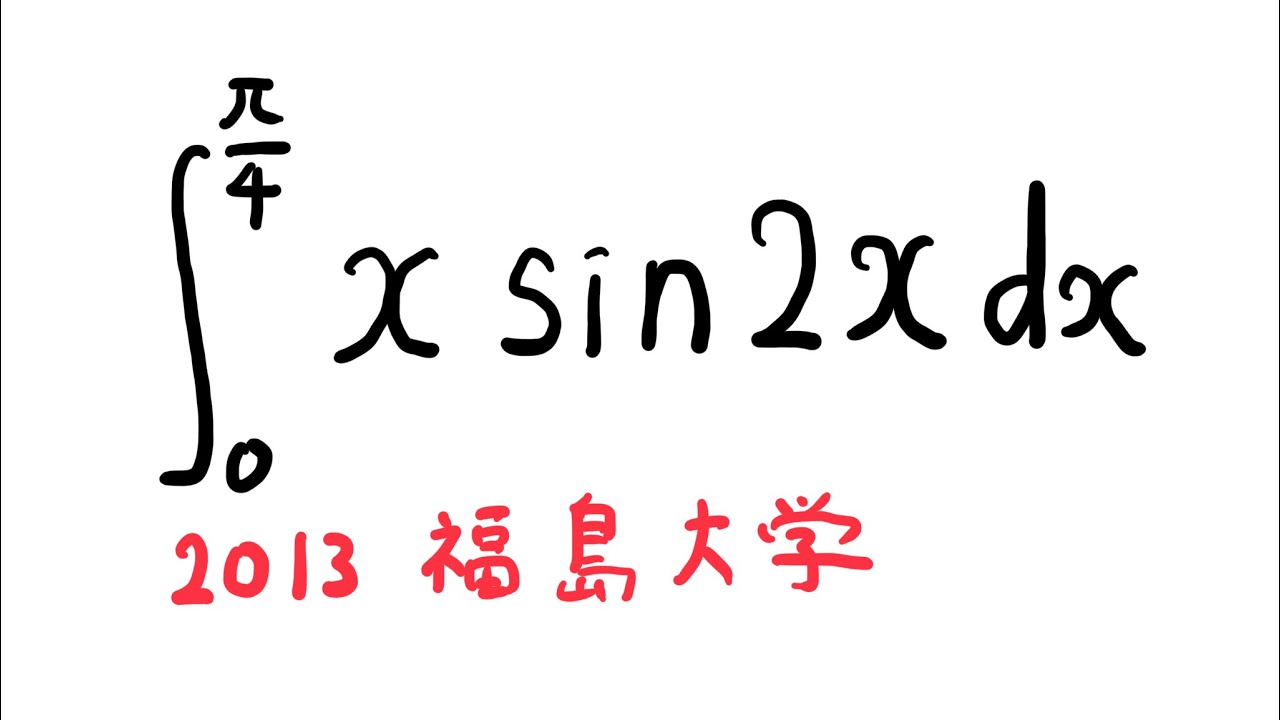
単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{4}} x$ $\sin2$ $x$ $dx$
出典:2013年福島大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}} x$ $\sin2$ $x$ $dx$
出典:2013年福島大学
#愛媛大学2014#極限#ますただ

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#愛媛大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{(\sqrt{ x^2+x+4 }-\sqrt{ x^2+4 })\sin2x}{x^2}$
出典:2024年愛媛大学
この動画を見る
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{(\sqrt{ x^2+x+4 }-\sqrt{ x^2+4 })\sin2x}{x^2}$
出典:2024年愛媛大学
大学入試問題#884「ミスれん」 #東京理科大学(2022) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#東京理科大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \displaystyle \frac{x-4}{2x^2+5x+2}$ $dx$
出典:2022年東京理科大学
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{x-4}{2x^2+5x+2}$ $dx$
出典:2022年東京理科大学
#小樽商科大学#不定積分#ますただ
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#小樽商科大学
指導講師:
ますただ
問題文全文(内容文):
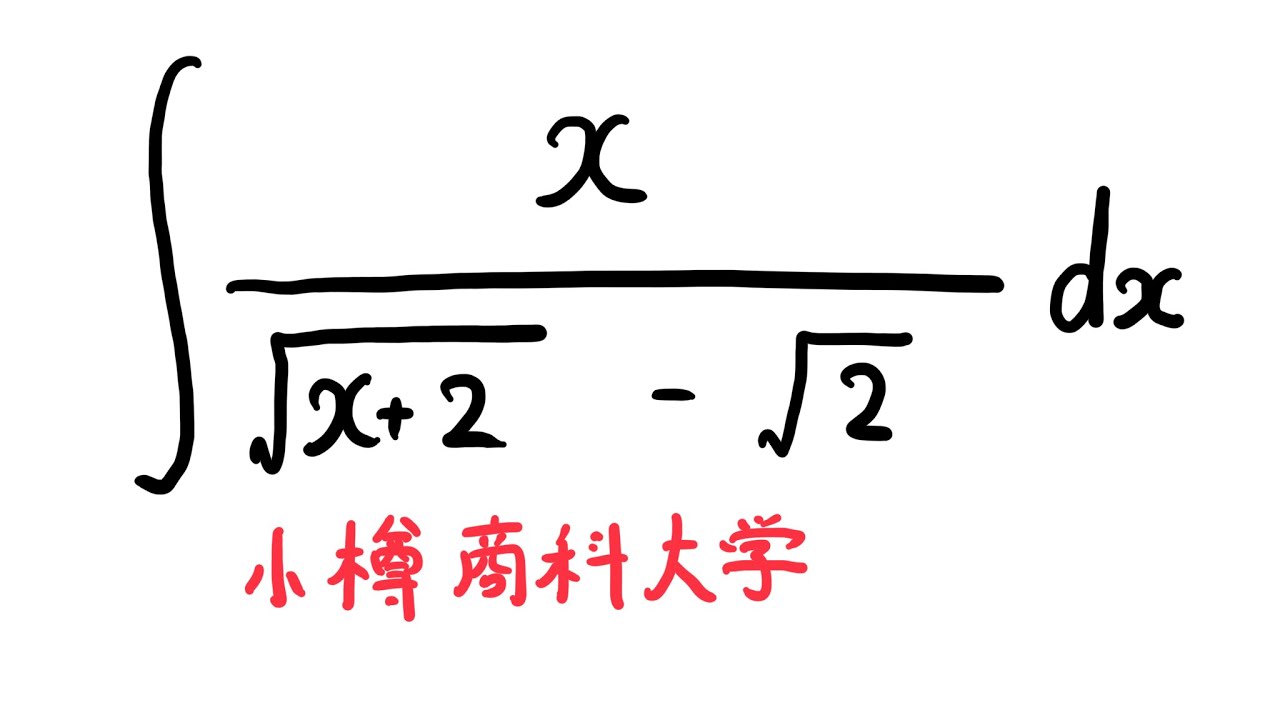
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ 2x+2}-\sqrt{ 2 }}$ $dx$
出典:小樽商科大学
この動画を見る
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ 2x+2}-\sqrt{ 2 }}$ $dx$
出典:小樽商科大学



