 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【受験算数】平面図形:角度わかるかな?【予習シリーズ算数・小5下】
単元:
#算数(中学受験)#平面図形#角度と面積
教材:
#予習シ#予習シ算数・小5下#中学受験教材#平面図形と比
指導講師:
理数個別チャンネル
問題文全文(内容文):
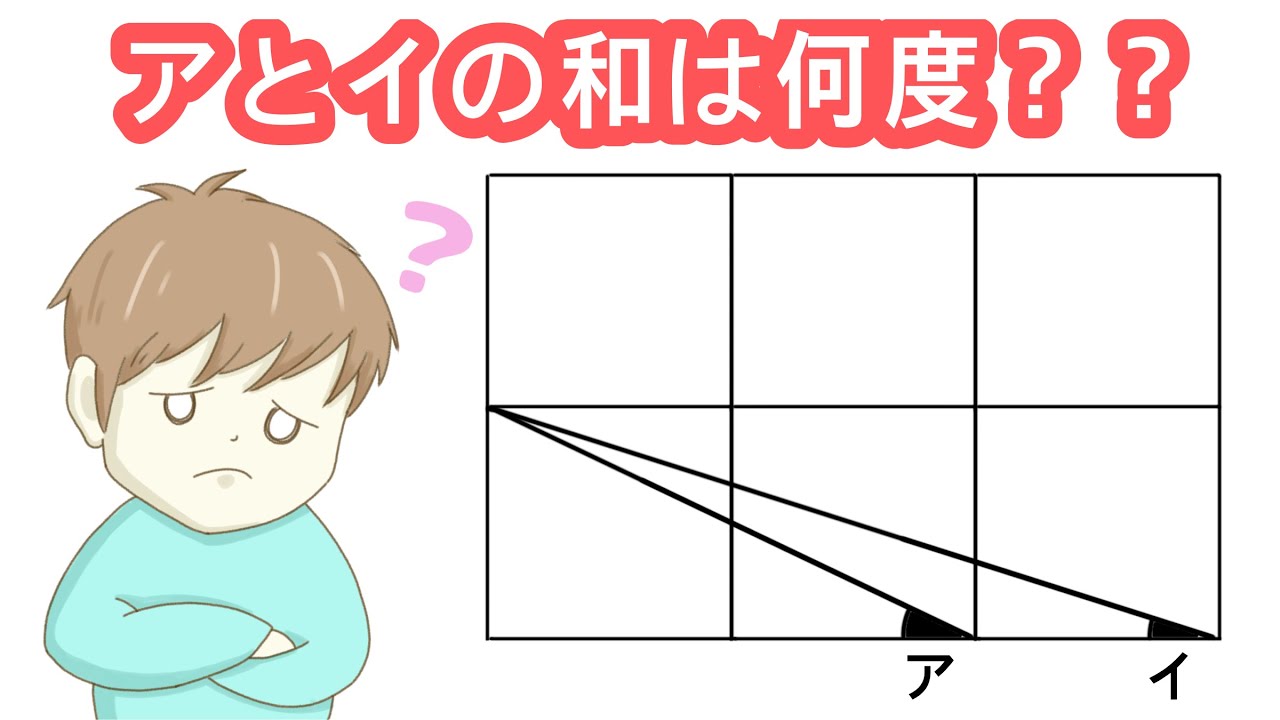
アとイの角度の和を求めよ
この動画を見る
アとイの角度の和を求めよ
【受験算数】場合の数:道順の場合の数 通ってはいけない場所がある場合~イチイチ解法【予習シリーズ算数・小5上】

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#予習シ#予習シ算数・小5上#中学受験教材#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
図のような、直角に交わる道があります。点Aから点Cを通って点Bまで行くとき、遠回りせずに行く道順は何通りありますか。
この動画を見る
図のような、直角に交わる道があります。点Aから点Cを通って点Bまで行くとき、遠回りせずに行く道順は何通りありますか。
【受験生応援】やる気が出ない受験生に伝えたい10の言葉

【数学】入試問題(国公立):一橋大学2018年(前期)第1問の解説

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
自然数nの各位の和をS(n)とする。n≧10000のとき、
n>30S(n)+2018が成り立つことを示せ。
この動画を見る
自然数nの各位の和をS(n)とする。n≧10000のとき、
n>30S(n)+2018が成り立つことを示せ。
【理数個別の過去問解説】2018年度一橋大学(前期) 数学 大問1解説

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
自然数nの各位の和を$S(n)$とする。$n\geqq 10000$のとき、
$n\gt 30S(n)+2018$が成り立つことを示せ。
この動画を見る
自然数nの各位の和を$S(n)$とする。$n\geqq 10000$のとき、
$n\gt 30S(n)+2018$が成り立つことを示せ。
【情報】ブロードキャストとデフォルトゲートウェイ

【数検3級】数学検定3級対策問題6(23)~(26)

単元:
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定3級
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題6.次の問いに答えなさい。
(23) yはxに反比例し、$x=-3$のとき$y=-12$です。yをxを用いて表しなさい。
(24) 右の度数分布表において、階級の幅は何㎝ですか。
(25) 等式$a=\dfrac{1}{2}(b+c)$ をbについて解きなさい。
(26) 右の図で、$\ell \parallel m$のとき、$∠x$の大きさは何度ですか。
この動画を見る
問題6.次の問いに答えなさい。
(23) yはxに反比例し、$x=-3$のとき$y=-12$です。yをxを用いて表しなさい。
(24) 右の度数分布表において、階級の幅は何㎝ですか。
(25) 等式$a=\dfrac{1}{2}(b+c)$ をbについて解きなさい。
(26) 右の図で、$\ell \parallel m$のとき、$∠x$の大きさは何度ですか。
【数C】ベクトルの基本⑧大きさを求めたいときの絶対値の2乗

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
教材:
#チャート式#青チャートⅡ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
ベクトルの絶対値を求めるために2乗の計算をする
この動画を見る
ベクトルの絶対値を求めるために2乗の計算をする
【数B】ベクトル:ベクトルの基本⑧大きさを求めたいときの絶対値の2乗

【受験算数】速さと比3:(練習❸)スタート地点が異なる【予習シリーズ演習問題集・小5下】

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#予習シ#予習シ演問・小5下#中学受験教材#速さと比(3)
指導講師:
理数個別チャンネル
問題文全文(内容文):
池を1周している道のP地点からA君が、Q地点からB君が、それぞれ一定の速さで図の矢印の方向へ向かって同時に歩き始めました。A君は出発してから10分後に初めてB君と出会い、それから6分後にQ地点を通過しました。さらに、P地点の少し手前で再びB君と出会い、その5分後にP地点に戻ってきました。これについて、次の問いに答えなさい。
(1)A君とB君の速さの比を求めなさい。
(2)A君がこの池を1周する時間は何分ですか。
この動画を見る
池を1周している道のP地点からA君が、Q地点からB君が、それぞれ一定の速さで図の矢印の方向へ向かって同時に歩き始めました。A君は出発してから10分後に初めてB君と出会い、それから6分後にQ地点を通過しました。さらに、P地点の少し手前で再びB君と出会い、その5分後にP地点に戻ってきました。これについて、次の問いに答えなさい。
(1)A君とB君の速さの比を求めなさい。
(2)A君がこの池を1周する時間は何分ですか。
【受験算数】場合の数:道順の場合の数~イチイチ解法【予習シリーズ算数・小5上】
単元:
#算数(中学受験)#場合の数#場合の数
教材:
#予習シ#予習シ算数・小5上#中学受験教材#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
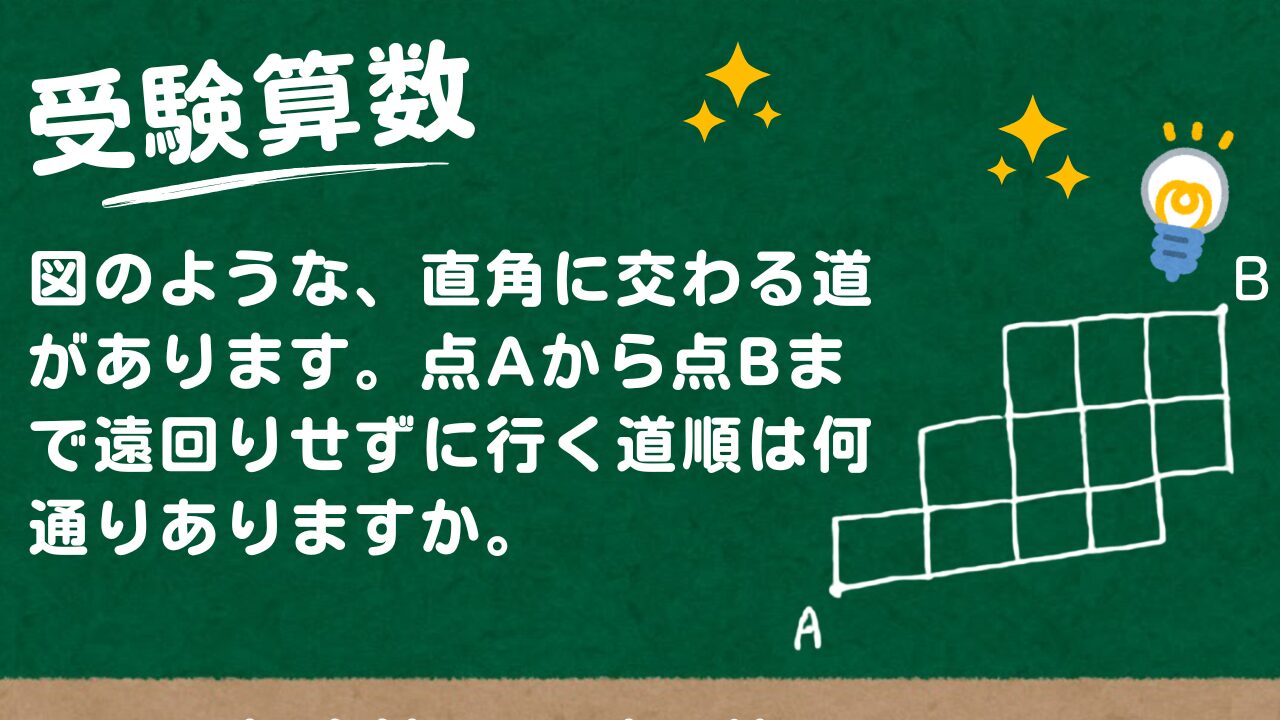
図のような、直角に交わる道があります。点Aから点Bまで遠回りせずに行く道順は何通りありますか。
この動画を見る
図のような、直角に交わる道があります。点Aから点Bまで遠回りせずに行く道順は何通りありますか。
【英語】今更誰にも聞けない『SVOC』を5分でおさらい!

単元:
#英語(中学生)#中2英語#文型(第1文型、第2文型、第3文型、第4文型、第5文型)
指導講師:
理数個別チャンネル
問題文全文(内容文):
SVOC(文型)って第一から第五まで分かれていますが、
そもそもバラにしてちゃんと考えたことありますか?
1つずつ丁寧に見ていきます!(分類の話ではありません)
この動画を見る
SVOC(文型)って第一から第五まで分かれていますが、
そもそもバラにしてちゃんと考えたことありますか?
1つずつ丁寧に見ていきます!(分類の話ではありません)
SVOC(文型)って第一から第五まで分かれていますが、 そもそもバラにしてちゃんと考えたことありますか? 1つずつ丁寧に見ていきます!(分類の話ではありません)

単元:
#英語(中学生)#英語(高校生)#英文法#品詞と文型、句と節#中1英語#中2英語#中3英語#分詞・分詞構文#接続詞#名詞・冠詞・代名詞#形容詞・副詞#前置詞#形容詞・副詞#接続詞(and,or,but,so・when,if,because,before,after・接続詞that)#文型(第1文型、第2文型、第3文型、第4文型、第5文型)#分詞(現在分詞の形容詞的用法、過去分詞の形容詞的用法)
指導講師:
理数個別チャンネル
問題文全文(内容文):
SVOC(文型)って第一から第五まで分かれていますが、
そもそもバラにしてちゃんと考えたことありますか?
1つずつ丁寧に見ていきます!(分類の話ではありません)
この動画を見る
SVOC(文型)って第一から第五まで分かれていますが、
そもそもバラにしてちゃんと考えたことありますか?
1つずつ丁寧に見ていきます!(分類の話ではありません)
【数学】高校入試:2022年度神奈川県立高校入試数学大問4(ア)(イ)

単元:
#数学(中学生)#高校入試過去問(数学)#神奈川県公立高校入試
指導講師:
理数個別チャンネル
問題文全文(内容文):
問4 右の図において、直線①は関数$y=x+3$のグラフであり、曲線②は関数$y=ax^2$のグラフである。 点Aは直線①と曲線②との交点で、そのx座標は6である。点Bは曲線②状の点で、線分ABはx軸に平行である。点Cは直線①上の点で、線分BCはy軸に平行である。
また、点Dは線分BCとx軸との交点である。
さらに、減点をOとするとき、点Eはx軸上の点で、$DO:OE=6:5$であり、そのx座標は正である。このとき、次の問いに答えなさい。
(ア)曲線②の式y=ax²のaの値として正しいものを次の1~6の中から1つ選び、その番号を答えなさい。
1.$a=\dfrac{1}{6}$ 2.$a=\dfrac{1}{4}$ 3.$a=\dfrac{1}{3}$ 4.$a=\dfrac{1}{2}$ 5.$a=\dfrac{3}{4}$ 6.$a=\dfrac{3}{2}$
(イ)直線CEの式をy=mx+nとするとき、(ⅰ)mの値と、(ⅱ)nの値として正しいものを、それぞれ次の1~6の中から1つずつ選び、その番号を答えなさい。
(ⅰ)mの値
1.$m=\dfrac{3}{13}$ 2.$m=\dfrac{1}{4}$ 3.$m=\dfrac{3}{11}$ 4.$m=\dfrac{3}{10}$ 5.$m=\dfrac{1}{3}$ 6.$m=\dfrac{3}{8}$
(ⅱ)nの値
1.$n=\dfrac{-17}{11}$ 2.$n=\dfrac{-20}{13}$ 3.$n=\dfrac{-3}{2}$
4.$n=\dfrac{-18}{13}$ 5.$n=\dfrac{-15}{11}$ 6.$n=\dfrac{-11}{10}$
この動画を見る
問4 右の図において、直線①は関数$y=x+3$のグラフであり、曲線②は関数$y=ax^2$のグラフである。 点Aは直線①と曲線②との交点で、そのx座標は6である。点Bは曲線②状の点で、線分ABはx軸に平行である。点Cは直線①上の点で、線分BCはy軸に平行である。
また、点Dは線分BCとx軸との交点である。
さらに、減点をOとするとき、点Eはx軸上の点で、$DO:OE=6:5$であり、そのx座標は正である。このとき、次の問いに答えなさい。
(ア)曲線②の式y=ax²のaの値として正しいものを次の1~6の中から1つ選び、その番号を答えなさい。
1.$a=\dfrac{1}{6}$ 2.$a=\dfrac{1}{4}$ 3.$a=\dfrac{1}{3}$ 4.$a=\dfrac{1}{2}$ 5.$a=\dfrac{3}{4}$ 6.$a=\dfrac{3}{2}$
(イ)直線CEの式をy=mx+nとするとき、(ⅰ)mの値と、(ⅱ)nの値として正しいものを、それぞれ次の1~6の中から1つずつ選び、その番号を答えなさい。
(ⅰ)mの値
1.$m=\dfrac{3}{13}$ 2.$m=\dfrac{1}{4}$ 3.$m=\dfrac{3}{11}$ 4.$m=\dfrac{3}{10}$ 5.$m=\dfrac{1}{3}$ 6.$m=\dfrac{3}{8}$
(ⅱ)nの値
1.$n=\dfrac{-17}{11}$ 2.$n=\dfrac{-20}{13}$ 3.$n=\dfrac{-3}{2}$
4.$n=\dfrac{-18}{13}$ 5.$n=\dfrac{-15}{11}$ 6.$n=\dfrac{-11}{10}$
【英検2級】スピーキング(2次試験)の質問1と質問2で15点中15点取る裏技大公開!!

単元:
#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英検2級
指導講師:
理数個別チャンネル
問題文全文(内容文):
スピーキング(2次試験)の質問1と質問2で15点中15点取る裏技大公開します.
この動画を見る
スピーキング(2次試験)の質問1と質問2で15点中15点取る裏技大公開します.
【削除覚悟】英検2級スピーキング(2次試験)の質問1と質問2で15点中15点取る裏技大公開!!

単元:
#英語(高校生)#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英検2級#勉強法・その他#勉強法#その他#英語リスニング・スピーキング#勉強法#スピーキング#英検
指導講師:
理数個別チャンネル
問題文全文(内容文):
★英検2級スピーキング(2次試験)完全対策★
・No.1とNo.2の裏技
https://youtu.be/-S5cDAHTTZ8
・No.3とNo.4の裏技
https://youtu.be/Z4CQomN75Qw
・音読・態度点の裏技
https://youtu.be/d4q-1PsLM60
この動画を見る
★英検2級スピーキング(2次試験)完全対策★
・No.1とNo.2の裏技
https://youtu.be/-S5cDAHTTZ8
・No.3とNo.4の裏技
https://youtu.be/Z4CQomN75Qw
・音読・態度点の裏技
https://youtu.be/d4q-1PsLM60
【受験算数】速さと比3:(練習❷)3人の旅人算【予習シリーズ演習問題集・小5下】

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#予習シ#予習シ演問・小5下#中学受験教材#速さと比(3)
指導講師:
理数個別チャンネル
問題文全文(内容文):
あるジョギングコースを、A君とB君は右回りに走っています。1周するのにかかる時間は、A君は20分、B君は12分です。また、C君は左回りに走り、A君12分ごとにすれ違います。これについて、次の問いに答えなさい。
(1)C君は1周するのに何分かかりますか。
(2)B君とC君は何分ごとにすれ違いますか。
この動画を見る
あるジョギングコースを、A君とB君は右回りに走っています。1周するのにかかる時間は、A君は20分、B君は12分です。また、C君は左回りに走り、A君12分ごとにすれ違います。これについて、次の問いに答えなさい。
(1)C君は1周するのに何分かかりますか。
(2)B君とC君は何分ごとにすれ違いますか。
【公民・現代社会】選挙:比例代表ドント式3分でマスター!

単元:
#社会(中学受験)#社会(中学生)#社会(高校生)#現代社会#公民#公民
指導講師:
理数個別チャンネル
問題文全文(内容文):
衆議院選挙の比例代表では党に投票しますが、それがどういうふうに当選者を決めるのか3分で解説しました!!
この動画を見る
衆議院選挙の比例代表では党に投票しますが、それがどういうふうに当選者を決めるのか3分で解説しました!!
【公民・現代社会】選挙:小選挙区比例代表並立制の全貌を5分で!!

単元:
#社会(中学受験)#社会(中学生)#社会(高校生)#現代社会#公民#公民
指導講師:
理数個別チャンネル
問題文全文(内容文):
衆議院選挙の小選挙区と比例代表それぞれをわかりやすく解説しました!5分でバッチリわかります。特徴はテストに頻出ですよ~
この動画を見る
衆議院選挙の小選挙区と比例代表それぞれをわかりやすく解説しました!5分でバッチリわかります。特徴はテストに頻出ですよ~
【数B】ベクトル:ベクトルの基本⑦内積を求めたいときの絶対値の2乗

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
$a=\sqrt3,b=5,a-b=\sqrt5$のとき、内積a・bを求めよ.
この動画を見る
$a=\sqrt3,b=5,a-b=\sqrt5$のとき、内積a・bを求めよ.
【数C】ベクトルの基本⑦内積を求めたいときの絶対値の2乗

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
教材:
#チャート式#青チャートⅡ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
a=√3,b=5,a-b=√5のとき、内積a・bを求めよ
この動画を見る
a=√3,b=5,a-b=√5のとき、内積a・bを求めよ
【受験算数】速さと比3:(練習❶)時間と速さは逆比、速さと距離は正比例【予習シリーズ演習問題集・小5下】

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#予習シ#予習シ演問・小5下#中学受験教材#速さと比(3)
指導講師:
理数個別チャンネル
問題文全文(内容文):
A君が4分で歩く道のりをB君は5分で歩きます。ある池のまわりを、A君とB君が同じ場所から同時に反対方向に向かって歩きました。A君が出発した場所を通り過ぎて、さらに60m進んだ地点でB君と2回目に出会いました。これについて、次の問に答えなさい。
(1)A君とB君の速さの比を求めなさい。
(2)この池のまわりの長さは何mですか。
この動画を見る
A君が4分で歩く道のりをB君は5分で歩きます。ある池のまわりを、A君とB君が同じ場所から同時に反対方向に向かって歩きました。A君が出発した場所を通り過ぎて、さらに60m進んだ地点でB君と2回目に出会いました。これについて、次の問に答えなさい。
(1)A君とB君の速さの比を求めなさい。
(2)この池のまわりの長さは何mですか。
2022年度神奈川県立高校入試数学大問3(ウ)

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
大問3 (ウ)
次の□の中の「あ」「い」に当てはまる数字をそれぞれ0~9の中から1つずつ選び、その数字を答えなさい。
右の図2において、5点A,B,C,D,Eは円Oの周上の点で、BE//CDであり、線分ADは∠BDEの二等分線である。
また、点Fは線分ADとCEとの交点である。
このとき、∠AFE=【あい】°である。
この動画を見る
大問3 (ウ)
次の□の中の「あ」「い」に当てはまる数字をそれぞれ0~9の中から1つずつ選び、その数字を答えなさい。
右の図2において、5点A,B,C,D,Eは円Oの周上の点で、BE//CDであり、線分ADは∠BDEの二等分線である。
また、点Fは線分ADとCEとの交点である。
このとき、∠AFE=【あい】°である。
英検準1級リスニング30%台でも合格/英検2級ライティング満点合格/小学5年生が英検準2級合格 etc

単元:
#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英検2級#英検準1級#英語リスニング・スピーキング#スピーキング#英検
指導講師:
理数個別チャンネル
問題文全文(内容文):
英検準1級リスニング30%台でも合格/英検2級ライティング満点合格/小学5年生が英検準2級合格など
この動画を見る
英検準1級リスニング30%台でも合格/英検2級ライティング満点合格/小学5年生が英検準2級合格など
【英語】英文の下線部を複数形に変えて、全文を書き換える問題を解説!

単元:
#英語(中学生)#中1英語#名詞・代名詞の複数形、How many~?、someとany
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の英文の下線部を複数形に変えて、全文書きなさい。
この動画を見る
次の英文の下線部を複数形に変えて、全文書きなさい。
2022年第1回英検1次試験結果発表日のコメ欄に・・・涙

【数C】ベクトルの基本⑥内積の基本計算2 成分を用いて計算する

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
教材:
#チャート式#青チャートⅡ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
内積の基本計算(直角三角形ABCにおける内積計算)
この動画を見る
内積の基本計算(直角三角形ABCにおける内積計算)
【数B】ベクトル:ベクトルの基本⑥内積の基本計算2 成分を用いて計算する

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
内積の基本計算(直角三角形ABCにおける内積計算)に関して解説していきます.
この動画を見る
内積の基本計算(直角三角形ABCにおける内積計算)に関して解説していきます.
【化学】原子量の定義から計算方法までを2分で解決!

単元:
#化学#化学基礎1ー物質の構成#原子の構成と元素の周期表#理科(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
化学基礎を初めてやる人向け。化学基礎の用語で困っている受験生へ。
この動画を見る
化学基礎を初めてやる人向け。化学基礎の用語で困っている受験生へ。
【化学】化学が嫌いになる要因No1!相対質量を理解して化学嫌いを脱しよう!

単元:
#化学#化学基礎2ー物質の変化#物質量と濃度#理科(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
化学基礎を初めてやる人向け。化学基礎の用語で困っている受験生へ。
この動画を見る
化学基礎を初めてやる人向け。化学基礎の用語で困っている受験生へ。




